Orta Taban
Bir üçgenin herhangi iki kenarının orta noktalarını birleştiren doğru parçasına orta taban denir.
Aşağıdaki şekilde \( D \) ve \( E \) noktaları sırasıyla \( [AB] \) ve \( [AC] \) kenarlarının orta noktalarıdır, dolayısıyla \( [DE] \) doğru parçası üçgenin bir orta tabanıdır.

Orta taban bir üçgeni biri üçgen diğeri yamuk olmak üzere iki parçaya ayırır.
Orta Taban Teoremi
Orta taban teoremine göre, bir üçgenin iki kenarının orta noktalarını birleştiren orta taban üçgenin üçüncü kenarına paraleldir ve uzunluğu bu üçüncü kenarın uzunluğunun yarısına eşittir.
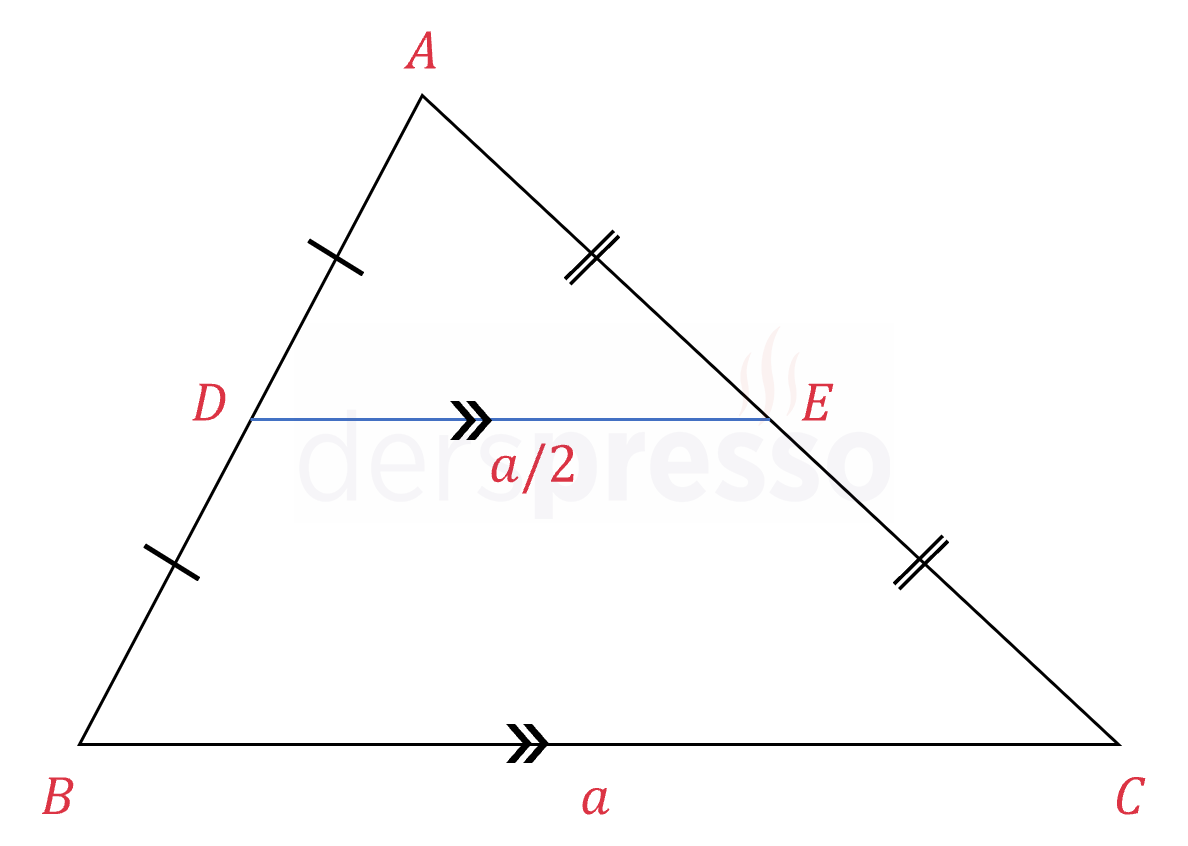
\( [DE] \) orta taban ise,
(1) \( [DE] \parallel [BC] \) ve
(2) \( \abs{DE} = \dfrac{\abs{BC}}{2} \)
İSPATI GÖSTER

\( C \) noktasından geçen ve \( [AB] \) kenarına paralel bir doğru çizelim ve \( [DE] \) kenarını bu doğru ile \( F \) noktasında kesişecek şekilde uzatalım (mavi kesikli çizgiler).
\( [CF] \parallel [BA] \)
Ters açılar oldukları için: \( m(\widehat{AED}) = m(\widehat{CEF}) \)
İç ters açılar oldukları için: \( m(\widehat{EAD}) = m(\widehat{ECF}) \)
\( E \) noktası orta nokta olduğu için: \( \abs{AE} = \abs{CE} \)
\( \overset{\triangle}{AED} \) ve \( \overset{\triangle}{CEF} \) üçgenlerinin ikişer açısı eşit olduğu için üçüncü açıları da eşittir ve benzer üçgenlerdir. Ayrıca üçgenlerin benzer kenarlarından birinin uzunlukları eşit olduğu için bu iki üçgenin benzerlik oranı 1'dir, yani eş üçgenlerdir.
\( \overset{\triangle}{AED} \cong \overset{\triangle}{CEF} \)
Bunun bir sonucu olarak iki üçgenin diğer kenar uzunlukları arasında da aşağıdaki eşitlikler geçerlidir.
\( \abs{AD} = \abs{CF} \)
\( \abs{ED} = \abs{EF} \)
\( D \) noktası \( [AB] \) kenarının orta noktasıdır.
\( \abs{AD} = \abs{DB} \)
Buna göre aşağıdaki iki kenar uzunluğu da eşit olmuş olur.
\( \abs{DB} = \abs{CF} \)
Bir dörtgenin karşılıklı iki kenarının paralel ve uzunluklarının eşit olması paralelkenar olması için yeterli koşullardan biri olduğu için \( BCFD \) dörtgeni bir paralelkenardır.
\( BCFD \) bir paralelkenar ise karşılıklı diğer iki kenarı için aşağıdakiler de doğrudur.
\( [DF] \parallel [BC] \)
\( \abs{DF} = \abs{BC} \)
Dolayısıyla orta taban teoreminin birinci önermesinin (paralellik) doğruluğunu göstermiş olduk.
Yukarıda benzer üçgenlerden aşağıdaki iki kenarın uzunluklarının eşit olduğunu göstermiştik.
\( \abs{ED} = \abs{EF} \)
Bu iki kenar uzunluğunun toplamı \( [BC] \) kenar uzunluğuna eşit olduğu için, her biri \( [BC] \) kenar uzunluğunun yarısına eşit olur.
\( \abs{DE} = \dfrac{\abs{BC}}{2} \)
Dolayısıyla orta taban teoreminin ikinci önermesinin (uzunluk) de doğruluğunu göstermiş olduk.
Orta taban teoreminin diğer iki yorumu aşağıdaki gibidir.
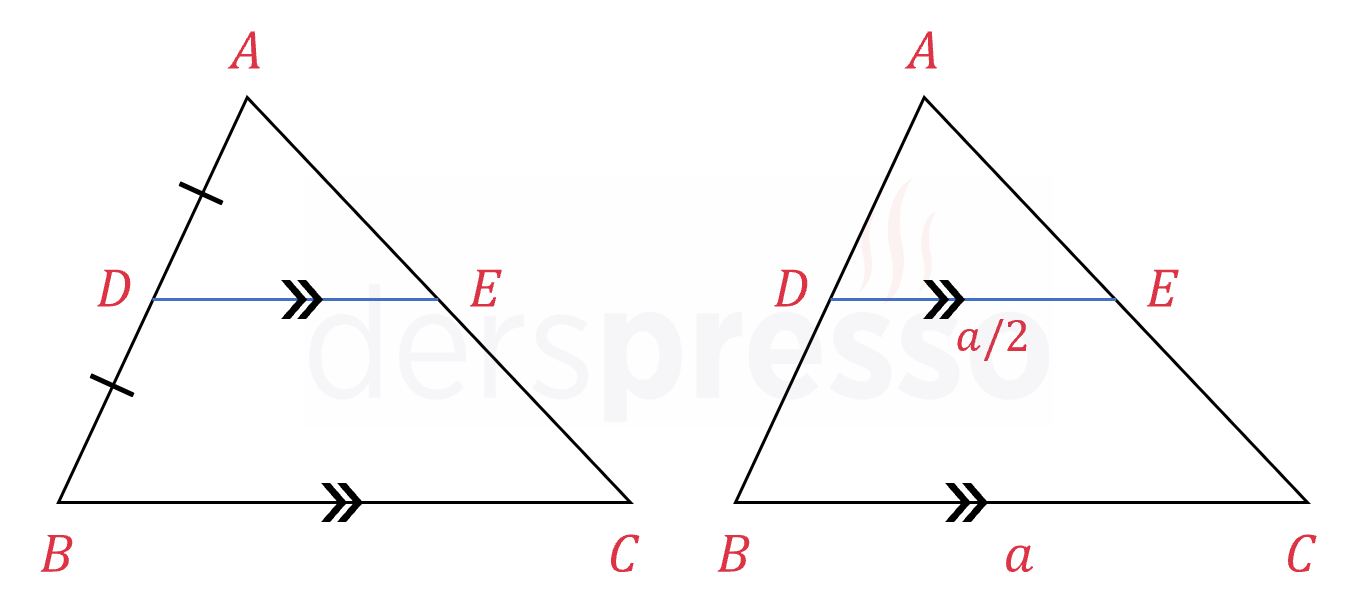
- Soldaki şekilde gösterildiği gibi, bir üçgenin bir yan kenarının orta noktasından tabana paralel çizeceğimiz bir doğru parçası orta taban olur, dolayısıyla diğer yan kenarı ortalar ve uzunluğu taban uzunluğunun yarısına eşittir.
- Sağdaki şekilde gösterildiği gibi, bir üçgenin yan kenarları arasında tabana paralel ve taban uzunluğunun yarı uzunluğunda çizeceğimiz bir doğru parçası orta taban olur, dolayısıyla her iki yan kenarı da ortalar.
Orta taban üçgenin yan kenarlarını olduğu gibi; tabana ait yüksekliği, açıortayı, kenarortayı ve tabana çizilen herhangi bir doğru parçasını ortalar.
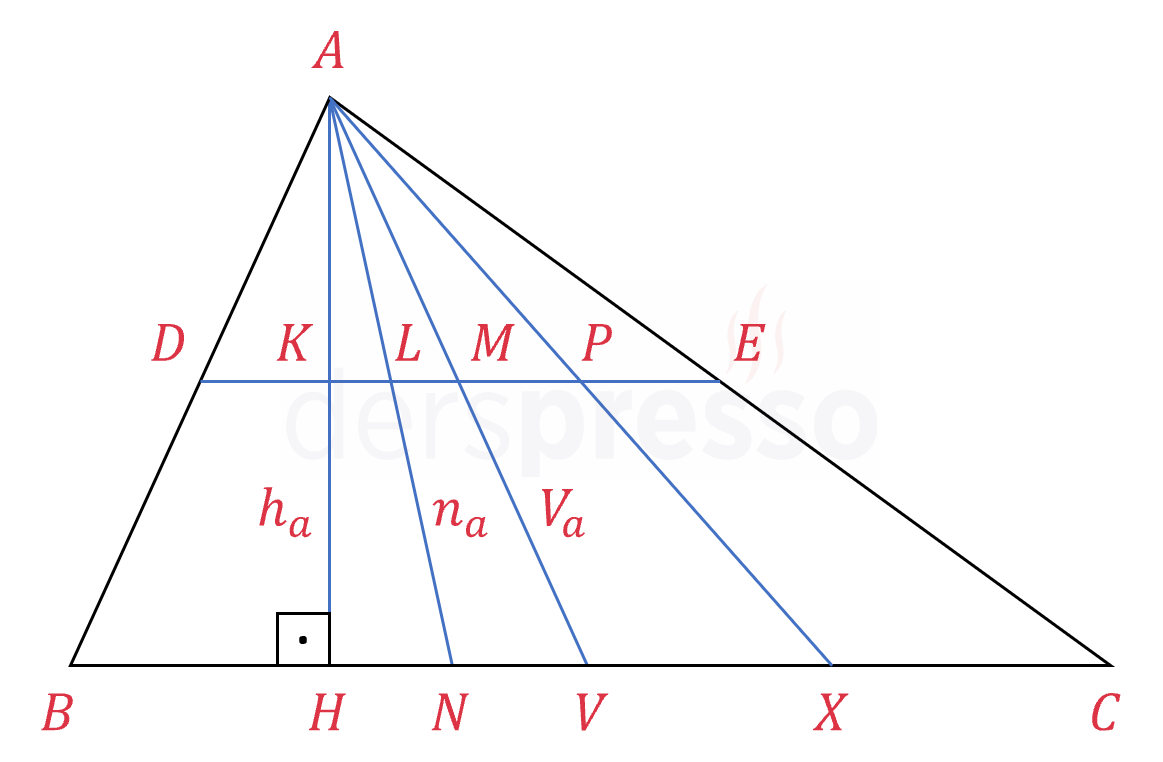
\( [DE] \) orta taban, \( [AH] \) yükseklik, \( [AN] \) açıortay, \( [AV] \) kenarortay, \( [AX] \) tabana çizilen herhangi bir doğru parçası olmak üzere,
\( \abs{AK} = \abs{KH} \)
\( \abs{AL} = \abs{LN} \)
\( \abs{AM} = \abs{MV} \)
\( \abs{AP} = \abs{PX} \)
İSPATI GÖSTER

\( [DE] \) doğru parçası \( ABC \) üçgeninin orta tabanı ise üçgenin her iki yan kenarını ortalar ve \( [BC] \) kenarına paraleldir.
\( [DE] \) doğru parçası aşağıdaki üçgenlerin ortak \( [AB] \) kenarını ortaladığı ve tümünün tabanına paralel olduğu için aşağıdaki dört üçgenin de orta tabanı olur.
(1) \( [AH] \) yüksekliğinin oluşturduğu \( ABH \) üçgeni,
(2) \( [AN] \) açıortayının oluşturduğu \( ABN \) üçgeni
(3) \( [AV] \) kenarortayının oluşturduğu \( ABV \) üçgeni
(4) \( [AX] \) doğru parçasının oluşturduğu \( ABX \) üçgeni
\( [DE] \) doğru parçası tüm bu üçgenlerin orta tabanı olduğu için sırasıyla \( [AH] \), \( [AN] \), \( [AV] \) ve \( [AX] \) kenarlarını ortalar.
Bir üçgenin yukarıdaki özellikleri gösteren üç orta tabanı vardır. Bu üç orta taban aşağıdaki şekildeki gibi ortalar üçgeni adı verilen bir üçgen oluştururlar.
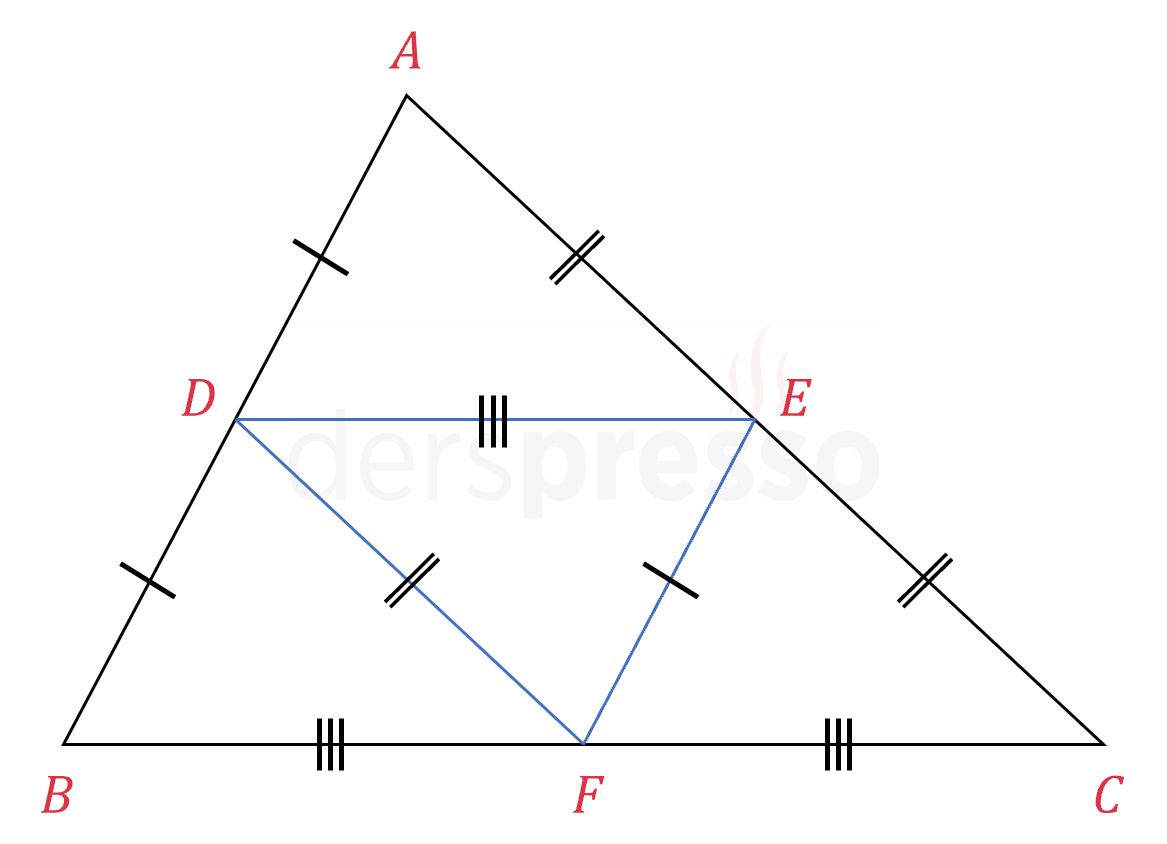
Bir kenara ait kenarortay o kenara ait orta tabanı da ortalar.
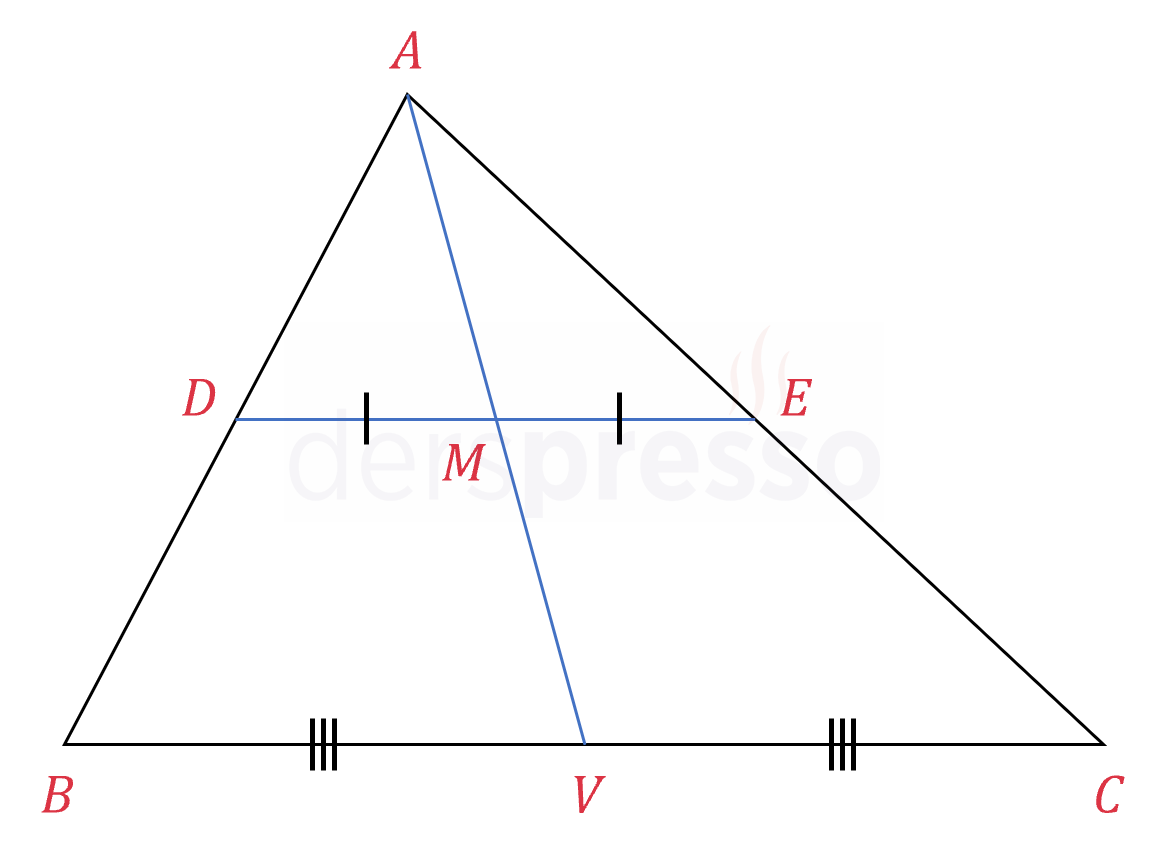
\( [DE] \) orta taban, \( [AV] \) kenarortay olmak üzere,
\( \abs{DM} = \abs{ME} \)
İSPATI GÖSTER
\( ABC \) üçgeninin ortalar üçgenini çizelim.
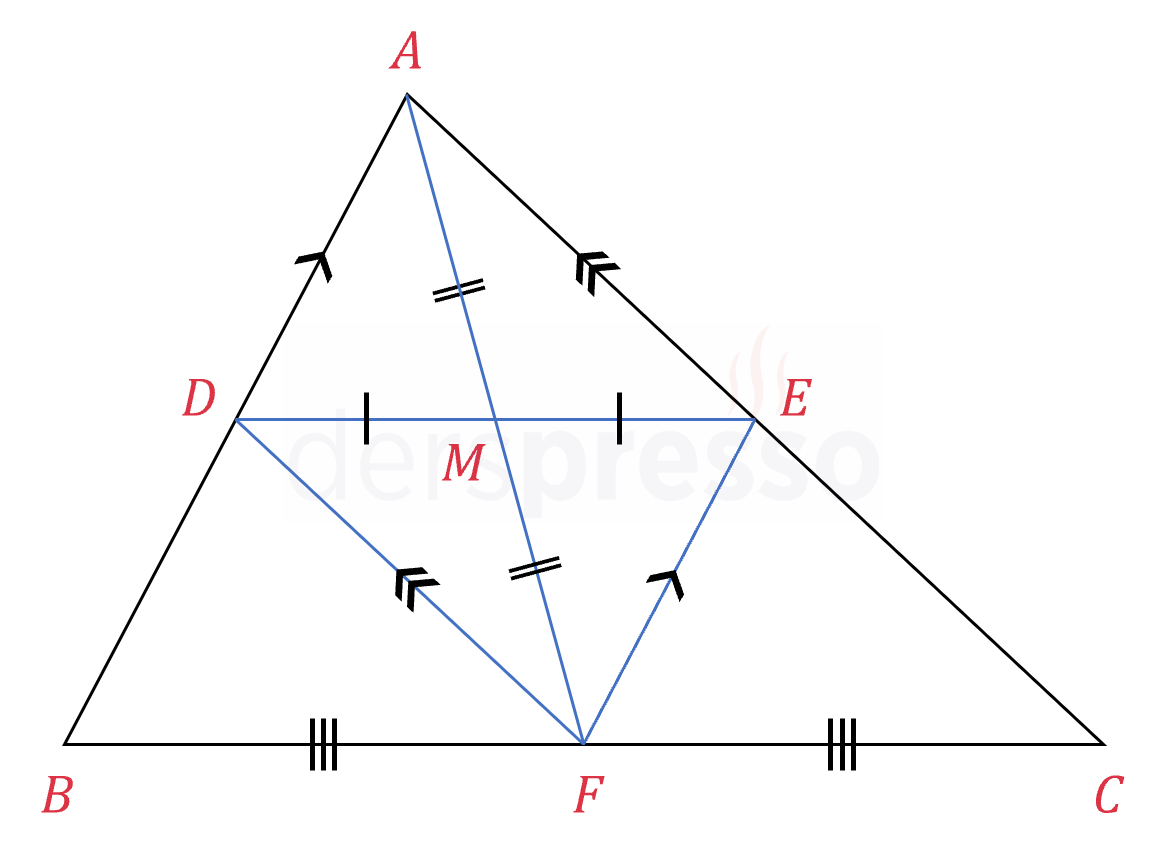
\( [DF] \) doğru parçası \( [AC] \) kenarının orta tabanı olduğu için bu kenara paraleldir.
\( [DF] \parallel [AC] \)
\( [EF] \) doğru parçası \( [AB] \) kenarının orta tabanı olduğu için bu kenara paraleldir.
\( [EF] \parallel [AB] \)
Buna göre \( ADFE \) dörtgeni bir paralelkenardır.
Paralelkenarın köşegenleri birbirini ortalar.
\( \abs{DM} = \abs{ME} \)
\( \abs{AM} = \abs{MF} \)
Bir üçgenin kenarortayları o üçgenin orta tabanlarını, dolayısıyla o üçgene ait ortalar üçgeninin kenarlarını da ortaladığı için, bir üçgenin ve ortalar üçgeninin kenarortayları çakışıktır ve ağırlık merkezleri aynı noktadır.
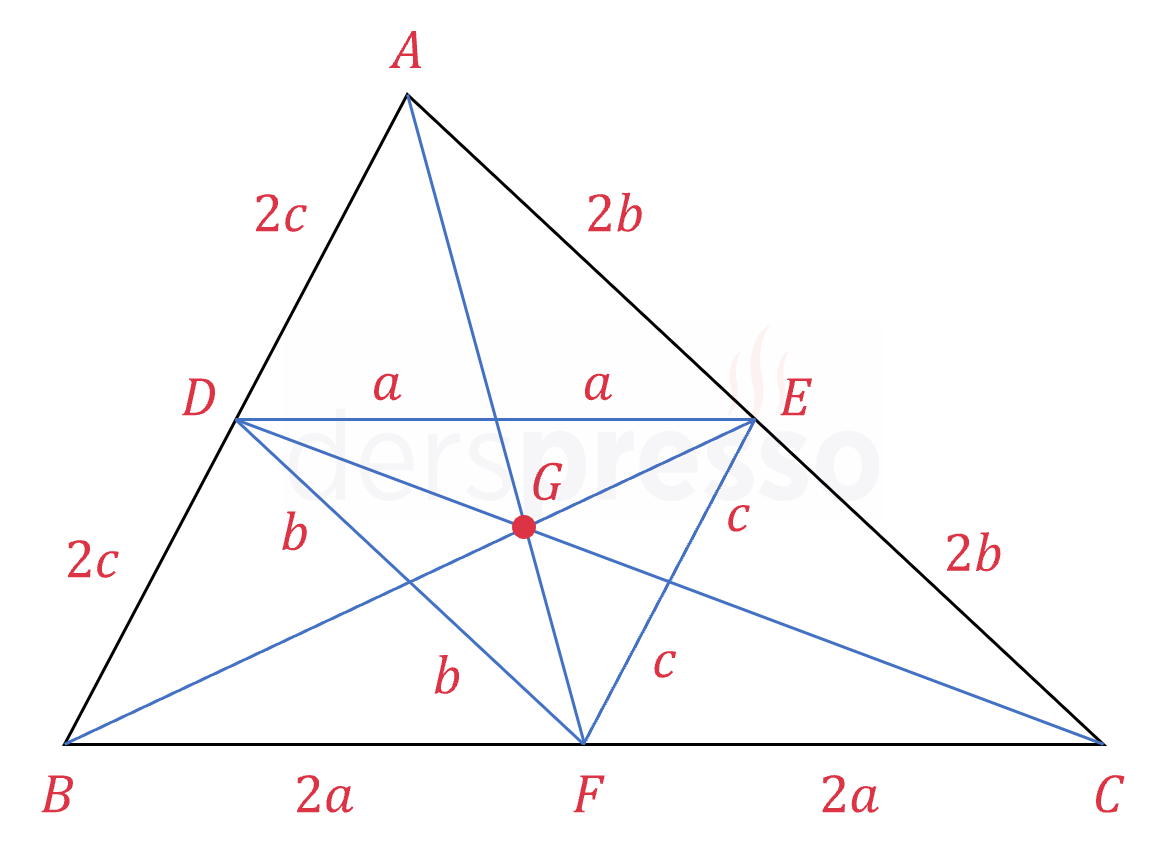
Bir üçgenin ortalar üçgeninin diklik merkezi (yüksekliklerin kesişim noktası) aynı zamanda o üçgenin (\( ABC \) üçgeni) orta dikmelerinin kesişim noktası, yani çevrel çemberinin merkezidir.
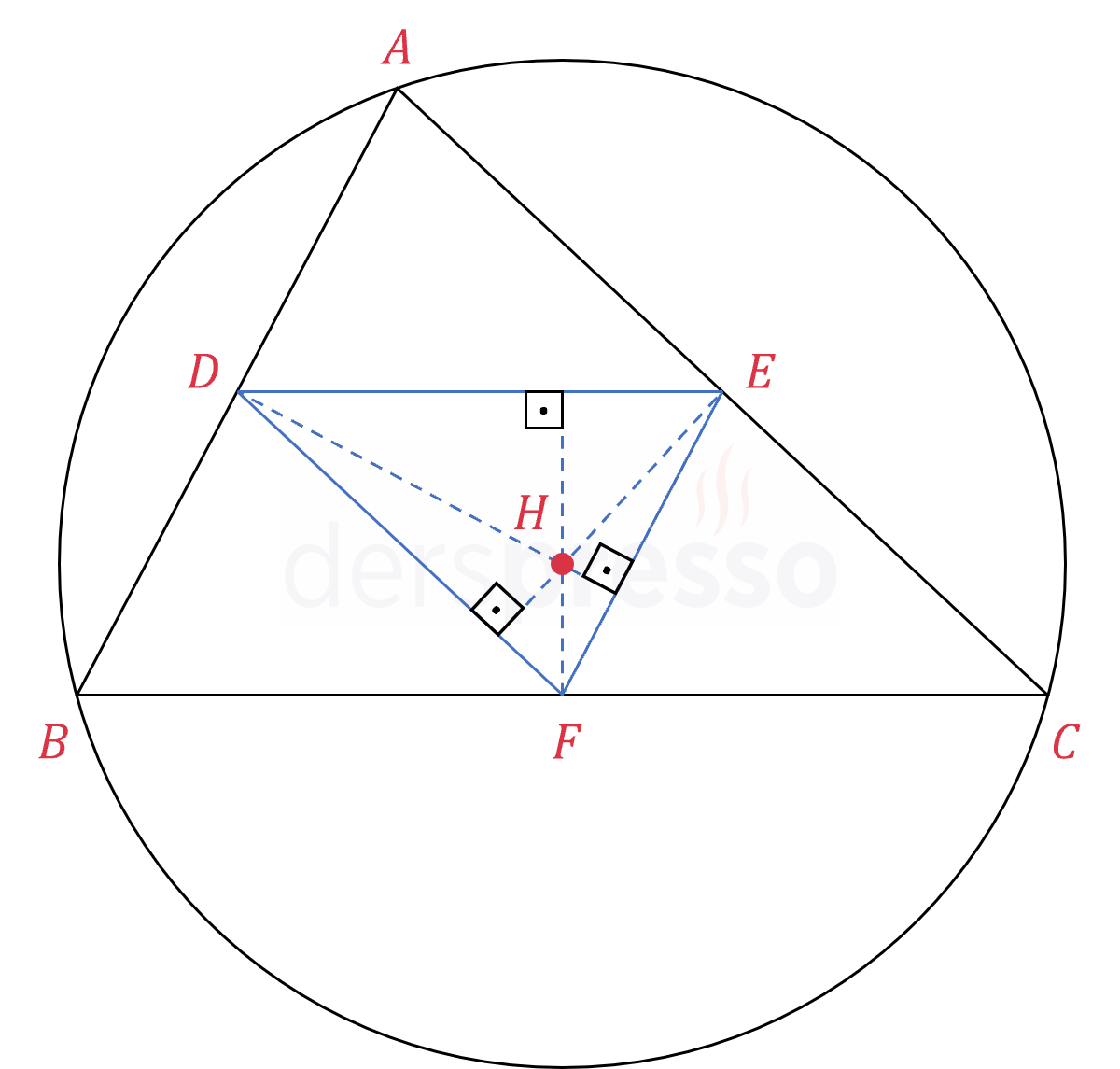
\( DE \) kenarı \( ABC \) üçgeninin \( BC \) kenarına ait orta tabanı olduğu için bu kenara paraleldir.
\( [DE] \parallel [BC] \)
Dolayısıyla \( DEF \) üçgeninin \( F \) köşesine ait yüksekliği \( [BC] \) kenarına da diktir.
\( [HF] \perp [BC] \)
Aynı durum diğer orta tabanlar için de geçerlidir.
\( [HD] \perp [AB] \)
\( [HE] \perp [AC] \)
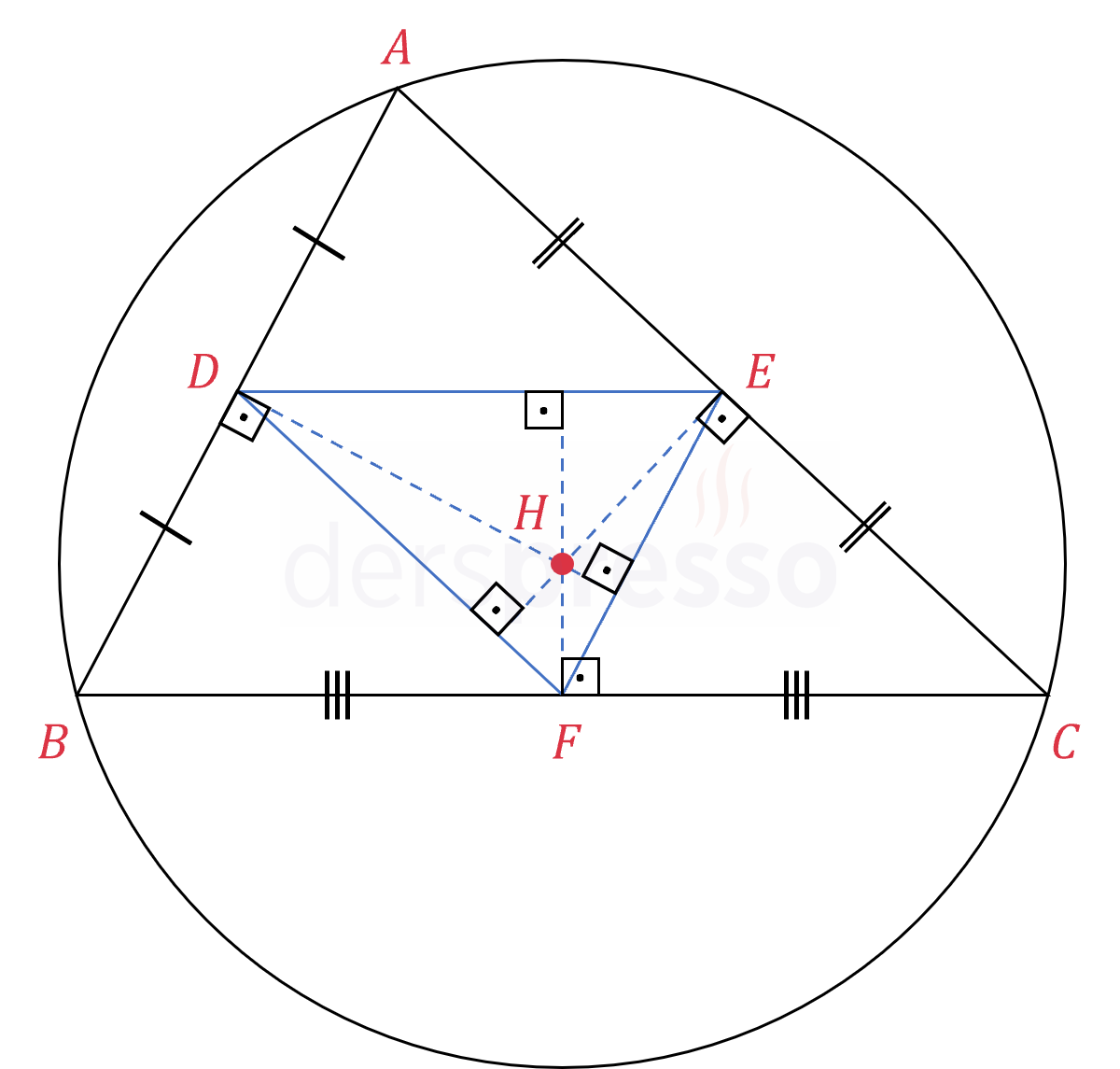
Buna göre \( D \), \( E \) ve \( F \) noktaları bulundukları kenarların orta noktaları olduğu için \( [DH] \), \( [EH] \) ve \( [FH] \) doğru parçaları aynı zamanda ilgili kenarların orta dikmeleri olur.
\( H \) noktası bu üç doğru parçasının kesişim noktası olduğu için, \( DEF \) üçgeninin diklik merkezi olmasına ek olarak \( ABC \) üçgeninin orta dikmelerinin kesişim noktası, yani \( ABC \) üçgeninin çevrel çemberinin merkezidir.
Bir üçgenin orta tabanlarının oluşturduğu dört üçgenin alanları birbirine eşittir.
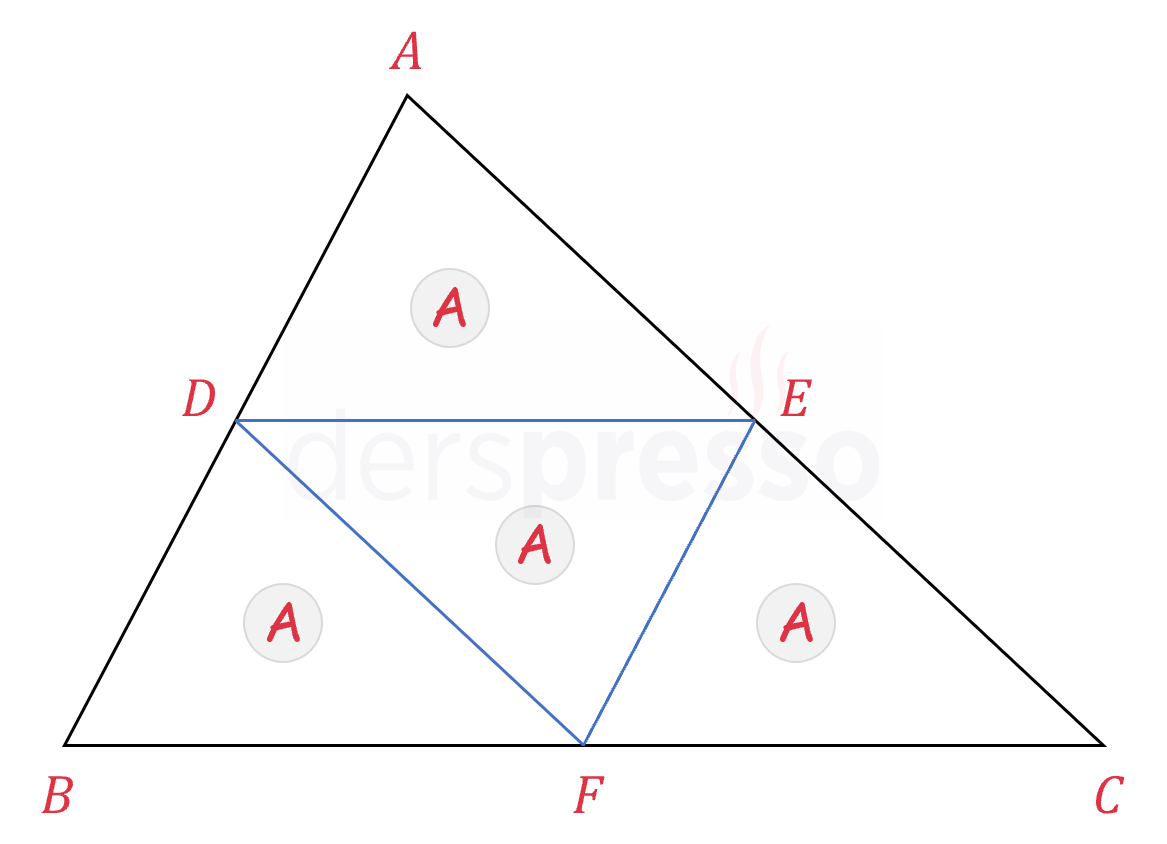
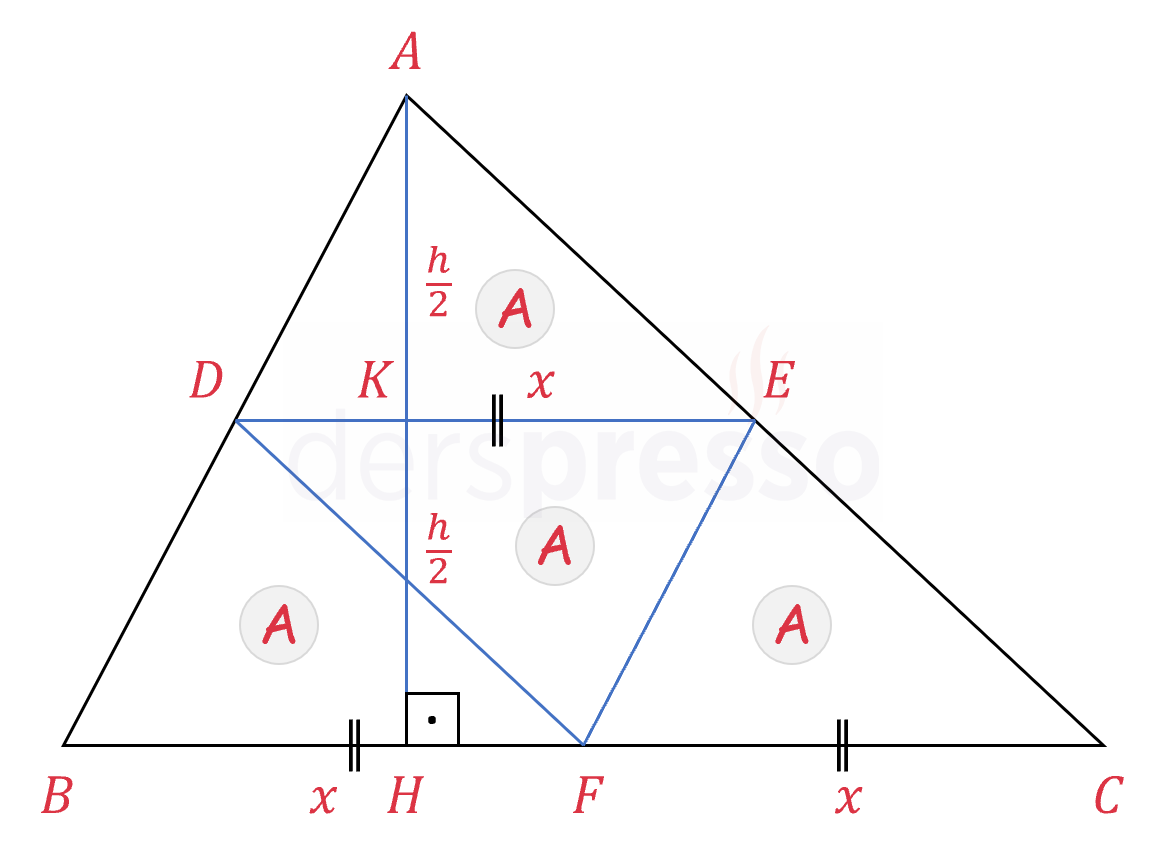
\( [EF] \) doğru parçası \( ABC \) üçgeninin orta tabanı ise \( [BC] \) kenarını ortalar.
\( \abs{BF} = \abs{FC} = x \)
\( [DE] \) doğru parçası \( ABC \) üçgeninin orta tabanı ise uzunluğu \( [BC] \) kenarının yarısına eşittir.
\( \abs{DE} = \abs{BF} = \abs{FC} = x \)
Yukarıda ispatını gösterdiğimiz üzere, \( [DE] \) doğru parçası tabana ait yüksekliği ortalar.
\( \abs{AK} = \abs{KH} = \dfrac{h}{2} \)
Buna göre \( ADE \), \( DBF \), \( DEF \) ve \( EFC \) üçgenlerinin tümünün tabanını \( x \) ve yüksekliğini \( \frac{h}{2} \) şeklinde ifade edebiliriz.
\( A = \dfrac{x \cdot \frac{h}{2}}{2} \)
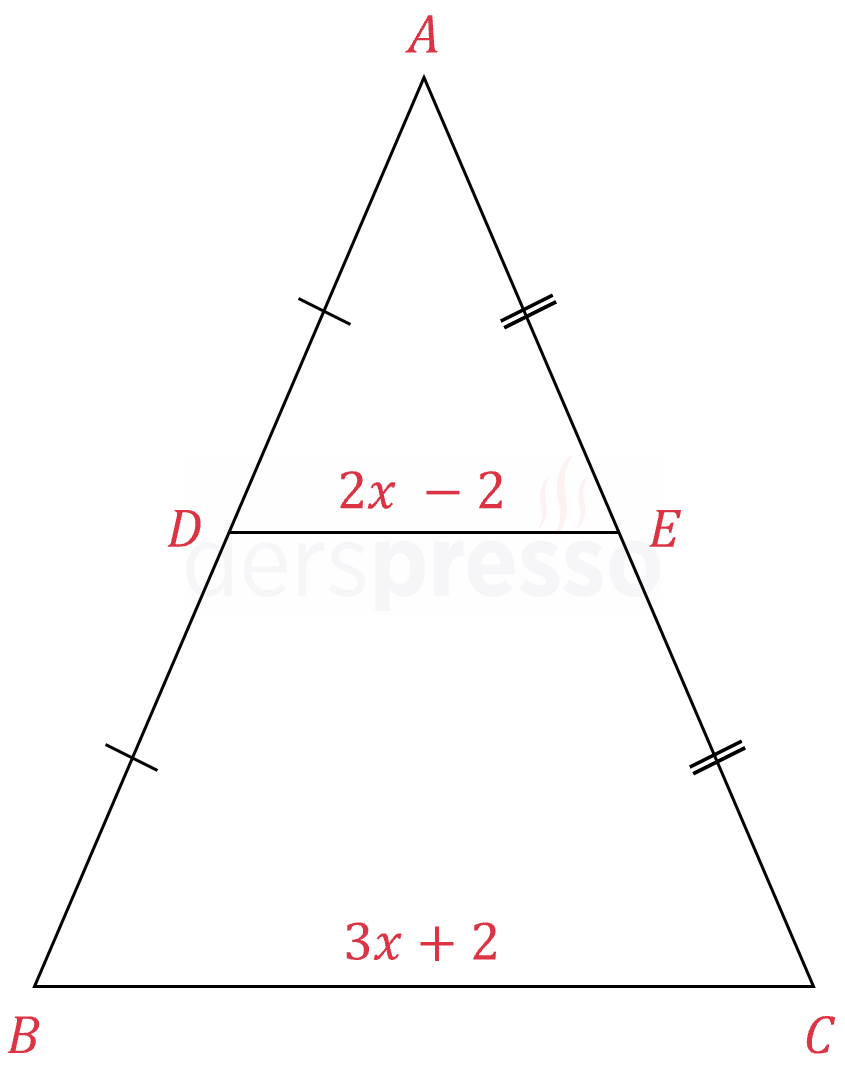
\( \abs{DE} = 2x- 2, \abs{BC} = 3x + 2 \)
\( \abs{AD} = \abs{DB}, \abs{AE} = \abs{EC} \)
olduğuna göre, \( x \) kaçtır?
Çözümü Göster\( [DE] \) üçgenin iki kenarının orta noktalarını birleştirdiği için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( 2\abs{DE} = \abs{BC} \)
\( 2(2x - 2) = 3x + 2 \)
\( 4x - 4 = 3x + 2 \)
\( x = 6 \) olarak bulunur.
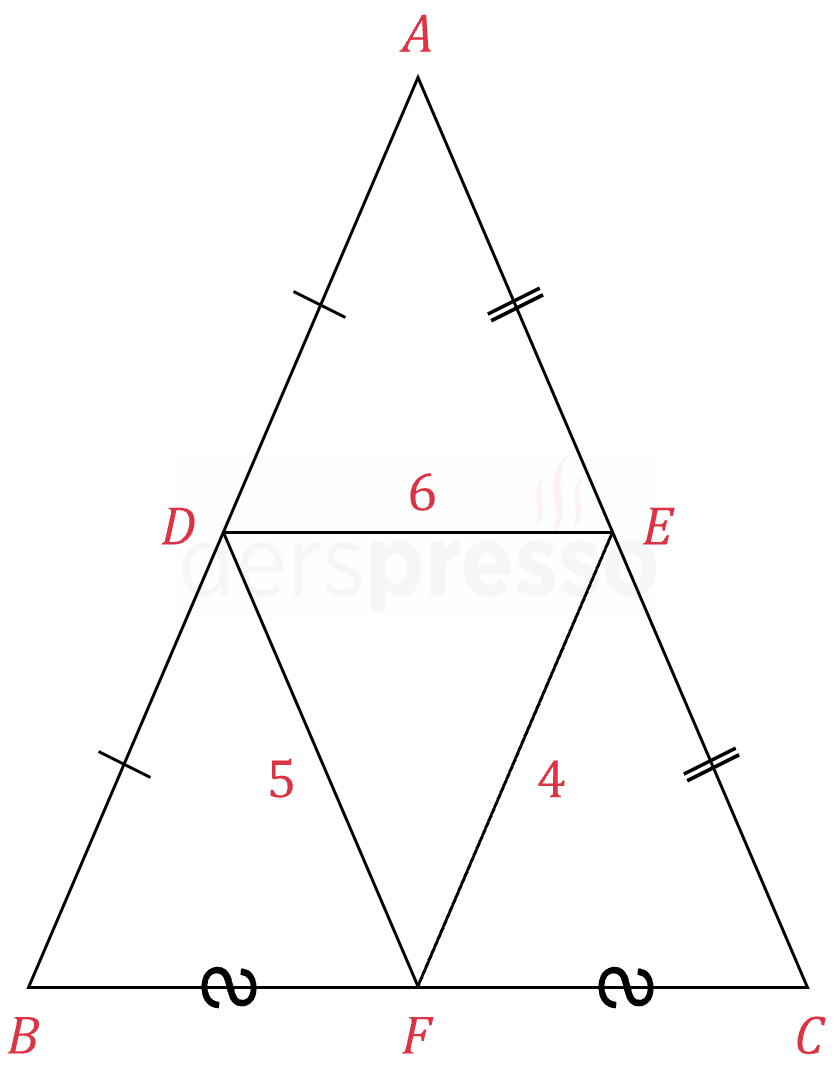
\( \abs{AD} = \abs{DB}, \abs{AE} = \abs{EC}, \abs{BF} = \abs{FC} \)
\( \abs{DE} = 6, \abs{DF} = 5, \abs{EF} = 4 \)
olduğuna göre, \( ABC \) üçgeninin çevre uzunluğu nedir?
Çözümü Göster\( D \), \( E \) ve \( F \) noktaları bulundukları kenarların orta noktaları oldukları için bu noktaları birleştiren doğru parçaları üçgenin birer orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{BC} = 2\abs{DE} = 12 \)
\( \abs{AC} = 2\abs{DF} = 10 \)
\( \abs{AB} = 2\abs{EF} = 8 \)
\( \abs{BC} + \abs{AC} + \abs{AB} = 12 + 10 + 8 = 30 \)
\( ABC \) üçgeninin çevre uzunluğu \( 30 \) olarak bulunur.

\( \abs{AD} = \abs{DC} \)
\( \abs{AB} = 4, \abs{BE} = 4, \abs{EC} = 8 \)
\( m(\widehat{DEC}) = 41° \)
olduğuna göre, \( m(\widehat{ABC}) = x \) değeri kaçtır?
Çözümü Göster\( D \) noktasından \( [AB] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [BC] \) kenarını kestiği noktaya \( F \) diyelim.

\( [DF] \parallel [AB] \)
\( [DF] \) \( [BC] \) kenarını ortaladığı ve \( [AB] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
\( \abs{FC} = 6, \abs{EF} = 2 \)
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{DF} = 2 \)
\( EDF \) üçgeni bir ikizkenar üçgendir.
İki iç açının toplamı bu açılara komşu olmayan bir dış açıya eşittir.
\( m(\widehat{FDE}) + m(\widehat{FED}) = m(\widehat{DFC}) = 82° \)
\( [AB] \parallel [DF] \) olduğu için,
\( m(\widehat{ABC}) = x = 82° \) bulunur.

\( [EF] \parallel [BC] \)
\( m(\widehat{ADE}) = m(\widehat{EDB}) \)
\( \abs{DA} = \abs{DB} \)
\( \abs{BC} = 8, \abs{AB} = 12, \abs{AC} = 10 \)
olduğuna göre, \( AEF \) üçgeninin çevre uzunluğu kaçtır?
Çözümü Göster\( ADB \) ikizkenar üçgeninde \( [DE] \) doğrusu açıortay olup aynı zamanda kenarortaydır.

\( [EF] \) \( [AB] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
\( \abs{AE} = \abs{EB} = 6 \)
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( 2\abs{EF} = \abs{BC} = 8 \)
\( \abs{EF} = 4 \)
\( [EF] \) orta taban olduğu için \( F \) noktası \( [AC] \) kenarının orta noktasıdır.
\( \abs{AF} = \abs{FC} = 5 \)
\( AEF \) üçgeninin çevre uzunluğunu bulalım.
\( \abs{AE} + \abs{EF} + \abs{FA} = 6 + 5 + 4 = 15 \) bulunur.

\( [AC] \perp [BC], \abs{AD} = \abs{DB} \)
\( \abs{BC} = 4k, \abs{AE} = 6k, \abs{EC} = 2k \)
olduğuna göre, \( m(\widehat{DEA}) = \alpha \) kaçtır?
Çözümü Göster\( D \) noktasından \( [BC] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [AC] \) kenarını kestiği noktaya \( F \) diyelim.

\( [DF] \parallel [BC] \)
\( [DF] \perp [AC]\)
\( [DF] \) \( [AB] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{DF} = 2k \)
\( [DF] \) orta taban olduğu için \( F \) noktası \( [AC] \) kenarının orta noktasıdır.
\( \abs{AF} = 4k, \abs{FE} = 2k \)
\( DFE \) üçgeni bir ikizkenar üçgendir.
\( m(\widehat{FDE}) = m(\widehat{FED}) = \alpha \)
\( m(\widehat{FDE}) + m(\widehat{FED}) = 90° \)
\( \alpha = 45° \) olarak bulunur.
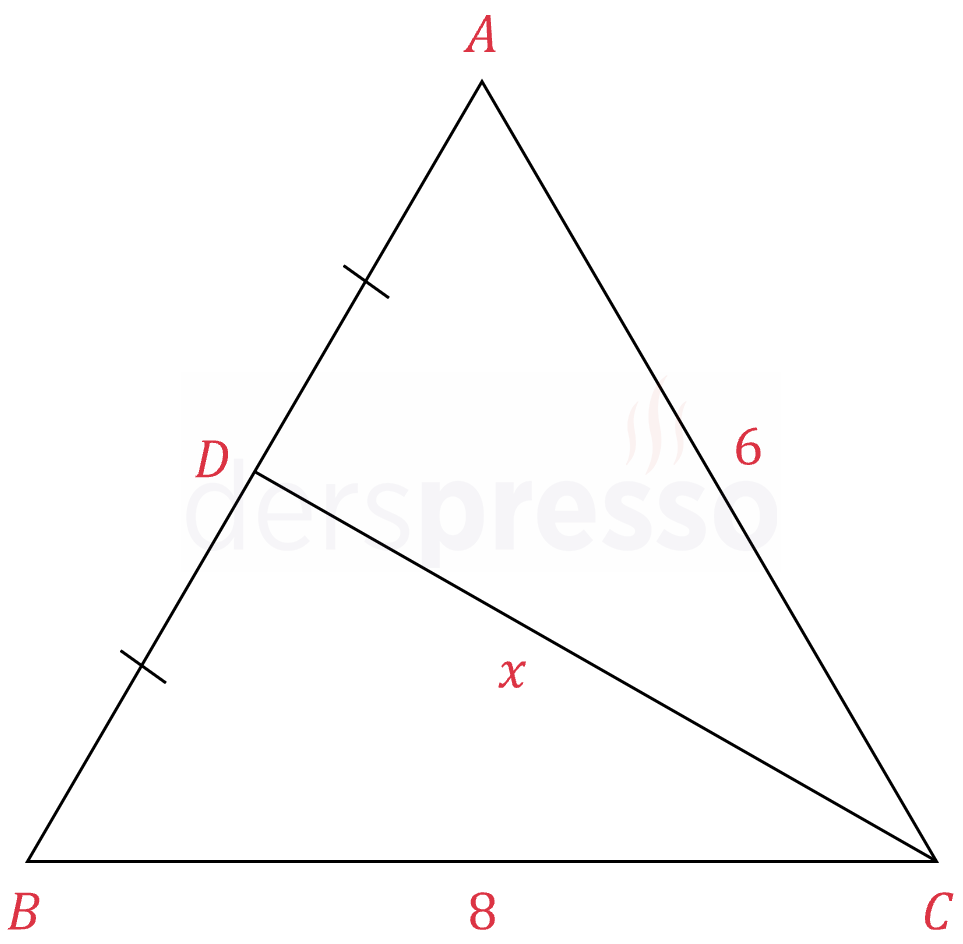
\( \abs{AD} = \abs{DB} \)
\( \abs{BC} = 8, \abs{AC} = 6\)
olduğuna göre, \( x \)'in alabileceği kaç tam sayı değeri vardır?
Çözümü Göster\( D \) noktasından \( [BC] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [AC] \) kenarını kestiği noktaya \( E \) diyelim.
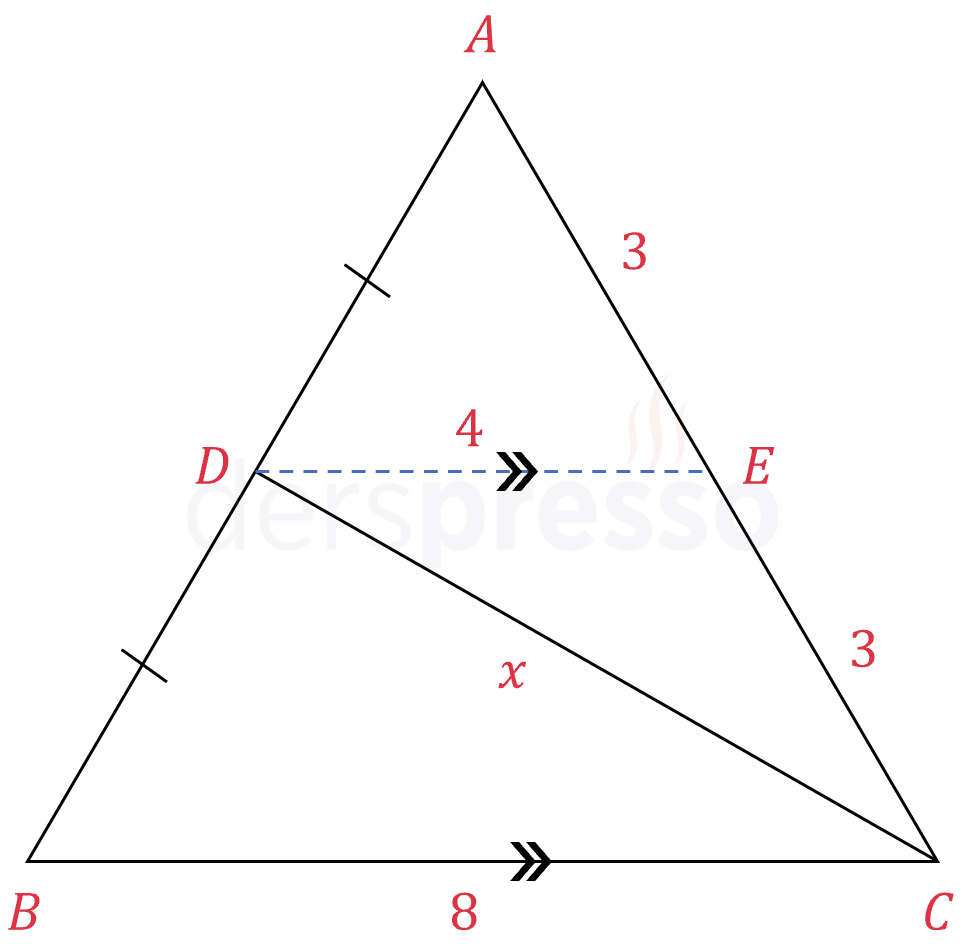
\( [DE] \parallel [BC] \)
\( [DE] \) \( [AB] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{DE} = 4 \)
\( [DE] \) orta taban olduğu için \( E \) noktası \( [AC] \) kenarının orta noktasıdır.
\( \abs{AE} = 3, \abs{EC} = 3 \)
\( DEC \) üçgeninde üçgen eşitsizliğini kullandığımızda aşağıdaki eşitsizliği elde ederiz.
\( \abs{4 - 3} \lt x \lt \abs{4 + 3} \)
\( 1 \lt x \lt 7 \)
\( x \) bu aralıkta 5 tam sayı değeri alabilir.

\( [AB] \perp [BC]\)
\( \abs{AF} = \abs{FC} \)
\( \abs{AD} = 1, \abs{DB} = 5, \abs{BC} = 8 \)
olduğuna göre, \( \abs{DF} = x \) kaçtır?
Çözümü Göster\( F \) noktasından \( [BC] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [AB] \) kenarını kestiği noktaya \( E \) diyelim.
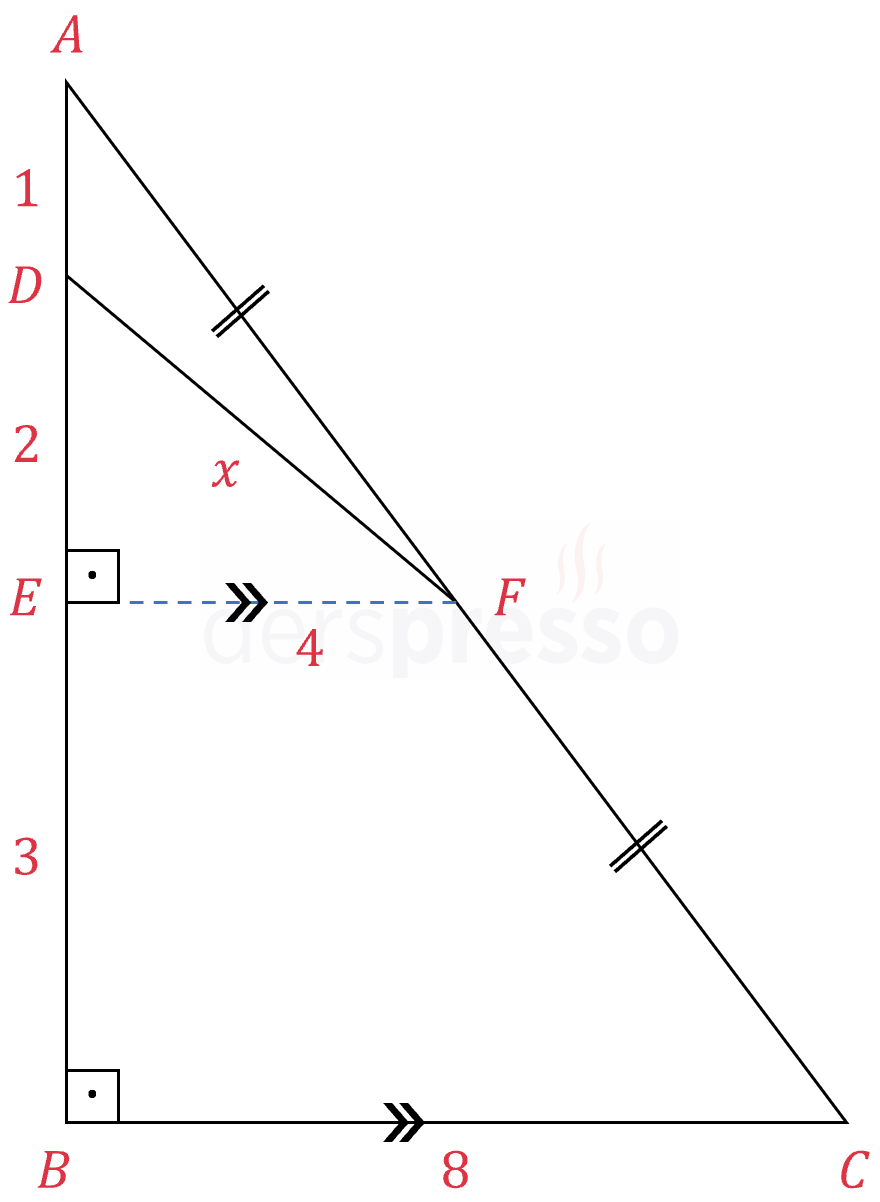
\( [EF] \parallel [BC] \)
\( [EF] \perp [AB] \)
\( [EF] \) \( [AC] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{EF} = 4 \)
\( [EF] \) orta taban olduğu için \( E \) noktası \( [AB] \) kenarının orta noktasıdır.
\( \abs{DE} = 2, \abs{EB} = 3 \)
\( DEF \) üçgeninde Pisagor teoremini kullanarak \( \abs{DF} \) uzunluğunu bulalım
\( \abs{DF}^2 = 2^2 + 4^2 \)
\( \abs{DF} = x = 2\sqrt{5} \) bulunur.

\( \abs{AB} = \abs{AC}, \abs{AD} = \abs{DB} \)
\( \abs{AF} = 7, \abs{FC} = 1, \abs{BC} = 6 \)
\( m(\widehat{BAC}) = 30° \)
olduğuna göre, \( m(\widehat{AFD}) = x \) kaçtır?
Çözümü Göster\( D \) noktasından \( [BC] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [AC] \) kenarını kestiği noktaya \( E \) diyelim.
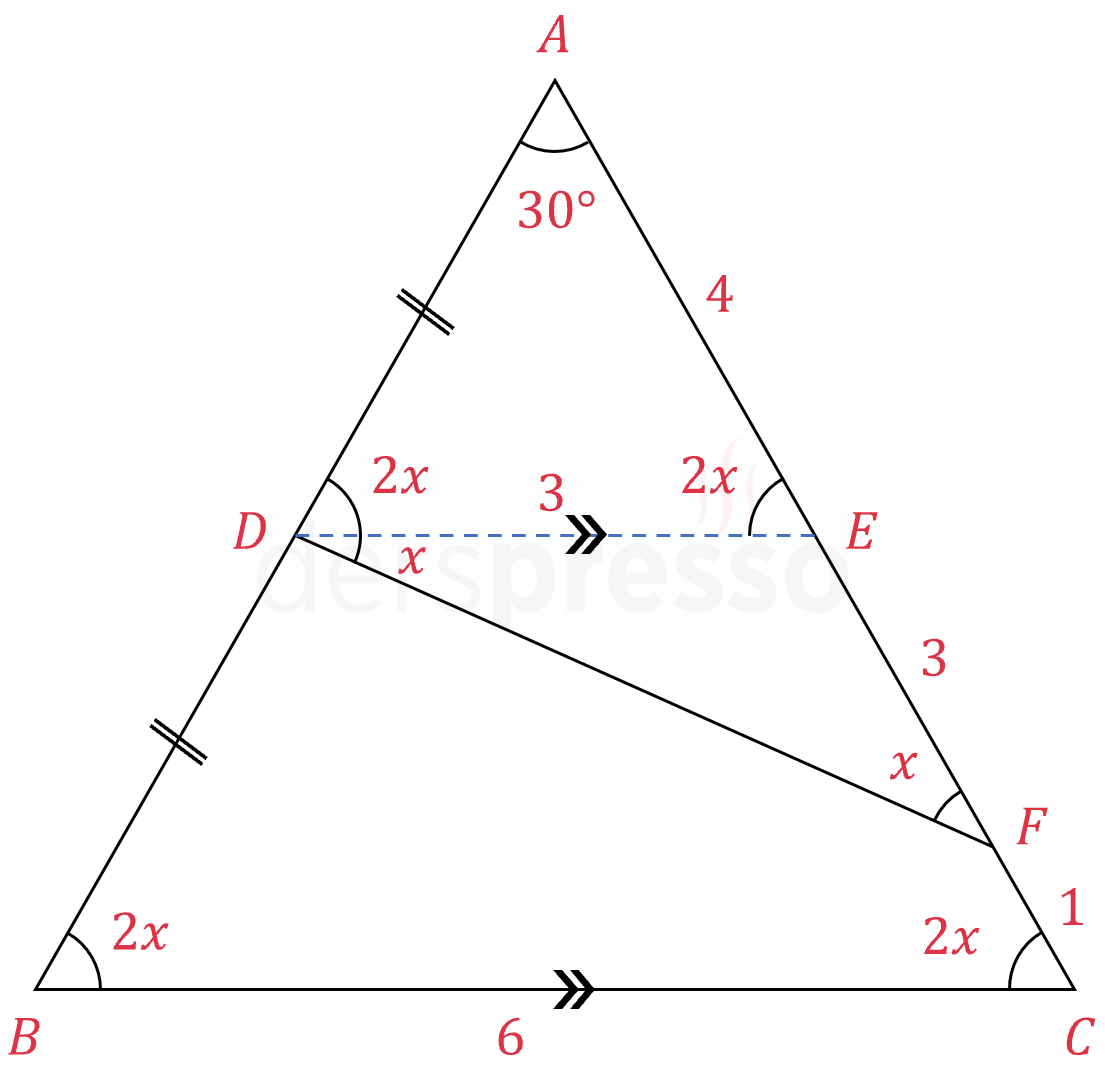
\( [DE] \parallel [BC] \)
\( [DE] \) \( [AB] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{DE} = 3 \)
\( [DE] \) orta taban olduğu için \( E \) noktası \( [AC] \) kenarının orta noktasıdır.
\( \abs{AE} = 4, \abs{EF} = 3 \)
\( DEF \) üçgeni bir ikizkenar üçgendir.
\( m(\widehat{EFD}) = m(\widehat{EDF}) = x \)
İki iç açının toplamı bu açılara komşu olmayan dış açıya eşittir.
\( m(\widehat{AED}) = m(\widehat{EFD}) + m(\widehat{EDF}) \)
\( = x + x = 2x \)
\( ABC \) üçgeni bir ikizkenar üçgendir, dolayısıyla orta tabanın oluşturduğu \( ADE \) üçgeni de ikizkenardır.
\( m(\widehat{ADE}) = m(\widehat{ABC}) = m(\widehat{ACB}) = 2x \)
\( ABC \) üçgeninin iç açıları toplamı 180°'dir.
\( 2x + 2x + 30 = 180 \)
\( 4x = 150 \)
\( x = 37,5° \) olarak bulunur.

\( [DB] \perp [BC] \)
\( \abs{AD} = \abs{DC} \)
\( \abs{DB} = 2, \abs{BC} = 5 \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( [BC] \) kenarını uzatalım ve \( [DB] \)'ye paralel olacak şekilde \( A \) köşesinden bu doğruya bir dik indirelim.
İki doğrunun kesişim noktasına \( E \) diyelim.
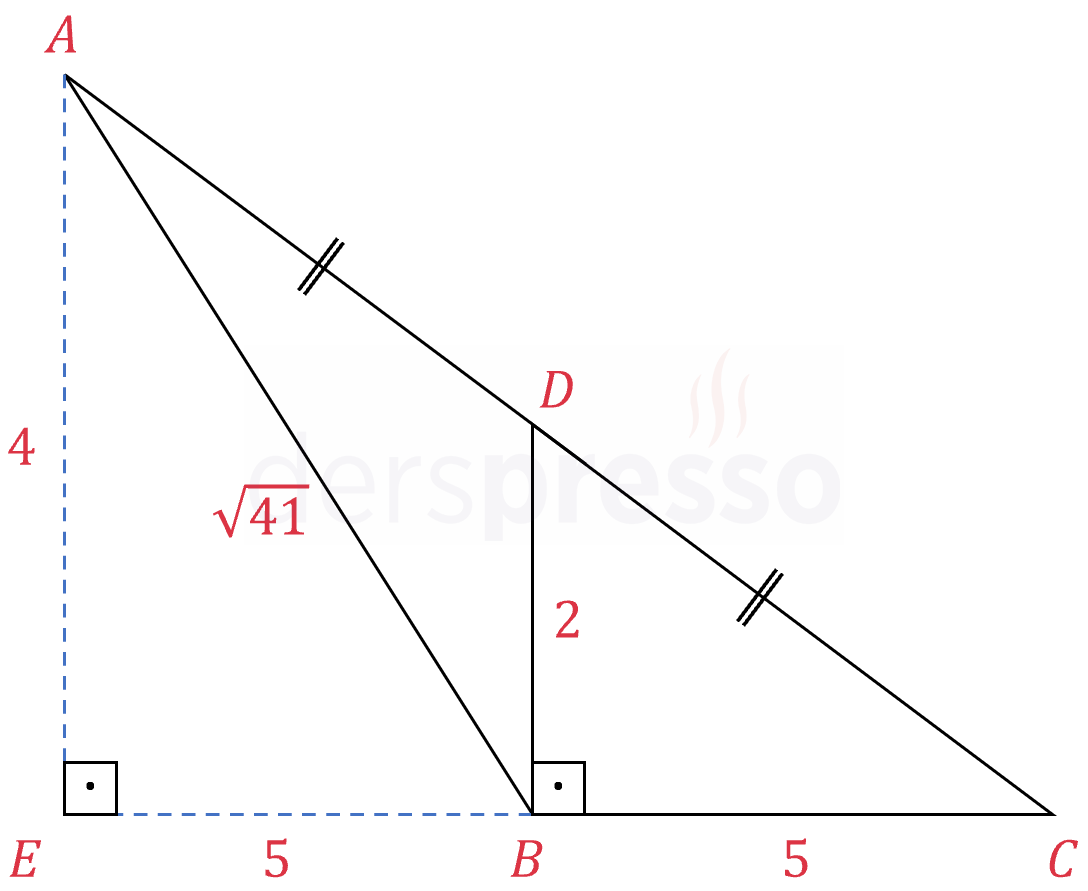
\( [AE] \perp [EC], [AE] \parallel [DB] \)
\( [DB] \) \( [AC] \) kenarını ortaladığı ve \( [AE] \) kenarına paralel olduğu için \( AEC) üçgeninin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{AE} = 2\abs{DB} = 4 \)
\( [DB] \) orta taban olduğu için \( B \) noktası \( [EC] \) kenarının orta noktasıdır.
\( \abs{EB} = \abs{BC} = 5 \)
\( AEB \) üçgeninde Pisagor teoremini kullanarak \( \abs{AB} \) uzunluğunu bulalım.
\( \abs{AB}^2 = x^2 = \abs{AE}^2 + \abs{EB}^2 \)
\( x = \sqrt{4^2 + 5^2} = \sqrt{41} \) bulunur.

\( [AB] \perp [BC] \)
\( \abs{ED} = \abs{DC}, \abs{AD} = \abs{BC} \)
\( m(\widehat{ECB}) = 40° \)
olduğuna göre, \( m(\widehat{ADE}) = x \) kaçtır?
Çözümü Göster\( D \) noktasından \( [BC] \) kenarına paralel bir doğru çizelim ve bu doğrunun \( [EB] \) kenarını kestiği noktaya \( F \) diyelim.

\( [DF] \perp [EB] \)
\( [DF] \) \( [EC] \) kenarını ortaladığı ve \( [BC] \) kenarına paralel olduğu için üçgenin bir orta tabanıdır.
Orta taban uzunluğu taban uzunluğunun yarısıdır.
\( \abs{FD} = a, \abs{BC} = 2a \)
\( \abs{AD} = \abs{BC} = 2a \)
\( [FD] \parallel [BC] \) olduğu için \( m(\widehat{EDF}) = m(\widehat{ECB}) = 40°\) olur.
\( 30-60-90°\) özel üçgeninde dik açının gördüğü kenar uzunluğu \( 30° \)'lik açının gördüğü kenarın 2 katıdır.
\( AFD \) üçgeninde hipotenüs \( 2a \) ve \( \hat{A} \) açısının gördüğü kenar \( a \) olduğuna göre, \( AFD \) üçgeninin \( 30-60-90° \) özel üçgeni olduğunu söyleyebiliriz
Bu durumda üçgenin açıları aşağıdaki gibi olur.
\( m(\widehat{FAD}) = 30° \)
\( m(\widehat{ADF}) = 40 + x = 60° \)
\( m(\widehat{ADE}) = x = 20° \) olarak bulunur.