Orta Dikme
Bir üçgenin kenarlarının orta noktalarından çizilen dikmelere orta dikme denir.
Bir üçgenin (ya da çokgenin) tüm köşelerinden geçen çembere çevrel çember denir. Her üçgenin bir çevrel çemberi vardır.
Bir üçgenin orta dikmeleri her zaman tek bir noktada kesişir. İki orta dikmenin kesiştiği nokta biliniyorsa üçüncü orta dikme de bu noktadan geçmek zorundadır. Orta dikmelerin kesişim noktası üçgenin \( R \) yarıçaplı çevrel çemberinin merkezidir.
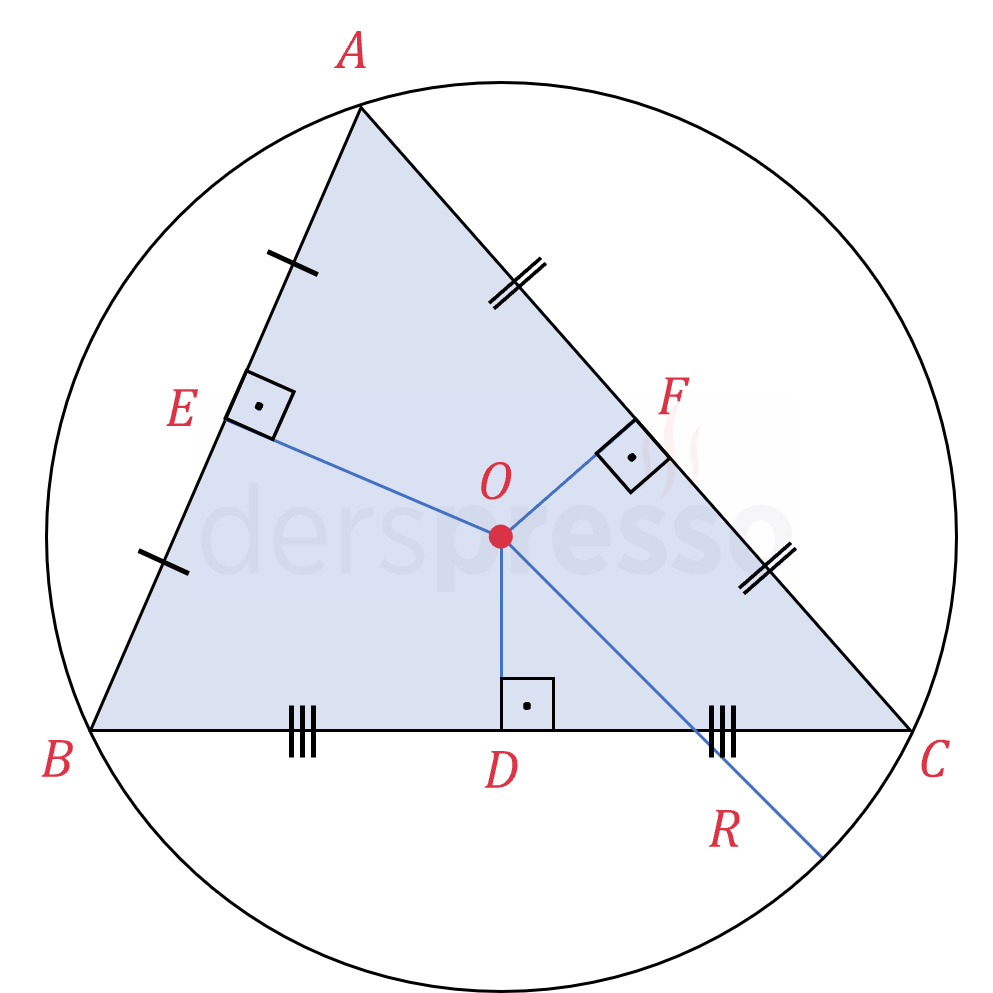
Orta dikmeler şekilde gösterildiği gibi üçgenin kenarlarını iki eşit parçaya böler.
Yukarıdaki şekilde gösterildiği gibi, dar açılı üçgenlerde orta dikmelerinin kesişim noktası üçgenin iç bölgesindedir.
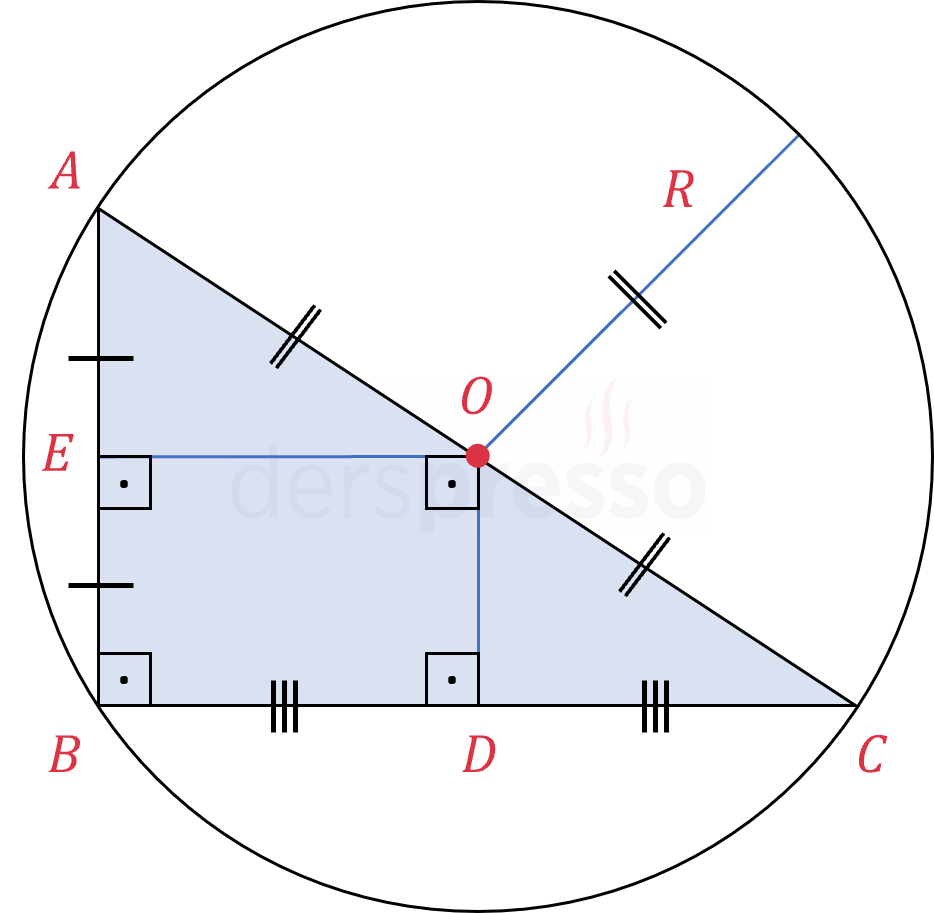
Dik açılı üçgenlerde orta dikmelerinin kesişim noktası hipotenüsün orta noktasıdır.
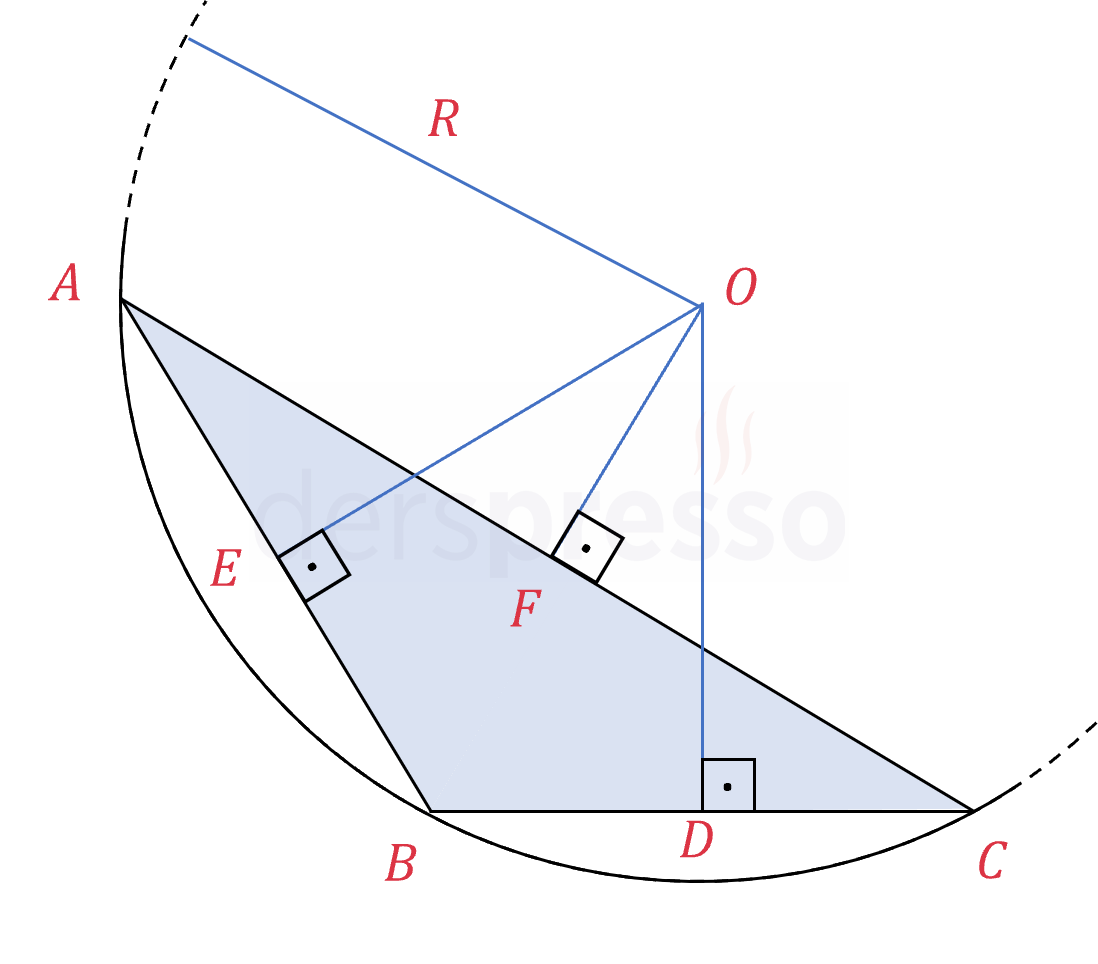
Geniş açılı üçgenlerde orta dikmelerinin kesişim noktası üçgenin dış bölgesindedir.
\( D \) noktası \( ABC \) üçgeninin çevrel çemberinin merkezidir.
\( \abs{BE} = 4, \abs{GC} = 6, \abs{FA} = 5 \)
Buna göre \( ABC \) üçgeninin çevresi kaç birimdir?
Çözümü Göster
\( D \) noktası üçgenin çevrel çemberinin merkezi olduğuna göre bu noktadan kenarlara indirilen dikmeler kenarları iki eşit parçaya böler.
\( \abs{EA} = \abs{BE} = 4 \)
\( \abs{BG} = \abs{GC} = 6 \)
\( \abs{CF} = \abs{FA} = 5 \)
Üçgenin çevresi \( 8 + 12 + 10 = 30 \) birim olur.
\( ABD \) ve \( BCD \) üçgenleri ile ilgili aşağıdakiler biliniyor.
\( [AE] \perp [BC], [AF] \perp [CD] \)
\( \abs{BE} = \abs{EC}, \abs{CF} = \abs{FD} \)
\( \abs{AB} = 2y + 8, \abs{AD} = 4y - 2 \)
olduğuna göre, \( \abs{AD} \) kaçtır?
Çözümü Göster\( [AE] \) ve \( [AF] \) doğruları indikleri doğruları dik ve ortalayarak kestikleri için \( BCD \) üçgeninin iki kenarının orta dikmelerdir.
Orta dikmelerin kesişim noktası çevrel çemberinin merkezidir.
Buna göre \( A \) noktası geniş açılı \( BCD \) üçgeninin çevrel çemberinin merkezi olup \( [AB] \) ve \( [AD] \) doğruları çemberin yarıçaplarıdır.
Bir çemberde yarıçap uzunlukları eşittir.
\( \abs{AB} = \abs{AD} \)
\( 2y + 8 = 4y - 2 \)
\( y = 5 \)
\( \abs{AD} = 4 \cdot 5 - 2 = 18 \) bulunur.
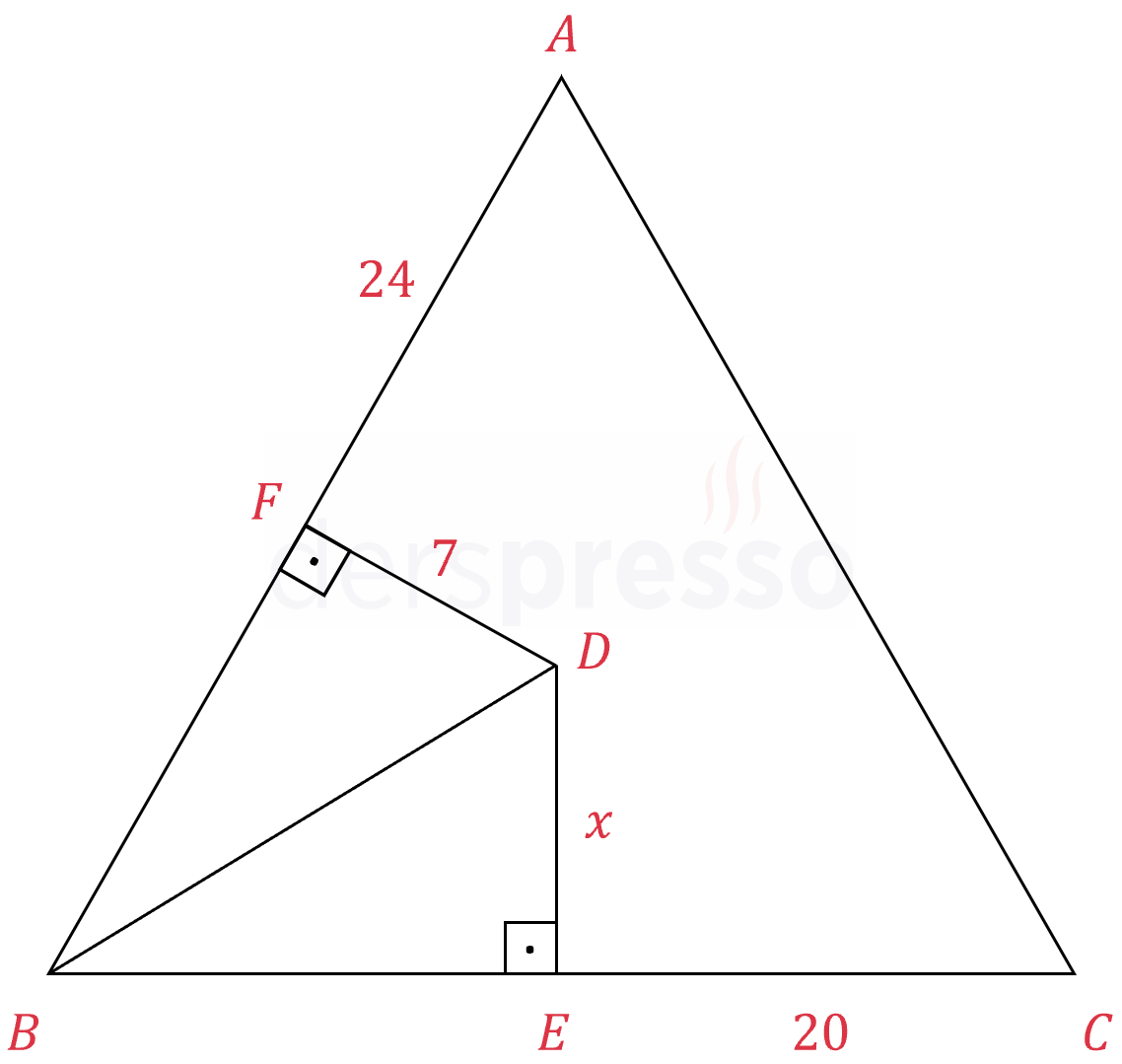
\( ABC \) üçgeninde \( [FD] \) doğru parçası \( [AB] \) kenarının, \( [DE] \) de \( [BC] \) kenarının orta dikmesidir.
\( \abs{FA} = 24, \abs{FD} = 7, \abs{EC} = 20 \)
olduğuna göre, \( \abs{DE} = x \) kaçtır?
Çözümü Göster
Bir kenarın orta dikmesi o kenarı iki eş parçaya böler.
\( \abs{BF} = \abs{FA} = 24 \)
\( \abs{BE} = \abs{EC} = 20 \)
\( BFD \) üçgeni 7-24-25 özel üçgenidir.
\( \abs{BD} = 25 \)
\( BDE \) üçgeninin kenar uzunlukları 3-4-5 özel üçgeninin 5 katıdır.
\( \abs{DE} = x = 15 \) bulunur.
\( [EC] \) üzerindeki \( D \) noktası \( ABC \) üçgeninin orta dikmelerinin kesişim noktasıdır.
\( m(\widehat{BAC}) = 60°, \abs{EB} = 2\sqrt{3} \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster
\( [BD] \) doğrusunu \( [AC] \) kenarına kadar uzatalım.
\( D \) noktası orta dikmelerin kesişim noktası ise bu noktadan geçen doğrular üçgenin kenarlarını dik keserler.
\( [BF] \perp [AC], [CE] \perp [BA] \)
\( m(\widehat{ACE}) = 90 - 60 = 30° \)
\( m(\widehat{FDC}) = m(\widehat{EDB}) = 60° \)
\( m(\widehat{EBD}) = 90 - 60 = 30° \)
\( BED \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde dik açının gördüğü kenar ve 60°'lik açının gördüğü kenar uzunlukları arasındaki oran \( 2:\sqrt{3} \) olur.
\( \abs{BD} = \dfrac{2 \cdot 2\sqrt{3}}{\sqrt{3}} = 4 \) olarak bulunur.
\( O \) noktası \( ABC \) üçgeninin çevrel çemberinin merkezidir.
\( \abs{OE} = 3, \abs{OF} = \sqrt{13}, \abs{BF} = 6 \)
olduğuna göre, \( \abs{EC} = x \) kaçtır?
Çözümü Göster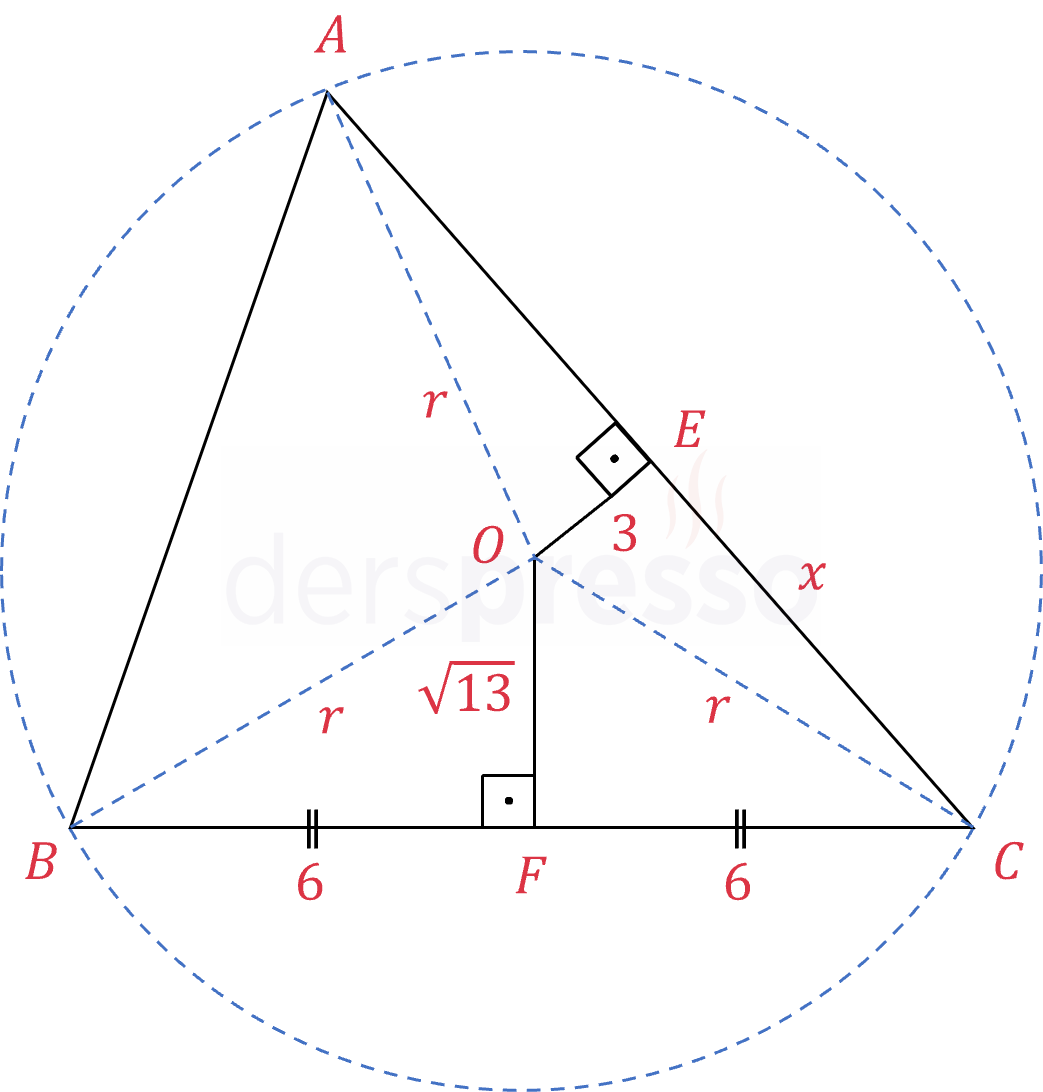
Bir üçgenin çevrel çemberinin merkezi üçgenin orta dikmelerinin kesişim noktasıdır.
\( O \) çevrel çemberin merkezi olduğundan bu noktanın üçgenin köşelerine olan uzaklıkları eşittir.
\( OBF \) üçgeninin iki dik kenarı bilindiğine göre Pisagor teoremi ile hipotenüsü bulalım.
\( r^2 = 6^2 + \sqrt{13}^2 \)
\( r = 7 \)
\( OEC \) üçgenine Pisagor teoremini uygulayalım.
\( 3^2 + x^2 = r^2 \)
\( x^2 = 7^2 - 3^2 = 40 \)
\( x = \sqrt{40} = 2\sqrt{10} \) olarak bulunur.
\( ABC \) üçgeninde \( O \) noktası çevrel çemberin merkezidir.
\( m(\widehat{OCA}) = 35° \)
olduğuna göre, \( m(\widehat{ABC}) = a \) kaçtır?
Çözümü Göster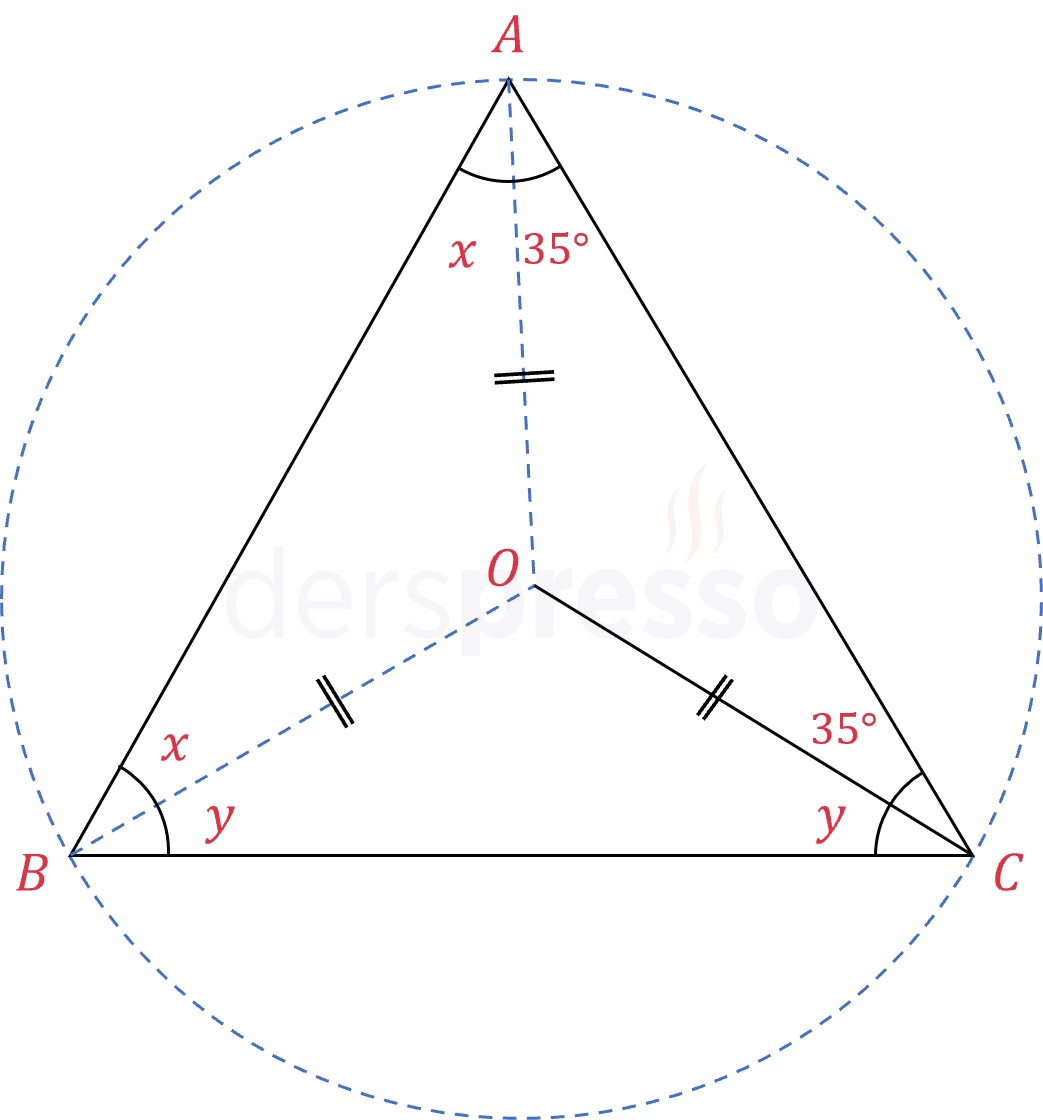
\( O \) noktası çevrel çemberin merkezi olduğu için bu noktanın üçgenin köşelerine olan uzaklıkları eşit olur.
\( \abs{OA} = \abs{OB} = \abs{OC} \)
\( m(\widehat{OCA}) = m(\widehat{OAC}) = 35° \)
\( m(\widehat{OBA}) = m(\widehat{OAB}) = x \)
\( m(\widehat{OBC}) = m(\widehat{OCB}) = y \)
\( x + y = a \) olur.
Üçgenin iç açılarının toplamı \( 180° \)'dir.
\( 2x + 2y + 70 = 180 \)
\( 2x + 2y = 110 \)
\( x + y = a = 55° \) bulunur.