Üçgende Benzerlik
İç açıları aynı olan üçgenlere benzer üçgenler denir.

\( ABC \) ve \( KLM \) üçgenlerinin benzerliği \( \overset{\triangle}{ABC} \sim \overset{\triangle}{KLM} \) şeklinde gösterilir. Bu gösterimde köşelerin yazım sırası önemli olup açı ölçüleri aynı olan köşeler her iki üçgenin yazılışında aynı konumda bulunmalıdır.
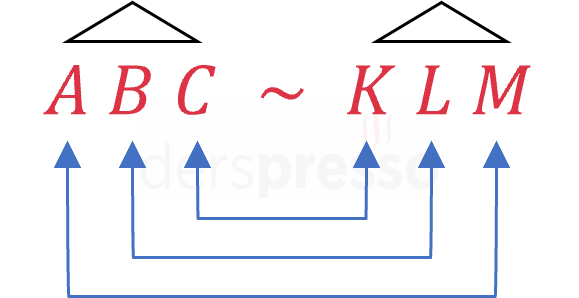
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{KLM} \) ise,
\( m(\widehat{A}) = m(\widehat{K}) \)
\( m(\widehat{B}) = m(\widehat{L}) \)
\( m(\widehat{C}) = m(\widehat{M}) \)
Benzer iki üçgende ölçüleri aynı olan açıların karşısındaki kenarların uzunlukları oranı sabittir ve bu orana benzerlik oranı denir.
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{KLM} \) ise,
\( k \) iki üçgen arasındaki benzerlik oranı olmak üzere,
\( \dfrac{\abs{AB}}{\abs{KL}} = \dfrac{\abs{AC}}{\abs{KM}} = \dfrac{\abs{BC}}{\abs{LM}} = k \)

\( \overset{\triangle}{DEF} \sim \overset{\triangle}{RQP} \) ise,
\( \dfrac{\abs{DE}}{\abs{RQ}} = \dfrac{\abs{DF}}{\abs{RP}} = \dfrac{\abs{EF}}{\abs{QP}} \)
\( \dfrac{25}{b} = \dfrac{30}{18} = \dfrac{35}{a} \)
\( a = 21, \quad b = 15 \)
Benzer iki üçgenin yükseklikleri, açıortayları, kenarortayları, orta dikmeleri ve çevreleri arasında da aynı \( k \) benzerlik oranı vardır.
\( \dfrac{h_a}{h_k} = \dfrac{h_b}{h_l} = \dfrac{h_c}{h_m} = k \)
\( \dfrac{n_a}{n_k} = \dfrac{n_b}{n_l} = \dfrac{n_c}{n_m} = k \)
\( \dfrac{V_a}{V_k} = \dfrac{V_b}{V_l} = \dfrac{V_c}{V_m} = k \)
\( \dfrac{\text{Ç}(ABC)}{\text{Ç}(KLM)} = k \)
Benzer iki üçgenin alanları arasındaki benzerlik oranı \( k^2 \)'dir.
\( \dfrac{A(ABC)}{A(KLM)} = k^2 \)
Üç açının eşitliğinin bilinmediği durumlarda, aşağıdaki koşullardan birini sağlayan üçgenler de benzerdir.
- Açı - Açı Benzerliği: İkişer açısı eşit olan iki üçgen, üçüncü açıları da eşit olacağı için benzerdir.
- Kenar - Kenar - Kenar Benzerliği: Tüm kenar uzunlukları arasında sabit orantı bulunan iki üçgenin iç açıları eşittir, dolayısıyla bu üçgenler benzerdir.
- Kenar - Açı - Kenar Benzerliği: İkişer kenarı orantılı ve bu iki kenar arasındaki açıları eşit olan iki üçgen, karşı kenar uzunlukları da aynı orantıya sahip olacağı için benzerdir (kosinüs teoreminden).
Bir dik üçgenin hipotenüsüne ait yükseklik, üçgeni birbirine ve büyük üçgene benzer iki küçük dik üçgene ayırır.

\( \overset{\triangle}{BDA} \sim \overset{\triangle}{ADC} \)
\( \overset{\triangle}{BDA} \sim \overset{\triangle}{BAC} \)
\( \overset{\triangle}{CDA} \sim \overset{\triangle}{CAB} \)
Bir üçgeni kesen bir doğru üçgenin iki kenarını orantılı olarak bölüyorsa bu doğru parçası üçgenin üçüncü kenarına paraleldir ve benzer iki üçgen oluşturur.
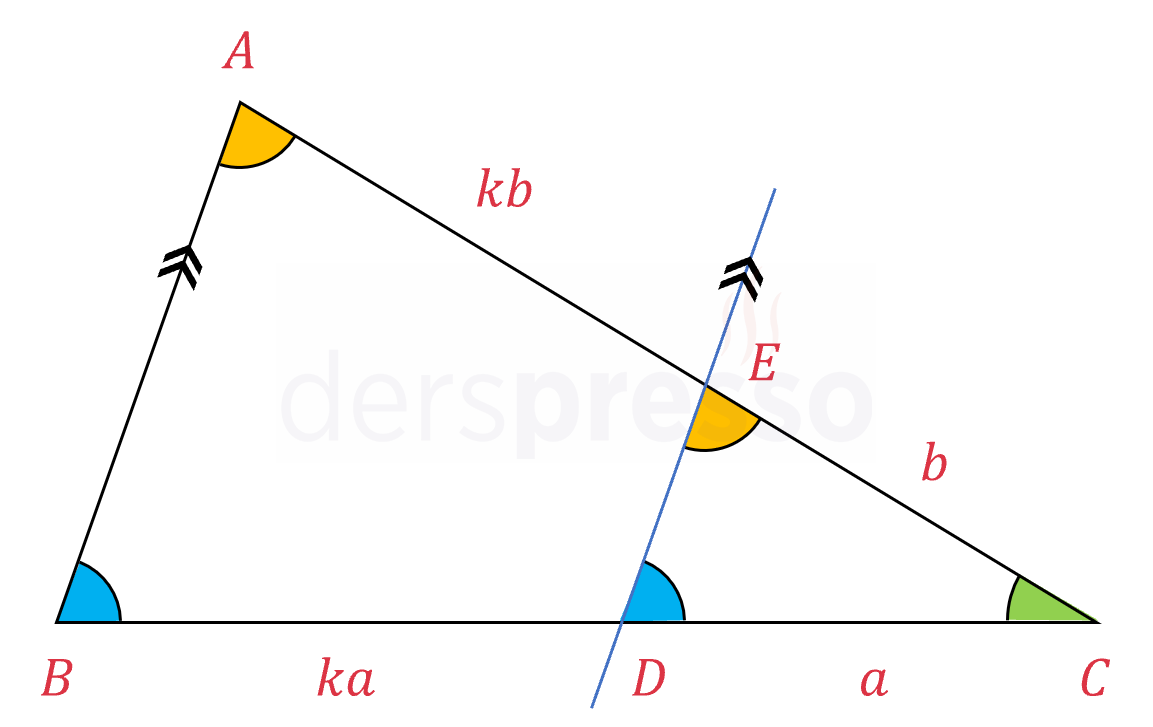
\( \dfrac{\abs{AE}}{\abs{EC}} = \dfrac{\abs{BD}}{\abs{DC}}\) ise,
\( [AB] \parallel [ED] \) ve \( \overset{\triangle}{ABC} \sim \overset{\triangle}{EDC} \)
Üçgende Eşlik
Tüm iç açıları ve kenar uzunlukları birbirine eşit olan, diğer bir deyişle benzerlik oranı 1 olan benzer üçgenlere eş üçgenler denir.

\( ABC \) ve \( KLM \) üçgenlerinin eşliği \( \overset{\triangle}{ABC} \cong \overset{\triangle}{KLM} \) şeklinde gösterilir. Bu gösterimde köşelerin yazım sırası önemli olup açı ölçüleri ve kenar uzunlukları aynı olan köşeler her iki üçgenin yazılışında aynı konumda bulunmalıdır.
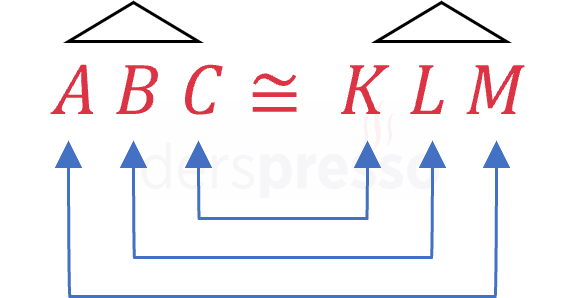
\( \overset{\triangle}{ABC} \cong \overset{\triangle}{KLM} \) ise,
\( m(\widehat{A}) = m(\widehat{K}) \)
\( m(\widehat{B}) = m(\widehat{L}) \)
\( m(\widehat{C}) = m(\widehat{M}) \)
\( \abs{AB} = \abs{KL} \)
\( \abs{AC} = \abs{KM} \)
\( \abs{BC} = \abs{LM} \)

\( \overset{\triangle}{DEF} \cong \overset{\triangle}{RQP} \) ise,
\( \abs{RQ} = \abs{DE} = 12 \)
\( \abs{RP} = \abs{DF} = 15 \)
\( \abs{QP} = \abs{EF} = 18 \)
Tüm açıların ve kenar uzunluklarının eşitliğinin bilinmediği durumlarda, aşağıdaki koşullardan birini sağlayan üçgenler de eştir.
- Kenar - Kenar - Kenar Eşliği: Tüm kenar uzunlukları eşit olan iki üçgenin iç açıları da eşittir, dolayısıyla bu üçgenler eştir.
- Kenar - Açı - Kenar Eşliği: İkişer kenarı ve bu iki kenar arasındaki açıları eşit olan iki üçgen, karşı kenar uzunlukları da eşit olacağı için eştir (kosinüs teoreminden).
- Açı - Kenar - Açı Eşliği: İkişer açısı ve bu açıların ortak kenarı eşit iki üçgen eştir (üçüncü açının eşitliği ve sinüs teoreminden).
Benzerlik Kuralları
Temel Orantı Teoremi
Bir üçgenin yan kenarlarını birleştiren ve tabana paralel doğru parçası iki benzer üçgen oluşturur.

\( [BC] \parallel [DE] \) ise,
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{ADE} \)
\( \dfrac{\abs{AB}}{\abs{AD}} = \dfrac{\abs{AC}}{\abs{AE}} = \dfrac{\abs{BC}}{\abs{DE}} = k \)
Thales Teoremi
Birbirine paralel doğruları kesen iki doğru ile paralel doğrular arasında kalan doğru parçalarının uzunlukları oranı sabittir.

\( [AD] \parallel [BE] \parallel [CF] \) olmak üzere,
\( \dfrac{\abs{AB}}{\abs{BC}} = \dfrac{\abs{DE}}{\abs{EF}} \)
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{\abs{DE}}{\abs{DF}} \)
İSPATI GÖSTER
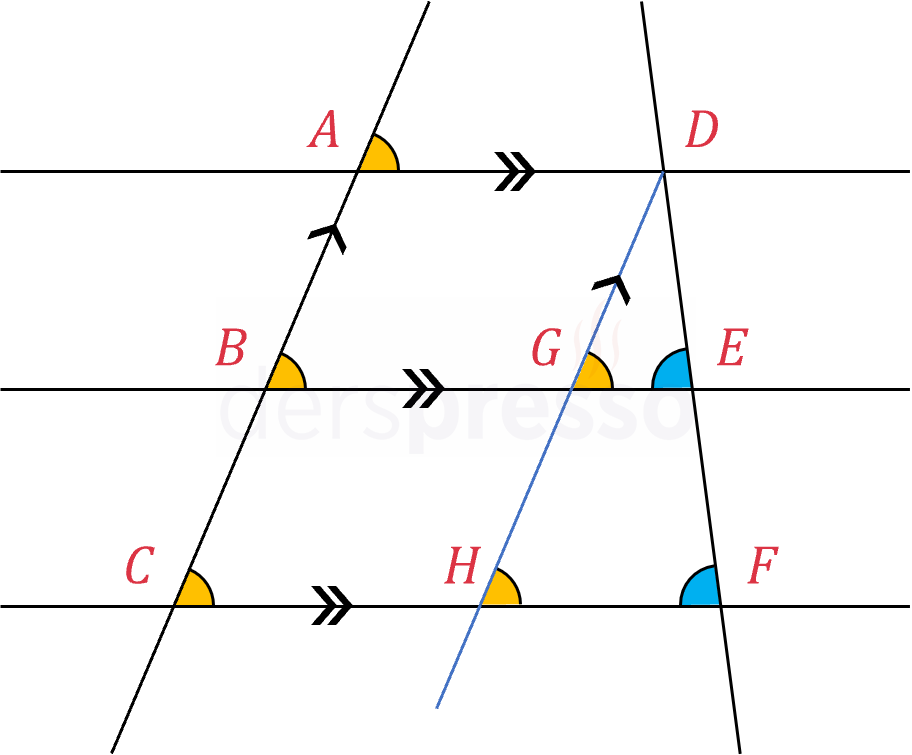
\( D \) noktasından geçen ve \( AC \) doğrusuna paralel bir doğru çizelim (mavi çizgi).
\( AC \parallel DH \)
Doğruların paralelliğinden dolayı aşağıdaki açılar yöndeş açılardır ve ölçüleri birbirine eşittir.
\( m(\widehat{ABE}) = m(\widehat{ACF}) = m(\widehat{DGE}) = m(\widehat{DHF}) \)
\( m(\widehat{DEB}) = m(\widehat{DFC}) \)
Buna göre tüm açıları eşit \( \overset{\triangle}{DGE} \) ve \( \overset{\triangle}{DHF} \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{DGE} \sim \overset{\triangle}{DHF} \)
\( \overset{\triangle}{DHF} \) üçgenine temel orantı teoremini uygulayalım.
\( \dfrac{\abs{DG}}{\abs{DH}} = \dfrac{\abs{DE}}{\abs{DF}} \)
İç terimleri aralarında yer değiştirelim.
\( \dfrac{\abs{DG}}{\abs{DE}} = \dfrac{\abs{DH}}{\abs{DF}} \)
Pay ve paydadaki terimler arasındaki toplama/çıkarma işlemi yapmamız orantıyı bozmaz.
\( \dfrac{\abs{DG}}{\abs{DE}} = \dfrac{\abs{DH}}{\abs{DF}} = \dfrac{\abs{DH} - \abs{DG}}{\abs{DF} - \abs{DE}} \)
\( \dfrac{\abs{DG}}{\abs{DE}} = \dfrac{\abs{GH}}{\abs{EF}} \)
İç terimleri yine aralarında yer değiştirelim.
\( \dfrac{\abs{DG}}{\abs{GH}} = \dfrac{\abs{DE}}{\abs{EF}} \)
\( ADGB \) ve \( BGHC \) dörtgenleri birer paralelkenar olduğu için karşılıklı kenar uzunlukları eşittir.
\( \abs{DG} = \abs{AB} \)
\( \abs{GH} = \abs{BC} \)
Buna göre yukarıdaki orantıyı aşağıdaki şekilde yazdığımızda Thales teoremini elde ederiz.
\( \dfrac{\abs{AB}}{\abs{BC}} = \dfrac{\abs{DE}}{\abs{EF}} \)
Kelebek Benzerliği
İki paralel doğru ve bu doğruları ve birbirini aşağıdaki şekildeki gibi kesen iki doğru arasında benzer iki üçgen oluşur.

\( [AB] \parallel [DE] \) ise,
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{EDC} \)
\( \dfrac{a}{f} = \dfrac{b}{e} = \dfrac{c}{d} = k \)
İSPATI GÖSTER
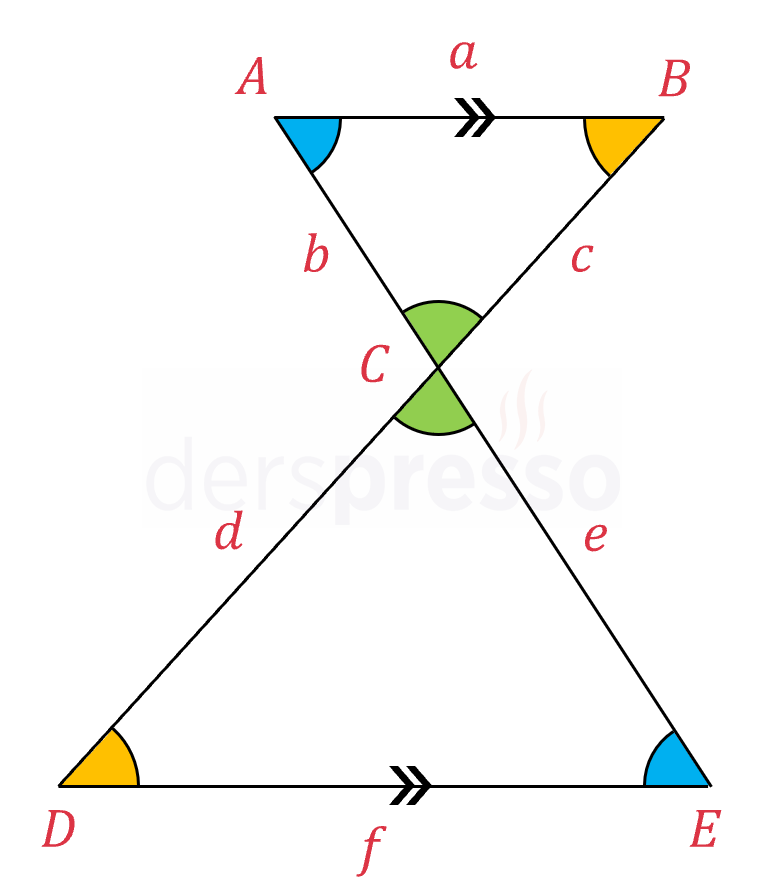
\( [AB] \) ve \( [DE] \) doğru parçaları paralel olduğu için aşağıdaki açılar iç ters açılardır ve ölçüleri eşittir.
\( m(\widehat{CAB}) = m(\widehat{CED}) \)
\( m(\widehat{CBA}) = m(\widehat{CDE}) \)
Aşağıdaki açılar ters açılardır ve ölçüleri eşittir.
\( m(\widehat{ACB}) = m(\widehat{ECD}) \)
Dolayısıyla tüm açıları eşit \( \overset{\triangle}{ABC} \) ve \( \overset{\triangle}{EDC} \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{EDC} \)
Buna göre bu iki üçgenin kenar uzunlukları arasında aşağıdaki orantıyı yazabiliriz.
\( \dfrac{\abs{AB}}{\abs{ED}} = \dfrac{\abs{AC}}{\abs{EC}} = \dfrac{\abs{BC}}{\abs{DC}} \)
\( \dfrac{a}{f} = \dfrac{b}{e} = \dfrac{c}{d} \)
Ceva Teoremi
Bir üçgenin iç bölgesinden (kenarlar üzerinde olmayan) herhangi bir \( M \) noktası seçelim ve üçgenin her köşesinden karşı kenara \( M \) noktasından geçen birer doğru parçası çizelim. Ceva teoremine göre, seçilecek her \( M \) noktası için aşağıdaki çarpım 1'e eşittir.

\( \dfrac{\abs{AD}}{\abs{DB}} \cdot \dfrac{\abs{BE}}{\abs{EC}} \cdot \dfrac{\abs{CF}}{\abs{FA}} = 1 \)
Bu formülde herhangi bir köşeden başlayarak ve saat yönünde ya da saat yönünün tersi yönde ilerleyerek her kenar üzerinde oluşan doğru parçalarının oranlarının çarpımı alınır.
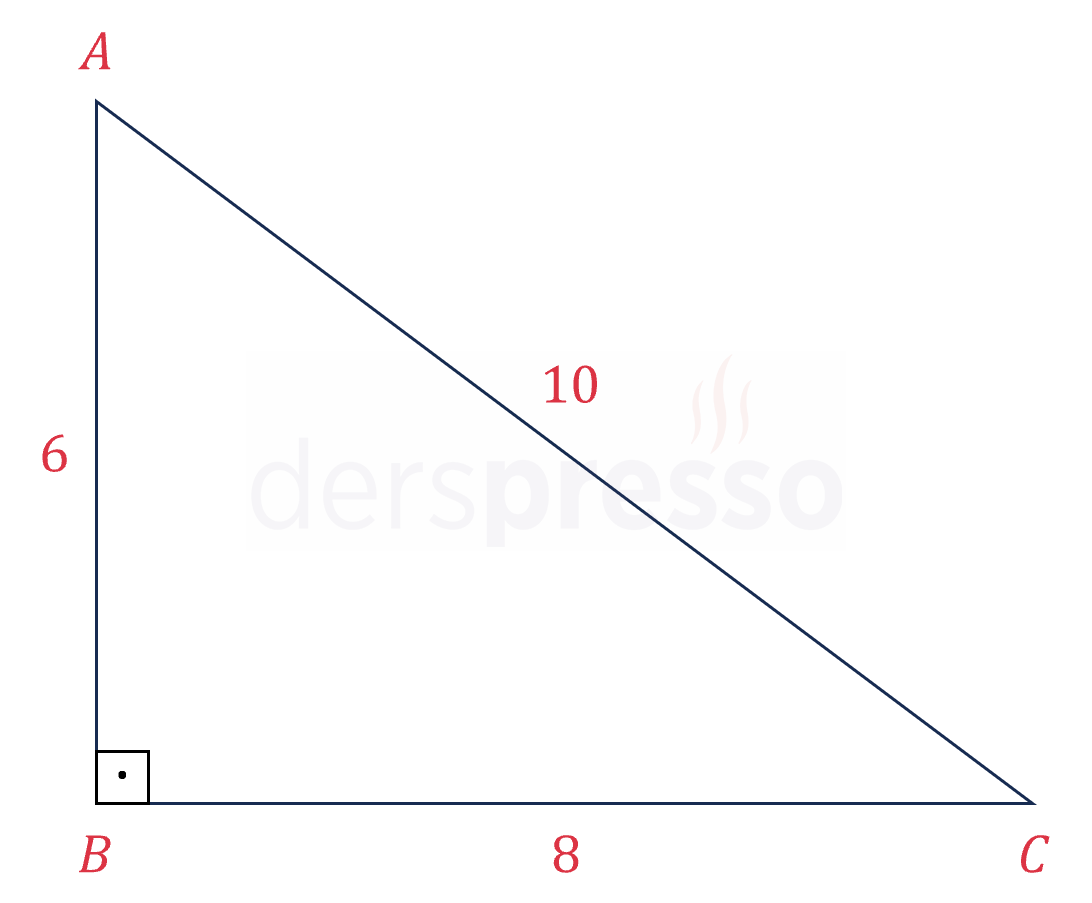
\( ABC \) dik üçgeni şekildeki gibidir.
\( C \) noktasının \( A \) noktasının üstüne gelecek şekilde katlanması sonucunda oluşan katlama çizgisinin uzunluğu kaç cm'dir?
Çözümü GösterKatlama çizgisinin uzunluğuna \( x \), katlama çizgisinin \( [AC] \) kenarını kestiği noktaya \( D \) diyelim.
Katlama sonucunda \( [AD] \) ve \( [DC] \) doğru parçaları çakışık ve uzunlukları eşit olması gerektiği için katlama çizgisi \( [AC] \) kenarına dik olmalıdır.
Katlama sonucu oluşan şekli çizelim.
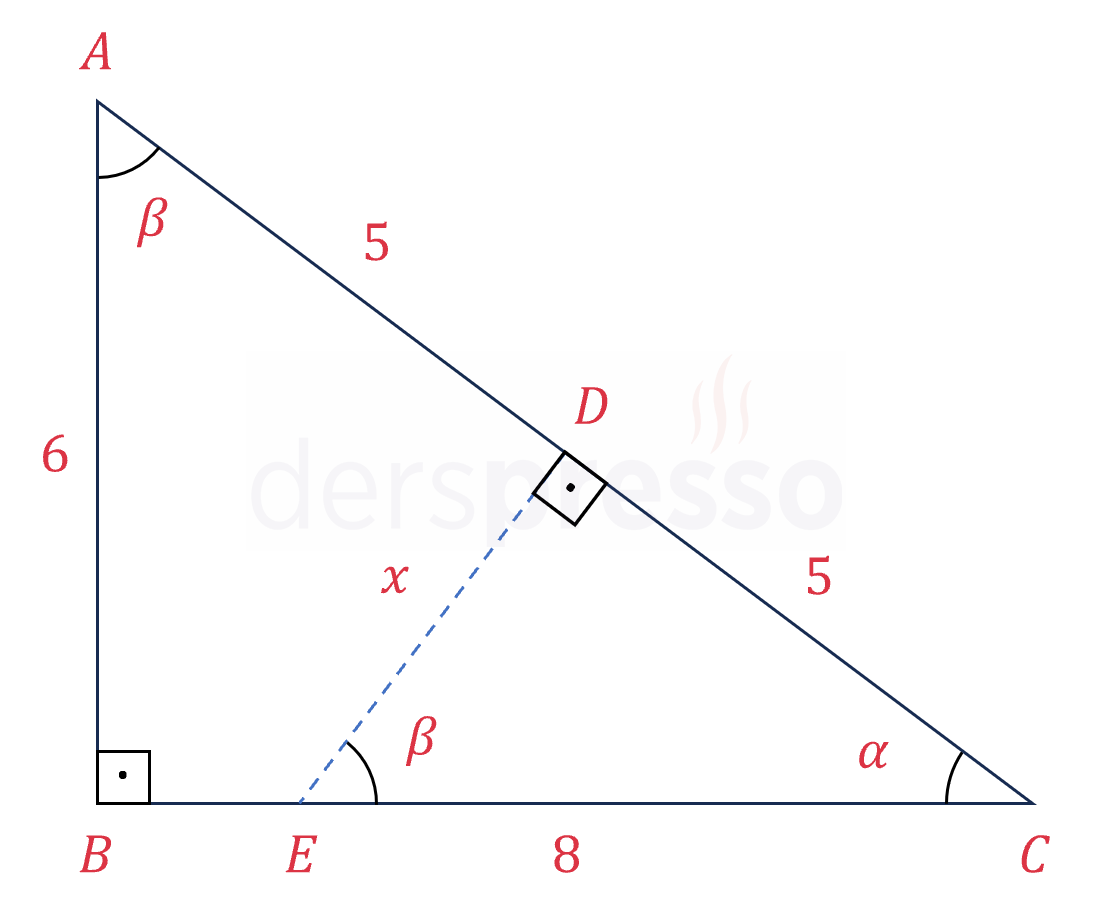
\( \abs{AD} = \abs{DC} = 5 \)
\( \hat{C} \) açısına \( \alpha \), \( \hat{A} \) açısına \( \beta \) diyelim.
\( \alpha \) ve \( \beta \) tümler açılar olduğundan \( \hat{E} \) açısı da \( \beta \) olur.
Tüm açıları aynı olan \( ABC \) ve \( EDC \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{ABC} \sim \overset{\triangle}{EDC} \)
\( \dfrac{\abs{AB}}{\abs{BC}} = \dfrac{\abs{ED}}{\abs{DC}} \)
\( \dfrac{6}{8} = \dfrac{x}{5} \)
\( x = \dfrac{6 \cdot 5}{8} \)
\( = \dfrac{15}{4} \) cm bulunur.

Yukarıdaki şekildeki karenin bir kenar uzunluğu 1 cm olduğuna göre, \( BEF \) üçgeninin alanı kaç cm\( ^2 \)'dir?
Çözümü Göster\( BDG \) üçgeninde Pisagor teoremini kullanarak \( \abs{BG} \) uzunluğunu bulalım.
\( \abs{BG}^2 = \abs{BD}^2 + \abs{DG}^2 \)
\( \abs{BG}^2 = 1^2 + (\dfrac{1}{2})^2 \)
\( \abs{BG} = \dfrac{\sqrt{5}}{2} \)
\( ABF \) ve \( BDG \) üçgenlerinin ikişer kenarı ve birer dik açısı eş olduğu için bu iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{ABF} \cong \overset{\triangle}{BDG} \)

\( m(BAF) = m(DGB) = a \)
\( m(AFB) = m(BGD) = b \)
\( ABF \) üçgeninde \( a + b = 90° \) olduğu için iki açısı \( a \) ve \( b \) olan \( BEF \) üçgeni de dik üçgendir.
Üç açısı da eş olan \( BEF \) ve \( BDG \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{BEF} \sim \overset{\triangle}{BDG} \)
\( BEF \) üçgeni ile \( BDG \) üçgeni arasındaki benzerliği kullanarak \( \abs{EF} \) uzunluğunu bulalım.
\( \dfrac{\abs{EF}}{\frac{1}{2}} = \dfrac{\frac{1}{2}}{\frac{\sqrt{5}}{2}} \)
\( \abs{EF} = \dfrac{1}{2\sqrt{5}} \)
\( BEF \) üçgeninde Pisagor teoremini kullanarak \( \abs{BE} \) uzunluğunu bulalım.
\( \abs{BF}^2 = \abs{BE}^2 + \abs{EF}^2 \)
\( \abs{BE}^2 = (\dfrac{1}{2})^2 - (\dfrac{1}{2\sqrt{5}})^2 \)
\( \abs{BE} = \dfrac{1}{\sqrt{5}} \)
Kenar uzunlukları bilinen \( BEF \) üçgeninin alanını bulalım.
\( A(BEF) = \dfrac{\abs{BE} \cdot \abs{EF}}{2} \)
\( = \dfrac{\frac{1}{\sqrt{5}} \cdot \frac{1}{2\sqrt{5}}}{2} \)
\( = \dfrac{1}{20} \) cm\( ^2 \) bulunur.
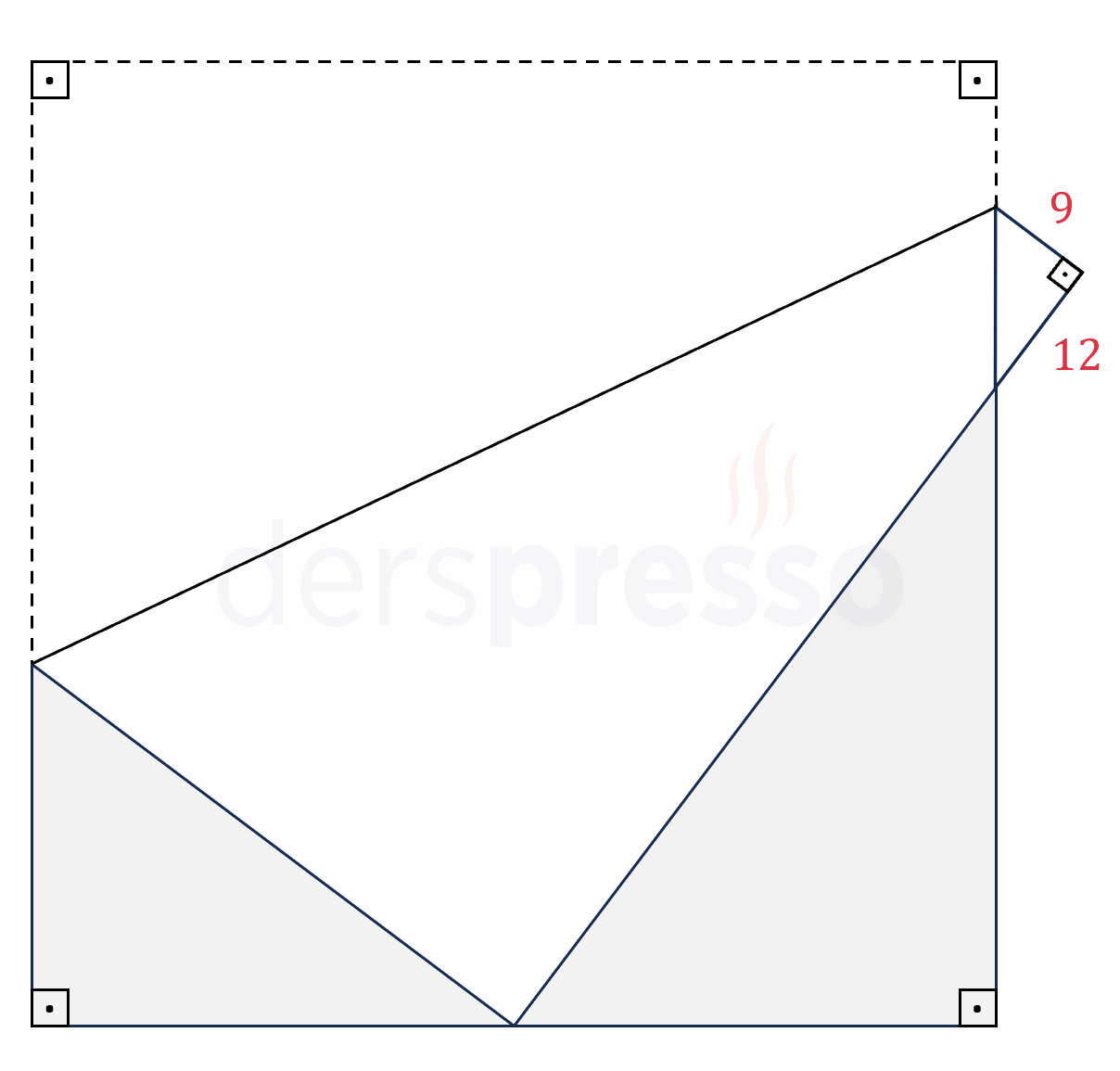
Kare bir kağıt parçası, köşelerinden biri kenarlarından birinin üzerinde gelecek şekilde katlanıyor.
Katlama sonucunda oluşan uzunluklar şekildeki gibi olduğuna göre, karenin bir kenar uzunluğu nedir?
Çözümü Gösterİki kenar uzunluğu verilen dik üçgenin açılarına \( \alpha \) ve \( \beta \) diyelim.
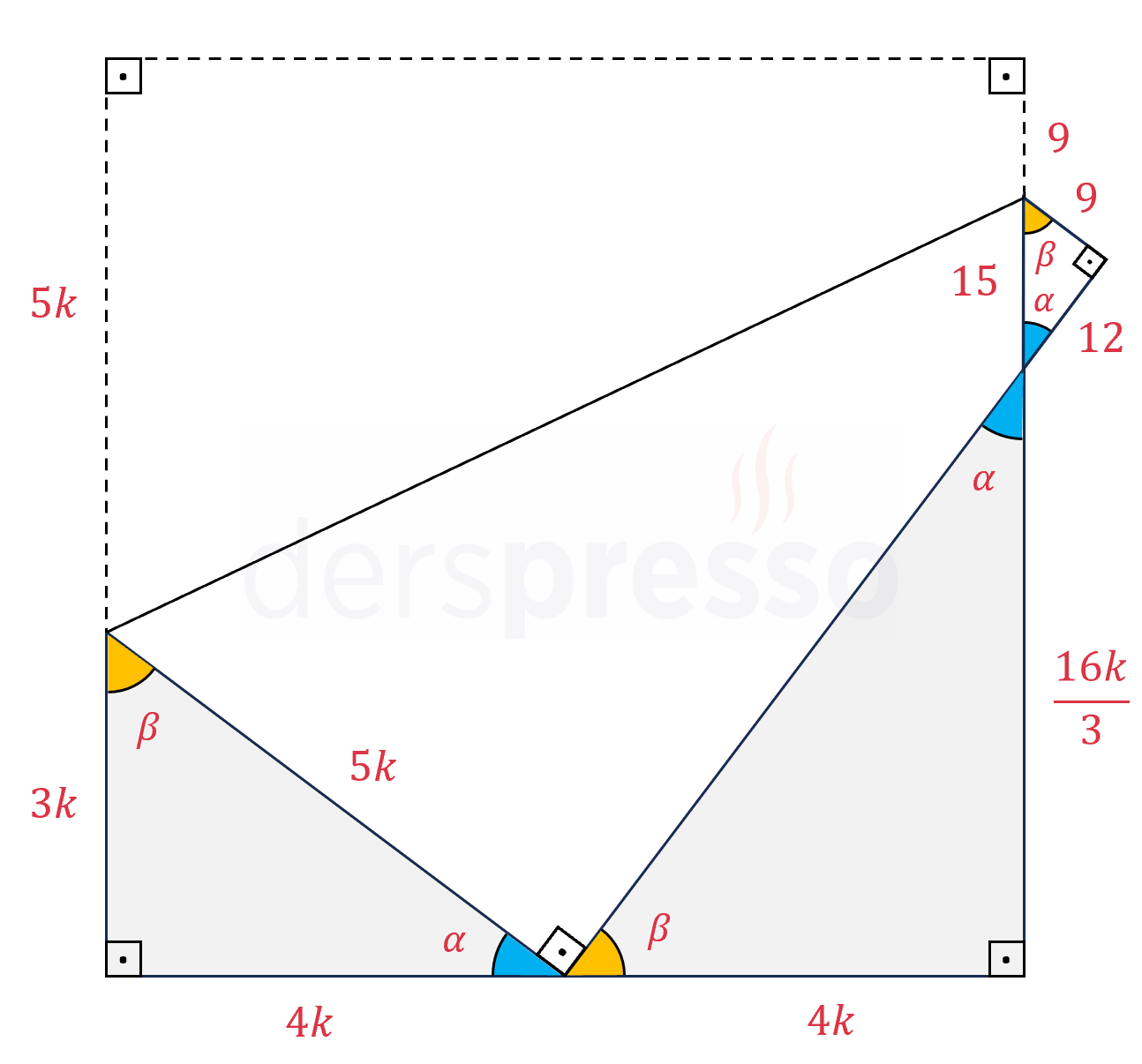
Şekildeki üç üçgen, tüm açıları aynı olduğu için benzer üçgenlerdir.
Üçgenlerin benzerliğinden yararlanarak sol alttaki üçgenin kenarlarına \( 3k \) ve \( 4k \) diyelim.
Pisagor teoreminden üçgenin hipotenüsü \( 5k \) olur.
Katlamayı açtığımızda \( 3k \)'nın üzerinde kalan uzunluğun \( 5k \) kenarı ile örtüştüğünü görürüz.
Buna göre karenin bir kenar uzunluğu \( 8k \) olur.
Dolayısıyla sağ altta kalan üçgende \( \alpha \) açısının gördüğü kenar \( 8k - 4k = 4k \) olur.
Aynı üçgende üçgen benzerliğinden dolayı \( \beta \) açısının gördüğü kenar \( \frac{16k}{3} \) olur.
Katlamayı açtığımızda kenarları verilen üçgenin hipotenüsünün üzerinde kalan uzunluğun üçgenin, uzunluğu 9 birim olan kenarı ile örtüştüğünü görürüz.
Karenin sağ kenarı üzerindeki parçaların uzunluklarının toplamını alıp \( 8k \)'ya eşitleyelim.
\( \dfrac{16k}{3} + 15 + 9 = 8k \)
\( \dfrac{8k}{3} = 24 \)
\( k = 9 \)
Buna göre, karenin bir kenarının uzunluğu \( 8k = 8 \cdot 9 = 72 \) olarak bulunur.