Yönlü Açılar
Geometride kullanılan açılarda açının yönü gözardı edilerek sadece büyüklüğü dikkate alınır. Trigonometride kullanılan açılarda ise açının yönü de önemlidir ve açı saat yönünün tersi yönde ise ölçüsü pozitif, saat yönünde ise ölçüsü negatif olur.
Yönüne göre ölçüsü pozitif ya da negatif olabilen bu tip açılar yönlü açı olarak adlandırılır.

Açı Ölçü Birimleri
Belirli bir uzunluğu ölçmek için kilometre ve mil gibi farklı birimler kullanıldığı gibi, açıların ölçüleri için de farklı birimler kullanılır. Trigonometride en sık kullanılan iki açı ölçü birimi derece ve radyandır (bir diğer birim olan graddan burada bahsetmeyeceğiz).
Derece
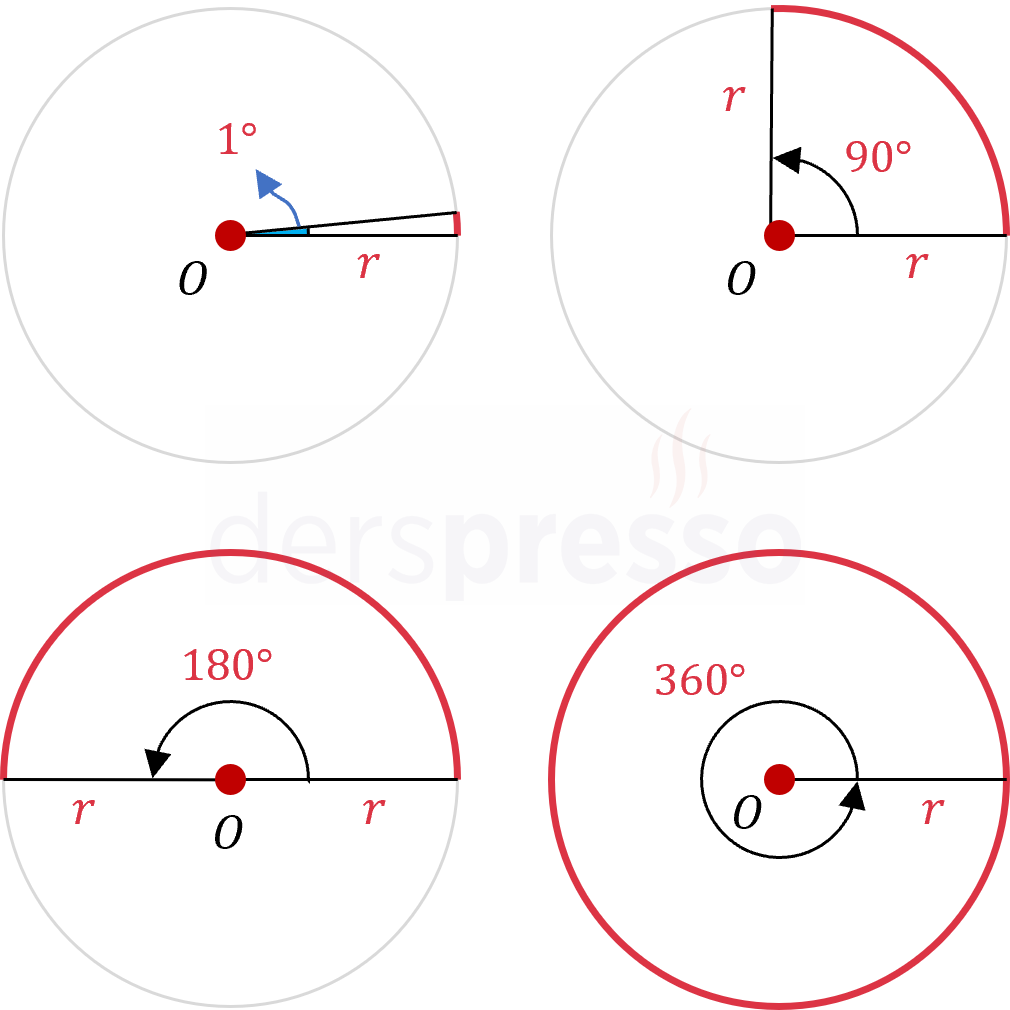
Bir tam çember yayının 360 eş parçaya bölünmesiyle elde edilen yaylardan her birini gören merkez açının ölçüsüne 1 derece denir ve \( 1° \) ile gösterilir. Dörtte bir, yarım ve tam çember yaylarını gören merkez açılar sırasıyla \( 90° \), \( 180° \) ve \( 360° \) olur.
Bir dereceden daha küçük açıları ifade etmek için dakika ve saniye birimleri kullanılır. Bir derecenin 60'ta birine dakika denir ve (') sembolü ile gösterilir. Bir dakikanın 60'ta birine saniye denir ve ('') sembolü ile gösterilir. Bir açının ölçüsü a derece b dakika ve c saniye ise bu açı a° b' c'' şeklinde gösterilir.
\( 1 \text{ derece} = 60 \text{ dakika} = 3600 \text{ saniye} \)
\( 1° = 60' = 3600'' \)
\( 1 \text{ tam çember yayı} = 360° = (360 \cdot 60)' = (360 \cdot 60 \cdot 60)'' \)
\( 45,625 \) dereceyi dakika ve saniye cinsinden yazalım.
Dereceyi tam ve ondalık kısımlarına ayıralım.
\( 45,625° = 45° + 0,625° \)
İkinci terimi dakikaya çevirelim.
\( = 45° + 0,625(60') \)
\( = 45° + 37,5' \)
Dakikayı tam ve ondalık kısımlarına ayıralım.
\( = 45° + 37' + 0,5' \)
Üçüncü terimi saniyeye çevirelim.
\( = 45° + 37' + 0,5(60'') \)
\( = 45° + 37' + 30'' \)
\( 45,625° = 45°\ 37'\ 30'' \)
\( 32°\ 18'\ 45'' \) dereceyi ondalık gösterimde yazalım.
Dakika ve saniye kısımlarını dereceye çevirelim.
\( = 32 + \dfrac{18}{60} + \dfrac{45}{3600} \)
\( = 32 + 0,3 + 0,0125 \)
\( = 32,3125° \)
Bir tam çemberin 360'a bölündüğü derece sisteminin en yaygın kullanılan açı ölçü birimlerinden olmasının bir sebebi 360'ın çok bölenli bir sayı olmasıdır. 360'ın 24 pozitif böleni vardır ve 1-10 arası sayılardan 7 hariç tümü 360'ın bir bölenidir, bu da kesirli sayılara girmeden bir tam çemberin farklı şekillerde bölünebilmesine imkan sağlar.
360 dışında akla gelebilecek bir diğer seçenek olan 100'ün ise sadece 9 pozitif böleni vardır.
İki pozitif açının ölçüleri toplamı 90° ise bu açılara tümler açılar denir. İki pozitif açının ölçüleri toplamı 180° ise bu açılara bütünler açılar denir.
Radyan
Bir çemberde yarıçap (\( r \)) uzunluğundaki bir yayı gören merkez açının ölçüsüne 1 radyan denir. Dörtte bir çemberin yay uzunluğu \( \frac{\pi r}{2} \), yarım çemberin yay uzunluğu \( \pi r \), tam çemberin yay uzunluğu \( 2\pi r \) olduğu için, bu yayları gören merkez açılar sırasıyla \( \frac{\pi}{2} \), \( \pi \) ve \( 2\pi \) radyandır.
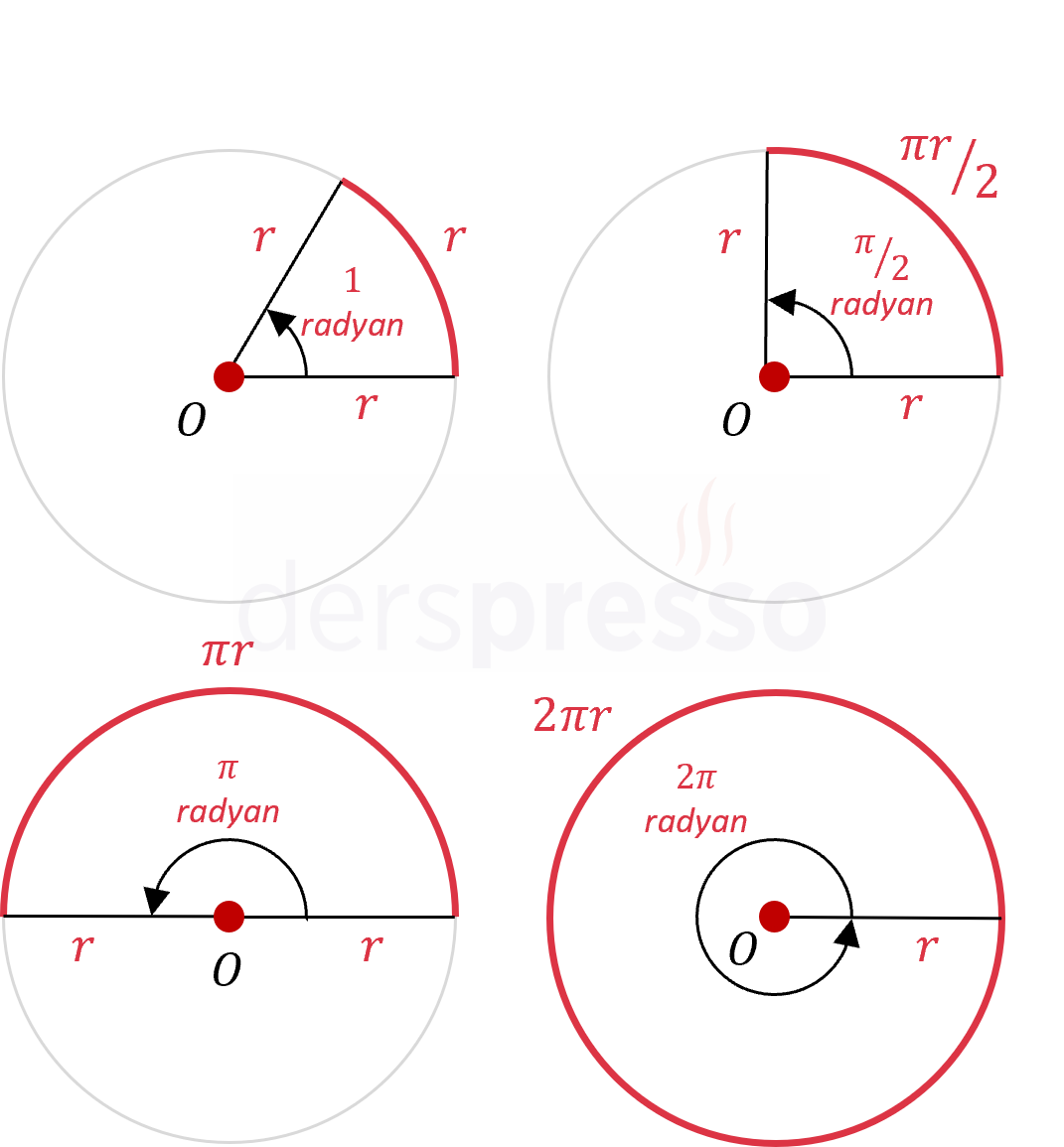
Yarıçap uzunluğunda yayı gören merkez açı \( = 1 \text{ radyan} \)
Dörtte bir çemberi gören merkez açı \( = \frac{\pi}{2} \text{ radyan} = 90° \)
Yarım çemberi gören merkez açı \( = \pi \text{ radyan} = 180° \)
Tam çemberi gören merkez açı \( = 2\pi \text{ radyan} = 360° \)
1 radyanın yaklaşık derece karşılığını bulalım.
\( 2\pi \text{ radyan} = 360° \) ise,
\( 1 \text{ radyan} = x° \)
Yukarıdaki orantıyı kullanarak \( x \) değerini bulalım.
\( x = \dfrac{360°}{2\pi} \)
\( \pi \approx 3,14 \)
\( x \approx 57,29° \)
Derece-Radyan Arası Dönüşümler
Bir tam çember yayını gören merkez açı derece cinsinden \( 360° \) ve radyan cinsinden \( 2\pi \) olduğu için, iki birim arasındaki ilişki aşağıdaki şekilde kurulabilir.
\( 360° = 2\pi \) radyan
\( 1° = \dfrac{\pi}{180} \) radyan
\( 1 \text{ radyan} = \dfrac{180°}{\pi} \)
Buna göre derece (\( D \)) cinsinden verilen bir açı ölçüsünü radyana (\( R \)) çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( R = D \cdot \dfrac{\pi}{180°} \) radyan
\( 60° = 60° \cdot \dfrac{\pi}{180°} = \dfrac{\pi}{3} \) radyan
\( 135° = 135° \cdot \dfrac{\pi}{180°} = \dfrac{3\pi}{4} \) radyan
\( 330° = 330° \cdot \dfrac{\pi}{180°} = \dfrac{11\pi}{6} \) radyan
Radyan cinsinden verilen bir açı ölçüsünü dereceye çevirmek için açı \( \frac{180°}{\pi} \) ile çarpılır. Alternatif olarak, açı ölçüsü \( \pi \) içeriyorsa \( \pi \) yerine \( 180° \) yazılarak da açı ölçüsü radyandan dereceye çevrilebilir.
\( D = R \cdot \dfrac{180°}{\pi} \)
\( \dfrac{5\pi}{6} \text{ radyan} = \dfrac{5 \cdot 180°}{6} = 150° \)
\( \dfrac{3\pi}{2} \text{ radyan} = \dfrac{3 \cdot 180°}{2} = 270° \)
\( \dfrac{5\pi}{4} \text{ radyan} = \dfrac{5 \cdot 180°}{4} = 225° \)
Esas Ölçü
Geometride açı ölçüleri 0° ile 360° aralığı ile sınırlanmıştır, ancak yönlü açılar için böyle bir sınırlama yoktur. Örneğin bir tekerleğin ya da CD'nin pek çok tur dönüşü sırasında katettiği toplam açı ölçüsü 360°'den büyük olmaktadır. Açı ölçüleri reel sayılar kümesinde herhangi bir değer alabiliyor olsa da, her açının bir tam çember üzerinde karşılık geldiği tek bir açı vardır ve işlemler çoğu zaman bu açı üzerinden yapılır.
Aşağıdaki şekildeki dereceleri 40°, 400° ve 760° olan üç açının gerçek ölçüleri farklı olsa da, 0-360° aralığında karşılık geldikleri açının ölçüsü aynıdır ve 40°'dir.
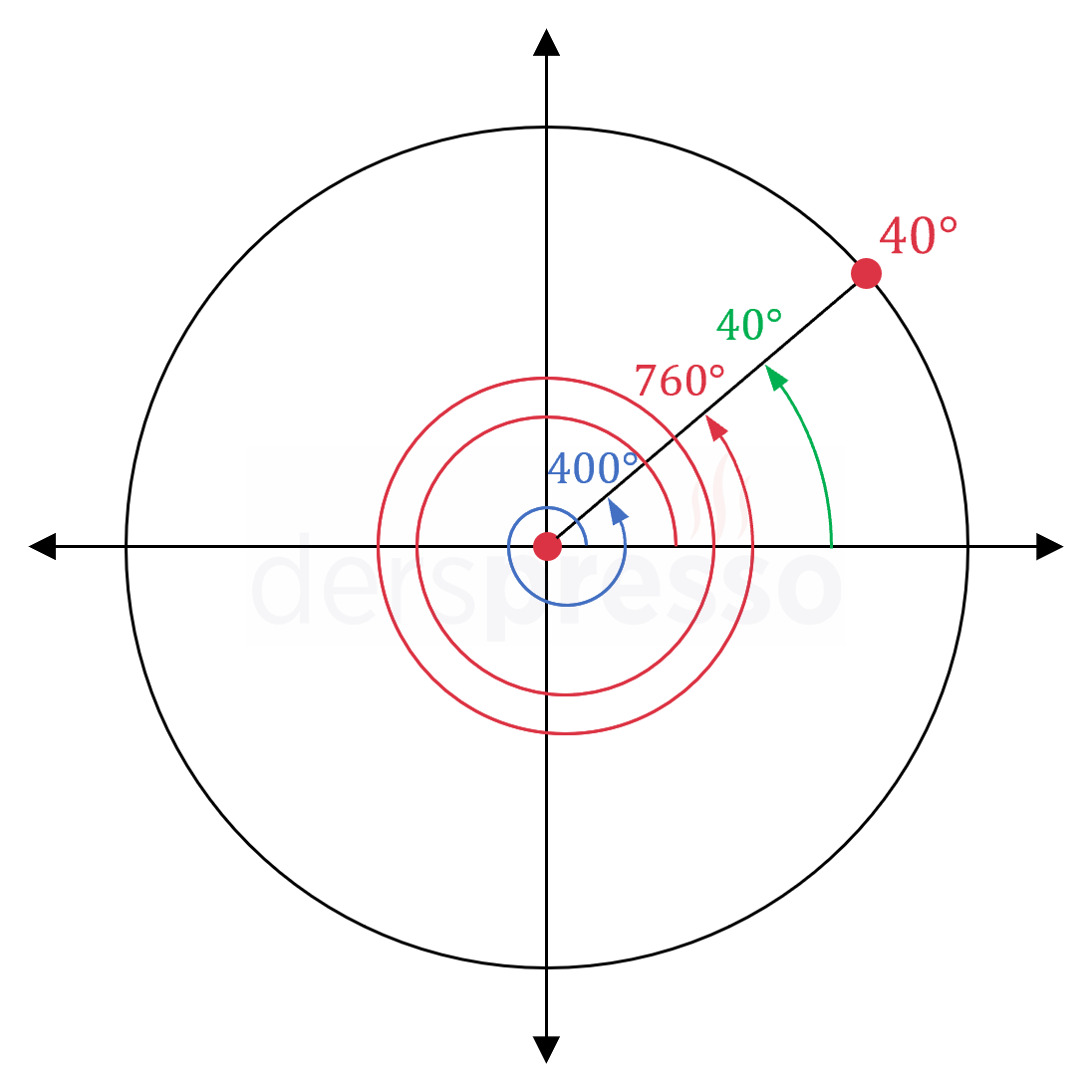
Bir açının içerdiği tam çember dönüşleri çıkarıldıktan sonra geriye kalan derece cinsinden \( [0°, 360°) \) ve radyan cinsinden \( [0, 2\pi) \) aralığındaki değere o açının esas ölçüsü denir. Bir açının gerçek ölçüsü negatif ise esas ölçü bu açıyı \( [0°, 360°) \) ya da \( [0, 2\pi) \) aralığına getirecek kadar tam çember dönüşü eklenerek elde edilir.
Derece Cinsinden Esas Ölçünün Bulunması
Bir açının derece birimindeki gerçek ve esas ölçüleri arasındaki ilişki aşağıda verilmiştir.
\( 0° \le \alpha \lt 360° \) ve \( k\in\mathbb{Z} \) olmak üzere,
\( \beta = \alpha + 360° \cdot k \) ise,
\( \alpha \) değeri \( \beta \) gerçek açı ölçüsünün derece cinsinden esas ölçüsüdür.
Aşağıda gerçek ölçüleri verilen açıların tümünün esas ölçüsü \( 220° \)'dir.
\( \ldots = -500° = -140° = \textcolor{red}{220°} = 580° = \ldots \)
\( 580° = 220° + 360° \cdot 1 \)
\( -140° = 220° + 360° \cdot (-1) \)
\( -500° = 220° + 360° \cdot (-2) \)
Ölçüsü derece biriminde verilmiş bir açının esas ölçüsünü bulmak için aşağıdaki yöntemler kullanılabilir.
Gerçek açı ölçüsü pozitif ise bu değer 360°'ye bölünür. Bölme işleminin kalanı açının esas ölçüsüdür.
\( 2000° \)'nin \( 360° \)'ye bölümünden kalan \( 200° \) olur.
\( 2000° = 200° + 360° \cdot 5 \)
Buna göre gerçek ölçüsü \( 2000° \) olan açının esas ölçüsü \( 200° \) olur.
Gerçek açı ölçüsü negatif ise bu değeri pozitif yapan 360°'nin en küçük tam sayı katı açı ölçüsüne eklenir (360°, 720°, 1080°, ... ). Bu işlemin sonucu açının esas ölçüsüdür.
\( -1000° \)'yi pozitif yapacak 360'ın en küçük katı \( 3 \cdot 360° = 1080° \)'dir.
\( -1000° + 360° \cdot 3 = 80° \)
Buna göre gerçek ölçüsü \( -1000° \) olan açının esas ölçüsü \( 80° \) olur.
Gerçek açı ölçüsünün negatif olduğu durumda kullanılabilecek bir diğer yöntemde, bu değerin mutlak değeri 360°'ye bölünür. Bölme işleminin kalanı 360°'den çıkarıldığında elde edilen değer açının esas ölçüsüdür.
\( -1000° \)'nin mutlak değeri olan \( 1000° \)'nin \( 360° \)'ye bölümünden kalan \( 280° \) olur.
\( 1000° = 280° + 360° \cdot 2 \)
Buna göre gerçek ölçüsü \( -1000° \) olan açının esas ölçüsü \( 360° - 280° = 80° \) olur.
Radyan Cinsinden Esas Ölçünün Bulunması
Bir açının radyan birimindeki gerçek ve esas ölçüleri arasındaki ilişki aşağıda verilmiştir.
\( 0 \le \alpha \lt 2\pi \) ve \( k\in\mathbb{Z} \) olmak üzere,
\( \beta = \alpha + 2\pi k \) ise,
\( \alpha \) değeri \( \beta \) gerçek açı ölçüsünün radyan cinsinden esas ölçüsüdür.
Aşağıda gerçek ölçüleri verilen açıların tümünün esas ölçüsü \( \frac{4\pi}{3} \) radyandır.
\( \ldots = -\dfrac{2\pi}{3} = \textcolor{red}{\dfrac{4\pi}{3}} = \dfrac{10\pi}{3} = \dfrac{16\pi}{3} = \ldots \)
\( \dfrac{16\pi}{3} = \dfrac{4\pi}{3} + 2\pi \cdot 2 \)
\( \dfrac{10\pi}{3} = \dfrac{4\pi}{3} + 2\pi \cdot 1 \)
\( -\dfrac{2\pi}{3} = \dfrac{4\pi}{3} + 2\pi \cdot (-1) \)
Ölçüsü radyan biriminde verilmiş bir açının esas ölçüsünü bulmak için aşağıdaki yöntemler kullanılabilir.
Gerçek açı ölçüsü pozitif ise bu değer içindeki \( 2\pi \)'nin katı olan en büyük sayı çıkarılır (\( 2\pi, 4\pi, 6\pi, \ldots \)). Bu işlemin kalanı açının esas ölçüsüdür. Eğer açı ölçüsü kesirli ise paydaki \( \pi \)'nin katsayısı paydanın 2 katına bölünerek kalan bulunur ve bu kalan paydaki katsayının yerine yazılır.
\( 23\pi \) içinde \( 2\pi \)'nin en büyük katı \( 22\pi \)'dir.
Buna göre gerçek ölçüsü \( 23\pi \) olan açının esas ölçüsü \( 23\pi - 22\pi = \pi \) olur.
\( \frac{23\pi}{3} \) ifadesinde paydaki \( \pi \)'nin katsayısı olan \( 23 \)'ün paydadaki \( 3 \)'ün iki katı olan \( 6 \)'ya bölümünden kalan \( 5 \) olur.
Buna göre gerçek ölçüsü \( \frac{23\pi}{3} \) olan açının esas ölçüsü \( \frac{5\pi}{3} \) olur.
Gerçek açı ölçüsü negatif ise bu değeri pozitif yapan \( 2\pi \)'nin en küçük tam sayı katı açı ölçüsüne eklenir (\( 2\pi, 4\pi, 6\pi, \ldots \)). Bu işlemin sonucu açının esas ölçüsüdür.
\( -\frac{7\pi}{2} \)'yi pozitif yapacak \( 2\pi \)'nin en küçük katı \( 2 \cdot 2\pi = 4\pi \)'dir.
\( -\dfrac{7\pi}{2} + 2\pi \cdot 2 = \dfrac{\pi}{2} \)
Buna göre gerçek ölçüsü \( -\frac{7\pi}{2} \) olan açının esas ölçüsü \( \frac{\pi}{2} \) olur.
Aşağıda \( a°\ b'\ c'' \) şeklinde verilen açıları saniye cinsinden gösteriniz.
(a) \( 120°\ 3'\ 59'' \)
(b) \( 42°\ 15'\ 45'' \)
(c) \( 19°\ 8'\ 14'' \)
Çözümü Göster\( 1° = 60' = 3600'' \)
(a) seçeneği:
\( 120°\ 3'\ 59'' = (120 \cdot 3600 + 3 \cdot 60 + 59)'' \)
\( = 432239'' \)
(b) seçeneği:
\( 42°\ 15'\ 45'' = (42 \cdot 3600 + 15 \cdot 60 + 45)'' \)
\( = 152145'' \)
(c) seçeneği:
\( 19°\ 8'\ 14'' = (19 \cdot 3600 + 8 \cdot 60 + 14)'' \)
\( = 68894'' \)
Aşağıda saniye cinsinden verilen açıları \( a°\ b'\ c'' \) şeklinde gösteriniz.
(a) 7446''
(b) 97677''
(c) 152316''
Çözümü Göster\( 1° = 60' = 3600'' \)
(a) seçeneği:
7446'' içinde kaç derece olduğunu bulalım.
\( 7446'' = (2 \cdot 3600 + 246)'' \)
\( = 2° + 246'' \)
246'' içinde kaç dakika olduğunu bulalım.
\( = 2° + (4 \cdot 60 + 6)'' \)
\( = 2° + 4' + 6'' \)
\( = 2°\ 4'\ 6'' \)
(b) seçeneği:
97677'' içinde kaç derece olduğunu bulalım.
\( 97677'' = (27 \cdot 3600 + 477)'' \)
\( = 27° + 477'' \)
477'' içinde kaç dakika olduğunu bulalım.
\( = 27° + (7 \cdot 60 + 57)'' \)
\( = 27° + 7' + 57'' \)
\( = 27°\ 7'\ 57'' \)
(c) seçeneği:
152316'' içinde kaç derece olduğunu bulalım.
\( 152316'' = (42 \cdot 3600 + 1116)'' \)
\( = 42° + 1116'' \)
1116'' içinde kaç dakika olduğunu bulalım.
\( = 42° + (18 \cdot 60 + 36)'' \)
\( = 42° + 18' + 36'' \)
\( = 42°\ 18'\ 36'' \)
Ölçüleri derece cinsinden verilen aşağıdaki açıların esas ölçülerini bulunuz.
(a) \( 736° \)
(b) \( 1663° \)
(c) \( 2880° \)
Çözümü GösterÖlçüsü pozitif olan açıların esas ölçüsünü bulmak için açı ölçüsü 360°'ye bölünür. Bölme işleminin kalanı açının esas ölçüsüdür.
(a) seçeneği:
\( 736° = 2 \cdot 360° + 16° \)
Buna göre 736°'nin esas ölçüsü 16° olur.
(b) seçeneği:
\( 1663° = 4 \cdot 360° + 223° \)
Buna göre 1663°'nin esas ölçüsü 223° olur.
(c) seçeneği:
\( 2880° = 8 \cdot 360° + 0° \)
Buna göre 2880°'nin esas ölçüsü 0° olur.
Ölçüleri derece cinsinden verilen aşağıdaki açıların esas ölçülerini bulunuz.
(a) \( -678° \)
(b) \( -2335° \)
(c) \( -3811° \)
Çözümü GösterÖlçüsü negatif olan açıların esas ölçüsünü bulmak için açı ölçüsünün mutlak değeri 360°'ye bölünür. Bölme işleminin kalanı 360°'den çıkarıldığında elde edilen değer açının esas ölçüsüdür.
(a) seçeneği:
\( -678° \)'nin mutlak değerinin 360°'ye bölümünden kalan 318° olur. Bu değeri 360°'den çıkardığımızda esas ölçü olarak 42° bulunur.
\( -678° = -2 \cdot 360° + 42° \)
(b) seçeneği:
\( -2335° \)'nin mutlak değerinin 360°'ye bölümünden kalan 175° olur. Bu değeri 360°'den çıkardığımızda esas ölçü olarak 185° bulunur.
\( -2335° = -7 \cdot 360° + 185° \)
(c) seçeneği:
\( -3811° \)'nin mutlak değerinin 360°'ye bölümünden kalan 211° olur. Bu değeri 360°'den çıkardığımızda esas ölçü olarak 149° bulunur.
\( -3811° = -11 \cdot 360° + 149° \)
Ölçüleri radyan cinsinden verilen aşağıdaki açıların esas ölçülerini bulunuz.
(a) \( \dfrac{13\pi}{6} \)
(b) \( \dfrac{79\pi}{12} \)
(c) \( \dfrac{104\pi}{9} \)
Çözümü GösterÖlçüsü pozitif olan açıların esas ölçüsünü bulmak için açı ölçüsü içindeki \( 2\pi \)'nin katı olan en büyük sayı çıkarılır. Eğer açı ölçüsü kesirli ise paydaki \( \pi \)'nin katsayısı paydanın 2 katına bölünerek kalan bulunur ve bu kalan paydaki katsayının yerine yazılır.
(a) seçeneği:
Paydaki katsayı olan 13'ün paydanın iki katı olan 12'ye bölümünden kalan 1 olduğu için esas ölçü \( \frac{\pi}{6} \) olur.
\( \dfrac{13\pi}{6} = 1 \cdot 2\pi + \dfrac{\pi}{6} \)
(b) seçeneği:
Paydaki katsayı olan 79'un paydanın iki katı olan 24'e bölümünden kalan 7 olduğu için esas ölçü \( \frac{7\pi}{12} \) olur.
\( \dfrac{79\pi}{12} = 3 \cdot 2\pi + \dfrac{7\pi}{12} \)
(c) seçeneği:
Paydaki katsayı olan 104'in paydanın iki katı olan 18'e bölümünden kalan 14 olduğu için esas ölçü \( \frac{14\pi}{9} \) olur.
\( \dfrac{104\pi}{9} = 5 \cdot 2\pi + \dfrac{14\pi}{9} \)
Ölçüleri derece cinsinden verilen aşağıdaki açıların esas ölçülerini bulunuz.
(a) \( -\dfrac{44\pi}{3} \)
(b) \( -\dfrac{82\pi}{15} \)
(c) \( -\dfrac{100\pi}{9} \)
Çözümü GösterÖlçüsü negatif olan açıların esas ölçüsünü bulmak için açı ölçüsünü pozitif yapan \( 2\pi \)'nin en küçük tam sayı katı açı ölçüsüne eklenir.
(a) seçeneği:
\( -\frac{44\pi}{3} \)'yi pozitif yapan \( 2\pi \)'nin en küçük tam sayı katı \( 16\pi \) olduğu için açının esas ölçüsü \( \frac{4\pi}{3} \) olur.
\( -\dfrac{44\pi}{3} = -8 \cdot 2\pi + \dfrac{4\pi}{3} \)
(b) seçeneği:
\( -\frac{82\pi}{15} \)'yi pozitif yapan \( 2\pi \)'nin en küçük tam sayı katı \( 6\pi \) olduğu için açının esas ölçüsü \( \frac{8\pi}{15} \) olur.
\( -\dfrac{82\pi}{15} = -3 \cdot 2\pi + \dfrac{8\pi}{15} \)
(c) seçeneği:
\( -\frac{100\pi}{9} \)'yi pozitif yapan \( 2\pi \)'nin en küçük tam sayı katı \( 12\pi \) olduğu için açının esas ölçüsü \( \frac{8\pi}{9} \) olur.
\( -\dfrac{100\pi}{9} = -6 \cdot 2\pi + \dfrac{8\pi}{9} \)
Aşağıda derece cinsinden verilen açıları radyan cinsinden yazınız.
(a) \( 275° \)
(b) \( 1683° \)
(c) \( -1305° \)
Çözümü GösterDerece cinsinden verilen bir açı ölçüsünü radyana çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( R = D \cdot \dfrac{\pi}{180°} \) radyan
(a) seçeneği:
\( 275° \cdot \dfrac{\pi}{180°} = \dfrac{55\pi}{36} \)
(b) seçeneği:
\( 1683° \cdot \dfrac{\pi}{180°} = \dfrac{187\pi}{20} \)
(c) seçeneği:
\( -1305° \cdot \dfrac{\pi}{180°} = -\dfrac{29\pi}{4} \)
Aşağıda radyan cinsinden verilen açıları derece cinsinden yazınız.
(a) \( \dfrac{101\pi}{60} \)
(b) \( \dfrac{35\pi}{12} \)
(c) \( -\dfrac{37\pi}{9} \)
Çözümü GösterRadyan cinsinden verilen bir açı ölçüsünü dereceye çevirmek için açı \( \frac{180°}{\pi} \) ile çarpılır. Alternatif olarak, açı ölçüsü \( \pi \) içeriyorsa \( \pi \) yerine \( 180° \) yazılarak açı ölçüsü radyandan dereceye çevrilebilir.
\( D = R \cdot \dfrac{180°}{\pi} \)
(a) seçeneği:
\( \dfrac{101\pi}{60} = \dfrac{101 \cdot 180°}{60} \)
\( = 101 \cdot 3° = 303° \)
(b) seçeneği:
\( \dfrac{35\pi}{12} = \dfrac{35 \cdot 180°}{12} \)
\( = 35 \cdot 15° = 525° \)
(c) seçeneği:
\( -\dfrac{37\pi}{9} = -\dfrac{37 \cdot 180°}{9} \)
\( = -37 \cdot 20° = -740° \)
Ölçüsü \( 100°\ 18'\ 40'' \) olan açı, ölçüsü \( 57°\ 43'\ 45'' \) olan açıdan ne kadar büyüktür?
Çözümü GösterÇıkarma işlemini saniyeden dakika ve derece değerlerine doğru yapalım.
\( 100°\ 18'\ 40'' \)
\( 57°\ 43'\ 45'' \)
40 saniyeden 45 saniye çıkmayacağı için 18 dakikadan 1 dakikayı saniyeye aktaralım.
\( 100°\ 17'\ 100'' \)
\( 57°\ 43'\ 45'' \)
17 dakikadan 43 dakika çıkmayacağı için 100 dereceden bir dereceyi dakikaya aktaralım.
\( 99°\ 77'\ 100'' \)
\( 57°\ 43'\ 45'' \)
Bu ifadeleri alt alta çıkardığımızda aşağıdaki sonuç bulunur.
\( 42°\ 34'\ 55'' \)
\( 152°\ 9'\ 54'' \) açısının altıda biri kaçtır?
Çözümü GösterVerilen açıyı derece, dakika ve saniye kısımları 6'ya bölünecek şekilde düzenleyelim.
Derece kısmını 6'ya bölünebilir yapmak için 2 dereceyi dakikaya çevirelim.
\( 152°\ 9'\ 54'' = 150°\ (2 \cdot 60 + 9)'\ 54'' \)
\( = 150°\ 129'\ 54'' \)
Dakika kısmını 6'ya bölünebilir yapmak için 3 dakikayı saniyeye çevirelim.
\( = 150°\ 126'\ (3 \cdot 60 + 54)'' \)
\( = 150°\ 126'\ 234'' \)
Bulduğumuz ifadedeki derece, dakika ve saniye kısımlarını ayrı ayrı 6'ya bölelim.
\( \dfrac{150°\ 126'\ 234''}{6} = 25°\ 21'\ 39'' \) bulunur.
\( x, y, z \in \mathbb{N} \) olmak üzere,
\( (471,42)° = x°\ y'\ z'' \) olduğuna göre, \( x + y + z \) toplamının en küçük değeri kaçtır?
Çözümü Göster\( x + y + z \) toplamının en küçük olması için \( y \) ve \( z \) değerlerini \( [0, 60) \) aralığında seçmeliyiz.
\( (471,42)° = x°\ y'\ z'' \)
\( 471° + (0,42)° = x° + y'\ z'' \)
Buradan \( x = 471 \) olarak bulunur.
\( (0,42)° = y'\ z'' \)
\( (0,42 \cdot 60)' = y\ 'z'' \)
\( (25,2)' = y'\ z'' \)
\( 25' + (0,2)' = y' + z'' \)
Buradan \( y = 25 \) olarak bulunur.
\( (0,2)' = z'' \)
\( (0,2 \cdot 60)'' = z'' \)
\( 12'' = z'' \)
Buradan \( z = 12 \) olarak bulunur.
\( (471,42)° = 471°\ 25'\ 12'' \)
\( x + y + z = 471 + 25 + 12 \)
\( = 508 \) bulunur.
Ali dairesel bir pistin bir turunu 10 dakikada koşmaktadır. Koşmaya başladıktan 61 dakika sonra mola veren Ali'nin koştuğu toplam açının esas ölçüsü kaç derecedir?
Çözümü GösterAli 10 dakikada 360° koşuyor.
Ali'nin 61 dakikada koştuğu açıya \( x° \) diyelim.
\( x = \dfrac{360 \cdot 61}{10} = 36 \cdot 61 \) derece
Ali'nin koştuğu bu açının esas ölçüsü, toplam açı ölçüsünün 360'a bölümünden kalandır.
\( 36 \cdot 61 = 36 \cdot 60 + 36 \)
Buna göre \( x = 36 \cdot 61 \) derecenin 360'a bölümünden kalan 36'dır, dolayısıyla açının esas ölçüsü 36° olur.
Bir diğer ifadeyle, Ali dairesel pist etrafında 6 tam tur tamamladıktan sonra 36° daha koşmuştur.
\( ABC \) üçgeninde \( A \) köşesinin dış açı ölçüsü \( 140° \), \( B \) köşesinin dış açı ölçüsü \( \frac{7\pi}{18} \) radyandır.
Buna göre \( C \) köşesinin iç açı ölçüsü kaç radyandır?
Çözümü Göster\( C \) köşesinin dış açı ölçüsüne \( x \) derece diyelim.
\( B \) köşesinin dış açı ölçüsünü dereceye çevirelim.
\( \dfrac{7\pi}{18} \text{ radyan } = \dfrac{7 \cdot 180°}{18} = 70° \)
Üçgenin dış açıları toplamı 360°'dir.
\( 140° + 70° + x = 360° \)
\( x = 150° \)
\( C \) köşesinin dış açı ölçüsü \( 150° \) olduğuna göre, iç açı ölçüsü \( 180 - 150 = 30° \) olur.
Derece cinsinden verilen bir açı ölçüsünü radyana çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( 30° \cdot \dfrac{\pi}{180°} = \dfrac{\pi}{6} \) radyan bulunur.
\( (456°, 3000°) \) aralığında olan ve esas ölçüsü 135° olan kaç tane açı vardır?
Çözümü Gösterİstenen koşulu sağlayan açıya \( x \) diyelim.
Buna göre \( x \) açısı aşağıdaki şekilde yazılabilir.
\( k \in \mathbb{Z} \) olmak üzere,
\( x = 135 + 360k \)
\( 456 \lt 135 + 360k \lt 3000 \)
\( 321 \lt 360k \lt 2865 \)
\( \dfrac{321}{360} \lt k \lt \dfrac{2865}{360} \)
\( 0,8\ldots \lt k \lt 7,9\ldots \)
\( k \in \{ 1, 2, 3, 4, 5, 6, 7 \} \)
İstenen koşulu sağlayan 7 tane açı vardır.
\( [133°, 3945°] \) aralığında olan ve esas ölçüsü 27° olan açılardan en büyük üçünün toplamı kaçtır?
Çözümü Gösterİstenen koşulu sağlayan açıya \( x \) diyelim.
Buna göre \( x \) açısı aşağıdaki şekilde yazılabilir.
\( k \in \mathbb{Z} \) olmak üzere,
\( x = 27 + 360k \)
\( 133 \le 27 + 360k \le 3945 \)
\( 106 \le 360k \le 3918 \)
\( \dfrac{106}{360} \le k \le \dfrac{3918}{360} \)
\( 0,2\ldots \le k \le 10,8\ldots \)
\( k \in \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \} \)
Bu açılardan en büyük üçü \( k \in \{ 8, 9, 10 \} \) için oluşur.
\( k = 8 \) için:
\( x = 27 + 360(8) = 2907° \)
\( k = 9 \) için:
\( x = 27 + 360(9) = 3267° \)
\( k = 10 \) için:
\( x = 27 + 360(10) = 3627° \)
İstenen koşulları sağlayan en büyük üç açının toplamını bulalım.
\( 2907° + 3267° + 3627° = 9801° \)
\( n \) kenarlı bir konveks çokgenin iki dış açı ölçüsü \( 25°\ 09'\ 39'' \) ve \( 14°\ 50'\ 21'' \) olarak veriliyor.
Geri kalan tüm dış açılar birbirine eşit ve 20° olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( 25°\ 09'\ 39'' \)
\( 14°\ 50'\ 21'' \)
Verilen bu iki dış açının ölçülerini toplayalım.
\( 40°\ 0'\ 0''\)
Konveks bir çokgenin dış açılarının ölçüleri toplamı 360°'dir.
Buna göre çokgenin iki dış açısının toplamı 40°, diğer \( n - 2 \) dış açısının her biri 20°'dir.
\( 40 + (n - 2) \cdot 20 = 360 \)
\( 40 + 20n - 40 = 360 \)
\( n = 18 \) bulunur.
Bir su sayacının göstergesi sabit bir hızla hareket ederek saniyede 19 derecelik bir yayı tarıyor. Buna göre bu gösterge bir saatte kaç tur atar?
Çözümü GösterGösterge sabit hızla hareket ettiği için taradığı yay zamanla doğru orantılıdır.
Bir saat \( 60 \cdot 60 = 3600 \) saniyedir.
Gösterge 1 saniyede 19 derece tarıyorsa 3600 saniyede \( x \) derece tarar.
\( \dfrac{19}{1} = \dfrac{x}{3600} \)
\( x = 19 \cdot 3600 \) derece
1 tur 360 derecelik yaya karşılık gelir.
Göstergenin attığı tur sayısına \( t \) diyelim.
\( t = \dfrac{19 \cdot 3600}{360} \)
\( = 190 \) tur atar.