Temel Trigonometrik Özdeşlikler
Trigonometride kullanılan temel özdeşlikler aşağıdaki gibidir. Bu özdeşlikler dışındaki indirgeme, toplam, fark, iki kat açı ve dönüşüm formüllerini ileriki bölümlerde inceleyeceğiz.

Pisagor Özdeşlikleri
Bir açının sinüs ve kosinüs değerlerinin kareleri toplamı 1'e eşittir. Bu özdeşlik sadece dar değil, tüm açılar için geçerlidir.
\( \sin^2{x} + \cos^2{x} = 1 \)

\( \sin^2{x} + \cos^2{x} = \left( \dfrac{2}{4} \right)^2 + \left( \dfrac{2\sqrt{3}}{4} \right)^2 \)
\( = \dfrac{4}{16} + \dfrac{12}{16} = 1 \)
İSPATI GÖSTER
Sinüs ve kosinüs fonksiyonlarını bir dik üçgenin kenarlarının oranı şeklinde yazalım.
\( \sin{x} = \dfrac{b}{a} \)
\( \cos{x} = \dfrac{c}{a} \)
\( \sin^2{x} + \cos^2{x} = {\left( \dfrac{b}{a} \right)}^2 + {\left( \dfrac{c}{a} \right)}^2 = \dfrac{b^2 + c^2}{a^2} \)
Pisagor teoremine göre, paydaki ifade \( a^2 \)'ye eşittir.
\( b^2 + c^2 = a^2 \)
\( \sin^2{x} + \cos^2{x} = \dfrac{a^2}{a^2} = 1 \)
İlgili fonksiyonların tanımlı olduğu açılar için aşağıdaki iki özdeşlik yukarıdaki Pisagor özdeşliğinden kolaylıkla türetilebilir.
\( \tan^2{x} + 1 = \sec^2{x} \)
\( 1 + \cot^2{x} = \csc^2{x} \)
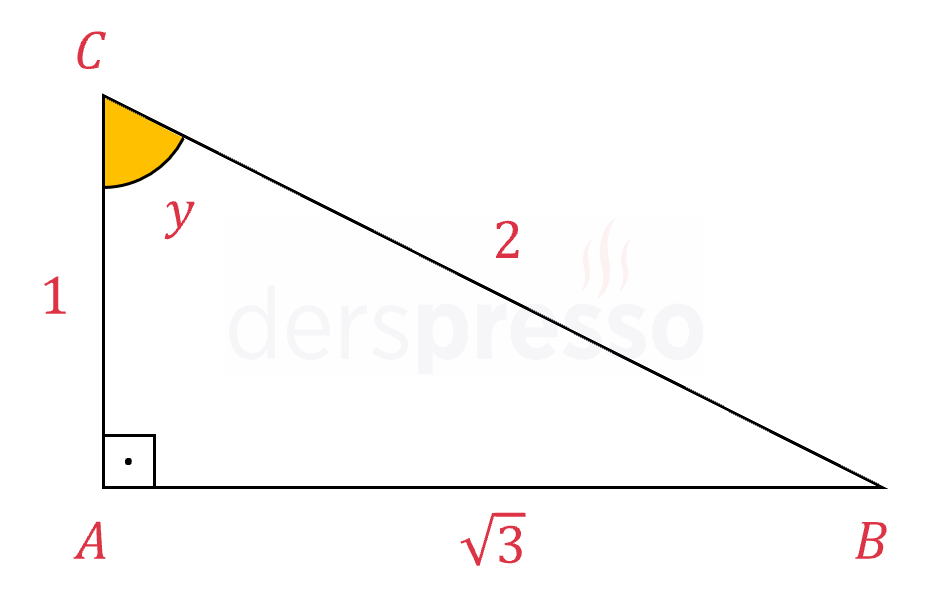
\( \tan^2{y} + 1 = \left( \dfrac{\sqrt{3}}{1} \right)^2 + 1 = 4 \)
\( \sec^2{y} = \left( \dfrac{2}{1} \right)^2 = 4 \)
\( 1 + \cot^2{y} = 1 + \left( \dfrac{1}{\sqrt{3}} \right)^2 = \dfrac{4}{3} \)
\( \csc^2{y} = \left( \dfrac{2}{\sqrt{3}} \right)^2 = \dfrac{4}{3} \)
İSPATI GÖSTER
Özdeşlik 1: \( \tan^2{x} + 1 = \sec^2{x} \)
\( \sin^2{x} + \cos^2{x} = 1 \)
Yukarıdaki Pisagor özdeşliğinin iki tarafını \( \cos^2{x} \) ifadesine bölelim.
\( \dfrac{\sin^2{x}}{\cos^2{x}} + \dfrac{\cos^2{x}}{\cos^2{x}} = \dfrac{1}{\cos^2{x}} \)
Sinüs fonksiyonunun kosinüs fonksiyonuna oranı tanjant fonksiyonunu verir. Kosinüs fonksiyonunun çarpmaya göre tersi sekant fonksiyonudur.
\( \tan^2{x} + 1 = \sec^2{x} \)
Özdeşlik 2: \( 1 + \cot^2{x} = \csc^2{x} \)
\( \sin^2{x} + \cos^2{x} = 1 \)
Yukarıdaki Pisagor özdeşliğinin iki tarafını \( \sin^2{x} \) ifadesine bölelim.
\( \dfrac{\sin^2{x}}{\sin^2{x}} + \dfrac{\cos^2{x}}{\sin^2{x}} = \dfrac{1}{\sin^2{x}} \)
Kosinüs fonksiyonunun sinüs fonksiyonuna oranı kotanjant fonksiyonunu verir. Sinüs fonksiyonunun çarpmaya göre tersi kosekant fonksiyonudur.
\( 1 + \cot^2{x} = \csc^2{x} \)
Bölüm Özdeşlikleri
Trigonometrik fonksiyonların tanımında gördüğümüz üzere, tanjant ve kotanjant fonksiyonları sinüs ve kosinüs fonksiyonları cinsinden aşağıdaki şekilde ifade edilebilir.
\( \tan{x} = \dfrac{\sin{x}}{\cos{x}} \)
\( \cot{x} = \dfrac{\cos{x}}{\sin{x}} \)
Çarpmaya Göre Ters Özdeşlikleri
Sinüs, kosinüs ve tanjant fonksiyonlarının çarpmaya göre tersleri sırasıyla kosekant, sekant ve kotanjant fonksiyonlarıdır.
\( x \) ilgili fonksiyonların tanımlı olduğu bir açı ölçüsü olmak üzere,
\( \sin{x} = \dfrac{1}{\csc{x}} \Longleftrightarrow \sin{x}\csc{x} = 1 \)
\( \cos{x} = \dfrac{1}{\sec{x}} \Longleftrightarrow \cos{x}\sec{x} = 1 \)
\( \tan{x} = \dfrac{1}{\cot{x}} \Longleftrightarrow \tan{x}\cot{x} = 1 \)

\( \sin{x}\csc{x} = \dfrac{2}{4} \cdot \dfrac{4}{2} = 1 \)
\( \cos{x}\sec{x} = \dfrac{2\sqrt{3}}{4} \cdot \dfrac{4}{2\sqrt{3}} = 1 \)
\( \tan{x}\cot{x} = \dfrac{2}{2\sqrt{3}} \cdot \dfrac{2\sqrt{3}}{2} = 1 \)
Negatif Açı Özdeşlikleri
Sinüs, tanjant, kotanjant ve kosekant fonksiyonları için bir açının negatifinin fonksiyon değeri açının kendisinin fonksiyon değerinin negatifine eşittir. Buna göre bu dört fonksiyon tek fonksiyondur.
\( \sin(-x) = -\sin{x} \)
\( \tan(-x) = -\tan{x} \)
\( \cot(-x) = -\cot{x} \)
\( \csc(-x) = -\csc{x} \)
Kosinüs ve sekant fonksiyonları için ise bir açının negatifinin fonksiyon değeri açının kendisinin fonksiyon değerine eşittir. Buna göre bu iki fonksiyon çift fonksiyondur.
\( \cos(-x) = \cos{x} \)
\( \sec(-x) = \sec{x} \)
Tümler Açı Özdeşlikleri
Birbirini \( 90° \)'ye tamamlayan açılar için sinüs-kosinüs, tanjant-kotanjant ve sekant-kosekant fonksiyonlarının değerleri birbirine eşittir. Bu özdeşlikler sadece dar açılar değil, tüm açılar için geçerlidir.
\( \sin{x} = \cos(\frac{\pi}{2} - x) \)
\( \cos{x} = \sin(\frac{\pi}{2} - x) \)
\( \tan{x} = \cot(\frac{\pi}{2} - x) \)
\( \cot{x} = \tan(\frac{\pi}{2} - x) \)
\( \sec{x} = \csc(\frac{\pi}{2} - x) \)
\( \csc{x} = \sec(\frac{\pi}{2} - x) \)

\( \sin{x} = \dfrac{3}{5} = \cos{y} \)
\( \tan{x} = \dfrac{3}{4} = \cot{y} \)
\( \sec{x} = \dfrac{5}{4} = \csc{y} \)
İSPATI GÖSTER

Yukarıdaki üçgende \( \hat{B} \) ve \( \hat{C} \) açıları tümler açılardır.
\( m(\hat{B}) + m(\hat{C}) = \dfrac{\pi}{2} \)
\( m(\hat{C}) = \dfrac{\pi}{2} - x \)
Üçgenin kenar uzunlukları arasındaki tüm oranları ve hem \( \hat{B} \) hem de \( \hat{C} \) açıları için her bir orana karşılık gelen trigonometrik fonksiyonları yazalım.
\( \dfrac{b}{a} = \sin{x} = \cos(\frac{\pi}{2} - x) \)
\( \dfrac{c}{a} = \cos{x} = \sin(\frac{\pi}{2} - x) \)
\( \dfrac{b}{c} = \tan{x} = \cot(\frac{\pi}{2} - x) \)
\( \dfrac{c}{b} = \cot{x} = \tan(\frac{\pi}{2} - x) \)
\( \dfrac{a}{c} = \sec{x} = \csc(\frac{\pi}{2} - x) \)
\( \dfrac{a}{b} = \csc{x} = \sec(\frac{\pi}{2} - x) \)
Bu şekilde altı özdeşliği de elde etmiş olduk.
Bu özdeşlikler tanjant, kotanjant, sekant ve kosekant fonksiyonlarını tanımsız yapan (tanım kümesi dışındaki) \( x \) değerleri için sağlanmaz.
Verilen bir trigonometrik özdeşliği ispatlamamız ya da bir trigonometrik ifadeyi en sade haline getirmemiz istendiğinde uygulanabilecek bazı adımlar aşağıdaki gibidir.
- Tanjant, kotanjant, sekant ve kosekant fonksiyonları sinüs ve kosinüs fonksiyonları cinsinden yazılır.
- Çarpanlara ayırma yöntemleri ile ifadeler çarpanlarına ayrılır.
- Pisagor özdeşlikleri ile ifadeler sadeleştirilir.
- Bu düzenlemeler sonrasında pay ve paydada oluşan ortak çarpanlar sadeleştirilir.
\( \dfrac{\tan{x}\sec{x}}{1 + \tan^2{x}} = \sin{x} \) olduğunu gösterelim.
Eşitliğin sol tarafındaki tanjant ve sekant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\tan{x}\sec{x}}{1 + \tan^2{x}} = \dfrac{\frac{\sin{x}}{\cos{x}}\frac{1}{\cos{x}}}{1 + \frac{\sin^2{x}}{\cos^2{x}}} \)
\( = \dfrac{\frac{\sin{x}}{\cos^2{x}}}{\frac{\cos^2{x} + \sin^2{x}}{\cos^2{x}}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{\frac{\sin{x}}{\cos^2{x}}}{\frac{1}{\cos^2{x}}} \)
Paydalardaki ortak ifadeleri sadeleştirdiğimizde eşitliğin sağ tarafını elde ederiz.
\( = \dfrac{\sin{x}}{1} = \sin{x} \)
\( \cos{x}\sin{x}(\cot{x} + \tan{x}) = 1 \) olduğunu gösterelim.
Eşitliğin sol tarafındaki tanjant ve kotanjant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \cos{x}\sin{x}(\cot{x} + \tan{x}) = \cos{x}\sin{x}\left( \dfrac{\cos{x}}{\sin{x}} + \dfrac{\sin{x}}{\cos{x}} \right) \)
Parantezi genişletelim.
\( = \cos{x}\sin{x}\dfrac{\cos{x}}{\sin{x}} + \cos{x}\sin{x}\dfrac{\sin{x}}{\cos{x}} \)
Pay ve paydadaki ortak çarpanları sadeleştirelim.
\( = \cos^2{x} + \sin^2{x} \)
Pisagor özdeşliğini kullanalım.
\( = 1 \)
\( \dfrac{\sin{40°}\tan{27°}}{\cos{50°}\cot{63°}} \) ifadesinin eşiti kaçtır?
Çözümü GösterTümler açıların sinüs ve kosinüs değerleri birbirine eşittir. Aynı şekilde tümler açıların tanjant ve kotanjant değerleri birbirine eşittir.
\( \sin{40°} = \cos{50°} \)
\( \tan{27°} = \cot{63°} \)
\( \dfrac{\sin{40°}\tan{27°}}{\cos{50°}\cot{63°}} \)
\( = \dfrac{\sin{40°}\tan{27°}}{\sin{40°}\tan{27°}} \)
\( = 1 \) bulunur.
\( \sin^4{x} + \cos^2{x}\sin^2{x} - \sin^2{x} \) ifadesinin en sade halini bulunuz.
Çözümü Göster\( \sin^4{x} + \cos^2{x}\sin^2{x} - \sin^2{x} \)
İfadeyi \( \sin^2{x} \) parantezine alalım.
\( = \sin^2{x}(\sin^2{x} + \cos^2{x} - 1) \)
Pisagor özdeşliğini kullanalım.
\( = \sin^2{x}(1 - 1) \)
\( = 0 \) bulunur.
\( (3\cos{x} + \sin{x})^2 + (\cos{x} - 3\sin{x})^2 \) ifadesinin en sade halini bulunuz.
Çözümü GösterParantez karesi ifadelerinin açılımını yazalım.
\( 9\cos^2{x} + 6\cos{x}\sin{x} + \sin^2{x} + \cos^2{x} - 6\cos{x}\sin{x} + 9\sin^2{x} \)
\( = 10\sin^2{x} + 10\cos^2{x} \)
\( = 10(\sin^2{x} + \cos^2{x}) \)
Pisagor özdeşliğini kullanalım.
\( = 10 \) bulunur.
\( \sec^3{x}\cos^6{x} + \cot{x}\csc{x}\sin^4{x} \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1}{\cos^3{x}} \cdot \cos^6{x} + \dfrac{\cos{x}}{\sin{x}} \cdot \dfrac{1}{\sin{x}} \cdot \sin^4{x} \)
\( = \cos^3{x} + \cos{x}\sin^2{x} \)
İfadeyi kosinüs parantezine alalım.
\( = \cos{x}(\cos^2{x} + \sin^2{x}) \)
Pisagor özdeşliğini kullanalım.
\( = \cos{x} \) bulunur.
\( \dfrac{\cot^2{x}}{1 + \cot^2{x}} \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\cot^2{x}}{1 + \cot^2{x}} = \dfrac{\frac{\cos^2{x}}{\sin^2{x}}}{1 + \frac{\cos^2{x}}{\sin^2{x}}} \)
\( = \dfrac{\frac{\cos^2{x}}{\sin^2{x}}}{\frac{\sin^2{x} + \cos^2{x}}{\sin^2{x}}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{\frac{\cos^2{x}}{\sin^2{x}}}{\frac{1}{\sin^2{x}}} \)
\( = \cos^2{x} \) bulunur.
\( \dfrac{1 + \sec{x}}{\sin{x} + \tan{x}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterSekant ve tanjant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1 + \sec{x}}{\sin{x} + \tan{x}} = \dfrac{1 + \frac{1}{\cos{x}}}{\sin{x} + \frac{\sin{x}}{\cos{x}}} \)
\( = \dfrac{\frac{\cos{x} + 1}{\cos{x}}}{\frac{\sin{x}\cos{x} + \sin{x}}{\cos{x}}} \)
\( = \dfrac{\cos{x} + 1}{\sin{x}\cos{x} + \sin{x}} \)
\( = \dfrac{\cos{x} + 1}{\sin{x}(\cos{x} + 1)} \)
\( = \dfrac{1}{\sin{x}} \)
\( = \csc{x} \) bulunur.
\( \dfrac{\sec{x} - \cos{x}}{\sin^2{x}\tan{x}} \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\sec{x} - \cos{x}}{\sin^2{x}\tan{x}} = \dfrac{\frac{1}{\cos{x}} - \cos{x}}{\sin^2{x} \cdot \frac{\sin{x}}{\cos{x}}} \)
\( = \dfrac{\frac{1 - \cos^2{x}}{\cos{x}}}{\frac{\sin^3{x}}{\cos{x}}} \)
\( = \dfrac{1 - \cos^2{x}}{\sin^3{x}} \)
\( = \dfrac{\sin^2{x}}{\sin^3{x}} \)
\( = \dfrac{1}{\sin{x}} = \csc{x} \) bulunur.
\( \sin{x} + \cos{x}\cot{x} \) ifadesinin en sade halini bulunuz.
Çözümü GösterKotanjant ifadesini sinüs ve kosinüs cinsinden yazalım.
\( \sin{x} + \cos{x} \cdot \dfrac{\cos{x}}{\sin{x}} \)
Terimlerin paydalarını eşitleyelim.
\( = \dfrac{\sin^2{x}}{\sin{x}} + \dfrac{\cos^2{x}}{\sin{x}} \)
\( = \dfrac{\sin^2{x} + \cos^2{x}}{\sin{x}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{1}{\sin{x}} = \csc{x} \) bulunur.
\( \csc^2{x}(\tan^2{x} - \sin^2{x}) \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1}{\sin^2{x}}\left( \dfrac{\sin^2{x}}{\cos^2{x}} - \sin^2{x} \right) \)
Parantez içerisinde paydaları eşitleyelim.
\( = \dfrac{1}{\sin^2{x}}\left( \dfrac{\sin^2{x}}{\cos^2{x}} - \dfrac{\cos^2{x}\sin^2{x}}{\cos^2{x}} \right) \)
\( = \dfrac{1}{\sin^2{x}} \cdot \dfrac{\sin^2{x}(1 - \cos^2{x})}{\cos^2{x}} \)
\( = \dfrac{1 - \cos^2{x}}{\cos^2{x}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{\sin^2{x}}{\cos^2{x}} \)
\( = \tan^2{x} \) bulunur.
\( \dfrac{\sin^2{x}}{1 + \cos{x}} \) ifadesinin en sade halini bulunuz.
Çözümü Göster\( \sin^2{x} + \cos^2{x} = 1 \)
\( \sin^2{x} = 1 - \cos^2{x} \)
Bu ifadeyi paydaki ifadenin yerine koyalım.
\( \dfrac{\sin^2{x}}{1 + \cos{x}} = \dfrac{1 - \cos^2{x}}{1 + \cos{x}} \)
Kare farkı özdeşliğini kullanalım.
\( = \dfrac{(1 - \cos{x})(1 + \cos{x})}{(1 + \cos{x})} \)
\( = 1 - \cos{x} \) bulunur.
\( \dfrac{\sin^3{x} - \cos^3{x}}{1 + \sin{x}\cos{x}} \)
ifadesinin en sade halini bulunuz.
Çözümü GösterPayda küp farkı özdeşliğini kullanalım.
\( a^3 - b^3 = (a - b)(a^2 + ab + b^2) \)
\( \dfrac{(\sin{x} - \cos{x})(\sin^2{x} + \sin{x}\cos{x} + \cos^2{x})}{1 + \sin{x}\cos{x}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{(\sin{x} - \cos{x})(1 + \sin{x}\cos{x})}{1 + \sin{x}\cos{x}} \)
\( = \sin{x} - \cos{x} \) bulunur.
\( \tan{x} - \cot{x} = \dfrac{3}{4} \) olduğuna göre,
\( \tan^2{x} + \cot^2{x} \) kaçtır?
Çözümü GösterEşitliğin taraflarının karesini alalım.
\( (\tan{x} - \cot{x})^2 = \left( \dfrac{3}{4} \right)^2 \)
\( = \tan{x}^2 - 2\tan{x}\cot{x} + \cot^2{x} = \dfrac{9}{16} \)
Bir açının tanjantı ile kotanjantının çarpımı 1'dir.
\( \tan^2{x} - 2 + \cot^2{x} = \dfrac{9}{16} \)
\( \tan^2{x} + \cot^2{x} = \dfrac{41}{16} \) bulunur.
\( \dfrac{\tan{x}}{\sec{x} - 1} - \dfrac{\sec{x} - 1}{\tan{x}} \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1}{\cos{x}} - 1} - \dfrac{\frac{1}{\cos{x}} - 1}{\frac{\sin{x}}{\cos{x}}} \)
\( = \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1 - \cos{x}}{\cos{x}}} - \dfrac{\frac{1 - \cos{x}}{\cos{x}}}{\frac{\sin{x}}{\cos{x}}} \)
\( = \dfrac{\sin{x}}{1 - \cos{x}} - \dfrac{1 - \cos{x}}{\sin{x}} \)
Terimlerin paydalarını eşitleyelim.
\( = \dfrac{\sin^2{x}}{(1 - \cos{x})\sin{x}} - \dfrac{(1 - \cos{x})^2}{\sin{x}(1 - \cos{x})} \)
\( = \dfrac{\sin^2{x} - 1 + 2\cos{x} - \cos^2{x}}{(1 - \cos{x})\sin{x}} \)
\( \sin^2{x} = 1 - \cos^2{x} \) yazalım.
\( = \dfrac{1 - \cos^2{x} - 1 + 2\cos{x} - \cos^2{x}}{(1 - \cos{x})\sin{x}} \)
\( = \dfrac{2\cos{x} - 2\cos^2{x}}{(1 - \cos{x})\sin{x}} \)
\( = \dfrac{2\cos{x}(1 - \cos{x})}{(1 - \cos{x})\sin{x}} \)
\( = \dfrac{2\cos{x}}{\sin{x}} \)
\( = 2\cot{x} \) bulunur.
\( \dfrac{\sec{x}}{1 + \sec{x}} - \dfrac{\sec{x}}{1 - \sec{x}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterSekant ifadelerini kosinüs cinsinden yazalım.
\( \dfrac{\frac{1}{\cos{x}}}{1 + \frac{1}{\cos{x}}} - \dfrac{\frac{1}{\cos{x}}}{1 - \frac{1}{\cos{x}}} \)
\( = \dfrac{\frac{1}{\cos{x}}}{\frac{\cos{x} + 1}{\cos{x}}} - \dfrac{\frac{1}{\cos{x}}}{\frac{\cos{x} - 1}{\cos{x}}} \)
Pay ve paydaların paydalarındaki kosinüs ifadeleri sadeleşir.
\( = \dfrac{1}{\cos{x} + 1} - \dfrac{1}{\cos{x} - 1} \)
Kesirlerin paydalarını eşitleyelim.
\( = \dfrac{\cos{x} - 1}{(\cos{x} + 1)(\cos{x} - 1)} - \dfrac{\cos{x} + 1}{(\cos{x} + 1)(\cos{x} - 1)} \)
\( = \dfrac{\cos{x} - 1 - \cos{x} - 1}{\cos^2{x} - 1} \)
Paydada Pisagor özdeşliğini kullanalım.
\( = \dfrac{-2}{-\sin^2{x}} \)
\( = \dfrac{2}{\sin^2{x}} = 2\csc^2{x} \) bulunur.
\( a = \csc^2{x} - \dfrac{1}{\tan^2{x}} \)
\( b = 3\tan^2{x} - \dfrac{3}{\cos^2{x}} \)
olduğuna göre, \( ab \) çarpımının değeri kaçtır?
Çözümü Gösterİfadelerdeki terimleri sinüs ve kosinüs cinsinden yazalım ve paydaları eşitleyelim.
\( a = \dfrac{1}{\sin^2{x}} - \dfrac{1}{\frac{\sin^2{x}}{\cos^2{x}}} \)
\( = \dfrac{1}{\sin^2{x}} - \dfrac{\cos^2{x}}{\sin^2{x}} \)
\( = \dfrac{1 - \cos^2{x}}{\sin^2{x}} \)
\( = \dfrac{\sin^2{x}}{\sin^2{x}} = 1 \)
\( b = \dfrac{3\sin^2{x}}{\cos^2{x}} - \dfrac{3}{\cos^2{x}} \)
\( = \dfrac{3(\sin^2{x} - 1)}{\cos^2x} \)
\( = \dfrac{3(-\cos^2{x})}{\cos^2{x}} = -3 \)
\( ab = 1 \cdot (-3) = -3 \) bulunur.
\( 0 \lt x \lt \dfrac{\pi}{2} \) olmak üzere,
\( 5\sin^2{x} + 2\cos^2{x} = \dfrac{11}{3} \) olduğuna göre,
\( \cot{x} + \tan{x} \) toplamı kaçtır?
Çözümü Gösterİfadede tek bir trigonometrik fonksiyon bırakmaya çalışalım.
\( 3\sin^2{x} + 2\sin^2{x} + 2\cos^2{x} = \dfrac{11}{3} \)
\( 3\sin^2{x} + 2(\sin^2{x} + \cos^2{x}) = \dfrac{11}{3} \)
Pisagor özdeşliğini kullanalım.
\( 3\sin^2{x} + 2 = \dfrac{11}{3} \)
\( \sin^2{x} = \dfrac{5}{9} \)
\( \sin{x} = \dfrac{\sqrt{5}}{3} \)
\( x \) açısının tanjant ve kotanjant değerlerini bulmak için bir dik üçgen çizelim.

\( x \) açısının komşu kenarı Pisagor teoremi ile \( 2k \) olarak bulunur.
\( (\sqrt{5}k)^2 + (2k)^2 = (3k)^2 \)
\( \tan{x} = \dfrac{\sqrt{5}}{2} \)
\( \cot{x} = \dfrac{2}{\sqrt{5}} \)
Bulduğumuz değerleri sorudaki ifadede yerlerine koyalım.
\( \cot{x} + \tan{x} = \dfrac{2}{\sqrt{5}} + \dfrac{\sqrt{5}}{2} \)
\( = \dfrac{4 + 5}{2\sqrt{5}} = \dfrac{9}{2\sqrt{5}} \)
Paydayı rasyonel hale getirelim.
\( = \dfrac{9\sqrt{5}}{10} \) bulunur.
\( \dfrac{\tan{x}}{\sec{x} - 1} - \dfrac{\sin{x}}{1 + \cos{x}} \) ifadesinin en sade halini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1}{\cos{x}} - 1} - \dfrac{\sin{x}}{1 + \cos{x}} \)
\( = \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1 - \cos{x}}{\cos{x}}} - \dfrac{\sin{x}}{1 + \cos{x}} \)
\( = \dfrac{\sin{x}}{1 - \cos{x}} - \dfrac{\sin{x}}{1 + \cos{x}} \)
Terimlerin paydalarını eşitleyelim.
\( = \dfrac{\sin{x}(1 + \cos{x})}{(1 - \cos{x})(1 + \cos{x})} - \dfrac{\sin{x}(1 - \cos{x})}{(1 + \cos{x})(1 - \cos{x})} \)
\( = \dfrac{\sin{x} + \sin{x}\cos{x} - \sin{x} + \sin{x}\cos{x}}{(1 - \cos{x})(1 + \cos{x})} \)
\( = \dfrac{2\sin{x}\cos{x}}{1 - \cos^2{x}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{2\sin{x}\cos{x}}{\sin^2{x}} \)
\( = \dfrac{2\cos{x}}{\sin{x}} = 2\cot{x} \) bulunur.
\( \sin{x} - \cos{x} = \dfrac{1}{3} \) olduğuna göre,
\( \tan{x} + \cot{x} \) ifadesinin değeri nedir?
Çözümü GösterEşitliğin taraflarının karesini alalım.
\( (\sin{x} - \cos{x})^2 = \left( \dfrac{1}{3} \right)^2 \)
\( \sin^2{x} - 2\sin{x}\cos{x} + \cos^2{x} = \dfrac{1}{9} \)
Pisagor özdeşliğini kullanalım.
\( 1 - 2\sin{x}\cos{x} = \dfrac{1}{9} \)
\( \sin{x}\cos{x} = \dfrac{4}{9} \)
Değeri sorulan ifadeyi düzenleyelim.
\( \tan{x} + \cot{x} = \dfrac{\sin{x}}{\cos{x}} + \dfrac{\cos{x}}{\sin{x}} \)
\( = \dfrac{\sin^2{x} + \cos^2{x}}{\sin{x}\cos{x}} \)
\( = \dfrac{1}{\sin{x}\cos{x}} \)
\( = \dfrac{1}{\frac{4}{9}} = \dfrac{9}{4} \) bulunur.
\( \dfrac{6\sin{\alpha} - 5}{\sqrt{11} - 6\cos{\alpha}} - \dfrac{6\cos{\alpha} + \sqrt{11}}{5 + 6\sin{\alpha}} \)
ifadesinin değeri kaçtır?
Çözümü GösterPaydaları eşitleyelim.
\( \dfrac{(6\sin{\alpha} - 5)(6\sin{\alpha} + 5) - (\sqrt{11} + 6\cos{\alpha})(\sqrt{11} - 6\cos{\alpha})}{(\sqrt{11} - 6\cos{\alpha})(5 + 6\sin{\alpha})} \)
Paydaki çarpanlar birbirinin eşleniği olduğu için kare farkı şeklinde yazalım.
\( \dfrac{((6\sin{\alpha})^2 - 5^2) - ((\sqrt{11})^2 - (6\cos{\alpha})^2)}{(\sqrt{11} - 6\cos{\alpha})(5 + 6\sin{\alpha})} \)
\( = \dfrac{36\sin^2{\alpha} - 25 - 11 + 36\cos^2{\alpha}}{(\sqrt{11} - 6\cos{\alpha})(5 + 6\sin{\alpha})} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{36 - 36}{(\sqrt{11} - 6\cos{\alpha})(5 + 6\sin{\alpha})} \)
\( = 0 \) bulunur.
\( 0 \lt \alpha \lt \dfrac{\pi}{2} \) olmak üzere,
\( \dfrac{\cos{\alpha} - \sin{\alpha}}{3(\sin{\alpha} + \cos{\alpha})} = \dfrac{1}{4} \)
olduğuna göre, \( \cos^4{\alpha} - \sin^4{\alpha} \) ifadesinin değeri kaçtır?
Çözümü Gösterİçler - dışlar çarpımı yapalım.
\( 4\cos{\alpha} - 4\sin{\alpha} = 3\sin{\alpha} + 3\cos{\alpha} \)
\( \cos{\alpha} = 7\sin{\alpha} \)
\( \dfrac{\sin{\alpha}}{\cos{\alpha}} = \dfrac{1}{7} \)
\( \tan{\alpha} = \dfrac{1}{7} \)
\( \alpha \) açısının karşı kenarına \( k \), komşu kenarına \( 7k \) dersek hipotenüs Pisagor teoreminden \( \sqrt{50}k \) olarak bulunur.
\( k^2 + (7k)^2 = (\sqrt{50}k)^2 \)
\( \cos{\alpha} = \dfrac{7k}{\sqrt{50}k} = \dfrac{7}{\sqrt{50}} \)
\( \sin{\alpha} = \dfrac{k}{\sqrt{50}k} = \dfrac{1}{\sqrt{50}} \)
Soruda istenen ifadenin değerini bulalım.
\( \cos^4{\alpha} - \sin^4{\alpha} = (\cos^2{\alpha} - \sin^2{\alpha})(\cos^2{\alpha} + \sin^2{\alpha}) \)
\( = \cos^2{\alpha} - \sin^2{\alpha} \)
\( = \left( \dfrac{7}{\sqrt{50}} \right)^2 - \left( \dfrac{1}{\sqrt{50}} \right)^2 \)
\( = \dfrac{49}{50} - \dfrac{1}{50} \)
\( = \dfrac{48}{50} = \dfrac{24}{25} \) bulunur.
\( \dfrac{\tan{x}}{(1 - \cos{x})(1 + \sec{x})} \) ifadesinin en sade halini bulunuz.
Çözümü GösterPaydadaki çarpma işlemini dağıtalım.
\( \dfrac{\tan{x}}{1 + \sec{x} - \cos{x} - \sec{x}\cos{x}} \)
Kosinüs ve sekant birbirinin çarpmaya göre tersidir.
\( = \dfrac{\tan{x}}{1 + \sec{x} - \cos{x} - 1} \)
\( = \dfrac{\tan{x}}{\sec{x} - \cos{x}} \)
İfadeleri sinüs ve kosinüs cinsinden yazalım.
\( = \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1}{\cos{x}} - \cos{x}} \)
\( = \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1 - \cos^2{x}}{\cos{x}}} \)
Pisagor özdeşliğini kullanalım.
\( = \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{\sin^2{x}}{\cos{x}}} \)
\( = \dfrac{\sin{x}}{\sin^2{x}} \)
\( = \dfrac{1}{\sin{x}} = \csc{x} \) bulunur.
\( \alpha \in (0, \frac{\pi}{2}) \) olmak üzere,
\( m = \sqrt{3}\sin{\alpha} + 2\cos{\alpha} \)
\( n = \sqrt{3}\cos{\alpha} - 2\sin{\alpha} \)
eşitlikleri veriliyor. Buna göre, \( m \)'nin \( n \) cinsinden eşiti kaçtır?
Çözümü GösterHer iki eşitlikte tarafların karesini alalım.
\( m^2 = 3\sin^2{\alpha} + 4\sqrt{3}\sin{\alpha}\cos{\alpha} + 4\cos^2{\alpha} \)
\( n^2 = 3\cos^2{\alpha} - 4\sqrt{3}\sin{\alpha}\cos{\alpha} + 4\sin^2{\alpha} \)
Eşitlikleri taraf tarafa toplayalım.
\( m^2 + n^2 = 7\sin^2{\alpha} + 7\cos^2{\alpha} \)
\( = 7(\sin^2{\alpha} + \cos^2{\alpha}) \)
Pisagor özdeşliğini kullanalım.
\( = 7 \)
\( m^2 = 7 - n^2 \)
\( (0, \frac{\pi}{2}) \) aralığında \( m \) pozitif olur.
\( m = \sqrt{7 - n^2} \) bulunur.
\( 0° \lt \theta \lt 90° \) olmak üzere,
\( \csc^2{\theta} + \cot^2{\theta} = 4 \) eşitliği veriliyor.
Buna göre, \( \tan{\theta} \) kaça eşittir?
Çözümü Göster\( \csc^2{\theta} + \cot^2{\theta} = 4 \)
\( \dfrac{1}{\sin^2{\theta}} + \dfrac{\cos^2{\theta}}{\sin^2{\theta}} = 4 \)
\( 1 + \cos^2{\theta} = 4\sin^2{\theta} \)
\( 1 + (1 - \sin^2{\theta}) = 4\sin^2{\theta} \)
\( 5\sin^2{\theta} = 2 \)
\( \sin^2{\theta} = \dfrac{2}{5} \)
\( \sin{\theta} = \dfrac{\sqrt{2}}{\sqrt{5}} \)
Sinüs değeri bilinen bir açının tanjant değerini bulmak için bir dik üçgen çizelim ve Pisagor teoremini kullanarak komşu kenar uzunluğunu bulalım.

\( \tan{\theta} = \dfrac{\sqrt{2}}{\sqrt{3}} \)
\( = \dfrac{\sqrt{6}}{3} \) bulunur.
\( 0° \lt \alpha \lt 90° \) olmak üzere,
\( \tan{\dfrac{\alpha}{2}}\tan{\dfrac{8\alpha}{9}} = 1 \) olduğuna göre, \( \alpha \) kaç derecedir?
Çözümü GösterBir açının tanjantı ile kotanjantının çarpımı 1'dir.
\( \tan{\dfrac{\alpha}{2}}\cot{\dfrac{\alpha}{2}} = 1 \)
Verilen eşitliğe göre aşağıdaki iki ifade birbirine eşit olmalıdır.
\( \tan{\dfrac{8\alpha}{9}} = \cot{\dfrac{\alpha}{2}} \)
Tümler açıların tanjant ve kotanjant değerleri birbirine eşittir.
Buna göre \( \frac{8\alpha}{9} \) ve \( \frac{\alpha}{2} \) tümler açılardır.
\( \dfrac{8\alpha}{9} + \dfrac{\alpha}{2} = 90° \)
\(\dfrac{25\alpha}{18} = 90° \)
\( \alpha = \dfrac{18}{25} \cdot 90° \)
\( = 64,8° \) olarak bulunur.
\( \sin{x} + \csc{x} = -2 \) olduğuna göre,
\( \csc^8{x} + \cos^4{x} \) ifadesinin değeri kaçtır?
Çözümü Göster\( \sin{x} + \dfrac{1}{\sin{x}} = -2 \)
\( \dfrac{\sin^2{x} + 1}{\sin{x}} = -2 \)
İçler - dışlar çarpımı yapalım.
\( \sin^2{x} + 1 = -2\sin{x} \)
\( \sin^2{x} + 2\sin{x} + 1 = 0 \)
\( (\sin{x} + 1)^2 = 0 \)
\( \sin{x} + 1 = 0 \)
\( \sin{x} = -1 \)
Değeri istenen ifadedeki terimlerin değerini bulalım.
\( \csc{x} = \dfrac{1}{\sin{x}} = -1 \)
Bu değeri Pisagor özdeşliğinde yerine koyalım.
\( \sin^2{x} + \cos^2{x} = 1 \)
\( (-1)^2 + \cos^2{x} = 1 \)
\( \cos^2{x} = 0 \Longrightarrow \cos{x} = 0 \)
Bulduğumuz değerleri istenen ifadede yerine koyalım.
\( \csc^8{x} + \cos^4{x} = (-1)^8 + 0^4 \)
\( = 1 \) olarak bulunur.
\( 2 \sin{x} + \sqrt{11} \cos{x} = \sqrt{15} \)
olduğuna göre, \( \cot{x} \) kaçtır?
Çözümü GösterVerilen eşitliğin taraflarının karesini alalım.
\( (2 \sin{x} + \sqrt{11} \cos{x})^2 = (\sqrt{15})^2 \)
\( 4\sin^2{x} + 4 \sqrt{11} \sin{x} \cos{x} + 11\cos^2{x} = 15 \)
Eşitliğin sağındaki 15 değeri yerine, \( \sin^2{x} + \cos^2{x} = 1 \) özdeşliğini kullanarak aşağıdaki eşitliği yazabiliriz.
\( 15(\sin^2{x} + \cos^2{x}) = 15 \cdot 1 = 15 \)
\( 4\sin^2{x} + 4 \sqrt{11} \sin{x} \cos{x} + 11\cos^2{x} = 15 (\sin^2{x} + \cos^2{x}) \)
\( 4\sin^2{x} + 4 \sqrt{11} \sin{x} \cos{x} + 11\cos^2{x} = 15\sin^2{x} + 15\cos^2{x} \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( -11\sin^2{x} + 4 \sqrt{11} \sin{x} \cos{x} - 4\cos^2{x} = 0 \)
Eşitliğin taraflarını \( -1 \) ile çarpalım.
\( 11\sin^2{x} - 4 \sqrt{11} \sin{x} \cos{x} + 4\cos^2{x} = 0 \)
Bu ifade bir parantez karesine eşittir.
\( (\sqrt{11} \sin{x} - 2\cos{x})^2 = 0 \)
\( \sqrt{11} \sin{x} - 2\cos{x} = 0 \)
\( \sqrt{11} \sin{x} = 2\cos{x} \)
\( \dfrac{\cos{x}}{\sin{x}} = \cot{x} = \dfrac{\sqrt{11}}{2} \) bulunur.
\( \tan^4{x} + \cot^4{x} = 2 \) olduğuna göre,
\( \tan{x} + \cot{x} \) toplamının pozitif değeri kaçtır?
Çözümü Göster\( \tan{x} + \cot{x} = k \) diyelim.
İki tarafın karesini alalım.
\( (\tan{x} + \cot{x})^2 = k^2 \)
\( \tan^2{x} + 2\tan{x}\cot{x} + \cot^2{x} = k^2 \)
Bir açının tanjantı ile kotanjantının çarpımı 1'dir.
\( \tan^2{x} + 2 + \cot^2{x} = k^2 \)
\( \tan^2{x} + \cot^2{x} = k^2 - 2 \)
İki tarafın tekrar karesini alalım.
\( (\tan^2{x} + \cot^2{x})^2 = (k^2 - 2)^2 \)
\( \tan^4{x} + 2\tan^2{x} \cot^2{x} + \cot^4{x} = (k^2 - 2)^2 \)
\( \tan^4{x} + 2 + \cot^4{x} = (k^2 - 2)^2 \)
Verilen \( \tan^4{x} + \cot^4{x} \) değerini yerine koyalım.
\( 2 + 2 = (k^2 - 2)^2 \)
\( k^2 - 2 = 2 \) veya \( k^2 - 2 = -2 \)
\( k^2 = 4 \) veya \( k^2 = 0 \)
\( k = 0 \) için yukarıda bulduğumuz aşağıdaki eşitlik sağlanmayacağı için geçerli bir çözüm değildir.
\( \tan^2{x} + \cot^2{x} = k^2 - 2 = -2 \)
\( k \in \{ -2, 2 \} \)
Buna göre \( \tan{x} + \cot{x} \) toplamının pozitif değeri 2 olur.
\( 4x^2 - x - k = 0 \) denkleminin kökleri \( \sin{t} \) ve \( \cos{t} \) olduğuna göre, \( k \) değeri nedir?
Çözümü Gösterİkinci dereceden denklemin kökler toplamı formülünü kullanalım.
\( \sin{t} + \cos{t} = -\dfrac{b}{a} = \dfrac{1}{4} \)
İkinci dereceden denklemin kökler çarpımı formülünü kullanalım.
\( \sin{t}\cos{t} = \dfrac{c}{a} = -\dfrac{k}{4} \)
Kökler toplamı eşitliğinde iki tarafın karesini alalım.
\( (\sin{t} + \cos{t})^2 = \left( \dfrac{1}{4} \right)^2 \)
\( \sin^2{t} + 2\sin{t}\cos{t} + \cos^2{t} = \dfrac{1}{16} \)
Pisagor özdeşliğini kullanalım.
\( 1 + 2\sin{t}\cos{t} = \dfrac{1}{16} \)
\( \sin{t}\cos{t} = -\dfrac{15}{32} \)
Kökler çarpımını yukarıda bulduğumuz değere eşitleyelim.
\( \sin{t}\cos{t} = -\dfrac{15}{32} = -\dfrac{k}{4} \)
\( \dfrac{k}{4} = \dfrac{15}{32} \)
\( k = \dfrac{15}{8} \) bulunur.