Trigonometrik Denklemler
Bir değişkenin trigonometrik fonksiyon içinde yer aldığı denklemlere trigonometrik denklem denir. Trigonometrik denklemlerin çözümü trigonometrik değerler, özdeşlikler, bölgeler arası dönüşümler, fonksiyonların grafikleri ve periyotları, dönüşüm formülleri gibi trigonometrinin tüm alt başlıklarını kullanmamızı gerektiren bir konudur.
Bir trigonometrik ifadenin fonksiyon, açı ve değişken değerleri arasındaki ayrıma denklem çözümünde dikkat edilmelidir.
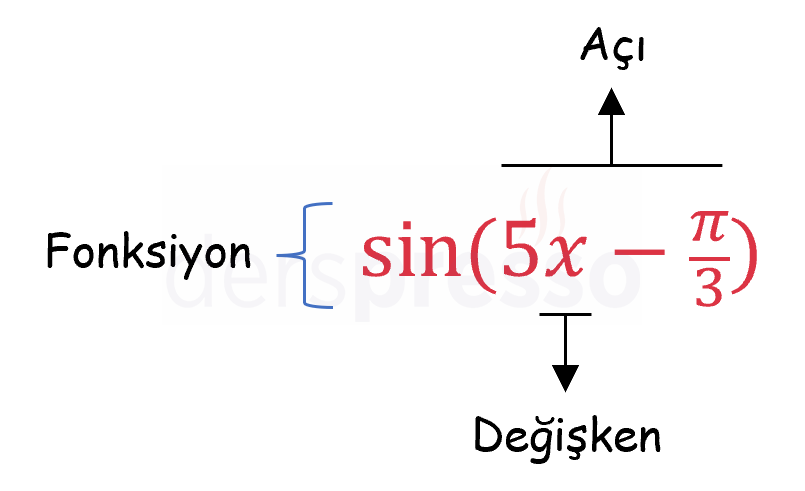
Trigonometrik fonksiyonlar periyodik oldukları için, bir denklem belirli bir açı ölçüsü için sağlanıyorsa denklemin sonsuz sayıda çözümü bulunur. Bir trigonometrik denklemi sağlayan açılar içinde \( [0, 2\pi) \) aralığındaki değerlere esas çözüm, tüm reel sayıları kapsayan değerlere genel çözüm denir.
Trigonometrik denklemleri üç başlık altında inceleyebiliriz.
Lineer Denklemler
Lineer trigonometrik denklemler tek bir trigonometrik fonksiyon ve bu fonksiyonun birinci kuvvetini içerir.
\( a\sin{x} + b = 0 \)
\( 2\sin{x} = -\sqrt{3} \)
\( \cos(2y) - 1 = 0 \)
\( \tan(3\alpha - \frac{\pi}{2}) = -1 \)
Birden fazla trigonometrik fonksiyon ve/veya yüksek dereceden ifadeler içeren denklemler çoğu zaman lineer ifadelerin çarpımı şeklinde yazılabildiği için lineer denklemlerin çözümünde kullanılan yöntemler daha karmaşık denklemlere de uygulanabilir.
Lineer trigonometrik denklemler dört adımda çözülebilir.
- Fonksiyon değerini bulma: İlk adımda trigonometrik fonksiyon yalnız bırakılır ve eşitliği sağlayan fonksiyon değeri bulunur.
- Açı ölçülerini bulma: Fonksiyonun bir tam periyodu içinde ilk adımda bulunan değeri aldığı açı ölçüleri bulunur.
- Genel çözümü bulma: İkinci adımda bulunan her açı ölçüsüne fonksiyonun periyodunun tam sayı katları eklenerek denklemin genel çözümü bulunur.
- Kısıtlamalar: Genel çözüm içinde soruda verilen tanım aralıkları içindeki çözüm değerleri seçilir.
\( 2\sin{x} + 1 = 0 \) denkleminin genel çözüm kümesini bulalım.
Adım 1: Fonksiyonu yalnız bırakarak eşitliği sağlayan fonksiyon değerini bulalım.
\( \sin{x} = -\dfrac{1}{2} \)
Adım 2: Fonksiyonun bir tam periyodu içinde bu değeri aldığı açı ölçülerini bulalım.
Sinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Sinüs fonksiyonu \( [0, 2\pi) \) aralığında \( -\frac{1}{2} \) değerini aşağıdaki açı değerlerinde alır.
\( x_1 = \dfrac{7\pi}{6} \)
\( x_2 = \dfrac{11\pi}{6} \)
Adım 3: Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
\( k \in \mathbb{Z} \) olmak üzere,
\( x_1 = \dfrac{7\pi}{6} + 2\pi k \)
\( x_2 = \dfrac{11\pi}{6} + 2\pi k \)
Adım 4: Soruda genel çözüm istendiği için bulduğumuz değerler denklemin çözüm kümesidir.
Çözüm kümesi: \( x \in \{\ldots, \frac{7\pi}{6}, \frac{11\pi}{6}, \frac{19\pi}{6}, \frac{23\pi}{6}, \ldots\} \)
Açı ölçüsünün \( x \)'ten farklı bir ifade olduğu duruma bir örnek verelim.
\( \pi \le x \lt 2\pi \) olmak üzere,
\( 3\tan(2x + \frac{\pi}{6}) + \sqrt{3} = 0 \) denkleminin çözüm kümesini bulalım.
Adım 1: Fonksiyonu yalnız bırakarak eşitliği sağlayan fonksiyon değerini bulalım.
\( \tan(2x + \frac{\pi}{6}) = -\dfrac{\sqrt{3}}{3} \)
Adım 2: Fonksiyonun bir tam periyodu içinde bu değeri aldığı açı ölçülerini bulalım.
Tanjant fonksiyonunun periyodu \( \pi \)'dir.
Tanjant fonksiyonu \( [0, \pi) \) aralığında \( -\frac{\sqrt{3}}{3} \) değerini aşağıdaki açı değerlerinde alır.
\( 2x + \dfrac{\pi}{6} = \dfrac{5\pi}{6} \)
Adım 3: Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x + \dfrac{\pi}{6} = \dfrac{5\pi}{6} + \pi k \)
\( x \) değişkenini yalnız bırakalım.
\( 2x = \dfrac{2\pi}{3} + \pi k \)
\( x = \dfrac{\pi}{3} + \dfrac{\pi}{2} k \)
Adım 4: Bulunan genel çözüm değerlerinden soruda verilen \( [\pi, 2\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{\frac{4\pi}{3}, \frac{11\pi}{6}\} \)
Lineer denklem formunda olmayan bazı denklemler özdeşlikler yardımıyla lineer denkleme dönüştürülerek çözülebilir.
\( 2\pi \le x \lt 4\pi \) olmak üzere,
\( \sin{x} - \sqrt{3}\cos{x} = 0 \) denkleminin çözüm kümesini bulalım.
Adım 1: Denklemi lineer forma getirelim ve fonksiyonu yalnız bırakarak eşitliği sağlayan fonksiyon değerini bulalım.
\( \sin{x} = \sqrt{3}\cos{x} \)
Eşitliğin iki tarafını kosinüse bölelim.
\( \dfrac{\sin{x}}{\cos{x}} = \sqrt{3} \)
\( \tan{x} = \sqrt{3} \)
Adım 2: Fonksiyonun bir tam periyodu içinde bu değeri aldığı açı ölçülerini bulalım.
Tanjant fonksiyonunun periyodu \( \pi \)'dir.
Tanjant fonksiyonu \( [0, \pi) \) aralığında \( \sqrt{3} \) değerini aşağıdaki açı değerlerinde alır.
\( x = \dfrac{\pi}{3} \)
Adım 3: Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
\( k \in \mathbb{Z} \) olmak üzere,
\( x = \dfrac{\pi}{3} + \pi k \)
Adım 4: Bulunan genel çözüm değerlerinden soruda verilen \( [2\pi, 4\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{\frac{7\pi}{3}, \frac{10\pi}{3}\} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \cos\left( 2x + \dfrac{\pi}{6} \right) = -\dfrac{1}{2} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Kosinüs fonksiyonu \( \frac{1}{2} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{2\pi}{3}, \dfrac{4\pi}{3} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( \dfrac{2\pi}{3} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x + \dfrac{\pi}{6} = \dfrac{2\pi}{3} + 2\pi k \)
\( 2x = \dfrac{\pi}{2} + 2\pi k \)
\( x = \dfrac{\pi}{4} + \pi k \)
Durum 2:
\( \dfrac{4\pi}{3} \) için:
\( 2x + \dfrac{\pi}{6} = \dfrac{4\pi}{3} + 2\pi k \)
\( 2x = \dfrac{7\pi}{6} + 2\pi k \)
\( x = \dfrac{7\pi}{12} + \pi k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, 2\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{4}, \dfrac{7\pi}{12}, \dfrac{5\pi}{4}, \dfrac{19\pi}{12} \right\} \)
\( -180° \le x \lt 180° \) olmak üzere,
\( \tan^2\left( \dfrac{3x}{2} - 30° \right) = 3 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitliğin taraflarının karekökünü alalım.
\( \tan\left( \dfrac{3x}{2} - 30° \right) = \pm \sqrt{3} \)
Tanjant fonksiyonunun periyodu \( 180° \)'dir.
Tanjant fonksiyonu \( \pm \sqrt{3} \) değerlerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ 60°, 120° \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( 60° \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{3x}{2} - 30 = 60 + 180 k \)
\( \dfrac{3x}{2} = 90 + 180 k \)
\( x = 60 + 120 k \)
Durum 2:
\( 120° \) için:
\( \dfrac{3x}{2} - 30 = 120 + 180 k \)
\( \dfrac{3x}{2} = 150 + 180 k \)
\( x = 100 + 120 k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [-180°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ -180°, -140°, -60°, -20°, 60°, 100° \right\} \)
\( 0 \le x \lt \pi \) olmak üzere,
\( \sqrt{3}\sin(2x) = \cos(2x)\)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \sqrt{3}\sin(2x) = \cos(2x) \)
\( \dfrac{\sin(2x)}{\cos(2x)} = \dfrac{1}{\sqrt{3}} \)
\( \tan(2x) = \dfrac{1}{\sqrt{3}} \)
Tanjant fonksiyonunun periyodu \( \pi \)'dir.
Tanjant fonksiyonu \( \frac{1}{\sqrt{3}} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{\pi}{6} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( \dfrac{\pi}{6} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = \dfrac{\pi}{6} + \pi k \)
\( x = \dfrac{\pi}{12} + \dfrac{\pi}{2} k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, \pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{12}, \dfrac{7\pi}{12} \right\} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \cos\left( x + \dfrac{\pi}{6} \right) = \sin{x} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs toplam formülünü kullanalım.
\( \cos{x}\cos{\dfrac{\pi}{6}} - \sin{x}\sin{\dfrac{\pi}{6}} = \sin{x} \)
\( \cos{x} \cdot \dfrac{\sqrt{3}}{2} - \sin{x} \cdot \dfrac{1}{2} = \sin{x} \)
\( \sqrt{3}\cos{x} - \sin{x} = 2\sin{x} \)
\( \sqrt{3}\cos{x} = 3\sin{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = \dfrac{\sqrt{3}}{3} \)
\( \tan{x} = \dfrac{\sqrt{3}}{3} \)
Tanjant fonksiyonu \( [0, 2\pi) \) aralığında \( \frac{\sqrt{3}}{3} \) değerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{6}, \dfrac{7\pi}{6} \right\} \)
\( -\pi \le x \lt \pi \) olmak üzere,
\( \sin\left( x + \dfrac{\pi}{3} \right) = \cos\left( x + \dfrac{\pi}{2} \right) \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterSinüs ve kosinüs toplam formüllerini kullanalım.
\( \sin{x}\cos{\dfrac{\pi}{3}} + \sin{\dfrac{\pi}{3}}\cos{x} = \cos{x}\cos{\dfrac{\pi}{2}} - \sin{\dfrac{\pi}{2}}\sin{x} \)
\( \sin{x} \cdot \dfrac{1}{2} + \dfrac{\sqrt{3}}{2} \cdot \cos{x} = \cos{x} \cdot 0 - 1 \cdot \sin{x} \)
\( \sin{x} + \sqrt{3}\cos{x} = -2\sin{x} \)
\( 3\sin{x} = -\sqrt{3}\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = -\dfrac{\sqrt{3}}{3} \)
\( \tan{x} = -\dfrac{\sqrt{3}}{3} \)
Tanjant fonksiyonu \( [-\pi, \pi) \) aralığında \( -\frac{\sqrt{3}}{3} \) değerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \left\{ -\dfrac{\pi}{6}, \dfrac{5\pi}{6} \right\} \)
\( 0° \le x \lt 360° \) olmak üzere,
\( 2\csc^2{x} + \cot^2{x} = 11 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosekant ifadesini kotanjant cinsinden yazalım.
\( 2(1 + \cot^2{x}) + \cot^2{x} = 11 \)
\( 2 + 3\cot^2{x} = 11 \)
\( \cot^2{x} = 3 \)
\( \cot{x} = \pm \sqrt{3} \)
Kotanjant fonksiyonu \( [0°, 360°) \) aralığında \( \pm \sqrt{3} \) değerlerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \{30°, 150°, 210°, 330°\} \)
\( 0° \le x \lt 360° \) olmak üzere,
\( \tan^2{x}\sin{x} + \cos{x} = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitliği düzenleyelim.
\( \tan^2{x}\sin{x} = -\cos{x} \)
Eşitliğin taraflarını \( \cos{x} \)'e bölelim.
\( \tan^2{x} \cdot \dfrac{\sin{x}}{\cos{x}} = -1 \)
\( \tan^2{x}\tan{x} = -1 \)
\( \tan^3{x} = -1 \)
\( \sqrt[3]{\tan^3{x}} = \sqrt[3]{-1} \)
\( \tan{x} = -1 \)
Tanjant fonksiyonu \( [0°, 360°) \) aralığında \( -1 \) değerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \{ 135°, 315° \} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \dfrac{\tan{x}}{\sec{x} - 1} + \dfrac{\sec{x} - 1}{\tan{x}} = 4 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitlikteki terimleri sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1}{\cos{x}} - 1} + \dfrac{\frac{1}{\cos{x}} - 1}{\frac{\sin{x}}{\cos{x}}} = 4 \)
\( \dfrac{\frac{\sin{x}}{\cos{x}}}{\frac{1 - \cos{x}}{\cos{x}}} + \dfrac{\frac{1 - \cos{x}}{\cos{x}}}{\frac{\sin{x}}{\cos{x}}} = 4 \)
Çözüm kümesinde \( \cos{x} = 0 \) yapan \( x \) değerleri bulunamayacağını not ederek \( \cos{x} \) ifadelerini sadeleştirelim.
\( \dfrac{\sin{x}}{1 - \cos{x}} + \dfrac{1 - \cos{x}}{\sin{x}} = 4 \)
Terimlerin paydalarını eşitleyelim.
\( \dfrac{\sin^2{x}}{(1 - \cos{x})\sin{x}} + \dfrac{(1 - \cos{x})^2}{(1 - \cos{x})\sin{x}} = 4 \)
\( \dfrac{\sin^2{x} + 1 - 2\cos{x} + \cos^2{x}}{(1 - \cos{x})\sin{x}} = 4 \)
Pisagor özdeşliğini kullanalım.
\( \dfrac{2 - 2\cos{x}}{(1 - \cos{x})\sin{x}} = 4 \)
\( \dfrac{2(1 - \cos{x})}{(1 - \cos{x})\sin{x}} = 4 \)
Çözüm kümesinde \( \cos{x} = 1 \) yapan \( x \) değerleri bulunamayacağını not ederek \( 1 - \cos{x} \) ifadelerini sadeleştirelim.
\( \dfrac{2}{\sin{x}} = 4 \)
\( \sin{x} = \dfrac{1}{2} \)
Sinüs fonksiyonu \( [0, 2\pi) \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{6}, \dfrac{5\pi}{6} \right\} \)
\( 0 \le x \le 2\pi \) olmak üzere,
\( \sin^2{x} = \dfrac{2 + \sqrt{3}}{4} \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs iki kat açı formülünü kullanalım.
\( \cos(2x) = 1 - 2\sin^2{x} \)
\( \sin^2{x} = \dfrac{1 - \cos(2x)}{2} \)
Bu değeri verilen eşitlikte yerine koyalım.
\( \dfrac{1 - \cos(2x)}{2} = \dfrac{2 + \sqrt{3}}{4} \)
\( 1 - \cos(2x) = \dfrac{2 + \sqrt{3}}{2} \)
\( \cos(2x) = -\dfrac{\sqrt{3}}{2} \)
Kosinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Kosinüs fonksiyonu \( -\frac{\sqrt{3}}{2} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{5\pi}{6}, \dfrac{7\pi}{6} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( \dfrac{5\pi}{6} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = \dfrac{5\pi}{6} + 2\pi k \)
\( x = \dfrac{5\pi}{12} + \pi k \)
Durum 2:
\( \dfrac{7\pi}{6} \) için:
\( 2x = \dfrac{7\pi}{6} + 2\pi k \)
\( x = \dfrac{7\pi}{12} + \pi k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, 2\pi] \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ \dfrac{5\pi}{12}, \dfrac{7\pi}{12}, \dfrac{17\pi}{12}, \dfrac{19\pi}{12} \right\} \)
Aşağıdaki gibi daha karmaşık yapıdaki trigonometrik denklemler (eğer mümkünse) çarpanlarına ayrılır, daha sonra her bir çarpanın yukarıda kullandığımız yöntemle çözüm kümesi bulunur. Bu tip denklemlerin çözüm kümesi, her bir çarpandan gelen çözümlerin birleşim kümesidir.
\( 0 \le x \lt 2\pi \) olmak üzere,
\( 3\sin^2{x} - 5\sin{x}\cos{x} - 2\cos^2{x} = 0 \)
denkleminin çözüm kümesi kaç elemanlıdır?
Çözümü GösterEşitliğin sol tarafını çarpanlarına ayıralım.
\( (3\sin{x} + \cos{x})(\sin{x} - 2\cos{x}) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 3\sin{x} + \cos{x} = 0 \)
\( 3\sin{x} = -\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = -\dfrac{1}{3} \)
\( \tan{x} = -\dfrac{1}{3} \)
Tanjant fonksiyonu \( [0, 2\pi) \) aralığında \( -\frac{1}{3} \) değerini II. ve IV. bölgelerde olmak üzere birer kez alır.
Durum 2:
\( \sin{x} - 2\cos{x} = 0 \)
\( \sin{x} = 2\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = 2 \)
\( \tan{x} = 2 \)
Tanjant fonksiyonu \( [0, 2\pi) \) aralığında \( 2 \) değerini I. ve III. bölgelerde olmak üzere birer kez alır.
Buna göre verilen denklemin çözüm kümesi 4 elemanlıdır.
\( 0° \lt x \lt 360° \) olmak üzere,
\( 1 + 2\cos{x} - 4\cos^2{x} - 8\cos^3{x} = 0 \) denkleminin çözüm kümesi kaç elemanlıdır?
Çözümü GösterEşitliğin sol tarafını çarpanlarına ayıralım.
\( 1 + 2\cos{x} - 4\cos^2{x}(1 + 2\cos{x}) = 0 \)
\( (1 + 2\cos{x})(1 - 4\cos^2{x}) = 0 \)
\( ( 1 + 2\cos{x})(1 - 2\cos{x})(1 + 2\cos{x}) = 0 \)
\( ( 1 + 2\cos{x})^2(1 - 2\cos{x}) = 0 \)
Bu denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 1 + 2\cos{x} = 0 \)
\( \cos{x} = -\dfrac{1}{2} \)
Kosinüs fonksiyonu \( (0°, 360°) \) aralığında \( -\frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \{ 120°, 240° \} \)
Durum 2:
\( 1 - 2\cos{x} = 0 \)
\( \cos{x} = \dfrac{1}{2} \)
Kosinüs fonksiyonu \( (0°, 360°) \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \{ 60°, 300° \} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
\( x \in \{ 60°, 120°, 240°, 300° \} \)
Buna göre denklemin çözüm kümesi 4 elemanlıdır.
\( 0° \le x \lt 360° \) olmak üzere,
\( 4\cot^2{x} - 9\csc{x} + 6 = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKotanjant ifadesini kosekant cinsinden yazalım.
\( 4(\csc^2{x} - 1) - 9\csc{x} + 6 = 0 \)
\( 4\csc^2{x} - 4 - 9\csc{x} + 6 = 0 \)
\( 4\csc^2{x} - 9\csc{x} + 2 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (\csc{x} - 2)(4\csc{x} - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \csc{x} - 2 = 0 \)
\( \csc{x} = 2 \)
\( \sin{x} = \dfrac{1}{2} \)
Sinüs fonksiyonu \( [0°, 360°) \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \{ 30°, 150° \} \)
Durum 2:
\( 4\csc{x} - 1 = 0 \)
\( \csc{x} = \dfrac{1}{4} \)
\( \sin{x} = 4 \)
Sinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığı olduğu için bu durumda geçerli bir çözüm oluşmaz.
\( x \in \emptyset \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ 30°, 150° \} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \sin^2{x} - \sin(2x) - 3 \cos^2{x} = 0 \)
denkleminin çözüm kümesi kaç elemanlıdır?
Çözümü GösterSinüs iki kat açı formülünü kullanalım.
\( \sin^2{x} - 2\sin{x}\cos{x} - 3 \cos^2{x} = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (\sin{x} - 3\cos{x})(\sin{x} + \cos{x}) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \sin{x} - 3\cos{x} = 0 \)
\( \sin{x} = 3\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = 3 \)
\( \tan{x} = 3 \)
Tanjant fonksiyonu bir tam periyodu içinde herhangi bir değeri bir kez alır, dolayısıyla bu değeri \( [0, 2\pi) \) aralığında iki kez alır.
Durum 2:
\( \sin{x} + \cos{x} = 0 \)
\( \sin{x} = -\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = -1 \)
\( \tan{x} = -1 \)
Tanjant fonksiyonu \( [0, 2\pi) \) aralığında \( -1 \) değerini aşağıdaki açı değerlerinde alır.
\( x \in \left\{ \dfrac{3\pi}{4}, \dfrac{7\pi}{4} \right\} \)
Buna göre verilen denklemin çözüm kümesi 4 elemanlıdır.
\( -\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2} \) olmak üzere,
\( 4\cos^2{x} - 2\sin^2{x} - 5\cos{x} = 2 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterPisagor özdeşliğini kullanalım.
\( 4\cos^2{x} - 2(1 - \cos^2{x}) - 5\cos{x} = 2 \)
\( 6\cos^2{x} - 5\cos{x} - 4 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (2\cos{x} + 1)(3\cos{x} - 4) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 2\cos{x} + 1 = 0 \)
\( \cos{x} = -\dfrac{1}{2} \)
Kosinüs fonksiyonu soruda verilen \( [-\frac{\pi}{2}, \frac{\pi}{2}] \) aralığında pozitiftir, dolayısıyla bu durumda geçerli bir çözüm oluşmaz.
\( x \in \emptyset \)
Durum 2:
\( 3\cos{x} - 4 = 0 \)
\( \cos{x} = \dfrac{4}{3} \)
Kosinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığı olduğu için bu durumda geçerli bir çözüm oluşmaz.
\( x \in \emptyset \)
Denklemin çözüm kümesi her çarpan için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \emptyset \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \sec{x} + \cos{x} = \dfrac{5}{2} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterSekant ifadesini kosinüs cinsinden yazalım.
\( \dfrac{1}{\cos{x}} + \cos{x} = \dfrac{5}{2} \)
\( \dfrac{1 + \cos^2{x}}{\cos{x}} = \dfrac{5}{2} \)
Çözüm kümesinde \( \cos{x} = 0 \) yapan \( x \) değerleri bulunamayacağını not ederek içler - dışlar çarpımı yapalım.
\( 2 + 2\cos^2{x} = 5\cos{x} \)
\( 2\cos^2{x} - 5\cos{x} + 2 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (2\cos{x} - 1)(\cos{x} - 2) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 2\cos{x} - 1 = 0 \)
\( \cos{x} = \dfrac{1}{2} \)
Kosinüs fonksiyonu \( [0, 2\pi) \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \left\{ \dfrac{\pi}{3}, \dfrac{5\pi}{3} \right\} \)
Durum 2:
\( \cos{x} - 2 = 0 \)
\( \cos{x} = 2 \)
Kosinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığı olduğu için bu durumda geçerli bir çözüm oluşmaz.
\( x \in \emptyset \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{3}, \dfrac{5\pi}{3} \right\} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( 2\cos{x} + 3\csc{x} = 6 + \cot{x} \)
denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİfadedeki terimleri sinüs ve kosinüs cinsinden yazalım.
\( 2\cos{x} + \dfrac{3}{\sin{x}} = 6 + \dfrac{\cos{x}}{\sin{x}} \)
Terimlerin paydalarını eşitleyelim.
\( \dfrac{2\sin{x}\cos{x} + 3}{\sin{x}} = \dfrac{6\sin{x} + \cos{x}}{\sin{x}} \)
Çözüm kümesinde \( \sin{x} = 0 \) yapan \( x \) değerleri bulunamayacağını not ederek \( \sin{x} \) ifadelerini sadeleştirelim.
\( 2\sin{x}\cos{x} + 3 = 6\sin{x} + \cos{x} \)
\( 2\sin{x}\cos{x} - \cos{x} - 6\sin{x} + 3 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( \cos{x}(2\sin{x} - 1) - 3(2\sin{x} - 1) = 0 \)
\( (\cos{x} - 3)(2\sin{x} - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos{x} - 3 = 0 \)
\( \cos{x} = 3 \)
Kosinüs fonksiyonunun görüntü kümesi \( [-1, 1] \) aralığı olduğu için bu durumda geçerli bir çözüm oluşmaz.
\( x \in \emptyset \)
Durum 2:
\( 2\sin{x} - 1 = 0 \)
\( \sin{x} = \dfrac{1}{2} \)
Sinüs fonksiyonu \( [0, 2\pi) \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \left\{ \dfrac{\pi}{6}, \dfrac{5\pi}{6} \right\} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{6}, \dfrac{5\pi}{6} \right\} \)
\( \cos(2x) - \cos{x} = 0 \)
denkleminin genel çözüm kümesini bulunuz.
Çözümü GösterTüm terimleri \( \cos{x} \) cinsinden yazalım.
Kosinüs iki kat açı formülünü kullanalım.
\( 2\cos^2{x} - 1 - \cos{x} = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (2\cos{x} + 1)(\cos{x} - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 2\cos{x} + 1 = 0 \)
\( \cos{x} = -\dfrac{1}{2} \)
Kosinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Kosinüs fonksiyonu bu değeri bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{2\pi}{3}, \dfrac{4\pi}{3} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek bu durum için genel çözümü bulalım.
\( k \in \mathbb{Z} \) olmak üzere,
\( x_1 = \dfrac{2\pi}{3} + 2\pi k \)
\( x_2 = \dfrac{4\pi}{3} + 2\pi k \)
Durum 2:
\( \cos{x} - 1 = 0 \)
\( \cos{x} = 1 \)
Kosinüs fonksiyonu bu değeri bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( x_3 = 0 \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek bu durum için genel çözümü bulalım.
\( x_3 = 0 + 2\pi k = 2\pi k \)
Denklemin genel çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ 2\pi k, \dfrac{2\pi}{3} + 2\pi k, \dfrac{4\pi}{3} + 2\pi k \right\} \)
\( 0° \lt x \lt 90° \) olmak üzere,
\( 4\sin^2(2x) + \cos(4x) = 3\sin(2x) \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs iki kat açı formülünü kullanalım.
\( 4\sin^2(2x) + (1 - 2\sin^2(2x)) = 3\sin(2x) \)
\( 2\sin^2(2x) - 3\sin(2x) + 1 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( (2\sin(2x) - 1)(\sin(2x) - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( 2\sin(2x) - 1 = 0 \)
\( \sin(2x) = \dfrac{1}{2} \)
Sinüs fonksiyonunun periyodu \( 360° \)'dir.
Sinüs fonksiyonu \( \frac{1}{2} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 30°, 150° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1.1:
30° için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = 30° + 360° k \)
\( x = 15° + 180° k \)
Durum 1.1:
150° için:
\( 2x = 150° + 360° k \)
\( x = 75° + 180° k \)
Durum 2:
\( \sin(2x) - 1 = 0 \)
\( \sin(2x) = 1 \)
Sinüs fonksiyonu \( 1 \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 90° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 2.1:
90° için:
\( 2x = 90° + 360° k \)
\( x = 45° + 180° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( (0, 90°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 15°, 45°, 75° \} \)
\( 0° \le x \lt 180° \) olmak üzere,
\( \sin(5x) + \sin{x} = \cos(2x) \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterSinüs toplam ve fark formüllerini kullanalım.
\( 2\sin{\dfrac{5x + x}{2}}\cos{\dfrac{5x - x}{2}} = \cos(2x) \)
\( 2\sin(3x)\cos(2x) = \cos(2x) \)
\( 2\sin(3x)\cos(2x) - \cos(2x) = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( \cos(2x)(2\sin(3x) - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos(2x) = 0 \)
Kosinüs fonksiyonunun periyodu \( 360° \)'dir.
Kosinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 90°, 270° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1.1:
90° için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = 90° + 360° k \)
\( x = 45° + 180° k \)
Durum 1.2:
270° için:
\( 2x = 270° + 360° k \)
\( x = 135° + 180° k \)
Durum 2:
\( 2\sin(3x) - 1 = 0 \)
\( \sin(3x) = \dfrac{1}{2} \)
Sinüs fonksiyonunun periyodu \( 360° \)'dir.
Sinüs fonksiyonu \( \frac{1}{2} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 30°, 150° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 2.1:
30° için:
\( 3x = 30° + 360° k \)
\( x = 10° + 120° k \)
Durum 2.2:
150° için:
\( 3x = 150° + 360° k \)
\( x = 50° + 120° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{10°, 45°, 50°, 130°, 135°, 170°\} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \cot^2{x}\cos{x} = \cot^2{x} \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \cot^2{x}\cos{x} - \cot^2{x} = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( \cot^2{x}(\cos{x} - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cot^2{x} = 0 \)
\( \cot{x} = 0 \)
Kotanjant fonksiyonu \( [0, 2\pi) \) aralığında \( 0 \) değerini aşağıdaki açı değerlerinde alır.
\( x \in \left\{ \dfrac{\pi}{2}, \dfrac{3\pi}{2} \right\} \)
Durum 2:
\( \cos{x} - 1 = 0 \)
\( \cos{x} = 1 \)
Kosinüs fonksiyonu \( [0, 2\pi) \) aralığında \( 1 \) değerini aşağıdaki açı değerinde alır.
\( x = 0 \)
Her ne kadar \( x = 0 \) değeri ikinci çarpanı sıfır yapıyor olsa da, birinci çarpandaki \( \cot{x} \) ifadesini tanımsız yaptığı için denklemin geçerli bir çözümü değildir.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{2}, \dfrac{3\pi}{2} \right\} \)
\( x \in [0, 2\pi] \) olmak üzere,
\( 2\cos^3{x} + 2\sin^3{x} = \sin{x} + \cos{x} \) eşitliğini sağlayan \( x \) değerlerinin toplamı kaçtır?
Çözümü GösterEşitliği düzenleyelim.
\( 2\cos^3{x} - \cos{x} - \sin{x} + 2\sin^3{x} = 0 \)
\( \cos{x}(2\cos^2{x} - 1) - \sin{x}(1 - 2\sin^2{x}) = 0 \)
Kosinüs iki kat açı formülünü kullanalım.
\( \cos{x}\cos(2x) - \sin{x}\cos(2x) = 0 \)
\( \cos(2x)(\cos{x} - \sin{x}) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos(2x) = 0 \)
Kosinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Kosinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{\pi}{2}, \dfrac{3\pi}{2} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1.1:
\( \dfrac{\pi}{2} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = \dfrac{\pi}{2} + 2\pi k \)
\( x = \dfrac{\pi}{4} + \pi k \)
Durum 1.2:
\( \dfrac{3\pi}{2} \) için:
\( 2x = \dfrac{3\pi}{2} + 2\pi k \)
\( x = \dfrac{3\pi}{4} + \pi k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, 2\pi] \) aralığında bulunan değerler bu durum için çözüm kümesini verir.
\( x \in \left\{ \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4} \right\} \)
Durum 2:
\( \cos{x} - \sin{x} = 0 \)
\( \sin{x} = \cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = 1 \)
\( \tan{x} = 1 \)
Tanjant fonksiyonu \( [0, 2\pi] \) aralığında \( 1 \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \left\{ \dfrac{\pi}{4}, \dfrac{5\pi}{4} \right\} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4} \right\} \)
Çözüm kümesindeki değerlerin toplamını bulalım.
\( \dfrac{\pi}{4} + \dfrac{3\pi}{4} + \dfrac{5\pi}{4} + \dfrac{7\pi}{4} = 4\pi \) bulunur.
\( 0 \le x \le \pi \) olmak üzere,
\( \cos(2x) = \sin{x}\sin(3x) \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs fark formülünü kullanalım.
\( \cos(3x - x) = \sin{x}\sin(3x) \)
\( \cos(3x)\cos{x} + \sin(3x)\sin{x} = \sin{x}\sin(3x) \)
Eşitliğin iki tarafındaki terimler birbirini götürür.
\( \cos{x}\cos(3x) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos{x} = 0 \)
Kosinüs fonksiyonu \( [0, \pi] \) aralığında \( 0 \) değerini aşağıdaki açı ölçülerinde alır.
\( x \in \left\{ \dfrac{\pi}{2} \right\} \)
Durum 2:
\( \cos(3x) = 0 \)
Kosinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Kosinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{\pi}{2}, \dfrac{3\pi}{2} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 2.1:
\( \dfrac{\pi}{2} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 3x = \dfrac{\pi}{2} + 2\pi k \)
\( x = \dfrac{\pi}{6} + \dfrac{2\pi}{3} k \)
Durum 2.2:
\( \dfrac{3\pi}{2} \) için:
\( 3x = \dfrac{3\pi}{2} + 2\pi k \)
\( x = \dfrac{\pi}{2} + \dfrac{2\pi}{3} k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, \pi] \) aralığında bulunan değerler bu durum için çözüm kümesini verir.
\( x \in \left\{ \dfrac{\pi}{6}, \dfrac{\pi}{2}, \dfrac{5\pi}{6} \right\} \)
Denklemin çözüm kümesi her çarpan için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( \left\{ \dfrac{\pi}{6}, \dfrac{\pi}{2}, \dfrac{5\pi}{6} \right\} \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( \cos^4{x} - \sin^4{x} = \cos{x} + \sin{x} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitliğin sol tarafını çarpanlarına ayıralım.
\( (\cos^2{x} - \sin^2{x})(\cos^2{x} + \sin^2{x}) = \cos{x} + \sin{x} \)
Pisagor özdeşliğini kullanalım.
\( \cos^2{x} - \sin^2{x} = \cos{x} + \sin{x} \)
Tüm terimleri eşitliğin solunda toplayalım ve ifadeyi çarpanlarına ayıralım.
\( (\cos{x} - \sin{x})(\cos{x} + \sin{x}) - (\cos{x} + \sin{x}) = 0 \)
\( (\cos{x} + \sin{x})(\cos{x} - \sin{x} - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos{x} + \sin{x} = 0 \)
\( \cos{x} = -\sin{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = -1 \)
\( \tan{x} = -1 \)
Tanjant fonksiyonunun \( [0, 2\pi) \) aralığında \( -1 \) değerini aldığı açı ölçüleri aşağıdaki gibidir.
\( x \in \left\{ \dfrac{3\pi}{4}, \dfrac{7\pi}{4} \right\} \)
Durum 2:
\( \cos{x} - \sin{x} - 1 = 0 \)
\( \cos{x} - \sin{x} = 1 \)
Tarafların karesini alalım.
\( \cos^2{x} - 2\sin{x}\cos{x} + \sin^2{x} = 1^2 \)
Pisagor özdeşliğini kullanalım.
\( 1 - 2\sin{x}\cos{x} = 1 \)
\( 2\sin{x}\cos{x} = 0 \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = 0 \)
Sinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Sinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ 0, \pi \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 2.1:
\( 0 \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = 0 + 2\pi k \)
\( x = \pi k \)
Durum 2.2:
\( \pi \) için:
\( 2x = \pi + 2\pi k \)
\( x = \dfrac{\pi}{2} + \pi k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, 2\pi) \) aralığında bulunan değerler bu durum için çözüm kümesini verir.
\( x \in \left\{ 0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2} \right\} \)
2. çarpanın çözümünde eşitliğin iki tarafının karesini aldığımız için bulduğumuz \( x \) değerlerinden bazıları geçersiz olabilir, bu yüzden bu dört değeri sorudaki eşitlikte yerine koyarak sağlamasını yapmalıyız.
\( x = 0 \) için:
\( \cos^4{0} - \sin^4{0} = \cos{0} + \sin{0} \)
\( 1^4 - 0^4 = 1 + 0 \Longrightarrow \) Eşitlik sağlanır.
\( x = \dfrac{\pi}{2} \) için:
\( \cos^4{\dfrac{\pi}{2}} - \sin^4{\dfrac{\pi}{2}} = \cos{\dfrac{\pi}{2}} + \sin{\dfrac{\pi}{2}} \)
\( 0^4 - 1^4 = 0 + 1 \Longrightarrow \) Eşitlik sağlanmaz.
\( x = \pi \) için:
\( \cos^4{\pi} - \sin^4{\pi} = \cos{\pi} + \sin{\pi} \)
\( (-1)^4 - 0^4 = -1 + 0 \Longrightarrow \) Eşitlik sağlanmaz.
\( x = \dfrac{3\pi}{2} \) için:
\( \cos^4{\dfrac{3\pi}{2}} - \sin^4{\dfrac{3\pi}{2}} = \cos{\dfrac{3\pi}{2}} + \sin{\dfrac{3\pi}{2}} \)
\( 0^4 - (-1)^4 = 0 + (-1) \Longrightarrow \) Eşitlik sağlanır.
Buna göre bu durum için geçerli çözümler aşağıdaki gibi olur.
\( x \in \left\{ 0, \dfrac{3\pi}{2} \right\} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ 0, \dfrac{3\pi}{4}, \dfrac{3\pi}{2}, \dfrac{7\pi}{4} \right\} \)
\( 90° \le x \lt 180° \) olmak üzere,
\( \cos{x} + \cos(3x) + \cos(5x) + \cos(7x) = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs dönüşüm formülünü kullanalım.
\( \cos{x} + \cos{y} = 2\cos{\dfrac{x + y}{2}}\cos{\dfrac{x - y}{2}} \)
Verilen eşitlikteki terimlerin sırasını düzenleyelim.
\( \cos(7x) + \cos{x} + \cos(5x) + \cos(3x) = 0 \)
\( 2\cos{\dfrac{7x + x}{2}}\cos{\dfrac{7x - x}{2}} + 2\cos{\dfrac{5x + 3x}{2}}\cos{\dfrac{5x - 3x}{2}} = 0 \)
\( 2\cos(4x)\cos(3x) + 2\cos(4x)\cos(x) = 0 \)
\( \cos(4x)(\cos(3x) + \cos(x)) = 0 \)
Tekrar kosinüs dönüşüm formülünü kullanalım.
\( \cos(4x)(2\cos{\dfrac{3x + x}{2}}\cos{\dfrac{3x - x}{2}}) = 0 \)
\( \cos{x}\cos(2x)\cos(4x) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( \cos{x} = 0 \)
Kosinüs fonksiyonu \( [90°, 180°) \) aralığında \( 0 \) değerini aşağıdaki açı ölçülerinde alır.
\( x = 90° \)
Durum 2:
\( \cos(2x) = 0 \)
Kosinüs fonksiyonunun periyodu \( 360° \)'dir.
Kosinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 90°, 270° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1.1:
90° için:
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = 90° + 360° k \)
\( x = 45° + 180° k \)
Durum 1.2:
270° için:
\( 2x = 270° + 360° k \)
\( x = 135° + 180° k \)
Durum 3:
\( \cos(4x) = 0 \)
Kosinüs fonksiyonunun periyodu \( 360° \)'dir.
Kosinüs fonksiyonu 0 değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \{ 90°, 270° \} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 2.1:
90° için:
\( 4x = 90° + 360° k \)
\( x = 22,5° + 90° k \)
Durum 2.2:
270° için:
\( 4x = 270° + 360° k \)
\( x = 67,5° + 90° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [90°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{90°, 112,5°, 135°, 157,5°\} \)
Aynı Fonksiyonların Eşitliği
İki sinüs, kosinüs, tanjant ya da kotanjant ifadesi arasındaki eşitlikler aşağıdaki yöntemlerle çözülebilir.
İki sinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
\( \sin{x} = \sin{y} \)
Çözüm 1: Açıların esas ölçüleri birbirine eşittir.
\( x = y + 2\pi k \)
Çözüm 2: Birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( x = (\pi - y) + 2\pi k \)
\( \sin(5x) = \sin{40°} \)
Çözüm 1:
\( 5x = 40° + 360° k \)
\( x = 8° + 72° k \)
Çözüm 2:
\( 5x = (180° - 40°) + 360° k \)
\( x = 28° + 72° k \)
Denklemin çözüm kümesi iki çözümün birleşim kümesidir.
Çözüm kümesi: \( x \in \{\ldots, 8°, 28°, 80°, 100°, \ldots\} \)
İSPATI GÖSTER
\( \sin{x} = \sin{y} \)
\( \sin{x} - \sin{y} = 0 \)
Sinüs fark dönüşüm formülünü kullanalım.
\( 2 \cos{\frac{x + y}{2}}\sin{\frac{x - y}{2}} = 0 \)
Bu denklemin çözümü her iki çarpanı sıfır yapan \( x \) ve \( y \) değerleridir.
Çözüm 1: \( \sin{\frac{x - y}{2}} = 0 \)
Sinüs esas ölçüsü \( 0 \) ve \( \pi \) olan açılarda sıfır olur.
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{x - y}{2} = \pi k \)
\( x - y = 2\pi k \)
\( x = y + 2\pi k \)
Bu çözüm iki açının esas ölçülerinin birbirine eşit olması anlamına gelir.
Çözüm 2: \( \cos{\frac{x + y}{2}} = 0 \)
Kosinüs esas ölçüsü \( \frac{\pi}{2} \) ve \( \frac{3\pi}{2} \) olan açılarda sıfır olur.
\( \dfrac{x + y}{2} = \dfrac{\pi}{2} + \pi k \)
\( x + y = \pi + 2\pi k \)
\( x = (\pi - y) + 2\pi k \)
Bu çözüm birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçülerinin birbirine eşit olması anlamına gelir.
İki kosinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
\( \cos{x} = \cos{y} \)
Çözüm 1: Açıların esas ölçüleri birbirine eşittir.
\( x = y + 2\pi k \)
Çözüm 2: Birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( x = (2\pi - y) + 2\pi k \)
\( \cos(4x - 32°) = \cos{48°} \)
Çözüm 1:
\( 4x - 32° = 48° + 360° k \)
\( x = 20° + 90° k \)
Çözüm 2:
\( 4x - 32° = (360° - 48°) + 360° k \)
\( x = 86° + 90° k \)
Denklemin çözüm kümesi iki çözümün birleşim kümesidir.
Çözüm kümesi: \( x \in \{\ldots, 20°, 86°, 110°, 176°, \ldots\} \)
İSPATI GÖSTER
\( \cos{x} = \cos{y} \)
\( \cos{x} - \cos{y} = 0 \)
Kosinüs fark dönüşüm formülünü kullanalım.
\( -2 \sin{\frac{x + y}{2}}\sin{\frac{x - y}{2}} = 0 \)
Bu denklemin çözümü her iki çarpanı sıfır yapan \( x \) ve \( y \) değerleridir.
Çözüm 1: \( \sin{\frac{x - y}{2}} = 0 \)
Sinüs esas ölçüsü \( 0 \) ve \( \pi \) olan açılarda sıfır olur.
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{x - y}{2} = \pi k \)
\( x - y = 2\pi k \)
\( x = y + 2\pi k \)
Bu çözüm iki açının esas ölçülerinin birbirine eşit olması anlamına gelir.
Çözüm 2: \( \sin{\frac{x + y}{2}} = 0 \)
Sinüs esas ölçüsü \( 0 \) ve \( \pi \) olan açılarda sıfır olur.
\( \dfrac{x + y}{2} = \pi k \)
\( x + y = 2\pi k \)
\( x = -y + 2\pi k \)
Eşitliğin sağ tarafına bir tam çember yayına karşılık gelen \( 2\pi \) ekleyebiliriz.
\( x = (2\pi - y) + 2\pi k \)
Bu çözüm birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının (ya da ikinci açının negatifinin) esas ölçülerinin birbirine eşit olması anlamına gelir.
İki tanjant ya da iki kotanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
\( \tan{x} = \tan{y} \)
\( \cot{x} = \cot{y} \)
Çözüm: Açıların farkı \( \pi \)'nin bir tam sayı katıdır.
\( x = y + \pi k \)
\( \tan(3x - 55°) = \tan(33° - x) \)
\( 3x - 55° = 33° - x + 180° k \)
\( x = 22° + 45° k \)
Çözüm kümesi: \( x \in \{\ldots, 22°, 67°, 112°, 157°, \ldots\} \)
İSPATI GÖSTER
\( \tan{x} = \tan{y} \)
\( \dfrac{\sin{x}}{\cos{x}} = \dfrac{\sin{y}}{\cos{y}} \)
İçler - dışlar çarpımı yapalım.
\( \sin{x}\cos{y} = \cos{x}\sin{y} \)
\( \sin{x}\cos{y} - \cos{x}\sin{y} = 0 \)
Eşitliğin sol tarafı sinüs fark formülüne eşittir.
\( \sin(x - y) = 0 \)
Sinüs esas ölçüsü \( 0 \) ve \( \pi \) olan açılarda sıfır olur.
\( k \in \mathbb{Z} \) olmak üzere,
\( x - y = \pi k \)
\( x = y + \pi k \)
Bu çözüm iki açının farkının \( \pi \)'nin bir tam sayı katı olması anlamına gelir.
Benzer bir ispat \( \cot{x} = \cot{y} \) eşitliği için de yapılabilir.
\( \sin{x} = \cos{y} \) ya da \( \tan{x} = \cot{y} \) formundaki denklemler fonksiyonlardan biri tümler açı özdeşliği ile diğerine dönüştürüldükten sonra yukarıdaki yöntemlerle çözülebilir.
\( \frac{\pi}{2} \le x \lt \pi \) olmak üzere,
\( \tan(2x - 21°) = \cot(3x - 34°) \) denkleminin çözüm kümesini bulalım.
Tümler açı özdeşliği ile kotanjant ifadesini tanjanta çevirelim.
\( \tan(2x - 21°) = \tan(90° - (3x - 34°)) \)
\( \tan(2x - 21°) = \tan(124° - 3x) \)
\( 2x - 21° = 124° - 3x + 180° k \)
\( x = 29° + 36° k \)
Çözüm kümesi: \( x \in \{101°, 137°, 173°\} \)
\( 0 \le x \le \pi \) olmak üzere,
\( \tan\left( 3x + \dfrac{\pi}{2} \right) = \tan{x} \)
denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİki tanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
Durum 1: Açıların farkı \( \pi \)'nin bir tam sayı katıdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( 3x + \dfrac{\pi}{2} = x + \pi k \)
\( 2x = -\dfrac{\pi}{2} + \pi k \)
\( x = -\dfrac{\pi}{4} + \dfrac{\pi}{2} k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, \pi] \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{4}, \dfrac{3\pi}{4} \right\} \)
\( 0 \le x \lt 2 \pi \) olmak üzere,
\( \tan\left( 2x + \dfrac{\pi}{4} \right) = \cot{\dfrac{\pi}{8}} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitliğin sağ tarafındaki kotanjant ifadesini tanjant cinsinden yazalım.
Tümler açıların tanjant - kotanjant değerleri birbirine eşittir.
\( \tan\left( 2x + \dfrac{\pi}{4} \right) = \tan\left( \dfrac{\pi}{2} - \dfrac{\pi}{8} \right) \)
\( \tan\left( 2x + \dfrac{\pi}{4} \right) = \tan{\dfrac{3\pi}{8}} \)
İki tanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
Durum 1: Açıların farkı \( \pi \)'nin bir tam sayı katıdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x + \dfrac{\pi}{4} = \dfrac{3\pi}{8} + \pi k \)
\( 2x = \dfrac{\pi}{8} + \pi k \)
\( x = \dfrac{\pi}{16} + \dfrac{\pi}{2} k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, 2\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{16}, \dfrac{9\pi}{16}, \dfrac{17\pi}{16}, \dfrac{25\pi}{16} \right\} \)
\( \pi \le x \le 2\pi \) olmak üzere,
\( \tan(8x) - \tan(4x) = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \tan(8x) = \tan(4x) \)
İki tanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
Durum 1: Açıların farkı \( \pi \)'nin bir tam sayı katıdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( 8x = 4x + \pi k \)
\( 4x = \pi k \)
\( x = \dfrac{\pi}{4} k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [\pi, 2\pi] \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \left\{\pi, \dfrac{5\pi}{4}, \dfrac{3\pi}{2}, \dfrac{7\pi}{4}, 2\pi \right\} \)
\( 180° \le x \lt 360° \) olmak üzere,
\( \sin(5x - 30°) = \sin(3x + 10°) \)
denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİki sinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 5x - 30° = 3x + 10° + 360° k \)
\( 2x = 40° + 360° k \)
\( x = 20° + 180° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 5x - 30° = (180° - (3x + 10°)) + 360° k \)
\( 8x = 200° + 360° k \)
\( x = 25° + 45° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [\pi, 2\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 200°, 205°, 250°, 295°, 340° \} \)
\( 0 \le x \lt \pi \) olmak üzere,
\( \cos(5x - 10°) = \sin(x - 20°) \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterEşitliğin sağ tarafındaki sinüs ifadesini kosinüs cinsinden yazalım.
Tümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( \cos(5x - 10°) = \cos(90° - (x - 20°)) \)
\( \cos(5x - 10°) = \cos(110° - x) \)
İki kosinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 5x - 10° = 110° - x + 360° k \)
\( 6x = 120° + 360° k \)
\( x = 20° + 60° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 5x - 10° = (360° - (110° - x)) + 360 k \)
\( 4x = 260° + 360° k \)
\( x = 65° + 90° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0, \pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 20°, 65°, 80°, 140°, 155° \} \)
\( 0° \le x \lt 180° \) olmak üzere,
\( \sin(6x) = \sin(3x) \)
denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİki sinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( 6x = 3x + 360° k \)
\( 3x = 360° k \)
\( x = 120° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 6x = (180° - 3x) + 360° k \)
\( 9x = 180° + 360° k \)
\( x = 20° + 40° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 0°, 20°, 60°, 100°, 120°, 140° \} \)
\( 0° \lt x \lt 360° \) olmak üzere,
\( \cos(23x) = \cos(22x) \)
denkleminin çözüm kümesi kaç elemanlıdır?
Çözümü Gösterİki kosinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 23x = 22x + 360° k \)
\( x = 360°k \)
Durum 2: Birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 23x = (360° - 22x) + 360° k \)
\( 45x = 360° + 360° k \)
\( x = 8° + 8° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( (0°, 360°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{8°, 16°, 24°, 32°, \ldots, 352°\} \)
Çözüm kümesinin eleman sayısı, terim sayısı formülü ile \( \frac{352 - 8}{8} + 1 = 44 \) olarak bulunur.
\( 0° \le x \lt 180° \) olmak üzere,
\( \sin(7x) + \sin(5x) = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \sin(7x) = -\sin(5x) \)
\( \sin(-x) = -\sin{x} \) olduğu için eşitliğin sağındaki negatif işaretini sinüs fonksiyonunun içine alabiliriz.
\( \sin(7x) = \sin(-5x) \)
İki sinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 7x = -5x + 360° k \)
\( 12x = 360° k \)
\( x = 30° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 7x = (180° - (-5x)) + 360° k \)
\( 2x = 180° + 360° k \)
\( x = 90° + 180° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{0°, 30°, 60°, 90°, 120°, 150°\} \)
\( 45° \le x \le 90° \) olmak üzere,
\( \tan(11x) + \tan(7x) = 0 \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \tan(11x) = -\tan(7x) \)
\( \tan(-x) = -\tan{x} \) olduğu için eşitliğin sağındaki negatif işaretini tanjant fonksiyonunun içine alabiliriz.
\( \tan(11x) = \tan(-7x) \)
İki tanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
Durum 1: Açıların farkı \( 180° \)'nin bir tam sayı katıdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( 11x = -7x + 180° k \)
\( 18x = 180° k \)
\( x = 10° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [45°, 90°] \)aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 50°, 60°, 70°, 80° \} \)
\( x = 90° \) sorudaki her iki tanjant ifadesini de tanımsız yaptığı için çözüm kümesine dahil değildir.
\( \tan(11 \cdot 90°) = \tan{990°} = \tan{270°} \)
\( \tan(7 \cdot 90°) = \tan{630°} = \tan{270°} \)
\( 0° \le x \lt 360° \) olmak üzere,
\( \sin(2x + 48°) + 2\sin^2{42°} = 1 \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \sin(2x + 48°) = 1 - 2\sin^2(42°) \)
Kosinüs iki kat açı formülünü kullanalım.
\( \sin(2x + 48°) = \cos{84°} \)
Tümler açıların sinüs - kosinüs değerleri birbirine eşittir.
\( \sin(2x + 48°) = \sin{6°} \)
İki sinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x + 48° = 6° + 360° k \)
\( 2x = -42° + 360° k \)
\( x = -21° + 180° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 180° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 2x + 48° = (180° - 6°) + 360° k \)
\( 2x = 126° + 360° k \)
\( x = 63° + 180° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0°, 360°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{63°, 159°, 243°, 339°\} \)
\( \tan(3x - 60°)\cot(x + 10°) = 1 \)
eşitliğini sağlayan en büyük negatif \( x \) açısı kaç derecedir?
Çözümü Göster\( \tan(3x - 60°) = \dfrac{1}{\cot(x + 10°)} \)
\( \tan{\alpha}\cot{\alpha} = 1 \) özdeşliğini kullanarak eşitliği aşağıdaki şekilde yazabiliriz.
\( \tan(3x - 60°) = \tan(x + 10°) \)
İki tanjant ifadesi arasındaki eşitlikte tek çözüm vardır.
Durum 1: Açıların farkı \( 180° \)'nin bir tam sayı katıdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( 3x - 60° = (x + 10°) + 180° k \)
\( 2x = 70° + 180° k \)
\( x = 35° + 90° k \)
Buna göre denklemi sağlayan en büyük negatif \( x \) açısı \( k = -1 \) için \( -55° \) olarak bulunur.
\( 0° \le x \lt 180° \) olmak üzere,
\( \cos(5x) = \cos{110°} + \cos{10°} \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterKosinüs toplam ve fark formüllerini kullanalım.
\( \cos(5x) = \cos(60° + 50°) + \cos(60° - 50°) \)
\( \cos(5x) = (\cos{60°}\cos{50°} - \sin{60°}\sin{50°}) + (\cos{60°}\cos{50°} + \sin{60°}\sin{50°}) \)
\( \cos(5x) = 2\cos{60°}\cos{50°} \)
\( \cos(5x) = 2 \cdot \dfrac{1}{2} \cdot \cos{50°} \)
\( \cos(5x) = \cos{50°} \)
İki kosinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 5x = 50° + 360° k \)
\( x = 10° + 72° k \)
Durum 2: Birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 5x = (360° - 50°) + 360° k \)
\( 5x = 310° + 360° k \)
\( x = 62° + 72° k \)
Bulduğumuz genel çözüm değerlerinden soruda verilen \( [0°, 180°) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{ 10°, 62°, 82°, 134°, 154° \} \)
\( \cos(2x) = \cos(x^2) \) ifadesini derece cinsinden sağlayan en küçük iki pozitif \( x \) değerinin toplamı kaçtır?
Çözümü Gösterİki kosinüs ifadesi arasındaki eşitlikte iki farklı çözüm vardır.
Durum 1: Açıların esas ölçüleri birbirine eşittir.
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = x^2 + 360° k \)
En küçük pozitif \( x \) değerlerini bulmak için \( k \in \{-1, 0\} \) değerlerini deneyelim.
\( k = 0 \) için:
\( 2x = x^2 + 360° (0) \)
\( x^2 - 2x = 0 \)
\( x(x - 2) = 0 \)
\( x \in \{ 0°, 2° \} \)
\( k = -1 \) için:
\( 2x = x^2 + 360° (-1) \)
\( x^2 - 2x - 360 = 0 \)
\( (x + 18)(x - 20) = 0 \)
\( x \in \{ -18°, 20° \} \)
Durum 2: Birinci açı ile ikinci açıyı \( 360° \)'ye tamamlayan açının esas ölçüleri birbirine eşittir.
\( 2x = (360° - x^2) + 360° k \)
En küçük pozitif \( x \) değerlerini bulmak için \( k \in \{-1, 0\} \) değerlerini deneyelim.
\( k = 0 \) için:
\( 2x = (360° - x^2) + 360° (0) \)
\( x^2 + 2x - 360° = 0 \)
\( (x + 20)(x - 18) = 0 \)
\( x \in \{ -20°, 18° \} \)
\( k = -1 \) için:
\( 2x = (360° - x^2) + 360° (-1) \)
\( x^2 + 2x = 0 \)
\( x(x + 2) = 0 \)
\( x \in \{ -2°, 0° \} \)
Buna göre verilen eşitliği sağlayan en küçük iki pozitif \( x \) değeri \( 2° \) ve \( 18° \) olur.
\( 2 + 18 = 20° \) bulunur.
Diğer Denklemler
Diğer bazı denklemler yukarıda bahsettiğimiz iki forma uymasa da her biri bu iki formdan birinde olan ifadelerin çarpımı şeklinde yazılabilir.
\( (2\sin{x} + 1)(\tan{x} - \sqrt{3}) = 0 \)
\( \sin{x}\cos(2x) = 0 \)
\( \sin{\frac{x}{2}}(\cos{x} - \cos{\frac{\pi}{3}}) = 0 \)
Bu tip denklemler aşağıdaki adımlar takip edilerek çözülebilir.
- Denklemin tüm terimleri eşitliğin sol tarafında toplanarak ifade sıfıra eşitlenir.
- Eşitliğin sol tarafı her bir çarpan \( a\sin{x} + b \) ya da \( \sin{x} - \sin{y} \) formunda olacak şekilde çarpanlarına ayrılmaya çalışılır.
- Her çarpan ifadeyi sıfır yapan değişken değerleri için çözülür.
- Denklemin çözümü tüm çarpanların çözümlerinin birleşim kümesidir.
\( 0 \le x \lt 2\pi \) olmak üzere,
\( 2\cos^2{x} + \sin{x} - 2 = 0 \) denkleminin çözüm kümesini bulalım.
Kosinüs ifadesini sinüs cinsinden yazalım.
\( 2(1 - \sin^2{x}) + \sin{x} - 2 = 0 \)
\( \sin{x}(2\sin{x} - 1) = 0 \)
Çarpanların her birini sıfır yapan değişken değerlerini bulalım.
Çarpan 1: \( \sin{x} = 0 \)
\( k \in \mathbb{Z} \) olmak üzere,
\( x_1 = \pi k \)
Çarpan 2: \( 2\sin{x} - 1 = 0 \)
\( \sin{x} = \dfrac{1}{2} \)
\( x_2 = \dfrac{\pi}{6} + 2\pi k \)
\( x_3 = \dfrac{5\pi}{6} + 2\pi k \)
Bulunan genel çözüm değerlerinden soruda verilen \( [0, 2\pi) \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{0, \frac{\pi}{6}, \frac{5\pi}{6}, \pi\} \)
Bir trigonometrik ifadeyi çarpanlarına ayırmak için trigonometrik özdeşlikler ve dönüşüm formülleri sıklıkla kullanılır.
\( 0 \le x \le \pi \) olmak üzere,
\( \sin(2x) = \tan{x} \) denkleminin çözüm kümesini bulalım.
Sinüs iki kat açı formülünü kullanalım.
\( 2\sin{x}\cos{x} = \dfrac{\sin{x}}{\cos{x}} \)
Çözüm kümesinde \( \cos{x} = 0 \) yapan \( x \) değerleri bulunamayacağını not ederek tarafları \( \cos{x} \) ile çarpalım.
\( 2\sin{x}\cos^2{x} = \sin{x} \)
\( 2\sin{x}\cos^2{x} - \sin{x} = 0 \)
\( \sin{x}(2\cos^2{x} - 1) = 0 \)
Parantez içindeki ifade kosinüs iki kat açı formülünün açılımıdır.
\( \sin{x}\cos(2x) = 0 \)
Çarpanların her birini sıfır yapan değişken değerlerini bulalım.
Çarpan 1: \( \sin{x} = 0 \)
\( k \in \mathbb{Z} \) olmak üzere,
\( x_1 = \pi k \)
Çarpan 2: \( \cos(2x) = 0 \)
\( 2x_2 = \dfrac{\pi}{2} + \pi k \)
\( x_2 = \dfrac{\pi}{4} + \dfrac{\pi}{2} k \)
Bulunan genel çözüm değerlerinden soruda verilen \( [0, \pi] \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( x \in \{0, \frac{\pi}{4}, \frac{3\pi}{4}, \pi\} \)
Denklem Çözümlerinin Grafik Yorumu
Trigonometrik fonksiyonların grafikleri denklemlerin çözümünde ve bulunan bir çözümün sağlamasını yapmak için sıklıkla kullanılır.
Aşağıda örnek bir trigonometrik denklem ve çözüm kümesi verilmiştir.
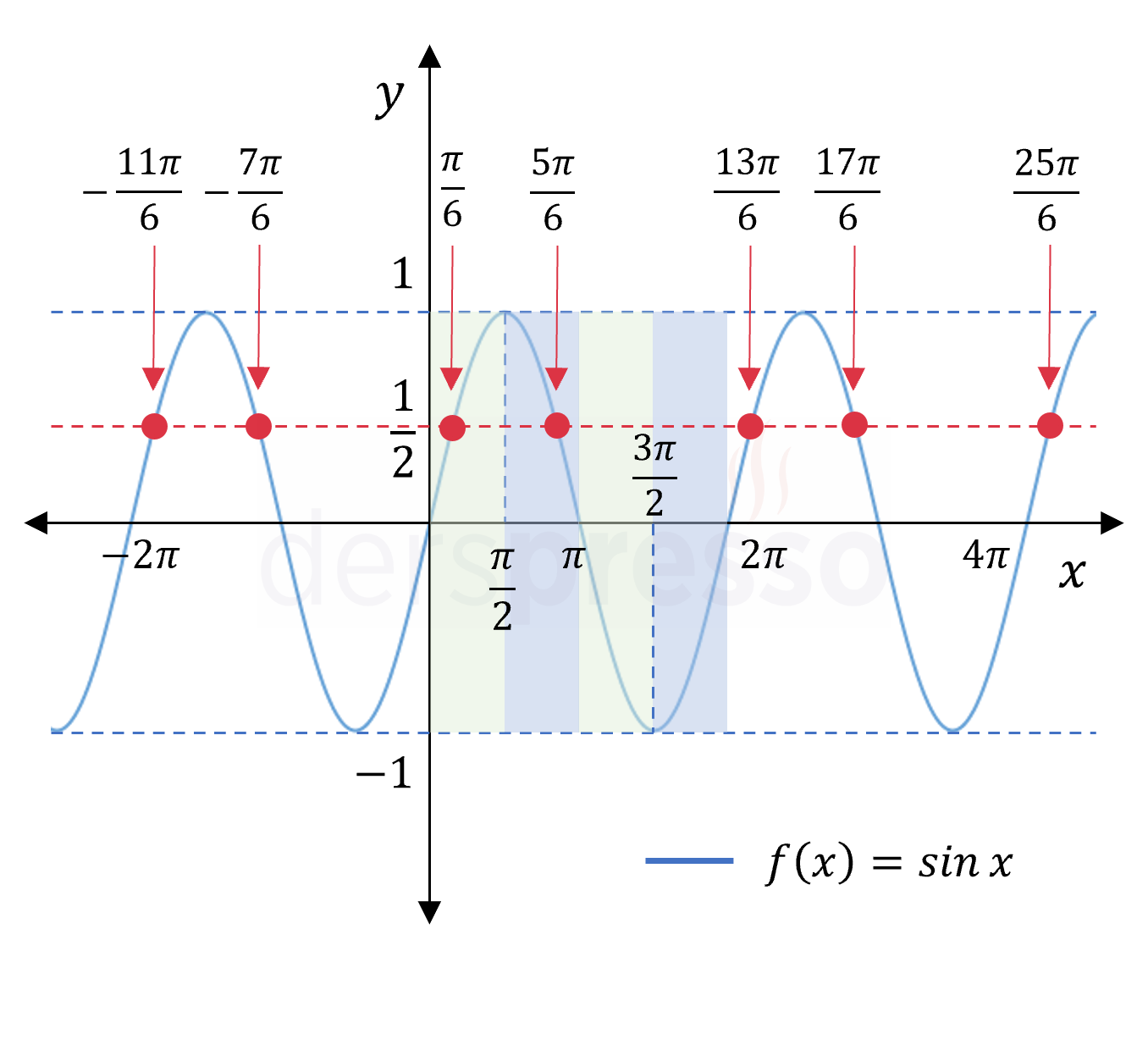
\( \sin(x) = \frac{1}{2} \)
Genel çözüm: \( x = \{ \frac{\pi}{6} + 2\pi k \} \cup \{ \frac{5\pi}{6} + 2\pi k \} \)
Aşağıdaki grafikte görebileceğimiz gibi, çözüm kümesi \( f(x) = \sin(x) \) fonksiyon grafiği ile \( y = \frac{1}{2} \) doğrusunun kesişim noktaları olmaktadır. Bu grafikte aynı zamanda \( [0, 2\pi) \) arasındaki her bir çözüm değerinin her periyotta tekrar eden sonsuz çözüme karşılık geldiğini görebiliriz.
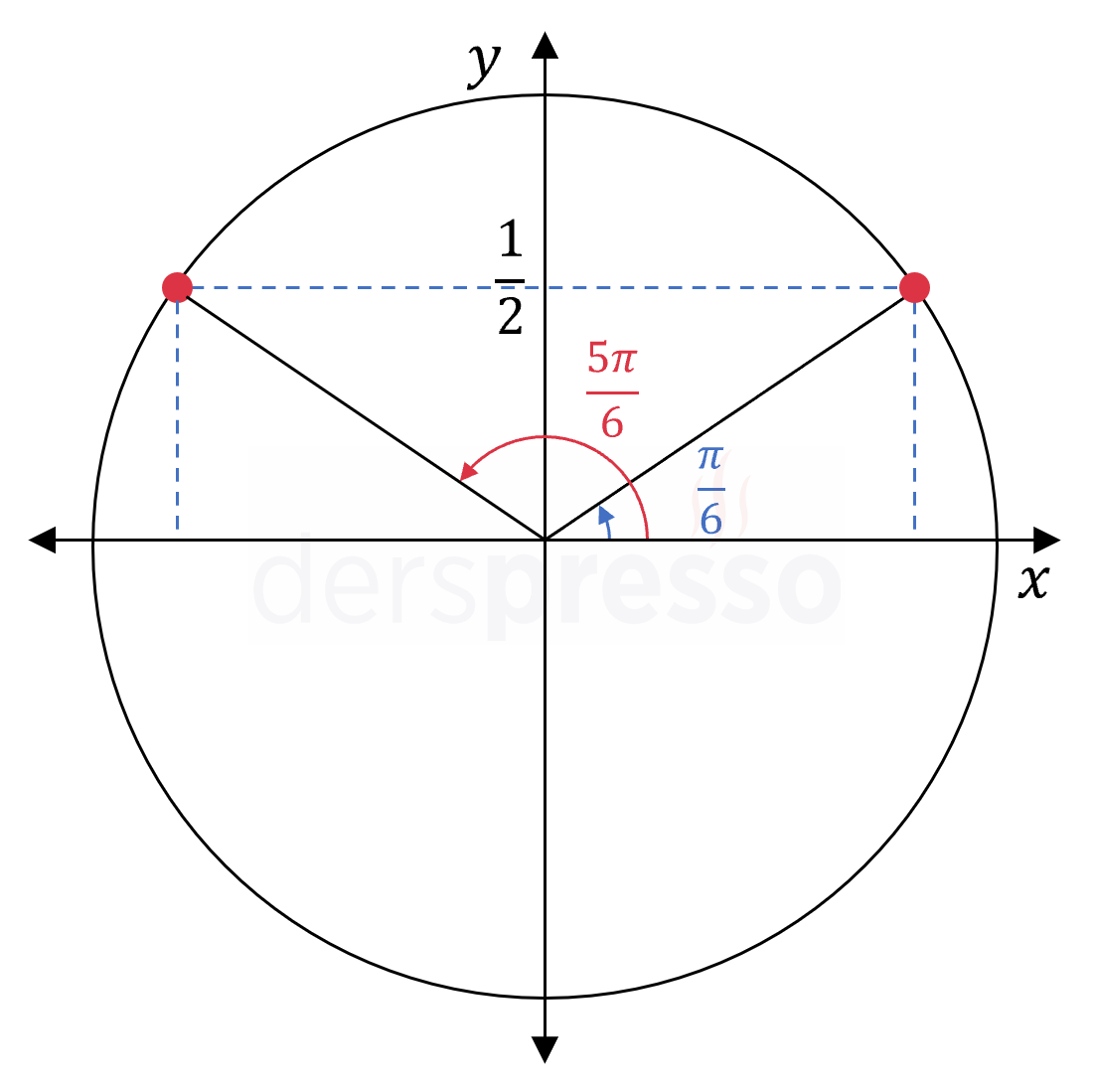
Denklem Çözümlerinin Birim Çember Yorumu
Yukarıdaki örnekteki denklemin çözümü birim çember üzerinde de gösterilebilir.
Birim çember üzerindeki bir noktanın ordinat değeri o noktanın karşılık geldiği yönlü açının sinüs değerine eşit olduğu için, birim çember üzerinde \( y = \frac{1}{2} \) olan noktalara ait açılar bu denklemin çözüm kümesini verir.
\( D \): Saat 00:00'dan başlayarak \( t \). saatte suyun metre cinsinden derinliği olmak üzere,
Belirli bir günde bir sahildeki suyun derinliği aşağıdaki fonksiyona göre değişmektedir.
\( D = 8 - 4\sin{\dfrac{\pi t}{6}} \)
Buna göre günün ikinci yarısında sahildeki suyun derinliğinin 6 metre olduğu saatleri bulunuz.
Çözümü GösterSuyun derinliğinin 6 metre olduğu saatleri bulmak için \( D = 6 \) yazalım.
\( 6 = 8 - 4\sin{\dfrac{\pi t}{6}} \)
\( \sin{\dfrac{\pi t}{6}} = \dfrac{1}{2} \)
Sinüs fonksiyonunun periyodu \( 2\pi \)'dir.
Sinüs fonksiyonu \( \frac{1}{2} \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{\pi}{6}, \dfrac{5\pi}{6} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( \dfrac{\pi}{6} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{\pi t}{6} = \dfrac{\pi}{6} + 2\pi k \)
\( t = 1 + 12k \)
Durum 2:
\( \dfrac{5\pi}{6} \) için:
\( \dfrac{\pi t}{6} = \dfrac{5\pi}{6} + 2\pi k \)
\( t = 5 + 12k \)
Bulduğumuz genel çözüm değerlerinden günün ikinci yarısına karşılık gelen \( [12, 24] \) aralığında bulunan değerler denklemin çözüm kümesini verir.
Çözüm kümesi: \( t \in \{13, 17\} \)
Buna göre sahildeki suyun derinliği öğleden sonra saat 13:00 ve 17:00'de 6 metre olur.
\( 0 \le x \le 2\pi \) olmak üzere,
\( \tan\left( \dfrac{\pi}{2}\cos{x} \right) = 1 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterDenklemi önce tanjant fonksiyonu için çözelim.
Tanjant fonksiyonunun periyodu \( \pi \)'dir.
Tanjant fonksiyonu \( 1 \) değerini bir tam periyodu içinde aşağıdaki açı değerlerinde alır.
\( \left\{ \dfrac{\pi}{4} \right\} \)
Bu açı ölçülerine fonksiyonun periyodunun tam sayı katlarını ekleyerek denklemin genel çözümünü bulalım.
Durum 1:
\( \dfrac{\pi}{4} \) için:
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{\pi}{2}\cos{x} = \dfrac{\pi}{4} + \pi k \)
\( \cos{x} = \dfrac{1}{2} + 2k \)
Kosinüs fonksiyonunun değer aralığı \( [-1, 1] \) olduğu için sadece \( k = 0 \) için geçerli bir kosinüs değeri vardır.
\( \cos{x} = \dfrac{1}{2} \)
Kosinüs fonksiyonu \( [0, 2\pi] \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{3}, \dfrac{5\pi}{3} \right\} \)
\( 0 \le x \le \dfrac{\pi}{2} \) olmak üzere,
\( 16^{\sin^2{x}} + 16^{\cos^2{x}} = 10 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterPisagor özdeşliğini kullanalım.
\( 16^{\sin^2{x}} + 16^{1 - \sin^2{x}} = 10 \)
\( 16^{\sin^2{x}} + \dfrac{16}{16^{\sin^2{x}}} = 10 \)
\( 16^{\sin^2{x}} = t \) şeklinde değişken değiştirelim.
\( t + \dfrac{16}{t} = 10 \)
\( t^2 + 16 = 10t \)
\( t^2 - 10t + 16 = 0 \)
\( (t - 2)(t - 8) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
Durum 1:
\( t - 2 = 0 \)
\( t = 2 = 16^{\sin^2{x}} \)
\( 2^{4\sin^2{x}} = 2^1 \)
Tabanları eşit ve -1, 0, 1'den farklı iki üslü ifadenin eşitliğinde üsler birbirine eşittir.
\( 4\sin^2{x} = 1 \)
\( \sin^2{x} = \dfrac{1}{4} \)
\( [0, \frac{\pi}{2}] \) aralığında sinüs pozitif olur.
\( \sin{x} = \dfrac{1}{2} \)
Sinüs fonksiyonu \( [0, \frac{\pi}{2}] \) aralığında \( \frac{1}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x = \dfrac{\pi}{6} \)
Durum 2:
\( t - 8 = 0 \)
\( t = 8 = 16^{\sin^2{x}} \)
\( 2^{4\sin^2{x}} = 2^3 \)
\( 4\sin^2{x} = 3 \)
\( \sin^2{x} = \dfrac{3}{4} \)
\( [0, \frac{\pi}{2}] \) aralığında sinüs pozitif olur.
\( \sin{x} = \dfrac{\sqrt{3}}{2} \)
Sinüs fonksiyonu \( [0, \frac{\pi}{2}] \) aralığında \( \frac{\sqrt{3}}{2} \) değerini aşağıdaki açı ölçülerinde alır.
\( x = \dfrac{\pi}{3} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{6}, \dfrac{\pi}{3} \right\} \)
\( \cos{x} + x^2 = 0 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \cos{x} = -x^2 \)
Bu denklemin çözümü cebirsel olarak kolay olmadığı için eşitliğin iki tarafındaki fonksiyonların grafiklerini çizerek kesişim noktalarını bulmaya çalışalım.
Kosinüs fonksiyonu \( [-1, 1] \) aralığında değer alır.
\( -x^2 \) fonksiyonu tepe noktası orijinde olan ve kolları aşağı yönlü bir paraboldür.
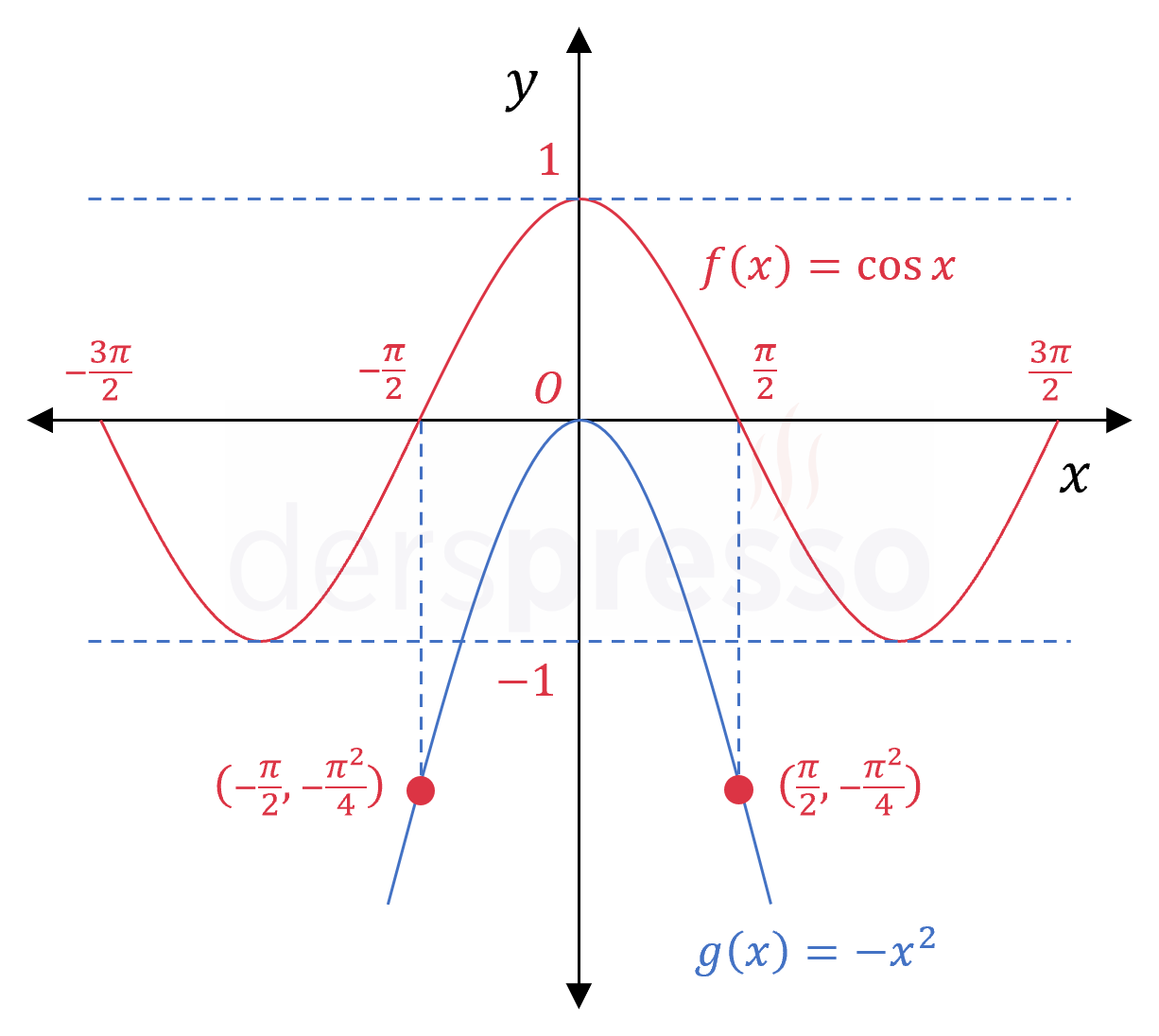
Grafik çiziminden iki fonksiyonun hiçbir noktada kesişmedikleri gözükse de bundan aşağıdaki şekilde emin olabiliriz.
Kosinüs grafiğinin negatif tarafa geçtiği \( x = -\frac{\pi}{2} \) ve \( x = \frac{\pi}{2} \) noktalarında parabol \( y = -\frac{\pi^2}{4} \approx -2,46 \) ordinat değerli noktalardan geçer. Bu iki nokta da kosinüs fonksiyonunun değer aralığının alt sınırı olan \( -1 \)'den küçüktür, dolayısıyla iki fonksiyon hiçbir noktada kesişmezler.
Çözüm kümesi: \( x \in \emptyset \)
\( 0 \le x \lt 2\pi \) olmak üzere,
\( (\sqrt{31 + 8\sqrt{15}})^{\sin{x}} + (\sqrt{31 - 8\sqrt{15}})^{\sin{x}} = 8 \)
denkleminin çözüm kümesini bulunuz.
Çözümü GösterBirinci terimin kök içini bir ifadenin parantez karesi şeklinde yazalım.
\( \sqrt{31 + 8\sqrt{15}} = \sqrt{31 + 2\sqrt{240}} \)
\( = \sqrt{16 + 15 + 2\sqrt{16}\sqrt{15}} \)
\( = \sqrt{(\sqrt{16} + \sqrt{15})^2} \)
\( = \sqrt{16} + \sqrt{15} = 4 + \sqrt{15} \)
Aynı işlemi ikinci terime uygulayalım.
\( \sqrt{31 - 8\sqrt{15}} = 4 - \sqrt{15} \)
Buna göre denklem aşağıdaki şekilde sadeleşir.
\( (4 + \sqrt{15})^{\sin{x}} + (4 - \sqrt{15})^{\sin{x}} = 8 \)
\( (4 - \sqrt{15})(4 + \sqrt{15}) = 1 \) özdeşliğinde birinci çarpanı yalnız bırakalım.
\( 4 - \sqrt{15} = \dfrac{1}{4 + \sqrt{15}} \)
Bu ifadeyi denklemde yerine koyalım.
\( (4 + \sqrt{15})^{\sin{x}} + \left( \dfrac{1}{4 + \sqrt{15}} \right)^{\sin{x}} = 8 \)
\( (4 + \sqrt{15})^{\sin{x}} + \dfrac{1}{(4 + \sqrt{15})^{\sin{x}}} = 8 \)
\( (4 + \sqrt{15})^{\sin{x}} = t \) şeklinde değişken değiştirelim.
\( t + \dfrac{1}{t} = 8 \)
\( t^2 + 1 = 8t \)
\( t^2 - 8t + 1 = 0 \)
İkinci dereceden denklemlerde kök bulma formülü ile kökleri bulalım.
\( t_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( = \dfrac{-(-8) \pm \sqrt{(-8)^2 - 4(1)(1)}}{2} \)
\( = \dfrac{8 \pm \sqrt{60}}{2} \)
\( = 4 \pm \sqrt{15} \)
Bulduğumuz değeri \( t \) değişkeninin değerine eşitleyelim.
\( (4 + \sqrt{15})^{\sin{x}} = t_1 = 4 + \sqrt{15} \) için:
\( \sin{x} = 1 \)
\( (4 + \sqrt{15})^{\sin{x}} = t_2 = 4 - \sqrt{15} \) için:
\( (4 + \sqrt{15})^{\sin{x}} = 4 - \sqrt{15} = \dfrac{1}{4 + \sqrt{15}} \)
\( (4 + \sqrt{15})^{\sin{x}} = (4 + \sqrt{15})^{-1} \)
\( \sin{x} = -1 \)
Buna göre \( \sin{x} \) için çözüm kümesi aşağıdaki gibidir.
\( \sin{x} = \pm 1 \)
Sinüs fonksiyonu \( [0, 2\pi) \) aralığında \( \pm 1 \) değerlerini aşağıdaki açı ölçülerinde alır.
Çözüm kümesi: \( x \in \left\{ \dfrac{\pi}{2}, \dfrac{3\pi}{2} \right\} \)