Parabolün Simetriği
Konu tekrarı için: Simetri Tipleri | Noktanın Simetriği
Bir parabolün eksenlere, bir doğruya ya da bir noktaya göre simetriğini bulmak için o parabolün denklemindeki değişkenlere belirli dönüşümler uygulanır.
Bir parabolün bir noktaya göre simetriği, parabolün üzerindeki her bir noktanın simetri noktasına göre simetriği olan noktalardan oluşur. Benzer şekilde; bir parabolün bir doğruya göre simetriği, parabolün üzerindeki her bir noktanın simetri doğrusuna göre simetriği olan noktalardan oluşur.
Bir parabolün farklı simetrileri için uygulanması gereken dönüşümler aşağıda belirtilmiştir.
\( x \) Eksenine Göre
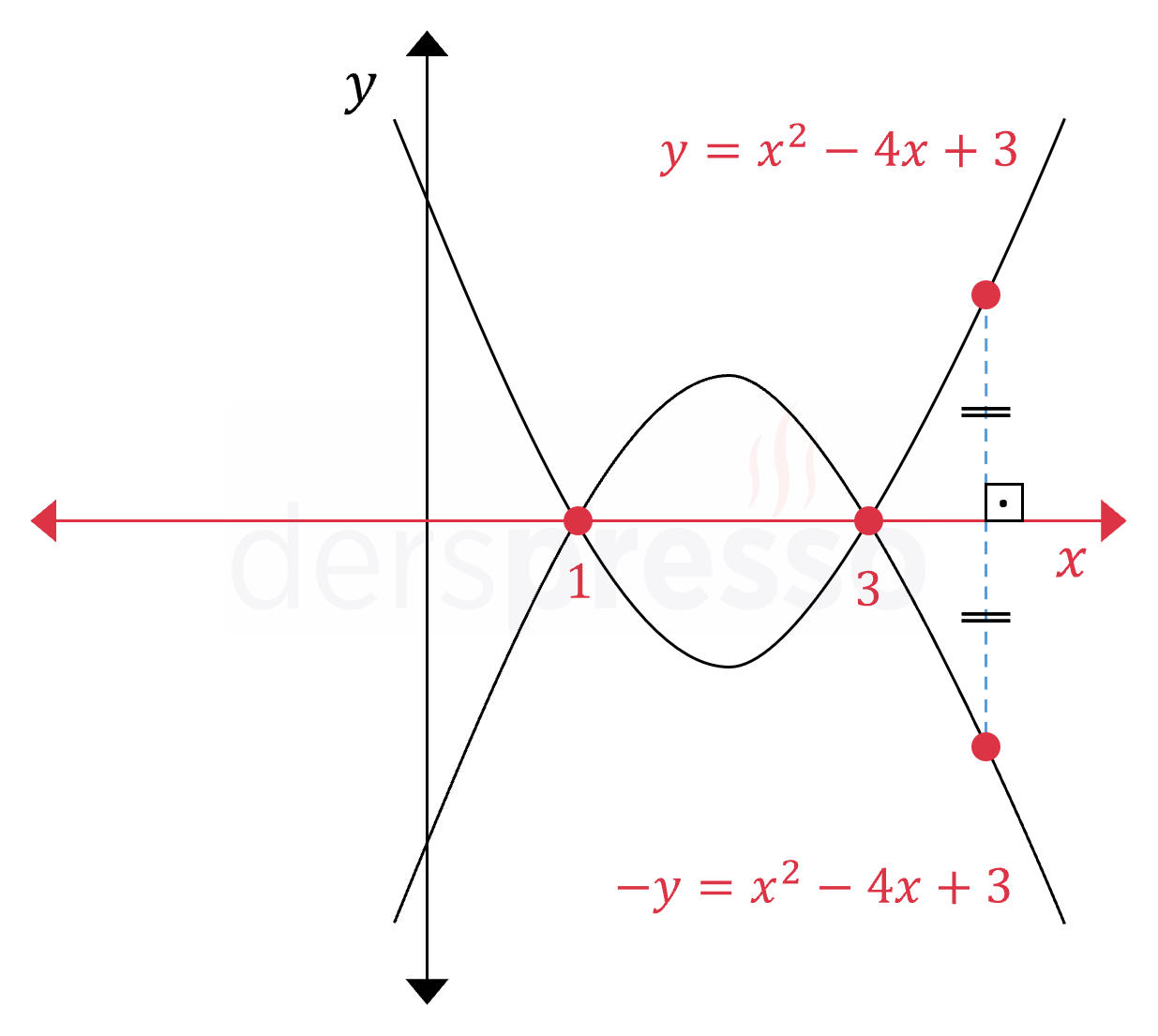
Bir parabolün \( x \) eksenine göre simetriği alınırken denklemde \( y \) işaret değiştirir.
\( y = ax^2 + bx + c \)
\( y \longmapsto -y \)
Simetrik parabolün denklemi:
\( -y = ax^2 + bx + c \)
\( y = x^2 - 4x + 3 \)
Simetrik parabolün denklemi:
\( -y = x^2 - 4x + 3 \)
Parabolün \( x \) eksenini kestiği noktaların bu eksene göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( x \) eksenini aynı noktalarda keser.
\( y \) Eksenine Göre
Bir parabolün \( y \) eksenine göre simetriği alınırken denklemde \( x \) işaret değiştirir.

\( y = ax^2 + bx + c \)
\( x \longmapsto -x \)
Simetrik parabolün denklemi:
\( y = ax^2 - bx + c \)
\( y = x^2 - 4x + 3 \)
Simetrik parabolün denklemi:
\( y = (-x)^2 - 4(-x) + 3 \)
\( y = x^2 + 4x + 3 \)
Parabolün \( y \) eksenini kestiği noktaların bu eksene göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( y \) eksenini aynı noktalarda keser.
Orijine Göre
Bir parabolün orijine göre simetriği alınırken denklemde \( x \) ve \( y \) işaret değiştirir.

\( y = ax^2 + bx + c \)
\( x \longmapsto -x, \quad y \longmapsto -y \)
Simetrik parabolün denklemi:
\( -y = ax^2 - bx + c \)
\( y = x^2 - 4x + 3 \)
Simetrik parabolün denklemi:
\( -y = (-x)^2 - 4(-x) + 3 \)
\( -y = x^2 + 4x + 3 \)
\( y = x \) Doğrusuna Göre
Bir parabolün \( y = x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) yer değiştirir.

\( y = ax^2 + bx + c \)
\( x \longmapsto y, \quad y \longmapsto x \)
Simetrik parabolün denklemi:
\( x = ay^2 + by + c \)
\( y = x^2 - 2x - 3 \)
Simetrik parabolün denklemi:
\( x = y^2 - 2y - 3 \)
Parabolün \( y = x \) doğrusunu kestiği noktaların bu doğruya göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( y = x \) doğrusunu aynı noktalarda keser.
\( y = -x \) Doğrusuna Göre
Bir parabolün \( y = -x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) işaret ve yer değiştirir.

\( y = ax^2 + bx + c \)
\( x \longmapsto -y, \quad y \longmapsto -x \)
Simetrik parabolün denklemi:
\( -x = ay^2 - by + c \)
\( y = x^2 - 4x + 3 \)
Simetrik parabolün denklemi:
\( -x = (-y)^2 - 4(-y) + 3 \)
\( -x = y^2 + 4y + 3 \)
Parabolün \( y = -x \) doğrusunu kestiği noktaların bu doğruya göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( y = -x \) doğrusunu aynı noktalarda keser.
Bir Noktaya Göre
Bir parabolün \( S(m, n) \) noktasına göre simetriği alınırken denklemde \( x \) yerine \( 2m - x \), \( y \) yerine \( 2n - y \) yazılır.
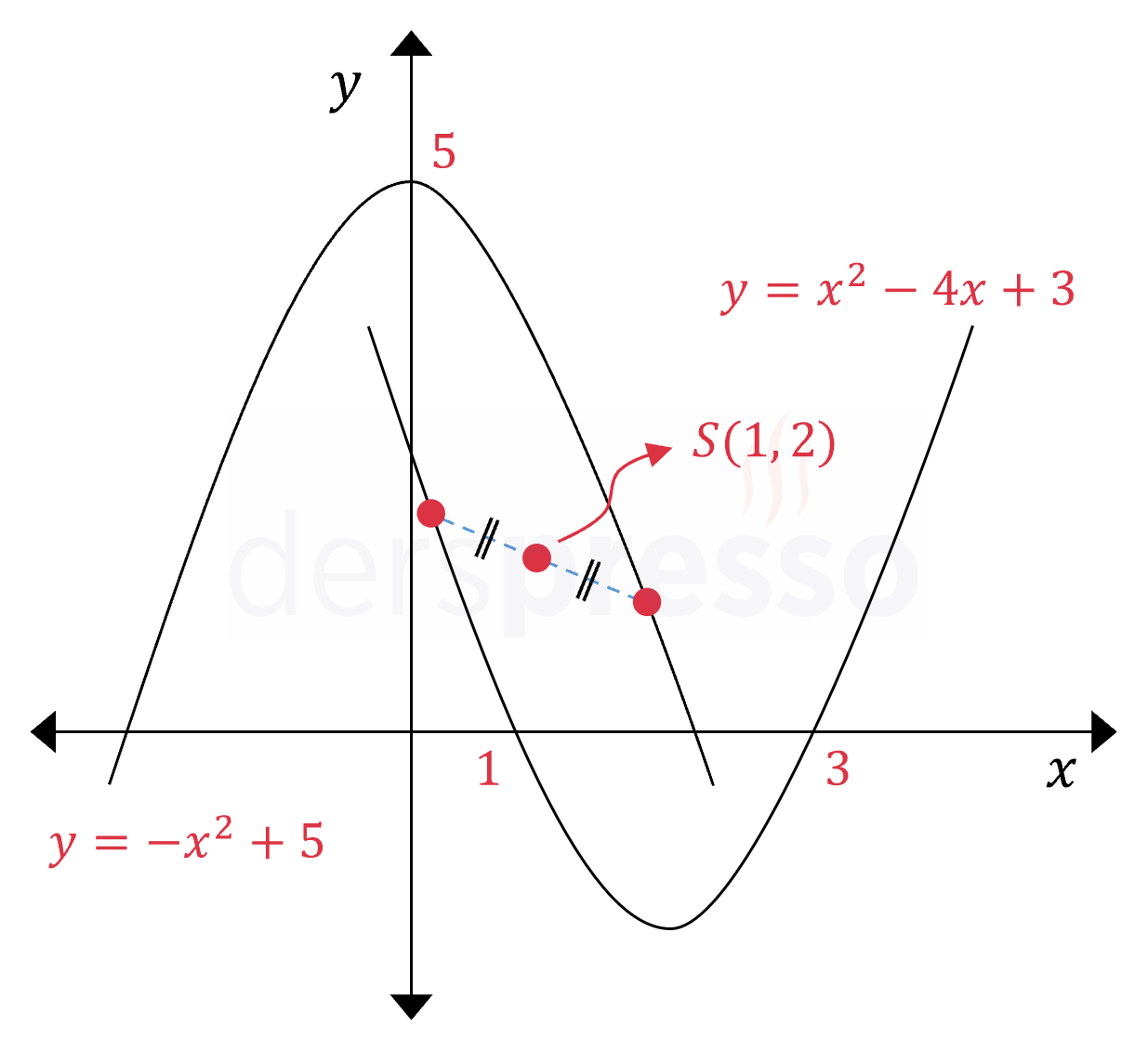
\( y = ax^2 + bx + c \)
Simetri noktası: \( S(m, n) \)
\( x \longmapsto 2m - x, \quad y \longmapsto 2n - y \)
Simetrik parabolün denklemi:
\( 2n - y = a(2m - x)^2 + b(2m - x) + c \)
\( y = x^2 - 4x + 3 \)
Simetri noktası: \( S(1, 2) \)
Simetrik parabolün denklemi:
\( 2(2) - y = (2(1) - x)^2 - 4(2(1) - x) + 3 \)
\( 4 - y = 4 - 4x + x^2 - 8 + 4x + 3 \)
\( y = -x^2 + 5 \)
\( y = n \) Doğrusuna Göre
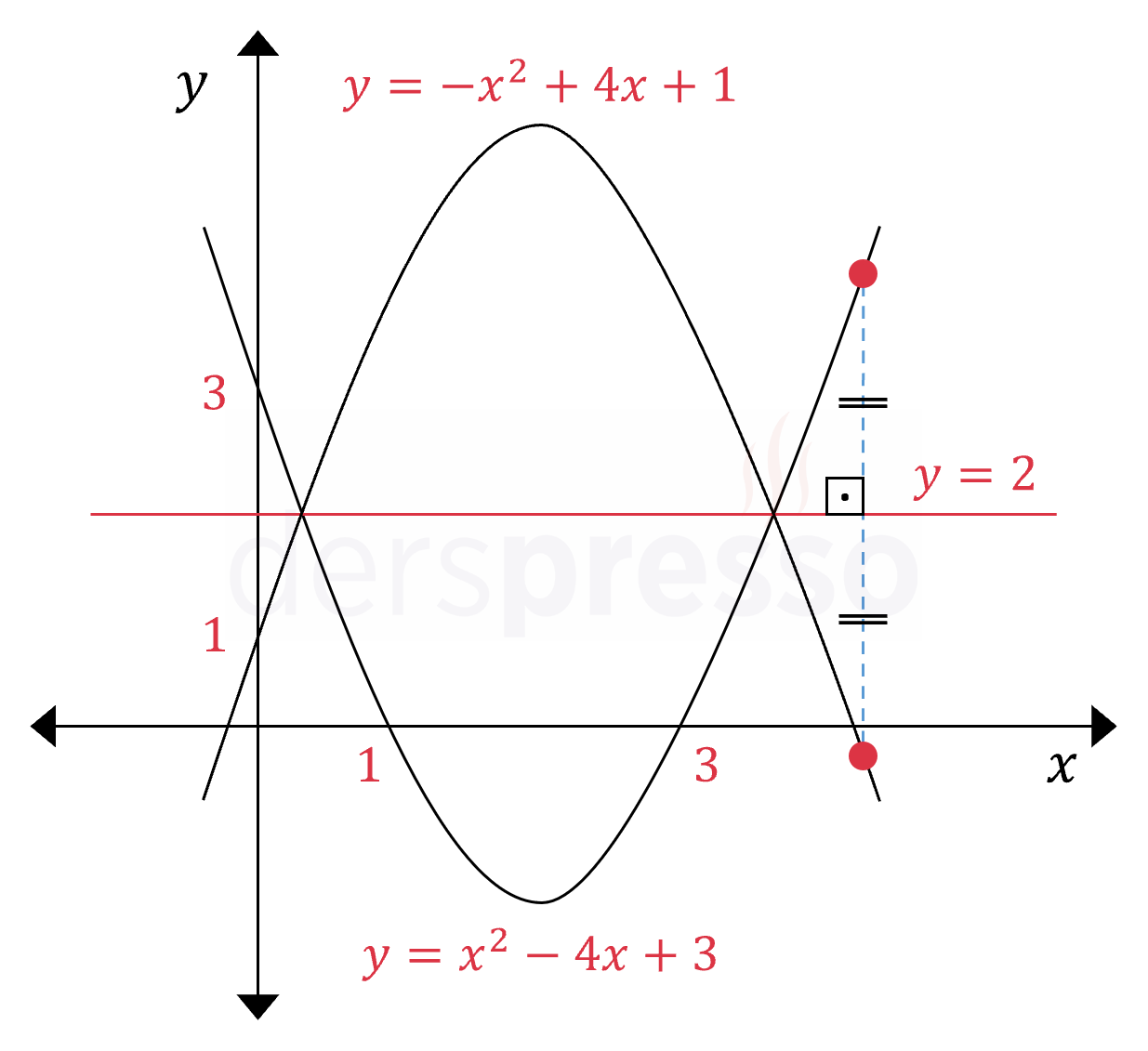
Bir parabolün \( y = n \) doğrusuna göre simetriği alınırken parabolün üzerindeki her noktanın simetri doğrusu üzerinde aynı apsis değerli noktaya göre simetriği alınır.
\( y = ax^2 + bx + c \)
\( y \longmapsto 2n - y \)
Simetrik parabolün denklemi:
\( 2n - y = ax^2 + bx + c \)
\( y = x^2 - 4x + 3 \)
Simetri doğrusu: \( y = 2 \)
Simetrik parabolün denklemi:
\( 2(2) - y = x^2 - 4x + 3 \)
\( 4 - y = x^2 - 4x + 3 \)
\( y = -x^2 + 4x + 1 \)
Parabolün \( y = n \) doğrusunu kestiği noktaların bu doğruya göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( y = n \) doğrusunu aynı noktalarda keser.
\( x = m \) Doğrusuna Göre
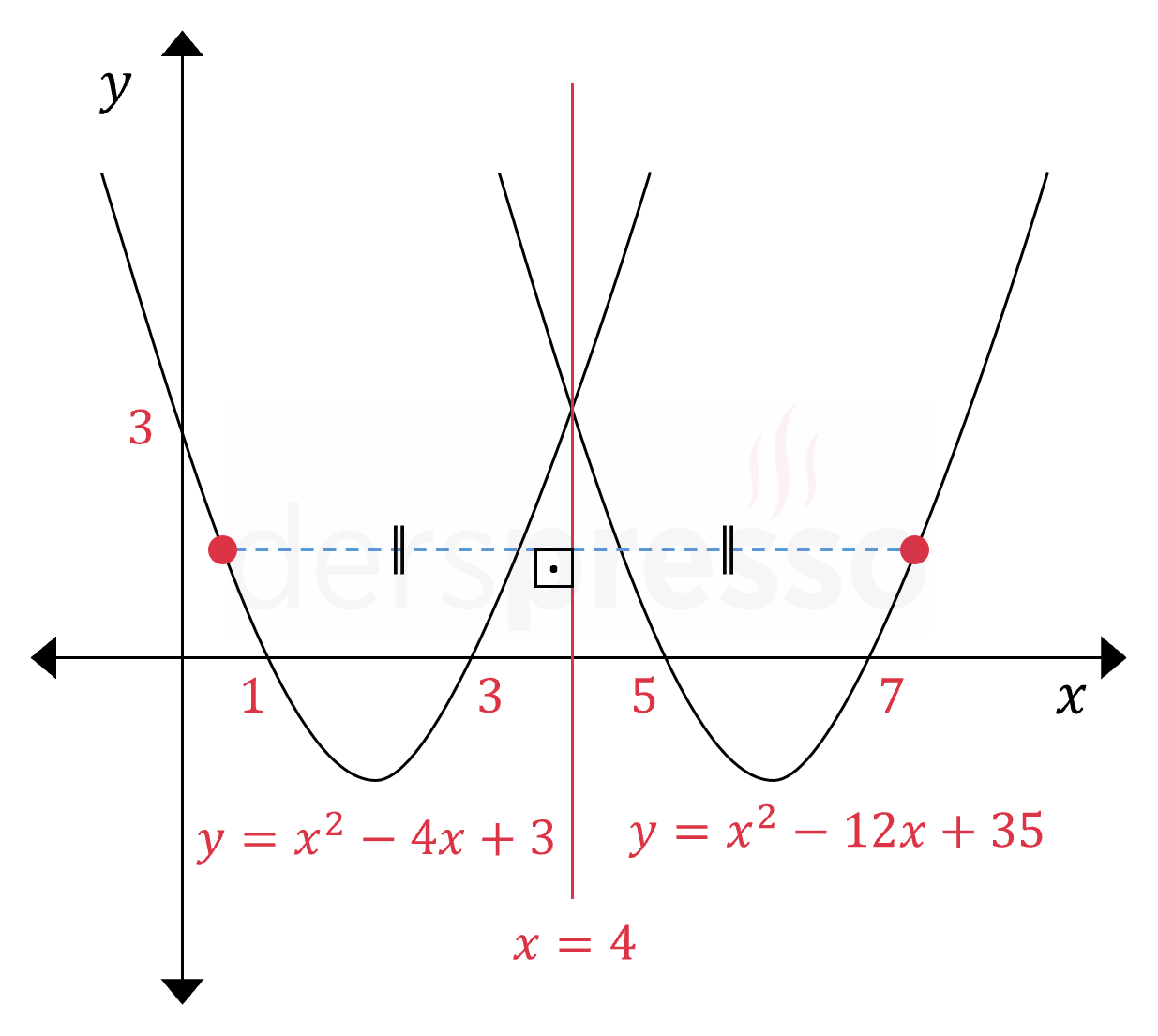
Bir parabolün \( x = m \) doğrusuna göre simetriği alınırken parabolün üzerindeki her noktanın simetri doğrusu üzerinde aynı ordinat değerli noktaya göre simetriği alınır.
\( y = ax^2 + bx + c \)
\( x \longmapsto 2m - x \)
Simetrik parabolün denklemi:
\( y = a(2m - x)^2 + b(2m - x) + c \)
\( y = x^2 - 4x + 3 \)
Simetri doğrusu: \( x = 4 \)
Simetrik parabolün denklemi:
\( y = (2(4) - x)^2 - 4(2(4) - x) + 3 \)
\( y = 64 - 16x + x^2 - 32 + 4x + 3 \)
\( y = x^2 - 12x + 35 \)
Parabolün \( x = m \) doğrusunu kestiği noktaların bu doğruya göre simetriği aynı noktalar olacağı için, parabolün kendisi ve simetriği \( x = m \) doğrusunu aynı noktalarda keser.
\( f(x) = 2x^2 - 3x + 12 \) parabolünün \( x = 5 \) doğrusuna göre simetriği \( g(x) \), \( x = -3 \) doğrusuna göre simetriği \( h(x) \) parabolüdür.
Buna göre \( g(2) + h(0) \) toplamının değeri kaçtır?
Çözümü Göster\( y = ax^2 + bx + c \) parabolünün \( x = m \) doğrusuna göre simetriğinin denklemini bulmak için aşağıdaki dönüşüm uygulanır.
\( x \longmapsto 2m - x \)
\( y = a(2m - x)^2 + b(2m - x) + c \)
Parabolün \( x = 5 \) doğrusuna göre simetriği \( y = g(x) \) parabolüdür.
\( g(x) = 2(2(5) - x)^2 - 3(2(5) - x) + 12 \)
\( g(2) \) değerini bulmak için denklemde \( x = 2 \) yazalım.
\( g(2) = 2(8)^2 - 3(8) + 12 = 116 \)
Parabolün \( x = -3 \) doğrusuna göre simetriği \( y = h(x) \) parabolüdür.
\( h(x) = 2(2(-3) - x)^2 - 3(2(-3) - x) + 12 \)
\( h(0) \) değerini bulmak için denklemde \( x = 0 \) yazalım.
\( h(0) = 2(-6)^2 - 3(-6) + 12 = 102 \)
\( g(2) + h(0) = 116 + 102 = 218 \) bulunur.