Parabolün Köklerinin Konumu
Bir parabol; köklerinin eksenlere, birbirine ve bir reel sayıya göre konumuna göre aşağıdaki şekillerde olabilir.
| Grafik | Köklerin Konumu |
|---|---|
|
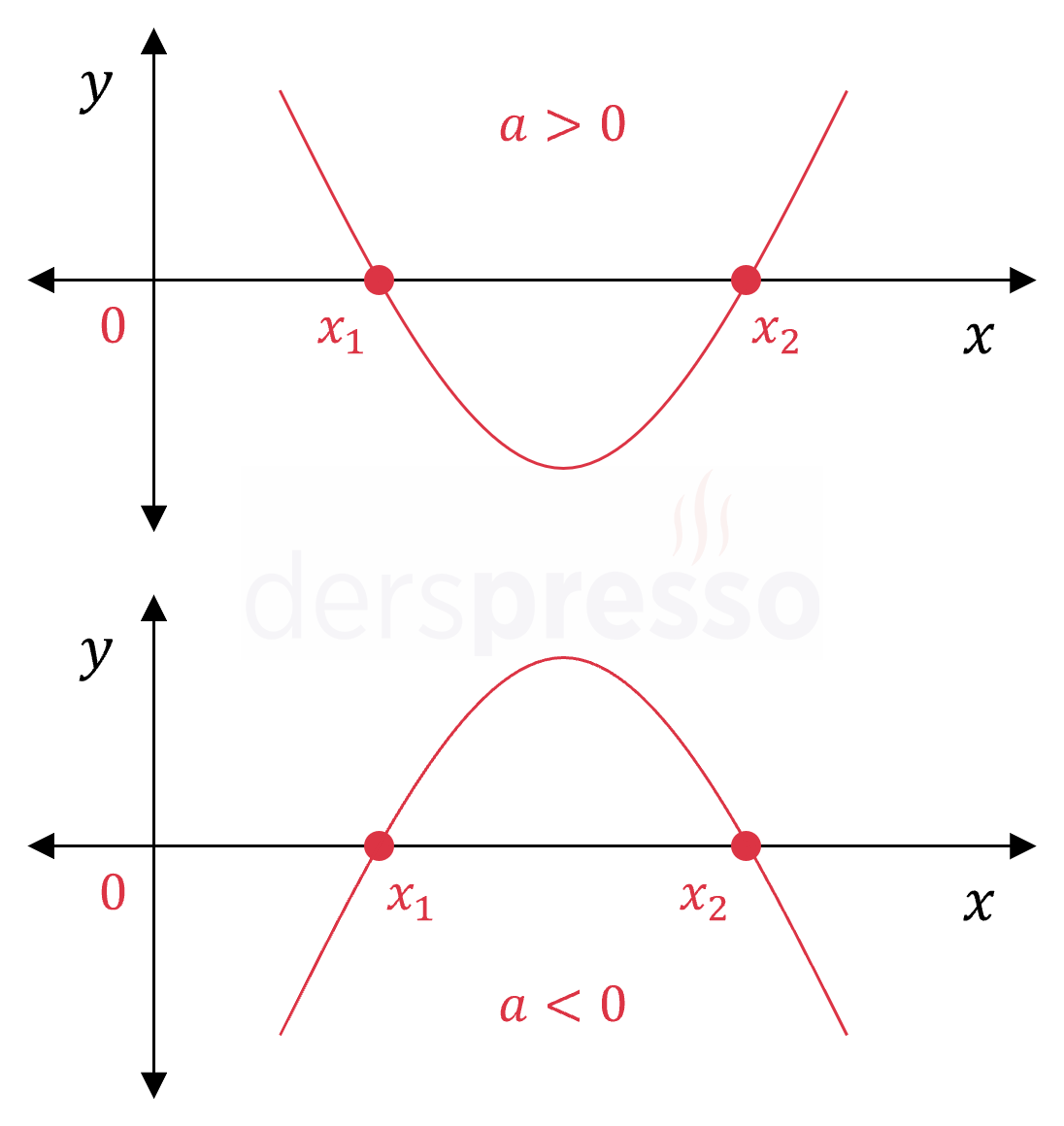
Birbirinden farklı ve pozitif iki kök: \( 0 \lt x_1 \lt x_2 \) Bu durumda delta sıfırdan büyük, kökler toplamı ve çarpımı pozitif olur. \( \Delta \gt 0 \) \( -\dfrac{b}{a} \gt 0 \) \( \dfrac{c}{a} \gt 0 \) |
|
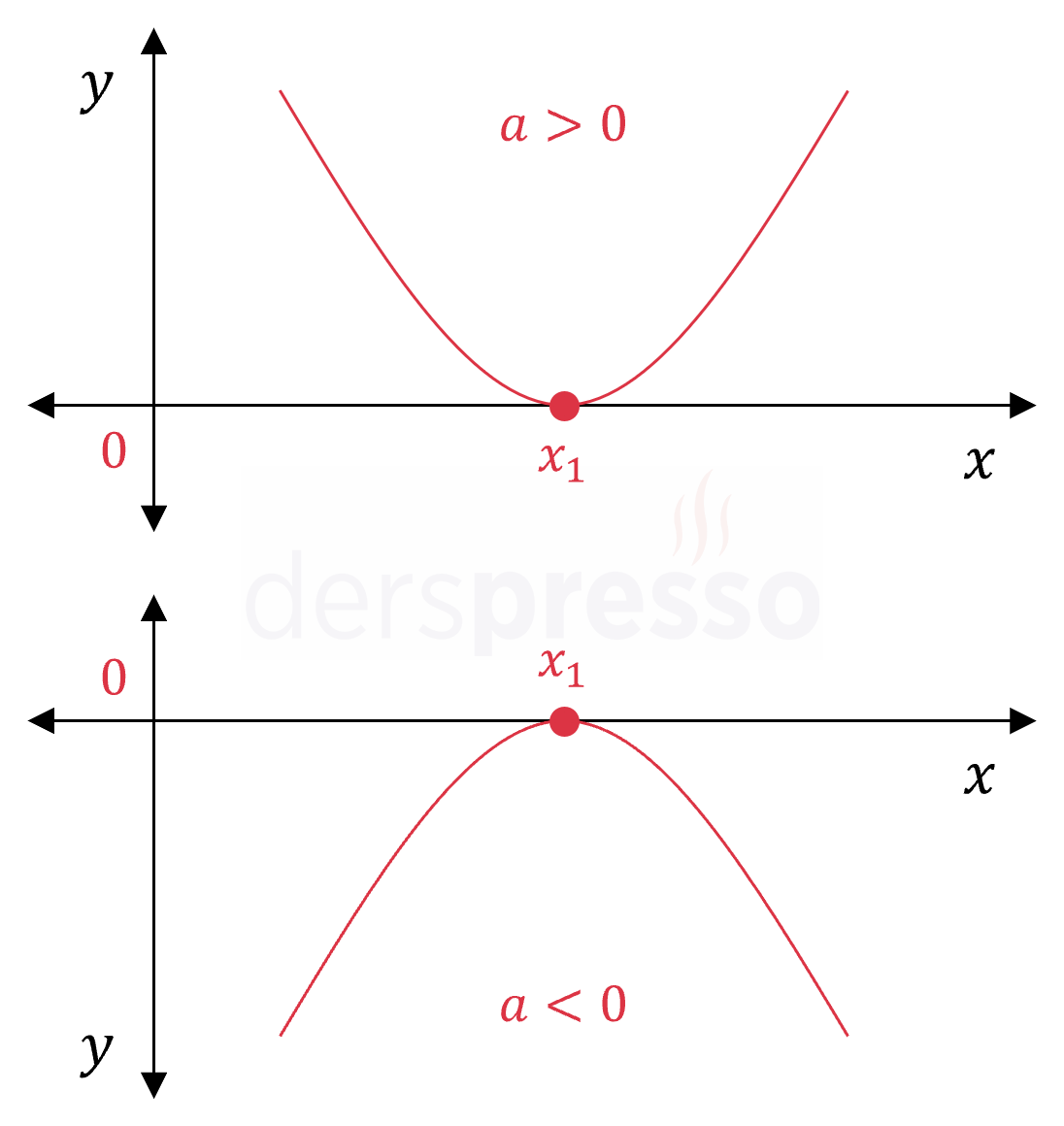
Çift katlı pozitif kök: \( 0 \lt x_1 = x_2 \) Bu durumda delta sıfıra eşit, kökler toplamı ve çarpımı pozitif olur. \( \Delta = 0 \) \( -\dfrac{b}{a} \gt 0 \) \( \dfrac{c}{a} \gt 0 \) |
|
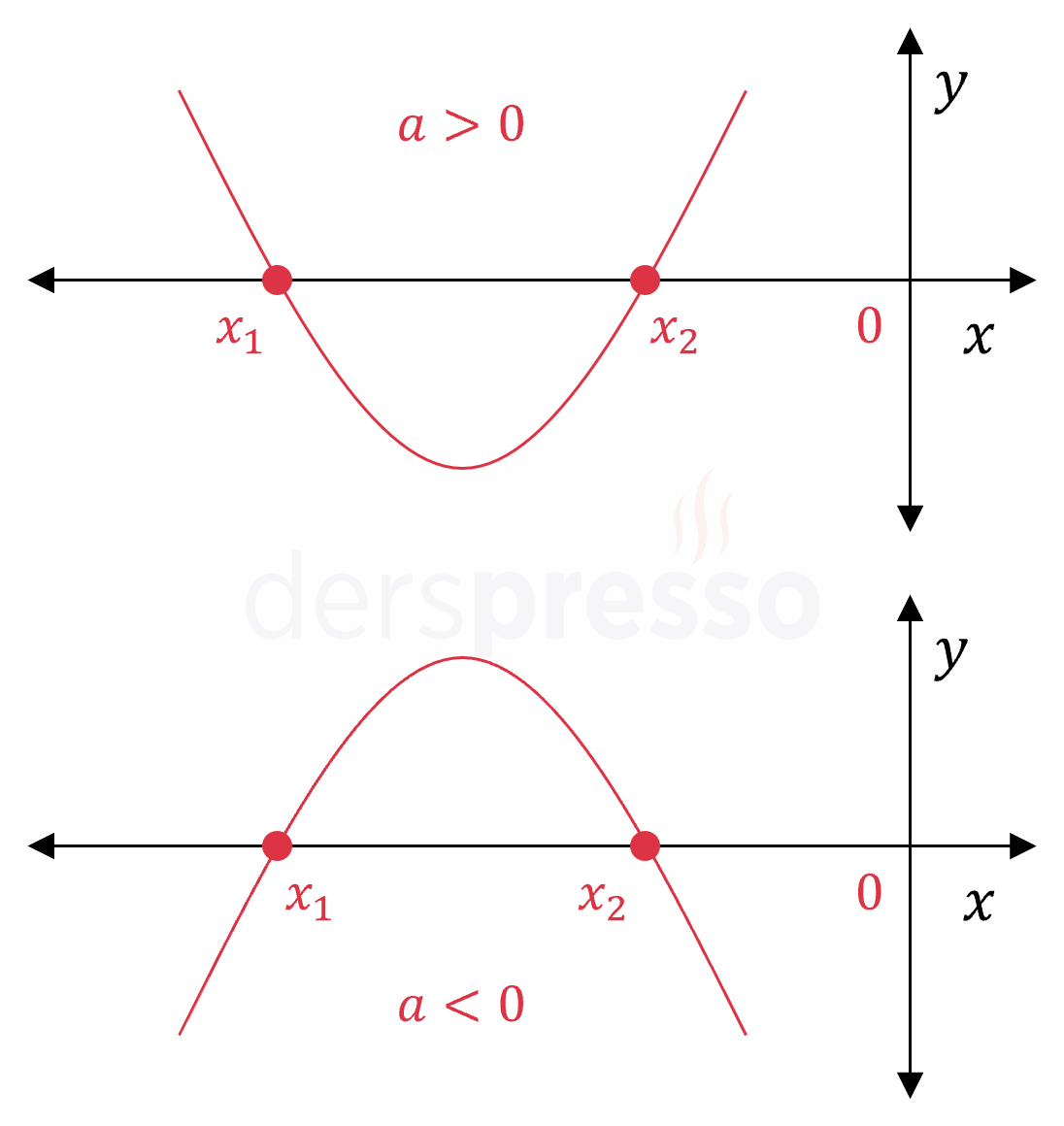
Birbirinden farklı ve negatif iki kök: \( x_1 \lt x_2 \lt 0 \) Bu durumda delta sıfırdan büyük, kökler toplamı negatif, kökler çarpımı pozitif olur. \( \Delta \gt 0 \) \( -\dfrac{b}{a} \lt 0 \) \( \dfrac{c}{a} \gt 0 \) |
|
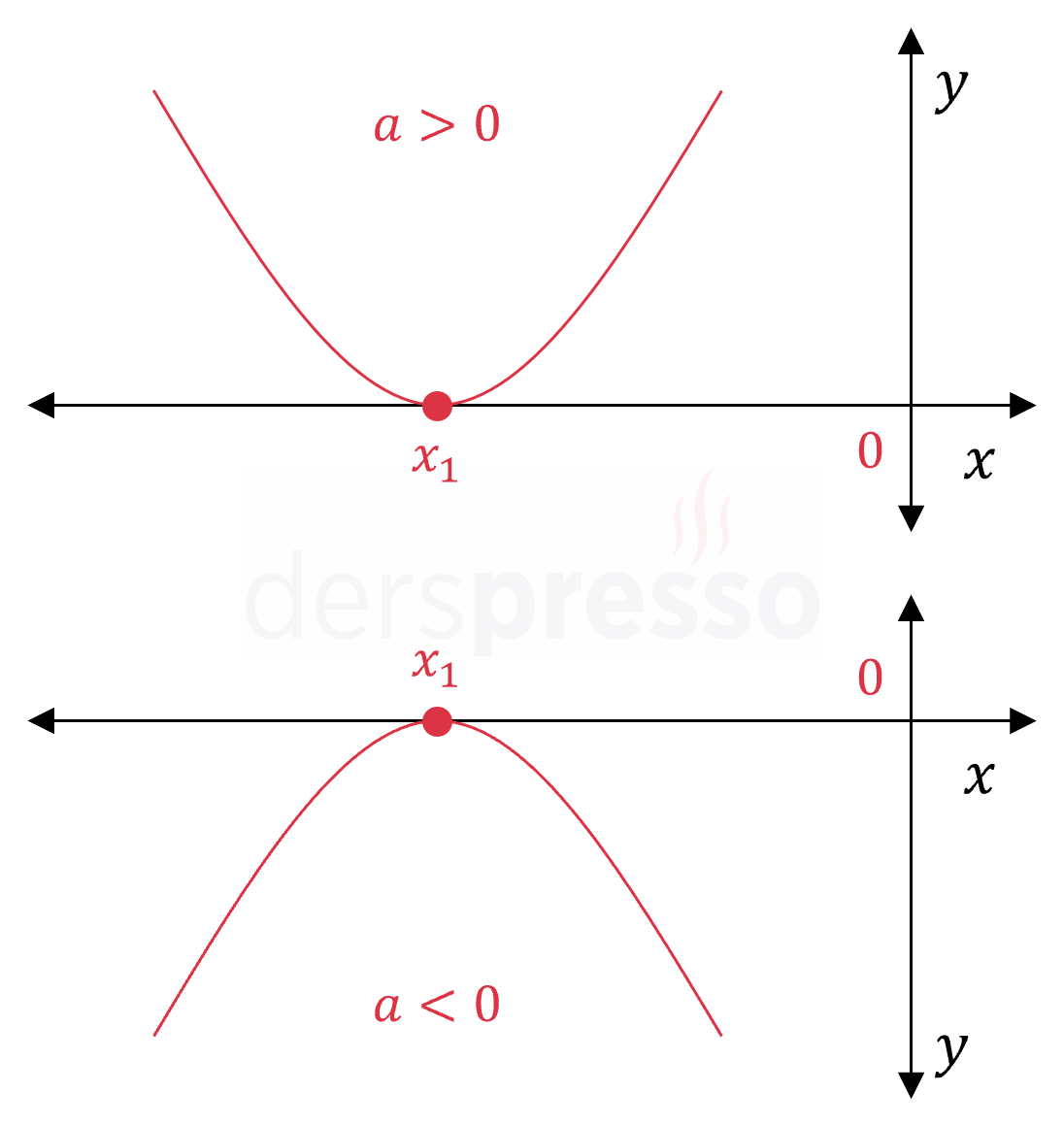
Çift katlı negatif kök: \( x_1 = x_2 \lt 0 \) Bu durumda delta sıfıra eşit, kökler toplamı negatif, kökler çarpımı pozitif olur. \( \Delta = 0 \) \( -\dfrac{b}{a} \lt 0 \) \( \dfrac{c}{a} \gt 0 \) |
|
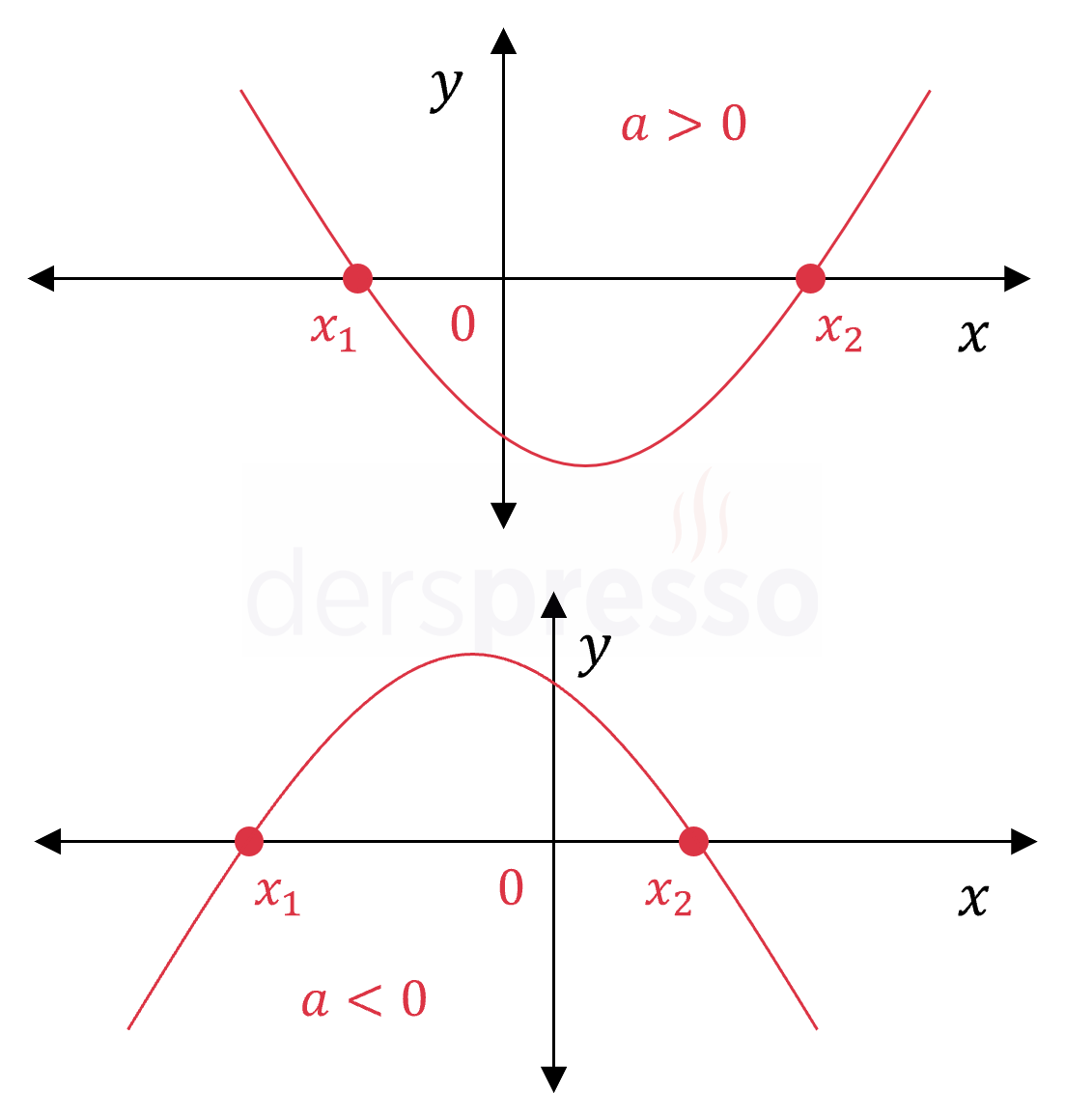
Ters işaretli iki kök: \( x_1 \lt 0 \lt x_2 \) Bu durumda delta sıfırdan büyük, kökler çarpımı negatif olur. \( \Delta \gt 0 \) \( \dfrac{c}{a} \lt 0 \) |
|
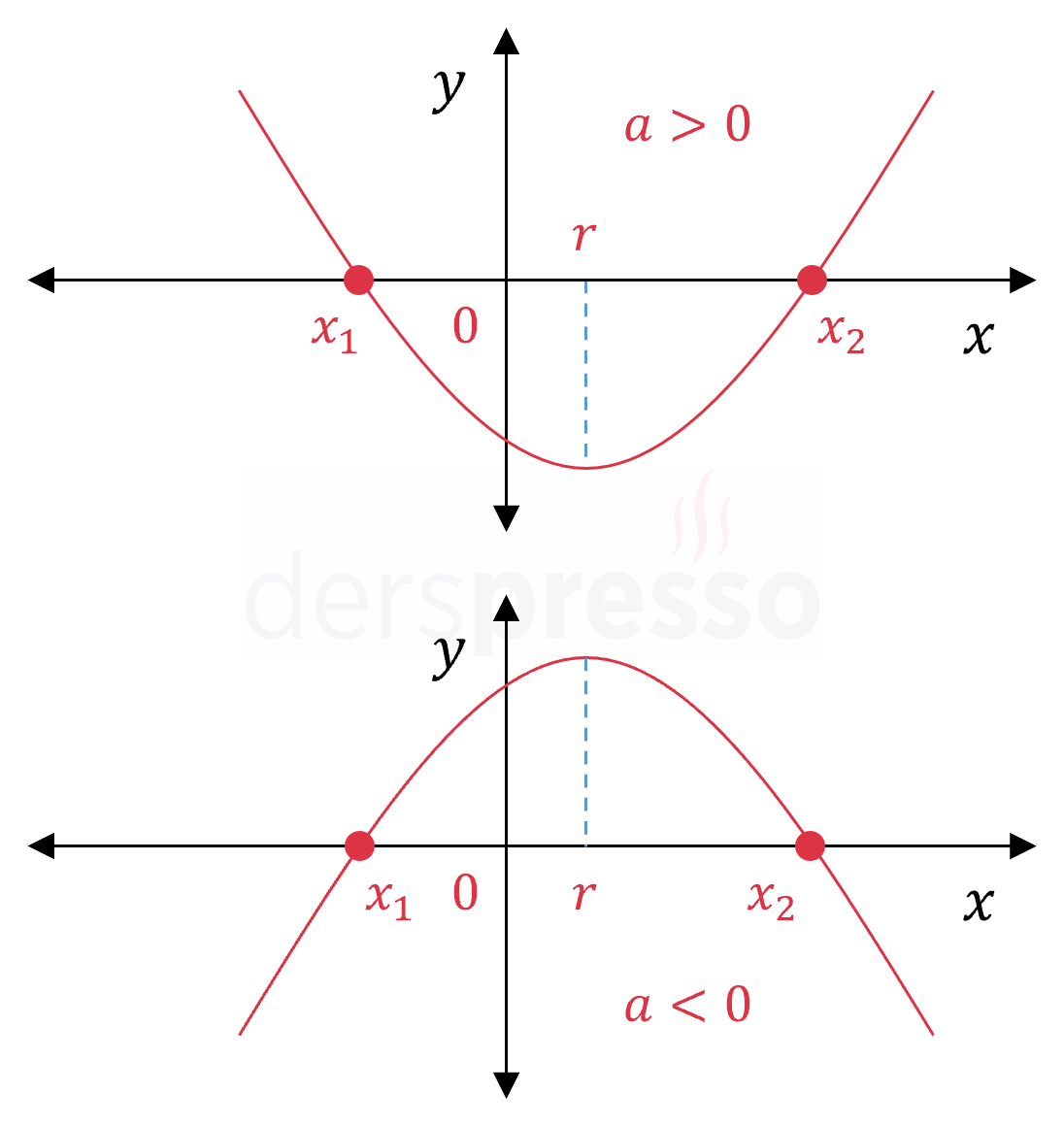
Ters işaretli iki kök (pozitif kök mutlak değerce büyük): \( x_1 \lt 0 \lt x_2 \) \( \abs{x_1} \lt \abs{x_2} \) Bu durumda delta sıfırdan büyük, kökler çarpımı negatif, tepe noktasının apsis değeri (\( r \)) pozitif olur. \( \Delta \gt 0 \) \( \dfrac{c}{a} \lt 0 \) \( r = -\dfrac{b}{2a} \gt 0 \) |
|
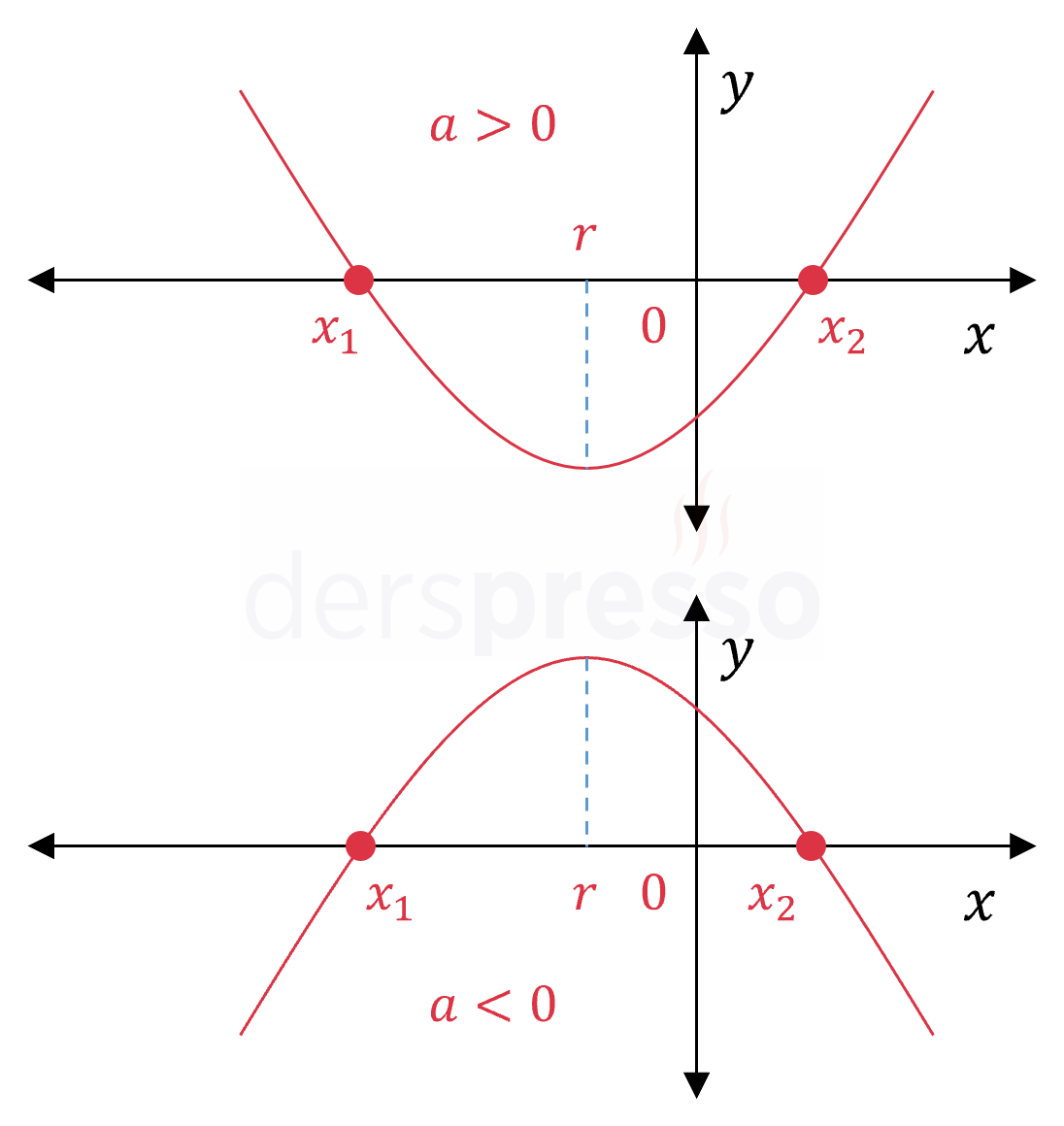
Ters işaretli iki kök (pozitif kök mutlak değerce küçük): \( x_1 \lt 0 \lt x_2 \) \( \abs{x_1} \gt \abs{x_2} \) Bu durumda delta sıfırdan büyük, kökler çarpımı negatif, tepe noktasının apsis değeri (\( r \)) negatif olur. \( \Delta \gt 0 \) \( \dfrac{c}{a} \lt 0 \) \( r = -\dfrac{b}{2a} \lt 0 \) |
|
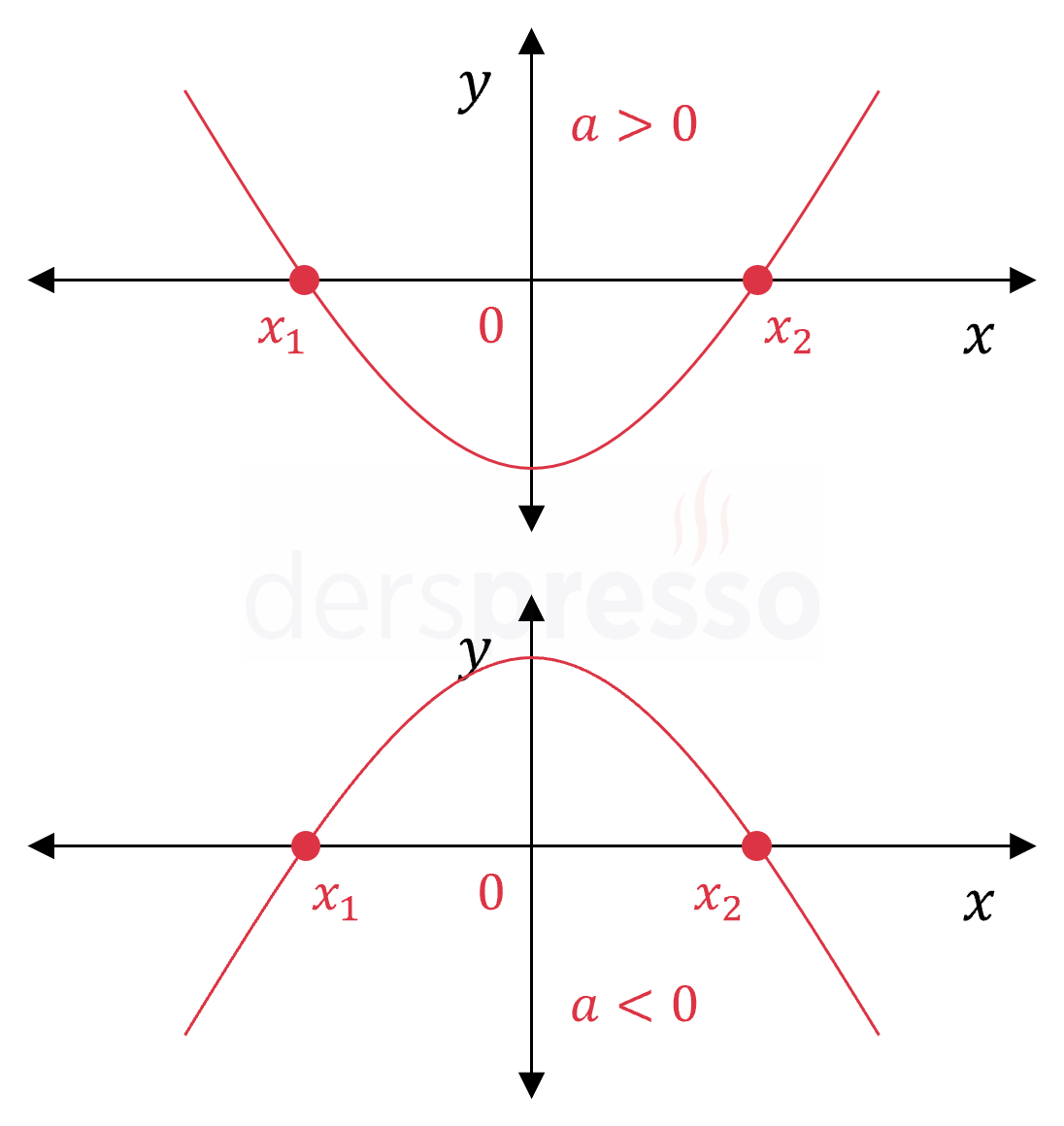
Simetrik kökler: \( x_1 \lt 0 \lt x_2 \) \( \abs{x_1} = \abs{x_2} \) Bu durumda delta sıfırdan büyük, kökler çarpımı negatif, tepe noktasının apsis değeri (\( r \)) sıfır olur. \( \Delta \gt 0 \) \( \dfrac{c}{a} \lt 0 \) \( r = -\dfrac{b}{2a} = 0 \Longrightarrow b = 0 \) |
|
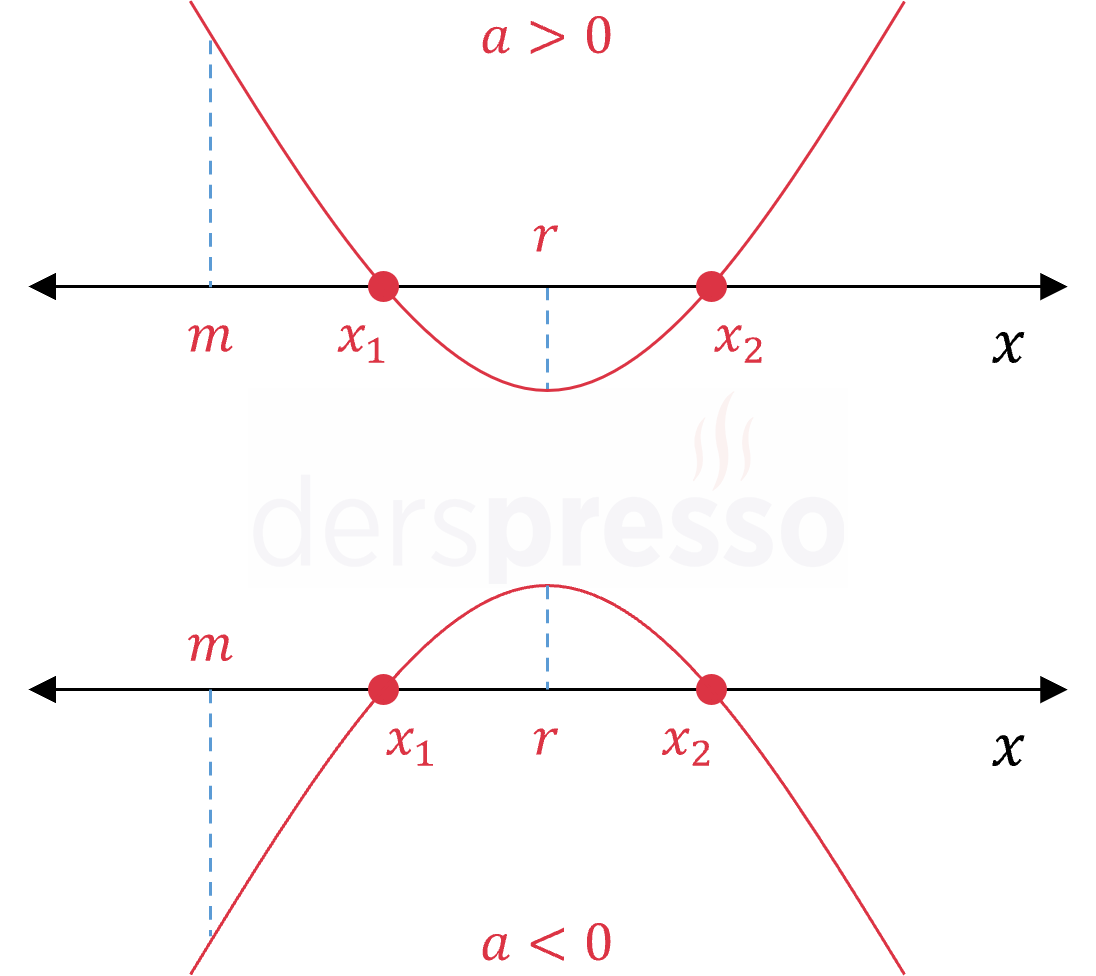
Birbirinden farklı ve \( m \) sayısından büyük iki kök: \( m \lt x_1 \lt x_2 \) Bu durumda delta sıfırdan büyük, tepe noktasının apsis değeri \( m \)'den büyük olur. Ayrıca parabolün kolları yukarı yönlü ise \( f(m) \gt 0 \), aşağı yönlü ise \( f(m) \lt 0 \) olur. \( \Delta \gt 0 \) \( a \cdot f(m) \gt 0 \) \( r = -\dfrac{b}{2a} \gt m \) |
|
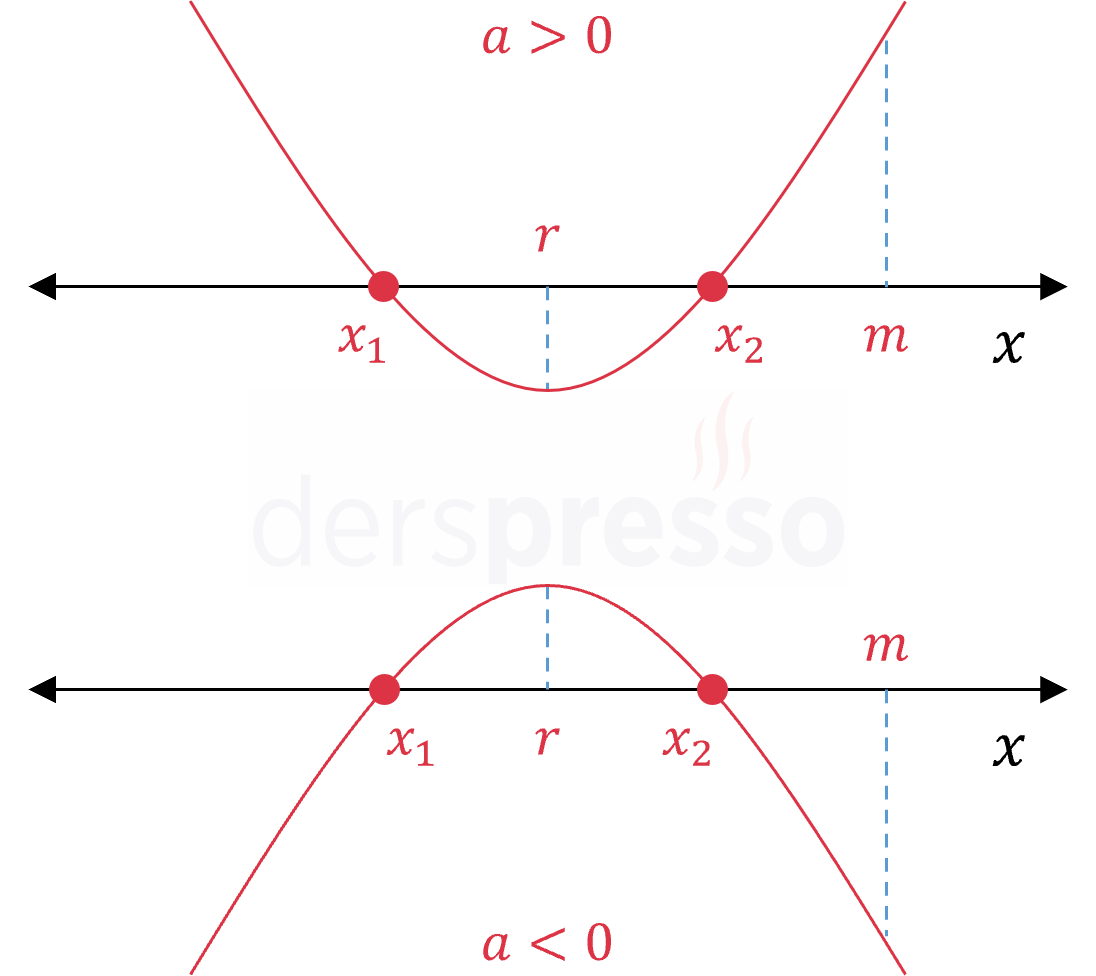
Birbirinden farklı ve \( m \) sayısından küçük iki kök: \( x_1 \lt x_2 \lt m \) Bu durumda delta sıfırdan büyük, tepe noktasının apsis değeri \( m \)'den küçük olur. Ayrıca parabolün kolları yukarı yönlü ise \( f(m) \gt 0 \), aşağı yönlü ise \( f(m) \lt 0 \) olur. \( \Delta \gt 0 \) \( a \cdot f(m) \gt 0 \) \( r = -\dfrac{b}{2a} \lt m \) |
|
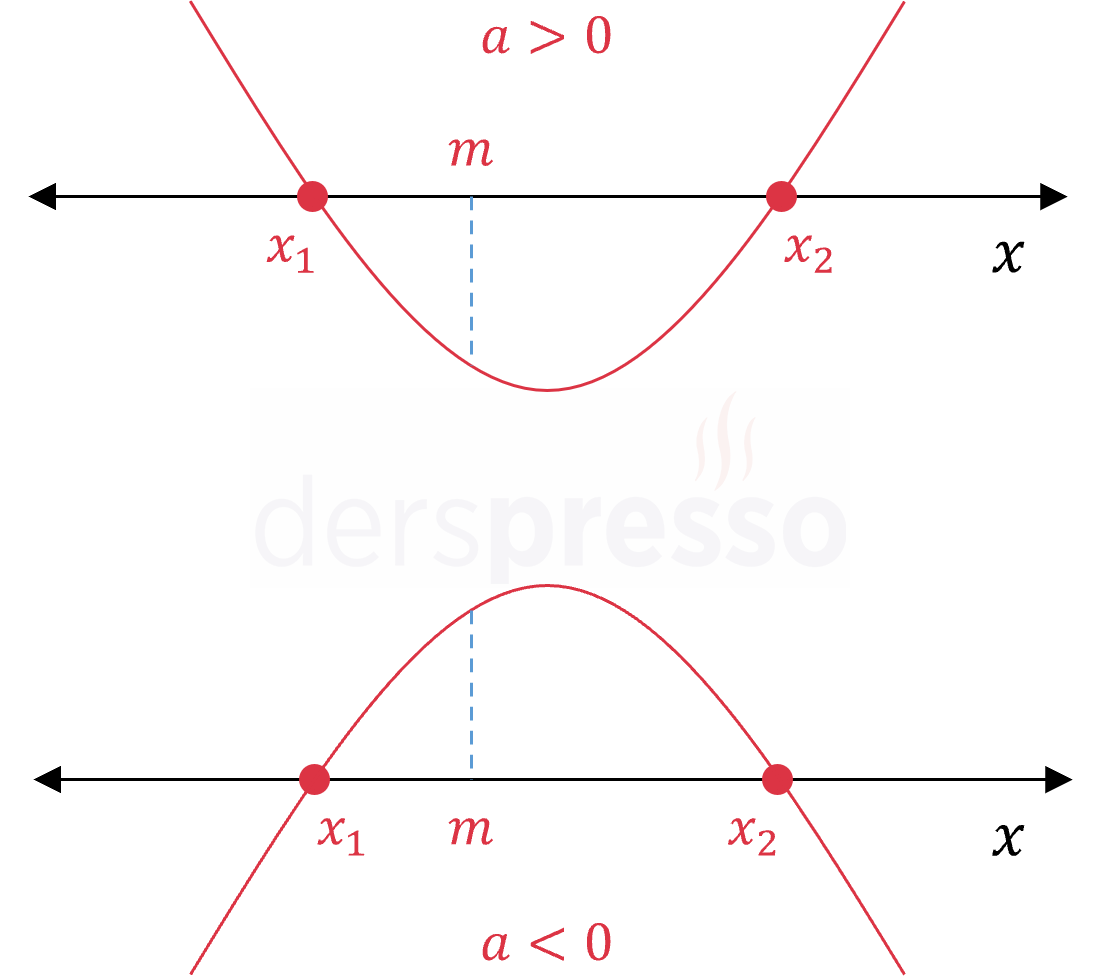
Biri \( m \) sayısından küçük, diğeri büyük iki kök: \( x_1 \lt m \lt x_2 \) Bu durumda delta sıfırdan büyük olur. Ayrıca parabolün kolları yukarı yönlü ise \( f(m) \lt 0 \), aşağı yönlü ise \( f(m) \gt 0 \) olur. \( \Delta \gt 0 \) \( a \cdot f(m) \lt 0 \) |
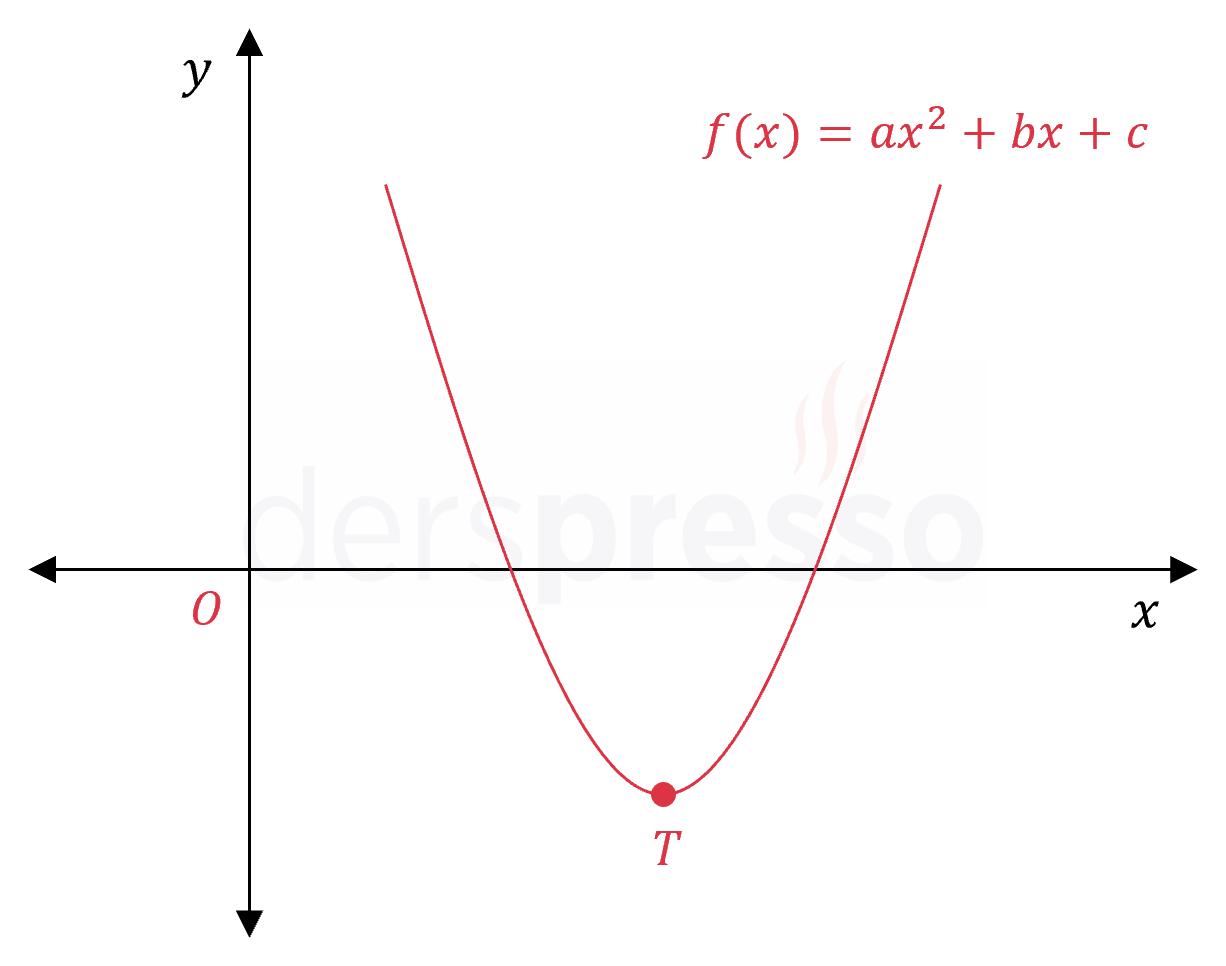
Şekildeki \( f(x) = ax^2 + bx + c \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. \( bc \lt 0 \)
II. \( ab \gt 0 \)
III. \( a \cdot \Delta \gt 0 \)
IV. \( abc \cdot \Delta \lt 0 \)
Çözümü GösterParabolün kolları yukarı yönlü olduğu için başkatsayısı pozitiftir.
\( a \gt 0 \)
Tepe noktasının apsisi IV. bölgede yer aldığı için pozitiftir.
\( -\dfrac{b}{2a} \gt 0 \)
\( a \) pozitif olduğuna göre \( b \) negatif olur.
\( b \lt 0 \)
Parabolün kökleri \( x \) ekseninin pozitif tarafında yer aldığına göre iki kök de pozitiftir, dolayısıyla çarpımları da pozitif olur.
\( x_1 \cdot x_2 = \dfrac{c}{a} \gt 0 \)
\( a \) pozitif olduğuna göre \( c \) de pozitif olur.
\( c \gt 0 \)
Parabol \( x \) eksenini iki farklı noktada kestiğine göre iki farklı reel kökü vardır, dolayısıyla deltası pozitiftir.
\( \Delta \gt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( bc \lt 0 \)
\( b \) negatif ve \( c \) pozitif olduğu için \( bc \) çarpımı negatif olur.
I. öncül doğrudur.
II. öncül:
\( ab \gt 0 \)
\( a \) pozitif ve \( b \) negatif olduğu için \( ab \) çarpımı negatif olur.
II. öncül yanlıştır.
III. öncül:
\( a \cdot \Delta \gt 0 \)
\( a \) ve delta pozitif olduğu için \( a \cdot \Delta \) çarpımı pozitif olur.
III. öncül doğrudur.
IV. öncül:
\( abc \cdot \Delta \lt 0 \)
\( a \), \( c \) ve \( \Delta \) pozitif, \( b \) negatif olduğu için \( abc \cdot \Delta \) çarpımı negatif olur.
IV. öncül doğrudur.
Buna göre I., III. ve IV. öncüller doğrudur.
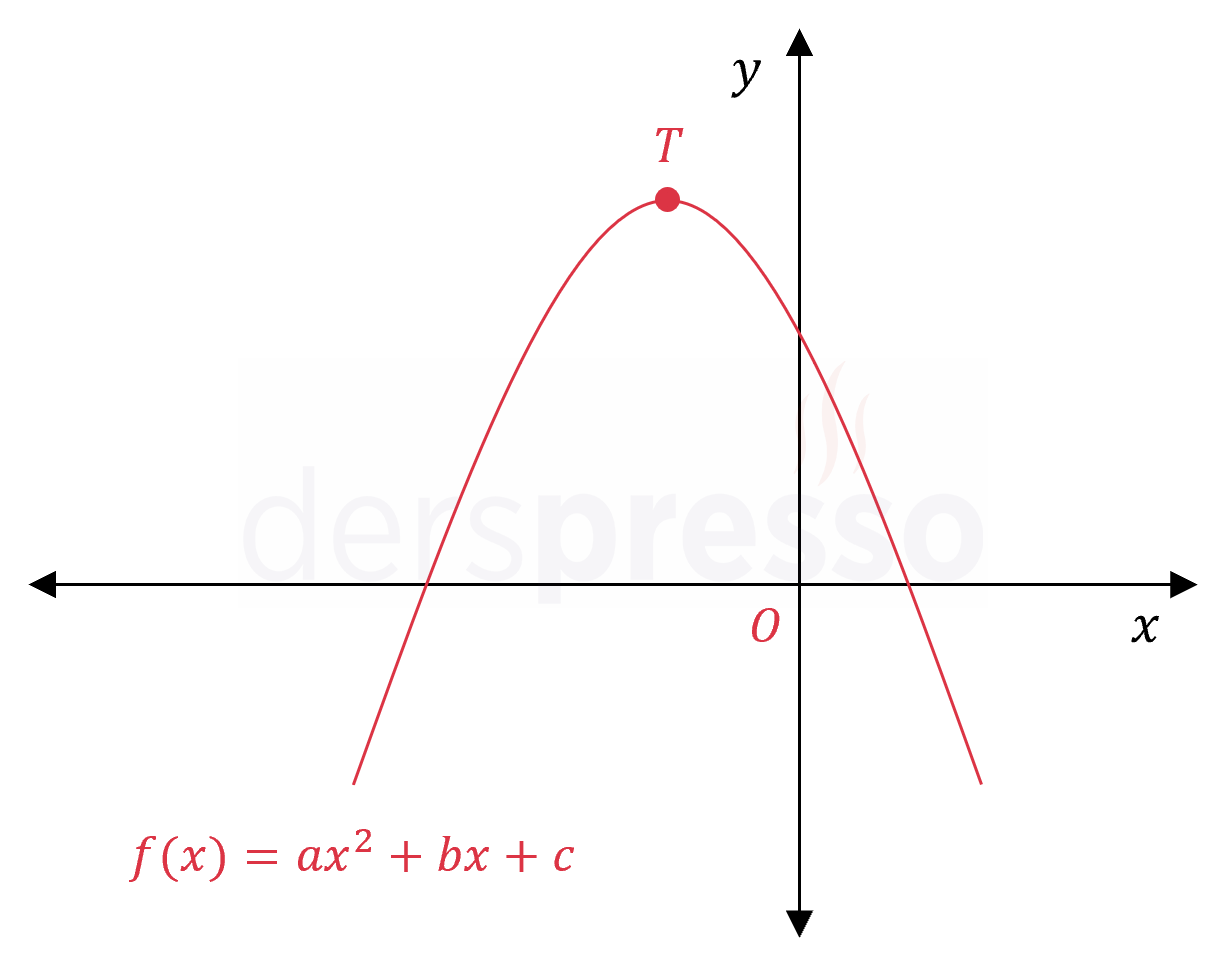
Şekildeki \( f(x) = ax^2 + bx + c \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. \( ab \gt 0 \)
II. \( ac \gt 0 \)
III. \( b \cdot \Delta \lt 0 \)
IV. \( abc \cdot \Delta \lt 0 \)
Çözümü GösterParabolün kolları aşağı yönlü olduğu için başkatsayısı negatiftir.
\( a \lt 0 \)
Tepe noktası II. bölgede yer aldığı için apsisi negatiftir.
\( -\dfrac{b}{2a} \lt 0 \)
\( a \) negatif olduğuna göre \( b \) de negatif olur.
\( b \lt 0 \)
Parabolün kökleri \( x \) ekseninin her iki tarafında yer aldığına göre köklerin biri pozitif diğeri negatiftir, dolayısıyla çarpımları negatif olur.
\( x_1 \cdot x_2 = \dfrac{c}{a} \lt 0 \)
\( a \) negatif olduğuna göre \( c \) pozitif olur.
\( c \gt 0 \)
Parabol \( x \) eksenini iki farklı noktada kestiğine göre iki farklı reel kökü vardır, dolayısıyla deltası pozitiftir.
\( \Delta \gt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( ab \lt 0 \)
\( a \) ve \( b \) negatif olduğu için \( ab \) çarpımı pozitif olur.
I. öncül yanlıştır.
II. öncül:
\( ac \gt 0 \)
\( a \) negatif ve \( c \) pozitif olduğu için \( ac \) çarpımı negatif olur.
II. öncül yanlıştır.
III. öncül:
\( b \cdot \Delta \lt 0 \)
\( b \) negatif ve delta pozitif olduğu için \( b \cdot \Delta \) çarpımı negatif olur.
III. öncül doğrudur.
IV. öncül:
\( abc \cdot \Delta \lt 0 \)
\( a \) ve \( b \) negatif, \( c \) ve \( \Delta \) pozitif olduğu için \( abc \cdot \Delta \) çarpımı pozitif olur.
IV. öncül yanlıştır.
Buna göre sadece III. öncül doğrudur.
\( ax^2 + bx + c = 0 \) denkleminin kökleri ters işaretli ve mutlak değerce büyük olan kök pozitif olduğuna göre, aşağıdakilerden hangileri kesinlikle doğrudur?
I. \( a \) ve \( b \) ters işaretlidir.
II. \( b \) ve \( c \) aynı işaretlidir.
III. \( a \) negatiftir.
Çözümü GösterKökler ters işaretli olduğundan çarpımları negatif olur.
\( \frac{c}{a} \) kökler çarpımına eşit olduğundan işareti negatif olur, dolayısıyla \( a \) ve \( c \) ters işaretlidir.
Mutlak değerce büyük olan kök pozitif olduğundan kökler toplamı pozitif olur.
\( -\frac{b}{a} \) kökler toplamına eşit olduğundan \( \frac{b}{a} \) negatif olur, dolayısıyla \( a \) ve \( b \) ters işaretlidir.
\( a \) hem \( b \) hem \( c \) ile zıt işaretli olduğundan \( b \) ve \( c \) aynı işaretli olur.
Bu bilgiler dışında katsayıların herhangi birinin işareti kesin olarak bilinemez.
Buna göre I. ve II. öncüller kesinlikle doğrudur.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = x^2 - (3 - m)x + 4 \)
parabolü \( x \) eksenine \( y \) ekseninin sol tarafında teğet ise \( m \) kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -(3 - m), \quad c = 4 \)
Parabol \( x \) eksenine teğet olduğuna göre, çakışık iki kökü vardır ve deltası sıfıra eşittir.
\( \Delta = b^2 - 4ac = 0 \)
\( (-(3 - m))^2 - 4(1)(4) = 0 \)
\( (3 - m)^2 = 16 \)
\( 3 - m = 4 \) ya da \( 3 - m = -4 \)
\( m = -1 \) ya da \( m = 7 \)
Parabol \( x \) eksenine \( y \) ekseninin sol tarafında teğet olduğuna göre, tepe noktasının apsisi negatif olmalıdır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} \lt 0 \)
\( -\dfrac{-(3 - m)}{2(1)} \lt 0 \)
\( 3 - m \lt 0 \)
\( 3 \lt m \)
Buna göre \( m \) için bulduğumuz iki değerden \( m = 7 \) istenen koşulu sağlar.
\( f(x) = 2x^2 + 5x + c \) fonksiyon \( x = -2 \) ve \( x = \frac{1}{2} \) noktalarında ters işaretlere sahiptir.
Buna göre, \( c \)'nin en geniş değer aralığını bulunuz.
Çözümü GösterFonksiyonun bu iki noktadaki değerini bulalım.
\( f(-2) = 2(2)^2 + 5(-2) + c = -2 + c \)
\( f(\frac{1}{2}) = 2(\frac{1}{2})^2 + 5(\frac{1}{2}) + c = 3 + c \)
Fonksiyon bu iki noktada ters işaretlere sahiptir.
\( f(-2) \cdot f(\frac{1}{2}) \lt 0 \)
\( (c - 2)(c + 3) \lt 0 \)
Başkatsayısı pozitif olan ve iki reel kökü olan ikinci dereceden ifade her bir çarpanı sıfır yapan \( c = -3 \) ve \( c = 2 \) kök değerlerinde sıfır, \( (-3, 2) \) aralığında negatif, köklerin dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için \( (c - 2)(c + 3) \) ifadesinin negatif olduğu aralık eşitsizliğin çözüm kümesi olur.
\( c \in (-3, 2) \) bulunur.
\( m \gt 0 \) olmak üzere,
\( f(x) = ax^2 + bx + c \) parabolü \( x \) eksenini \( m \) ve \( 3m \) noktalarında kesmektedir.
\( f(-2m) \lt 0 \) olduğuna göre, aşağıdaki ifadelerden hangileri kesinlikle doğrudur?
I. \( f(2m) \gt 0 \)
II. \( f(c) \lt 0 \)
III. \( f(ab) \lt 0 \)
IV. \( f(10000) \lt 0 \)
Çözümü GösterParabolün kökleri \( x = m \) ve \( x = 3m \) olup \( f(-2m) \lt 0 \) olduğu için parabol kök değerlerinin dışındaki aralıkta negatif, arasındaki aralıkta pozitif değer alır, dolayısıyla parabolün kolları aşağı yönlüdür.
Kolları aşağı yönlü olan parabollerin başkatsayısı negatiftir.
\( a \lt 0 \)
Parabolün kökleri pozitif ve kolları aşağı yönlü olduğu için \( y \) eksenini negatif tarafta keser, dolayısıyla sabit terimi negatiftir.
\( c \lt 0 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün tepe noktasının apsisi kökler toplamının yarısına eşittir.
\( r = \dfrac{m + 3m}{2} = 2m \)
\( T(2m, f(2m)) \)
Parabolün iki pozitif kökü olduğu ve kolları aşağı yönlü olduğu için tepe noktası noktası I. bölgede yer alır.
Tepe noktasın apsis formülünü kullanarak \( b \) değerinin işaretini bulalım.
\( r = -\dfrac{b}{2a} \)
\( 2m = -\dfrac{b}{2a} \)
\( b = -4am \)
\( a \) negatif, \( m \) pozitif olduğu için \( b \) pozitif olur.
\( b \gt 0 \)
Buna göre parabolün grafiği aşağıdaki gibidir.
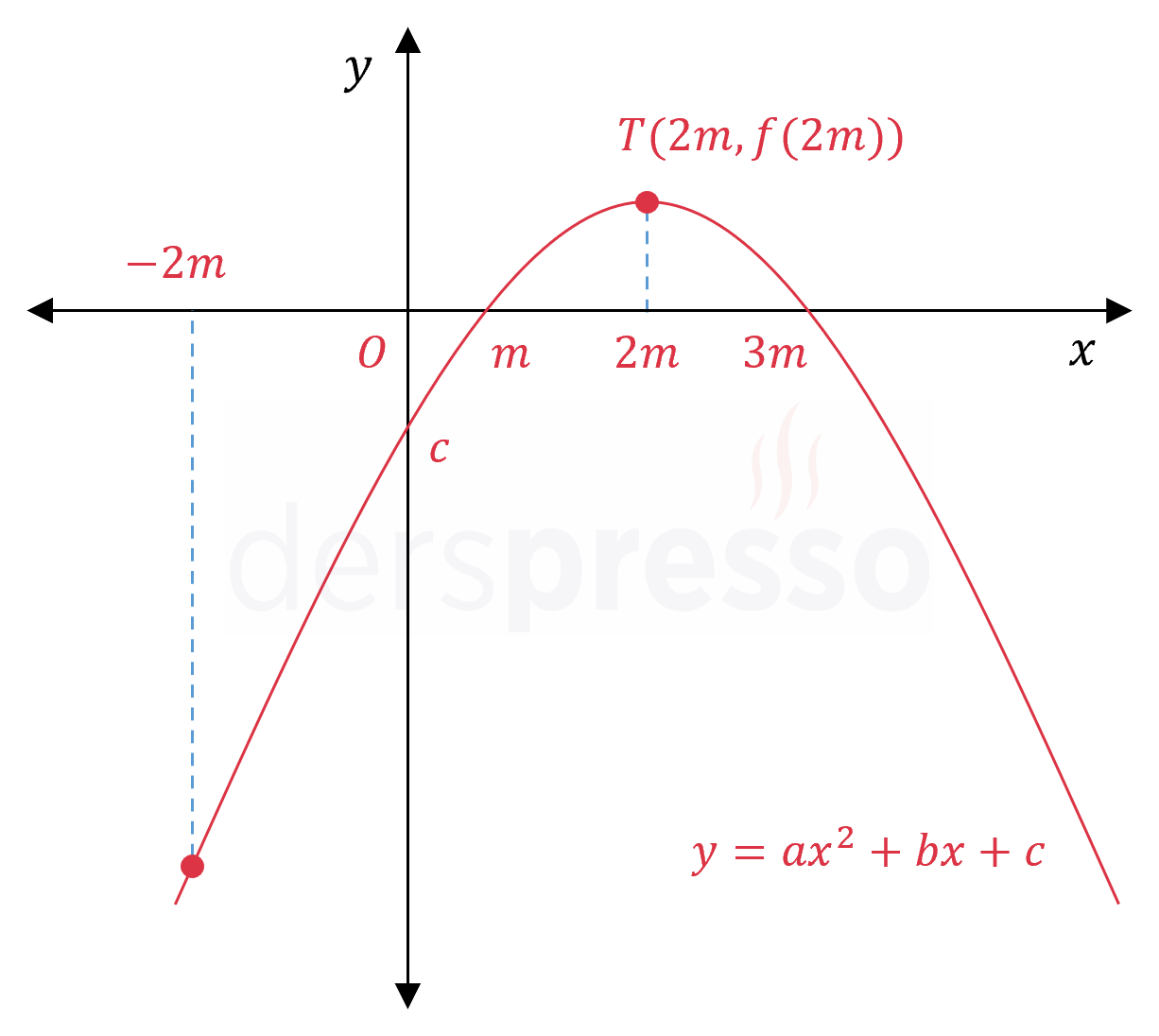
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( f(2m) \gt 0 \)
Bu öncül kesinlikle doğrudur.
II. öncül:
\( f(c) \lt 0 \)
\( c \) negatiftir. \( x \)'in negatif değerlerinde parabol negatif değer alır.
Bu öncül kesinlikle doğrudur.
III. öncül:
\( f(ab) \lt 0 \)
\( a \) negatif ve \( b \) pozitif olduğu için \( ab \) çarpımı negatif olur.
\( x \)'in negatif değerlerinde parabol negatif değer alır.
Bu öncül kesinlikle doğrudur.
IV. öncül:
\( f(10000) \lt 0 \)
Parabol \( x \gt 3m \) için negatif değer alır, ancak 10000 sayısının \( 3m \)'den küçük mü büyük mü olduğunu bilemeyiz.
Bu öncül doğru ya da yanlış olabilir.
Buna göre I., II. ve III. öncüller kesinlikle doğrudur.