Parabolde Eşitsizlikler

Denklemi \( y = f(x) \) şeklinde verilen bir parabol, analitik düzlemdeki noktaları üç bölgeye ayırır.

Parabolün kendisi: Bu noktalar \( y = f(x) \) eşitliğini sağlayan \( (x, y) \) noktalarından oluşur.
Parabolün üstündeki bölge: Bu noktalar \( y \gt f(x) \) eşitsizliğini sağlayan \( (x, y) \) noktalarından oluşur.
Parabolün altındaki bölge: Bu noktalar \( y \lt f(x) \) eşitsizliğini sağlayan \( (x, y) \) noktalarından oluşur.

Bu doğrultuda parabollere ait eşitsizliklerin analitik düzlemde karşılık geldiği bölgeleri inceleyelim.

Eşitsizliklerin Gösterimi

Bir parabolün analitik düzlemde oluşturduğu bölgelerin eşitsizlik gösterimleri aşağıdaki gibidir.

Grafik	Eşitsizlik
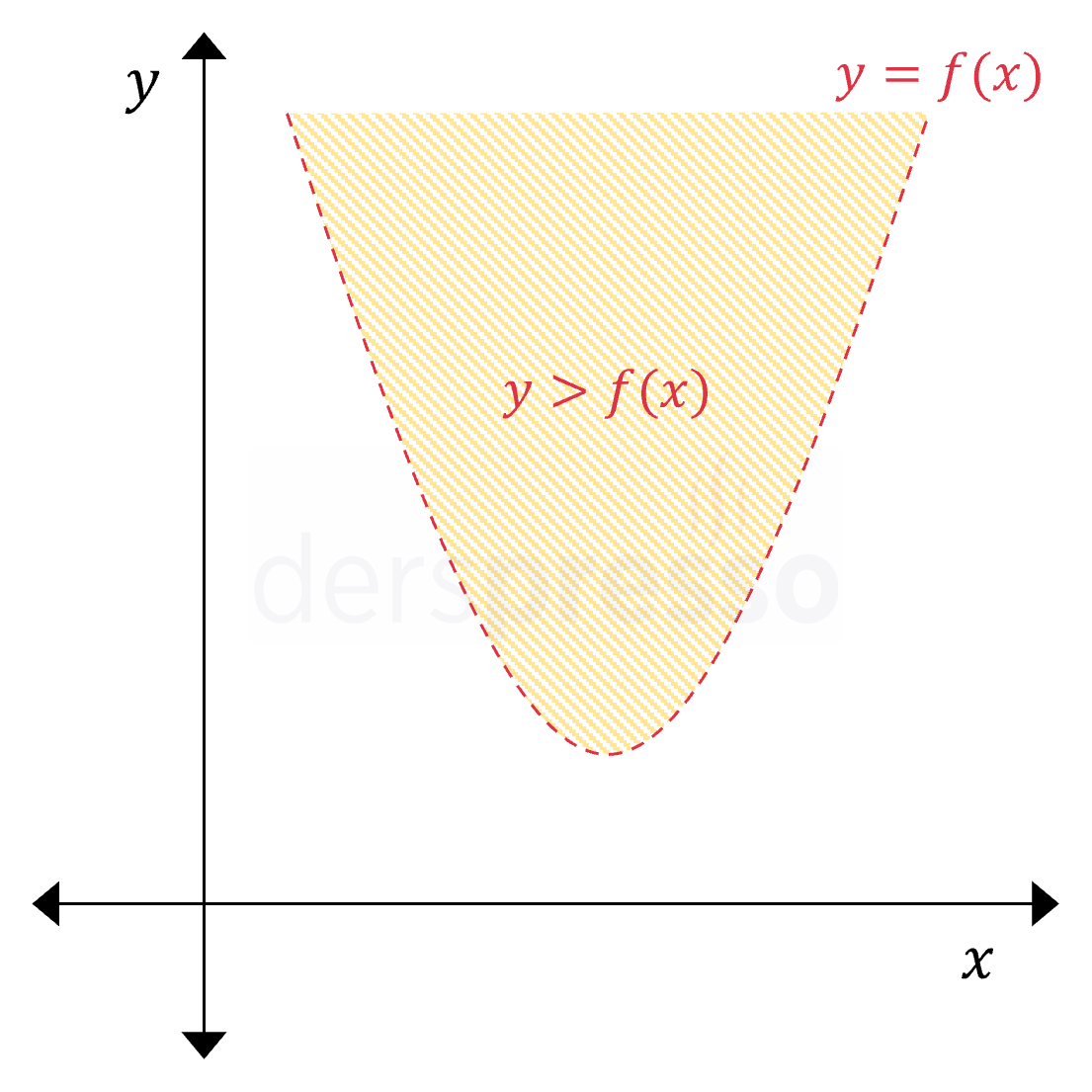
	Kollar yukarı yönlü (\( a \gt 0 \)) \( y \gt f(x) \) Eşitsizlik herhangi bir \( x \) değeri için ordinat değeri \( f(x) \) değerinden büyük olan noktaları kapsar ve parabolün iç/üst bölgesine karşılık gelir. Eşitsizlikte \( \gt \) sembolü kullanıldığı için parabolün üzerindeki noktalar taralı bölgeye dahil değildir, dolayısıyla parabol kesikli çizgi ile gösterilir.
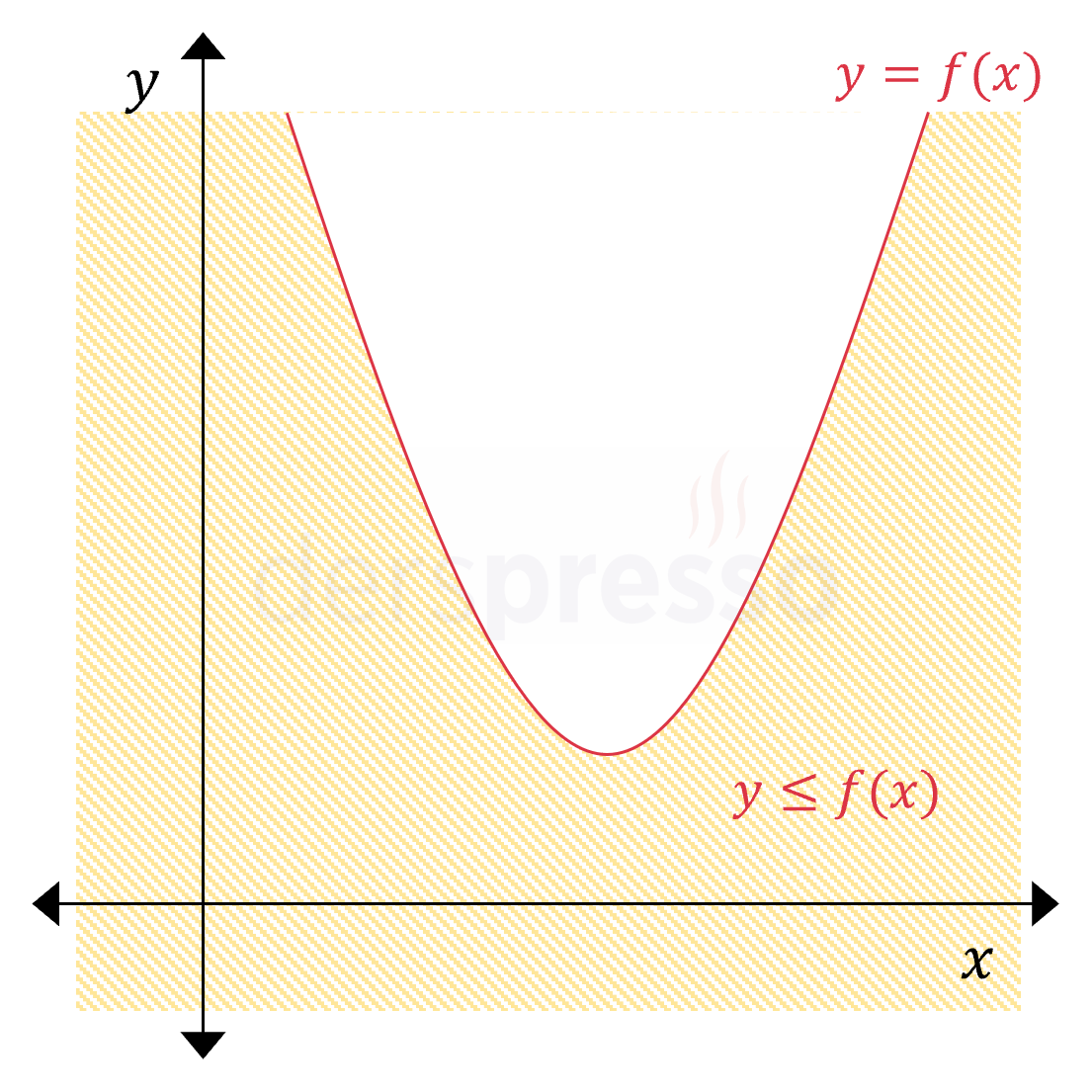
	Kollar yukarı yönlü (\( a \gt 0 \)) \( y \le f(x) \) Eşitsizlik herhangi bir \( x \) değeri için ordinat değeri \( f(x) \) değerinden küçük ya da \( f(x) \) değerine eşit olan noktaları kapsar ve parabolün kendisine ve dış/alt bölgesine karşılık gelir. Eşitsizlikte \( \le \) sembolü kullanıldığı için parabolün üzerindeki noktalar taralı bölgeye dahildir, dolayısıyla parabol sürekli çizgi ile gösterilir.
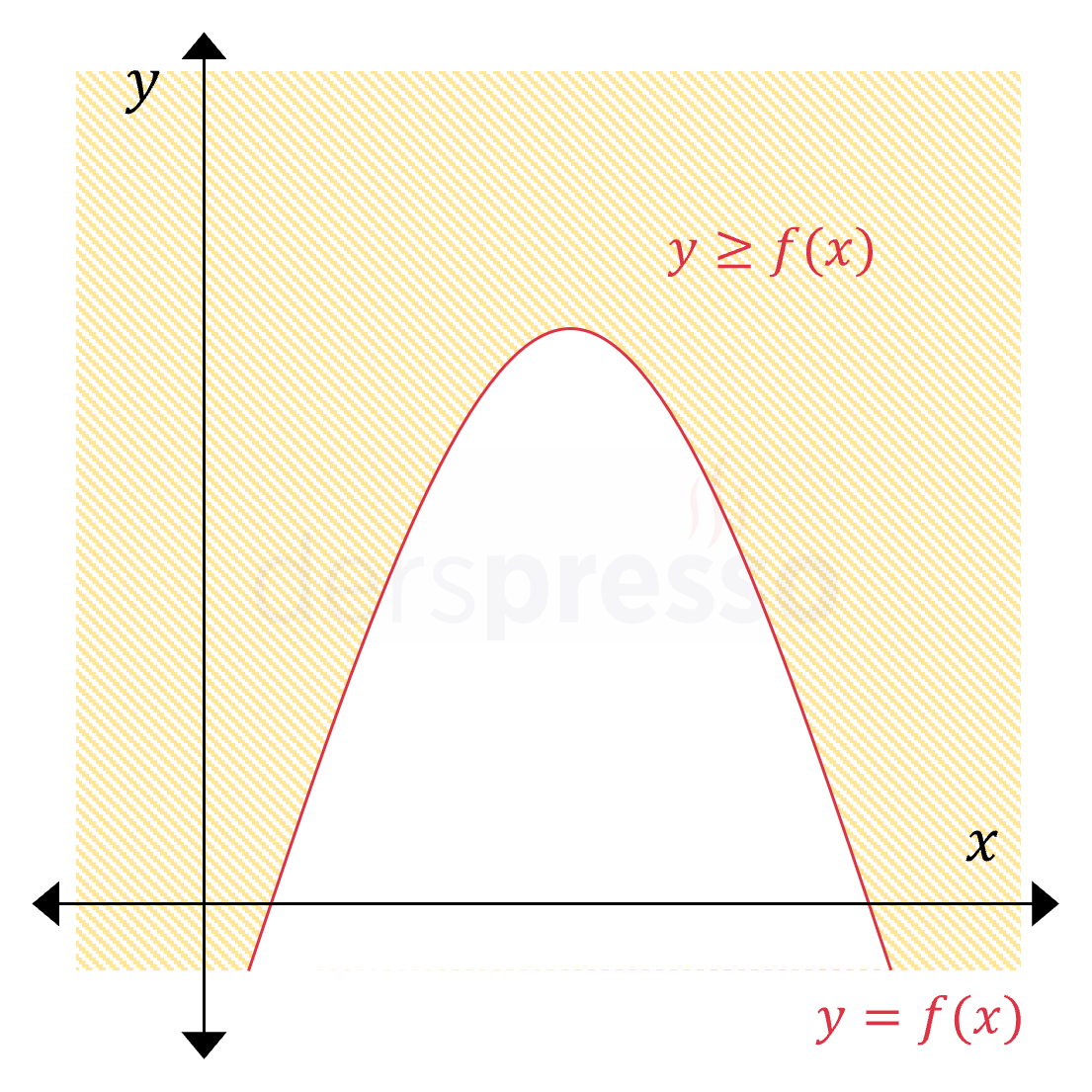
	Kollar aşağı yönlü (\( a \lt 0 \)) \( y \ge f(x) \) Eşitsizlik herhangi bir \( x \) değeri için ordinat değeri \( f(x) \) değerinden büyük ya da \( f(x) \) değerine eşit olan noktaları kapsar ve parabolün kendisine ve dış/üst bölgesine karşılık gelir. Eşitsizlikte \( \ge \) sembolü kullanıldığı için parabolün üzerindeki noktalar taralı bölgeye dahildir, dolayısıyla parabol sürekli çizgi ile gösterilir.
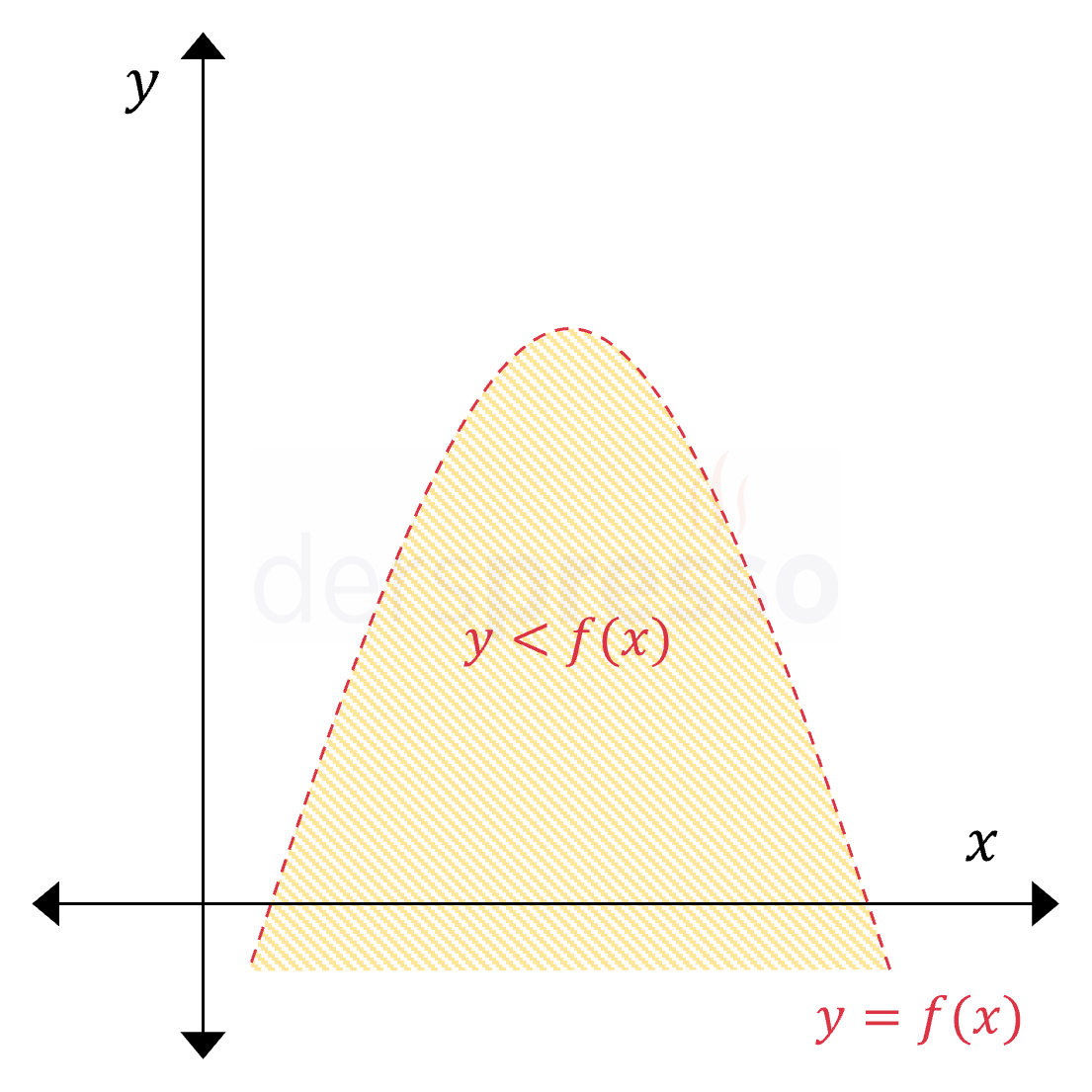
	Kollar aşağı yönlü (\( a \lt 0 \)) \( y \lt f(x) \) Eşitsizlik herhangi bir \( x \) değeri için ordinat değeri \( f(x) \) değerinden küçük olan noktaları kapsar ve parabolün iç/alt bölgesine karşılık gelir. Eşitsizlikte \( \lt \) sembolü kullanıldığı için parabolün üzerindeki noktalar taralı bölgeye dahil değildir, dolayısıyla parabol kesikli çizgi ile gösterilir.

Eşitsizlik Sistemlerinin Gösterimi

Aşağıda bazı örnek eşitsizlik sistemlerinin karşılık geldiği bölgeler taralı şekilde gösterilmiştir.

Grafik	Eşitsizlik Sistemi
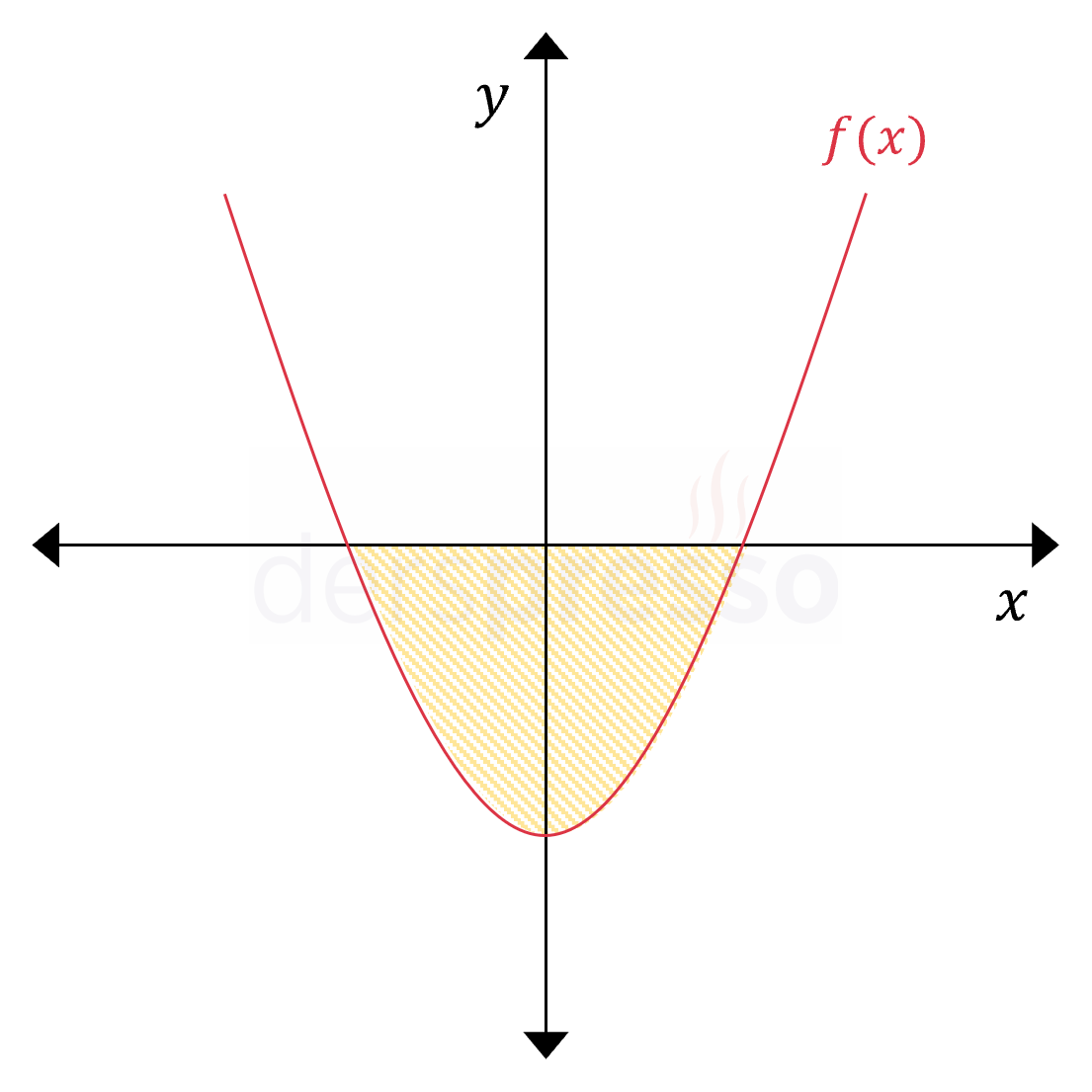
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \ge f(x) \) \( y \le 0 \) Küçük/büyük eşit sembolleri kullanıldığı için parabol ve \( x \) ekseni üzerindeki noktalar taralı alana dahildir.
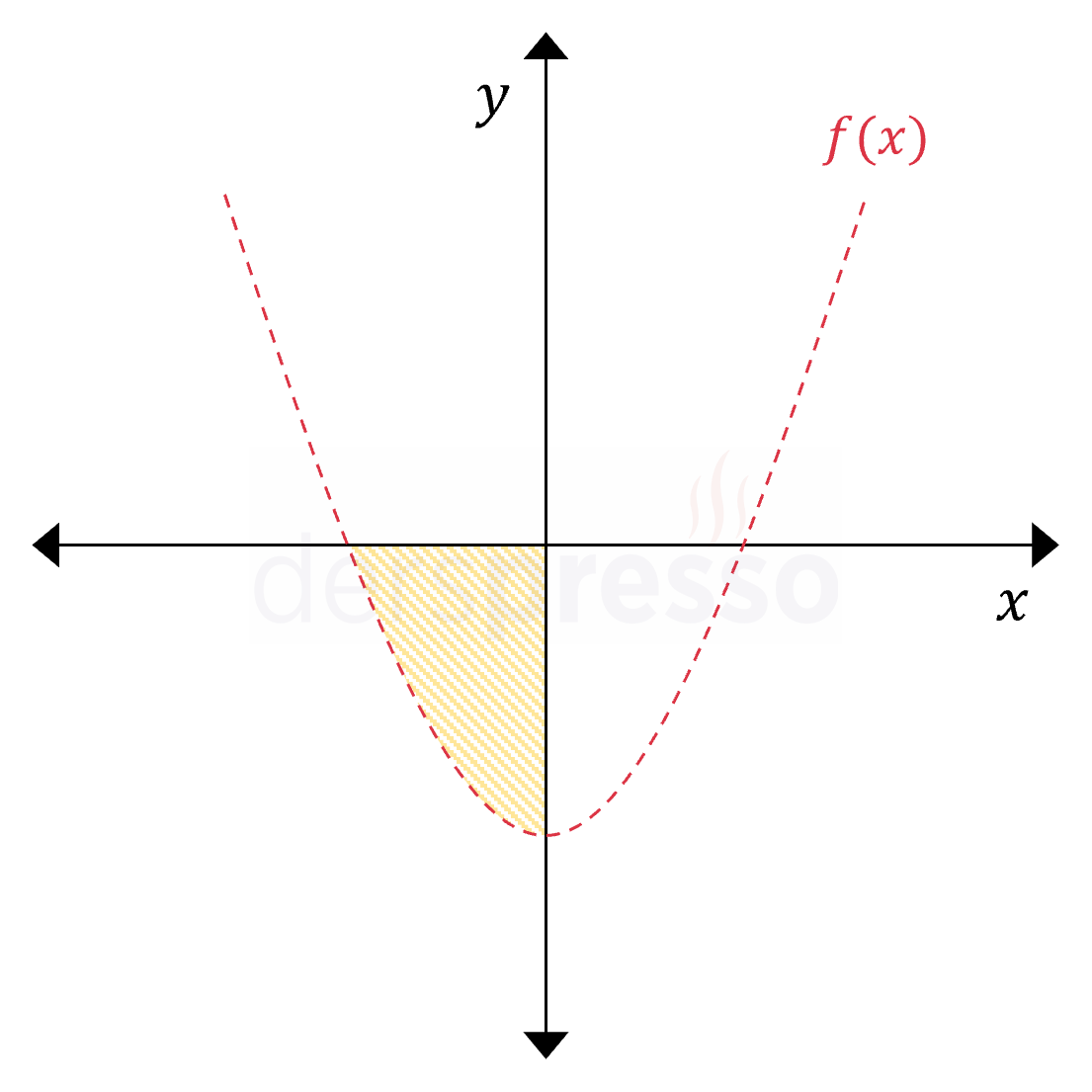
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \gt f(x) \) \( x \le 0 \) \( y \le 0 \) Küçük eşit sembolü kullanıldığı için eksenler üzerindeki noktalar taralı alana dahildir, ancak parabol üzerindeki noktalar değildir.
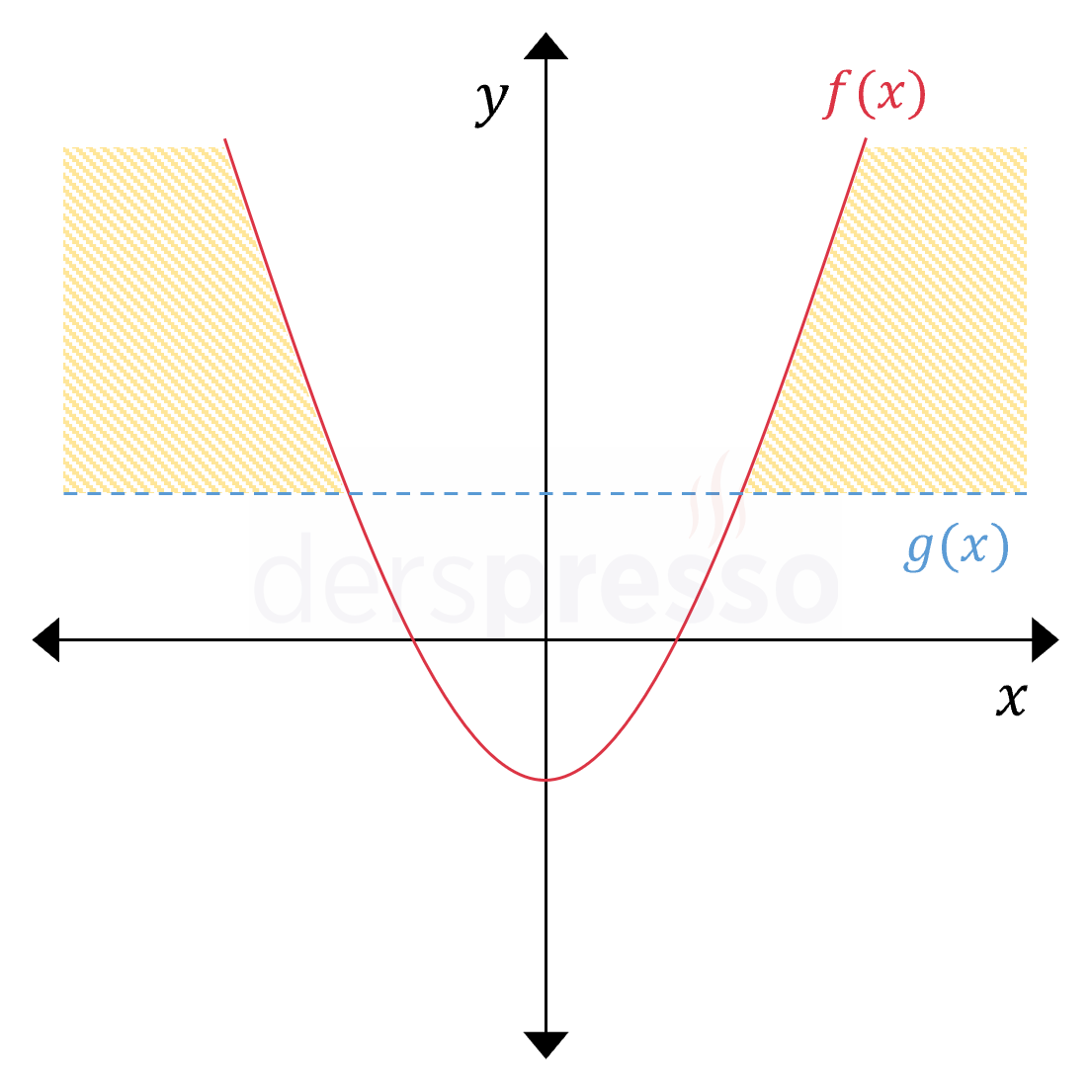
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \le f(x) \) \( y \gt g(x) \) Küçük eşit sembolü kullanıldığı için parabol üzerindeki noktalar taralı alana dahildir, ancak \( g(x) \) doğrusu üzerindeki noktalar değildir.
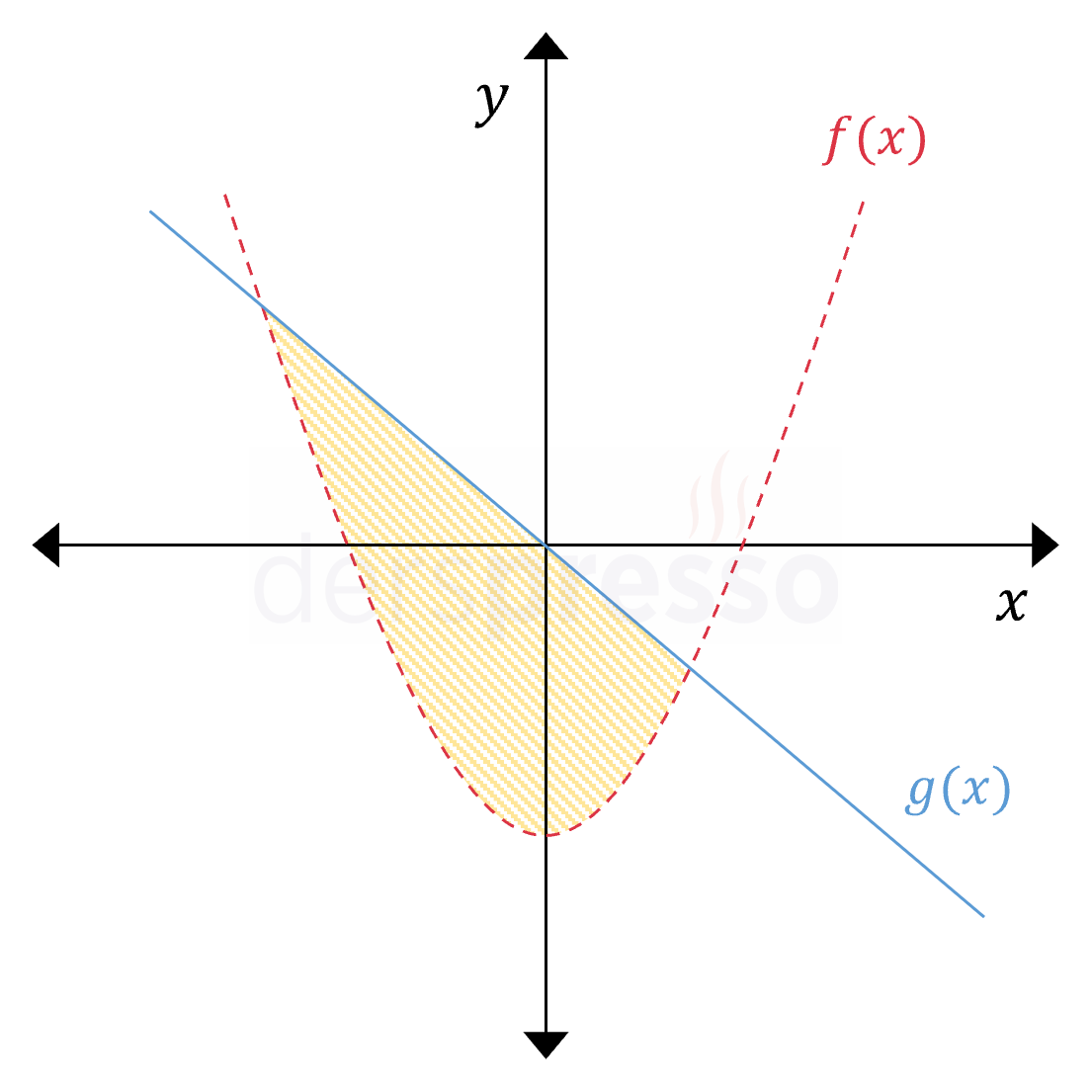
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \gt f(x) \) \( y \le g(x) \) Küçük eşit sembolü kullanıldığı için \( g(x) \) doğrusu üzerindeki noktalar taralı alana dahildir, ancak parabol üzerindeki noktalar değildir.
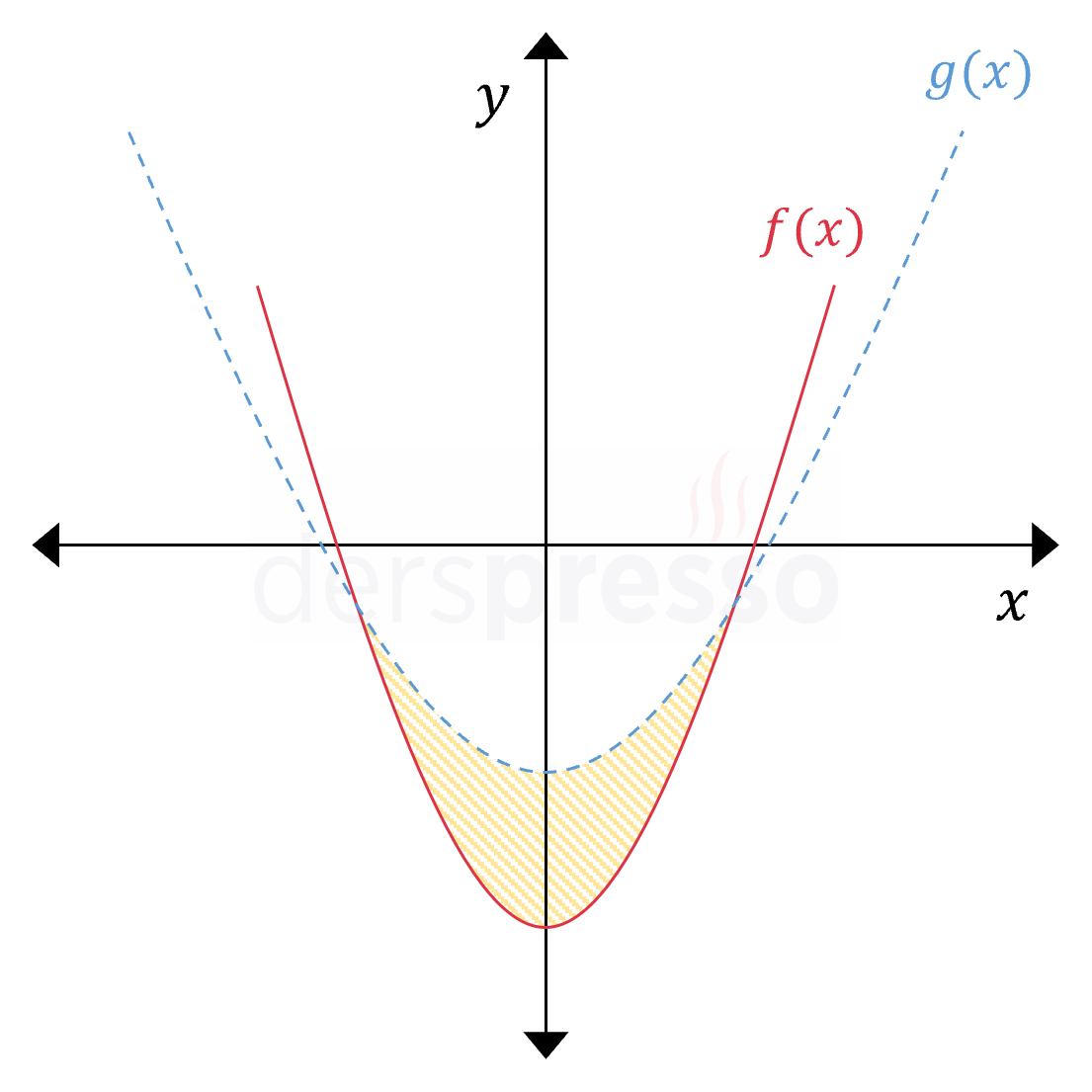
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \ge f(x) \) \( y \lt g(x) \) Büyük eşit sembolü kullanıldığı için \( f(x) \) parabolü üzerindeki noktalar taralı alana dahildir, ancak \( g(x) \) parabolü üzerindeki noktalar değildir.
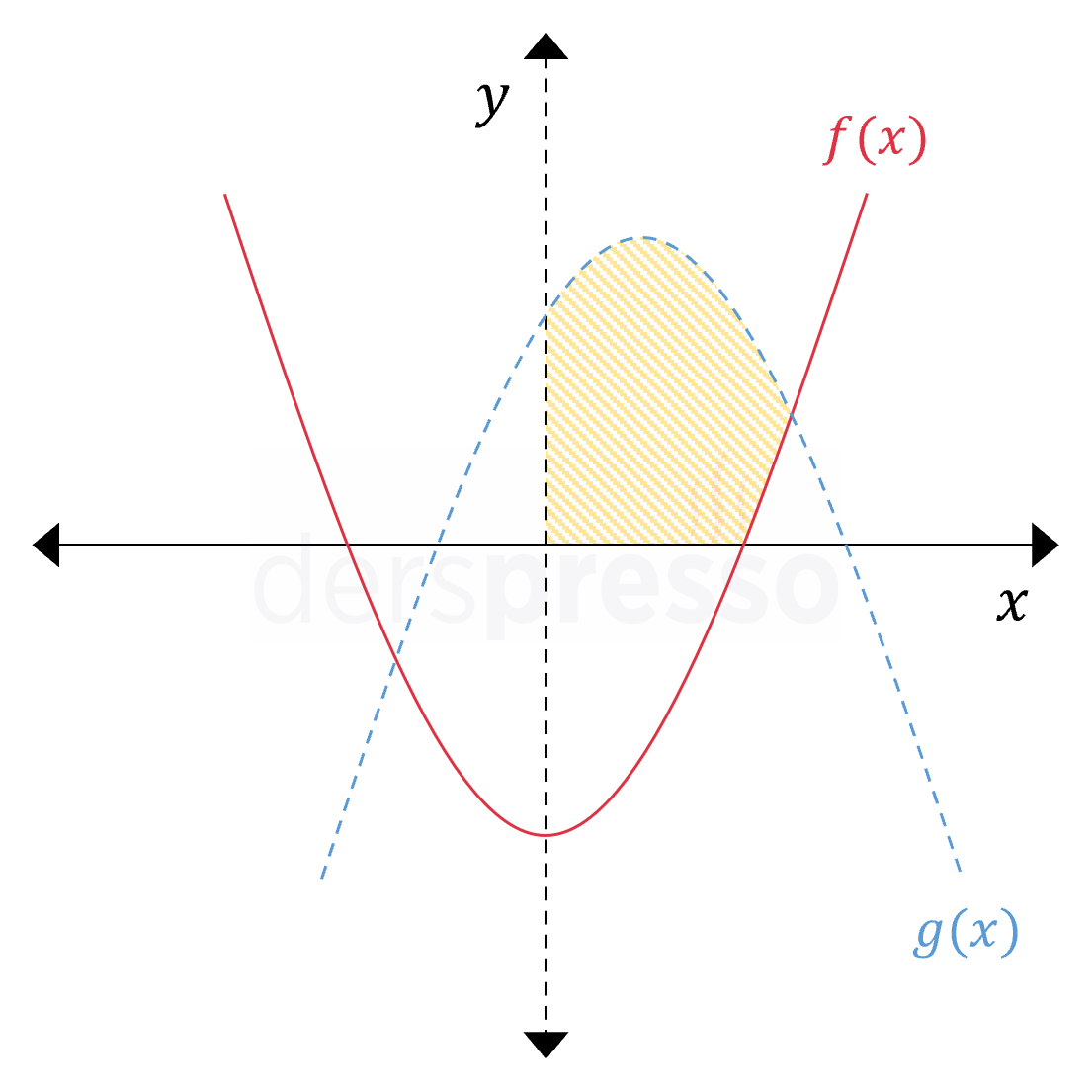
	Grafikteki taralı alan aşağıdaki eşitsizliklerin kesişimini temsil eder. \( y \ge f(x) \) \( y \lt g(x) \) \( x \gt 0 \) \( y \ge 0 \) Büyük eşit sembolü kullanıldığı için \( f(x) \) parabolü ve \( x \) ekseni üzerindeki noktalar taralı alana dahildir, ancak \( g(x) \) parabolü ve \( y \) ekseni üzerindeki noktalar değildir.

SORU 1 :

\( A(2, 7) \) noktası \( f(x) = x^2 + nx - 5 \) parabolünün iç bölgesinde, \( B(3, -8) \) noktası parabolün dış bölgesinde yer almaktadır.

Buna göre \( n \) sayısının alabileceği kaç farklı tam sayı değeri vardır?

Çözümü Göster

Parabolün iç bölgesindeki bir noktanın ordinatı, o nokta için parabolün değerinden büyük olur.

\( f(x) \) parabolünün iç bölgesindeki \( A(2, 7) \) noktası için aşağıdaki eşitsizliği yazabiliriz.

\( 7 \gt f(2) \)

\( 7 \gt 2^2 + 2n - 5 \)

\( 4 \gt n \)

Parabolün dış bölgesindeki bir noktanın ordinatı, o nokta için parabolün değerinden küçük olur.

\( f(x) \) parabolünün dış bölgesindeki \( B(3, -8) \) noktası için aşağıdaki eşitsizliği yazabiliriz.

\( -8 \lt f(3) \)

\( -8 \lt 3^2 + 3n - 5 \)

\( -4 \lt n \)

İki eşitsizliğin kesişimini bulalım.

\( -4 \lt n \lt 4 \)

\( n \) bu aralıkta \( 3 - (-3) + 1 = 7 \) tane tam sayı değer alabilir.

Soru sorun Soruda hata bildirin