Mantığın Elektrik Devrelerinde Kullanımı
Elektrik devrelerinde kullanılan anahtarları mantıksal önermeler, bu anahtarların farklı bağlama şekillerini de bileşik önermeler şeklinde modelleyerek devrelerin akımı geçirip geçirmeme durumlarını bulabiliriz.
Açık ve Kapalı Anahtarlar
Anahtarlar elektrik devrelerinde açma/kapama işlevi görerek devreden akımın geçip geçmemesini kontrol ederler.
Açık Anahtarlar
Bir anahtarın açık olması anahtarın akımı geçirmemesi anlamına gelir. Açık anahtarlar mantıkta doğruluk değeri 0 olan basit önermelerle (\( p \equiv 0 \)) temsil edilir.
Açık anahtarlar aşağıdaki şekildeki gibi gösterilir.

Kapalı Anahtarlar
Bir anahtarın kapalı olması anahtarın akımı geçirmesi anlamına gelir. Kapalı anahtarlar mantıkta doğruluk değeri 1 olan basit önermelerle (\( p \equiv 1 \)) temsil edilir.
Kapalı anahtarlar aşağıdaki şekildeki gibi gösterilir.
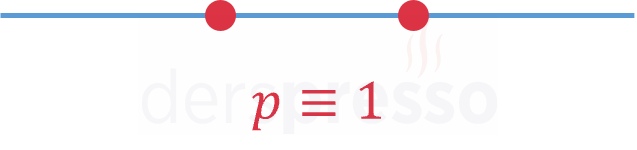
Seri ve Paralel Bağlı Anahtarlar
Anahtarların birbirine farklı şekillerde bağlanması sonucunda oluşan bir devrenin elektrik akımını geçirip geçirmediğini mantıktaki bileşik önermeler yardımıyla bulabiliriz.
Seri Bağlı Anahtarlar
İki ya da daha fazla anahtarın devrenin aynı kolunda uç uca eklenmesi ile elde edilen bağlama şekline seri bağlama denir. Anahtarların seri bağlandığı bir devre, sadece anahtarların tümü kapalı olduğunda elektrik akımını geçirir.

Seri bağlı anahtarlar birbirine "ve" bağlacı ile bağlı önermelerle (\( p \land q \)) ifade edilir, dolayısıyla sadece bileşik önermeyi oluşturan önermelerin tümü doğru olduğunda (tüm anahtarlar kapalı olduğunda) doğru olurlar (elektrik akımını geçirirler).
Paralel Bağlı Anahtarlar
İki ya da daha fazla anahtarın uçlarının devrede farklı kollar oluşturacak şekilde birleştirilmesi ile elde edilen bağlama şekline paralel bağlama denir. Anahtarların paralel bağlandığı bir devre, anahtarlardan en az biri kapalı olduğunda elektrik akımını geçirir.

Paralel bağlı anahtarlar birbirine "veya" bağlacı ile bağlı önermelerle (\( p \lor q \)) ifade edilir, dolayısıyla bileşik önermeyi oluşturan önermelerin en az biri doğru olduğunda (en az bir anahtar kapalı olduğunda) doğru olurlar (elektrik akımını geçirirler).
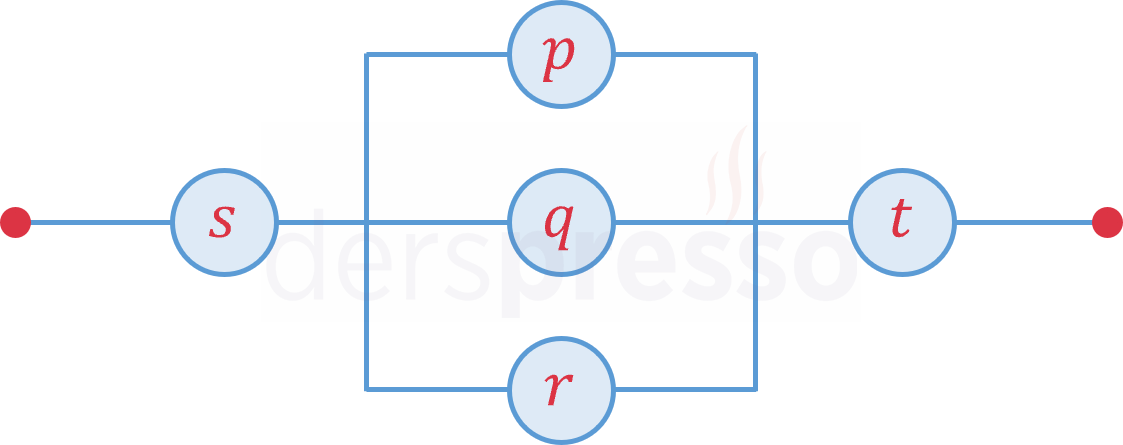
Yukarıdaki şekildeki devredeki anahtarları bir bileşik önerme şeklinde yazalım ve aşağıdaki doğruluk değerleri için devrenin akımı geçirip geçirmediğini bulalım.
\( s \equiv p \equiv q \equiv 1 \)
\( r \equiv t \equiv 0 \)
Şekilde \( p \), \( q \) ve \( r \) anahtarlarının paralel bağlı olduğunu, \( s \) ve \( t \) anahtarlarının da bu paralel anahtar grubuna seri bağlı olduğunu görüyoruz.
Buna göre, verilen devreyi bir bileşik önerme şeklinde aşağıdaki gibi yazabiliriz.
\( s \land (p \lor q \lor r) \land t \)
Verilen doğruluk değerlerini ifadede yerine koyalım.
\( 1 \land (1 \lor 1 \lor 0) \land 0 \)
\( \equiv 1 \land 1 \land 0 \equiv 0 \)
0 sonucu elde ettiğimiz için devrenin akımı geçirmediği sonucuna varabiliriz.
\( ((p \land q) \lor r) \land s \land (t \lor v) \)
bileşik önermesini bir elektrik devresi şeklinde gösterelim ve aşağıdaki doğruluk değerleri için devrenin akımı geçirip geçirmediğini bulalım.
\( r \equiv s \equiv v \equiv 1 \)
\( p \equiv q \equiv t \equiv 0 \)
Verilen bileşik önermeyi incelediğimizde, \( p \) ve \( q \) anahtarlarının seri bağlı ve \( r \) anahtarının bu iki anahtara paralel bağlı olduğunu, ayrıca \( t \) ve \( v \) anahtarlarının paralel bağlı olduğunu görüyoruz. \( s \) anahtarı ve bu iki anahtar grubu da birbirine seri bağlı durumdadır.
Buna göre verilen bileşik önermeyi devre şeklinde aşağıdaki gibi gösterebiliriz.

Verilen doğruluk değerlerini ifadede yerine koyalım.
\( ((p \land q) \lor r) \land s \land (t \lor v) \)
\( \equiv ((0 \land 0) \lor 1) \land 1 \land (0 \lor 1) \)
\( \equiv (0 \lor 1) \land 1 \land 1 \)
\( \equiv 1 \land 1 \land 1 \equiv 1 \)
1 sonucu elde ettiğimiz için devrenin akımı geçirdiği sonucuna varabiliriz.
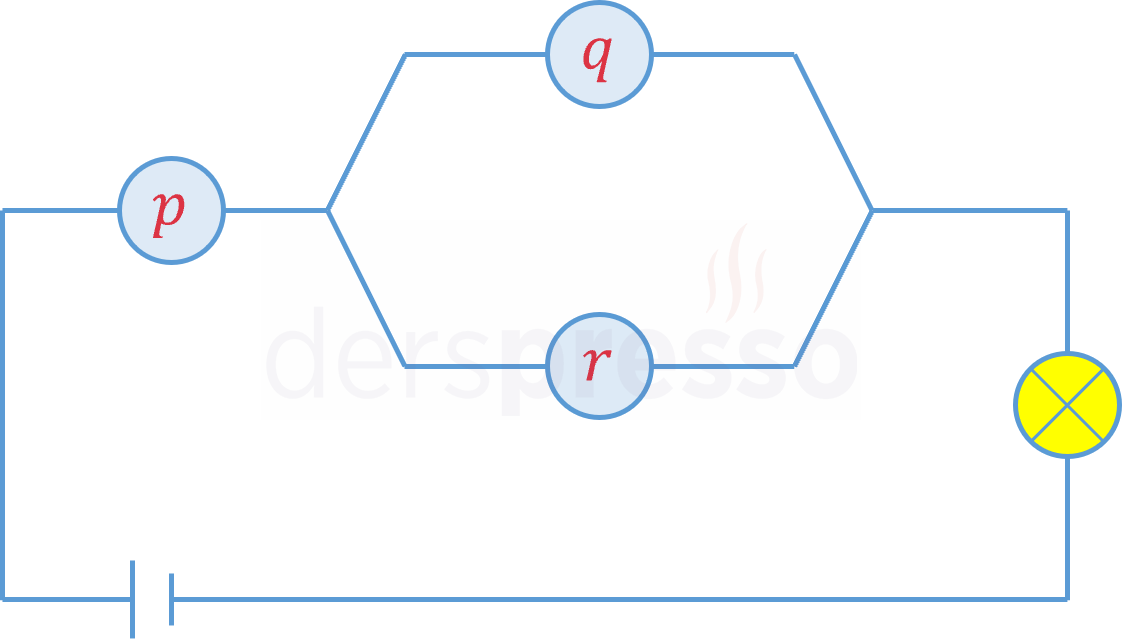
Şekildeki elektrik devresindeki lamba \( p \), \( q \) ve \( r \)'nin hangi doğruluk değerleri için yanar?
Çözümü GösterVerilen elektrik devresi aşağıdaki bileşik önermeye karşılık gelir.
\( p \land (q \lor r) \)
Lamba bu bileşik önermenin doğruluk değeri 1 olduğunda yanar.
"Ve" bileşik önermesi her iki bileşeni de doğru olduğunda doğru olur.
\( p \equiv 1 \) ve \( q \lor r \equiv 1 \)
"Veya" bileşik önermesi bileşenlerinden en az biri doğru olduğunda doğru olur.
\( q \equiv 1 \) veya \( r \equiv 1 \)
Buna göre verilen bileşik önerme aşağıdaki üç durumda doğru olur, dolayısıyla karşılık geldiği devredeki lamba yanar.
\( p \equiv 1, q \equiv 1, r \equiv 1 \)
\( p \equiv 1, q \equiv 1, r \equiv 0 \)
\( p \equiv 1, q \equiv 0, r \equiv 1 \)
Bir salonun ışıklandırması için kullanılan ampuller iki farklı düğme ile kontrol ediliyor.
Düğmelerin ikisi de aynı konumda ise (ikisi de açık ya da ikisi de kapalı ise) ampuller yanmıyor. Düğmelerden biri açık diğeri kapalı konumda ise ampuller yanıyor.
Düğmelerin durumu \( p \) ve \( q \), devredeki güç kaynağının durumu \( r \) ile gösterildiğine göre, ampullerin yanmasını sağlayan önerme nedir?
Çözümü GösterDüğmelerden biri açık diğeri kapalı konumda ise ampuller yanıyor, diğer durumlarda yanmıyor.
O halde \( p \) ve \( q \) düğmeleri aşağıdaki şekilde gösterilir.
\( (p \land q') \lor (p' \land q) \)
Ampüllerin yanması için güç kaynağı her durumda devrede olmalıdır. O halde yukarıda belirtilen bileşik önermeye "ve" bağlacı ile bağlanmalıdır.
\( r \land [(p \land q') \lor (p' \land q)] \)