3 Boyutlu Koordinat Sistemi
Bir noktanın bir doğru üzerindeki konumunu ifade etmek için her noktası bir reel sayıya karşılık gelen sayı doğrusu kullanılır.

Bir noktanın bir düzlem üzerindeki konumunu ifade etmek için iki boyutlu kartezyen düzlemi ve kutupsal koordinat sistemi gibi koordinat sistemleri kullanılır. Bu sistemlerden iki boyutlu kartezyen düzlemi, birbirine dik ve her biri birer sayı doğrusu olan \( x \) ve \( y \) eksenlerinden ve bu eksenlerin oluşturduğu düzlemden oluşur.
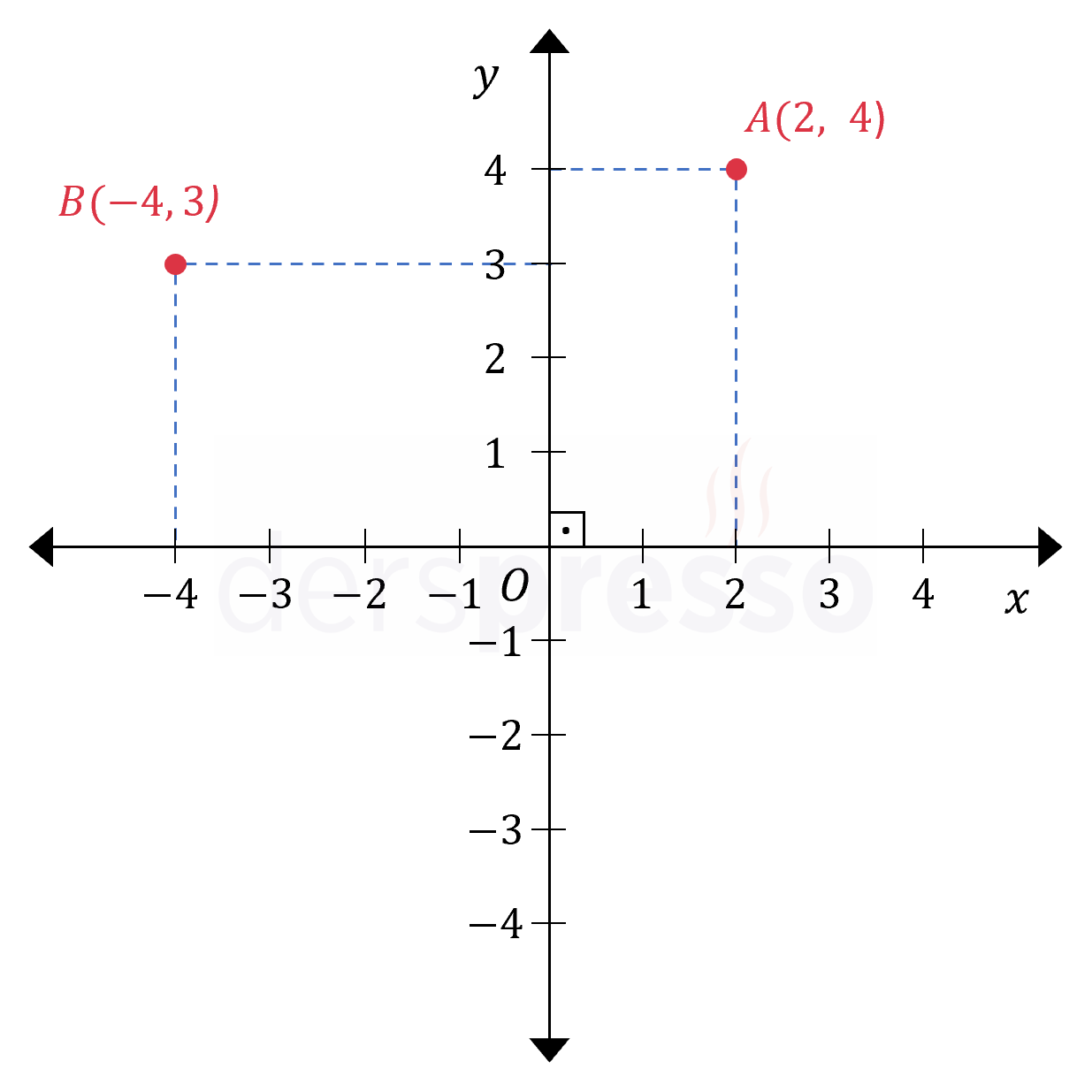
İki boyutlu kartezyen koordinat sistemindeki tüm noktaların kümesi, reel sayılar kümesinin ikili kartezyen çarpımı şeklinde ifade edilir.
\( \mathbb{R}^2 = \mathbb{R} \times \mathbb{R} = \{ (x, y) \mid x, y \in \mathbb{R} \} \)
Bir noktanın uzaydaki konumunu ifade etmek için ise üç boyutlu bir koordinat sistemine ihtiyaç duyulur. Bu sistemlerden biri olan üç boyutlu kartezyen koordinat sistemi, birbirine dik \( x \), \( y \) ve \( z \) eksenlerinden ve bu eksenlerin oluşturduğu koordinat uzayından oluşur. Bu üç eksene koordinat eksenleri denir.

Bu koordinat sisteminde \( x \) ve \( y \) eksenlerinin oluşturduğu düzleme \( xy \) düzlemi, \( x \) ve \( z \) eksenlerinin oluşturduğu düzleme \( xz \) düzlemi, \( y \) ve \( z \) eksenlerinin oluşturduğu düzleme de \( yz \) düzlemi denir. Bu üç düzleme koordinat düzlemleri denir. Koordinat düzlemleri koordinat uzayını sekiz bölgeye ayırır.
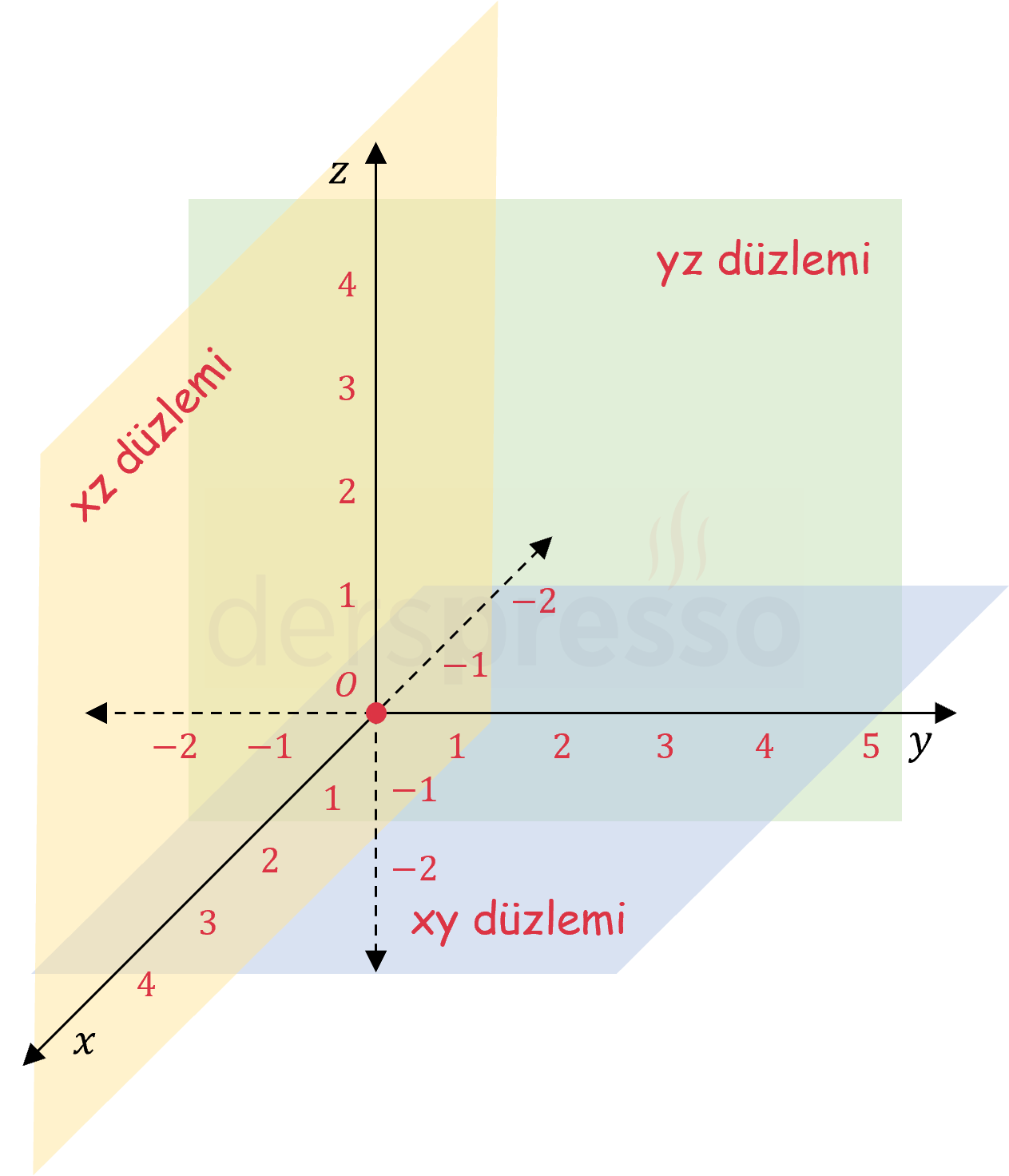
Kartezyen koordinat sisteminde uzaydaki bir noktanın koordinatları \( (x, y, z) \) sıralı üçlüsü ile ifade edilir. Bu koordinatlarda \( x \) değeri noktanın \( yz \) düzlemine, \( y \) değeri \( xz \) düzlemine, \( z \) değeri de \( xy \) düzlemine pozitif ya da negatif yöndeki uzaklığını verir. Aşağıda bir \( A \) noktasının koordinatları ile koordinat düzlemleri ve eksenleri üzerindeki izdüşümleri verilmiştir.

Üç boyutlu kartezyen koordinat sistemindeki tüm noktaların kümesi, reel sayılar kümesinin üçlü kartezyen çarpımı şeklinde ifade edilir.
\( \mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R} = \{ (x, y, z) \mid x, y, z \in \mathbb{R} \} \)
Uzayda İki Nokta Arasındaki Uzaklık
Üç boyutlu uzayda iki nokta arasındaki uzaklık aşağıdaki formülle bulunur.
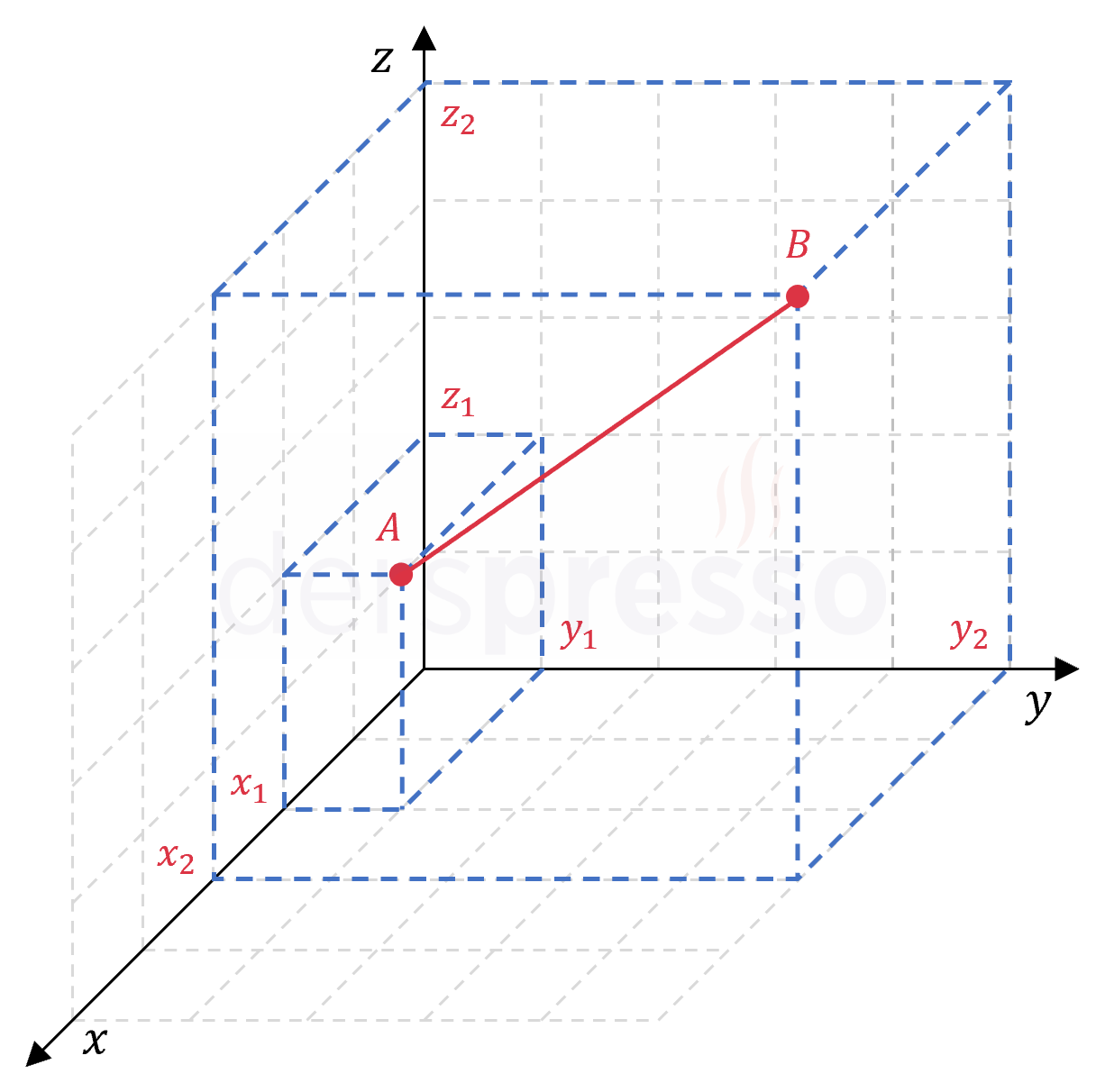
\( A(x_1, y_1, z_1) \) ve \( B(x_2, y_2, z_2) \) noktaları arasındaki uzaklık:
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \)
\( A(-4, 5, 2) \) ve \( B(2, 3, -1) \) noktaları arasındaki uzaklık:
\( \abs{AB} = \sqrt{(2 - (-4))^2 + (3 - 5)^2 + (-1 - 2)^2} \)
\( = \sqrt{36 + 4 + 9} = 7 \)
İSPATI GÖSTER
\( z \) koordinatı \( A \) noktası, \( x \) ve \( y \) koordinatları \( B \) noktası ile aynı olacak şekilde \( C \) noktası belirleyelim.
\( C(x_2, y_2, z_1) \)
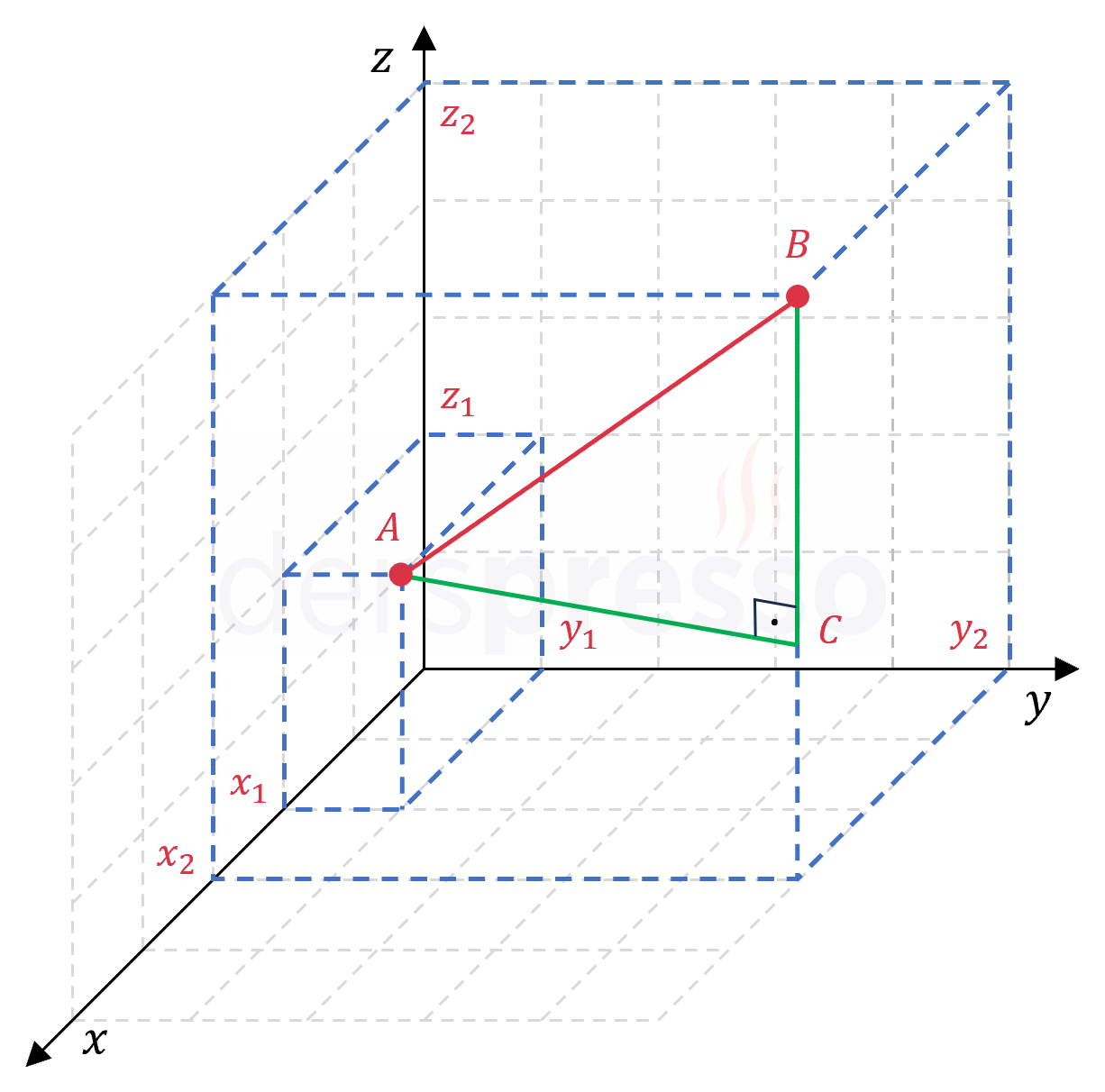
\( z \) koordinatları aynı olan ve \( xy \) düzlemine paralel bir düzlem üzerinde bulunan \( A \) ve \( C \) noktaları arasındaki \( \abs{AC} \) uzaklığını iki boyutlu kartezyen düzlemi uzaklık formülü ile bulabiliriz.
\( \abs{AC} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( x \) ve \( y \) koordinatları aynı olan ve \( z \) eksenine paralel bir doğru üzerinde bulunan \( B \) ve \( C \) noktaları arasındaki \( \abs{BC} \) uzaklığı, iki noktanın \( z \) koordinatları arasındaki farka eşittir.
\( \abs{BC} = z_2 - z_1 \)
Oluşan \( ACB \) dik üçgenine Pisagor teoremini uygulayarak \( \abs{AB} \) uzunluğunu bulalım.
\( (\abs{AB})^2 = (\abs{AC})^2 + (\abs{BC})^2 \)
\( \abs{AB} = \sqrt{(\abs{AC})^2 + (\abs{BC})^2} \)
Yukarıda bulduğumuz ifadeleri bu formülde yerine koyduğumuzda üç boyutlu uzayda iki nokta arasındaki uzaklık formülünü elde ederiz.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \)
Noktalardan biri orijin olarak alınırsa bir noktanın orijine uzaklığı aşağıdaki formülle bulunur.
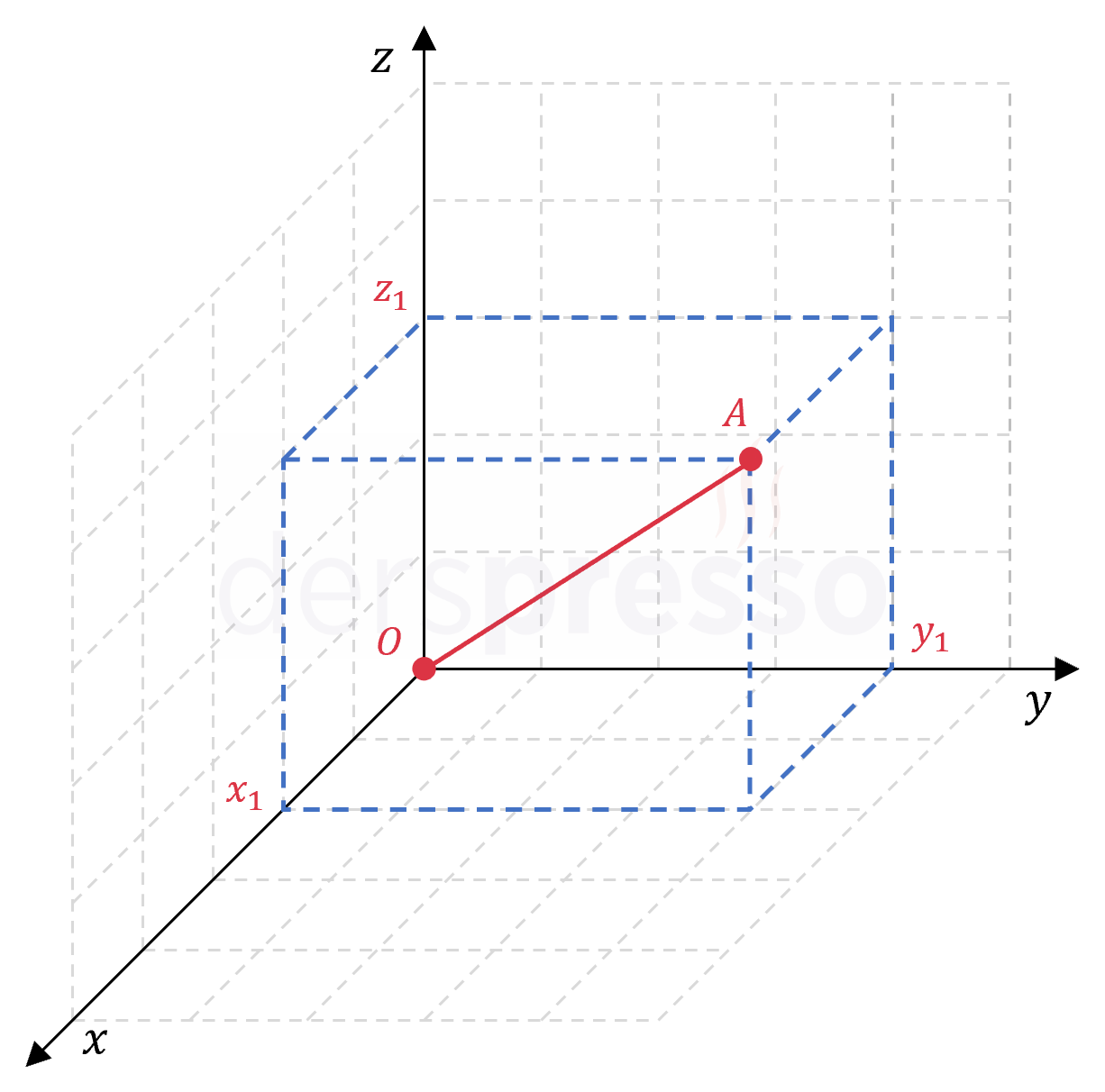
\( A(x_1, y_1, z_1) \) noktasının orijine uzaklığı:
\( \abs{AO} = \sqrt{x_1^2 + y_1^2 + z_1^2} \)
\( A(-3, 6, 2) \) noktasının orijine uzaklığı:
\( \abs{AO} = \sqrt{(-3)^2 + 6^2 + 2^2} \)
\( = \sqrt{9 + 36 + 4} = 7 \)
İSPATI GÖSTER
Üç boyutlu uzayda iki nokta arasındaki uzaklık formülünde noktalardan birini orijin olarak kabul edelim.
\( O(0, 0, 0) \)
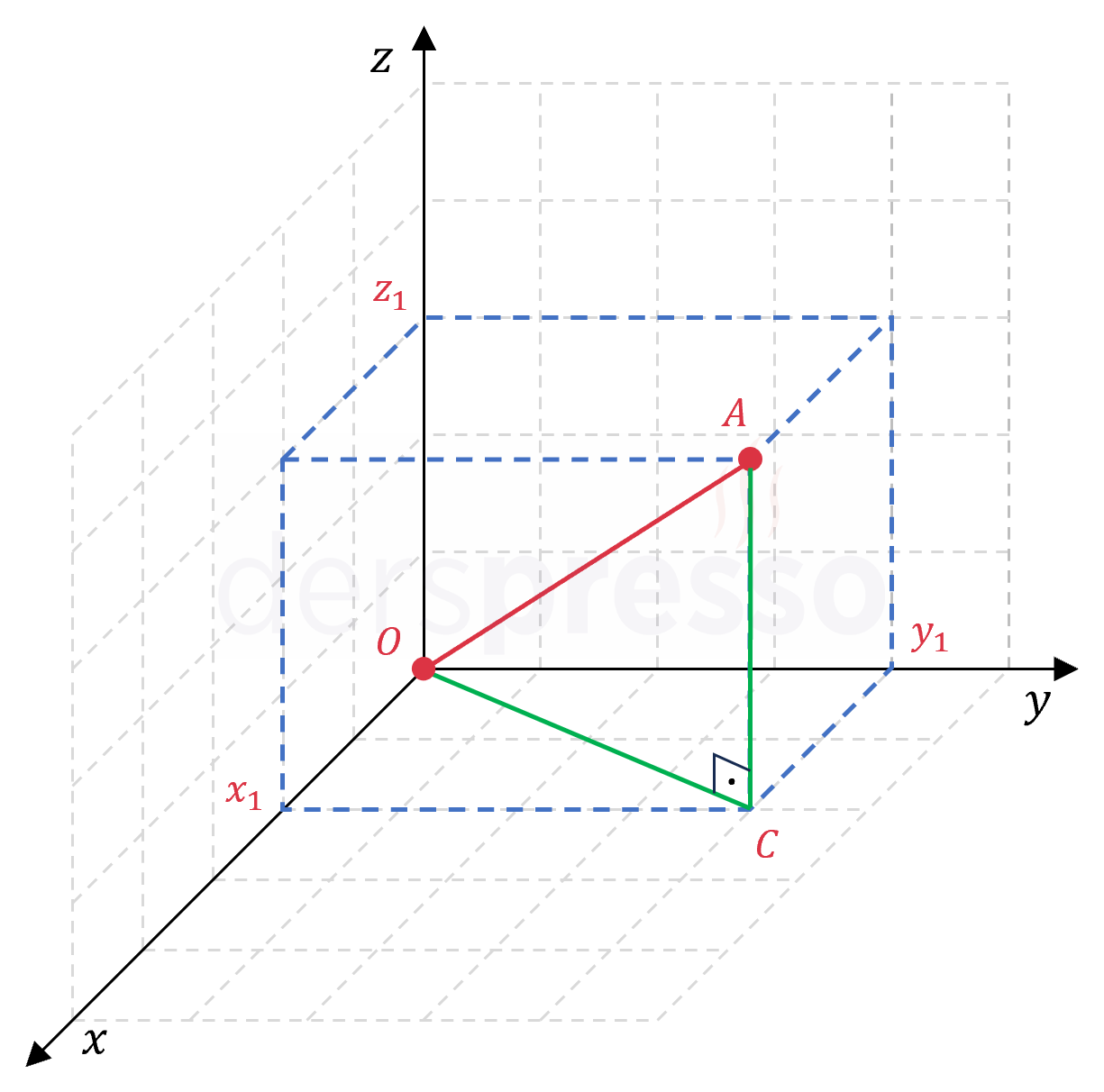
\( \abs{AO} = \sqrt{(x_1 - 0)^2 + (y_1 - 0)^2 + (z_1 - 0)^2} \)
\( = \sqrt{x_1^2 + y_1^2 + z_1^2} \)