Kutupsal Koordinat Sistemi
Bir koordinat sistemi bir noktanın düzlemdeki ya da uzaydaki konumunu belirli eksenleri veya noktaları referans alarak bir sıralı ikili ya da üçlü şeklinde temsil eder. Bu konuma noktanın o koordinat sistemindeki koordinatları denir.
En sık kullanılan koordinat sistemi olan kartezyen koordinat sisteminde bir noktanın koordinatları noktanın birbirine dik eksenlere olan yönlü (pozitif ve negatif olabilen) uzaklıkları ile ifade edilir. İki boyutlu kartezyen koordinat sisteminde eksenler \( x \) ve \( y \), noktanın koordinatları da \( (x, y) \) sıralı ikilisidir. Üç boyutlu koordinat sisteminde ise eksenler \( x \), \( y \) ve \( z \), noktanın koordinatları da \( (x, y, z) \) sıralı üçlüsüdür.
Bu bölümde inceleyeceğimiz kutupsal koordinat sisteminde ise bir noktanın koordinatları noktanın orijine olan yönlü uzaklığı ve noktayı orijinle birleştiren doğru parçasının yatay eksen ile yaptığı yönlü açıdan oluşan \( (r, \theta) \) sıralı ikilisi ile ifade edilir.

Kutupsal koordinat sisteminde orijine kutup noktası, \( x \) eksenine kutup ekseni de denir. Kutup ekseni kartezyen koordinat sistemindeki \( x \) ekseninin pozitif tarafına karşılık gelir.
Aşağıdaki şekilde bazı noktaların kutupsal koordinat sistemindeki koordinatları verilmiştir.

Bir noktaya ait \( \theta \) açısının ölçüsü pozitif ise açı yatay eksenin pozitif tarafından saat yönünün tersi yönde, negatif ise saat yönünde ölçülür.
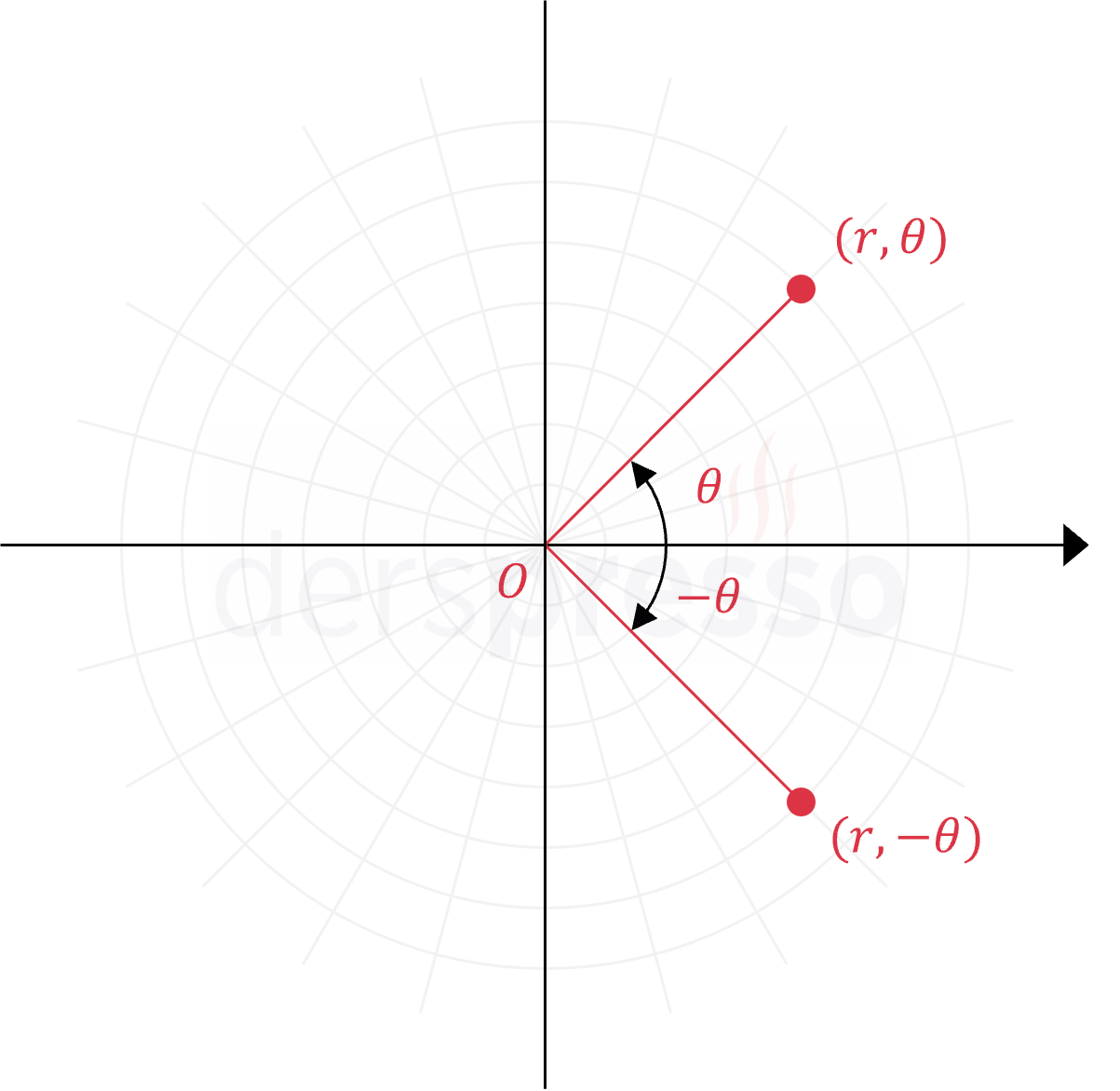
Kutupsal koordinat sisteminde kullanılan uzaklık da yönlü bir kavramdır, dolayısıyla negatif olabilir. Bir noktaya ait \( r \) uzaklığı pozitif ise nokta açının bitim kolu boyunca orijinden \( \abs{r} \) birim uzaklıktadır, negatif ise bitiş kolu ile aynı doğrultuda ve ters yönde orijinden \( \abs{r} \) birim uzaklıktadır. Bu nokta aynı zamanda birinci noktanın orijine göre simetriğidir ve iki doğru arasındaki açı \( \pi \) radyandır.

Noktanın Farklı Gösterimleri
Bir noktanın kartezyen koordinat sisteminde tek bir gösterimi varken kutupsal koordinat sisteminde sonsuz sayıda farklı gösterimi vardır. Bu farklı gösterimler üç şekilde olabilir.
Denk Açılar
Trigonometride tanımladığımız yönlü açılara \( 2\pi \) radyanın herhangi bir tam sayı katı eklendiğinde ya da çıkarıldığında elde edilen açı orijinal açıya denktir. Bu sebeple kutupsal koordinat sisteminde aynı nokta birbirine denk açılarla sonsuz sayıda farklı şekilde ifade edilebilir.
Aşağıda \( A \) noktasının kutupsal koordinatlarının birbirine denk üç açı ile farklı gösterimleri verilmiştir.

\( k \in \mathbb{Z} \) olmak üzere,
\( (r, \theta) = (r, \theta + k \cdot 2\pi) \)
\( \ldots = (r, -\frac{11\pi}{6}) = (r, \frac{\pi}{6}) = (r, \frac{13\pi}{6}) = \ldots \)
Negatif Uzaklık
Kutupsal koordinat sisteminde uzaklık da yönlü bir kavramdır, dolayısıyla negatif olabilir.
Aşağıda \( B \) noktasının kutupsal koordinatları standart gösterime ek olarak, orijine göre simetriği olan \( A \) noktasının koordinatları cinsinden ve negatif uzaklıkla verilmiştir. Buna göre, \( A \) noktasının sonsuz sayıda gösterimindeki uzaklıkların negatif işaretlileri alındığında \( B \) noktası için birer gösterim elde edilir.

\( k \in \mathbb{Z} \) olmak üzere,
\( (r, \theta) = (-r, \theta + (2k + 1) \cdot \pi) \)
\( (5, \frac{\pi}{4}) = (-5, \frac{5\pi}{4}) = (-5, \frac{13\pi}{4}) \)
İSPATI GÖSTER
Kutupsal koordinat sisteminde bir \( (r, \theta) \) noktasının koordinatları orijine göre simetrik olduğu ve aralarında \( \pi \) radyan açı bulunan diğer bir nokta cinsinden aşağıdaki şekilde de yazılabilir.
\( (r, \theta) = (-r, \theta + \pi) \)
Bu ikinci noktanın açı ölçüsüne \( 2\pi \)'nin tam sayı katlarının eklenmesiyle ya da çıkarılmasıyla denk açılar elde edilir.
\( k \in \mathbb{Z} \) olmak üzere,
\( (r, \theta) = (-r, \theta + \pi + k \cdot 2\pi) \)
Parantez içindeki açıyı düzenleyelim.
\( (r, \theta) = (-r, \theta + \pi + 2k \cdot \pi) \)
\( (r, \theta) = (-r, \theta + (2k + 1) \cdot \pi) \)
Orijin Noktası
Orijin noktası \( r = 0 \) olduğu sürece herhangi bir \( \theta \) değeri ile ifade edilebilir.
Orijin noktasının koordinatları:
\( (0, \theta) \)
\( (0, 0) = (0, \frac{\pi}{3}) = (0, -\frac{3\pi}{4}) \)
Bir nokta kutupsal koordinat sisteminde benzersiz şekilde ifade edilmek istenirse \( r \) pozitif, \( \theta \) da \( [0, 2\pi) \) aralığında seçilmelidir.
Kutupsal > Kartezyen Denklemi Dönüşümü
Kutupsal koordinatları verilen bir noktanın kartezyen koordinatları dik üçgenin trigonometrik özellikleri kullanılarak aşağıdaki formüllerle bulunabilir.
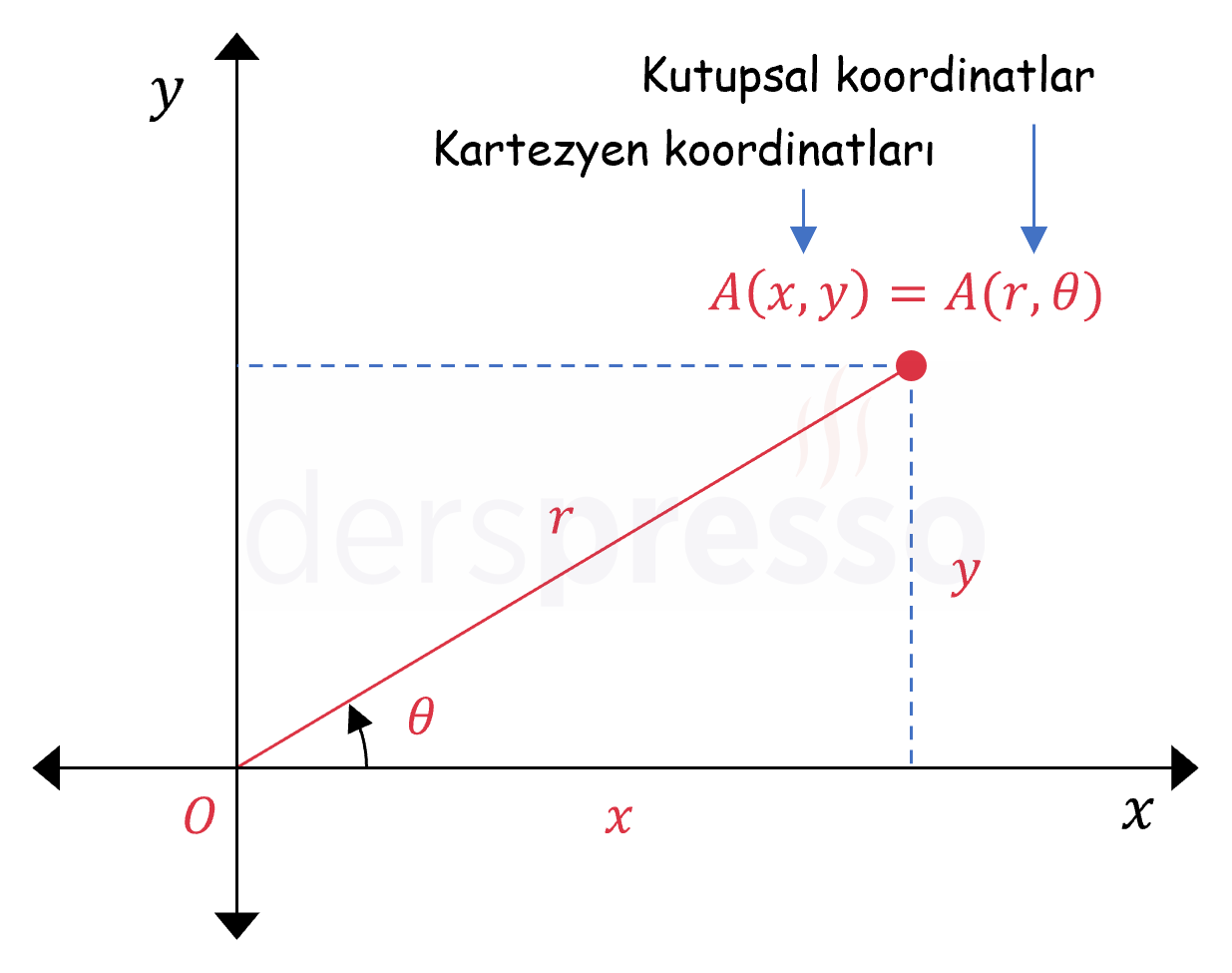
\( x = r\cos{\theta} \)
\( y = r\sin{\theta} \)
Kutupsal koordinatları \( (8, \frac{\pi}{3}) \) olan \( A \) noktasının kartezyen koordinatları:
\( x = 8\cos{\frac{\pi}{3}} = 8 \cdot \dfrac{1}{2} = 4 \)
\( y = 8\sin{\frac{\pi}{3}} = 8 \cdot \dfrac{\sqrt{3}}{2} = 4\sqrt{3} \)
Buna göre \( A \) noktasının kartezyen koordinatları \( (4, 4\sqrt{3}) \) olur.
Bu dönüşümler tüm bölgelerdeki pozitif ve negatif \( \theta \) ve \( r \) değerleri için geçerlidir.
Kartezyen > Kutupsal Denklem Dönüşümü
Kartezyen koordinatları verilen bir noktanın kutupsal koordinatları aşağıdaki formüllerle bulunabilir.
\( r^2 = x^2 + y^2 \)
\( \theta = \arctan{\frac{y}{x}} \)
Kartezyen koordinatları \( (4, 4\sqrt{3}) \) olan noktanın kutupsal koordinatları:
\( r = \sqrt{4^2 + (4\sqrt{3})^2} = 8 \)
\( \theta = \arctan{\frac{4\sqrt{3}}{4}} = \dfrac{\pi}{3} \)
Buna göre verilen noktanın kutupsal koordinatları \( (8, \frac{\pi}{3}) \) olur.
\( r^2 = x^2 + y^2 \) eşitliğinin \( r \) için çözümü pozitif ve negatif olmak üzere iki değer içerse de standart bir gösterim için pozitif değer seçilir.
\( \theta \) değerini ters tanjant fonksiyonu ile bulurken verilen \( x \) ve \( y \) değerlerinin işaretleri doğrultusunda noktanın bulunduğu bölgeye karşılık gelen doğru açı alınmalıdır.
Kartezyen koordinatları \( (-3\sqrt{2}, -3\sqrt{2}) \) olan noktanın kutupsal koordinatları:
\( r = \sqrt{((-3\sqrt{2})^2 + (-3\sqrt{2})^2} = 6 \)
\( \dfrac{y}{x} = \dfrac{-3\sqrt{2}}{-3\sqrt{2}} = 1 \)
\( \arctan(1) = \dfrac{\pi}{4} \)
Tanjant I. ve III. bölgelerde pozitiftir, verilen nokta ise III. bölgededir.
\( \theta = \dfrac{5\pi}{4} \)
Buna göre verilen noktanın kutupsal koordinatları \( (6, \frac{5\pi}{4}) \) olur.
\( \theta = \arctan{\frac{y}{x}} \) formülü bazı \( x \) ve \( y \) değerleri için tanımsız olabileceği için aşağıdaki üç özel duruma dikkat edilmelidir.
(1) \( x = 0, \quad y \gt 0 \) ise:
\( \theta = \dfrac{\pi}{2} \)
(2) \( x = 0, \quad y \lt 0 \) ise:
\( \theta = \dfrac{3\pi}{2} \)
(3) \( x = 0, \quad y = 0 \) ise:
\( r = 0 \) olacağı için \( \theta \) sıfır ya da herhangi bir değer seçilebilir.