Kutupsal Denklemlerde Analitik Uygulamalar
Bu bölümde kutupsal denklemlerin bazı analitik uygulamalarını inceleyeceğiz.
İki Nokta Arasındaki Uzaklık
Kutupsal koordinatları verilen iki nokta arasındaki uzaklık aşağıdaki formülle bulunabilir. Aşağıdaki şekilde oluşan \( AOB \) üçgeni ile birlikte incelendiğinde, bu formülün trigonometride gördüğümüz kosinüs teoremi formülü ile aynı olduğu görülebilir.
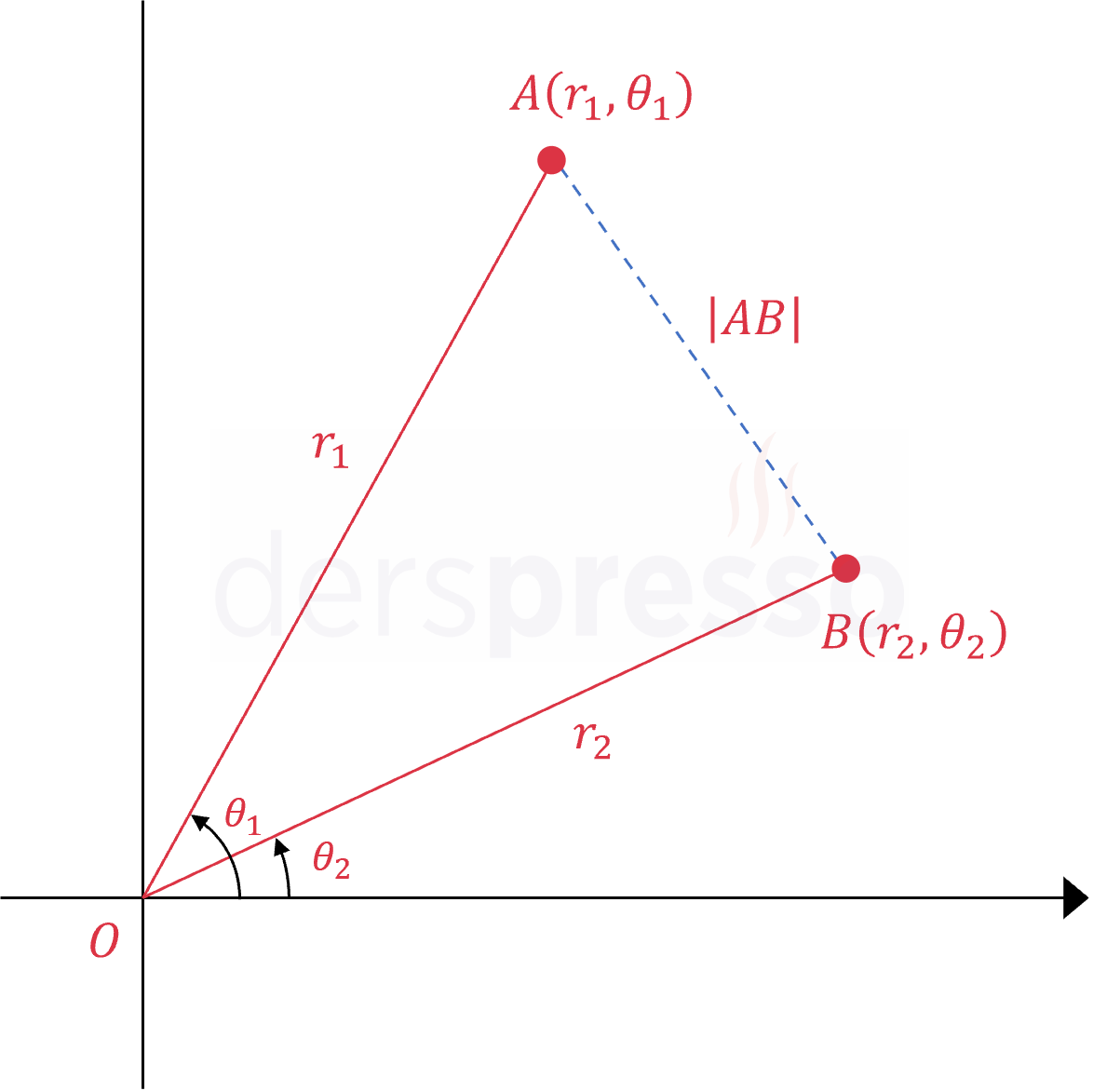
\( A(r_1, \theta_1), B(r_2, \theta_2) \) olmak üzere,
\( \abs{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2\cos(\theta_1 - \theta_2)} \)
\( A(3, \frac{5\pi}{6}), \quad B(8, \frac{\pi}{2}) \)
\( \abs{AB} = \sqrt{3^2 + 8^2 - 2(3)(8)\cos(\frac{5\pi}{6} - \frac{\pi}{2})} \)
\( = \sqrt{9 + 64 - 48\cos{\frac{\pi}{3}}} = 7 \)
İSPATI GÖSTER
Kartezyen koordinatları verilen iki nokta arasındaki uzaklık formülünü yazalım.
\( A(x_1, y_1), \quad B(x_2, y_2) \) olmak üzere,
\( \abs{AB} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \)
Kartezyen koordinatlarını kutupsal koordinatlara dönüştürme formüllerini bu formülde yerine koyalım.
\( x = r\cos{\theta} \)
\( y = r\sin{\theta} \)
\( = \sqrt{(r_1\cos{\theta_1} - r_2\cos{\theta_2})^2 + (r_1\sin{\theta_1} - r_2\sin{\theta_2})^2} \)
\( = \sqrt{r_1^2\cos^2{\theta_1} - 2r_1r_2\cos{\theta_1}\cos{\theta_2} + r_2^2\cos^2{\theta_2} + r_1^2\sin^2{\theta_1} - 2r_1r_2\sin{\theta_1}\sin{\theta_2} + r_2^2\sin^2{\theta_2}} \)
\( = \sqrt{r_1^2(\cos^2{\theta_1} + \sin^2{\theta_1}) + r_2^2(\cos^2{\theta_2} + \sin^2{\theta_2}) - 2r_1r_2(\cos{\theta_1}\cos{\theta_2} + \sin{\theta_1}\sin{\theta_2})} \)
\( \sin^2{x} + \cos^2{x} = 1 \) özdeşliğini kullanalım.
\( = \sqrt{r_1^2 + r_2^2 - 2r_1r_2(\cos{\theta_1}\cos{\theta_2} + \sin{\theta_1}\sin{\theta_2})} \)
Kosinüs fark formülünü kullanalım.
\( \cos(x - y) = \cos{x}\cos{y} + \sin{x}\sin{y} \)
\( = \sqrt{r_1^2 + r_2^2 - 2r_1r_2\cos(\theta_1 - \theta_2)} \)
Kutupsal Denklemlerin Kesişimi
İki kutupsal denklem belirli bir \( \theta \) değeri için aynı \( r \) değerine sahipse bu iki denklem aynı \( (r, \theta) \) noktasından geçiyordur, dolayısıyla bu nokta denklemlerin bir kesişim noktasıdır.
Kutupsal koordinat sistemi sayfasında üç farklı sebeple farklı kutupsal koordinatların aynı noktaya karşılık gelebileceğini belirtmiştik. İki kutupsal denklemin kesişim noktalarını bulurken bu üç durum ayrı ayrı kontrol edilmelidir.
- Denklemlerin esas ölçüsü aynı olan açılarda aynı \( r \) değerine sahip olduğu durumlar
- Denklemlerin aralarında 180° olan iki açı için birbirinin ters işaretlisi \( r \) değerlerine sahip olduğu durumlar
- Denklemlerin farklı açı değerlerinde \( r = 0 \) olduğu, yani orijinden geçtiği durumlar
Alternatif bir yöntem olarak kutupsal denklemler kartezyen denklemine dönüştürülerek ve ortak çözülerek de kesişim noktaları bulunabilir. Bulunan kesişim noktalarının kartezyen koordinatları daha sonra kutupsal koordinatlara dönüştürülür. Bu çözüm ek işlem gerekirse de tek adımda tüm kesişim noktalarını bulmamızı sağlar.
Aşağıda verilen iki kutupsal denklemin kesişim noktalarını bulalım.
\( r_1(\theta) = \sin{\theta} \)
\( r_2(\theta) = \sin(2\theta) \)
Durum 1: İki denklemi birbirine eşitleyerek ortak çözelim.
\( r_1(\theta) = r_2(\theta) \)
\( \sin{\theta} = \sin(2\theta) \)
\( \sin{\theta} - \sin(2\theta) = 0 \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin{\theta} - 2\sin{\theta}\cos{\theta} = 0 \)
\( \sin{\theta}(1 - 2\cos{\theta}) = 0 \)
\( \sin{\theta} = 0 \) veya \( 1 - 2\cos{\theta} = 0 \)
\( \sin{\theta} = 0 \) için:
\( \theta \in \{0, \pi\} \)
\( 1 - 2\cos{\theta} = 0 \) için:
\( \cos{\theta} = \dfrac{1}{2} \)
\( \theta \in \{\frac{\pi}{3}, \frac{5\pi}{3}\} \)
Bulduğumuz dört \( \theta \) değerini birinci denklemde yerine koyarak kutupsal koordinatlarını bulalım.
\( r_1(0) = \sin{0} = 0 \)
\( r_1(\pi) = \sin{\pi} = 0 \)
\( r_1(\frac{\pi}{3}) = \sin{\frac{\pi}{3}} = \frac{\sqrt{3}}{2} \)
\( r_1(\frac{5\pi}{3}) = \sin{\frac{5\pi}{3}} = -\frac{\sqrt{3}}{2} \)
\( (0, 0) \) ve \( (0, \pi) \) noktalarının ikisinde de \( r = 0 \) olduğu için koordinat sisteminde aynı noktaya karşılık gelirler.
Noktaları pozitif \( r \) değeri ile gösterme prensibiyle \( (-\frac{\sqrt{3}}{2}, \frac{5\pi}{3}) \) noktasını \( (\frac{\sqrt{3}}{2}, \frac{2\pi}{3}) \) şeklinde ifade edelim.
Buna göre eğrilerin üç kesişim noktasını bulmuş olduk.
\( (r, \theta) \in \{(0, 0), (\frac{\sqrt{3}}{2}, \frac{\pi}{3}), (\frac{\sqrt{3}}{2}, \frac{2\pi}{3})\} \)
Durum 2: Açılar arasında \( \pi \) radyan olduğu durumda \( r_1 = -r_2 \) denkleminin çözümlerini kontrol edelim.
\( r_1(\theta) = -r_2(\theta + \pi) \)
\( \sin{\theta} = -\sin(2(\theta + \pi)) \)
\( \sin{\theta} = -\sin(2\theta) \)
\( \sin{\theta} + 2\sin(\theta)\cos(\theta) = 0 \)
\( \sin{\theta}(1 + 2\cos(\theta)) = 0 \)
\( \sin{\theta} = 0 \) eşitliğinin çözümü yukarıda bulduğumuz çözüme dahildir.
\( 1 + 2\cos{\theta} = 0 \) için:
\( \cos{\theta} = -\frac{1}{2} \)
\( \theta \in \{\frac{2\pi}{3}, \frac{4\pi}{3}\} \)
Bulduğumuz yeni iki \( \theta \) değerini birinci denklemde yerine koyarak kutupsal koordinatlarını bulalım.
\( r_1(\frac{2\pi}{3}) = \sin{\frac{2\pi}{3}} = \frac{\sqrt{3}}{2} \)
\( r_1(\frac{4\pi}{3}) = \sin{\frac{4\pi}{3}} = -\frac{\sqrt{3}}{2} \)
Noktaları pozitif \( r \) değeri ile gösterme prensibiyle \( (-\frac{\sqrt{3}}{2}, \frac{4\pi}{3}) \) noktasını \( (\frac{\sqrt{3}}{2}, \frac{\pi}{3}) \) şeklinde ifade edelim.
Buna göre bulduğumuz yeni iki nokta yukarıda bulduğumuz üç noktaya dahildir, dolayısıyla yeni bir çözüm yoktur.
Durum 3: Bulduğumuz çözüm kümesi \( (0, 0) \) noktasını da içerdiği için farklı açı değerlerinde \( r = 0 \) olma durumunu kontrol etmemize gerek yoktur.
Buna göre eğrilerin üç kesişim noktası aşağıdaki gibidir.
\( (r, \theta) \in \{(0, 0), (\frac{\sqrt{3}}{2}, \frac{\pi}{3}), (\frac{\sqrt{3}}{2}, \frac{2\pi}{3})\} \)
Aşağıdaki şekilde eğrilerin grafikleri ve kesişim noktaları gösterilmiştir.

Şimdi de \( r = 0 \) kesişim noktasının denklemlerin ortak çözümü ile elde edilemediği duruma bir örnek verelim.
Aşağıda verilen iki kutupsal denklemin kesişim noktalarını bulalım.
\( r_1(\theta) = 1 - \sin{\theta} \)
\( r_2(\theta) = 1 + \cos{\theta} \)
Durum 1: İki denklemi birbirine eşitleyerek ortak çözelim.
\( r_1(\theta) = r_2(\theta) \)
\( 1 - \sin{\theta} = 1 + \cos{\theta} \)
\( \dfrac{\sin{\theta}}{\cos{\theta}} = \tan{\theta} = -1 \)
\( \theta \in \{\frac{3\pi}{4}, \frac{7\pi}{4}\} \)
Bulduğumuz iki \( \theta \) değerini birinci denklemde yerine koyarak kutupsal koordinatlarını bulalım.
\( r_1(\frac{3\pi}{4}) = 1 - \sin{\frac{3\pi}{4}} = 1 - \frac{\sqrt{2}}{2} \)
\( r_1(\frac{7\pi}{4}) = 1 - \sin{\frac{7\pi}{4}} = 1 + \frac{\sqrt{2}}{2} \)
Buna göre eğrilerin iki kesişim noktası aşağıdaki gibidir.
\( (r, \theta) \in \{(1 - \frac{\sqrt{2}}{2}, \frac{3\pi}{4}), (1 + \frac{\sqrt{2}}{2}, \frac{7\pi}{4})\} \)
Durum 2: Sinüs ve kosinüs fonksiyonlarının görüntü kümeleri \( [-1, 1] \) olduğu için her iki denklem de \( r \) hiçbir \( \theta \) değeri için negatif olmaz, dolayısıyla \( -r \) durumunu kontrol etmemize gerek yoktur.
Durum 3: Bulduğumuz çözüm kümesi \( (0, \theta) \) noktasını içermediği için iki denklemin farklı \( \theta \) değerlerinde orijinden geçip geçmediğini kontrol edelim.
\( r_1(\theta) = 1 - \sin{\theta} = 0 \)
\( \theta = \frac{\pi}{2} \) değerinde \( r_1 = 0 \) olur.
\( r_2(\theta) = 1 + \cos{\theta} = 0 \)
\( \theta = \pi \) değerinde \( r_2 = 0 \) olur.
Her iki denklem de farklı \( \theta \) değerlerinde olsa da \( r = 0 \) değeri aldığı için denklemler orijinden geçer, dolayısıyla orijin de denklemlerin bir kesişim noktasıdır.
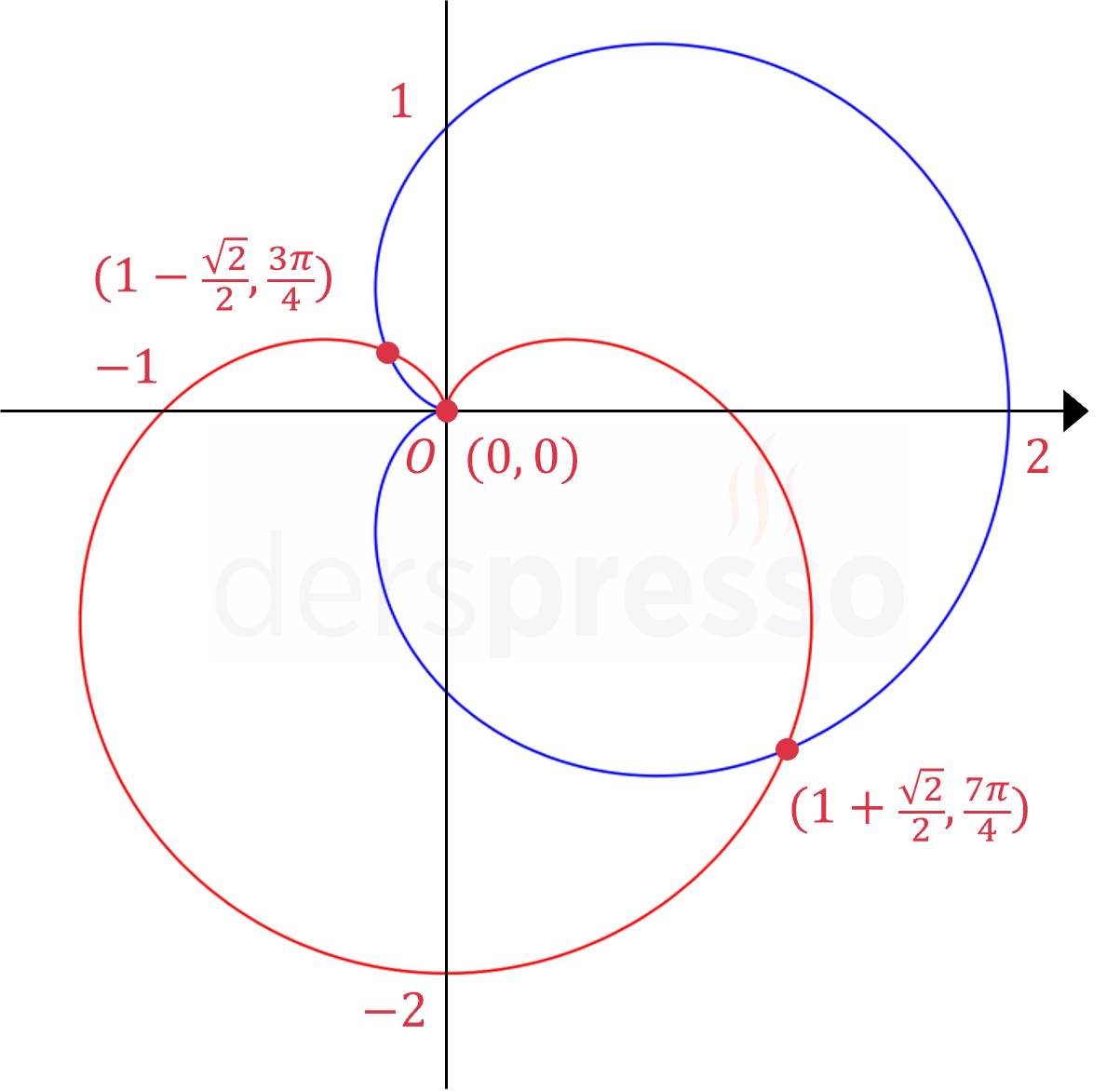
Buna göre eğrilerin üç kesişim noktası aşağıdaki gibidir.
\( (r, \theta) \in \{(0, 0), (1 - \frac{\sqrt{2}}{2}, \frac{3\pi}{4}), (1 + \frac{\sqrt{2}}{2}, \frac{7\pi}{4})\} \)
Aşağıdaki şekilde eğrilerin grafikleri ve kesişim noktaları gösterilmiştir.