Uzayda Doğruların Birbirine Göre Durumu
Uzayda iki doğrunun birbirine göre durumu dört şekilde olabilir.
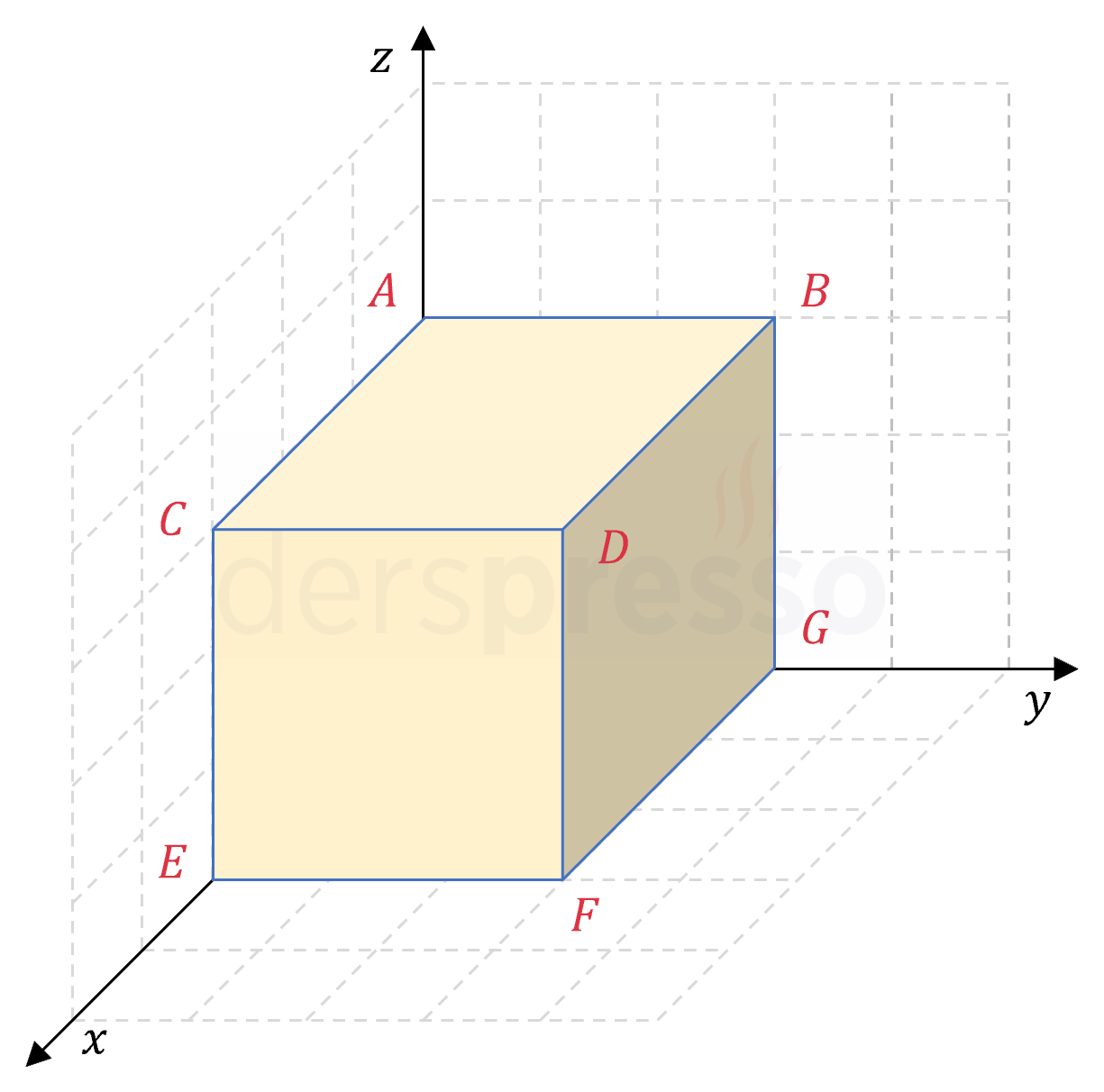
- Doğrular çakışıktır (sonsuz noktada kesişir): Bu durumda doğruların doğrultman vektörleri paraleldir ve denklemlerinin ortak çözüm kümesi sonsuz elemanlıdır.
- Doğrular paraleldir (ve kesişmez): Bu durumda doğruların doğrultman vektörleri paraleldir ve denklemlerinin ortak çözüm kümesi boş kümedir. Yukarıdaki şekildeki küpün \( [AB] \) ve \( [CD] \) kenarları paraleldir.
- Doğrular tek noktada kesişir: Bu durumda doğruların doğrultman vektörleri paralel değildir ve denklemlerinin ortak çözüm kümesi tek elemanlıdır. Yukarıdaki şekildeki küpün \( [CD] \) ve \( [DF] \) kenarları tek noktada kesişir.
- Doğrular aykırıdır (paralel değildir ve kesişmez): Bu durumda doğruların doğrultman vektörleri paralel değildir ve denklemlerinin ortak çözüm kümesi boş kümedir. Yukarıdaki şekildeki küpün \( [AB] \) ve \( [DF] \) kenarları aykırıdır.
Denklemi verilen iki doğrunun birbirine göre durumunu anlamak için aşağıdaki yöntem izlenebilir.
- Doğruların doğrultman vektörlerinin paralel olup olmadığı kontrol edilir.
- Doğrultman vektörleri paralel ise: İki doğru denklemini de sağlayan en az bir nokta varsa doğrular çakışıktır, aksi takdirde paraleldir (kesişmez).
- Doğrultman vektörleri paralel değilse: İki doğru denkleminin ortak bir çözümü varsa doğrular tek bir noktada kesişir, aksi takdirde doğrular aykırıdır (kesişmez).
Uzayda iki doğrunun birbirine göre durumunu, sırasıyla \( P_1 \) ve \( P_2 \) noktalarından geçen ve doğrultman vektörleri \( \vec{d_1} \) ve \( \vec{d_2} \) olan örnek \( L_1 \) ve \( L_2 \) doğruları üzerinden inceleyelim.
Çakışık Doğrular
Uzayda çakışık iki doğrunun doğrultman vektörleri paraleldir ve her iki doğru denklemini de sağlayan en az bir \( K \) noktası vardır. Çakışık iki doğru aynı doğrulardır.
\( \vec{d_1} \parallel \vec{d_2} \)
\( L_1 \cap L_2 = L_1 = L_2 \)
İki doğrunun çakışık olduğu durum için bir örnek yapalım.
Aşağıdaki iki doğrunun birbirine göre durumunu bulalım.
\( \vec{r_1} = (-2, 3, -1) + t(-1, 2, 3) \)
\( \vec{r_2} = (-4, 7, 5) + t(3, -6, -9) \)
\( r_1 \) doğrusunun parametrik denklemini yazalım.
\( x = -2 - t \)
\( y = 3 + 2t \)
\( z = -1 + 3t \)
\( r_2 \) doğrusunun parametrik denklemini yazalım.
\( x = -4 + 3s \)
\( y = 7 - 6s \)
\( z = 5 - 9s \)
Önce iki doğrunun doğrultman vektörlerinin paralel olup olmadığını kontrol edelim.
İki vektör birbirine paralel ise vektörlerden biri diğerinin bir skaler ile çarpımına eşittir.
\( (3, -6, -9) \stackrel{?}{=} \lambda(-1, 2, 3) \)
\( (3, -6, -9) = -3(-1, 2, 3) \)
\( \lambda = -3 \) için eşitlik sağlandığı için iki vektör birbirine paraleldir.
\( \vec{d_1} \parallel \vec{d_2} \)
Buna göre iki doğru ya paraleldir (kesişmez) ya da çakışıktır (sonsuz noktada kesişir).
İki doğrunun paralel mi çakışık mı olduğunu bulmak için birinci doğrunun geçtiği herhangi bir noktanın ikinci doğru üzerinde de olup olmadığını kontrol edelim.
Birinci doğrunun herhangi bir \( t = 2 \) değerinde geçtiği \( K \) noktasının koordinatlarını bulalım.
\( K(-2 - t, 3 + 2t, -1 + 3t) \)
\( K(-2 - 2, 3 + 2(2), -1 + 3(2)) \)
\( K(-4, 7, 5) \)
İkinci doğrunun bu noktadan geçip geçmediğini bulmak için önce hangi \( s \) değerinde \( x = -4 \) değerini aldığını bulalım.
\( x = -4 + 3s = -4 \)
\( s = 0 \)
İkinci doğrunun \( s = 0 \) değerinde geçtiği noktanın koordinatlarını bulalım.
\( y = 7 - 6s = 7 - 6(0) = 7 \)
\( z = 5 - 9s = 5 - 9(0) = 5 \)
Buna göre ikinci doğru da aynı \( K(-4, 7, 5) \) noktasından geçer.
Doğruların hem doğrultman vektörleri paralel olduğu hem de ortak bir noktaları bulunduğu için iki doğru çakışıktır.
Paralel Doğrular
Uzayda paralel iki doğrunun doğrultman vektörleri paraleldir ve denklemlerinin ortak çözüm kümesi boş kümedir. Paralel doğrular aynı düzlem üzerinde bulunurlar.
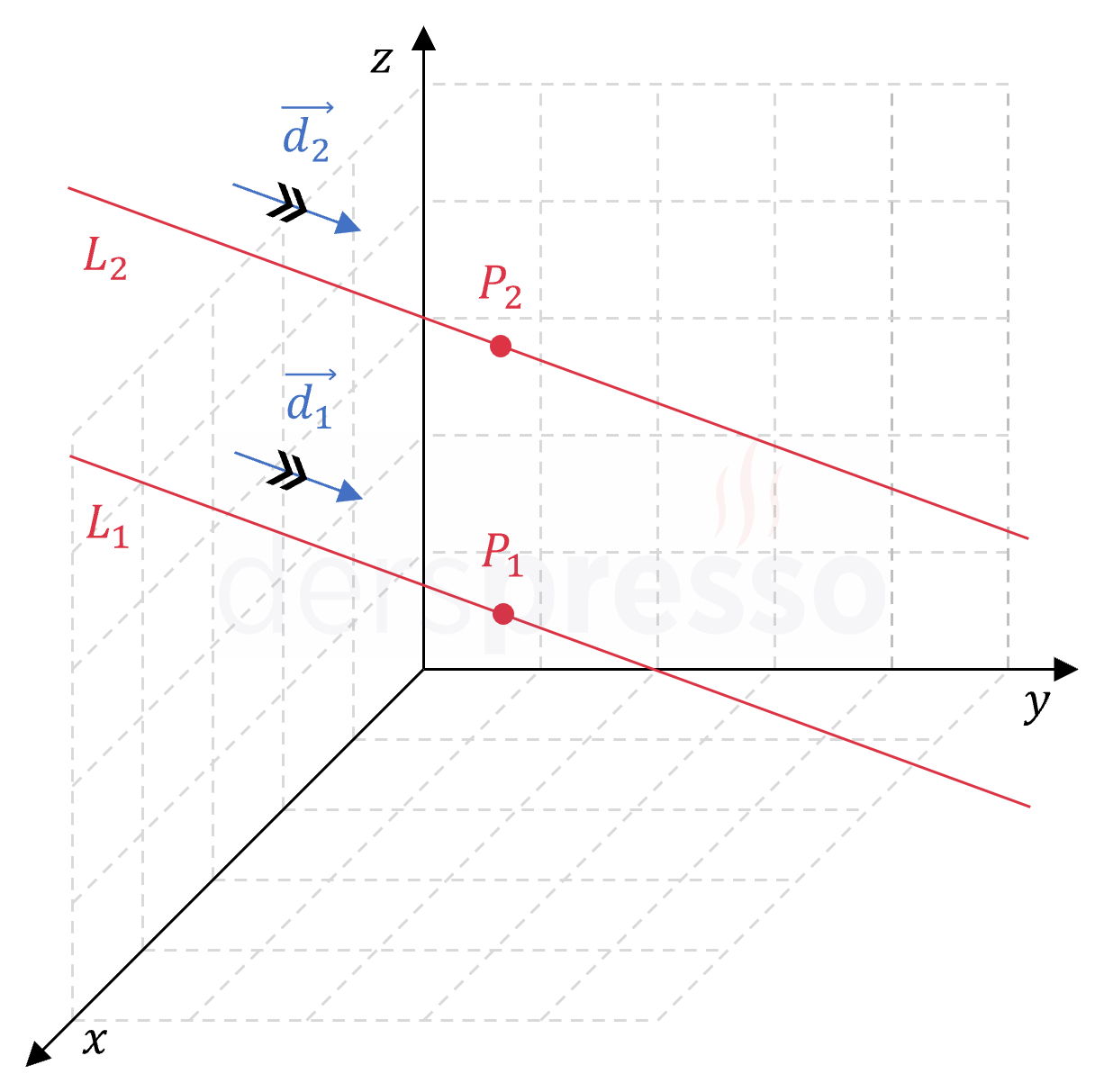
\( \vec{d_1} \parallel \vec{d_2} \)
\( L_1 \cap L_2 = \emptyset \)
İki doğrunun paralel olduğu durum için bir örnek yapalım.
Aşağıdaki iki doğrunun birbirine göre durumunu bulalım.
\( \vec{r_1} = (1, 5, -3) + t(4, 0, -2) \)
\( \vec{r_2} = (-5, 5, 2) + t(-2, 0, 1) \)
\( r_1 \) doğrusunun parametrik denklemini yazalım.
\( x = 1 + 4t \)
\( y = 5 + 0t = 5 \)
\( z = -3 - 2t \)
\( r_2 \) doğrusunun parametrik denklemini yazalım.
\( x = -5 - 2s \)
\( y = 5 + 0t = 5 \)
\( z = 2 + s \)
Önce iki doğrunun doğrultman vektörlerinin paralel olup olmadığını kontrol edelim.
İki vektör birbirine paralel ise vektörlerden biri diğerinin bir skaler ile çarpımına eşittir.
\( (-2, 0, 1) \stackrel{?}{=} \lambda(4, 0, -2) \)
\( (-2, 0, 1) = -\frac{1}{2}(4, 0, -2) \)
\( \lambda = -\frac{1}{2} \) için eşitlik sağlandığı için iki vektör birbirine paraleldir.
\( \vec{d_1} \parallel \vec{d_2} \)
Buna göre iki doğru ya paraleldir (kesişmez) ya da çakışıktır (sonsuz noktada kesişir).
İki doğrunun paralel mi çakışık mı olduğunu bulmak için birinci doğrunun geçtiği herhangi bir noktanın ikinci doğru üzerinde de olup olmadığını kontrol edelim.
Birinci doğrunun herhangi bir \( t = 0 \) değerinde geçtiği \( K \) noktasının koordinatlarını bulalım.
\( K(1 + 4t, 5, -3 - 2t) \)
\( K(1 + 4(0), 5, -3 - 2(0)) \)
\( K(1, 5, -3) \)
İkinci doğrunun bu noktadan geçip geçmediğini bulmak için önce hangi \( s \) değerinde \( x = 1 \) değerini aldığını bulalım.
\( x = -5 - 2s = 1 \)
\( s = -3 \)
İkinci doğrunun \( s = -3 \) değerinde geçtiği noktanın koordinatlarını bulalım.
\( y = 5 \)
\( z = 2 + s = 2 + (-3) = -1 \)
Buna göre ikinci doğru \( x = 1 \) değerini aldığında \( K(1, 5, -3) \) noktasından farklı \( M(1, 5, -1) \) noktasından geçer.
Doğruların doğrultman vektörleri paralel olsa da ortak bir noktaları bulunmadığı için iki doğru çakışık değil paraleldir.
Kesişen Doğrular
Bir düzlemdeki iki doğru paralel değilse mutlaka bir noktada kesişir, ancak uzayda paralel olmayan iki doğru kesişebilir ya da kesişmeyebilir.
Uzayda tek bir noktada kesişen iki doğrunun doğrultman vektörleri paralel değildir ve denklemlerinin ortak çözüm kümesi tek elemanlıdır. Kesişen doğrular aynı düzlem üzerinde bulunurlar.
\( \vec{d_1} \not\parallel \vec{d_2} \)
\( L_1 \cap L_2 = K \)
Kesişen iki doğrunun kesişim noktası bulunurken eğer doğruların parametrik denklemleri kullanılıyorsa iki denklemde farklı parametre kullanılmasına dikkat edilmelidir (örneğin \( t \) ve \( s \)), aksi takdirde bulunan çözüm doğruların sadece aynı parametre değerindeki kesişimini içerecektir.
İki doğrunun tek bir noktada kesiştiği durum için bir örnek yapalım.
Aşağıda vektör denklemleri verilen iki doğrunun birbirine göre durumunu bulalım.
\( \vec{r_1} = (3, 0, -4) + t(-1, 2, 3) \)
\( \vec{r_2} = (4, 1, 3) + s(3, -3, 1) \)
\( r_1 \) doğrusunun parametrik denklemini yazalım.
\( x = 3 - t \)
\( y = 0 + 2t = 2t \)
\( z = -4 + 3t \)
\( r_2 \) doğrusunun parametrik denklemini yazalım.
\( x = 4 + 3s \)
\( y = 1 - 3s \)
\( z = 3 + s \)
Önce iki doğrunun doğrultman vektörlerinin paralel olup olmadığını kontrol edelim.
İki vektör birbirine paralel ise vektörlerden biri diğerinin bir skaler ile çarpımına eşittir.
\( (3, -3, 1) \stackrel{?}{=} \lambda(-1, 2, 3) \)
Bu eşitliği sağlayan bir \( \lambda \) değeri bulunmadığı için iki vektör birbirine paralel değildir.
\( \vec{d_1} \not\parallel \vec{d_2} \)
Buna göre iki doğru ya tek bir noktada kesişir ya da aykırıdır (kesişmez).
İki doğrunun kesişip kesişmediğini bulmak için iki doğru denkleminde de aynı \( (x, y, z) \) koordinatlarını üreten bir \( (t, s) \) ikilisinin bulunup bulunmadığını bulalım.
İki doğrunun \( x \) ve \( y \) denklemlerini ortak çözelim.
\( 3 - t = 4 + 3s \)
\( 2t = 1 - 3s \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki \( t \) ve \( s \) değerlerini buluruz.
\( t = 2, \quad s = -1 \)
Aynı \( x \) ve \( y \) değerlerini veren \( (t, s) = (2, -1) \) değerlerinin aynı \( z \) değerini verip vermediğini kontrol edelim.
\( -4 + 3t \stackrel{?}{=} 3 + s \)
\( -4 + 3(2) \stackrel{?}{=} 3 + (-1) \)
\( 2 = 2 \)
Buna göre iki doğru \( (t, s) = (2, -1) \) değerlerinde aynı \( (x, y, z) \) değerlerini alır, dolayısıyla tek bir noktada kesişir.
İki doğrunun kesişim noktasını bulmak için \( t = 2 \) için birinci doğrunun koordinatlarını bulalım.
\( x = 3 - t = 3 - 2 = 1 \)
\( y = 2t = 2(2) = 4 \)
\( z = -4 + 3t = -4 + 3(2) = 2 \)
Buna göre doğrular \( K(1, 4, 2) \) noktasında kesişir.
Yaptığımız işlemlerin sağlaması olarak \( s = -1 \) için ikinci doğrunun koordinatlarını bulalım.
\( x = 4 + 3s = 4 + 3(-1) = 1 \)
\( y = 1 - 3s = 1 - 3(-1) = 4 \)
\( z = 3 + s = 3 + (-1) = 2 \)
İkinci doğrunun da \( K(1, 4, 2) \) noktasından geçtiğini, dolayısıyla doğruların bu noktada kesiştiğini doğrulamış olduk.
İki doğru dik kesişiyorsa doğrultman vektörlerinin nokta çarpımı sıfıra eşit olur.
\( \vec{d_1} \perp \vec{d_2} \)
\( \vec{d_1} \cdot \vec{d_2} = 0 \)
Aykırı Doğrular
Uzayda aykırı iki doğrunun doğrultman vektörleri paralel değildir ve denklemlerinin ortak çözüm kümesi boş kümedir. Aykırı doğrular farklı düzlemler üzerinde bulunurlar.
\( \vec{d_1} \not\parallel \vec{d_2} \)
\( L_1 \cap L_2 = \emptyset \)
İki doğrunun aykırı olduğu durum için bir örnek yapalım.
Aşağıda vektör denklemleri verilen iki doğrunun birbirine göre durumunu bulalım.
\( \vec{r_1} = (-2, 4, 3) + t(2, -3, 0) \)
\( \vec{r_2} = (2, -8, 3) + s(-4, 3, 1) \)
\( r_1 \) doğrusunun parametrik denklemini yazalım.
\( x = -2 + 2t \)
\( y = 4 - 3t \)
\( z = 3 + 0t = 3 \)
\( r_2 \) doğrusunun parametrik denklemini yazalım.
\( x = 2 - 4s \)
\( y = -8 + 3s \)
\( z = 3 + s \)
Önce iki doğrunun doğrultman vektörlerinin paralel olup olmadığını kontrol edelim.
İki vektör birbirine paralel ise vektörlerden biri diğerinin bir skaler ile çarpımına eşittir.
\( (-4, 3, 1) \stackrel{?}{=} \lambda(2, -3, 0) \)
Bu eşitliği sağlayan bir \( \lambda \) değeri bulunmadığı için iki vektör birbirine paralel değildir.
\( \vec{d_1} \not\parallel \vec{d_2} \)
Buna göre iki doğru ya tek bir noktada kesişir ya da aykırıdır (kesişmez).
İki doğrunun kesişip kesişmediğini bulmak için iki doğru denkleminde de aynı \( (x, y, z) \) koordinatlarını üreten bir \( (t, s) \) ikilisinin bulunup bulunmadığını bulalım.
İki doğrunun \( x \) ve \( y \) denklemlerini ortak çözelim.
\( -2 + 2t = 2 - 4s \)
\( 4 - 3t = -8 + 3s \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki \( t \) ve \( s \) değerlerini buluruz.
\( t = 6, \quad s = -2 \)
Aynı \( x \) ve \( y \) değerlerini veren \( (t, s) = (6, -2) \) değerlerinin aynı \( z \) değerini verip vermediğini kontrol edelim.
\( 3 \stackrel{?}{=} 3 + s \)
\( 3 \stackrel{?}{=} 3 + (-2) \)
\( 3 \ne 1 \)
Buna göre iki doğru \( (t, s) = (6, -2) \) değerlerinde aynı \( (x, y) \) değerlerini alsa da aynı \( z \) değerini almadığı için bu iki doğru kesişmez.