Doğru ve Düzlemin Birbirine Göre Durumu
Doğru ve Düzlemin Birbirine Göre Durumu
Bir doğrunun bir düzleme göre durumu üç şekilde olabilir.
- Doğru düzlemin üzerindedir.
- Doğru düzleme paraleldir (düzlemin dışındadır).
- Doğru düzlemi tek bir noktada keser.
Bu üç durumu aşağıdaki örnek doğru ve düzlem üzerinden inceleyelim.
\( P_1 \) noktasından geçen ve \( \vec{d} \) vektörüne paralel olan \( L \) doğrusu:
\( P_1(x_1, y_1, z_1) \)
\( \vec{d} = (d_1, d_2, d_3) \)
\( P_2 \) noktasından geçen ve \( \vec{n} \) vektörüne dik olan \( N \) düzlemi:
\( P_2(x_2, y_2, z_2) \)
\( \vec{n} = (a, b, c) \)
\( ax + by + cz + d = 0 \)
Düzlem Üzerindeki Doğru
Bir doğru bir düzlemin üzerinde ise doğrunun doğrultman vektörü ile düzlemin normal vektörü birbirine dik olur, ayrıca doğru üzerindeki her nokta düzlem denklemini sağlar.
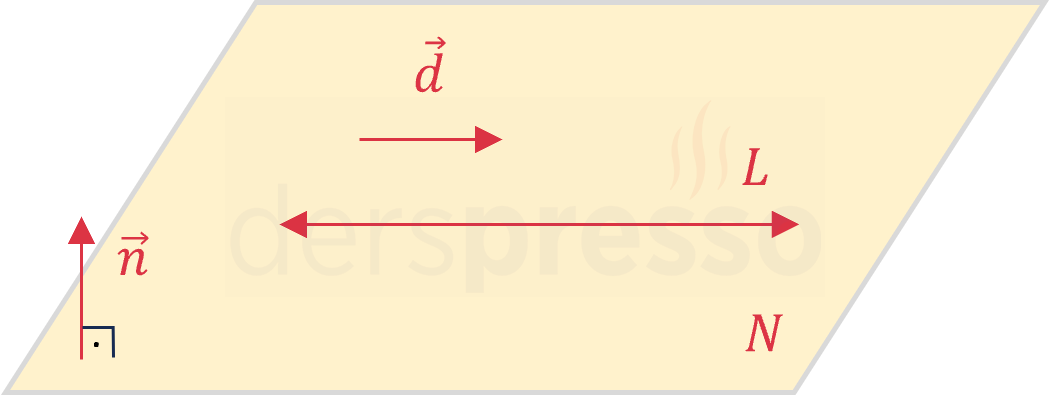
\( \vec{d} \perp \vec{n} \)
\( \vec{d} \cdot \vec{n} = 0 \)
\( ax_1 + by_1 + cz_1 + d = 0 \)
Bir doğru bir düzlemin üzerinde ise kesişim kümeleri doğrudur.
\( L \cap N = L \)
Düzleme Paralel Doğru
Bir doğru bir düzlemin üzerinde ise doğrunun doğrultman vektörü ile düzlemin normal vektörü birbirine dik olur, ayrıca doğru üzerindeki hiçbir nokta düzlem denklemini sağlamaz.
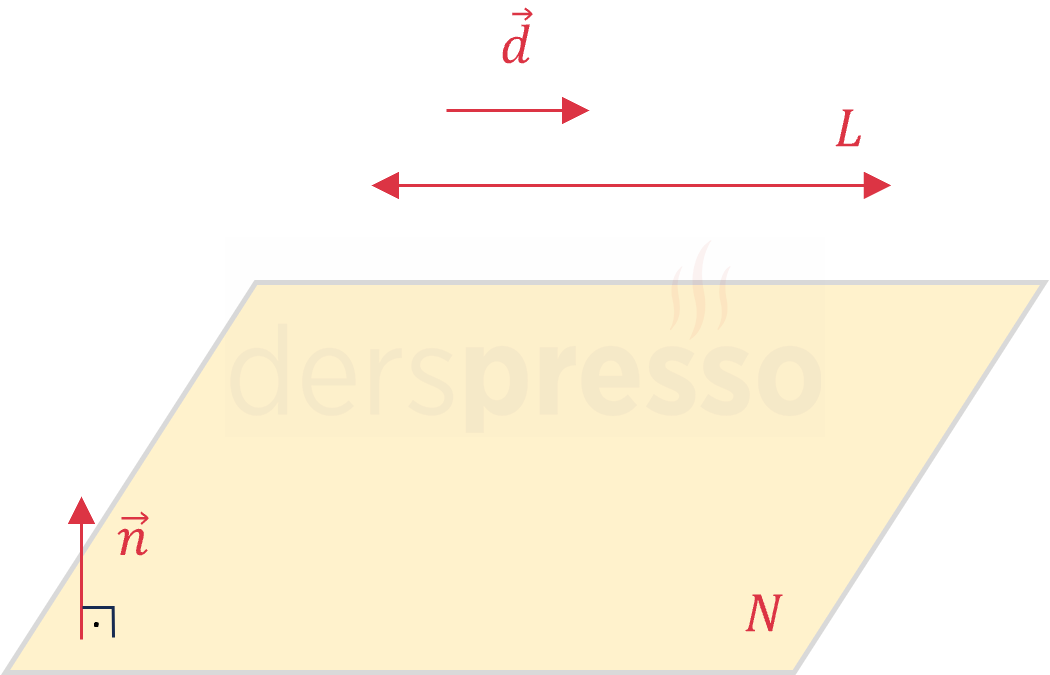
\( \vec{d} \perp \vec{n} = 0 \)
\( \vec{d} \cdot \vec{n} = 0 \)
\( ax_1 + by_1 + cz_1 + d \ne 0 \)
Bir doğru bir düzlemin dışında ise kesişim kümeleri boş kümedir.
\( L \cap N = \emptyset \)
Düzlemi Kesen Doğru
Bir doğru bir düzlemi kesiyorsa doğrunun doğrultman vektörü ile düzlemin normal vektörü birbirine dik değildir.
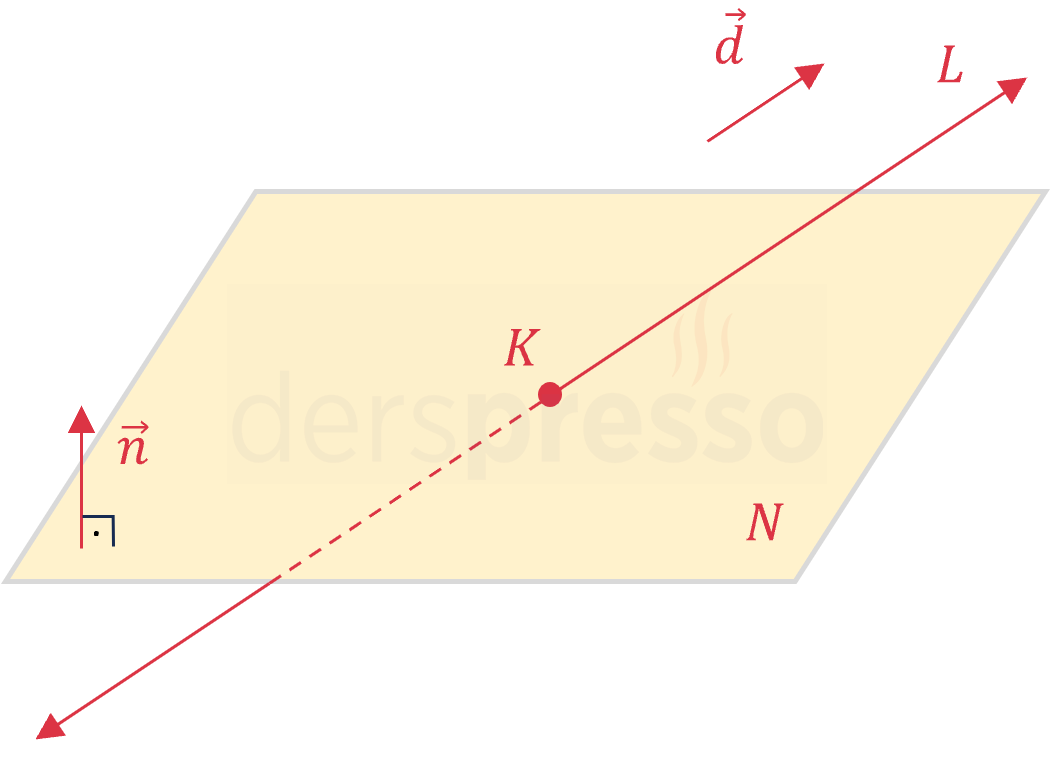
\( \vec{d} \cdot \vec{n} \ne 0 \)
Bir doğru bir düzlemi kesiyorsa kesişim kümeleri bir noktadır.
\( L \cap N = K \)
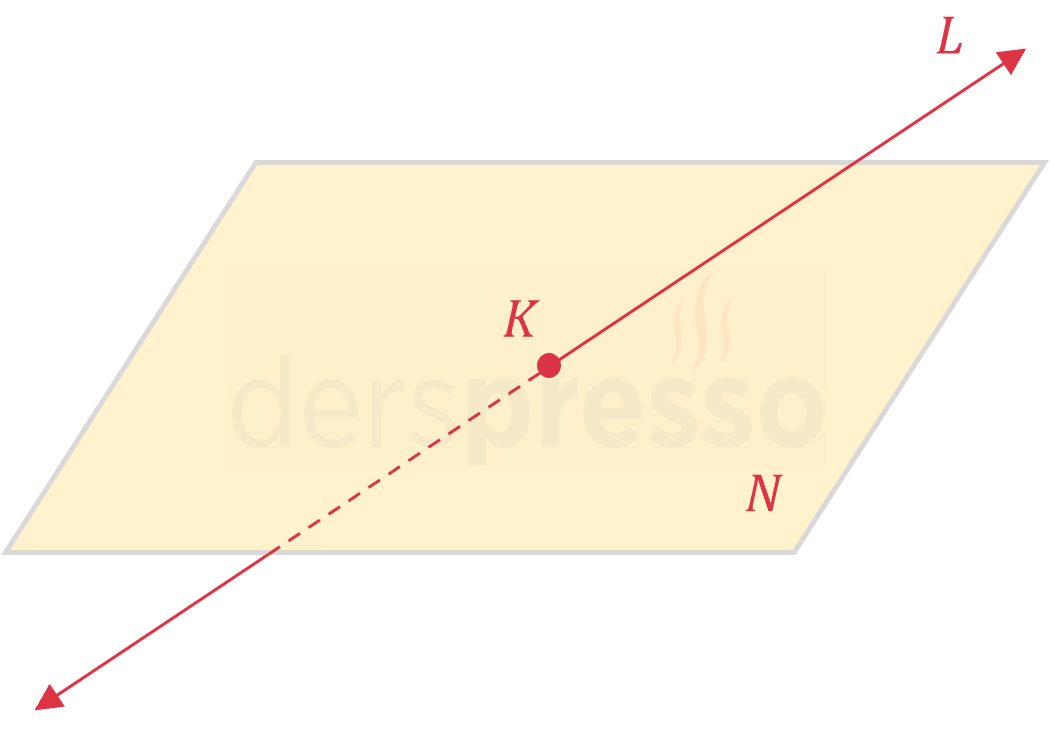
Düzlemi Dik Kesen Doğru
Bir doğru bir düzlemi dik kesiyorsa doğrunun doğrultman vektörü ile düzlemin normal vektörü birbirine paraleldir.
\( \vec{d} \parallel \vec{n} \)
\( \dfrac{d_1}{a} = \dfrac{d_2}{b} = \dfrac{d_3}{c} \)
Doğrunun Düzlemi Kestiği Nokta
Bir doğrunun bir düzlemi kestiği nokta aşağıdaki yöntemle bulunabilir.
- Doğrunun parametrik denklemi bulunur.
- Doğrunun \( x \), \( y \) ve \( z \) değişkenleri için parametrik denklemleri düzlem denkleminde yerine yazılır.
- Düzlem denklemini sağlayan \( t \) değeri bulunur.
- Bu \( t \) değeri doğrunun parametrik denklemlerinde yerine yazıldığında doğrunun düzlemi kestiği noktanın koordinatları elde edilir.
Aşağıda denklemleri verilen \( L \) doğrusunun \( N \) düzlemini kestiği noktayı bulalım.
\( L: \dfrac{x - 1}{2} = \dfrac{y + 3}{1} = \dfrac{z - 1}{-4} \)
\( N: 3x - 2y + 4z = -11 \)
\( L \) doğrusunun parametrik denklemi:
\( x = 1 + 2t \)
\( y = -3 + t \)
\( z = 1 - 4t \)
Bu değerleri düzlem denkleminde yerine koyalım.
\( 3(1 + 2t) - 2(-3 + t) + 4(1 - 4t) = -11 \)
\( 3 + 6t + 6 - 2t + 4 - 16t = -11 \)
\( 13 - 12t = -11 \)
\( t = 2 \)
Doğrunun \( t = 2 \) değerindeki koordinatlarını bulalım.
\( x = 1 + 2(2) = 5 \)
\( y = -3 + 2 = -1 \)
\( z = 1 - 4(2) = -7 \)
Buna göre \( L \) doğrusu \( N \) düzlemini \( K(5, -1, -7) \) noktasında keser.