Düzleme Uzaklık
Bu bölümde bir noktanın, doğrunun ya da bir diğer düzlemin verilen bir düzleme olan uzaklığını hesaplama yöntemlerini inceleyeceğiz.
Noktanın Düzleme Uzaklığı
Bir noktanın bir düzleme olan en kısa uzaklığı aşağıdaki formülle bulunur.
Bir Noktası ve Normal Vektörü Bilinen Düzleme Uzaklık
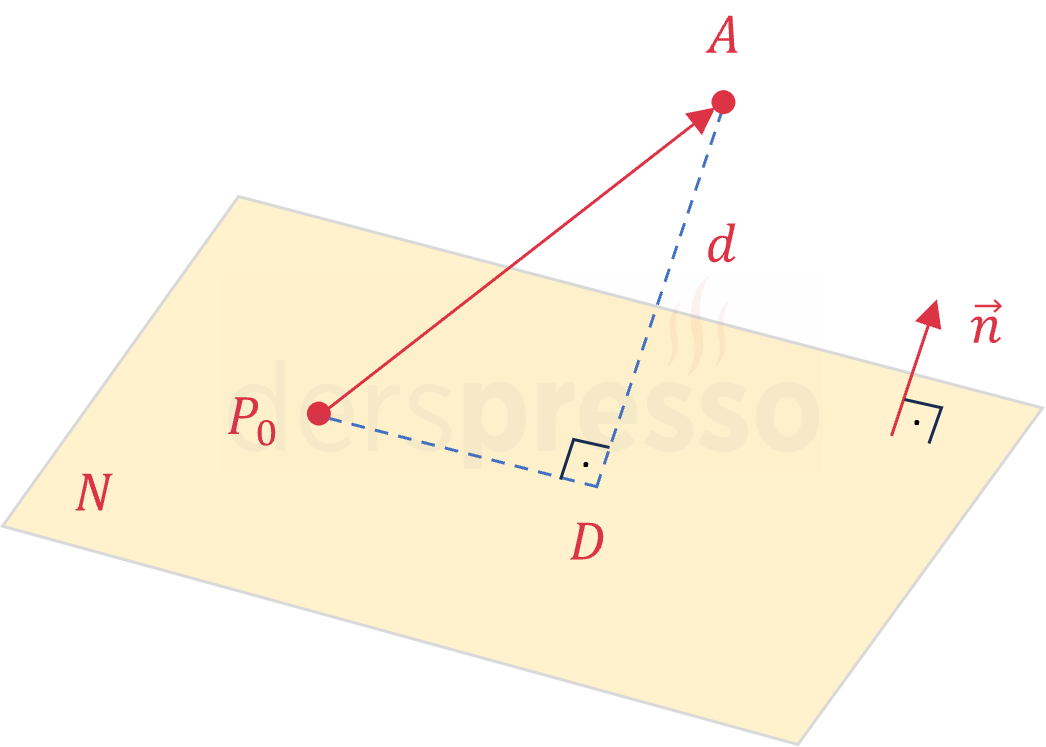
Bir noktanın, bir noktası ve normal vektörü bilinen düzleme olan en kısa uzaklığı aşağıdaki formülle bulunur.
\( A \) noktası ile \( P_0 \) noktasından geçen ve \( \vec{n} \) vektörüne dik olan düzlem arasındaki uzaklık:
\( d = \dfrac{\abs{\vec{P_0A} \cdot \vec{n}}}{\norm{\vec{n}}} \)
\( A(-2, 1, 5) \) noktası ile \( P_0(1, 3, -2) \) noktasından geçen ve \( \vec{n} = (2, 1, -2) \) vektörüne dik olan düzlem arasındaki uzaklık:
\( \vec{P_0A} = (-2 - 1, 1 - 3, 5 - (-2)) \)
\( = (-3, -2, 7) \)
\( \norm{\vec{n}} = \sqrt{2^2 + 1^2 + (-2)^2} = 3 \)
\( d = \dfrac{\abs{(-3, -2, 7) \cdot (2, 1, -2)}}{3} \)
\( = \dfrac{\abs{-3(2) + (-2)(1) + 7(-2)}}{3} \)
\( = \dfrac{22}{3} \)
İSPATI GÖSTER
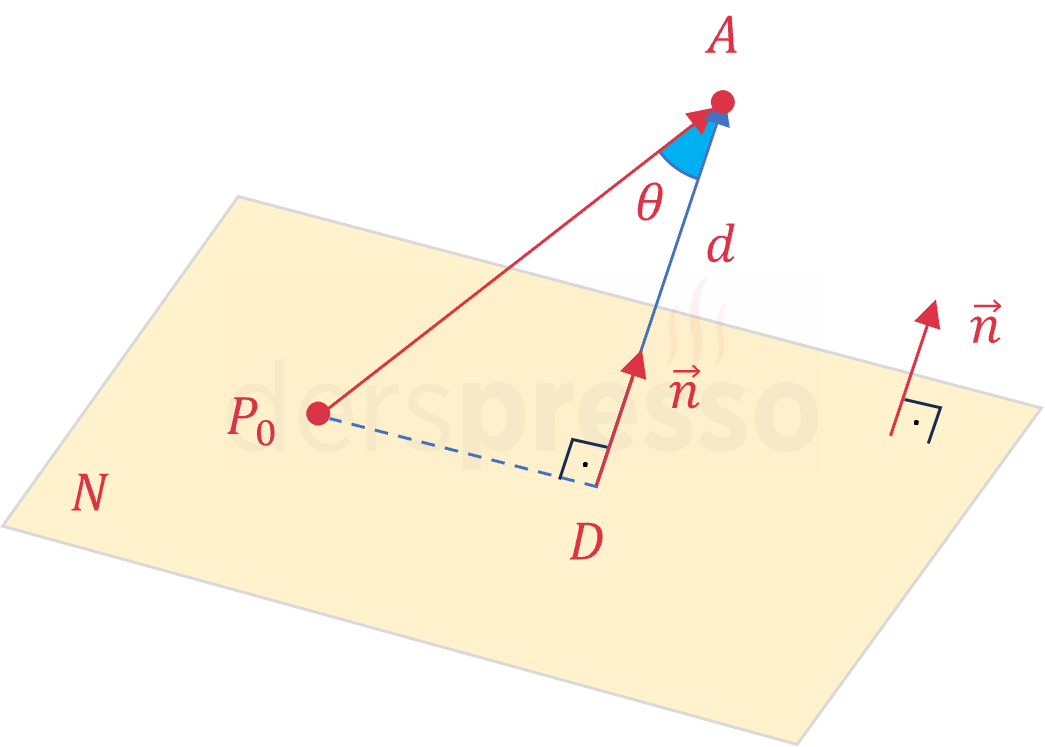
\( N \) düzlemi üzerinde \( A \) noktasına en yakın olan noktaya \( D \) diyelim.
\( D \) noktasından \( A \) noktasına çizeceğimiz \( \vec{DA} \) vektörü \( N \) düzlemine dik ve \( \vec{n} \) vektörüne paraleldir.
\( A \) noktasının \( N \) düzlemine en yakın uzaklığı \( \vec{DA} \) vektörünün normuna eşittir.
\( d = \norm{\vec{DA}} \)
\( N \) düzlemi üzerindeki \( P_0 \) noktasından \( A \) noktasına bir vektör tanımlayalım.
\( \vec{P_0A} = A - P_0 \)
\( \vec{P_0A} \) ve \( \vec{DA} \) vektörleri arasındaki dar açıya \( \theta \) diyelim.
\( d \) uzunluğunu \( \vec{P_0A} \) vektörünün normu ve \( \theta \) açısı cinsinden aşağıdaki şekilde yazabiliriz.
\( d = \norm{\vec{P_0A}}\cos{\theta} \)
Bu eşitliğin sağ tarafını \( \vec{n} \) vektörünün normu ile çarpıp bölelim.
\( = \dfrac{\norm{\vec{P_0A}}\norm{\vec{n}}\cos{\theta}}{\norm{\vec{n}}} \)
Eşitliğin sağ tarafının payı \( \vec{P_0A} \) ve \( \vec{n} \) vektörlerinin nokta çarpımına eşittir.
\( = \dfrac{\vec{P_0A} \cdot \vec{n}}{\norm{\vec{n}}} \)
Formüldeki vektörlerin yönüne göre nokta çarpımının sonucu negatif olabileceği için ifadenin mutlak değerini alalım.
\( = \dfrac{\abs{\vec{P_0A} \cdot \vec{n}}}{\norm{\vec{n}}} \)
Genel Denklemi Bilinen Düzleme Uzaklık
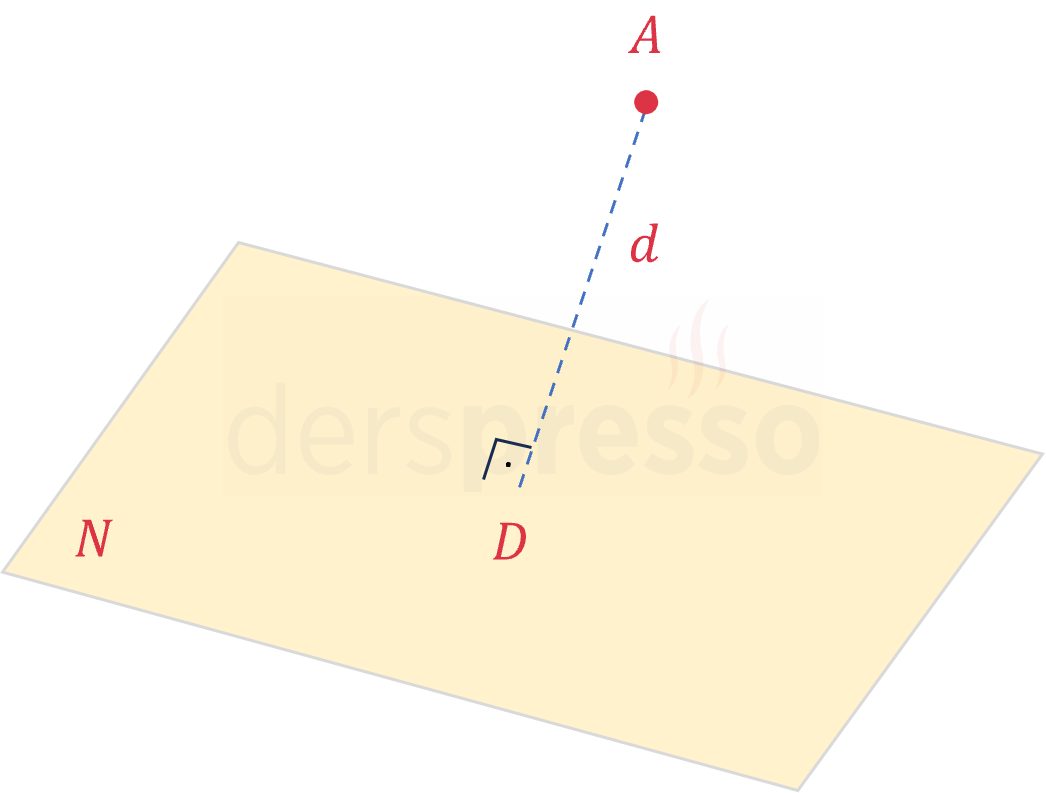
Bir noktanın, genel denklemi bilinen düzleme olan en kısa uzaklığı aşağıdaki formülle bulunur.
\( A(x_1, y_1, z_1) \) noktası ile genel denklemi \( ax + by + cz + d = 0 \) olan düzlem arasındaki uzaklık:
\( d = \dfrac{\abs{ax_1 + by_1 + cz_1 + d}}{\sqrt{a^2 + b^2 + c^2}} \)
\( A(-2, 1, 5) \) noktası ile genel denklemi \( 2x + y - 2z - 9 = 0 \) olan düzlem arasındaki uzaklık:
\( d = \dfrac{\abs{2(-2) + 1(1) + (-2)(5) - 9}}{\sqrt{2^2 + 1^2 + (-2)^2}} \)
\( = \dfrac{22}{3} \)
İSPATI GÖSTER
Yukarıda bulduğumuz \( A(x_1, y_1, z_1) \) noktası ile \( P_0(x_0, y_0, z_0) \) noktasından geçen ve \( \vec{n} = (a, b, c) \) vektörüne dik olan düzlem arasındaki uzaklık formülünü yazalım.
\( d = \dfrac{\abs{\vec{P_0A} \cdot \vec{n}}}{\norm{\vec{n}}} \)
Formüldeki vektörlerin koordinatlarını yazalım.
\( = \dfrac{\abs{(x_1 - x_0, y_1 - y_0, z_1 - z_0) \cdot (a, b, c)}}{\sqrt{a^2 + b^2 + c^2}} \)
Paydaki iki vektör arasındaki nokta çarpım işlemini yapalım.
\( = \dfrac{\abs{a(x_1 - x_0) + b(y_1 - y_0) + c(z_1 - z_0)}}{\sqrt{a^2 + b^2 + c^2}} \)
Parantezleri genişletelim.
\( = \dfrac{\abs{ax_1 - ax_0 + by_1 - by_0 + cz_1 - cz_0}}{\sqrt{a^2 + b^2 + c^2}} \)
Terimleri düzenleyelim.
\( = \dfrac{\abs{ax_1 + by_1 + cz_1 - (ax_0 + by_0 + cz_0}}{\sqrt{a^2 + b^2 + c^2}} \)
Payda parantez içindeki \( (x_0, y_0, z_0) \) koordinatları \( N \) düzlemi üzerindeki \( P_0 \) noktasının koordinatlarıdır, dolayısıyla bu koordinatları düzlemin genel denkleminde yerine koyduğumuzda düzlem denklemini sağlar.
\( ax + by + cz + d = 0 \)
\( ax_0 + by_0 + cz_0 + d = 0 \)
\( ax_0 + by_0 + cz_0 = -d \)
Bu ifadenin değerini uzaklık formülünde yerine koyduğumuzda \( A \) noktasının \( N \) düzlemine olan uzaklığının ikinci formülünü elde ederiz.
\( = \dfrac{\abs{ax_1 + by_1 + cz_1 + d}}{\sqrt{a^2 + b^2 + c^2}} \)
Paralel Doğrunun Düzleme Uzaklığı
Bir doğrunun paralel olduğu bir düzleme uzaklığı doğru üzerindeki her noktada eşittir, dolayısıyla doğrunun düzleme uzaklığını bulmak için doğru üzerinde herhangi bir nokta seçilir ve noktanın düzleme uzaklığı formülü ile istenen uzaklık bulunur.
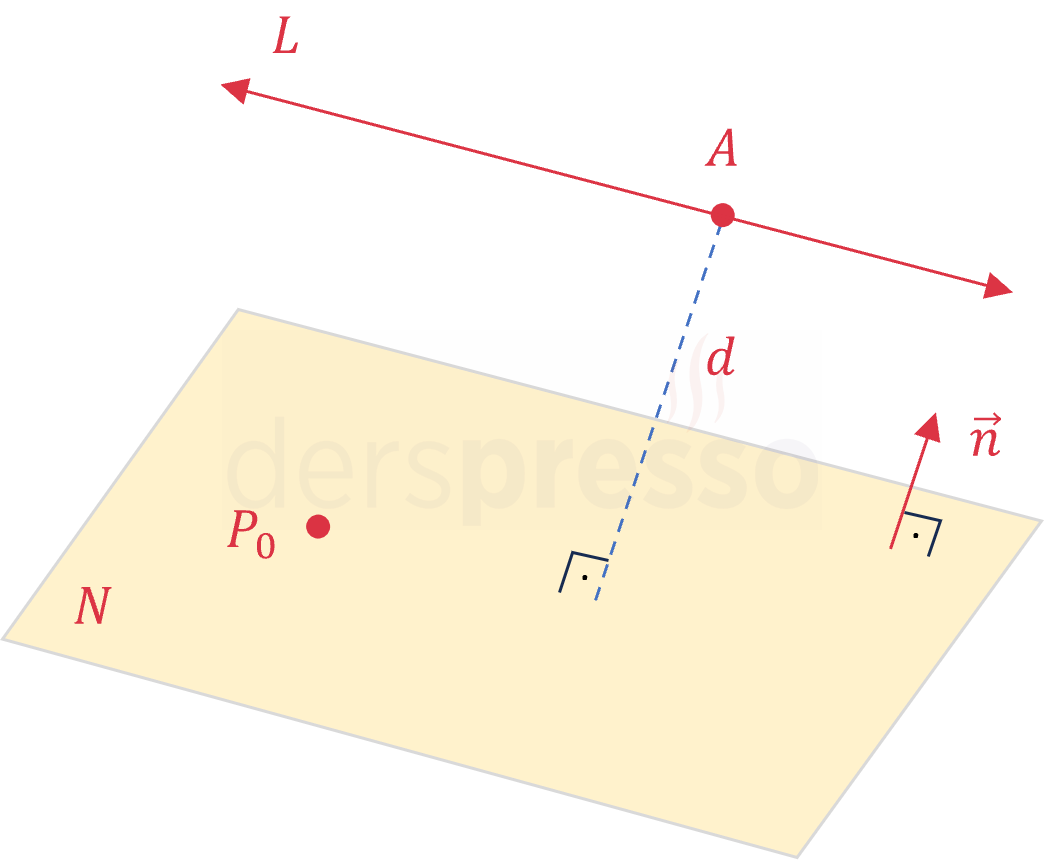
\( A \) noktasından geçen doğru ile \( P_0 \) noktasından geçen ve \( \vec{n} \) vektörüne dik olan paralel düzlem arasındaki uzaklık:
\( d = \dfrac{\abs{\vec{P_0A} \cdot \vec{n}}}{\norm{\vec{n}}} \)
\( A(0, 4, -5) \) noktasından geçen doğru ile \( P_0(2, -1, 3) \) noktasından geçen ve \( \vec{n} = (4, 0, -3) \) vektörüne dik olan paralel düzlem arasındaki uzaklık:
\( \vec{P_0A} = (0 - 2, 4 - (-1), -5 - 3) \)
\( = (-2, 5, -8) \)
\( \norm{\vec{n}} = \sqrt{4^2 + 0^2 + (-3)^2} = 5 \)
\( d = \dfrac{\abs{(4, 0, -3) \cdot (-2, 5, -8)}}{5} \)
\( = \dfrac{\abs{4(-2) + 0(5) + (-3)(-8)}}{5} \)
\( = \dfrac{32}{5} \)
Paralel İki Düzlem Arasındaki Uzaklık
Bir düzlemin paralel olduğu bir diğer düzleme uzaklığı düzlem üzerindeki her noktada eşittir. Paralel iki düzlem arasındaki uzaklık aşağıdaki formülle bulunur.
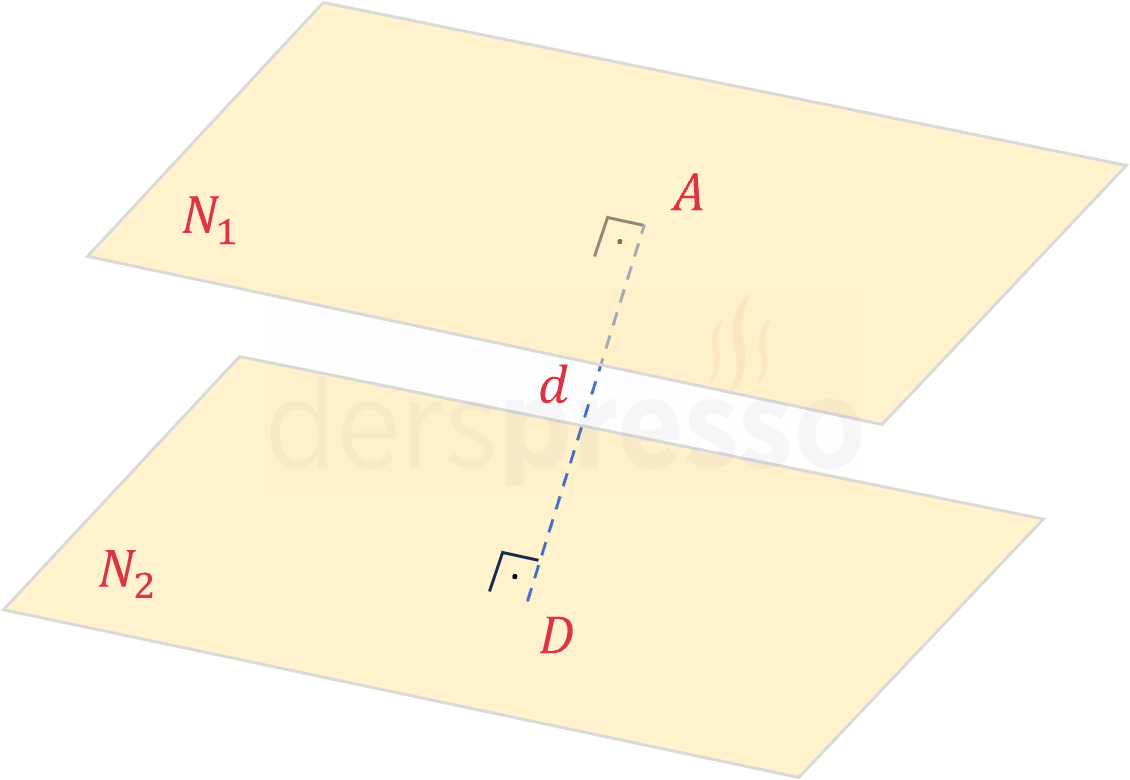
\( N_1: ax + by + cz + d_1 = 0 \)
\( N_2: ax + by + cz + d_2 = 0 \)
Birbirine paralel \( N_1 \) ve \( N_2 \) düzlemleri arasındaki uzaklık:
\( d = \dfrac{\abs{d_1 - d_2}}{\sqrt{a^2 + b^2 + c^2}} \)
\( N_1: 3x - 6y + 2z + 9 = 0 \)
\( N_2: 3x - 6y + 2z - 5 = 0 \)
Yukarıda denklemleri verilen düzlemler arasındaki uzaklık:
Denklemlerin \( a, b, c \) katsayılarının oranı eşit olduğu için düzlemler paraleldir.
\( d = \dfrac{\abs{9 - (-5)}}{\sqrt{3^2 + (-6)^2 + 2^2}} \)
\( = \dfrac{14}{7} = 2 \)
İSPATI GÖSTER
Genel denklemleri sırasıyla \( ax + by + cz + d_1 = 0 \) ve \( ax + by + cz + d_2 = 0 \) olan birbirine paralel \( N_1 \) ve \( N_2 \) düzlemleri arasındaki uzaklık formülünü bulalım.
\( N_1 \) düzlemi üzerinde herhangi bir \( A \) noktası seçelim.
\( A(x_1, y_1, z_1) \)
Bu noktanın \( N_2 \) düzlemine uzaklığını bir noktanın düzleme olan uzaklığı formülü ile bulabiliriz.
\( d = \dfrac{\abs{ax_1 + by_1 + cz_1 + d_2}}{\sqrt{a^2 + b^2 + c^2}} \)
Paydaki \( (x_a, y_a, z_a) \) koordinatları \( N_1 \) düzlemi üzerindeki \( A \) noktasının koordinatlarıdır, dolayısıyla bu koordinatları \( N_1 \) düzleminin genel denkleminde yerine koyduğumuzda düzlem denklemini sağlar.
\( ax + by + cz + d_1 = 0 \)
\( ax_1 + by_1 + cz_1 + d_1 = 0 \)
\( ax_1 + by_1 + cz_1 = -d_1 \)
Bu ifadenin değerini uzaklık formülünde yerine koyduğumuzda birbirine paralel \( N_1 \) ve \( N_2 \) düzlemleri arasındaki uzaklık formülünü elde ederiz.
\( = \dfrac{\abs{-d_1 + d_2}}{\sqrt{a^2 + b^2 + c^2}} \)
\( = \dfrac{\abs{d_1 - d_2}}{\sqrt{a^2 + b^2 + c^2}} \)