Dizilerde Yakınsaklık/Iraksaklık
Fonksiyonların limitine benzer şekilde, bir dizinin \( n \) sonsuza giderkenki limiti dizinin terimlerinin (eğer varsa) yaklaştığı reel sayı \( L \) değerine eşittir. Bir dizinin sonsuzdaki limiti matematiksel analizin önemli konularından biridir.
\( \lim\limits_{n \to \infty} {a_n} = L \)
ya da
\( n \to \infty \) iken \( a_n \to L \)
Bir dizi; sonsuzdaki limiti bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
Aşağıda yakınsak dizilere birkaç örnek verilmiştir. Bu örneklerde görülebileceği gibi yakınsak diziler \( n \) sonsuza giderken tek bir reel sayı \( L \) değerine yaklaşır.
| Grafik | Dizi |
|---|---|
|
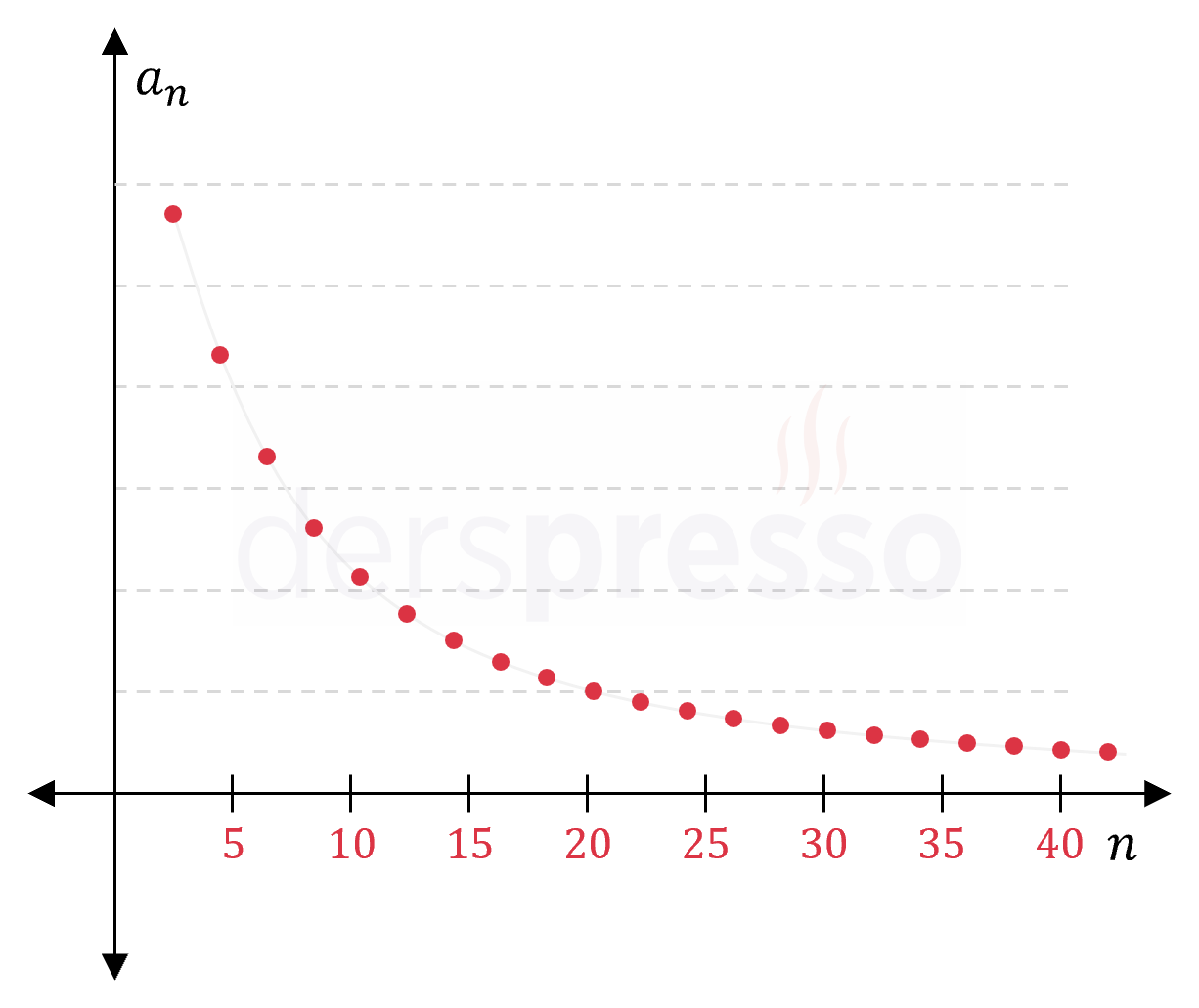
Azalan yakınsak dizi: Bu tip bir dizide terimler monoton azalarak limit değerine yaklaşır. \( (a_n) = \dfrac{1}{n} \) \( = \{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \} \) \( n \to \infty \) iken \( a_n \to 0 \) |
|
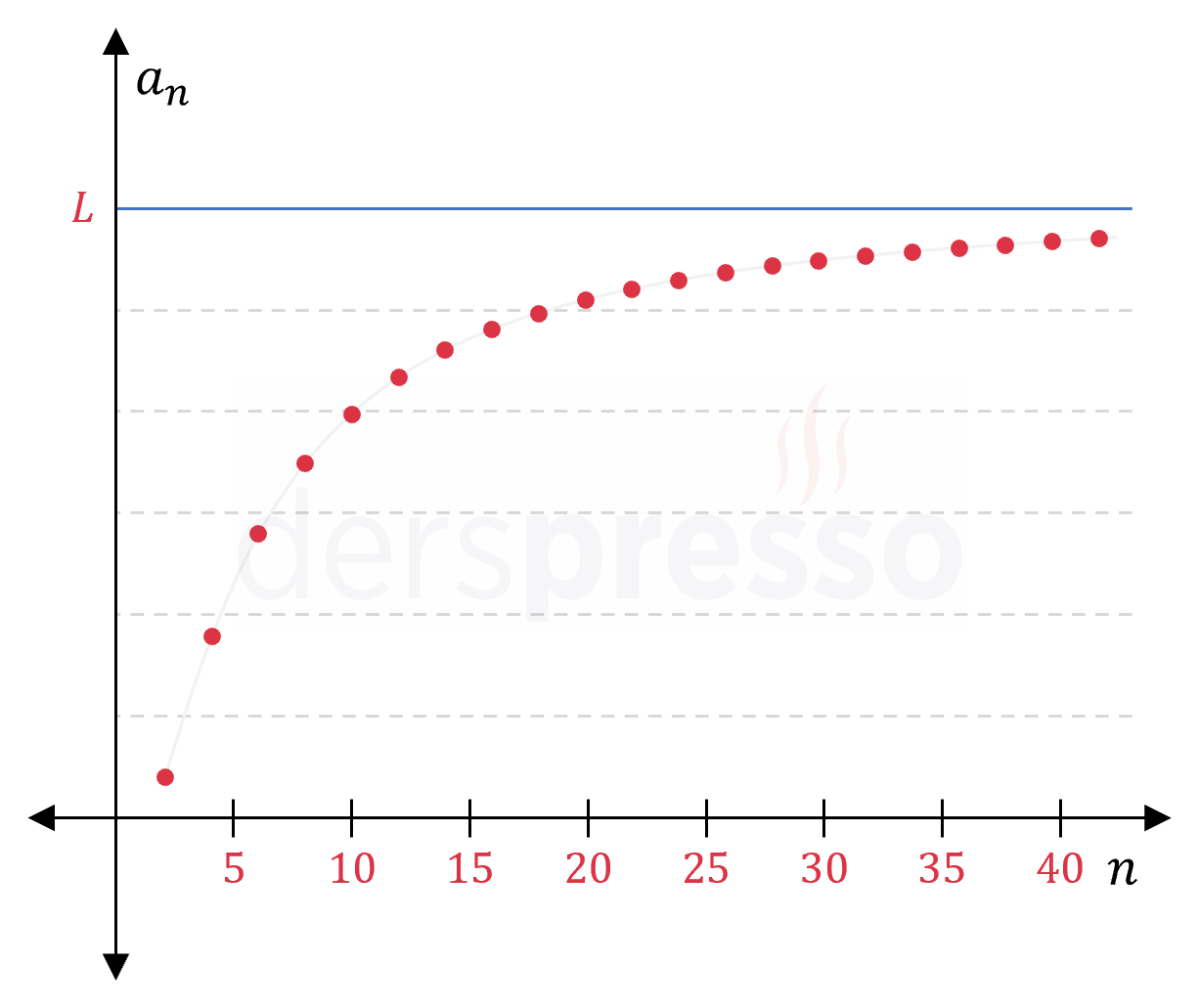
Artan yakınsak dizi: Bu tip bir dizide terimler monoton artarak limit değerine yaklaşır. \( (b_n) = \left( 1 + \dfrac{2}{n} \right)^n \) \( = (3, 4, \frac{125}{27}, \frac{81}{16}, \ldots) \) \( n \to \infty \) iken \( b_n \to e^2 \) |
|
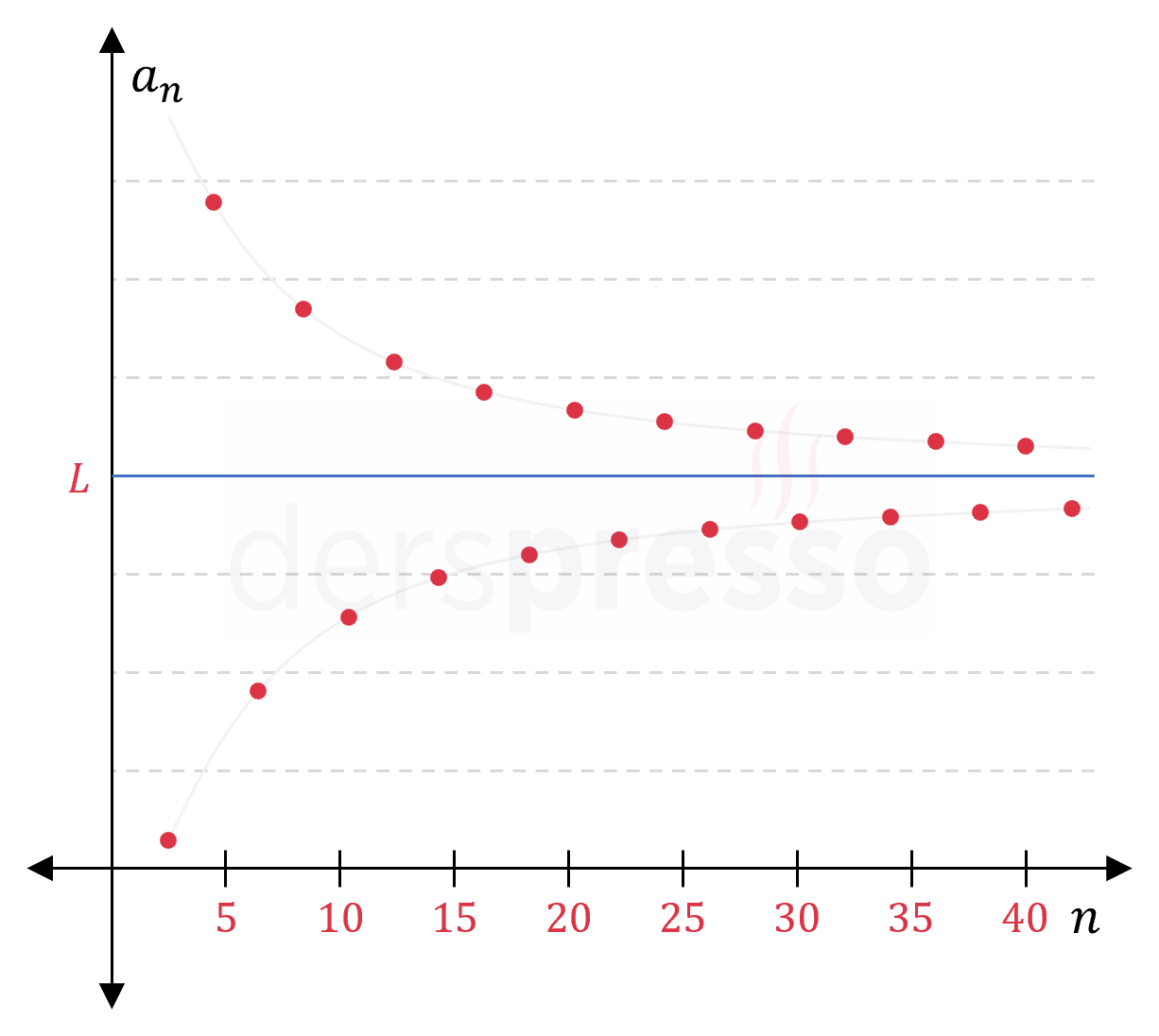
Salınımlı yakınsak dizi: Bu tip bir dizide terimler limit değeri etrafında salınım hareketi yaparak limit değerine yaklaşır. \( (c_n) = 4 + \dfrac{4(-1)^n}{n} \) \( = \{0, 6, \frac{8}{3}, 5, \frac{16}{5}, \ldots \} \) \( n \to \infty \) iken \( c_n \to 4 \) |
|
Sabit dizi: Sabit bir dizide limit değeri dizinin sabit değerine eşittir. \( (d_n) = 5 \) \( = (5, 5, 5, 5, 5, \ldots) \) \( n \to \infty \) iken \( d_n \to 5 \) |
Aşağıda ıraksak dizilere birkaç örnek verilmiştir. Bu örneklerde görülebileceği gibi bir dizi iki sebeple ıraksak olabilir.
- Dizinin terimleri pozitif ya da negatif sonsuza gider. Bu durumda dizinin sonsuzdaki limiti de sonsuzdur.
- Son örnekte olduğu gibi, \( n \) sonsuza giderken dizi sonlu değerler alsa da tek bir değere yakınsamaz. Bu durumda dizinin sonsuzdaki limiti tanımsızdır.
| Grafik | Dizi |
|---|---|
|
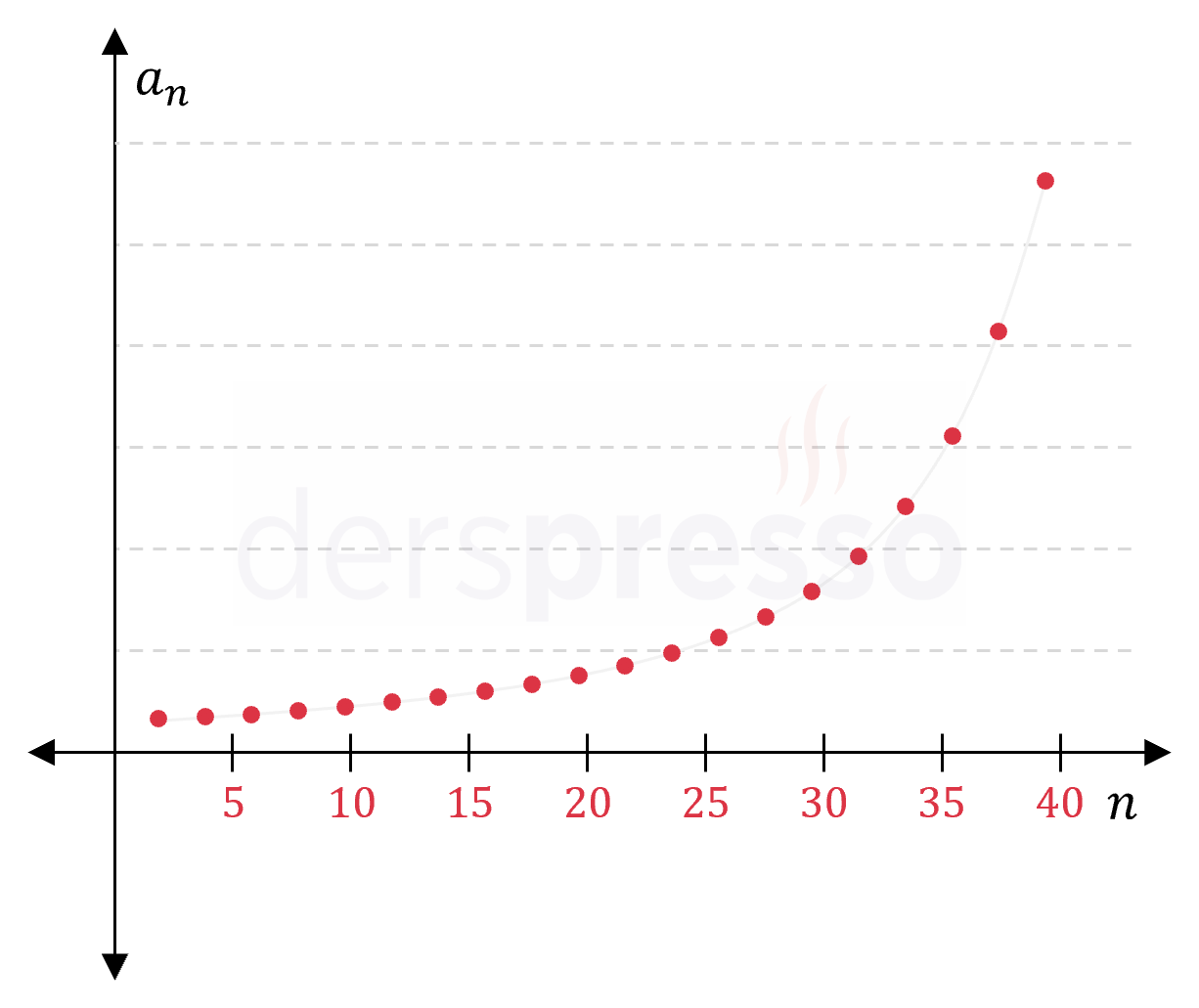
Artan ıraksak dizi: Bu tip bir dizide terimler monoton artarak ıraksar. \( (a_n) = n^2 \) \( = \{1, 4, 9, 16, 25, 36, \ldots \} \) \( n \to \infty \) iken \( a_n \to \infty \) |
|
Azalan ıraksak dizi: Bu tip bir dizide terimler monoton azalarak ıraksar. \( (b_n) = -n^2 \) \( = \{-1, -4, -9, -16, -25, -36, \ldots \} \) \( n \to \infty \) iken \( b_n \to -\infty \) |
|
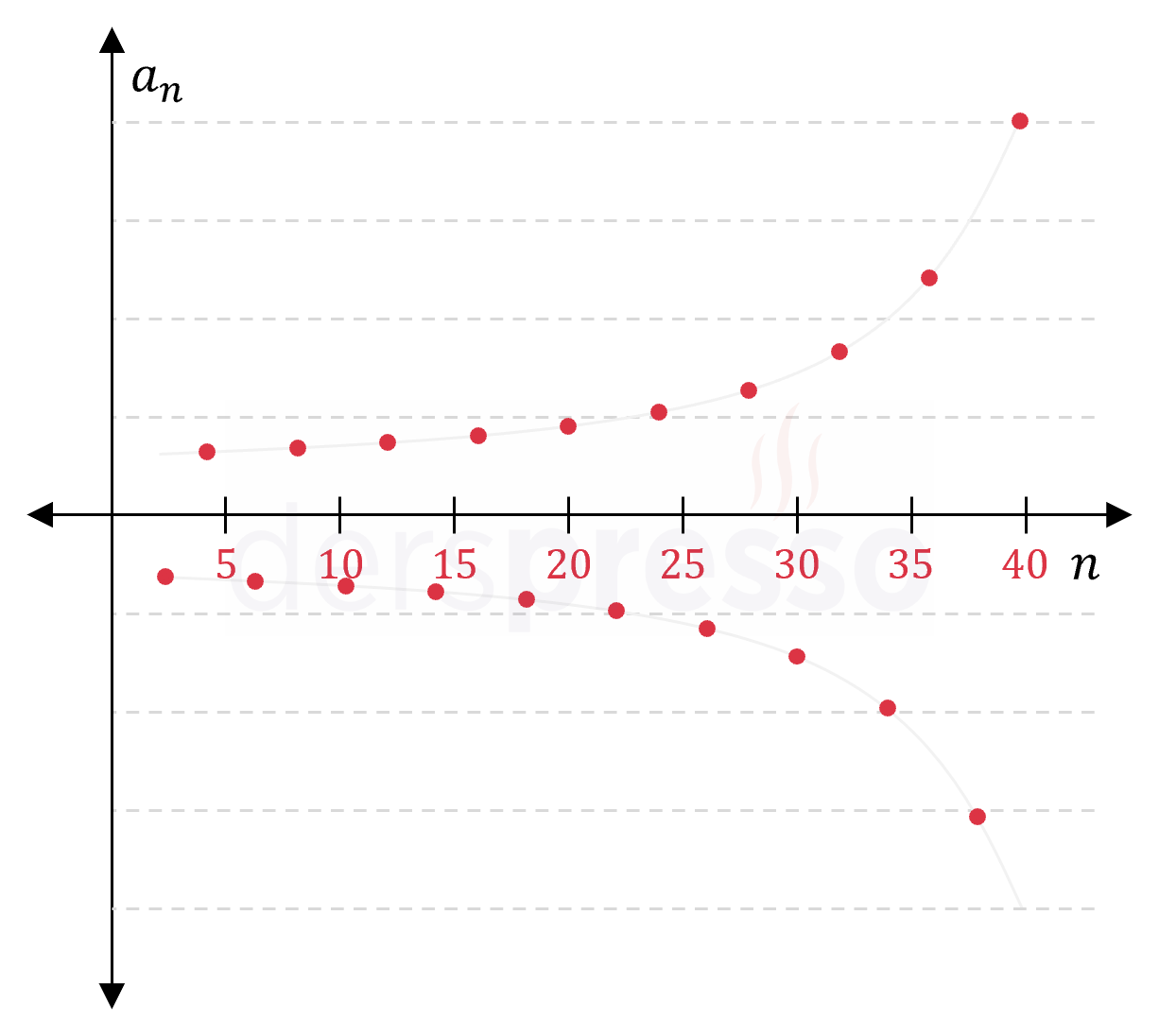
Salınımlı ıraksak dizi: Bu tip bir dizide terimler salınım hareketi yaparak ıraksar. \( (c_n) = (-1)^n\ n^2 \) \( = \{-1, 4, -9, 16, -25, 36, \ldots \} \) |
|
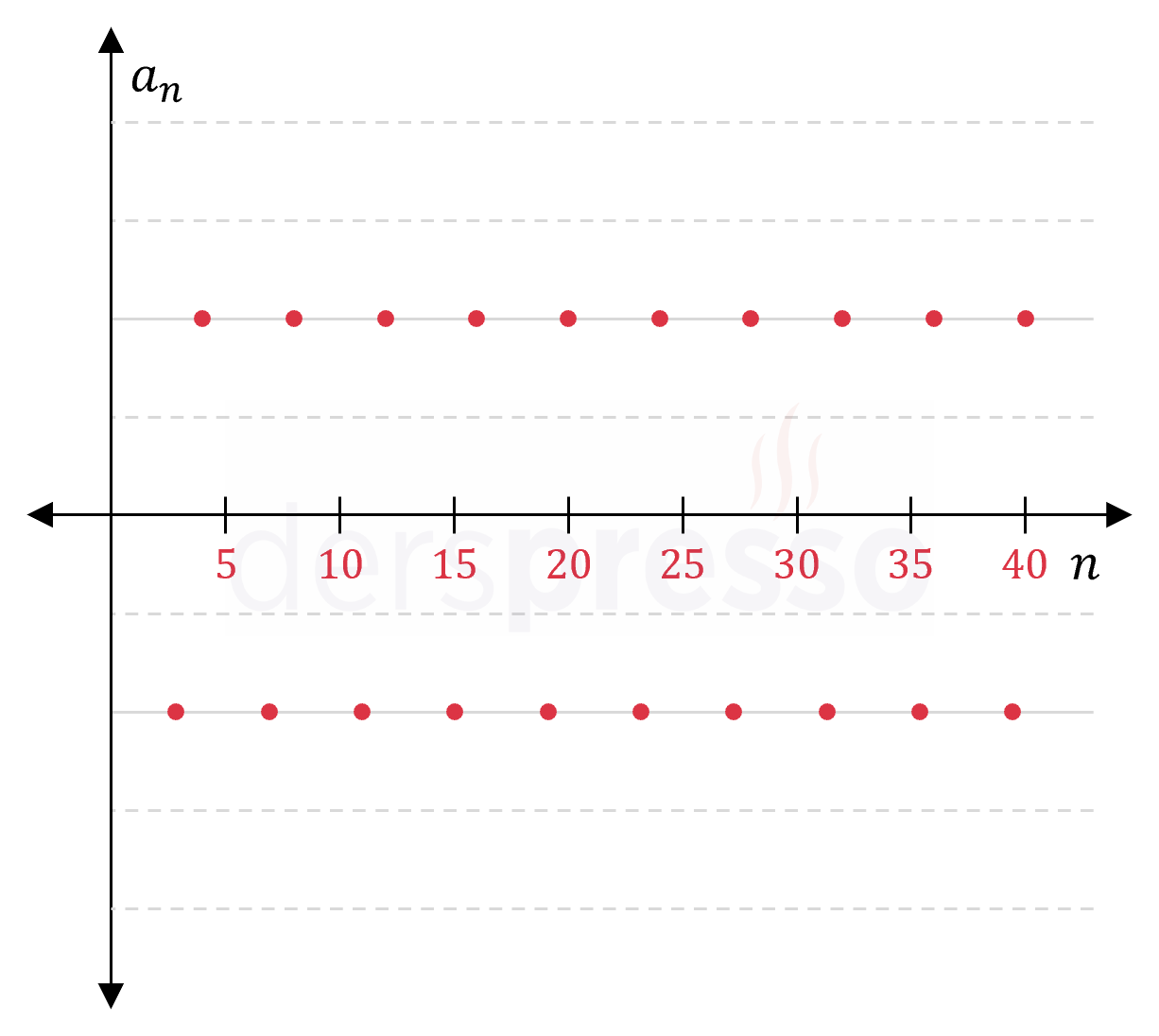
İki değer alan ıraksak dizi: Bu tip bir dizide terimler iki sabit değer arasında gidip gelir. \( (d_n) = (-1)^n\ 4 \) \( = (4, -4, 4, -4, 4, -4, \ldots) \) |
Yakınsak Dizi Tanımı
Dizilerde yakınsaklık tanımı, limit konusunda gördüğümüz sonsuzda limitin epsilon-delta tanımı kullanılarak aşağıdaki şekilde yapılır.
\( a_n \) dizisi aşağıdaki koşulu sağlıyorsa yakınsaktır ve yakınsadığı değer \( L \)'dir.
\( \lim\limits_{n \to \infty} {a_n} = L \) limiti,
seçilebilecek her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşulu sağlayan bir \( N \gt 0 \) değeri bulunabiliyorsa mevcuttur.
Her \( n \gt N \) değeri için, \( \abs{a_n - L} \lt \varepsilon \)
Aşağıdaki koşul sağlandığı durumda ise \( a_n \) dizisinin limiti sonsuzdur.
\( \lim\limits_{n \to \infty} {a_n} = \infty \) limiti,
her \( M \gt 0 \) değeri için aşağıdaki koşulu sağlayan bir \( N \gt 0 \) değeri bulunabiliyorsa mevcuttur.
Her \( n \gt N \) değeri için, \( a_n \gt M \)
Dizilerin Sürekli Fonksiyonlarla İlişkisi
\( f(x) \) fonksiyonu tam sayı \( x = n \) değerlerinde bir \( a_n \) dizisi ile aynı değerlere sahip olan sürekli bir fonksiyon olsun. \( f \) fonksiyonunun sonsuzdaki limiti bir reel sayı olarak tanımlı ya da sonsuz ise \( a_n \) dizisinin limiti de fonksiyonun bu limitine eşittir. Bunun sebebi, sonsuz sayıda noktadan oluşan sürekli bir fonksiyonun limiti belirli bir değere (ya da sonsuza) yaklaşıyorsa bu noktaların bir alt kümesi olan noktalar da aynı değere (ya da sonsuza) yaklaşır.
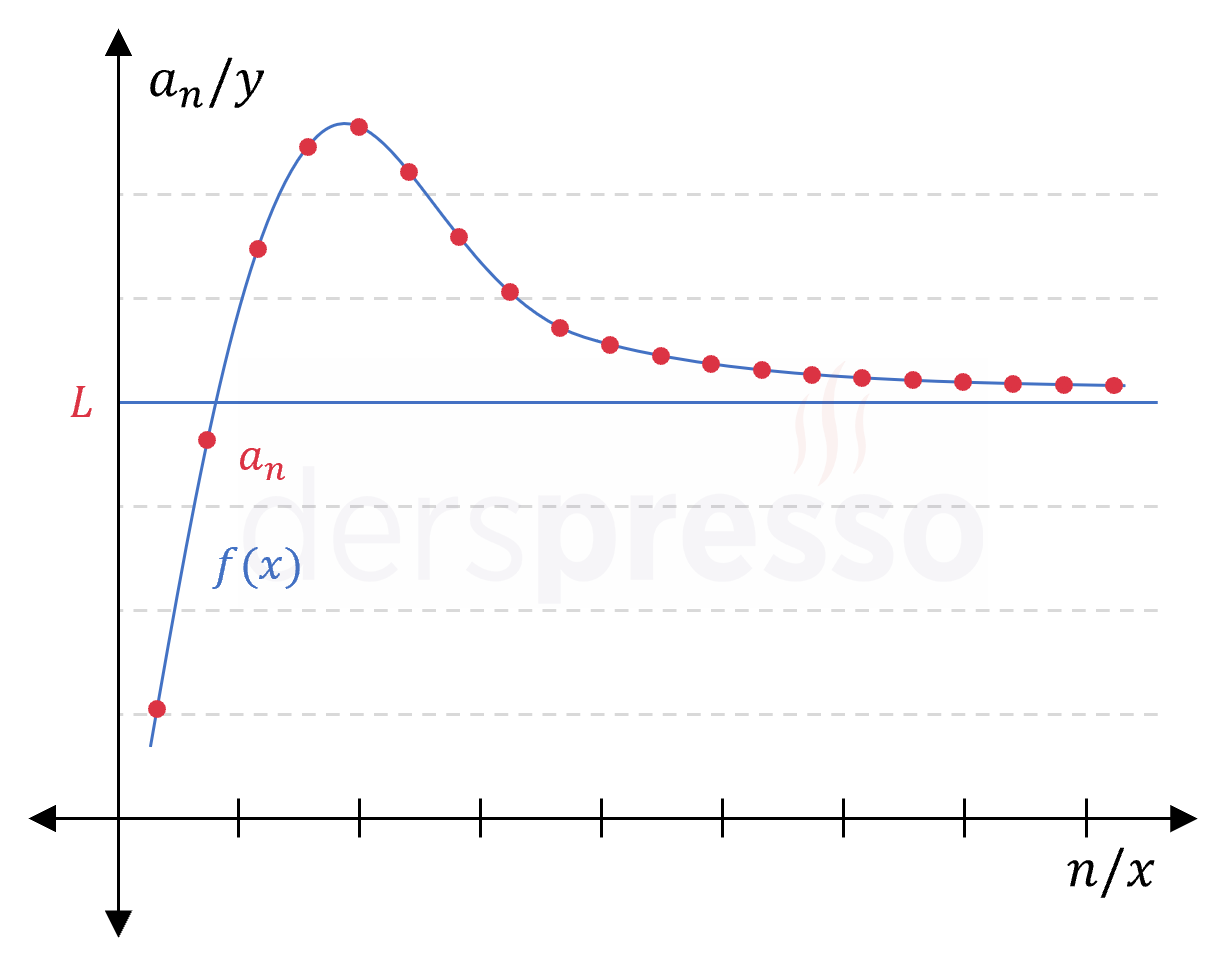
\( a_n \) bir dizi, \( f(x) \) bir fonksiyon olmak üzere,
Her \( n \gt N \) değeri için \( a_n = f(n) \) ve,
\( \lim\limits_{x \to \infty} {f(x)} = L \) ya da sonsuz ise,
\( a_n \) dizisinin limiti fonksiyonun limitine eşittir.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{x \to \infty} {f(x)} \)
Bu teorem fonksiyonun limiti tanımlı ya da sonsuz ise dizinin limitinin fonksiyonun limitine eşit olduğunu söyler. Bununla birlikte fonksiyonun limiti tanımlı olmadığı durumda dizinin limiti tanımlı olabilir. Aşağıda bu duruma bir örnek verilmiştir.
\( (a_n) = \sin(n\pi) \) ve \( f(x) = \sin(x\pi) \) olmak üzere,
\( \lim\limits_{n \to \infty} {a_n} \ne \lim\limits_{x \to \infty} f(x) \) olduğunu gösterelim.
\( a_n \) dizisinin terimlerini listeleyelim.
\( (a_n) = (\sin(0\pi), \sin(1\pi), \sin(2\pi), \sin(3\pi), \ldots) \)
\( = (0, 0, 0, 0, \ldots) \)
\( \lim\limits_{n \to \infty} {a_n} = 0 \)
\( f \) fonksiyonu ise \( x \) sonsuza giderken belirli bir değere yaklaşmaz, \( [-1, 1] \) aralığında salınım hareketi yapar, dolayısıyla sonsuzdaki limiti tanımlı değildir.
\( \lim\limits_{n \to \infty} {a_n} \ne \lim\limits_{x \to \infty} f(x) \)
Sadece sürekli fonksiyonların türevi tanımlı olduğu için tanım kümeleri tam sayılardan oluşan ve sürekli olmayan dizilerin genel terimlerinin türevi alınamaz, dolayısıyla bir dizinin limiti alınırken L'hospital kuralı kullanılamaz. Ancak yukarıda paylaştığımız dizi - sürekli fonksiyon ilişkisi kullanılarak dizinin sürekli ve türevlenebilir bir fonksiyon şeklinde yazılabildiği durumlarda fonksiyonun limiti L'hospital kuralı ile bulunabilir ve bulunan limit değeri dizinin limiti olarak alınabilir.
Alterne diziler için yukarıdaki koşulu sağlayan sürekli bir fonksiyon yazılamayacağı için bu dizilerin limitinde L'hospital kuralı kullanılamaz.
Dizilerde Yakınsaklık Teoremleri
Her yakınsak dizi sınırlıdır.
Her yakınsak dizi sınırlıdır.
İSPATI GÖSTER
\( a_n \) yakınsak bir dizi olsun ve yakınsadığı değere \( L \) diyelim.
\( \lim\limits_{n \to \infty} {a_n} = L \)
Yakınsak dizilerin epsilon - delta tanımına göre, seçilebilecek her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşulu sağlayan bir \( N \gt 0 \) değeri vardır.
Her \( n \gt N \) değeri için, \( \abs{a_n - L} \lt \varepsilon \)
\( \varepsilon = 1 \) seçelim.
Buna göre \( \varepsilon = 1 \) için aşağıdaki koşulu sağlayan bir \( N \gt 0 \) değeri vardır.
Her \( n \gt N \) değeri için, \( \abs{a_n - L} \lt 1 \)
\( -1 \lt a_n - L \lt 1 \)
\( L - 1 \lt a_n \lt L + 1 \)
Buna göre, \( a_n \) dizisinin \( N \). teriminden sonraki terimleri için bir alt sınır (\( L - 1 \)) ve üst sınır (\( L + 1 \)) değeri bulmuş olduk.
Dizinin 1 ve \( N \) arasındaki terimlerini de dahil ederek dizinin tümü için alt ve üst sınır değerleri bulalım.
Dizinin 1 ve \( N \) arasındaki terimleri ile \( N \)'den sonraki terimleri için bir alt sınır değeri olan \( L - 1 \) değerinin en küçüğüne \( m \) diyelim.
\( m = min\{ a_1, a_2, \ldots, a_N, L - 1 \} \)
Dizinin 1 ve \( N \) arasındaki terimleri ile \( N \)'den sonraki terimleri için bir üst sınır değeri olan \( L + 1 \) değerinin en büyüğüne \( M \) diyelim.
\( M = max\{ a_1, a_2, \ldots, a_N, L + 1 \} \)
Dolayısıyla dizinin tüm terimlerinin aşağıdaki alt ve üst sınır değerleri arasında olduğunu söyleyebiliriz.
\( m \le a_n \le M \)
Buna göre yakınsak \( a_n \) dizisi sınırlıdır.
Bu koşullu önermenin karşıt tersi de doğru olacağı için, sınırlı olmayan her dizi ıraksaktır.
Bu koşullu önermenin tersi doğru değildir, yani sınırlı bir dizi yakınsak ya da ıraksak olabilir. Bununla birlikte monoton yakınsaklık teoremine göre, monoton ve sınırlı diziler yakınsaktır.
Monoton Yakınsaklık Teoremi
Monoton yakınsaklık teoremine (bir diğer adıyla monoton dizi teoremi) göre, her monoton ve sınırlı dizi yakınsaktır.
\( a_n \) bir reel sayı dizisi olmak üzere,
- \( a_n \) monoton artan ve üstten sınırlı ise yakınsaktır.
- \( a_n \) monoton azalan ve alttan sınırlı ise yakınsaktır.
Yakınsak bir dizi sınırlıdır, ancak bunun tersi doğru olmayabilir, yani sınırlı bir dizi yakınsak olmayabilir. Örnek olarak aşağıdaki sınırlı dizinin değerleri \( -1 \) ve \( 1 \) değerleri arasında gidip geldiği için yakınsak değildir.
\( ((-1)^n) = (-1, 1, -1, 1, \ldots) \)
Dizilerde Sıkıştırma Teoremi
Limit konusunda gördüğümüz sıkıştırma teoremi dizilere de uyarlanabilir.
Sıkıştırma teoremine göre, bir \( b_n \) dizisi sonsuzdaki limit değerleri birbirine eşit ve \( L \) olan \( a_n \) ve \( c_n \) dizileri arasında kalıyorsa \( b_n \) dizisinin sonsuzdaki limiti de \( L \) olmak zorundadır.
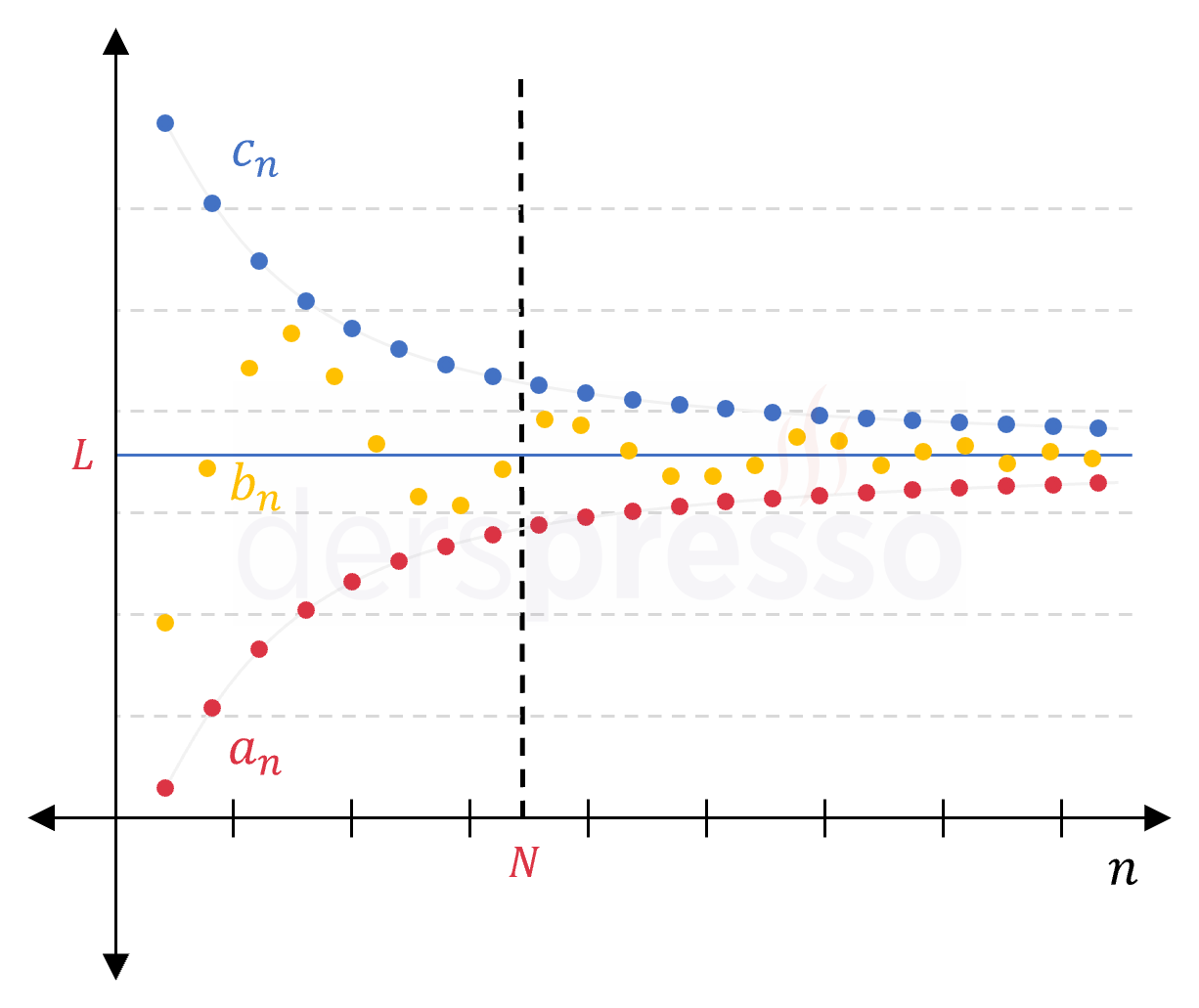
\( a_n, b_n, c_n \) reel sayılarda tanımlı üç dizi olsun.
Her \( n \gt N \) pozitif tam sayısı için,
\( a_n \le b_n \le c_n \) ve
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {c_n} = L \) ise,
\( \lim\limits_{n \to \infty} {b_n} = L \) olur.
Dizilerde Mutlak Değer Teoremi
Sıkıştırma teoreminin bir uygulaması olarak, bir dizinin mutlak değerinin sonsuzdaki limiti sıfır ise dizinin limiti de sıfırdır.
\( \lim\limits_{n \to \infty} {\abs{a_n}} = 0 \) ise,
\( \lim\limits_{n \to \infty} {a_n} = 0 \) olur.
\( (a_n) = \dfrac{(-1)^n}{n} \) olmak üzere,
\( \lim\limits_{n \to \infty} {\abs{a_n}} = \lim\limits_{n \to \infty} {\dfrac{1}{n}} = 0 \) olduğu için,
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{(-1)^n}{n}} = 0 \) olur.
İSPATI GÖSTER
Mutlak değerinin sonsuzdaki limiti sıfır olan bir \( a_n \) dizisi tanımlayalım.
\( \lim\limits_{n \to \infty} {\abs{a_n}} = 0 \)
Limit işlem kurallarına göre, \( -1 \) ile çarptığımızda elde edeceğimiz dizinin de sonsuzdaki limiti sıfır olur.
\( \lim\limits_{n \to \infty} ((-1)\abs{a_n}) = (-1)0 \)
\( \lim\limits_{n \to \infty} (-\abs{a_n}) = 0 \)
Her sayı mutlak değerinden küçük ya da ona eşit, mutlak değerinin negatifinden büyük ya da ona eşittir.
\( -\abs{a_n} \le a_n \le \abs{a_n} \)
Eşitsizliğin taraflarının limitini alalım.
\( \lim\limits_{n \to \infty} (-\abs{a_n}) \le \lim\limits_{n \to \infty} {a_n} \le \lim\limits_{n \to \infty} {\abs{a_n}} \)
Yukarıda bulduğumuz limit değerlerini yerine yazalım.
\( 0 \le \lim\limits_{n \to \infty} {a_n} \le 0 \)
Sıkıştırma teoremine göre, \( \lim\limits_{n \to \infty} {a_n} \) limitinin değeri de sıfır olmak zorundadır.
Dizilerde Limit İşlem Kuralları
Fonksiyonların limiti konusunda gördüğümüz aşağıdaki işlem kuralları diziler için de geçerlidir.
İki yakınsak dizi sırasıyla \( L \) ve \( M \) değerlerine yakınsıyorsa toplamları (farkları) olan dizi de yakınsaktır ve \( L + M \) (\( L - M \)) değerine yakınsar.
\( \lim\limits_{n \to \infty} (a_n + b_n) = L + M \)
\( \lim\limits_{n \to \infty} (a_n - b_n) = L - M \)
Bir yakınsak dizi \( L \) değerine yakınsıyorsa bir \( c \) sayısı ile çarpımı olan dizi de yakınsaktır ve \( cL \) değerine yakınsar.
\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{n \to \infty} (c\ a_n) = cL \)
İki yakınsak dizi sırasıyla \( L \) ve \( M \) değerlerine yakınsıyorsa çarpımları olan dizi de yakınsaktır ve \( LM \) değerine yakınsar.
\( \lim\limits_{n \to \infty} (a_nb_n) = LM \)
İki yakınsak dizi sırasıyla \( L \) ve \( M \) değerlerine yakınsıyorsa bölümleri olan dizi de yakınsaktır ve \( \frac{L}{M} \) değerine yakınsar.
\( M \ne 0 \) olmak üzere,
\( \lim\limits_{n \to \infty} {\dfrac{a_n}{b_n}} = \dfrac{L}{M} \)
Sık Kullanılan Limitler
Sık kullanılan bazı dizilerin limit değerleri aşağıda verilmiştir.
\( \abs{a} \lt 1 \) olmak üzere,
\( \lim\limits_{n \to \infty} {a^n} = 0 \)
\( a \gt 0 \) olmak üzere,
\( \lim\limits_{n \to \infty} {\sqrt[n]{a}} = 1 \)
\( \lim\limits_{n \to \infty} {\sqrt[n]{n}} = 1 \)
\( \lim\limits_{n \to \infty} \left( 1 + \dfrac{a}{n} \right)^n = e^a \)
\( \lim\limits_{n \to \infty} {\dfrac{\ln{n}}{n}} = 0 \)
\( (a_n) = (-\dfrac{1}{5})^n \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {(-\dfrac{1}{5})^n} \)
\( -1 \lt a \lt 1 \) olduğunda \( n \to \infty \) iken \( a^n \to 0 \) olur.
\( = 0 \)
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = 5 + (0,2)^n \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} (5 + (0,2)^n) \)
\( = \lim\limits_{n \to \infty} {5} + \lim\limits_{n \to \infty} {(0,2)^n} \)
\( -1 \lt a \lt 1 \) olduğunda \( n \to \infty \) iken \( a^n \to 0 \) olur.
\( = 5 + 0 = 5 \)
Verilen dizinin sonsuzdaki limiti \( 5 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{3n + (-1)^n}{n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{3n + (-1)^n}{n}} \)
\( = \lim\limits_{n \to \infty} (3 + \dfrac{(-1)^n}{n}) \)
\( = \lim\limits_{n \to \infty} {3} + \lim\limits_{n \to \infty} {\dfrac{(-1)^n}{n}} \)
\( \frac{(-1)^n}{n} \) ifadesi salınımlı yakınsak bir dizidir. Bu tip bir dizide terimler limit değeri etrafında salınım hareketi yaparak limit değerine yaklaşır.
\( n \to \infty \) iken \( \dfrac{(-1)^n}{n} \to 0 \) olur.
\( = 3 + 0 = 3 \)
Verilen dizinin sonsuzdaki limiti \( 3 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \pi^{\frac{1}{n}} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\pi^{\frac{1}{n}}} \)
\( = \lim\limits_{n \to \infty}{\sqrt[n]{\pi}} \)
\( a \gt 0 \) olduğu durumda \( \lim\limits_{n \to \infty} {\sqrt[n]{a}} = 1 \) olur.
\( \pi \gt 0 \) olduğu için \( \lim\limits_{n \to \infty} {\sqrt[n]{\pi}} = 1 \) olur.
Verilen dizinin sonsuzdaki limiti \( 1 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{3 - 5n}{3 + 5n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{3 - 5n}{3 + 5n}} \)
Payı ve paydayı \( n \) parantezine alalım.
\( = \lim\limits_{n \to \infty} {\dfrac{n(\frac{3}{n} - 5)}{n(\frac{3}{n} + 5)}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{\frac{3}{n} - 5}{\frac{3}{n} + 5}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {\frac{3}{n}} - \lim\limits_{n \to \infty} {5}}{\lim\limits_{n \to \infty} {\frac{3}{n}} + \lim\limits_{n \to \infty} {5}} \)
\( n \to \infty \) iken \( \dfrac{3}{n} \to 0 \) olur.
\( = \dfrac{0 - 5}{0 + 5} = -1 \)
Verilen dizinin sonsuzdaki limiti \( -1 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{3n + 2}{4 - 5\sqrt{n}} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{3n + 2}{4 - 5\sqrt{n}}} \)
Payı ve paydayı \( \sqrt{n} \) parantezine alalım.
\( = \lim\limits_{n \to \infty} {\dfrac{\sqrt{n}(3\sqrt{n} + \frac{2}{\sqrt{n}})}{\sqrt{n}(\frac{4}{\sqrt{n}} - 5)}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{3\sqrt{n} + \frac{2}{\sqrt{n}}}{\frac{4}{\sqrt{n}} - 5}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {3\sqrt{n}} + \lim\limits_{n \to \infty} {\frac{2}{\sqrt{n}}}}{\lim\limits_{n \to \infty} {\frac{4}{\sqrt{n}}} - \lim\limits_{n \to \infty} {5}} \)
\( n \to \infty \) iken \( \dfrac{2}{\sqrt{n}} \to 0 \ \) ve \( \dfrac{4}{\sqrt{n}} \to 0 \) olur.
\( n \to \infty \) iken \( \sqrt{n} \to \infty \) olur.
\( = \dfrac{3 \cdot \infty + 0}{0 - 5} \)
\( = -\infty \)
Verilen dizinin sonsuzdaki limiti \( -\infty \) olduğu için dizi ıraksaktır.
\( (a_n) = \dfrac{2 - 7n^5}{n^5 + 6n^4} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{2 - 7n^5}{n^5 + 6n^4}} \)
Payı ve paydayı \( n^5 \) parantezine alalım.
\( = \lim\limits_{n \to \infty} {\dfrac{n^5(\frac{2}{n^5} - 7)}{n^5(1 + \frac{6}{n})}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{\frac{2}{n^5} - 7}{1 + \frac{6}{n}}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {\frac{2}{n^5}} - \lim\limits_{n \to \infty} {7}}{\lim\limits_{n \to \infty} {1} + \lim\limits_{n \to \infty} {\frac{6}{n}}} \)
\( n \to \infty \) iken \( \dfrac{2}{n^5} \to 0 \) ve \( \dfrac{6}{n} \to 0 \) olur.
\( = \dfrac{0 - 7}{1 + 0} = -7 \)
Verilen dizinin sonsuzdaki limiti \( -7 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{n - 2}{n^2 + 2n - 8} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{n - 2}{n^2 + 2n - 8}} \)
Paydayı çarpanlarına ayıralım.
\( = \lim\limits_{n \to \infty} {\dfrac{n - 2}{(n - 2)(n + 4)}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{1}{n + 4}} \)
\( n \to \infty \) iken \( \dfrac{1}{n + 4} \to 0 \) olur.
\( = 0 \)
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{n^2 + 4n + 1}{n - 3} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{n^2 + 4n + 1}{n - 3}} \)
Payı ve paydayı \( n \) parantezine alalım.
\( = \lim\limits_{n \to \infty} {\dfrac{n(n + 4 + \frac{1}{n})}{n(1 - \frac{3}{n})}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{n + 4 + \frac{1}{n}}{1 - \frac{3}{n}}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {n} + \lim\limits_{n \to \infty} {4} + \lim\limits_{n \to \infty} {\frac{1}{n}}}{\lim\limits_{n \to \infty} {1} - \lim\limits_{n \to \infty} {\frac{3}{n}}} \)
\( n \to \infty \) iken \( \dfrac{1}{n} \to 0 \) ve \( \dfrac{3}{n} \to 0 \) olur.
\( = \dfrac{\infty + 4 + 0}{1 - 0} \)
\( = \infty \)
Verilen dizinin sonsuzdaki limiti \( \infty \) olduğu için dizi ıraksaktır.
\( (a_n) = \sqrt{\dfrac{8n}{2n + 3}} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\sqrt{\dfrac{8n}{2n + 3}}} \)
Karekök fonksiyonu tanım kümesi içinde sürekli olduğu için limiti karekök içine alabiliriz.
\( = \sqrt{\lim\limits_{n \to \infty} {\dfrac{8n}{2n + 3}}} \)
Paydayı \( n \) parantezine alalım.
\( = \sqrt{\lim\limits_{n \to \infty} {\dfrac{8n}{n(2 + \frac{3}{n})}}} \)
\( = \sqrt{\lim\limits_{n \to \infty} {\dfrac{8}{2 + \frac{3}{n}}}} \)
\( = \sqrt{\dfrac{\lim\limits_{n \to \infty} {8}}{\lim\limits_{n \to \infty} {2} + \lim\limits_{n \to \infty} {\frac{3}{n}}}} \)
\( n \to \infty \) iken \( \dfrac{3}{n} \to 0 \) olur.
\( = \sqrt{\dfrac{8}{2 + 0}} \)
\( = \sqrt{4} = 2 \)
Verilen dizinin sonsuzdaki limiti \( 2 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \sin(\dfrac{3\pi}{2} + \dfrac{2}{n}) \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\sin(\dfrac{3\pi}{2} + \dfrac{2}{n})} \)
Sinüs fonksiyonu tüm reel sayılarda sürekli olduğu için limiti sinüs ifadesinin içine alabiliriz.
\( = \sin{\lim\limits_{n \to \infty} (\dfrac{3\pi}{2} + \dfrac{2}{n})} \)
\( = \sin(\lim\limits_{n \to \infty} {\dfrac{3\pi}{2}} + \lim\limits_{n \to \infty} {\dfrac{2}{n}}) \)
\( n \to \infty \) iken \( \dfrac{2}{n} \to 0 \) olur.
\( = \sin(\dfrac{3\pi}{2} + 0) \)
\( = -1 \)
Verilen dizinin sonsuzdaki limiti \( -1 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{\sin{n}}{n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterSıkıştırma teoremini uygulayalım.
Sinüs fonksiyonu \( [-1, 1] \) aralığında değer alır.
\( -1 \le \sin{n} \le 1 \)
Eşitsizliğin taraflarını \( \frac{1}{n} \) ile çarpalım.
\( -\dfrac{1}{n} \le \dfrac{\sin{n}}{n} \le \dfrac{1}{n} \)
Tarafların \( n \) sonsuza giderken limitini alalım.
\( \lim\limits_{n \to \infty} {-\dfrac{1}{n}} \le \lim\limits_{n \to \infty} {\dfrac{\sin{n}}{n}} \le \lim\limits_{n \to \infty} {\dfrac{1}{n}} \)
\( n \to \infty \) iken \( \dfrac{1}{n} \to 0 \) ve \( -\dfrac{1}{n} \to 0 \) olur.
\( 0 \le \lim\limits_{n \to \infty} {\dfrac{\sin{n}}{n}} \le 0 \)
Buna göre sıkıştırma teoremine göre \( \lim\limits_{n \to \infty} {\frac{\sin{n}}{n}} = 0 \) olur.
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{3n}{5^n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{3n}{5^n}} \)
\( \lim\limits_{n \to \infty} (3n) = \infty \)
ve
\( \lim\limits_{n \to \infty} {5^n} = \infty \)
olduğu için, \( \dfrac{\infty}{\infty} \) belirsizliği vardır. Dolayısıyla L'Hospital kuralını uygulayabiliriz.
\( = \lim\limits_{n \to \infty} {\dfrac{(3n)'}{(5^n)'}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{3}{5^n\ln{5}}} \)
\( n \to \infty \) iken \( 5^n \to \infty \) olur.
\( = \dfrac{3}{\infty \cdot \ln{5}} \)
\( = 0 \)
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = (\dfrac{n + 4}{n})^n \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {(\dfrac{n + 4}{n})^n} \)
\( = \lim\limits_{n \to \infty} {(1 + \dfrac{4}{n})^n} \)
Aşağıdaki limit kuralını kullanalım.
\( \lim\limits_{n \to \infty} {(1 + \dfrac{a}{n})^n} = e^a \)
\( \lim\limits_{n \to \infty} {(1 + \dfrac{4}{n})^n} = e^4 \)
Verilen dizinin sonsuzdaki limiti \( e^4 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \sqrt[n]{7n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\sqrt[n]{7n}} \)
\( = \lim\limits_{n \to \infty} (\sqrt[n]{7} \cdot \sqrt[n]{n}) \)
\( = \lim\limits_{n \to \infty} {\sqrt[n]{7}} \cdot \lim\limits_{n \to \infty} {\sqrt[n]{n}} \)
Aşağıdaki limit kurallarını kullanalım.
\( a \gt 0 \) olmak üzere,
\( \lim\limits_{n \to \infty} {\sqrt[n]{a}} = 1 \)
\( \lim\limits_{n \to \infty} {\sqrt[n]{n}} = 1 \)
\( 7 \gt 0 \) olduğu için \( \lim\limits_{n \to \infty} {\sqrt[n]{7}} = 1 \) olur.
\( = 1 \cdot 1 = 1 \)
Verilen dizinin sonsuzdaki limiti \( 1 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = (\dfrac{e}{n})^{\frac{1}{n}} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {(\dfrac{e}{n})^{\frac{1}{n}}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{e^{\frac{1}{n}}}{n^{\frac{1}{n}}}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{\sqrt[n]{e}}{\sqrt[n]{n}}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {\sqrt[n]{e}}}{\lim\limits_{n \to \infty} {\sqrt[n]{n}}} \)
Aşağıdaki limit kurallarını kullanalım.
\( a \gt 0 \) olmak üzere,
\( \lim\limits_{n \to \infty} {\sqrt[n]{a}} = 1 \)
\( \lim\limits_{n \to \infty} {\sqrt[n]{n}} = 1 \)
\( e \gt 0 \) olduğu için \( \lim\limits_{n \to \infty} {\sqrt[n]{e}} = 1 \) olur.
\( = \dfrac{1}{1} = 1 \)
Verilen dizinin sonsuzdaki limiti \( 1 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \sqrt[n]{2^{3n + 4}} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\sqrt[n]{2^{3n + 4}}} \)
\( = \lim\limits_{n \to \infty} {2^{\frac{3n + 4}{n}}} \)
\( = \lim\limits_{n \to \infty} {2^{3 + \frac{4}{n}}} \)
\( = 8\lim\limits_{n \to \infty} {2^{\frac{4}{n}}} \)
Üstel fonksiyon tüm reel sayılarda sürekli olduğu için limit ifadesini üsse alabiliriz.
\( = 8 \cdot 2^{\lim\limits_{n \to \infty} {{\frac{4}{n}}}} \)
\( n \to \infty \) iken \( \dfrac{4}{n} \to 0 \) olur.
\( = 8 \cdot 2^0 = 8 \)
Verilen dizinin sonsuzdaki limiti \( 8 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \ln{(1 + \dfrac{5}{n})^n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\ln{(1 + \dfrac{5}{n})^n}} \)
Doğal logaritma fonksiyonu pozitif tam sayılarda sürekli olduğu için limiti logaritma içine alabiliriz.
\( = \ln(\lim\limits_{n \to \infty} {(1 + \dfrac{5}{n})^n}) \)
Aşağadaki limit kuralını kullanalım.
\( \lim\limits_{n \to \infty} {(1 + \dfrac{a}{n})^n} = e^a \)
\( = \ln{e^5} = 5 \)
Verilen dizinin sonsuzdaki limiti \( 5 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{(-1)^{n + 1}}{5n - 3} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{(-1)^{n + 1}}{5n - 3}} \)
Payı ve paydayı \( n \) parantezine alalım.
\( = \lim\limits_{n \to \infty} {\dfrac{n \cdot \frac{(-1)^{n + 1}}{n}}{n(5 - \frac{3}{n})}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{\frac{(-1)^{n + 1}}{n}}{5 - \frac{3}{n}}} \)
\( = \dfrac{\lim\limits_{n \to \infty} {\frac{(-1)^{n + 1}}{n}}}{\lim\limits_{n \to \infty} {5} - \lim\limits_{n \to \infty} {\frac{3}{n}}} \)
\( \frac{(-1)^{n + 1}}{n} \) ifadesi salınımlı yakınsak bir dizidir. Bu tip bir dizide terimler limit değeri etrafında salınım hareketi yaparak limit değerine yaklaşır.
\( n \to \infty \) iken \( \dfrac{(-1)^{n + 1}}{n} \to 0 \) olur.
\( n \to \infty \) iken \( \dfrac{3}{n} \to 0 \) olur.
\( = \dfrac{0}{5 - 0} = 0 \)
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = n^2\pi\cos(n\pi) \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} (n^2\pi\cos(n\pi)) \)
Tam sayı \( n \) değerlerinde \( \cos(n\pi) \) ifadesi \( \pm 1 \) değerlerini alır, dolayısıyla \( \cos(n\pi) \) yerine \( (-1)^n \) yazabiliriz.
\( = \lim\limits_{n \to \infty} (n^2\pi(-1)^n) \)
\( n \) sonsuza giderken \( n^2\pi \) ifadesi sonsuza giderken dizi \( (-1)^n \) ifadesi ile ardışık \( n \) değerlerinde işaret değiştirir.
Verilen dizinin sonsuzdaki limiti tanımsız olduğu için dizi ıraksaktır.
\( (a_n) = \dfrac{2^n}{n^3} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{2^n}{n^3}} \)
\( \lim\limits_{n \to \infty} {2^n} = \infty \)
ve
\( \lim\limits_{n \to \infty} {n^3} = \infty \)
olduğu için, \( \dfrac{\infty}{\infty} \) belirsizliği vardır. Dolayısıyla L'Hospital kuralını uygulayabiliriz.
\( = \lim\limits_{n \to \infty} {\dfrac{(2^n)'}{(n^3)'}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{2^n\ln{2}}{3n^2}} \)
\( \dfrac{\infty}{\infty} \) belirsizliği devam ettiği için L'Hospital kuralını tekrar uygulayalım.
\( = \lim\limits_{n \to \infty} {\dfrac{(2^n\ln{2})'}{(3n^2)'}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{2^n(\ln{2})^2}{6n}} \)
\( \dfrac{\infty}{\infty} \) belirsizliği devam ettiği için L'Hospital kuralını tekrar uygulayalım.
\( = \lim\limits_{n \to \infty} {\dfrac{(2^n(\ln{2})^2)'}{(6n)'}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{2^n(\ln{2})^3}{6}} \)
\( n \to \infty \) iken \( 2^n \to \infty \) olur.
\( = \dfrac{\infty \cdot (\ln{2})^3}{6} \)
\( = \infty \)
Verilen dizinin sonsuzdaki limiti \( \infty \) olduğu için dizi ıraksaktır.
\( (a_n) = (\dfrac{5n + 2}{5n - 2})^n \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {(\dfrac{5n + 2}{5n - 2})^n} \)
\( = \lim\limits_{n \to \infty} {(1 + \dfrac{4}{5n - 2})^n} \)
\( = \lim\limits_{n \to \infty} {(1 + \dfrac{\frac{4}{5}}{n - \frac{2}{5}})^n} \)
\( n \to \infty \) iken \( (n - \frac{2}{5}) \to \infty \) olur, dolayısıyla aşağıdaki limit kuralını kullanabiliriz.
\( \lim\limits_{n \to \infty} {(1 + \dfrac{a}{n})^n} = e^a \)
\( = e^{\frac{4}{5}} \)
Verilen dizinin sonsuzdaki limiti \( e^{\frac{4}{5}} \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{(-7)^n}{n!} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{(-7)^n}{n!}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{(-1)^n \cdot 7^n}{n!}} \)
\( n \) sonsuza giderken \( n! \) ifadesi \( a^n \) ifadesinden daha hızlı büyür.
\( n \to \infty \) iken \( \dfrac{7^n}{n!} \to 0 \) olur.
Buna göre verilen dizi \( n \) sonsuza giderken pozitif ve negatif değerler arasında salınım hareketi yaparak sıfır değerine yaklaşır.
Verilen dizinin sonsuzdaki limiti \( 0 \) olarak tanımlı olduğu için dizi yakınsaktır.
\( (a_n) = \dfrac{n!}{5^n7^n} \) dizisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü GösterBir dizi sonsuzdaki limiti tek bir reel sayı olarak tanımlı ise yakınsaktır, aksi takdirde ıraksaktır.
\( \lim\limits_{n \to \infty} {a_n} = \lim\limits_{n \to \infty} {\dfrac{n!}{5^n7^n}} \)
\( = \lim\limits_{n \to \infty} {\dfrac{n!}{35^n}} \)
\( n \) sonsuza giderken \( n! \) ifadesi \( a^n \) ifadesinden daha hızlı büyür.
\( n \to \infty \) iken \( \dfrac{n!}{35^n} \to \infty \) olur.
\( = \infty \)
Verilen dizinin sonsuzdaki limiti \( \infty \) olduğu için dizi ıraksaktır.
\( (a_n) = 1 - \dfrac{3^n}{(n + 3)!} \) dizisinin yakınsak olduğunu monoton yakınsaklık teoremini kullanarak gösteriniz.
Çözümü GösterÖnce \( \dfrac{3^n}{(n + 3)!} \) dizisinin azalan olduğunu gösterelim.
Oran testini kullanalım.
\( \dfrac{a_{n + 1}}{a_n} = \dfrac{\frac{3^{n + 1}}{(n + 4)!}}{\frac{3^n}{(n + 3)!}} \)
\( = \dfrac{3 \cdot 3^{n}}{(n + 4)(n + 3)!} \cdot \dfrac{(n + 3)!}{3^n} \)
\( = \dfrac{3}{n + 4} \lt 1 \)
Bu ifade her \( n \ge 1 \) için 1'den küçük olduğu için \( \frac{3^n}{(n + 3)!} \) ifadesi kesin monoton azalandır.
O halde \( (1 - \frac{3^n}{(n + 3)!}) \) ifadesi kesin monoton artan olur.
Her \( n \ge 1 \) için \( \frac{3^n}{(n + 3)!} \gt 0 \) olduğu için \( a_n \) dizisi üstten 1 ile sınırlıdır.
Monoton yakınsaklık teoremine göre, \( a_n \) dizisi monoton artan ve üstten sınırlı olduğu için yakınsak bir dizidir.
\( (b_n) = \dfrac{2n}{n + 2} \) dizisinin yakınsak olduğunu monoton yakınsaklık teoremini kullanarak gösteriniz.
Çözümü GösterÖnce \( b_n \) dizisinin monotonluğunu inceleyelim.
Fark testini kullanalım.
\( b_{n + 1} - b_n = \dfrac{2(n + 1)}{(n + 1) + 2} - \dfrac{2n}{n + 2} \)
\( = \dfrac{2n + 2}{n + 3} - \dfrac{2n}{n + 2} \)
\( = \dfrac{(2n + 2)(n + 2) - (n + 3)2n}{(n + 3)(n + 2)} \)
\( = \dfrac{2n^2 + 6n + 4 - (2n^2 + 6n)}{(n + 3)(n + 2)} \)
\( = \dfrac{4}{(n + 3)(n + 2)} \gt 0 \)
Bu ifade her \( n \ge 1 \) için pozitif olduğu için \( b_n \) kesin monoton artan bir dizidir.
Şimdi \( b_n \) dizisinin üst sınırını bulalım.
\( \dfrac{2n}{n + 2} \lt \dfrac{2n}{n} = 2 \)
Buna göre \( b_n \) dizisi üstten 2 ile sınırlıdır.
Monoton yakınsaklık teoremine göre, \( b_n \) dizisi monoton artan ve üstten sınırlı olduğu için yakınsak bir dizidir.
\( (c_n) = \dfrac{n^2 + 3}{2n^2 + 1} \) dizisinin yakınsak olduğunu monoton yakınsaklık teoremini kullanarak gösteriniz.
Çözümü GösterÖnce \( c_n \) dizisinin monotonluğunu inceleyelim.
Fark testini kullanalım.
\( c_{n + 1} = \dfrac{(n + 1)^2 + 3}{2(n + 1)^2 + 1} \)
\( = \dfrac{n^2 + 2n + 1 + 3}{2(n^2 + 2n + 1) + 1} \)
\( = \dfrac{n^2 + 2n + 4}{2n^2 + 4n + 3} \)
\( c_{n + 1} - c_n = \dfrac{n^2 + 2n + 4}{2n^2 + 4n + 3} - \dfrac{n^2 + 3}{2n^2 + 1} \)
\( = \dfrac{(n^2 + 2n + 4)(2n^2 + 1) - (n^2 + 3)(2n^2 + 4n + 3)}{(2n^2 + 4n + 3)(2n^2 + 1)} \)
Paydaki parantezleri genişletelim.
\( = \dfrac{(2n^4 + 2n^2 + 4n^2 + 4 + 2n^2 + 4n + 4) - (2n^4 + 4n^3 + 3n^2 + 6n^2 + 12n + 9)}{(2n^2 + 4n + 3)(2n^2 + 1)} \)
\( = \dfrac{2n^4 + 6n^2 + 4n + 4 - 2n^4 - 4n^3 - 9n^2 - 12n - 9}{(2n^2 + 4n + 3)(2n^2 + 1)} \)
\( = \dfrac{-(4n^3 + 3n^2 + 8n + 5)}{(2n^2 + 4n + 3)(2n^2 + 1)} \)
Parantez içindeki ifadeler pozitif terimlerin toplamı olduğu için pozitiftir, dolayısıyla bu ifade her \( n \ge 1 \) için negatiftir, bu yüzden \( c_n \) kesin monoton azalan bir dizidir.
Şimdi \( c_n \) dizisinin üst sınırını bulalım.
\( \dfrac{n^2 + 3}{2n^2 + 1} \gt \dfrac{n^2 + \frac{1}{2}}{2n^2 + 1} = \dfrac{1}{2} \)
Buna göre \( c_n \) dizisi alttan \( \frac{1}{2} \) ile sınırlıdır.
Monoton yakınsaklık teoremine göre, \( c_n \) dizisi monoton azalan ve alttan sınırlı olduğu için yakınsak bir dizidir.