Sonsuz Diziler
Belirli bir sıraya sahip sayı listelerine dizi denir.
\( (a_n) = (1, 2, 3, 4, 5, \ldots) \)
\( (b_n) = (\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \ldots) \)
\( (c_n) = (1, -2, 4, -9, 16, \ldots) \)
Diziler bölümünde dizi kavramından, farklı dizi tiplerinden ve dizilerle işlemlerden bahsetmiştik. Bu bölümde seriler konusuna bir giriş olarak sonsuz sayıda terimden oluşan ve terimleri reel sayılar olan sonsuz dizileri inceleyeceğiz.
Dizilerle ilgili önemli birkaç bilgiyi hatırlayalım.
- Bir dizinin her bir elemanına o dizinin terimi denir.
- Bir dizinin \( k \). terimi \( a_k \) şeklinde gösterilir. Bir terimin dizinin kaçıncı terimi olduğunu gösteren bu \( k \) sayısına indis denir.
- Dizilerde (kümelerden farklı olarak) terimler tekrar edebilir ve sıra önemlidir.
- Diziler tanım kümesi bir tam sayı aralığı olan birer fonksiyondur.
- Dizilerin indisi 0, 1 ya da herhangi bir tam sayıdan başlayabilir.
Terimleri arasında matematiksel bir ilişki bulunan diziler genellikle \( n \). terimi belirten bir formül ile tanımlanır. Bu formüle dizinin genel terimi denir.
\( (a_n) = n^2 - n \)
\( = (0, 2, 6, 12, 20, 30, 42, \ldots) \)
\( (b_n) = \dfrac{n + 1}{5n} \)
\( = (\frac{2}{5}, \frac{3}{10}, \frac{4}{15}, \ldots) \)
Diziler alternatif olarak terimleri listelenerek de tanımlanabilir.
Asal sayılar dizisi:
\( (a_n) = (2, 3, 5, 7, 11, 13, \ldots) \)
"Mükemmel" sayılar dizisi:
\( (b_n) = (6, 28, 496, 8128, 33550336, \ldots) \)
Bir dizinin indisinin başlangıç ve bitiş değerleri aşağıdaki şekilde belirtilebilir.
\( (2n)_{n=1}^{\infty} \)
\( (n^2 - 4n)_{n=4}^{\infty} \)
Dizilerin Grafiksel Gösterimi
Bir dizinin terimleri iki boyutlu kartezyen düzleminde aşağıdaki şekilde gösterilebilir.
| Grafik | Dizi |
|---|---|
|
\( (a_n) = n^2 - 5n \) \( = (-4, -6, -6, -4, 0, 6, 14, 24, \ldots) \) |
|
\( (b_n) = \dfrac{n - 1}{n} \) \( = (0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8}, \ldots) \) |
|
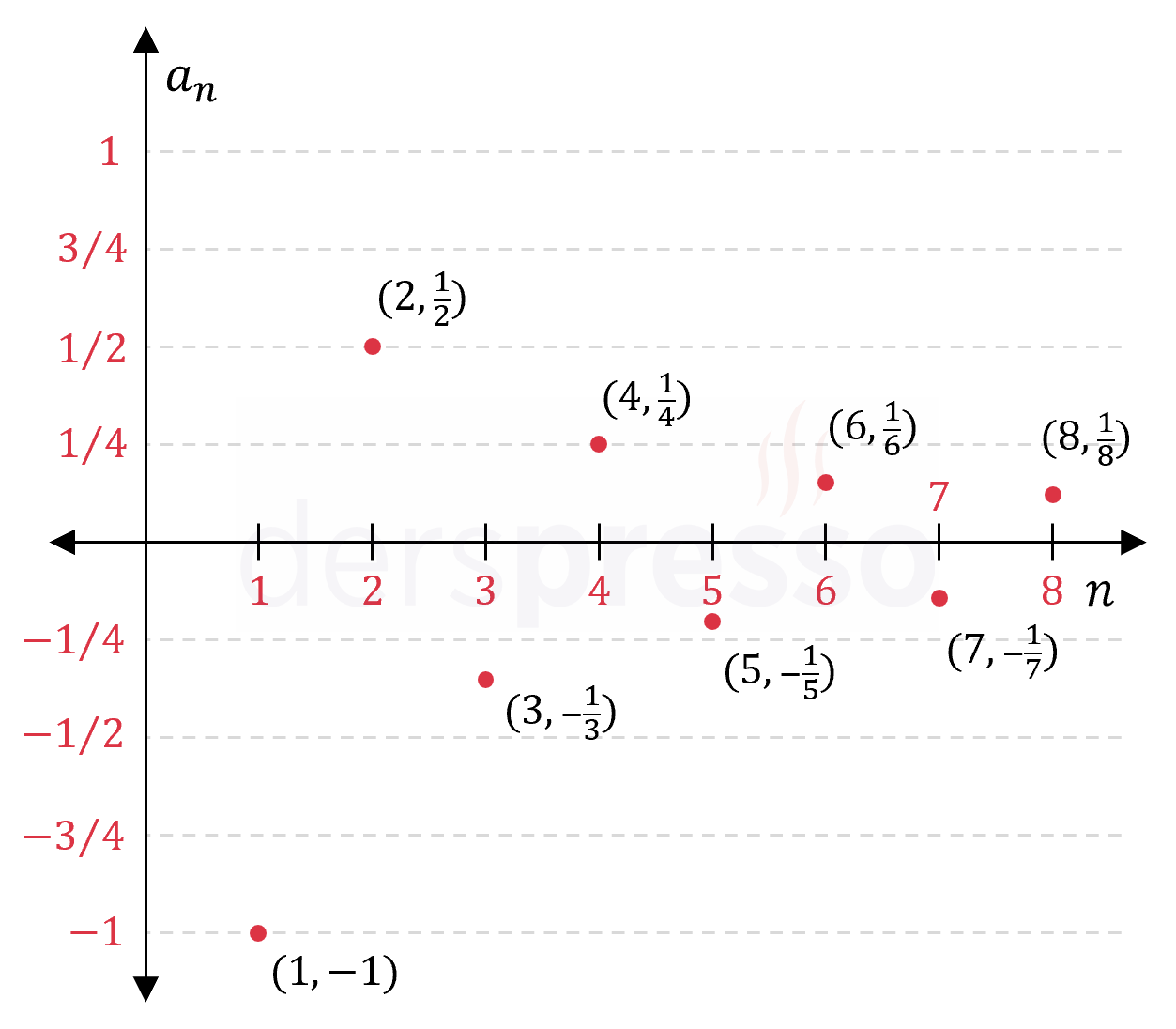
\( (c_n) = \dfrac{(-1)^n}{n} \) \( = (-1, \frac{1}{2}, -\frac{1}{3}, \frac{1}{4}, -\frac{1}{5}, \frac{1}{6}, -\frac{1}{7}, \frac{1}{8}, \ldots) \) |
Artan ve Azalan Diziler
Terimlerinin değeri sürekli artan ya da sabit kalan (\( a_k \le a_{k + 1} \)) dizilere monoton artan dizi denir.
Terimlerinin değeri sürekli artan (\( a_k \lt a_{k + 1} \)) dizilere kesin monoton artan dizi denir.
Terimlerinin değeri sürekli azalan ya da sabit kalan (\( a_k \ge a_{k + 1} \)) dizilere monoton azalan dizi denir.
Terimlerinin değeri sürekli azalan (\( a_k \gt a_{k + 1} \)) dizilere kesin monoton azalan dizi denir.
Yukarıdaki dört durumdan herhangi birine uyan dizilere monoton dizi denir. Buna göre monoton bir dizi tanım kümesindeki bir aralıkta artan diğer bir aralıkta azalan olamaz.
Monotonluk Testi
Bir dizinin monotonluk ve artan/azalan olma durumu aşağıdaki üç testten biri kullanılarak belirlenebilir.
- Fark testi: Bu testte ardışık terimlerin farkının sıfırdan büyük ya da küçük olma durumuna bakılır.
- Oran testi: Pozitif terimli dizilerde kullanılabilecek bu testte, ardışık terimlerin oranının 1'den büyük ya da küçük olma durumuna bakılır.
- Türev testi: Genel terimi her yerde türevlenebilir bir fonksiyona karşılık gelen dizilerde kullanılabilecek bu testte, türev fonksiyonunun sıfırdan büyük ya da küçük olma durumuna bakılır.
Bu üç test aşağıdaki tabloda özetlenmiştir.
| Artan/Azalan | Fark Testi | Oran Testi | Türev Testi |
|---|---|---|---|
| Monoton artan | \( a_{n+1} - a_n \ge 0 \) | \( \dfrac{a_{n+1}}{a_n} \ge 1 \) | \( f'(x) \ge 0 \) |
| Kesin monoton artan | \( a_{n+1} - a_n \gt 0 \) | \( \dfrac{a_{n+1}}{a_n} \gt 1 \) | \( f'(x) \gt 0 \) |
| Monoton azalan | \( a_{n+1} - a_n \le 0 \) | \( \dfrac{a_{n+1}}{a_n} \le 1 \) | \( f'(x) \le 0 \) |
| Kesin monoton azalan | \( a_{n+1} - a_n \lt 0 \) | \( \dfrac{a_{n+1}}{a_n} \lt 1 \) | \( f'(x) \lt 0 \) |
Bu üç testin birer örnek üzerinden uygulamasını yapalım.
\( (a_n) = \dfrac{n - 1}{n} \) dizisinin monotonluk durumunu inceleyelim.
Fark testini kullanalım.
\( a_{n+1} - a_n = \dfrac{(n + 1) - 1}{n + 1} - \dfrac{n - 1}{n} \)
\( = \dfrac{n^2 - (n^2 - 1)}{n(n + 1)} \)
\( = \dfrac{1}{n(n + 1)} \gt 0 \)
Bu ifade her \( n \ge 1 \) için pozitif olduğu için \( a_n \) kesin monoton artan bir dizidir.
\( (b_n) = \dfrac{5^n}{(2n)!} \) dizisinin monotonluk durumunu inceleyelim.
Verilen dizinin terimleri her \( n \ge 1 \) için pozitiftir.
Oran testini kullanalım.
\( \dfrac{b_{n+1}}{b_n} = \dfrac{5^{n+1}}{[2(n + 1)]!} \cdot \dfrac{(2n)!}{5^n} \)
\( = \dfrac{5 \cdot 5^n}{(2n + 2)(2n + 1)(2n)!} \cdot \dfrac{(2n)!}{5^n} \)
\( = \dfrac{5}{(2n + 2)(2n + 1)} \lt 1 \)
Bu ifade her \( n \ge 1 \) için 1'den küçük olduğu için \( b_n \) kesin monoton azalan bir dizidir.
\( (c_n) = ne^{-2n} \) dizisinin monotonluk durumunu inceleyelim.
Türev testini kullanalım.
Dizinin genel teriminin karşılık geldiği sürekli ve her yerde türevlenebilir bir fonksiyon tanımlayalım.
\( f: [1, \infty) \to \mathbb{R} \)
\( f(x) = xe^{-2x} \)
\( f'(x) = e^{-2x} - 2xe^{-2x} \)
\( = e^{-2x}(1 - 2x) \lt 0 \)
Bu ifade her \( x \ge 1 \) için negatif olduğu için \( c_n \) kesin monoton azalan bir dizidir.
Sınırlı Diziler
Eğer her \( n \) için \( a_n \le M \) koşulunu sağlayan bir \( M \) sayısı varsa \( a_n \) dizisi üstten sınırlı bir dizidir ve bu \( M \) sayısı dizinin bir üst sınırıdır.
Eğer her \( n \) için \( m \le a_n \) koşulunu sağlayan bir \( m \) sayısı varsa \( a_n \) dizisi alttan sınırlı bir dizidir ve bu \( m \) sayısı dizinin bir alt sınırıdır.
Bir dizinin üstten (alttan) sınırlı olması, dizinin grafiğinde tüm noktaların altında (üstünde) kaldığı yatay bir çizgi çizebilmemiz anlamına gelir.
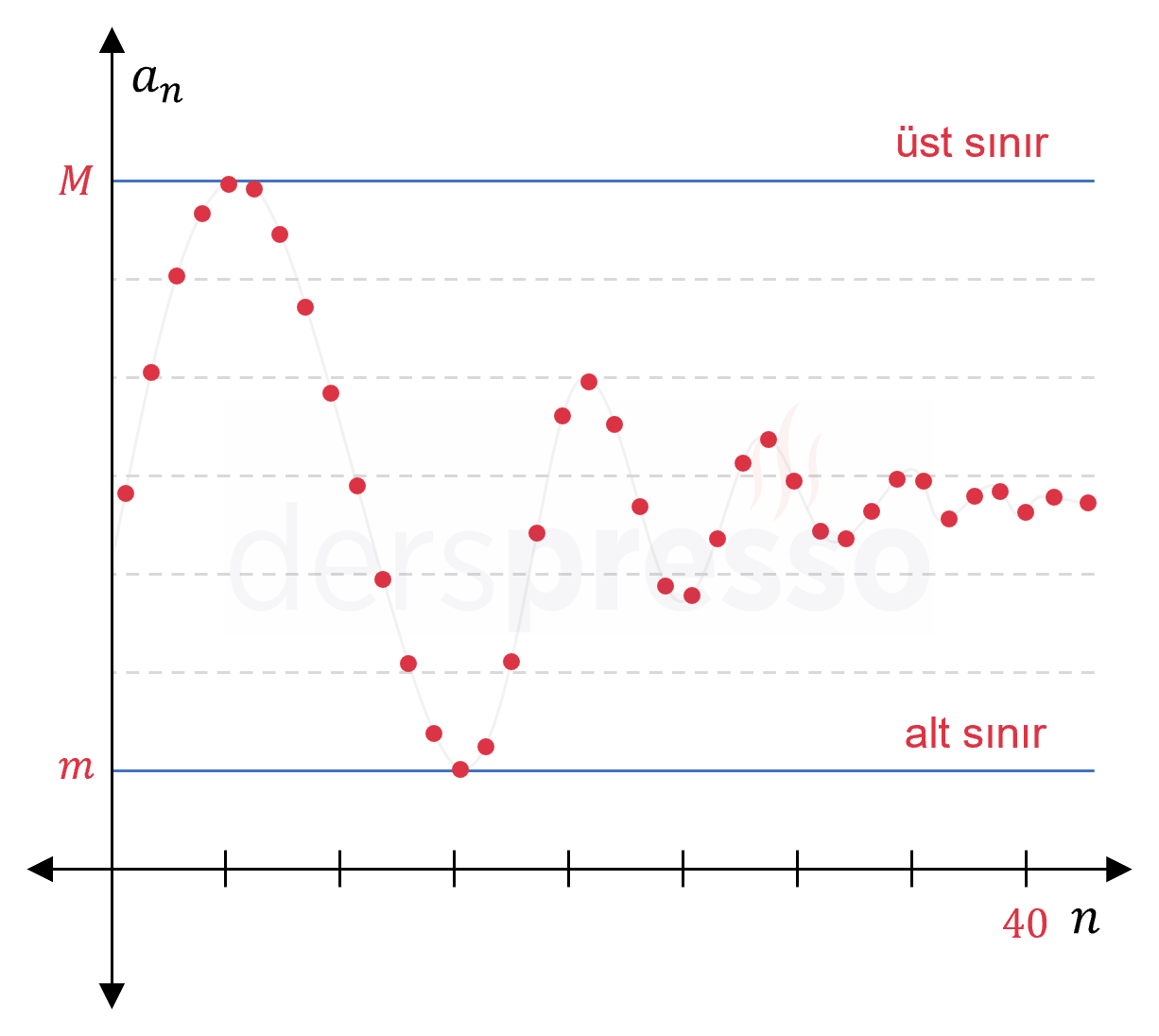
Hem üstten hem alttan sınırlı olan dizilere sınırlı dizi denir. Bu iki yönden en az birinde sınırlı olmayan dizilere sınırsız dizi denir.
Alterne Diziler
Ardışık terimlerinin işaretleri birbirinden farklı olan (pozitif ve negatif arasında değişerek ilerleyen) dizilere alterne dizi denir.
\( (a_n) = (-1)^n\ b_n \)
\( (a_n) = \left( -\dfrac{1}{2} \right)^n \)
\( = (-\frac{1}{2}, \frac{1}{4}, -\frac{1}{8}, \frac{1}{16}, \ldots) \)
\( (b_n) = \cos(n\pi) \)
\( = (-1, 1, -1, 1, \ldots) \)
Aşağıdaki dizilerin monotonluk durumlarını inceleyiniz.
(a) \( (a_n) = \dfrac{3n - 2}{5n - 1} \)
(b) \( (b_n) = 2^n \cdot n! \)
(c) \( (c_n) = \dfrac{n!}{n^n} \)
Çözümü Göster(a) seçeneği:
\( (a_n) = \dfrac{3n - 2}{5n - 1} \)
Fark testini kullanalım.
\( a_{n + 1} - a_n = \dfrac{3(n + 1) - 2}{5(n + 1) - 1} - \dfrac{3n - 2}{5n - 1} \)
\( = \dfrac{(3n + 1)(5n - 1) - (5n + 4)(3n - 2)}{(5n + 4)(5n - 1)} \)
\( = \dfrac{15n^2 + 2n - 1 - (15n^2 + 2n - 8)}{(5n + 4)(5n - 1)} \)
\( = \dfrac{7}{(5n + 4)(5n - 1)} \gt 0 \)
Bu ifade her \( n \ge 1 \) için pozitif olduğu için \( a_n \) kesin monoton artan bir dizidir.
(b) seçeneği:
\( (b_n) = 2^n \cdot n! \)
Verilen dizinin terimleri her \( n \ge 1 \) için pozitiftir.
Oran testini kullanalım.
\( \dfrac{b_{n + 1}}{b_n} = \dfrac{2^{n + 1} \cdot (n + 1)!}{2^n \cdot n!} \)
\( = \dfrac{2^n \cdot 2 \cdot (n + 1)n!}{2^n \cdot n!} \)
\( = 2(n + 1) \gt 1 \)
Bu ifade her \( n \ge 1 \) için 1'den büyük olduğu için \( b_n \) kesin monoton artan bir dizidir.
(c) seçeneği:
\( (c_n) = \dfrac{n!}{n^n} \)
Verilen dizinin terimleri her \( n \ge 1 \) için pozitiftir.
Oran testini kullanalım.
\( \dfrac{c_{n + 1}}{c_n} = \dfrac{\frac{(n + 1)!}{(n + 1)^{n + 1}}}{\frac{n!}{n^n}} \)
\( = \dfrac{(n + 1)!}{(n + 1)^{n + 1}} \cdot \dfrac{n^n}{n!} \)
\( = \dfrac{(n + 1) \cdot n! \cdot n^n}{(n + 1)^n \cdot (n + 1) \cdot n!} \)
\( = \dfrac{n^n}{(n + 1)^n} \)
\( = (\dfrac{n}{n + 1})^n \lt 1 \)
Bu ifade her \( n \ge 1 \) için 1'den küçük olduğu için \( c_n \) kesin monoton azalan bir dizidir.
Aşağıdaki dizilerin monotonluk durumlarını inceleyiniz.
(a) \( (a_n) = n\ln{n} - n \)
(b) \( (b_n) = \dfrac{2n + 1}{n + 2} \)
(c) \( (c_n) = \dfrac{n + 3}{2^n} \)
Çözümü Göster(a) seçeneği:
\( (a_n) = n\ln{n} - n \)
Türev testini kullanalım.
Dizinin genel teriminin karşılık geldiği sürekli ve türevlenebilir bir fonksiyon tanımlayalım.
\( f: [1, \infty] \to \mathbb{R} \)
\( f(x) = x\ln{x} - x \)
\( f'(x) = 1\ln{x} + x \cdot \dfrac{1}{x} - 1 \)
\( = \ln{x} \)
Bu ifade her \( x \ge 2 \) için sıfırdan büyüktür.
\( a_1 = 1\ln{1} - 1 = -1 \)
\( a_2 = 2\ln{2} - 2 \approx -0,61 \)
\( a_1 \lt a_2 \) olduğu için \( a_n \) kesin monoton artan bir dizidir.
(b) seçeneği:
\( (b_n) = \dfrac{2n + 1}{n + 2} \)
Türev testini kullanalım.
Dizinin genel teriminin karşılık geldiği sürekli ve türevlenebilir bir fonksiyon tanımlayalım.
\( f: [1, \infty] \to \mathbb{R} \)
\( f(x) = \dfrac{2x + 1}{x + 2} \)
\( f'(x) = \dfrac{2(x + 2) - 1(2x + 1)}{(x + 2)^2} \)
\( = \dfrac{3}{(x + 2)^2} \gt 0 \)
Bu ifade her \( x \ge 1 \) için sıfırdan büyük olduğu için \( b_n \) kesin monoton artan bir dizidir.
(c) seçeneği:
\( (c_n) = \dfrac{n + 3}{2^n} \)
Fark testini kullanalım.
\( c_{n + 1} - c_n = \dfrac{(n + 1) + 3}{2^{n + 1}} - \dfrac{n + 3}{2^n} \)
\( = \dfrac{n + 4}{2 \cdot 2^n} - \dfrac{n + 3}{2^n} \)
\( = \dfrac{n + 4 - 2(n + 3)}{2 \cdot 2^n} \)
\( = \dfrac{-(n + 2)}{2 \cdot 2^n} \lt 0 \)
Bu ifade her \( n \ge 1 \) için negatif olduğu için \( c_n \) kesin monoton azalan bir dizidir.