Üçgen Eşitsizliği
Üçgen eşitsizliği matematikteki en önemli eşitsizliklerden biridir ve matematiğin pek çok alanında kullanılır.
Geometride Üçgen Eşitsizliği
Geometride kullanılan üçgen eşitsizliğine göre, bir üçgenin herhangi bir kenarının uzunluğu diğer iki kenarının uzunlukları toplamından küçük, farkının mutlak değerinden ise büyüktür.
\( \abs{b - c} \lt a \lt b + c \)
\( \abs{a - c} \lt b \lt a + c \)
\( \abs{a - b} \lt c \lt a + b \)
İki kenar uzunluğu 5 ve 7 br olan bir üçgenin üçüncü kenar uzunluğu için değer aralığı:
\( \abs{5 - 7} \lt a \lt 5 + 7 \)
\( 2 \lt a \lt 12 \)
İSPATI GÖSTER
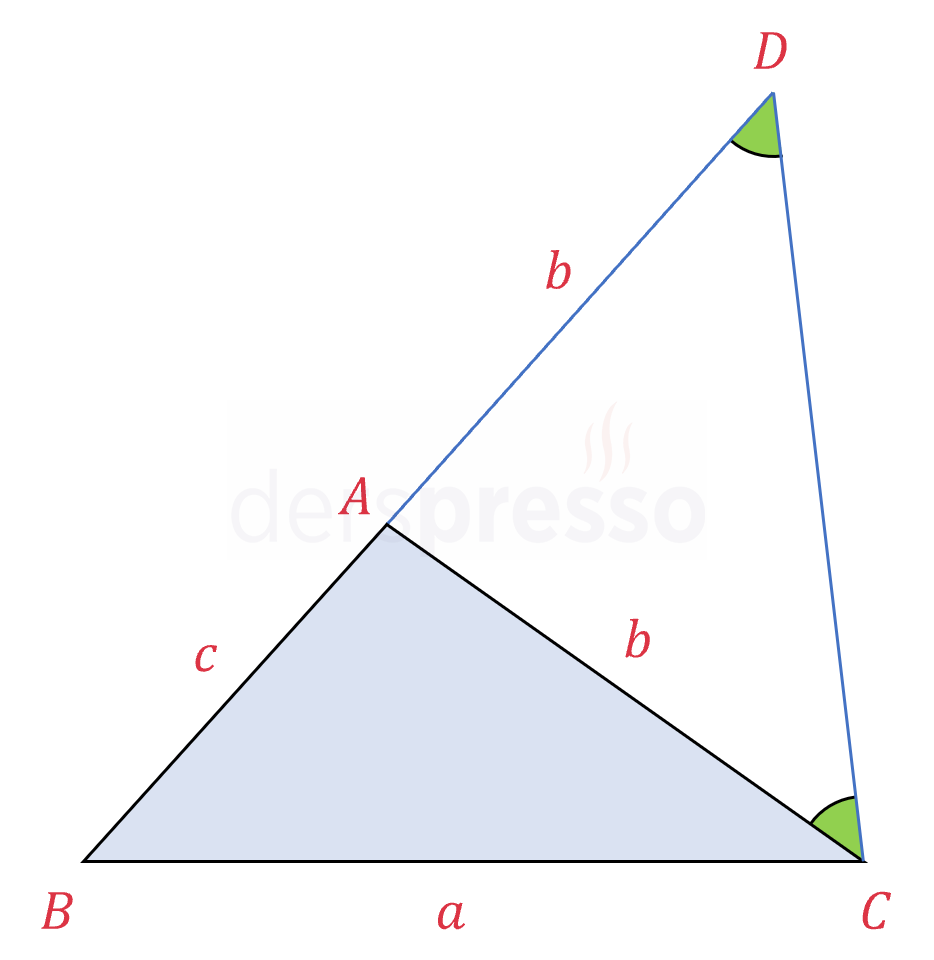
Şekildeki \( \overset{\triangle}{ABC} \) üçgeninin \( [BA] \) kenarını \( [AC] \) kenarı uzunluğunda \( b \) birim uzatalım (mavi çizgi). Bu doğru parçasının sonlandığı \( D \) noktası ile üçgenin \( C \) köşesini birleştirelim.
Oluşan \( \overset{\triangle}{ADC} \) üçgeni iki kenar uzunluğu eşit olduğu için bir ikizkenar üçgendir, dolayısıyla iki açısı da eşittir.
\( \abs{AD} = \abs{AC} = b \)
\( m(\widehat{ADC}) = m(\widehat{ACD}) \)
Bir üçgende daha geniş olan açının gördüğü kenar daha uzundur. Buna göre büyük üçgende \( \widehat{BCD} \) açısı \( \widehat{ACD} \) açısından büyük olduğu için bu açıya eşit \( \widehat{BDC} \) açısından da büyüktür, dolayısıyla \( [BD] \) kenarı \( [BC] \) kenarından uzun olur.
\( m(\widehat{ACD}) \lt m(\widehat{BCD}) \) olduğu için,
\( m(\widehat{BDC}) \lt m(\widehat{BCD}) \)
\( \abs{BC} \lt \abs{BD} \)
\( \abs{BC} \lt \abs{BA} + \abs{AD} \)
\( \abs{AD} = \abs{AC} = b \) olduğu için,
\( \abs{BC} \lt \abs{BA} + \abs{AC} \)
\( a \lt b + c \)
Buna göre \( [BC] \) kenarı için üçgen eşitsizliğinin sağ tarafını bulmuş oluruz. Aynı ispat diğer kenarlar için de tekrarlanabilir.
Üçgen eşitsizliğinin sol tarafını elde etmek için diğer iki kenara ait eşitsizliklerin sağ tarafını yazalım.
\( b \lt a + c \)
\( c \lt a + b \)
Bu eşitsizliklerde \( a \)'yı yalnız bırakalım.
\( b - c \lt a \)
\( c - b \lt a \Longrightarrow -(b - c) \lt a \)
\( a \) sayısı bir ifadenin hem pozitif hem de negatif işaretlisinden büyükse bu iki ifadenin daha büyüğüne eşit olan mutlak değerinden de büyüktür.
\( \abs{b - c} \lt a \)
Buna göre \( [BC] \) kenarı için üçgen eşitsizliğinin sol tarafını da bulmuş oluruz. Buna göre bu kenar için tüm eşitsizlik aşağıdaki şekilde olur.
\( \abs{b - c} \lt a \lt b + c \)
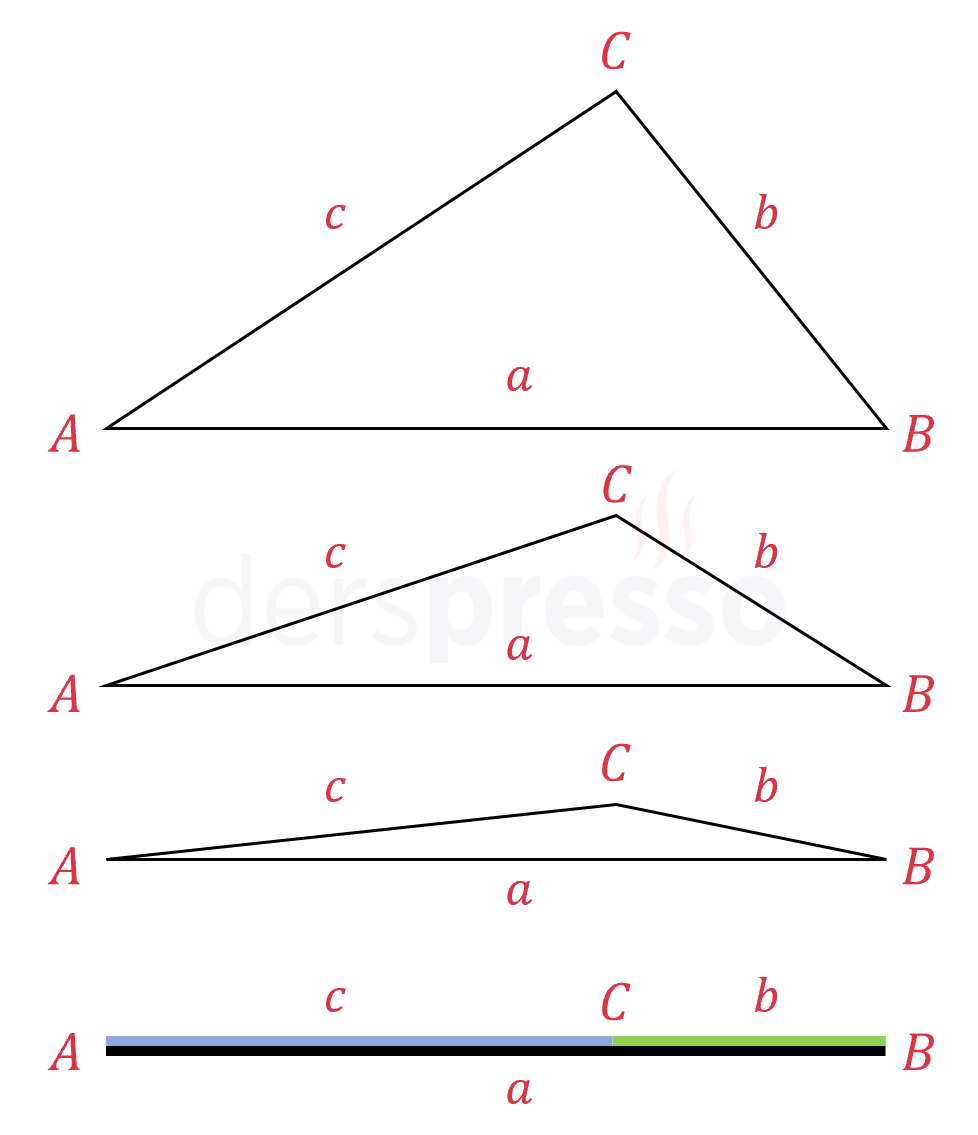
Üçgen eşitsizliğini yukarıdaki şekildeki üçgen üzerinden anlatmaya çalışalım. Bu eşitsizliğe göre, \( a \) uzunluğu \( b \) ve \( c \) uzunlukları toplamından küçüktür. Üçgenin \( C \) köşesi gitgide \( [AB] \) kenarına yaklaştırıldığında \( b + c \) uzunluğu gitgide küçülerek \( a \) uzunluğuna yaklaşır. \( a = b + c \) olduğu nokta \( C \) köşesinin \( [AB] \) doğru parçası üzerine geldiği noktadır, ancak bu durumda üç nokta üçgen değil bir doğru oluşturur, dolayısıyla \( C \) köşesi \( [AB] \) kenarına ne kadar yaklaşırsa yaklaşsın \( a \lt b + c \) eşitsizliği sağlanır.
Benzer şekilde \( b \) uzunluğu \( a \) ve \( c \) uzunlukları farkından büyüktür. Üçgenin \( C \) köşesi gitgide \( [AB] \) kenarına yaklaştırıldığında (\( c \) uzunluğu kısaldığı için) \( a - c \) uzunluğu gitgide büyüyerek gitgide küçülen \( b \) uzunluğuna yaklaşır. \( b = a - c \) olduğu nokta \( C \) köşesinin \( [AB] \) doğru parçası üzerine geldiği noktadır, ancak bu durumda üç nokta üçgen değil bir doğru oluştururlar, dolayısıyla \( C \) köşesi \( [AB] \) kenarına ne kadar yaklaşırsa yaklaşsın \( \abs{a - c} \lt b \) eşitsizliği sağlanır.
Reel Sayılarda Üçgen Eşitsizliği
Reel sayılardaki üçgen eşitsizliğine göre, iki sayının toplamının mutlak değeri sayıların mutlak değerlerinin toplamından büyük olamaz. Üçgen eşitsizliği iki sayının toplamının alabileceği değer için bir üst sınır belirler.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( a = -3, b = 4 \) ise,
\( \abs{-3 + 4} \le \abs{-3} + \abs{4} \)
\( 1 \le 7 \)
İSPATI GÖSTER
İspat 1:
Mutlak değerin tanımı gereği bir reel sayı ya mutlak değerinin kendisine ya da negatifine eşittir.
\( a = \abs{a} \) veya \( a = -\abs{a} \)
\( a \) sayısı bu iki değerden birine eşit olduğu için aşağıdaki eşitsizliği yazabiliriz.
\( -\abs{a} \le a \le \abs{a} \)
Benzer bir eşitsizliği \( b \) reel sayısı için yazalım.
\( -\abs{b} \le b \le \abs{b} \)
Bu iki eşitsizliği taraf tarafa toplayalım.
\( -\abs{a} - \abs{b} \le a + b \le \abs{a} + \abs{b} \)
\( -(\abs{a} + \abs{b}) \le a + b \le \abs{a} + \abs{b} \)
Mutlak değer eşitsizliklerinde gördüğümüz aşağıdaki kurala göre, bir sayının mutlak değeri \( c \) sayısından küçükse ya da ona eşitse bu sayı \( [-c, c] \) aralığındadır.
\( \abs{x} \le c \Longleftrightarrow -c \le x \le c \)
Bu ifadede \( x \) yerine \( a + b \) ve \( c \) yerine \( \abs{a} + \abs{b} \) yazarsak yukarıda bulduğumuz eşitsizliği elde ederiz.
\( -(\abs{a} + \abs{b}) \le a + b \le \abs{a} + \abs{b} \)
Bu eşitsizliği de \( \abs{x} \le c \) formunda aşağıdaki şekilde yazabiliriz.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
İspat 2:
Alternatif olarak \( a \) ve \( b \) sayılarının tüm olası durumları için eşitsizliğin sağlanıp sağlanmadığını kontrol edelim.
Durum 1: \( a \ge 0, b \ge 0 \)
Mutlak değer içindeki ifadeler sıfır ya da pozitif olduğu için mutlak değer dışına pozitif işaretli çıkar.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( a + b \le a + b \)
Taraflar birbirine eşit olduğu için \( \le \) eşitsizliği sağlanır.
Durum 2: \( a \lt 0, b \lt 0 \)
Mutlak değer içindeki ifadeler negatif olduğu için mutlak değer dışına negatif işaretli çıkar.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( -(a + b) \le (-a) + (-b) \)
\( -a - b \le -a - b \)
Taraflar birbirine eşit olduğu için \( \le \) eşitsizliği sağlanır.
Durum 3.1: \( a \ge 0, b \lt 0, \abs{a} \ge \abs{b} \)
\( a + b \) toplamı sıfır ya da pozitif olduğu için mutlak değer dışına pozitif işaretli çıkar.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( a + b \le a + (-b) \)
\( b \le -b \)
\( b \lt 0 \) olduğu için eşitsizliğin sol tarafı negatif, sağ tarafı pozitiftir, dolayısıyla eşitsizlik sağlanır.
Durum 3.2: \( a \ge 0, b \lt 0, \abs{a} \lt \abs{b} \)
\( a + b \) toplamı negatif olduğu için mutlak değer dışına negatif işaretli çıkar.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( -(a + b) \le a + (-b) \)
\( -a - b \le a - b \)
\( -a \le a \)
\( a \ge 0 \) olduğu için eşitsizliğin sol tarafı sıfır ya da negatif, sağ tarafı sıfır ya da pozitiftir, dolayısıyla \( \le \) eşitsizliği sağlanır.
Durum 4: \( a \lt 0, b \ge 0 \)
Bu durum \( a \) ve \( b \) sayıları aralarında yer değiştirmiş şekilde 3. durumun tekrarı olduğu için eşitsizlik yine sağlanır.
Buna göre üçgen eşitsizliği \( a \) ve \( b \)'nin her değeri için sağlanır.
Üçgen eşitsizliğinde \( b \) yerine \( -b \) yazıldığında aşağıdaki eşitsizlik elde edilir.
\( \abs{a - b} \le \abs{a} + \abs{b} \)
\( a = -2, \quad b = -4 \) ise,
\( \abs{-2 - (-4)} \le \abs{-2} + \abs{-4} \)
\( 2 \le 6 \)
İSPATI GÖSTER
\( \abs{a + b} \le \abs{a} + \abs{b} \)
İspatını verdiğimiz yukarıdaki üçgen eşitsizliğinde \( b \) yerine \( -b \) koyalım.
\( \abs{a + (-b)} \le \abs{a} + \abs{-b} \)
Bir sayının ve negatif işaretlisinin mutlak değerleri birbirine eşittir.
\( \abs{a - b} \le \abs{a} + \abs{b} \)
Ters Üçgen Eşitsizliği
Ters üçgen eşitsizliğine göre, iki sayının farkının mutlak değeri sayıların mutlak değerlerinin farkının mutlak değerinden küçük olamaz. Ters üçgen eşitsizliği iki sayının farkının alabileceği değer için bir alt sınır belirler.
\( \abs{\abs{a} - \abs{b}} \le \abs{a - b} \)
\( a = 5, \quad b = -4 \) ise,
\( \abs{\abs{5} - \abs{-4}} \le \abs{5 - (-4)} \)
\( 1 \le 9 \)
İSPATI GÖSTER
Üçgen eşitsizliğinde \( a \) yerine \( a - b \) yazalım.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( \abs{(a - b) + b} \le \abs{a - b} + \abs{b} \)
\( \abs{a} \le \abs{a - b} + \abs{b} \)
Terimleri yeniden düzenleyelim.
\( \abs{a} - \abs{b} \le \abs{a - b} \)
Şimdi de üçgen eşitsizliğinde \( b \) yerine \( b - a \) yazalım.
\( \abs{a + b} \le \abs{a} + \abs{b} \)
\( \abs{a + (b - a)} \le \abs{a} + \abs{b - a} \)
\( \abs{b} \le \abs{a} + \abs{b - a} \)
Terimleri yeniden düzenleyelim.
\( -\abs{b - a} \le \abs{a} - \abs{b} \)
\( \abs{b - a} \) ifadesinin içini -1 ile çarpalım.
\( -\abs{a - b} \le \abs{a} - \abs{b} \)
Mutlak değer eşitsizliklerinde gördüğümüz aşağıdaki kurala göre, bir sayının mutlak değeri \( c \) sayısından küçükse ya da ona eşitse bu sayı \( [-c, c] \) aralığındadır.
\( \abs{x} \le c \Longleftrightarrow -c \le x \le c \)
Buna göre, yukarıda elde ettiğimiz iki eşitsizlikte \( \abs{a} - \abs{b} \) ifadesi pozitif ve negatif \( \abs{a - b} \) aralığında olduğu için bu eşitsizliği aşağıdaki şekilde yazabiliriz.
\( -\abs{a - b} \le \abs{a} - \abs{b} \le \abs{a - b} \)
\( \abs{\abs{a} - \abs{b}} \le \abs{a - b} \)
Genelleştirilmiş Üçgen Eşitsizliği
Üçgen eşitsizliği ikiden fazla reel sayı içeren durumlara da uygulanabilir. Buna göre \( n \) tane sayının toplamının mutlak değeri sayıların mutlak değerlerinin toplamından büyük olamaz.
\( \abs{a_1 + a_2 + \ldots + a_n} \le \) \( \abs{a_1} + \abs{a_2} + \ldots + \abs{a_n} \)
\( a_1 = -2, \quad a_2 = 5, \quad a_3 = -7 \) ise,
\( \abs{-2 + 5 + (-7)} \le \abs{-2} + \abs{5} + \abs{-7} \)
\( 4 \le 14 \)
Genelleştirilmiş üçgen eşitsizliğinin ispatı, başlangıç adımı olarak temel üçgen eşitsizliği kullanılarak tümevarım yöntemiyle yapılabilir.
Yukarıda \( ABC \) üçgeni verilmiştir.
\( \hat{C} \) açısı geniş açı olduğuna göre, \( x \)'in alabileceği tam sayı değerlerinin toplamı nedir?
Çözümü GösterVerilen bilgiler doğrultusunda üçgen eşitsizliği oluşturalım.
\( \abs{7x - x} \lt 96 \lt 7x + x \)
\( 6x \lt 96 \lt 8x \)
Eşitsizlikleri ayrı ayrı çözelim.
\( 6x \lt 96 \Longrightarrow x \lt 16 \)
\( 96 \lt 8x \Longrightarrow 12 \lt x \)
\( 12 \lt x \lt 16 \)
\( \hat{C} \) geniş açı olduğuna göre, üçgendeki en uzun kenar \( \abs{AB} \) olmalıdır. Bulduğumuz değer aralığındaki hangi \( x \) tam sayı değerlerinin bunu sağlayıp sağlamadığını kontrol edelim.
\( x = 13 \Longrightarrow 7x = 91 \)
\( x = 14 \Longrightarrow 7x = 98 \)
\( x = 15 \Longrightarrow 7x = 105 \)
\( 91 \le 96 \) olduğundan \( x = 13 \) için istenen durum sağlanmamaktadır.
Bu durumda \( x \)'in alabileceği tam sayı değerler \( \{14, 15\} \) olur.
Kenar uzunlukları birer tam sayı ve çevre uzunluğu 30 cm olacak şekilde oluşturulabilecek ikizkenar üçgenlerin, farklı uzunluktaki kenarının uzunluğunun alabileceği en büyük ve en küçük değerler arasındaki fark en çok kaç olabilir?
Çözümü Gösterİkizkenar üçgenin eşit uzunluktaki kenarlarının uzunluğuna \( a \) cm, diğer kenarının uzunluğuna \( b \) cm diyelim.
Üçgen eşitsizliğine göre; bir üçgenin herhangi bir kenarının uzunluğu, diğer iki kenarının uzunlukları toplamından küçük, farkının mutlak değerinden büyük olmalıdır.
Bu kuralı uzunluğu \( b \) olan kenara uygulayalım.
\( \abs{a - a} \lt b \lt a + a \)
\( 0 \lt b \lt 2a \)
İkizkenar üçgenin çevre uzunluğu 30 cm'dir.
\( 2a + b = 30 \)
\( b = 30 - 2a \)
Bu değeri yukarıda elde ettiğimiz eşitsizlikte yerine yazalım.
\( 0 \lt 30 - 2a \lt 2a \)
\( 2a \lt 30 \lt 4a \)
\( a \lt 15 \lt 2a \)
Bu eşitsizliği iki ayrı eşitsizlik olarak inceleyelim ve \( a \) değer aralığını bulalım.
\( a \lt 15 \)
\( 15 \lt 2a\Longrightarrow 7,5 \lt a \)
Buna göre \( a \) değer aralığı aşağıdaki gibi bulunur.
\( 7,5 \lt a \lt 15 \)
\( a \)'nın bu aralıkta alabileceği tam sayı değerleri 8, 9, 10, 11, 12, 13 ve 14'tür.
\( a \) bu değerleri alırken, \( 2a + b = 30 \) denklemine göre \( b \) sırasıyla 14, 12, 10, 8, 6, 4, 2 değerlerini alır.
\( b \) değerinin alabileceği en büyük ve en küçük değerler arasındaki fark \( 14 - 2 = 12 \) olarak bulunur.
\( 2 + \dfrac{\abs{5x} + \abs{5y}}{\abs{3x + 3y}} \) ifadesinin alabileceği en küçük değer kaçtır?
Çözümü Göster\( 2 + \dfrac{\abs{5x} + \abs{5y}}{\abs{3(x + y)}} \)
Mutlak değer içindeki pozitif katsayı mutlak değer dışına olduğu gibi çıkar.
\( = 2 + \dfrac{5\abs{x} + 5\abs{y}}{3\abs{x + y}} \)
\( = 2 + \dfrac{5(\abs{x} + \abs{y})}{3\abs{x + y}} \)
\( = 2 + \dfrac{5}{3} \cdot \dfrac{\abs{x} + \abs{y}}{\abs{x + y}} \)
Reel sayılardaki üçgen eşitsizliğine göre, iki sayının toplamının mutlak değeri sayıların mutlak değerlerinin toplamından büyük olamaz.
\( \abs{x + y} \le \abs{x} + \abs{y} \)
Buna göre verilen ifade en küçük değerini \( \abs{x + y} = \abs{x} + \abs{y} \) olduğunda alır.
\( = 2 + \dfrac{5}{3} \cdot \dfrac{\abs{x + y}}{\abs{x + y}} \)
\( = 2 + \dfrac{5}{3} = \dfrac{11}{3} \) bulunur.