Mutlak Değer Denklemleri
Mutlak değer içinde bir değişkenin olduğu denklemlere mutlak değer denklemi denir. Mutlak değer denklemleri aşağıda detaylandıracağımız yöntemler kullanılarak çözülebilir.
Bu bölümdeki tüm denklem tiplerinde geçerli olmak üzere,
\( x, y, z, c \in \mathbb{R} \)
\( \abs{x} = c \) Formundaki Denklemler
Mutlak değer içinde bir ifade negatif bir sayıya eşitse mutlak değer işleminin sonucu negatif olamayacağı için çözüm kümesi boş kümedir.
\( \abs{x} = c \) denkleminde,
\( c \lt 0 \) ise \( x \in \emptyset \)
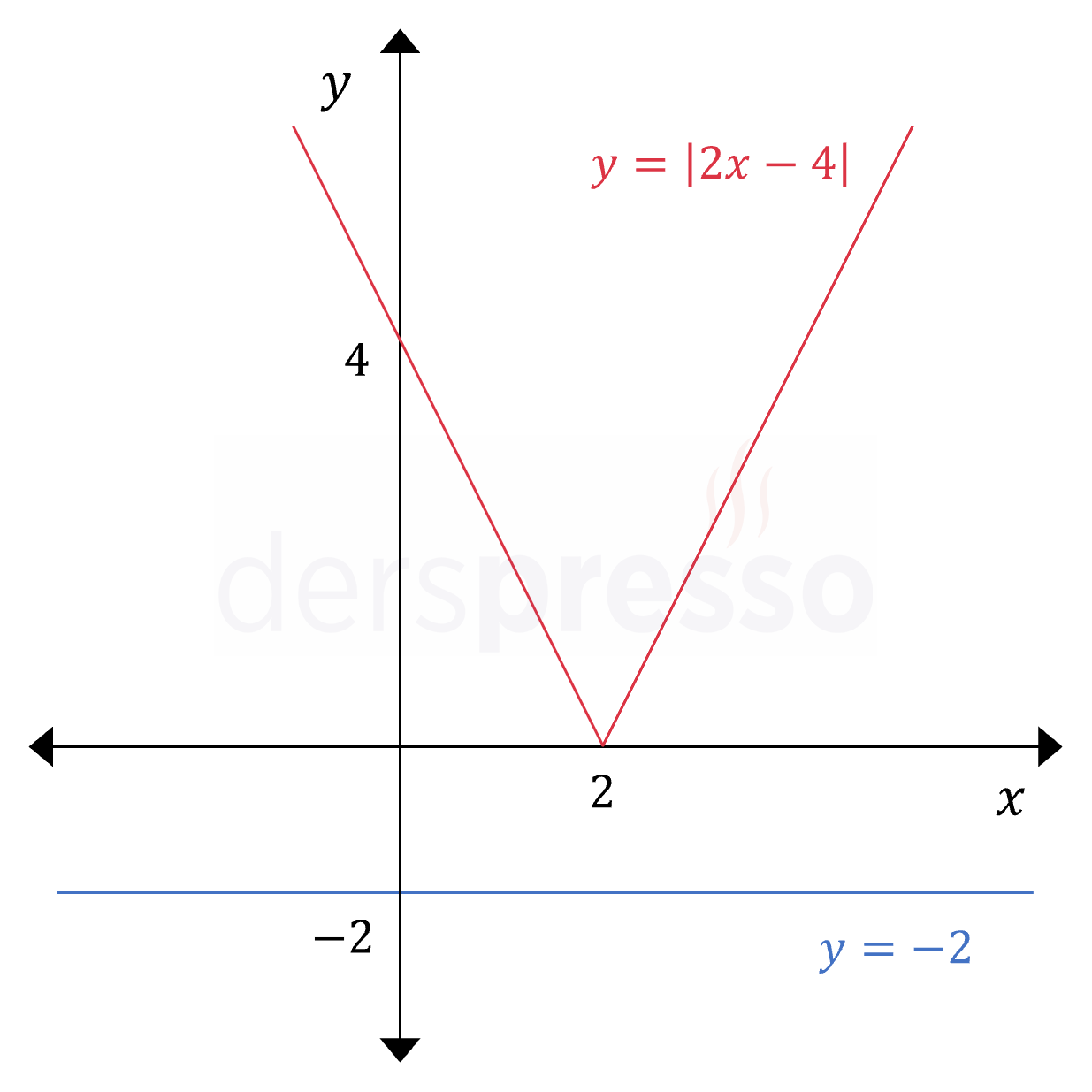
\( \abs{2x - 4} = -2 \)
Çözüm kümesi: \( x \in \emptyset \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların hiçbir noktada kesişmediklerini görebiliriz.
Mutlak değer içinde bir ifade sıfıra eşitse mutlak değer içindeki ifade de sıfıra eşittir.
\( \abs{x} = c \) denkleminde,
\( c = 0 \) ise \( x = 0 \)
\( \abs{2x - 4} = 0 \) ise,
\( 2x - 4 = 0 \)
Çözüm kümesi: \( x = 2 \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların sadece \( x = 2 \) noktasında kesiştiklerini görebiliriz.

Mutlak değer içinde bir ifade pozitif bir \( c \) sayısına eşitse \( x = c \) ve \( x = -c \) denklemleri ayrı ayrı çözülür. Her iki denklem \( x \) için farklı olası değerleri temsil ettiği için, çözüm kümesi bu iki denklemin çözüm kümelerinin birleşimi olur.
\( \abs{x} = c \) denkleminde,
\( c \gt 0 \) ise \( x = c \) ya da \( x = -c \)
\( \abs{2x - 4} = 2 \) ise,
Durum 1: \( 2x - 4 = 2 \)
\( x = 3 \)
Durum 2: \( 2x - 4 = -2 \)
\( x = 1 \)
Çözüm kümesi bu iki denklemin çözüm kümelerinin birleşimidir.
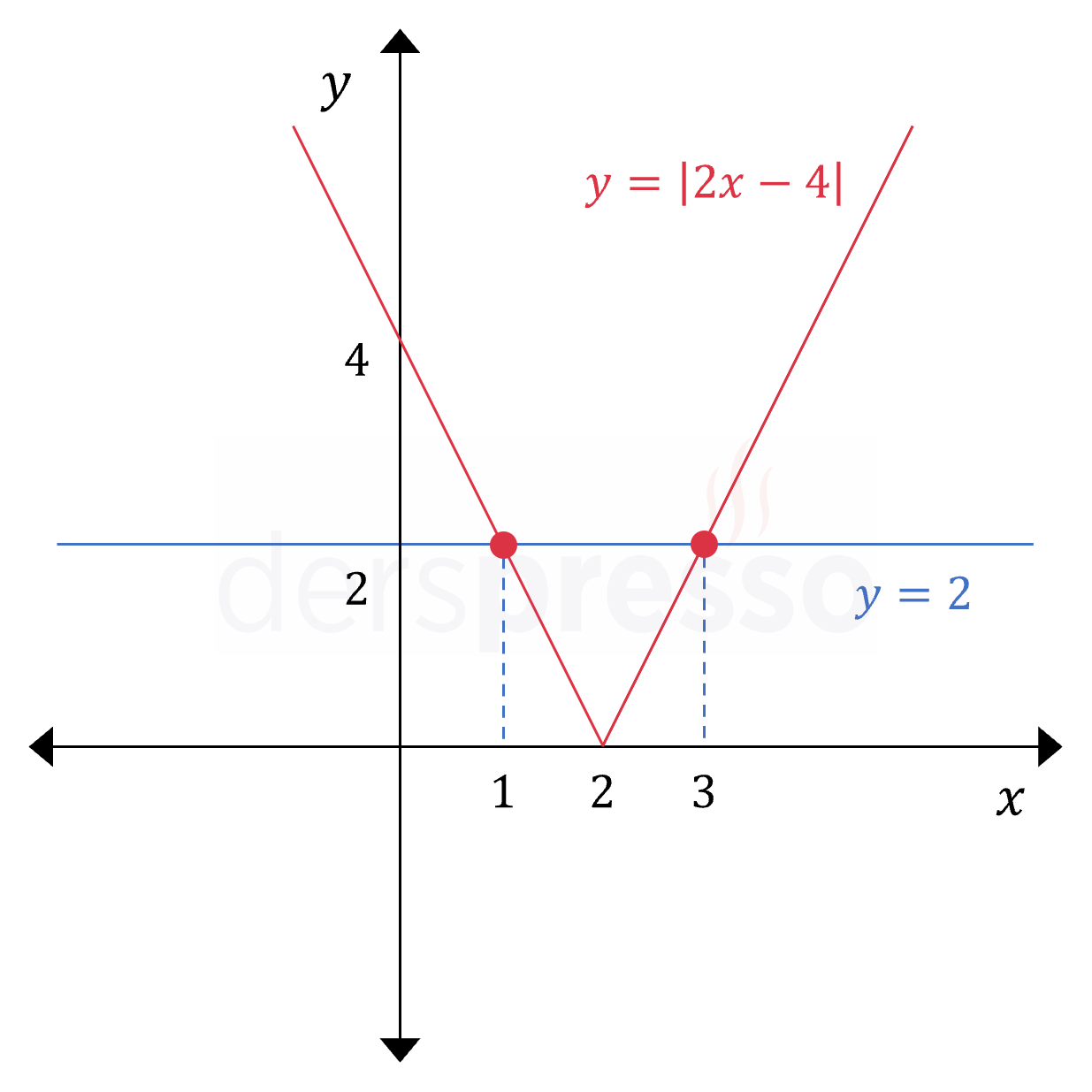
Çözüm kümesi: \( x \in \{ 1, 3 \} \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların \( x = 1 \) ve \( x = 3 \) noktalarında kesiştiklerini görebiliriz.
\( \abs{x} = y \) Formundaki Denklemler
Mutlak değer içinde bir ifade mutlak değer içinde olmayan bir ifadeye eşitse \( x = y \) ve \( x = -y \) denklemleri ayrı ayrı çözülür. Çözüm kümesi bu iki denklemin çözüm kümelerinin birleşimi olur.
Bu denklem tipinde elde edilen sonuçlar orijinal denklemde yerine konarak sağlaması yapılmalıdır, bu değerlerden mutlak değer içinde olmayan ifadeyi negatif yapan değerler orijinal denklemi sağlamayacaktır.
\( \abs{x} = y \) ise,
\( x = y \) veya \( x = -y \)
\( \abs{2x - 4} = 3x - 1 \) ise,
Durum 1: \( 2x - 4 = 3x - 1 \)
\( x = -3 \)
Durum 2: \( 2x - 4 = -(3x - 1) \)
\( 2x - 4 = 1 - 3x \)
\( x = 1 \)
Bu değerleri orijinal denklemde yerine koyduğumuzda sadece \( x = 1 \)'in denklemi sağladığını görürüz.
Çözüm kümesi: \( x \in \{ 1 \} \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların sadece \( x = 1 \) noktasında kesiştiklerini ve \( x = -3 \)'ün gerçek bir çözüm olmadığını görebiliriz.

\( \abs{x} = \abs{y} \) Formundaki Denklemler
Bu denklem tipinde eşitliğin iki tarafı da negatif olamayacağı için denklem çözümünde orijinal denklemi sağlamayan çözümler oluşmaz. Bu nedenle bulunan \( x \) değerleri sağlaması yapılmadan çözüm kümesine dahil edilebilir.
Yöntem 1
Mutlak değerli iki ifade birbirine eşitse \( x = y \) ve \( x = -y \) olacak şekilde iki denklem yazılır ve ayrı ayrı çözülür. Çözüm kümesi bu iki denklemin çözüm kümelerinin birleşimidir.
\( \abs{x} = \abs{y} \) ise,
\( x = y \) veya \( x = -y \)
\( \abs{x - 5} = \abs{2x - 4} \) ise,
Durum 1: \( x - 5 = 2x - 4 \)
\( x = -1 \)
Durum 2: \( x - 5 = -(2x - 4) \)
\( x - 5 = 4 - 2x \)
\( x = 3 \)
Çözüm kümesi bu iki denklemin çözüm kümelerinin birleşimidir.
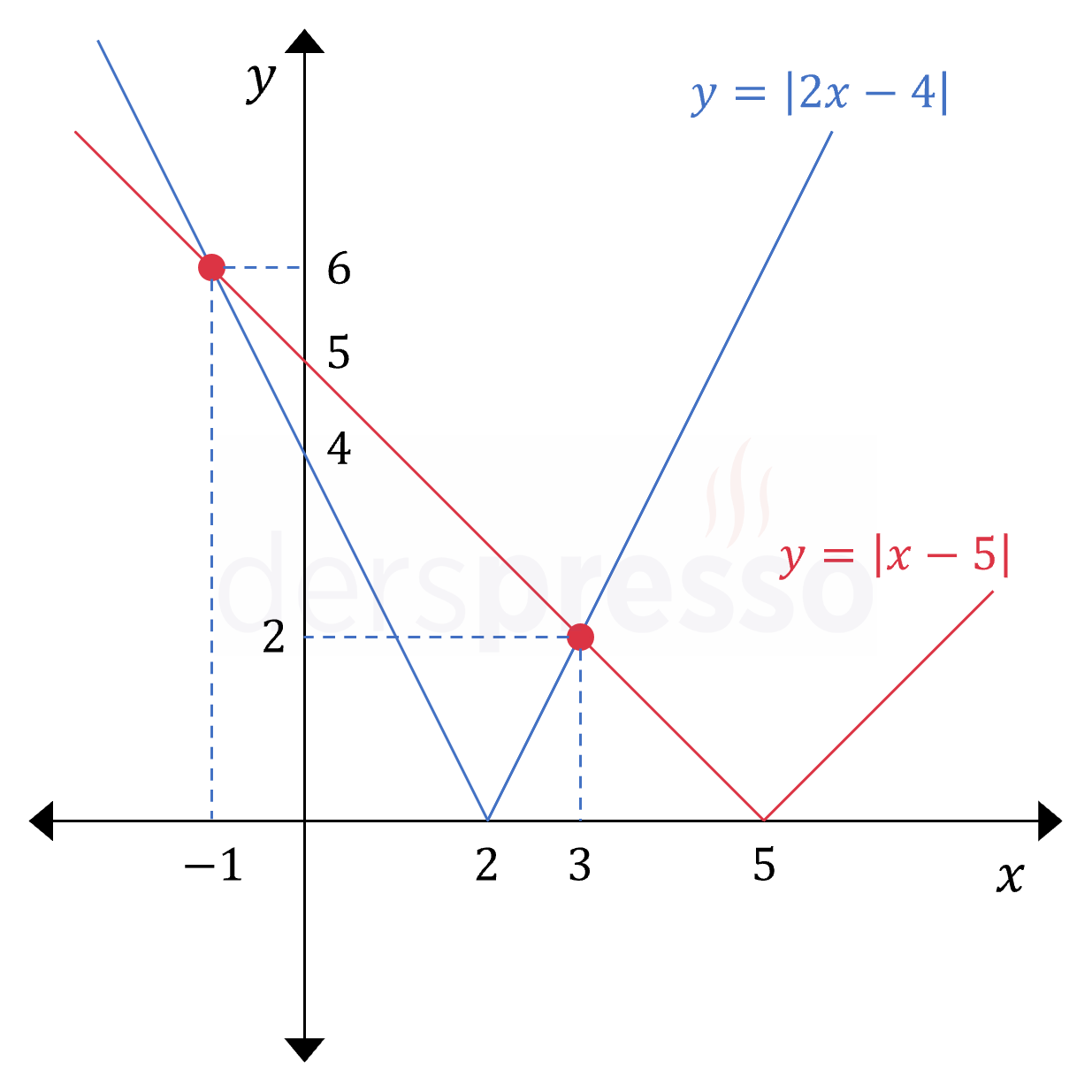
Çözüm kümesi: \( x \in \{ -1, 3 \} \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların \( x = -1 \) ve \( x = 3 \) noktalarında kesiştiklerini görebiliriz.
Yöntem 2
İkinci bir yöntem olarak eşitliğin her iki tarafının karesi alınarak denklem tek adımda çözülebilir.
Birinci yöntemde kullandığımız örneği şimdi bu yöntemle çözelim.
\( \abs{x - 5} = \abs{2x - 4} \) ise,
\( {\abs{x - 5}}^2 = {\abs{2x - 4}}^2 \)
\( x^2 - 10x + 25 = 4x^2 - 16x + 16 \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( 3x^2 - 6x - 9 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( 3(x + 1)(x - 3) = 0 \)
Çözüm kümesi: \( x \in \{ -1, 3 \} \)
Diğer Denklemler
Yukarıdaki \( \abs{x} = c \), \( \abs{x} = y \) ve \( \abs{x} = \abs{y} \) formundaki denklemlerin ortak özelliği, mutlak değerli ifadelerin eşitliğin bir ya da her iki tarafında yalnız bırakılabilmesiydi. Bunu yapmanın mümkün olmadığı bazı denklem formları aşağıdaki gibidir.
\( \abs{x} + \abs{y} = c \)
\( \abs{x} + \abs{y} = z \)
\( \abs{x + 1} + \abs{2x - 1} = 3 \)
\( \abs{2x + 2} - \abs{x - 3} = x + 1 \)
Bu tip denklemler her mutlak değerli ifade için kritik noktalar belirlenerek, bu kritik noktalar arasında kalan her aralık için ayrı ayrı çözülür. Her aralık için denklem çözülürken mutlak değerli ifadeler ilgili aralıktaki işaretlerine göre mutlak değerden çıkarılır. Denklemin çözüm kümesi her aralık için bulunan çözümlerin birleşim kümesi olur.
\( \abs{2x - 4} + \abs{x - 6} = 7 \) denklemini çözelim.
Mutlak değerli ifadelerin kritik noktalarını bulalım.
\( 2x - 4 = 0 \Longrightarrow x = 2 \)
\( x - 6 = 0 \Longrightarrow x = 6 \)
Bu kritik noktalar reel sayılar kümesini aşağıdaki gibi üç aralığa böler.

(1) \( -\infty \lt x \lt 2 \)
(2) \( 2 \le x \lt 6 \)
(3) \( 6 \le x \lt \infty \)
Her aralık için mutlak değer içindeki ifadeleri mutlak değerde çıkaralım ve denklemi çözelim.
(1) \( -\infty \lt x \lt 2 \) aralığı için:
\( |\underbrace{2x - 4}_{-}| + |\underbrace{x - 6}_{-}| = 7 \)
\( -(2x - 4) - (x - 6) = 7 \)
\( -3x + 10 = 7 \)
\( x = 1 \Longrightarrow \) Değer ilgili aralıkta olduğu için geçerli bir çözümdür.
(2) \( 2 \le x \lt 6 \) aralığı için:
\( |\underbrace{2x - 4}_{+}| + |\underbrace{x - 6}_{-}| = 7 \)
\( (2x - 4) - (x - 6) = 7 \)
\( x + 2 = 7 \)
\( x = 5 \Longrightarrow \) Değer ilgili aralıkta olduğu için geçerli bir çözümdür.
(3) \( 6 \le x \lt \infty \) aralığı için:
\( |\underbrace{2x - 4}_{+}| + |\underbrace{x - 6}_{+}| = 7 \)
\( (2x - 4) + (x - 6) = 7 \)
\( 3x - 10 = 7 \)
\( x = \frac{17}{3} \Longrightarrow \) Değer ilgili aralıkta olmadığı için geçersiz bir çözümdür.
Buna göre denklemin çözüm kümesi (1). ve (2). aralıklarda bulduğumuz değerlerden oluşur.
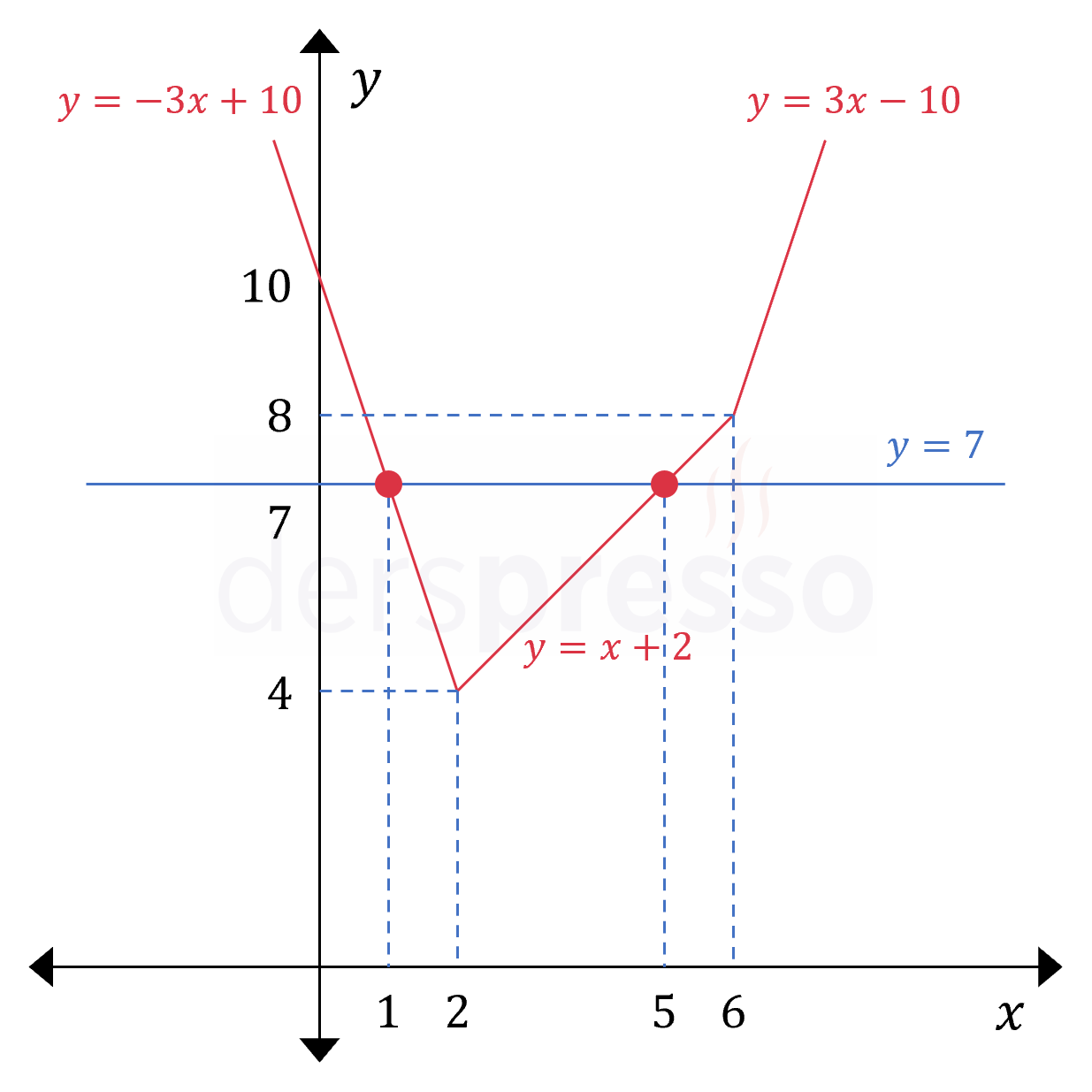
Çözüm kümesi: \( x \in \{ 1, 5 \} \)
Aşağıdaki grafikte denklemin sol tarafını parçalı fonksiyon şeklinde yazdığımızda oluşan grafik ve sağ tarafını temsil eden doğrunun \( x = 1 \) ve \( x = 5 \) noktalarında kesiştiklerini görebiliriz.
İç İçe Mutlak Değerli İfadeler
Denklem iç içe birden fazla mutlak değerli ifade içeriyorsa yukarıda paylaştığımız yöntemler en dıştaki mutlak değerden başlayıp içtekine doğru ilerleyerek birden fazla adımda uygulanabilir.
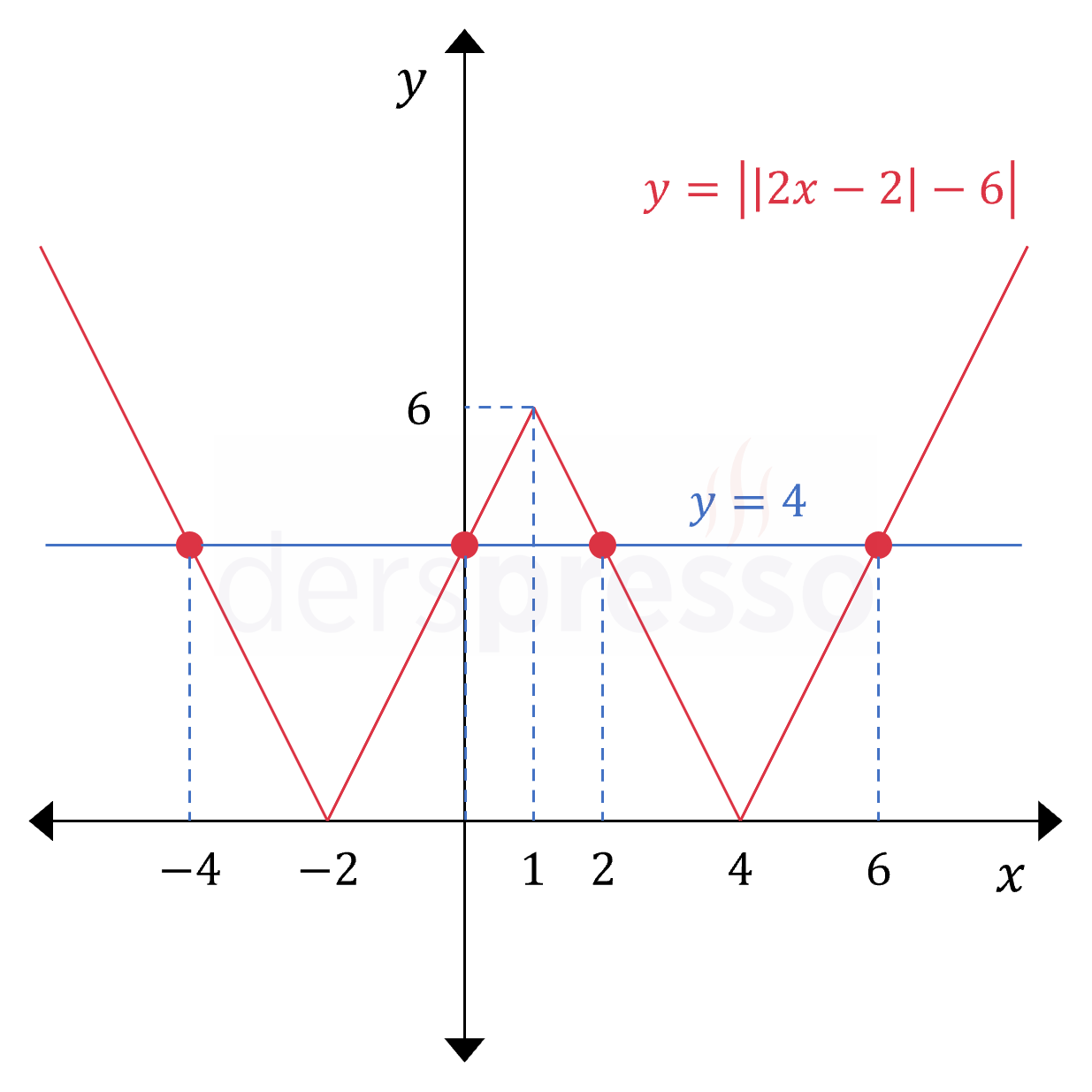
\( \abs{\abs{2x - 2} - 6} = 4 \) denklemini çözelim.
İlk adımda en dıştaki mutlak değerli ifadenin içini +4 ve -4'e eşitleyelim ve iki denklemi ayrı ayrı çözelim.
Denklem 1: \( \abs{2x - 2} - 6 = 4 \)
\( \abs{2x - 2} = 10 \)
Şimdi bu mutlak değerli ifadenin içini +10 ve -10'a eşitleyelim ve iki denklemi ayrı ayrı çözelim.
Denklem 1.1: \( 2x - 2 = 10 \)
\( x = 6 \)
Denklem 1.2: \( 2x - 2 = -10 \)
\( x = -4 \)
Denklem 2: \( \abs{2x - 2} - 6 = -4 \)
\( \abs{2x - 2} = 2 \)
Şimdi bu mutlak değerli ifadenin içini +2 ve -2'ye eşitleyelim ve iki denklemi ayrı ayrı çözelim.
Denklem 2.1: \( 2x - 2 = 2 \)
\( x = 2 \)
Denklem 2.2: \( 2x - 2 = -2 \)
\( x = 0 \)
Bu durumda denklemin çözüm kümesi aşağıdaki gibi olur.
Çözüm kümesi: \( x \in \{ -4, 0, 2, 6 \} \)
Aşağıdaki grafikte denklemin sol ve sağ tarafını temsil eden doğruların bulduğumuz bu dört noktada kesiştiklerini görebiliriz.
\( \abs{x} + \abs{y} = 0 \) Formundaki Denklemler
İki ya da daha fazla sayıda mutlak değerli ifadenin toplamı sıfır ise her ifade ayrı ayrı sıfıra eşittir. Bunun sebebi, herhangi bir mutlak değerli ifade sıfırdan büyük olursa ifadelerin toplamının da sıfırdan büyük olacak olmasıdır.
\( \abs{x} + \abs{y} + \abs{z} = 0 \) ise,
Çözüm kümesi: \( (x, y, z) = (0, 0, 0) \)
\( \abs{x + 2} + \abs{2y - 6} + \abs{z} = 0 \) ise,
\( x + 2 = 0 \Longrightarrow x = -2 \)
\( 2y - 6 = 0 \Longrightarrow y = 3 \)
\( z = 0 \Longrightarrow z = 0 \)
Çözüm kümesi: \( (x, y, z) = (-2, 3, 0) \)
Aşağıdaki eşitlikleri sağlayan \( x \) değer aralıklarını bulunuz.
(a) \( \abs{-2x} = -2x \)
(b) \( \abs{2x + 5} = -2x - 5 \)
(c) \( \abs{-8 + 3x} = 3x - 8 \)
Çözümü Göster(a) seçeneği:
\( \abs{-2x} = -2x \)
Mutlak değer içindeki ifade mutlak değerden olduğu gibi çıktığına göre değeri sıfır ya da pozitiftir.
\( -2x \ge 0 \)
\( x \le 0 \)
(b) seçeneği:
\( \abs{2x + 5} = -2x - 5 = -(2x + 5) \)
Mutlak değer içindeki ifade mutlak değerden negatif işaretli çıktığına göre değeri sıfır ya da negatiftir.
\( 2x + 5 \le 0 \)
\( x \le -\dfrac{5}{2} \)
(c) seçeneği:
\( \abs{-8 + 3x} = 3x - 8 = -8 + 3x \)
Mutlak değer içindeki ifade mutlak değerden olduğu gibi çıktığına göre değeri sıfır ya da pozitiftir.
\( -8 + 3x \ge 0 \)
\( x \ge \dfrac{8}{3} \)
Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( \abs{6 - 2x} + \abs{3x - 9} = 25 \)
(b) \( \abs{5 - 5x} - \abs{x - 1} = 72 \)
(c) \( 4\abs{7 - x} + \abs{2x - 14} = 90 \)
Çözümü Göster(a) seçeneği:
\( \abs{6 - 2x} + \abs{3x - 9} = 25 \)
\( \abs{2(3 - x)} + \abs{3(x - 3)} = 25 \)
Mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( 2\abs{3 - x} + 3\abs{x - 3} = 25 \)
\( \abs{3 - x} \) ve \( \abs{x - 3} \) ifadeleri birbirine eşittir.
\( 2\abs{x - 3} + 3\abs{x - 3} = 25 \)
\( 5\abs{x - 3} = 25 \)
\( \abs{x - 3} = 5 \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( x - 3 = 5 \)
\( x = 8 \)
Durum 2:
\( x - 3 = -5 \)
\( x = -2 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-2, 8\} \)
(b) seçeneği:
\( \abs{5 - 5x} - \abs{x - 1} = 72 \)
\( \abs{5(1 - x)} - \abs{x - 1} = 72 \)
Mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( 5\abs{1 - x} - \abs{x - 1} = 72 \)
\( \abs{1 - x} \) ve \( \abs{x - 1} \) ifadeleri birbirine eşittir.
\( 5\abs{x - 1} - \abs{x - 1} = 72 \)
\( 4\abs{x - 1} = 72 \)
\( \abs{x - 1} = 18 \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( x - 1 = 18 \)
\( x = 19 \)
Durum 2:
\( x - 1 = -18 \)
\( x = -17 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-17, 19\} \)
(c) seçeneği:
\( 4\abs{7 - x} + \abs{2x - 14} = 90 \)
\( 4\abs{7 - x} + \abs{2(x - 7)} = 90 \)
Mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( 4\abs{7 - x} + 2\abs{x - 7} = 90 \)
\( \abs{7 - x} \) ve \( \abs{x - 7} \) ifadeleri birbirine eşittir.
\( 4\abs{x - 7} + 2\abs{x - 7} = 90 \)
\( 6\abs{x - 7} = 90 \)
\( \abs{x - 7} = 15 \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( x - 7 = 15 \)
\( x = 22 \)
Durum 2:
\( x - 7 = -15 \)
\( x = -8 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-8, 22\} \)
\( \abs{\sqrt[3]{x} + \sqrt[3]{-8}} = 3 \)
eşitliğini sağlayan \( x \) değerlerinin toplamı kaçtır?
Çözümü Göster\( \sqrt[3]{-8} = -2 \)
\( \abs{\sqrt[3]{x} - 2} = 3 \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( \sqrt[3]{x} - 2 = 3 \)
\( \sqrt[3]{x} = 5 \)
\( x = 125 \)
Durum 2:
\( \sqrt[3]{x} - 2 = -3 \)
\( \sqrt[3]{x} = -1 \)
\( x = -1 \)
Eşitliği sağlayan \( x \) değerlerinin toplamı \( 125 + (-1) = 124 \) olarak bulunur.
\( \abs{x + k} = 40 \)
eşitliğini sağlayan \( x \) değerleri toplamı 22 olduğuna göre, \( k \) kaçtır?
Çözümü GösterBu denklem iki durumda sağlanır.
Durum 1:
\( x + k = 40 \)
\( x = 40 - k \)
Durum 2:
\( x + k = -40 \)
\( x = -40 - k \)
Bu iki çözümün toplamı 22 olarak veriliyor.
\( (40 - k) + (-40 - k) = 22 \)
\( -2k = 22 \)
\( k = -11 \) bulunur.
\( x, y \in \mathbb{R} \) olmak üzere,
\( \abs{3x - 6} = 12 \)
\( \abs{y - 9} = 5 \)
olduğuna göre, \( xy \) çarpımının en küçük değeri kaçtır?
Çözümü GösterBirinci denklemin çözüm kümesini bulalım.
\( \abs{3x - 6} = 12 \)
\( 3x - 6 = 12 \) ya da \( 3x - 6 = -12 \)
\( x = 6 \) ya da \( x = -2 \)
\( x \in \{6, -2\} \)
İkinci denklemin çözüm kümesini bulalım.
\( \abs{y - 9} = 5 \)
\( y - 9 = 5 \) ya da \( y - 9 = -5 \)
\( y = 14 \) ya da \( y = 4 \)
\( y \in \{4, 14\} \)
Bulduğumuz \( x \) ve \( y \) değerlerinin çarpımları içinden en küçük olanı bulmak için \( x \)'in negatif değerini, \( y \)'nin de büyük değerini seçmeliyiz.
\( xy = (-2) \cdot 14 = -28 \) bulunur.
Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( \abs{x - \abs{3x + 8} - 1} = 13 \)
(b) \( \abs{12x - \abs{-10x + 5} + 4} = 45 \)
(c) \( \abs{6x + \abs{-x} - 8} = 20 \)
Çözümü Göster(a) seçeneği:
\( \abs{x - \abs{3x + 8} - 1} = 13 \)
Mutlak değer içini sıfır yapan \( x = -\frac{8}{3} \) değerinin oluşturduğu \( x \lt -\frac{8}{3} \) ve \( x \ge -\frac{8}{3} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt -\dfrac{8}{3} \)
Bu aralıkta \( 3x + 8 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \abs{x - [-(3x + 8)] - 1} = 13 \)
\( \abs{x + 3x + 8 - 1} = 13 \)
\( \abs{4x + 7} = 13 \)
Bu denklem iki durumda sağlanır.
Durum 1.1:
\( 4x + 7 = 13 \)
\( x = \dfrac{3}{2} \)
Bu değer incelediğimiz \( x \lt -\frac{8}{3} \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 1.2:
\( 4x + 7 = -13 \)
\( x = -5 \)
Bu değer incelediğimiz \( x \lt -\frac{8}{3} \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2:
\( x \ge -\dfrac{8}{3} \)
Bu aralıkta \( 3x + 8 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \abs{x - (3x + 8) - 1} = 13 \)
\( \abs{-2x - 9} = 13 \)
Bu denklem iki durumda sağlanır.
Durum 2.1:
\( -2x - 9 = 13 \)
\( x = -11 \)
Bu değer incelediğimiz \( x \ge -\frac{8}{3} \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 2.2:
\( -2x - 9 = -13 \)
\( x = 2 \)
Bu değer incelediğimiz \( x \ge -\frac{8}{3} \) aralığında bulunduğu için geçerli bir çözümdür.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-5, 2\} \)
(b) seçeneği:
\( \abs{12x - \abs{-10x + 5} + 4} = 45 \)
Mutlak değer içini sıfır yapan \( x = \frac{1}{2} \) değerinin oluşturduğu \( x \lt \frac{1}{2} \) ve \( x \ge \frac{1}{2} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt \dfrac{1}{2} \)
Bu aralıkta \( -10x + 5 \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \abs{12x - (-10x + 5) + 4} = 45 \)
\( \abs{12x + 10x - 5 + 4} = 45 \)
\( \abs{22x - 1} = 45 \)
Bu denklem iki durumda sağlanır.
Durum 1.1:
\( 22x - 1 = 45 \)
\( x = \dfrac{23}{11} \)
Bu değer incelediğimiz \( x \lt \frac{1}{2} \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 1.2:
\( 22x - 1 = -45 \)
\( x = -2 \)
Bu değer incelediğimiz \( x \lt \frac{1}{2} \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2:
\( x \ge \dfrac{1}{2} \)
Bu aralıkta \( -10x + 5 \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \abs{12x - [-(-10x + 5)] + 4} = 45 \)
\( \abs{12x - 10x + 5 + 4} = 45 \)
\( \abs{2x + 9} = 45 \)
Bu denklem iki durumda sağlanır.
Durum 2.1:
\( 2x + 9 = 45 \)
\( x = 18 \)
Bu değer incelediğimiz \( x \ge \frac{1}{2} \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2.2:
\( 2x + 9 = -45 \)
\( x = -27 \)
Bu değer incelediğimiz \( x \ge \frac{1}{2} \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-2, 18\} \)
(c) seçeneği:
\( \abs{6x + \abs{-x} - 8} = 20 \)
Mutlak değer içini sıfır yapan \( x = 0 \) değerinin oluşturduğu \( x \lt 0 \) ve \( x \ge 0 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 0 \)
Bu aralıkta \( x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \abs{6x + (-x) - 8} = 20 \)
\( \abs{5x - 8} = 20 \)
Bu denklem iki durumda sağlanır.
Durum 1.1:
\( 5x - 8 = 20 \)
\( x = \dfrac{28}{5} \)
Bu değer incelediğimiz \( x \lt 0 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 1.2:
\( 5x - 8 = -20 \)
\( x = -\dfrac{12}{5} \)
Bu değer incelediğimiz \( x \lt 0 \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2:
\( x \ge 0 \)
Bu aralıkta \( x \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \abs{6x + [-(-x)] - 8} = 20 \)
\( \abs{6x + x - 8} = 20 \)
\( \abs{7x - 8} = 20 \)
Bu denklem iki durumda sağlanır.
Durum 2.1:
\( 7x - 8 = 20 \)
\( x = 4 \)
Bu değer incelediğimiz \( x \ge 0 \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2.2:
\( 7x - 8 = -20 \)
\( x = -\dfrac{12}{7} \)
Bu değer incelediğimiz \( x \ge 0 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-\frac{12}{5}, 4\} \)
\( \abs{3x^2 - 5x + 2} + 5x - 2 = 3x^2 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterMutlak değer ifadesini yalnız bırakalım.
\( \abs{3x^2 - 5x + 2} = 3x^2 - 5x + 2 \)
Mutlak değer içindeki ifade mutlak değerden olduğu gibi çıktığına göre değeri sıfır ya da pozitiftir.
\( 3x^2 - 5x + 2 \ge 0 \)
Eşitsizliğin sol tarafını çarpanlarına ayıralım.
\( (3x - 2)(x - 1) \ge 0 \)
İkinci dereceden ifadeyi sıfır yapan değerler \( x = \frac{2}{3} \) ve \( x = 1 \)'dir.
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Eşitsizlikte \( \ge \) sembolü kullanıldığı için eşitsizliğin pozitif ve sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in \left( -\infty, \dfrac{2}{3} \right] \cup [1, \infty) \)
\( x, y \in \mathbb{R} \) olmak üzere,
\( \abs{3x - 4y + 14} + \abs{2x + 3y - 19} = 0 \)
olduğuna göre, \( x^2 - y^2 \) ifadesinin değeri kaçtır?
Çözümü GösterMutlak değerli bir ifade negatif olamayacağı için, iki ya da daha fazla sayıda mutlak değer ifadesinin toplamı sıfır ise her ifade ayrı ayrı sıfıra eşittir.
\( \abs{3x - 4y + 14} = 0 \)
\( \abs{2x + 3y - 19} = 0 \)
Bir ifadenin mutlak değeri sıfıra eşitse kendisi de sıfırdır.
\( 3x - 4y + 14 = 0 \)
\( 2x + 3y - 19 = 0 \)
İki denklemi de birlikte sağlayan \( x \) ve \( y \) değerlerini bulmak için denklemleri ortak çözelim.
Birinci denklemin taraflarını 3 ile, ikinci denklemin taraflarını 4 ile çarpalım.
\( 9x - 12y + 42 = 0 \)
\( 8x + 12y - 76 = 0 \)
İki denklemi taraf tarafa toplayalım.
\( 17x - 34 = 0 \)
\( x = 2 \)
\( x = 2 \) değerini birinci denklemde yerine yazarak \( y \) değerini bulalım.
\( 3(2) - 4y + 14 = 0 \)
\( -4y = -20 \)
\( y = 5 \)
İstenen ifadenin sonucunu bulalım.
\( x^2 - y^2 = 2^2 - 5^2 = -21 \) bulunur.
\( \abs{x - 4}^2 - 4\abs{x - 4} = 5 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterMutlak değer içini sıfır yapan \( x = 4 \) değerinin oluşturduğu \( x \lt 4 \) ve \( x \ge 4 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 4 \)
Bu aralıkta \( x - 4 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \abs{x - 4} = -(x - 4) = 4 - x \)
\( (4 - x)^2 - 4(4 - x) = 5 \)
\( 16 - 8x + x^2 - 16 + 4x = 5 \)
\( x^2 - 4x - 5 = 0 \)
\( (x + 1)(x - 5) = 0 \)
\( x = -1, \quad x = 5 \)
İncelediğimiz \( x \lt 4 \) aralığında sadece \( x = -1 \) geçerli bir çözümdür.
\( x = -1 \)
Durum 2:
\( x \ge 4 \)
Bu aralıkta \( x - 4 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \abs{x - 4} = x - 4 \)
\( (x - 4)^2 - 4(x - 4) = 5 \)
\( x^2 - 8x + 16 - 4x + 16 = 5 \)
\( x^2 - 12x + 27 = 0 \)
\( (x - 3)(x - 9) = 0 \)
\( x = 3, \quad x = 9 \)
İncelediğimiz \( x \ge 4 \) aralığında sadece \( x = 9 \) geçerli bir çözümdür.
\( x = 9 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ -1, 9 \} \)
\( \abs{x - 3} + (x - 3)^2 - 12 = 0 \) denkleminin kökler toplamı kaçtır?
Çözümü GösterMutlak değer içini sıfır yapan \( x = 3 \) değerinin oluşturduğu \( x \lt 3 \) ve \( x \ge 3 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 3 \)
Bu aralıkta \( x - 3 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(x - 3) + (x - 3)^2 - 12 = 0 \)
\( 3 - x + x^2 - 6x + 9 - 12 = 0 \)
\( x^2 - 7x = 0 \)
\( x(x - 7) = 0 \)
\( x = 0, \quad x = 7 \)
İncelediğimiz \( x \lt 3 \) aralığında sadece \( x = 0 \) geçerli bir çözümdür.
\( x = 0 \)
Durum 2:
\( x \ge 3 \)
Bu aralıkta \( x - 3 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (x - 3) + (x - 3)^2 - 12 = 0 \)
\( x - 3 + x^2 - 6x + 9 - 12 = 0 \)
\( x^2 - 5x - 6 = 0 \)
\( (x + 1)(x - 6) = 0 \)
\( x = -1, \quad x = 6 \)
İncelediğimiz \( x \ge 3 \) aralığında sadece \( x = 6 \) geçerli bir çözümdür.
\( x = 6 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ 0, 6 \} \)
Bulduğumuz çözüm değerlerinin toplamı \( 0 + 6 = 6 \) olarak bulunur.
\( x^2 - 8\abs{x} + 7 = 0 \) denkleminin kökler çarpımı kaçtır?
Çözümü GösterMutlak değer içini sıfır yapan \( x = 0 \) değerinin oluşturduğu \( x \lt 0 \) ve \( x \ge 0 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 0 \)
Bu aralıkta \( x \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( x^2 - 8(-x) + 7 = 0 \)
\( x^2 + 8x + 7 = 0 \)
\( (x + 7)(x + 1) = 0 \)
\( x = -7, \quad x = -1 \)
İncelediğimiz \( x \lt 0 \) aralığında her iki değer de geçerli birer çözümdür.
\( x \in \{ -7, -1 \} \)
Durum 2:
\( x \ge 0 \)
Bu aralıkta \( x \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( x^2 - 8x + 7 = 0 \)
\( (x - 1)(x - 7) = 0 \)
\( x = 1, \quad x = 7 \)
İncelediğimiz \( x \ge 0 \) aralığında her iki değer de geçerli birer çözümdür.
\( x \in \{ 1, 7 \} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ -7, -1, 1, 7 \} \)
Bulduğumuz çözüm değerlerinin çarpımı \( (-7)(-1)(1)(7) = 49 \) olarak bulunur.
\( x^2 - \abs{4x} = 21 \)
eşitliğini sağlayan \( x \) değerlerinin çarpımı kaçtır?
Çözümü Göster\( x^2 \) ifadesi her zaman pozitiftir, dolayısıyla verilen denklemde \( x^2 = \abs{x}^2 \) yazabiliriz.
Mutlak değer içindeki pozitif çarpanlar mutlak değer dışına çıkarılabilir.
\( \abs{x}^2 - 4\abs{x} - 21 = 0 \)
İkinci dereceden denklemi çarpanlarına ayıralım.
\( (\abs{x} - 7)(\abs{x} + 3) = 0\)
\( \abs{x} - 7 = 0 \) ya da \( \abs{x} + 3 = 0 \)
\( \abs{x} = 7 \) ya da \( \abs{x} = -3 \)
\( \abs{x} = 7 \Longrightarrow x \in \{-7, 7\} \)
Mutlak değerli bir ifadenin sonucu negatif olamayacağı için \( \abs{x} = -3 \) eşitliğinin bir çözümü yoktur.
Çözüm kümesi: \( x \in \{-7, 7\} \)
Buna göre \( x \)'in alabileceği değerler çarpımı \( -7 \cdot 7 = -49 \) olur.
\( \abs{x + 5} + \abs{x - 7} = 15 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterMutlak değer ifadelerini sıfır yapan değerler \( x \in \{-5, 7\} \) noktalarıdır.
Bu iki kritik noktanın oluşturduğu üç aralığı ayrı ayrı inceleyelim ve her aralıkta mutlak değer içindeki ifadeleri o aralıktaki işaretlerine göre mutlak değerden çıkaralım.
Durum 1:
\( x \lt -5 \)
Bu aralıkta her iki mutlak değer ifadesi de negatif olur, dolayısıyla mutlak değerden negatif işaretli çıkar.
\( -(x + 5) - (x - 7) = 15 \)
\( -2x + 2 = 15 \)
\( x = -\dfrac{13}{2} \)
Bulduğumuz değer denklemi çözdüğümüz \( x \lt -5 \) aralığında olduğu için geçerli bir çözümdür.
Durum 2:
\( -5 \le x \lt 7 \)
Bu aralıkta \( x + 5 \) ifadesi pozitif, \( x - 7 \) ifadesi negatif olur, dolayısıyla birinci ifade mutlak değerden olduğu gibi, ikinci ifade negatif işaretli çıkar.
\( (x + 5) - (x - 7) = 15 \)
\( 12 = 15 \)
Elde ettiğimiz eşitlik herhangi bir \( x \) değeri için sağlanmadığı için bu aralıkta geçerli bir çözüm yoktur.
Durum 3:
\( 7 \le x \)
Bu aralıkta her iki mutlak değer ifadesi de pozitif olur, dolayısıyla mutlak değerden olduğu gibi çıkar.
\( (x + 5) + (x - 7) = 15 \)
\( 2x - 2 = 15 \)
\( x = \dfrac{17}{2} \)
Bulduğumuz değer denklemi çözdüğümüz \( 7 \le x \) aralığında olduğu için geçerli bir çözümdür.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ -\dfrac{13}{2}, \dfrac{17}{2} \right\} \)
Denklemin iki tarafına ait denklemlerin grafiklerini analitik düzlemde çizdiğimizde, kesişim noktalarının apsis değerleri olarak aynı değerleri buluruz.

Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( \abs{3x - 2} + \abs{x - 2} = 12 \)
(b) \( \abs{2 - x} - \abs{2x - 1} = -6 \)
(c) \( \abs{12 - 4x} + \abs{8 - x} = 4 \)
Çözümü Göster(a) seçeneği:
\( \abs{3x - 2} + \abs{x - 2} = 12 \)
Mutlak değer içini sıfır yapan \( x \in \{\frac{2}{3}, 2\} \) değerlerinin oluşturduğu \( x \lt \frac{2}{3} \), \( \frac{2}{3} \le x \lt 2 \) ve \( x \ge 2 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt \dfrac{2}{3} \)
Bu aralıkta \( 3x - 2 \) ve \( x - 2 \) ifadeleri negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(3x - 2) + [-(x - 2)] = 12 \)
\( -3x + 2 + 2 - x = 12 \)
\( 4 - 4x = 12 \)
\( x = -2 \)
Bu değer incelediğimiz \( x \lt \frac{2}{3} \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2:
\( \dfrac{2}{3} \le x \lt 2 \)
Bu aralıkta \( 3x - 2 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
Bu aralıkta \( x - 2 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( (3x - 2) + [-(x - 2)] = 12 \)
\( 3x - 2 + 2 - x = 12 \)
\( x = 6 \)
Bu değer incelediğimiz \( \frac{2}{3} \le x \lt 2 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 3:
\( x \ge 2 \)
Bu aralıkta \( 3x - 2 \) ve \( x - 2 \) ifadeleri sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (3x - 2) + (x - 2) = 12 \)
\( 4x - 4 = 12 \)
\( x = 4 \)
Bu değer incelediğimiz \( x \ge 2 \) aralığında bulunduğu için geçerli bir çözümdür.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-2, 4\} \)
(b) seçeneği:
\( \abs{2 - x} - \abs{2x - 1} = -6 \)
Mutlak değer içini sıfır yapan \( x \in \{\frac{1}{2}, 2\} \) değerlerinin oluşturduğu \( x \lt \frac{1}{2} \), \( \frac{1}{2} \le x \lt 2 \) ve \( x \ge 2 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt \dfrac{1}{2} \)
Bu aralıkta \( 2x - 1 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
Bu aralıkta \( 2 - x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (2 - x) - [-(2x - 1)] = -6 \)
\( 2 - x + 2x - 1 = -6 \)
\( x = -7 \)
Bu değer incelediğimiz \( x \lt \frac{1}{2} \) aralığında bulunduğu için geçerli bir çözümdür.
Durum 2:
\( \dfrac{1}{2} \le x \lt 2 \)
Bu aralıkta \( 2x - 1 \) ve \( 2 - x \) ifadeleri sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (2 - x) - (2x - 1) = -6 \)
\( 2 - x - 2x + 1 = -6 \)
\( x = 3 \)
Bu değer incelediğimiz \( \frac{1}{2} \le x \lt 2 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 3:
\( x \ge 2 \)
Bu aralıkta \( 2x - 1 \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
Bu aralıkta \( 2 - x \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(2 - x) - (2x - 1) = -6 \)
\( -2 + x - 2x + 1 = -6 \)
\( x = 5 \)
Bu değer incelediğimiz \( x \ge 2 \) aralığında bulunduğu için geçerli bir çözümdür.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-7, 5\} \)
(c) seçeneği:
\( \abs{12 - 4x} + \abs{8 - x} = 4 \)
Mutlak değer içini sıfır yapan \( x \in \{3, 8\} \) değerlerinin oluşturduğu \( x \lt 3 \), \( 3 \le x \lt 8 \) ve \( x \ge 8 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 3 \)
Bu aralıkta \( 12 - 4x \) ve \( 8 - x \) ifadeleri pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (12 - 4x) + (8 - x) = 4 \)
\( 12 - 4x + 8 - x = 4 \)
\( x = \dfrac{16}{5} \)
Bu değer incelediğimiz \( x \lt 3 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 2:
\( 3 \le x \lt 8 \)
Bu aralıkta \( 12 - 4x \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
Bu aralıkta \( 8 - x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( -(12 - 4x) + (8 - x) = 4 \)
\( -12 + 4x + 8 - x = 4 \)
\( x = \dfrac{8}{3} \)
Bu değer incelediğimiz \( 3 \le x \lt 8 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 3:
\( x \ge 8 \)
Bu aralıkta \( 12 - 4x \) ve \( 8 - x \) ifadeleri sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(12 - 4x) + [-(8 - x)] = 4 \)
\( -12 + 4x - 8 + x = 4 \)
\( x = \dfrac{24}{5} \)
Bu değer incelediğimiz \( x \ge 8 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Her üç durumda da geçerli bir çözüm bulunmadığı için denklemin çözüm kümesi boş kümedir.
Çözüm kümesi: \( x \in \emptyset \)
Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( \abs{x - 1} = x^2 + 4x - 5 \)
(b) \( \abs{3x - 18} = 3x^2 - 4x - 12 \)
(c) \( \abs{10 - 8x} = 5x^2 + 15x \)
Çözümü Göster(a) seçeneği:
\( \abs{x - 1} = x^2 + 4x - 5 \)
Mutlak değer içini sıfır yapan \( x = 1 \) değerinin oluşturduğu \( x \lt 1 \) ve \( x \ge 1 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 1 \)
Bu aralıkta \( x - 1 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(x - 1) = x^2 + 4x - 5 \)
\( x^2 + 5x - 6 = 0 \)
\( (x + 6)(x - 1) = 0 \)
\( x = -6, \quad x = 1 \)
İncelediğimiz \( x \lt 1 \) aralığında sadece \( x = -6 \) geçerli bir çözümdür.
\( x = -6 \)
Durum 2:
\( x \ge 1 \)
Bu aralıkta \( x - 1 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( x - 1 = x^2 + 4x - 5 \)
\( x^2 + 3x - 4 = 0 \)
\( (x + 4)(x - 1) = 0 \)
\( x = -4, \quad x = 1 \)
İncelediğimiz \( x \ge 1 \) aralığında sadece \( x = 1 \) geçerli bir çözümdür.
\( x = 1 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{-6, 1\} \)
(b) seçeneği:
\( \abs{3x - 18} = 3x^2 - 4x - 12 \)
Mutlak değer içini sıfır yapan \( x = 6 \) değerinin oluşturduğu \( x \lt 6 \) ve \( x \ge 6 \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 6 \)
Bu aralıkta \( 3x - 18 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(3x - 18) = 3x^2 - 4x - 12 \)
\( 3x^2 - x - 30 = 0 \)
\( (3x - 10)(x + 3) = 0 \)
\( x = \dfrac{10}{3}, \quad x = -3 \)
Bu iki değer incelediğimiz \( x \lt 6 \) aralığında bulunduğu için geçerli birer çözümdür.
\( x \in \{-3, \frac{10}{3}\} \)
Durum 2:
\( x \ge 6 \)
Bu aralıkta \( 3x - 18 \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( 3x - 18 = 3x^2 - 4x - 12 \)
\( 3x^2 - 7x + 6 = 0 \)
Denklemin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( a = 3, \quad b = -7, \quad c = 6 \)
\( \Delta = (-7)^2 - 4(3)(6) = -23 \)
\( \Delta \lt 0 \) olduğu için denklemin reel sayı kökü yoktur.
\( x \in \emptyset \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ -3, \dfrac{10}{3} \right\} \)
(c) seçeneği:
\( \abs{10 - 8x} = 5x^2 + 15x \)
Mutlak değer içini sıfır yapan \( x = \frac{5}{4} \) değerinin oluşturduğu \( x \lt \frac{5}{4} \) ve \( x \ge \frac{5}{4} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt \dfrac{5}{4} \)
Bu aralıkta \( 10 - 8x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( 10 - 8x = 5x^2 + 15x \)
\( 5x^2 + 23x - 10 = 0 \)
\( (5x - 2)(x + 5) = 0 \)
\( x = \dfrac{2}{5}, \quad x = -5 \)
Bu iki değer incelediğimiz \( x \lt \frac{5}{4} \) aralığında bulunduğu için geçerli birer çözümdür.
\( x \in \left\{ -5, \dfrac{2}{5} \right\} \)
Durum 2:
\( x \ge \dfrac{5}{4} \)
Bu aralıkta \( 10 - 8x \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(10 - 8x) = 5x^2 + 15x \)
\( -10 + 8x = 5x^2 + 15x \)
\( 5x^2 + 7x + 10 = 0 \)
Denklemin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( a = 5, \quad b = 7, \quad c = 10 \)
\( \Delta = 7^2 - 4(5)(10) = -151 \)
\( \Delta \lt 0 \) olduğu için denklemin reel sayı kökü yoktur.
\( x \in \emptyset \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ -5, \dfrac{2}{5} \right\} \)
\( \abs{2x^2 + 7x + 3} = 10x + 12 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterMutlak değer içindeki ifadeyi çarpanlarına ayıralım.
\( \abs{(2x + 1)(x + 3)} = 10x + 12 \)
Mutlak değer içini sıfır yapan \( x \in \{-3, -\frac{1}{2}\} \) değerlerinin oluşturduğu \( x \lt -3 \), \( -3 \le x \lt -\frac{1}{2} \) ve \( x \ge -\frac{1}{2} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt -3 \)
Bu aralıkta \( 2x + 1 \) ve \( x + 3 \) ifadeleri negatif olur, dolayısıyla çarpımları pozitif olur ve mutlak değerden olduğu gibi çıkar.
\( (2x + 1)(x + 3) = 10x + 12 \)
\( 2x^2 + 7x + 3 = 10x + 12 \)
\( 2x^2 - 3x - 9 = 0 \)
\( (2x + 3)(x - 3) = 0 \)
\( x = -\dfrac{3}{2}, \quad x = 3 \)
İncelediğimiz \( x \lt -3 \) aralığında iki değer de geçerli birer çözüm değildir.
\( x \in \emptyset \)
Durum 2:
\( -3 \le x \lt -\dfrac{1}{2} \)
Bu aralıkta \( x + 3 \) ifadesi sıfır ya da pozitif, \( 2x + 1 \) ifadesi negatif olur, dolayısıyla çarpımları sıfır ya da negatif olur ve mutlak değerden negatif işaretli çıkar.
\( -(2x + 1)(x + 3) = 10x + 12 \)
\( -2x^2 - 7x - 3 = 10x + 12 \)
\( 2x^2 + 17x + 15 = 0 \)
\( (2x + 15)(x + 1) = 0 \)
\( x = -\dfrac{15}{2}, \quad x = -1 \)
İncelediğimiz \( -3 \le x \lt -\frac{1}{2} \) aralığında sadece \( x = -1 \) geçerli bir çözümdür.
\( x = -1 \)
Durum 3:
\( x \ge -\dfrac{1}{2} \)
Bu aralıkta \( 2x + 1 \) ve \( x + 3 \) ifadeleri sıfır ya da pozitif olur, dolayısıyla çarpımları sıfır ya da pozitif olur ve mutlak değerden olduğu gibi çıkar.
\( (2x + 1)(x + 3) = 10x + 12 \)
\( 2x^2 + 7x + 3 = 10x + 12 \)
\( 2x^2 - 3x - 9 = 0 \)
\( (2x + 3)(x - 3) = 0 \)
\( x = -\dfrac{3}{2}, \quad x = 3 \)
İncelediğimiz \( x \ge -\frac{1}{2} \) aralığında sadece \( x = 3 \) geçerli bir çözümdür.
\( x = 3 \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ -1, 3 \} \)
\( a, b, c \in \mathbb{Z} \) olmak üzere,
\( \abs{4a + 24} + \abs{5b + 10} + \abs{3c - 9} + \abs{2d - 4} = 2 \)
olduğuna göre, \( a + b + c + d \) toplamının alabileceği en küçük değer kaçtır?
Çözümü Gösterİfadeyi düzenleyelim.
\( \abs{4(a + 6)} + \abs{5(b + 2)} + \abs{3(c - 3)} + \abs{2(d - 2)} = 2 \)
Mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( 4\abs{a + 6} + 5\abs{b + 2} + 3\abs{c - 3} + 2\abs{d - 2} = 2 \)
\( a, b, c \) tam sayı oldukları için \( 4\abs{a + 6}, 5\abs{b + 2},3\abs{c - 3} \) ifadeleri sırasıyla 4'ün, 5'in ve 3'ün katları olur.
Mutlak değer ifadesi hiçbir zaman negatif olamayacağı için ve verilen ifade ikiye eşit olduğu için, bu ifadeler ayrı ayrı sıfıra eşit olmalıdır.
Bu ifadeleri sıfıra eşitleyerek \( a, b, c \) değerlerini bulalım.
\( 4\abs{a + 6} = 0 \)
\( a = -6 \)
\( 5\abs{b + 2} = 0 \)
\( b = -2 \)
\( 3\abs{c - 3} = 0 \)
\( c = 3 \)
Bulduğumuz değerleri denklemde yerine koyalım.
\( 0 + 2\abs{d - 2} = 2 \)
\( \abs{d - 2} = 1 \)
\( d - 2 = \pm 1 \)
\( d \in \{ 1, 3 \} \)
Toplamın en küçük değeri istendiği için \( d = 1 \) seçilir.
\( a + b + c + d = -6 - 2 + 3 + 1 = -4 \) bulunur.
\( \abs{\dfrac{\abs{x}}{x} + 4 + x} = 4x + 5 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterMutlak değer içini sıfır yapan \( x = 0 \) değerinin oluşturduğu \( x \lt 0 \), \( x = 0 \) ve \( x \gt 0 \) durumlarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt 0 \)
Bu aralıkta \( x \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \abs{x} = -x \)
\( \abs{\dfrac{-x}{x} + 4 + x} = 4x + 5 \)
\( \abs{3 + x} = 4x + 5 \)
Bu eşitlikte \( 3 + x \) ifadesinin işaretine göre iki durum oluşur.
Durum 1.1:
\( -3 \le x \lt 0 \)
Bu aralıkta \( 3 + x \) ifadesi sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( 3 + x = 4x + 5 \)
\( x = -\dfrac{2}{3} \)
Bu değer incelediğimiz \( -3 \le x \lt 0 \) aralığında bulunduğu için geçerli bir çözümdür.
\( x \in \{-\frac{2}{3}\} \)
Durum 1.2:
\( x \lt -3 \)
Bu aralıkta \( 3 + x \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( -(3 + x) = 4x + 5 \)
\( -3 - x = 4x + 5 \)
\( x = -\dfrac{8}{5} \)
Bu değer incelediğimiz \( x \lt -3 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Durum 2:
\( x = 0 \)
\( x = 0 \) değeri \( \frac{\abs{x}}{x} \) ifadesini tanımsız yaptığı için geçerli bir çözüm değildir.
Durum 3:
\( x \gt 0 \)
Bu aralıkta \( x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \abs{x} = x \)
\( \abs{\dfrac{x}{x} + 4 + x} = 4x + 5 \)
\( \abs{5 + x} = 4x + 5 \)
\( x \gt 0 \) aralığında \( 5 + x \) pozitif olur.
\( 5 + x = 4x + 5 \)
\( x = 0 \)
Bu değer incelediğimiz \( x \gt 0 \) aralığında bulunmadığı için geçerli bir çözüm değildir.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ -\dfrac{2}{3} \right\} \)
\( x \in \mathbb{R} \) olmak üzere,
\( \abs{x - 6}\abs{2x^2 + 6x - 36} = 30\abs{3x - 9} \)
olduğuna göre, \( x \) ifadesinin alabileceği kaç farklı değer vardır?
Çözümü Gösterİkinci dereceden ifadeyi çarpanlarına ayıralım.
\( \abs{x - 6}\abs{2(x + 6)(x - 3)} = 30\abs{3x - 9} \)
Bir çarpımın mutlak değeri mutlak değerlerin çarpımı şeklinde yazılabilir.
Ayrıca pozitif çarpanlar mutlak değer dışına çıkarılabilir.
\( 2\abs{x - 6}\abs{x + 6}\abs{x - 3} = 90\abs{x - 3} \)
Eşitliğin iki tarafındaki \( \abs{x - 3} \) çarpanları birbirini götürür, ancak \( x = 3 \) değerinin denklemi sağlayan köklerden biri olduğu not edilir.
\( \abs{x - 6} \abs{x + 6} = 45 \)
\( \abs{(x - 6)(x + 6)} = 45 \)
\( \abs{x^2 - 36} = 45 \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( x^2 - 36 = 45 \)
\( x^2 = 81 \)
\( x \in \{ -9, 9 \} \)
Durum 2:
\( x^2 - 36 = -45 \)
\( x^2 = -9 \)
Bir tam kare ifade negatif olamayacağı için bu durum için reel sayı bir çözüm yoktur.
Çözüm kümesi: \( x \in \{ -9, 3, 9 \} \)
Buna göre \( x \)'in alabileceği 3 farklı değer vardır.
\( \abs{x - n} + \abs{7n - 7x} = 48n \)
denkleminin kökleri \( x_1 \) ve \( x_2 \) olarak veriliyor.
\( \abs{x_1 - x_2} = 108 \) olduğuna göre, \( n \) kaçtır?
Çözümü GösterVerilen eşitliği düzenleyelim.
Mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( \abs{x - n} + 7\abs{n - x} = 48n \)
Mutlak değer içini \( -1 \) ile çarpıp terimlerin yerini değiştirebiliriz.
\( \abs{x - n} + 7\abs{x - n} = 48n \)
\( 8\abs{x - n} = 48n \)
\( \abs{x - n} = 6n \)
Bu denklem iki durumda sağlanır.
Durum 1:
\( x - n = 6n \)
\( x = 7n \)
Durum 2:
\( x - n = -6n \)
\( x = -5n \)
Buna göre denklemi sağlayan değerler aşağıdaki gibidir.
\( x_1 = 7n, \quad x_2 = -5n \)
\( \abs{x_1 - x_2} = 108 \)
\( \abs{7n - (-5n)} = 108 \)
\( \abs{12n} = 108 \)
\( 12\abs{n} = 108 \)
\( \abs{n} = 9 \)
\( n = 9 \) ya da \( n = -9 \) olabilir, ancak soruda verilen eşitlikte iki mutlak değer ifadesinin toplamı negatif olamayacağı için \( n = -9 \) denklemi sağlamaz.
Buna göre \( n = 9 \) bulunur.
\( \dfrac{1}{\abs{1 - 2x}} + \dfrac{2}{\abs{4x + 1}} = 1 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterRasyonel ifadenin paydalarını eşitleyelim.
\( \dfrac{1}{\abs{1 - 2x}} + \dfrac{2}{\abs{4x + 1}} = 1 \)
\( \dfrac{\abs{4x + 1} + 2\abs{1 - 2x}}{\abs{1 - 2x}\abs{4x + 1}} = 1 \)
İçler - dışlar çarpımı yapalım.
İçler - dışlar çarpımı yaparken paydadaki iki çarpanı sıfır yapan \( x = \frac{1}{2} \) ve \( x = -\frac{1}{4} \) değerlerinin çözüm kümesine dahil olamayacağını not edelim.
\( \abs{4x + 1} + 2\abs{1 - 2x} = \abs{4x + 1}\abs{1 - 2x} \)
Mutlak değer içini sıfır yapan \( x \in \{-\frac{1}{4}, \frac{1}{2} \} \) değerlerinin oluşturduğu \( x \lt -\frac{1}{4} \), \( -\frac{1}{4} \le x \lt \frac{1}{2} \) ve \( x \ge \frac{1}{2} \) aralıklarını ayrı ayrı inceleyelim ve her durumda oluşan denklemi çözelim.
Durum 1:
\( x \lt -\dfrac{1}{4} \)
Bu aralıkta \( 4x + 1 \) ifadesi negatif olur ve mutlak değer dışına negatif işaretli çıkar.
Bu aralıkta \( 1 - 2x \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( -(4x + 1) + 2(1 - 2x) = -(4x + 1)(1 - 2x) \)
\( -4x - 1 + 2 - 4x = 8x^2 - 4x + 2x - 1 \)
\( 8x^2 + 6x - 2 = 0 \)
\( 2(4x - 1)(x + 1) = 0 \)
\( x = \dfrac{1}{4}, \quad x = -1 \)
İncelediğimiz \( x \lt -\frac{1}{4} \) aralığında sadece \( x = -1 \) geçerli bir çözümdür.
\( x = -1 \)
Durum 2:
\( -\dfrac{1}{4} \le x \lt \dfrac{1}{2} \)
Bu aralıkta \( 4x + 1 \) ve \( 1 - 2x \) ifadeleri sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( (4x + 1) + 2(1 - 2x) = (4x + 1)(1 - 2x) \)
\( 4x + 1 + 2 - 4x = -8x^2 + 4x - 2x + 1 \)
\( 8x^2 - 2x + 2 = 0 \)
\( 4x^2 - x + 1 = 0 \)
Denklemin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( a = 4, \quad b = -1, \quad c = 1 \)
\( \Delta = (-1)^2 - 4(4)(1) = -15 \)
\( \Delta \lt 0 \) olduğundan denklemin reel sayı kökü yoktur.
\( x \in \emptyset \)
Durum 3:
\( x \ge \dfrac{1}{2} \)
Bu aralıkta \( 4x + 1 \) ifadesi pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
Bu aralıkta \( 1 - 2x \) ifadesi sıfır ya da negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( (4x + 1) + 2[-(1 - 2x)] = (4x + 1)[-(1 - 2x)] \)
\( 4x + 1 - 2 + 4x = 8x^2 - 4x + 2x - 1 \)
\( 8x^2 - 10x = 0 \)
\( 2x(4x - 5) = 0 \)
\( x = 0, \quad x = \dfrac{5}{4} \)
İncelediğimiz \( x \ge \frac{1}{2} \) aralığında sadece \( x = \frac{5}{4} \) geçerli bir çözümdür.
\( x = \dfrac{5}{4} \)
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \left\{ -1, \dfrac{5}{4} \right\} \)
\( f \) ve \( g \) reel sayılarda tanımlı birer fonksiyondur.
\( f(x) = \abs{4x + 3} \)
\( g(x) = \abs{3x + 2} \)
Buna göre \( (g \circ f)(x) = 99^4 \) eşitliğini sağlayan \( x \) değerlerinin toplamı kaçtır?
Çözümü Göster\( g \circ f \) bileşke fonksiyonunu bulalım.
\( g(f(x)) = \abs{3\abs{(4x + 3)} +2} \)
\( = \abs{ \abs{12x + 9} + 2} = 99^4 \)
Mutlak değer içindeki ifade mutlak değer dışına iki farklı şekilde çıkabilir.
Durum 1:
\( \abs{12x + 9} + 2 = 99^4 \)
\( \abs{12x + 9} = 99^4 - 2 \)
Bu eşitlik için de iki farklı durum vardır.
Durum 1.1:
\( 12x + 9 = 99^4 - 2 \)
\( 12x = 99^4 - 11 \)
\( x = \dfrac{99^4 - 11}{12} \)
Durum 1.2:
\( 12x + 9 = -99^4 + 2 \)
\( 12x = -99^4 - 7 \)
\( x = \dfrac{-99^4 - 7}{12} \)
Durum 2:
\( \abs{12x + 9} + 2 = -99^4 \)
\( \abs{12x + 9} = -99^4 - 2 \)
Mutlak değerli bir ifadenin sonucu negatif olamayacağı için bu durumda geçerli bir çözüm yoktur.
Bu durumda denklemi sağlayan \( x \) değerlerinin toplamı aşağıdaki gibi olur.
\( \dfrac{99^4 - 11}{12} + \dfrac{-99^4 - 7}{12} = \dfrac{-18}{12} \)
\( = -\dfrac{3}{2} \) bulunur.
\( x \in \mathbb{R} \) olmak üzere,
\( \abs{x^3 - 1} + \abs{4x - 4} = x^2 - 6x + 5 \)
denklemini sağlayan \( x \) tam sayılarının toplamı kaçtır?
Çözümü GösterTüm ifadeleri çarpanlarına ayıralım.
\( \abs{(x - 1)(x^2 + x + 1)} + \abs{4(x - 1)} = (x - 1)(x - 5) \)
Bir çarpımın mutlak değeri mutlak değerlerin çarpımı şeklinde yazılabilir.
Ayrıca mutlak değer içindeki pozitif çarpan mutlak değer dışına çıkarılabilir.
\( \abs{x - 1}\abs{x^2 + x + 1} + 4\abs{x - 1} = (x - 1)(x - 5) \)
\( \abs{x - 1}(\abs{x^2 + x + 1} + 4) = (x - 1)(x - 5) \)
\( x^2 + x + 1 \) ifadesinin deltası negatif olduğu için reel kökü yoktur ve her zaman pozitiftir, dolayısıyla mutlak değerden olduğu gibi çıkar.
\( \abs{x - 1}(x^2 + x + 5) = (x - 1)(x - 5) \)
Denklemi mutlak değer içindeki ifadenin üç farklı durumu için ayrı ayrı çözelim.
Durum 1:
\( x \gt 1 \)
\( (x - 1)(x^2 + x + 5) = (x - 1)(x - 5) \)
\( x^2 + x + 5 = x - 5 \)
\( x^2 = -10 \)
\( x^2 \) negatif bir değere sahip olamaz, dolayısıyla bu durum için geçerli bir çözüm yoktur.
Durum 2:
\( x = 1 \)
Bu durumda eşitliğin her iki tarafı sıfır olduğu ve eşitlik sağlandığı için \( x = 1 \) geçerli bir çözümdür.
Durum 3:
\( x \lt 1 \)
\( -(x - 1)(x^2 + x + 5) = (x - 1)(x - 5) \)
\( -x^2 - x - 5 = x - 5 \)
\( x^2 + 2x = 0 \)
\( x(x + 2) = 0 \)
Bu eşitliği sağlayan değerler \( x = 0 \) ve \( x = -2 \) olur.
Her iki değer de çözüm yaptığımız aralık içinde olduğu için geçerli birer çözümdür.
Denklemin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in \{ -2, 0, 1 \} \)
Buna göre eşitliği sağlayan \( x \) değerlerinin toplamı \( -2 + 0 + 1 = -1 \) olur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \abs{3x - a} = b \) denkleminin çözüm kümesi \( \{ -4, 10 \} \) olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü GösterVerilen denklem iki durumda sağlanır.
Durum 1:
\( 3x - a \ge 0 \)
\( 3x - a = b \)
\( 3x - a \) ifadesi \( x \) daha büyük olan \( 10 \) değerini aldığında pozitif olur.
\( 3(10) = a + b \)
\( a + b = 30 \)
Durum 2:
\( 3x - a \lt 0 \)
\( 3x - a = -b \)
\( 3x - a \) ifadesi \( x \) daha küçük olan \( -4 \) değerini aldığında negatif olur.
\( 3(-4) - a = -b \)
\( a - b = -12 \)
Bulduğumuz iki denklemi taraf tarafa toplayalım.
\( (a + b) + (a - b) = 30 + (-12) \)
\( a = 9 \)
Bulduğumuz \( a \) değerini birinci denklemde yerine koyalım.
\( a + b = 30 \)
\( b = 21 \)
Buna göre \( ab = 9 \cdot 21 = 189 \) olarak bulunur.
\( \abs{\abs{x - 21} - a} = 6 \) denkleminin 4 reel kökü bulunduğuna göre, \( a \) değer aralığı nedir?
Çözümü GösterEn dıştaki mutlak değer ifadesini açalım.
\( \abs{x - 21} - a = \pm 6 \)
\( \abs{x - 21} = \pm 6 + a \)
Denklemin 4 reel kökü olabilmesi için \( \pm 6 + a \) ve \( \pm 6 + a \) değerlerinin ikisi de içteki mutlak değer açıldığında ikişer çözüm üretecek şekilde pozitif birer reel sayıya karşılık gelmelidir.
\( 6 + a \ge 0 \Longrightarrow a \ge -6 \)
\( -6 + a \ge 0 \Longrightarrow a \ge 6 \)
\( a \) için bulduğumuz iki değer aralığını da sağlayan değerler için denklemin 4 reel kökü olur.
\( a \in [6, \infty) \)
\( a, b, m \in \mathbb{Z} \) olmak üzere,
\( \abs{a} + \abs{b} = m \)
eşitliğini sağlayan 32 tane \( (a, b) \) ikilisi olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( a = 0 \) olduğu durumda \( b = m \) ya da \( b = -m \) olmak üzere iki çözüm vardır.
\( b = 0 \) olduğu durumda \( a = m \) ya da \( a = -m \) olmak üzere iki çözüm vardır.
\( 0 \lt \abs{a} \lt m \) olduğu \( m - 1 \) durumun her birinde ise \( (a, b) \) ikilileri için \( (+, +), (+, -), (-, +), (-, -) \) olmak üzere dörder çözüm vardır.
Buna göre verilen denklemin toplam çözüm sayısı aşağıdaki sayıda olur.
\( 2 + 2 + 4(m - 1) = 4m \)
\( 4m = 32 \)
\( m = 8 \) bulunur.
Yukarıdaki açıklamaları netleştirmek adına, denklemin 32 çözümü aşağıdaki gibi olur.
\( a = 0 \) için:
\( (0, 8), (0, -8) \)
\( \abs{a} = 1 \) için:
\( (1, 7), (1, -7), (-1, 7), (-1, -7) \)
\( \abs{a} = 2 \) için:
\( (2, 6), (2, -6), (-2, 6), (-2, -6) \)
\( \vdots \)
\( a = 8 \) için:
\( (8, 0), (-8, 0) \)
\( \abs{x}, x + 12, x^2 \) sayıları sadece iki farklı sayı içerdiğine göre, \( x \)'in alabileceği kaç farklı değer vardır?
Çözümü GösterSayıları sırasıyla ikili olarak birbirine eşitleyerek denklemleri çözelim.
Durum 1:
\( \abs{x} = x + 12 \)
Durum 1.1: \( x \ge 0 \)
\( x = x + 12 \)
\( 0 = 12 \)
Bu durumda geçerli bir çözüm yoktur.
Durum 1.2: \( x \lt 0 \)
\( -x = x + 12 \)
\( x = -6 \)
Bu durumda verilen 3 sayı aşağıdaki gibi olur.
\( \abs{-6}, -6 + 12, (-6)^2 \)
\( 6, 6, 36 \)
Durum 2:
\( \abs{x} = x^2 \)
Durum 2.1: \( x \ge 0 \)
\( x = x^2 \)
\( x(x - 1) = 0 \)
\( x = 0 \) ya da \( x = 1 \)
\( x = 0 \) için verilen 3 sayı aşağıdaki gibi olur.
\( \abs{0}, 0 + 12, 0^2 \)
\( 0, 12, 0 \)
\( x = 1 \) için verilen 3 sayı aşağıdaki gibi olur.
\( \abs{1}, 1 + 12, 1^2 \)
\( 1, 13, 1 \)
Durum 2.2: \( x \lt 0 \)
\( -x = x^2 \)
\( x(x + 1) = 0 \)
\( x = 0 \) ya da \( x = -1 \)
\( x = 0 \) için verilen 3 sayıyı yukarıda bulmuştuk.
\( x = -1 \) için verilen 3 sayı aşağıdaki gibi olur.
\( \abs{-1}, -1 + 12, (-1)^2 \)
\( 1, 11, 1 \)
Durum 3:
\( x + 12 = x^2 \)
\( (x - 4)(x + 3) = 0 \)
\( x = 4 \) ya da \( x = -3 \)
\( x = 4 \) için verilen 3 sayı aşağıdaki gibi olur.
\( \abs{4}, 4 + 12, 4^2 \)
\( 4, 16, 16 \)
\( x = -3 \) için verilen 3 sayı aşağıdaki gibi olur.
\( \abs{-3}, -3 + 12, (-3)^2 \)
\( 3, 9, 9 \)
İstenen koşulu sağlayan farklı \( x \) değerleri aşağıdaki gibi bulunur.
\( x \in \{ -6, -3, -1, 0, 1, 4 \} \)
\( \abs{x - a} + \abs{x + 5} = 14 \) denkleminin çözüm kümesini sonsuz elemanlı yapan \( a \) değerlerinin toplamı kaçtır?
Çözümü GösterDenklemin çözüm kümesinin sonsuz elemanlı olması için belirli bir aralıkta \( x \) değişkenleri birbirini götürmeli ve \( 14 = 14 \) şeklinde bir eşitlik oluşmalıdır.
\( x \) değişkenleri birbirini iki durumda götürür.
Durum 1:
Bu durumda birinci mutlak değer ifadesi negatif, ikinci mutlak değer ifadesi sıfır ya da pozitif olur.
\( x - a \lt 0 \) ve \( x + 5 \ge 0 \)
\( a - x + x + 5 = 14 \)
\( a + 5 = 14 \)
\( a = 9 \)
Durum 2:
Bu durumda ikinci mutlak değer ifadesi negatif, birinci mutlak değer ifadesi sıfır ya da pozitif olur.
\( x - a \ge 0 \) ve \( x + 5 \lt 0 \)
\( x - a - x - 5 = 14 \)
\( -a - 5 = 14 \)
\( a = -19 \)
Buna göre \( a \) değerlerinin toplamı \( 9 + (-19) = -10 \) olur.