Logaritma Fonksiyonu Tanım ve Görüntü Kümesi
Logaritma ve üstel fonksiyonların birbirinin tersi fonksiyonlar olduğunu görmüştük.
\( y = \log_a{x} \Longleftrightarrow a^y = x \)
Tanım gereği \( a \) tabanı 1'den farklı pozitif bir sayı olduğu için, \( a \)'nın tüm reel sayı kuvvetleri (\( y \)) tanımlıdır ve sonucu (\( x \)) her zaman bir pozitif reel sayıdır.
Buna göre logaritma fonksiyonunun tanım kümesi (\( x \)) pozitif reel sayılarla sınırlıdır ve görüntü kümesi (\( y \)) tüm reel sayılardır.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
|
\( y = \log_a{x} \) \( a \in \mathbb{R^+} - \{ 1 \} \) |
\( \mathbb{R^+} \) | \( \mathbb{R} \) |
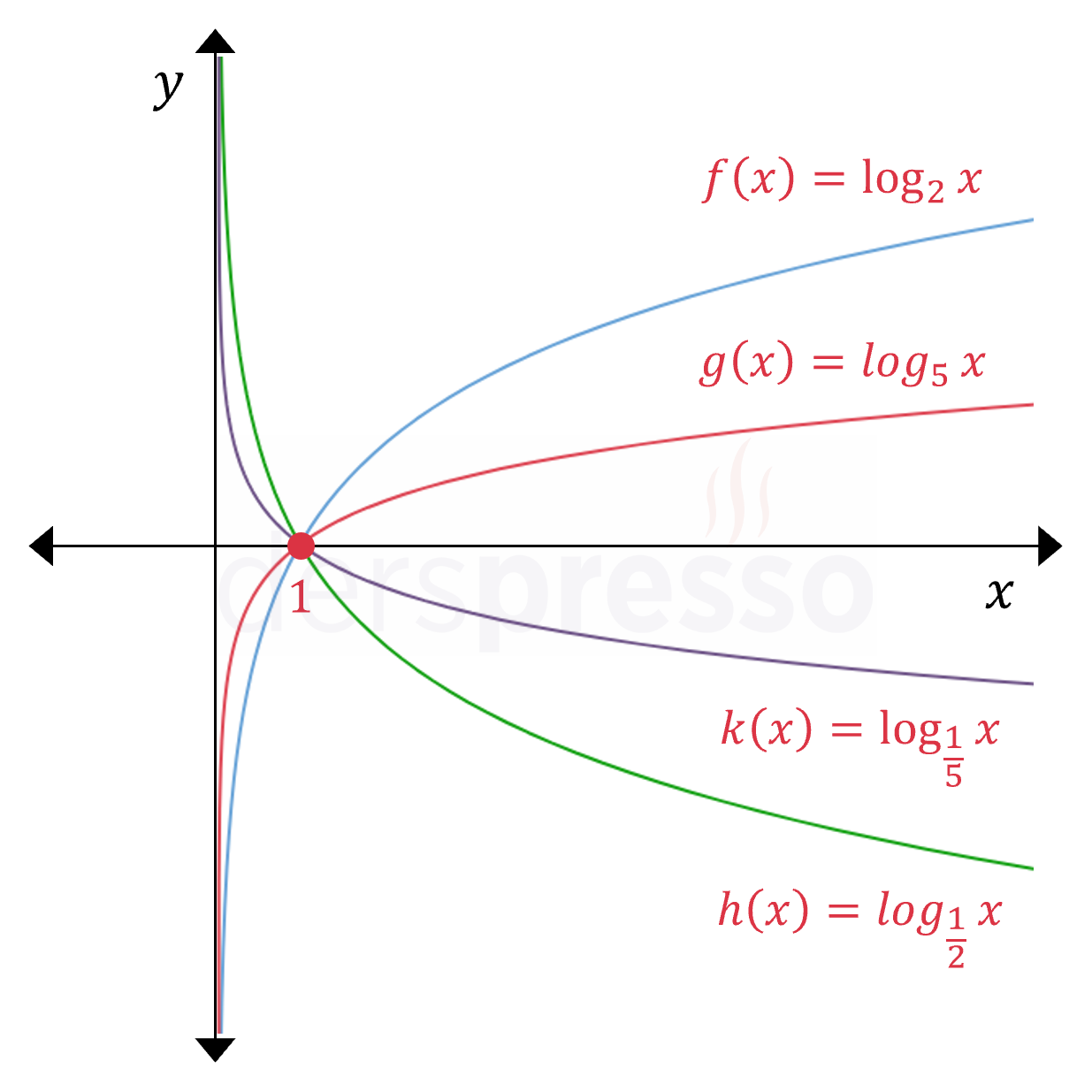
Logaritma fonksiyonlarının tanım ve görüntü kümeleri farklı tabanlar için aşağıda verilen grafikler üzerinden de teyit edilebilir.
\( f(x) = \log_5(10 - x) + 8\log_3(x - 4) \)
fonksiyonunun en geniş tanım kümesindeki tam sayı \( x \) değerlerinin toplamı kaçtır?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 10 - x \gt 0 \Longrightarrow x \lt 10 \)
\( x - 4 \gt 0 \Longrightarrow x \gt 4 \)
Bulduğumuz aralıkların kesişimi fonksiyonun en geniş tanım kümesini verir.
\( 4 \lt x \lt 10 \)
Tanım kümesi: \( x \in (4, 10) \)
Bu aralıktaki tam sayıların toplamı \( 5 + 6 + 7 + 8 + 9 = 35 \) olur.
\( f(x) = \log_{x - 2}(5 - x) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 5 - x \gt 0 \Longrightarrow x \lt 5 \)
Logaritma işleminde taban sıfırdan büyük ve 1'den farklı olmalıdır.
\( x - 2 \gt 0 \Longrightarrow x \gt 2 \)
\( x - 2 \ne 1 \Longrightarrow x \ne 3 \)
Bulduğumuz aralıkların kesişimi fonksiyonun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (2, 5) - \{3\} \)
\( m \in \mathbb{R} \) olmak üzere,
\( f(x) = \log_7(x^2 - mx + 9) \)
fonksiyonu tüm reel sayılarda tanımlı olduğuna göre, \( a \) değer aralığını bulunuz.
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( x^2 - mx + 9 \gt 0 \)
İkinci dereceden bir polinomun her \( x \) için pozitif olması için başkatsayısı pozitif olmalıdır ve \( x \) eksenini kesmemelidir.
Buna göre ifadenin deltası 0'dan küçük olmalıdır, yani reel bir kökü olmamalıdır.
\( \Delta = b^2 - 4ac \lt 0 \)
\( (-m)^2 - 4(1)(9) \lt 0 \)
\( m^2 \lt 36 \)
\( -6 \lt m \lt 6 \) bulunur.
\( f(x) = \log_{x - 3}(-x^2 + 5x + 6) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( -x^2 + 5x + 6 \gt 0 \)
\( -(x - 6)(x + 1) \gt 0 \)
\( (x - 6)(x + 1) \lt 0 \)
Pozitif başkatsayılı ikinci dereceden bir ifade kök değerlerinin arasındaki aralıkta negatif olur.
\( -1 \lt x \lt 6 \)
Logaritma işleminde taban sıfırdan büyük ve 1'den farklı olmalıdır.
\( x - 3 \gt 0 \Longrightarrow x \gt 3 \)
\( x - 3 \ne 1 \Longrightarrow x \ne 4 \)
Bulduğumuz aralıkların kesişimi fonksiyonun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (3, 6) - \{4\} \)
\( f(x) = 5\log_4{\dfrac{x - 7}{3 - x}} - 3 \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{x - 7}{3 - x} \gt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{3, 7\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, 3) \), \( (3, 7) \) ve \( (7, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (3, 7) \)
Bulduğumuz aralık aynı zamanda verilen fonksiyonun en geniş tanım kümesidir.
Tanım kümesi: \( x \in (3, 7) \)
\( f(x) = -\ln{\dfrac{16 + 6x - x^2}{x - 5}} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{16 + 6x - x^2}{x - 5} \gt 0 \)
Payı çarpanlarına ayıralım.
\( \dfrac{(x + 2)(8 - x)}{x - 5} \gt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-2, 5, 8\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -2) \), \( (-2, 5) \), \( (5, 8) \) ve \( (8, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
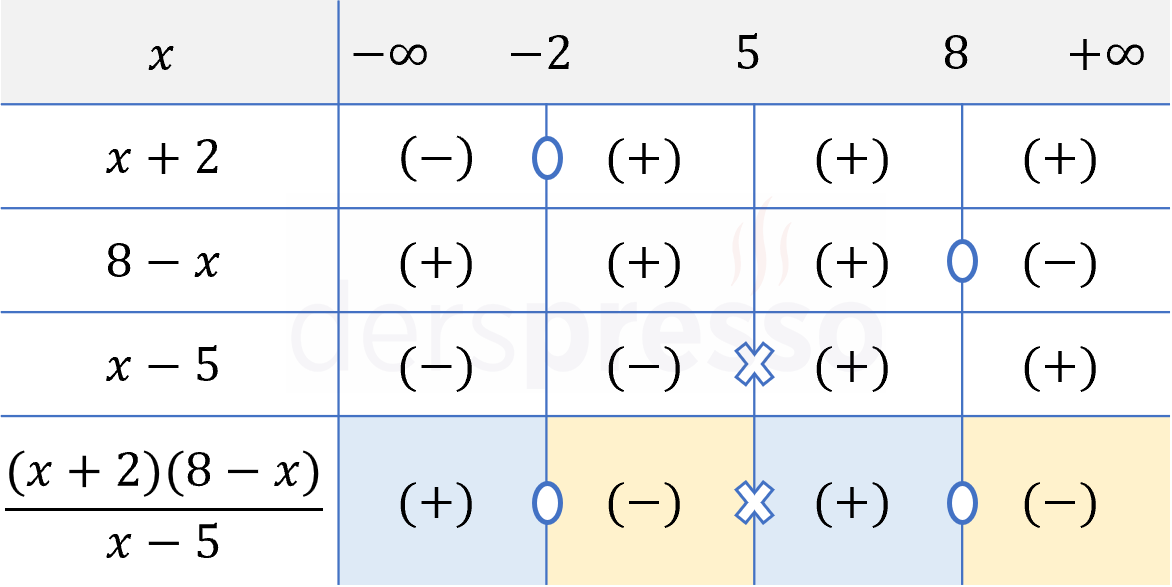
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -2) \cup (5, 8) \)
Bulduğumuz aralık aynı zamanda verilen fonksiyonun en geniş tanım kümesidir.
Tanım kümesi: \( x \in (-\infty, -2) \cup (5, 8) \)
\( f(x) = \ln(9 - x) + \sqrt{x - 2} + \cot{\dfrac{\pi x}{2}} \)
reel değerli fonksiyonunun en geniş tanım kümesindeki tam sayı \( x \) değerlerinin toplamı kaçtır?
Çözümü GösterLogaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 9 - x \gt 0 \)
\( x \lt 9 \)
Karekök ifadesinin reel sayılarda tanımlı olması için kök içi sıfır ya da sıfırdan büyük olmalıdır.
\( x - 2 \ge 0 \)
\( x \ge 2 \)
Kotanjant fonksiyonu \( \pi \) açısının tam sayı katlarında tanımsızdır.
\( k \in \mathbb{Z} \) olmak üzere,
\( \dfrac{\pi x}{2} \ne k\pi \)
\( x \ne 2k \)
Buna göre \( x \) çift sayı olamaz.
Fonksiyonun en geniş tanım kümesindeki tam sayı \( x \) değerleri aşağıdaki gibidir.
\( x \in \{ 3, 5, 7 \} \)
\( x \)'in alabileceği tam sayı değerlerin toplamı \( 3 + 5 + 7 = 15 \) olarak bulunur.
\( f(x) = \log_{64 - x^2}{\abs{3 - \abs{2 - \abs{x - 1}}}} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterLogaritma işleminde taban sıfırdan büyük ve 1'den farklı olmalıdır.
\( 64 - x^2 \gt 0 \)
\( x^2 \lt 64 \)
\( -8 \lt x \lt 8 \)
\( 64 - x^2 \ne 1 \)
\( x^2 \ne 63 \)
\( x \ne \pm 3\sqrt{7} \)
Logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
Logaritma içinde mutlak değer ifadesi bulunduğu için değeri negatif olamaz, dolayısıyla sadece ifadenin sıfır olmama durumunu kontrol etmemiz yeterlidir.
Mutlak değer ifadesini sıfır yapan ve tanım kümesi dışında bırakılması gereken değerleri bulalım.
\( \abs{3 - \abs{2 - \abs{x - 1}}} = 0 \)
\( \abs{2 - \abs{x - 1}} = 3 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2 - \abs{x - 1} = 3 \)
\( \abs{x - 1} = -1 \)
Mutlak değer ifadesi negatif olamayacağı için bu durumda geçerli bir çözüm yoktur.
Durum 2:
\( 2 - \abs{x - 1} = -3 \)
\( \abs{x - 1} = 5 \)
\( x - 1 = 5 \) veya \( x - 1 = -5 \)
\( x = 6 \) veya \( x = -4 \)
Bu iki değer fonksiyonu tanımsız yapar, dolayısıyla tanım kümesi dışında bırakılmalıdır.
Bulduğumuz aralıkların kesişimi fonksiyonun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (-8, 8) - \{\pm 3\sqrt{7}, -4, 6\} \)
\( f(x) = \sqrt{\log_{\pi}{\dfrac{x + 3}{x - 2}}} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterKarekök ifadesinin içi negatif olamaz.
\( \log_{\pi}{\dfrac{x + 3}{x - 2}} \ge 0 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( \pi \gt 1 \) olduğu için bu işlemde eşitsizliğin yönü değişmez.
\( \dfrac{x + 3}{x - 2} \ge \pi^0 = 1 \)
\( \dfrac{x + 3}{x - 2} - 1 \ge 0 \)
\( \dfrac{x + 3 - x + 2}{x - 2} \ge 0 \)
\( \dfrac{5}{x - 2} \ge 0 \)
Rasyonel ifadenin payı 5 olduğu için ifadenin değeri sıfır olamaz.
İfadenin pozitif olması için payda pozitif olmalıdır.
\( x - 2 \gt 0 \)
\( x \gt 2 \)
Logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{x + 3}{x - 2} \gt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-3, 2\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -3) \), \( (-3, 2) \) ve \( (2, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -3) \cup (2, \infty) \)
Bulduğumuz aralıkların kesişimi fonksiyonun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (2, \infty) \)
\( x \in \mathbb{R} \) olmak üzere,
\( \sqrt{\ln{\dfrac{2x^2 - x}{10}}} \) ifadesini reel sayılarda tanımlı yapan \( x \) değer aralığı nedir?
Çözümü GösterVerilen ifadenin sonucunun reel sayı olması için iki koşul sağlanmalıdır.
Durum 1:
Karekök içindeki ifade sıfır ya da sıfırdan büyük olmalıdır.
\( \ln{\dfrac{2x^2 - x}{10}} \ge 0 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( \dfrac{2x^2 - x}{10} \ge e^0 = 1 \)
\( 2x^2 - x \ge 10 \)
\( 2x^2 - x - 10 \ge 0 \)
\( (2x - 5)(x + 2) \ge 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif ya da sıfır olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( x \in (-\infty, -2] \cup [\frac{5}{2}, \infty) \)
Durum 2:
Logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{2x^2 - x}{10} \gt 0 \)
\( 2x^2 - x \gt 0 \)
\( x(2x - 1) \gt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( x \in (-\infty, 0) \cup (\frac{1}{2}, \infty) \)
Bulduğumuz aralıkların kesişimi sorudaki ifadenin sonucunu reel sayı yapan \( x \) değer aralığını verir.
\( x \in (-\infty, -2] \cup [\frac{5}{2}, \infty) \)
\( f(x) = \log{x} \) olduğuna göre,
\( (f \circ f)(x) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterDetaylarını bileşke fonksiyon konusunda gördüğümüz üzere, \( g \circ f \) fonksiyonunun tanım kümesindeki elemanlar aşağıdaki iki koşulu sağlamalıdır.
Koşul 1:
\( f \) fonksiyonunun tanım kümesinde bulunmalıdır.
Logaritma fonksiyonu pozitif reel sayılarda tanımlıdır.
\( x \gt 0 \)
Koşul 2:
\( f \) fonksiyonuna göre görüntüleri \( g \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( f(x) \gt 0 \)
\( \log{x} \gt 0 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( x \gt 10^0 = 1 \)
Bulduğumuz aralıkların kesişimi bileşke fonksiyonun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (1, \infty) \)