Logaritmik Eşitsizlikler
Bu bölümde bazı logaritmik eşitsizlik tiplerini ve her biri için çözüm yöntemlerini inceleyeceğiz.
Eşitsizliklerin çözümünde her logaritma ifadesi için aşağıdaki iki koşul da çözüme ek birer koşul olarak eklenmelidir.
- Logaritma içinin pozitif olması
- Logaritma tabanı değişken içeriyorsa tabanın pozitif ve 1'den farklı olması
Logaritma kaynaklı tanımsızlıklar dışında fonksiyonların tanım ve görüntü kümesi bölümünde listelediğimiz tüm tanımsızlık tipleri eşitsizlik çözümlerinde akılda tutulmalıdır.
Sabit Değer
Bir logaritma ifadesi ile sabit bir reel sayı arasındaki eşitsizlikte eşitsizlik üstel ifadeye çevrilir.
Logaritma tabanı birden büyükse eşitsizlik işareti yön değiştirmez.
\( a \gt 1 \) olmak üzere,
\( m \le \log_a{x} \lt n \) ise,
\( a^m \le x \lt a^n \)
\( -3 \le \log_2(x + 1) \lt 6 \)
\( 2^{-3} \le x + 1 \lt 2^6 \)
\( \frac{1}{8} \le x + 1 \lt 64 \)
\( -\frac{7}{8} \le x \lt 63 \)
\( x + 1 \) aralığındaki tüm değerler pozitif olduğu için bu aralıktaki tüm değerler geçerli birer çözümdür.
Çözüm kümesi: \( x \in [-\frac{7}{8}, 63) \)
\( \log_4(x - 3) \lt 2 \)
\( x - 3 \lt 4^2 \)
\( x \lt 19 \)
Ayrıca logaritma içi sıfırdan büyük olmalıdır.
\( x - 3 \gt 0 \Longrightarrow x \gt 3 \)
Çözüm kümesi: \( x \in (3, 19) \)
Logaritma tabanı sıfır ve bir aralığındaysa eşitsizlik işareti yön değiştirir.
\( 0 \lt a \lt 1 \) olmak üzere,
\( m \le \log_a{x} \lt n \) ise,
\( a^m \ge x \gt a^n \)
\( -4 \le \log_{\frac{1}{3}}(3x) \lt 2 \)
\( (\frac{1}{3})^{-4} \ge 3x \gt (\frac{1}{3})^2 \)
\( 81 \ge 3x \gt \frac{1}{9} \)
\( 27 \ge x \gt \frac{1}{27} \)
\( 3x \) aralığındaki tüm değerler pozitif olduğu için bu aralıktaki tüm değerler geçerli birer çözümdür.
Çözüm kümesi: \( x \in (\frac{1}{27}, 27] \)
Eşit Tabanlar
Tabanları aynı iki logaritma ifadesi arasındaki eşitsizlik logaritma içleri arasında eşitsizliğe dönüştürülebilir.
Logaritma tabanı birden büyükse logaritma içi daha büyük olan taraf daha büyüktür.
\( a \gt 1 \) olmak üzere,
\( \log_a{x_1} \gt \log_a{x_2} \) ise,
\( x_1 \gt x_2 \)
\( \log_3{x} \le \log_3{8} \Longrightarrow 0 \lt x \le 8 \)
Logaritma tabanı sıfır ve bir aralığındaysa logaritma içi daha küçük olan taraf daha büyüktür.
\( 0 \lt a \lt 1 \) olmak üzere,
\( \log_a{x_1} \gt \log_a{x_2} \) ise,
\( x_1 \lt x_2 \)
\( \log_{\frac{1}{2}}{x} \ge \log_{\frac{1}{2}}{4} \Longrightarrow 0 \lt x \le 4 \)
Eşitlenebilir Tabanlar
İki logaritma ifadesi arasındaki eşitsizlikte tabanlar farklı ama eşitlenebilir ise önce tabanlar eşitlenir, daha sonra tabanın birden büyük ya da (0, 1) aralığında olma durumuna göre yukarıdaki iki eşit taban kuralından biri uygulanır.
\( \log_{\frac{1}{64}}{x} \gt \log_{8}{\sqrt{2}} \)
\( \log_{2^{-6}}{x} \gt \log_{2^3}{2^{\frac{1}{2}}} \)
\( -\frac{1}{6} \cdot \log_{2}{x} \gt \frac{1}{3} \cdot \frac{1}{2} \)
\( \log_{2}{x} \lt -1 \)
\( 0 \lt x \lt \frac{1}{2} \)
Bir Sayının Logaritma Değer Aralığını Tahmin Etme
Bir sayının logaritma değerinin hangi iki tam sayı arasında bulunduğunu bulmak için aşağıdaki gibi bir yöntem izlenebilir.
20'nin 2 tabanında logaritmasının bulunduğu tam sayı aralığı bulalım.
Önce 20'nin 2 tabanında hangi iki tam sayının üsleri arasında bulunduğunu bulalım.
\( 16 \lt 20 \lt 32 \)
\( 2^4 \lt 20 \lt 2^5 \)
Üç ifadenin de 2 tabanında logaritmasını alalım.
\( \log_2{2^4} \lt \log_2{20} \lt \log_2{2^5} \)
\( 4\log_2{2} \lt \log_2{20} \lt 5\log_2{2} \)
\( 4 \lt \log_2{20} \lt 5 \)
Buna göre 20'nin 2 tabanında logaritma değeri \( (4, 5) \) aralığındadır.
\( \log_{\frac{1}{2}}(x - 5) \gt -2 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma ifadesini üstel ifade şeklinde yazalım.
\( 0 \lt a \lt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu azalan olduğu için, bu adımda eşitsizlik yön değiştirir.
\( x - 5 \lt \left( \dfrac{1}{2} \right)^{-2} \)
\( x - 5 \lt 4 \)
\( x \lt 9 \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( x - 5 \gt 0 \Longrightarrow x \gt 5 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in (5, 9) \)
\( 2 \lt \log_{\frac{1}{3}}{\dfrac{x + 1}{36}} \lt 3 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü Göster\( \log_{\frac{1}{3}}\left( \dfrac{1}{3} \right)^2 \lt \log_{\frac{1}{3}}{\dfrac{x + 1}{36}} \lt \log_{\frac{1}{3}}\left( \dfrac{1}{3} \right)^3 \)
\( 0 \lt a \lt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu azalan olduğu için, fonksiyon değeri büyük olan tarafın logaritma içi küçüktür.
\( \left( \dfrac{1}{3} \right)^2 \gt \dfrac{x + 1}{36} \gt \left( \dfrac{1}{3} \right)^3 \)
\( \dfrac{1}{9} \gt \dfrac{x + 1}{36} \gt \dfrac{1}{27} \)
\( 4 \gt x + 1 \gt \dfrac{4}{3} \)
\( 3 \gt x \gt \dfrac{1}{3} \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{x + 1}{36} \gt 0 \Longrightarrow x \gt -1 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in \left( \dfrac{1}{3}, 3 \right) \)
\( \log_5(x^2 + 8x + 41) \le 3 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
\( x^2 + 8x + 41 \le 5^3 = 125 \)
\( x^2 + 8x - 84 \le 0 \)
\( (x + 14)(x - 6) \le 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlanır.
\( -14 \le x \le 6 \)
Çözüm kümesi: \( x \in [-14, 6] \)
\( \log_9{27} \le \log_4{x} \lt \log_{\sqrt{5}}{5\sqrt{5}} \)
eşitsizliğini sağlayan kaç tam sayı \( x \) değeri vardır?
Çözümü Göster\( \log_{3^2}{3^3} \le \log_{2^2}{x} \lt \log_{5^{\frac{1}{2}}}{5^{\frac{3}{2}}} \)
Logaritma içinin üssü olduğu gibi, tabanın üssünün çarpmaya göre tersi logaritma önüne katsayı olarak alınabilir.
\( \dfrac{3}{2}\log_3{3} \le \dfrac{1}{2}\log_2{x} \lt \dfrac{3}{2 \cdot \frac{1}{2}}\log_5{5} \)
\( 3 \le \log_2{x} \lt 6 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
\( 2^3 \le x \lt 2^6 \)
\( 8 \le x \lt 64 \)
Bu aralıkta \( 63 - 8 + 1 = 56 \) tam sayı vardır.
\( \log_{\sqrt{3}}(8 - x) \le \log_3(x^2 - 2) \) eşitsizliğini sağlayan tam sayıların toplamı kaçtır?
Çözümü Göster\( \log_{3^\frac{1}{2}}(8 - x) \le \log_3(x^2 - 2) \)
\( 2\log_3(8 - x) \le \log_3(x^2 - 2) \)
\( \log_3(8 - x)^2 \le \log_3(x^2 - 2) \)
Tabanları aynı ve birden büyük olan iki logaritma ifadesi arasındaki eşitlikte logaritma içi daha büyük olan taraf daha büyüktür.
\( (8 - x)^2 \le x^2 - 2 \)
\( 64 - 16x + x^2 \le x^2 - 2 \)
\( 66 \le 16x \)
\( x \ge \dfrac{66}{16} = \dfrac{33}{8} \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 8 - x \gt 0 \)
\( x \lt 8 \)
\( x^2 - 2 \gt 0 \)
\( x \in (-\infty, -\sqrt{2}) \cup (\sqrt{2}, \infty) \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in \left[ \dfrac{33}{8}, 8 \right) \)
Bu aralıktaki tam sayıların toplamı \( 5 + 6 + 7 = 18 \) olarak bulunur.
\( \log_3{\dfrac{x - 2}{x - 3}} \gt 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
\( \dfrac{x - 2}{x - 3} \gt 3^0 = 1 \)
\( \dfrac{x - 2}{x - 3} - 1 \gt 0 \)
\( \dfrac{x - 2 - x + 3}{x - 3} \gt 0 \)
\( \dfrac{1}{x - 3} \gt 0 \)
Bu eşitsizlik payda sıfırdan büyük olduğunda pozitif olur.
\( x - 3 \gt 0 \)
\( x \gt 3 \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \dfrac{x - 2}{x - 3} \gt 0 \)
\( x \in (-\infty, 2) \cup (3, \infty) \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in (3, \infty) \)
\( x^{\log_3{x}} \gt 81 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin taraflarının 3 tabanında logaritmasını alalım.
\( \log_3{x^{\log_3{x}}} \gt \log_3{81} \)
\( \log_3{x}\log_3{x} \gt 4 \)
\( (\log_3{x})^2 - 4 \gt 0 \)
\( \log_3{x} = t \) şeklinde değişken değiştirelim.
\( t^2 - 4 \gt 0 \)
\( (t - 2)(t + 2) \gt 0 \)
\( t \lt -2 \) ya da \( t \gt 2 \)
\( \log_3{x} \lt -2 \) ya da \( \log_3{x} \gt 2 \)
\( x \lt \dfrac{1}{9} \) ya da \( x \gt 9 \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( x \gt 0 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in (0, \frac{1}{9}) \cup (9, \infty) \)
\( 5 - 3e^{-x} \ge 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü Göster\( e^{-x} \) ifadesini yalnız bırakalım.
\( - 3e^{-x} \ge -4 \)
\( e^{-x} \le \dfrac{4}{3} \)
Eşitsizliğin her iki tarafının doğal logaritmasını alalım.
\( \ln{e^{-x}} \le \ln{\dfrac{4}{3}} \)
\( -x \ln{e} \le \ln{\dfrac{4}{3}} \)
\( x \ge -\ln{\dfrac{4}{3}} \)
\( x \ge \ln\left( \dfrac{4}{3} \right)^{-1} \)
\( x \ge \ln{\dfrac{3}{4}} \)
Çözüm kümesi: \( x \in \left[ \ln{\dfrac{3}{4}}, \infty \right) \)
\( \log_3(\log_2(x - 7)) \lt 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEn dıştaki logaritma ifadesini üstel ifade şeklinde yazalım.
\( \log_2(x - 7) \lt 3^1 = 3 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( x - 7 \lt 2^3 = 8 \)
\( x \lt 15 \)
İçteki logaritma ifadesinin içi sıfırdan büyük olmalıdır.
\( x - 7 \gt 0 \)
\( x \gt 7 \)
Ayrıca dıştaki logaritma ifadesinin de içi sıfırdan büyük olmalıdır.
\( \log_2(x - 7) \gt 0 \)
\( x - 7 \gt 2^0 = 1 \)
\( x \gt 8 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in (8, 15) \)
\( x^{\ln{x}} \lt (xe^6) \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin taraflarının doğal logaritmasını alalım.
\( \ln{x}^{\ln{x}} \lt \ln(xe^6) \)
\( \ln{x}\ln{x} \lt \ln{x} + \ln{e^6} \)
\( (\ln{x})^2 \lt \ln{x} + 6 \)
\( \ln{x} = t \) şeklinde değişken değiştirelim.
\( t^2 \lt t + 6 \)
\( t^2 - t - 6 \lt 0 \)
\( (t - 3)(t + 2) \lt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlanır.
\( -2 \lt t \lt 3 \)
\( -2 \lt \ln{x} \lt 3 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
\( e^{-2} \lt x \lt e^3 \)
Çözüm kümesi: \( x \in (e^{-2}, e^3) \)
\( \log_{0,5}(x^2 - x + 1) \gt 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma ifadesini üstel ifade şeklinde yazalım.
\( 0 \lt a \lt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu azalan olduğu için, bu adımda eşitsizlik yön değiştirir.
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 0 \lt x^2 - x + 1 \lt (0,5)^0 = 1 \)
\( x^2 - x + 1 \) ifadesinin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac = (-1)^2 - 4(1)(1) = -3 \lt 0 \)
İkinci dereceden ifadenin başkatsayısı pozitif ve deltası negatif olduğu için grafiği \( x \) ekseninin üstünde kalır, dolayısıyla \( x^2 - x + 1 \) ifadesi her \( x \) için sıfırdan büyük olur.
\( x^2 - x + 1 \lt 1 \)
\( x(x - 1) \lt 0 \)
Çözüm kümesi: \( 0 \lt x \lt 1 \)
\( \log_3{\abs{x - 2}} \lt 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma ifadesini üstel ifade şeklinde yazalım.
\( \abs{x - 2} \lt 3^1 = 3 \)
\( -3 \lt x - 2 \lt 3 \)
\( -1 \lt x \lt 5 \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \abs{x - 2} \gt 0 \)
Mutlak değerli bir ifadenin sonucu her zaman sıfır ya da pozitiftir.
\( x - 2 \ne 0 \)
\( x \ne 2 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( x \in (-1, 5) - \{2\} \)
\( 3x^2 - 6x - \log_3{n} = 0 \) denkleminin reel kökü bulunmadığına göre, \( n \)'nin değer aralığı nedir?
Çözümü Gösterİkinci dereceden denklemin reel kökü yoksa deltası sıfırdan küçük olmalıdır.
\( a = 3, \quad b = -6, \quad c = -\log_3{n} \)
\( \Delta = b^2 - 4ac \lt 0 \)
\( = (-6)^2 - 4(3)(-\log_3{n}) \lt 0 \)
\( 36 + 12\log_3{n} \lt 0 \)
\( \log_3{n} \lt -3 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( 0 \lt n \lt \dfrac{1}{27} \) bulunur.
\( 121 \approx 125 \) yaklaşımını kullanarak \( \log_5{11} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Göster\( 11^2 \approx 5^3 \)
Her iki tarafın 5 tabanında logaritmasını alalım.
\( \log_5{11^2} \approx \log_5{5^3} \)
\( 2\log_5{11} \approx 3 \)
\( \log_5{11} \approx \dfrac{3}{2} \) bulunur.
\( n \in \mathbb{Z} \) olmak üzere,
\( -2,50 \le 2^{3n - 1} - 3 \le 347 \) eşitsizliğini sağlayan \( n \) değerlerinin toplamı kaçtır?
Çözümü GösterEşitsizliğin taraflarına 3 ekleyelim.
\( 0,50 \le 2^{3n-1} \le 350 \)
\( 2^{-1} \le 2^{3n-1} \le 350 \)
Eşitsizliğin her tarafının 2 tabanında logaritmasını alalım.
\( \log_2{2^{-1}} \le \log_2{2^{3n-1}} \le \log_2{350} \)
\( 2^8 \lt 350 \lt 2^9 \) olduğu için \( \log_2{350} \) değeri \( (8, 9) \) aralığındadır.
\( -1 \le 3n - 1 \le 8,\dots \)
Eşitsizliğin taraflarına 1 ekleyelim.
\( 0 \le 3n \le 9,\dots \)
Eşitsizliğin taraflarını 3'e bölelim.
\( 0 \le n \le 3,\dots \)
\( n \) tam sayısının bu aralıkta alabileceği değerler 0, 1, 2 ve 3'tür.
\( 0 + 1 + 2 + 3 = 6 \) bulunur.
\( (x + 2)\ln{\abs{x}} \gt 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin sol tarafı \( x + 2 \) ve \( \ln{\abs{x}} \) ifadelerinin ikisi de pozitif ya da ikisi de negatif olduğunda pozitif olur.
Durum 1: İki çarpan da pozitif
\( x + 2 \gt 0 \)
\( x \gt -2 \)
\( \ln{\abs{x}} \gt 0 \)
\( \abs{x} \gt e^0 = 1 \)
\( x \lt -1 \) ya da \( x \gt 1 \)
\( x \in (-2, -1) \cup (1, \infty) \)
Durum 2: İki çarpan da negatif
\( x + 2 \lt 0 \)
\( x \lt -2 \)
\( \ln{\abs{x}} \lt 0 \)
\( \abs{x} \lt e^0 = 1 \)
\( -1 \lt x \lt 1 \)
\( x = \emptyset \)
Ayrıca logaritma işleminde logaritma içi sıfırdan büyük olmalıdır.
\( \abs{x} \gt 0 \)
Mutlak değerli bir ifadenin sonucu her zaman sıfır ya da pozitiftir.
\( x \ne 0 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin birleşiminden oluşur.
Çözüm kümesi: \( x \in (-2, -1) \cup (1, \infty) \)
\( \dfrac{\log_3{a} - 3}{7 - \log_2{a}} \gt 0 \) eşitsizliğini sağlayan kaç farklı \(a\) tam sayı değeri vardır?
Çözümü GösterÖnce pay ve paydadaki ifadeleri sıfır yapan değerleri bulalım.
\( \log_3{a} - 3 = 0 \)
\( \log_3{a} = 3 \)
\( a = 3^3 = 27 \)
\( 7 - \log_2{a} = 0 \)
\( \log_2{a} = 7 \)
\( a = 2^7 = 128 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{27, 128\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bir işaret tablosu hazırlayalım.
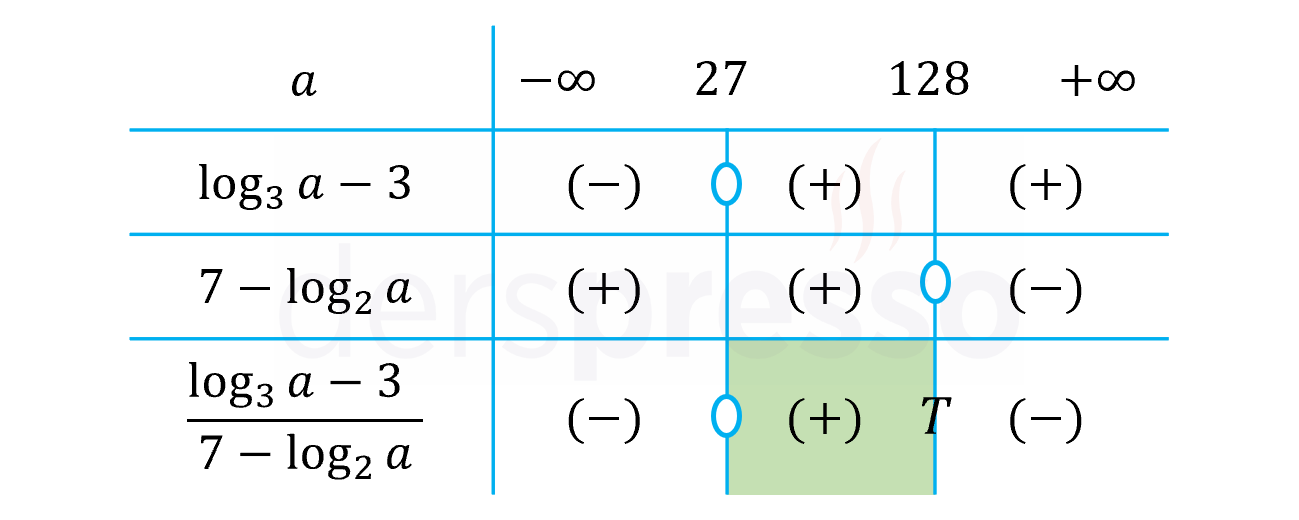
Rasyonel ifade paydayı sıfır yapan \( x = 128 \) değerinde tanımsız, payı sıfır yapan \( x = 27 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( a \in (27, 128) \)
Terim sayısı formülünü kullanarak \( a \)'nın bu aralıkta alabileceği \( 127 - 28 + 1 = 100 \) farklı tam sayı değer bulunur.
\( f(x) = \log_{\frac{1}{25}}{\dfrac{1}{x^3 - 2}} \) en geniş tanım kümesi içinde tanımlı bir fonksiyondur.
\( 0 \lt f(x) \le 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterLogaritma tabanını ve içini üslü ifade şeklinde yazalım.
\( f(x) = \log_{5^{-2}}(x^3 - 2)^{-1} \)
Logaritma içinin üssü olduğu gibi, tabanın üssünün çarpmaya göre tersi logaritma önüne katsayı olarak alınabilir.
\( = \dfrac{-1}{-2}\log_5(x^3 - 2) \)
\( = \dfrac{1}{2}\log_5(x^3 - 2) \)
Verilen eşitsizliğin çözüm kümesini bulalım.
\( 0 \lt \dfrac{1}{2}\log_5(x^3 - 2) \le 1 \)
\( 0 \lt \log_5(x^3 - 2) \le 2 \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
\( a \gt 1 \) olmak üzere \( \log_{a}{x} \) fonksiyonu artan olduğu için, bu adımda eşitsizlik yön değiştirmez.
\( 5^0 \lt x^3 - 2 \le 5^2 \)
\( 1 \lt x^3 - 2 \le 25 \)
\( 3 \lt x^3 \le 27 \)
\( \sqrt[3]{3} \lt x \le 3 \)
Ek bir koşul olarak bir logaritma ifadesinin içi her zaman pozitif olmalıdır.
\( \dfrac{1}{x^3 - 2} \gt 0 \)
Bu eşitsizlik paydanın pozitif olduğu her durumda sağlanır.
\( x^3 - 2 \gt 0 \)
\( x^3 \gt 2 \)
\( x \gt \sqrt[3]{2} \)
Eşitsizliğin çözüm kümesi bulduğumuz iki aralığın kesişim kümesidir.
Çözüm kümesi: \( x \in (\sqrt[3]{3}, 3] \)