Logaritmik Fonksiyonlarının Grafiği
Önceki bölümde gördüğümüz üzere, logaritma fonksiyonunun tanım kümesi pozitif reel sayılar, görüntü kümesi ise tüm reel sayılardır.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
|
\( y = \log_a{x} \) \( a \in \mathbb{R^+} - \{ 1 \} \) |
\( \mathbb{R^+} \) | \( \mathbb{R} \) |
Logaritma fonksiyonunun grafiği taban değerine göre aşağıdaki şekillerde oluşur.
Taban Birden Büyükse
Tabanın birden büyük olduğu (\( a \gt 1 \)) iki farklı logaritma fonksiyonu için grafik aşağıdaki gibi olur.
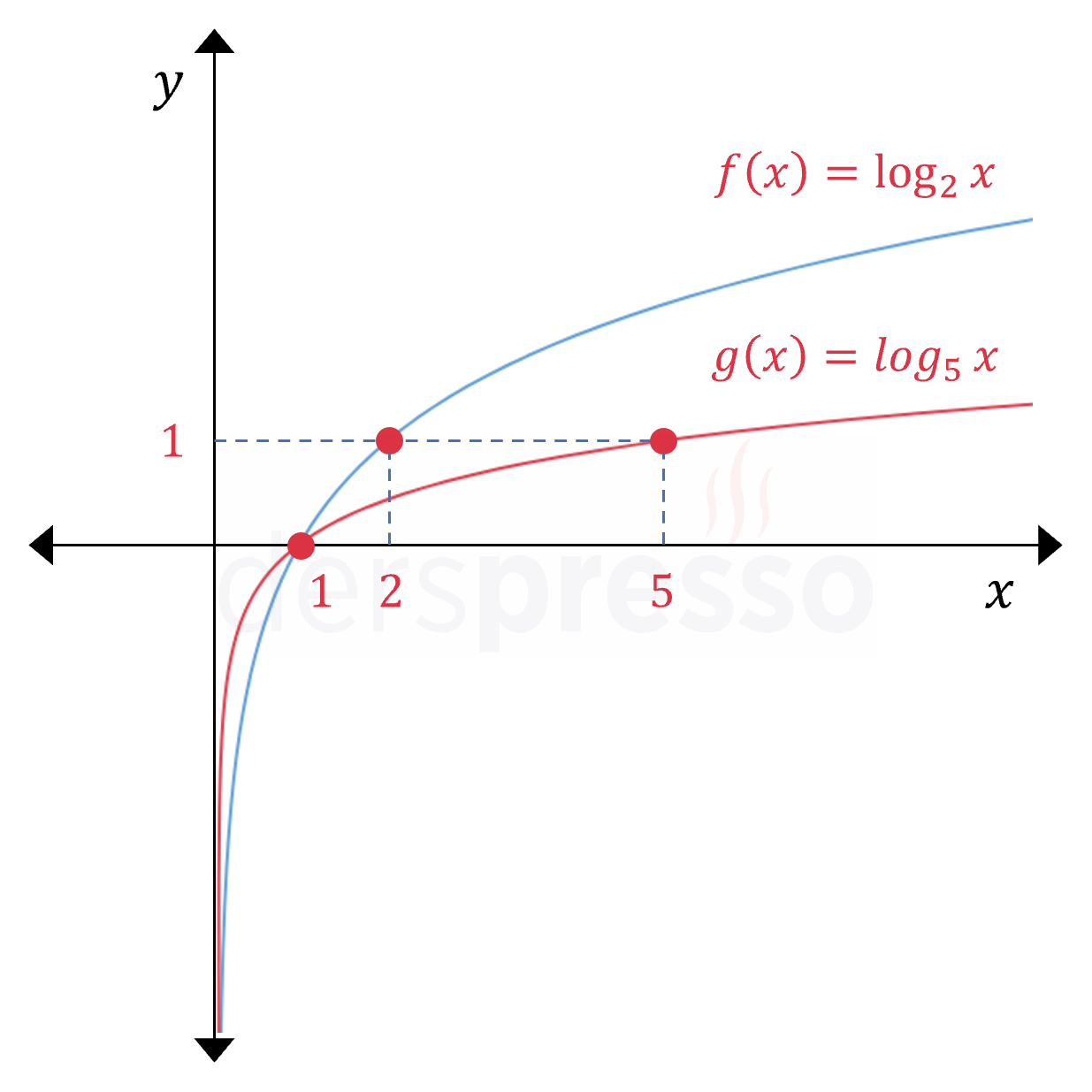
Bu fonksiyonların grafikleri ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Logaritma tanım kümesi gereği grafik \( x \in (0, \infty) \) aralığında tanımlıdır.
- Grafik tüm tanım aralığında artandır.
- Grafik \( y \) eksenine yaklaşır ama kesmez, dolayısıyla \( y \) ekseni grafiğin bir dikey asimptotudur.
- Grafik \( x \) eksenini her zaman \( (1, 0) \) noktasında keser.
- Taban \( a \) olmak üzere, \( \log_a{a} = 1 \) olduğu için grafik her zaman \( (a, 1) \) noktasından geçer.
- Fonksiyon birebir ve örtendir, bu yüzden ters fonksiyonu tanımlıdır ve \( f^{-1} = a^x \) üstel fonksiyondur.
- Pozitif \( y \) değerlerinde (I. bölge) daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin altında kalır, çünkü belirli bir \( x \) değerini elde etmek için daha büyük tabanlı bir sayının daha küçük bir üssünü almak yeterlidir.
- Negatif \( y \) değerlerinde (IV. bölge) daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin üstünde kalır.
Taban Sıfır ve Bir Aralığındaysa
Tabanın sıfır ve bir arasında olduğu (\( 0 \lt a \lt 1 \)) iki farklı logaritma fonksiyonu için grafik aşağıdaki gibi olur.
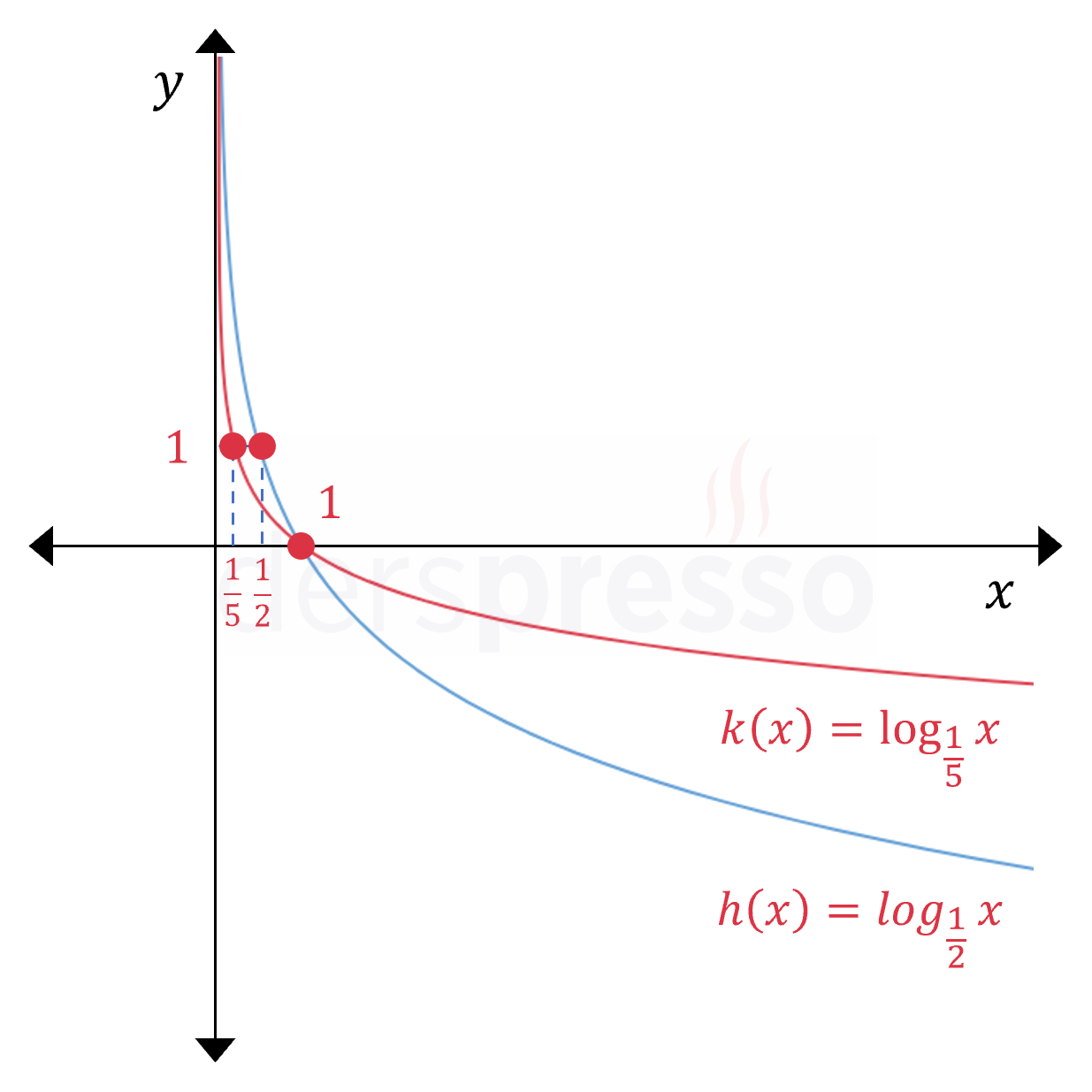
Bu fonksiyonların grafikleri ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Logaritma tanım kümesi gereği grafik \( x \in (0, \infty) \) aralığında tanımlıdır.
- Grafik tüm tanım aralığında azalandır.
- Grafik \( y \) eksenine yaklaşır ama kesmez, dolayısıyla \( y \) ekseni grafiğin bir dikey asimptotudur.
- Grafik \( x \) eksenini her zaman \( (1, 0) \) noktasında keser.
- Taban \( a \) olmak üzere, \( \log_a{a} = 1 \) olduğu için grafik her zaman \( (a, 1) \) noktasından geçer.
- Fonksiyon birebir ve örtendir, bu yüzden ters fonksiyonu tanımlıdır ve üstel fonksiyondur.
- Negatif \( y \) değerlerinde (IV. bölge) daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin altında kalır.
- Pozitif \( y \) değerlerinde (I. bölge) daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin üstünde kalır.
Logaritma Değerinin İşareti
\( \log_a{x} \) ifadesinin sonucunun işareti, \( a \) ve \( x \) değerlerinin bulundukları aralıklara göre değişir. Yukarıdaki grafiklere göre \( a \), \( x \) ve logaritma değeri arasındaki ilişkiyi aşağıdaki şekilde özetleyebiliriz.
| \( a \) ve \( x \) Değer Aralıkları | \( 0 \lt x \lt 1 \) | \( x \gt 1 \) |
|---|---|---|
| \( a \gt 1 \) | \( \log_a{x} \lt 0 \) | \( \log_a{x} \gt 0 \) |
| \( 0 \lt a \lt 1 \) | \( \log_a{x} \gt 0 \) | \( \log_a{x} \lt 0 \) |
Aşağıdaki ifadelerden hangilerinin değeri negatiftir?
I. \( \log_3{2} \)
II. \( \log_3{\frac{1}{2}} \)
III. \( \log_\frac{1}{3}{2} \)
IV. \( \log_\frac{1}{3}{\frac{1}{2}} \)
Çözümü GösterKonu anlatımında ve fonksiyon grafiklerinde gösterdiğimiz üzere, \( \log_a{x} \) formundaki bir logaritma ifadesinde \( a \gt 1 \) ise \( 0 \lt x \lt 1 \) aralığında, \( 0 \lt a \lt 1 \) ise \( x \gt 1 \) aralığında logaritma değeri negatif olur.
Buna göre II. ve III. ifadelerin sonucu negatiftir.
Aşağıdaki ifadelerden hangilerinin değeri 1'den küçüktür?
I. \( \log_3{2} \)
II. \( \log_2{3} \)
III. \( \log_\frac{1}{3}{\frac{1}{2}} \)
IV. \( \log_\frac{1}{2}{\frac{1}{3}} \)
Çözümü GösterKonu anlatımında ve fonksiyon grafiklerinde gösterdiğimiz üzere, \( \log_a{x} \) formundaki bir logaritma ifadesinde \( a \gt 1 \) ise \( 0 \lt x \lt a \) aralığında, \( 0 \lt a \lt 1 \) ise \( x \gt a \) aralığında logaritma değeri 1'den küçük olur.
Buna göre I. ve III. ifadelerin sonucu 1'den küçüktür.
\( a = \log_5{3} \)
\( b = \log_{25}{16} \)
\( c = \log_{125}{216} \)
olduğuna göre, \( a, b, c \) değerlerini küçükten büyüğe doğru sıralayınız.
Çözümü Gösterİfadeleri aynı tabana getirelim.
\( a = \log_5{3} \)
\( b = \log_{5^2}{4^2} = \log_5{4} \)
\( c = \log_{5^3}{6^3} = \log_5{6} \)
\( f(x) = \log_a{x} \) fonksiyonu \( a \gt 1 \) için artan olduğu için, \( x \) değeri büyüdükçe fonksiyon değeri de büyür.
Buna göre ifadelerin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( a \lt b \lt c \)
\( \log_{\frac{1}{5}}{a} \lt \log_{\frac{1}{5}}{b} \lt \log_{\frac{1}{5}}{c} \)
olduğuna göre, \( a, b, c \) değerlerini küçükten büyüğe doğru sıralayınız.
Çözümü Göster\( f(x) = \log_a{x} \) fonksiyonu \( 0 \lt a \lt 1 \) için azalan olduğu için, \( x \) değeri büyüdükçe fonksiyon değeri küçülür.
Buna göre ifadelerin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( c \lt b \lt a \)
Aşağıdaki ifadelerden hangilerinin değeri negatiftir?
I. \( \log_2{\log_3{2}} \)
II. \( \log_2{\log_2{3}} \)
III. \( \log_{\frac{1}{2}}{\log_3{2}} \)
IV. \( \log_{\frac{1}{2}}{\log_2{3}} \)
Çözümü GösterLogaritma fonksiyonunun farklı taban ve \( x \) değerleri için değer aralıklarını logaritma grafiklerini dikkate alarak özetleyelim.
\( y = \log_a{x} \) logaritma ifadesinde,
Taban 1'den büyükse:
- \( 0 \lt x \lt 1 \Longrightarrow y \lt 0 \)
- \( 1 \lt x \Longrightarrow y \gt 0 \)
Taban 0 - 1 aralığında ise:
- \( 0 \lt x \lt 1 \Longrightarrow y \gt 0 \)
- \( 1 \lt x \Longrightarrow y \lt 0 \)
I. öncül:
\( 0 \lt \log_3{2} \lt 1 \)
\( \log_2{\log_3{2}} \lt 0 \)
İfadenin değeri negatiftir.
II. öncül:
\( \log_2{3} \gt 1 \)
\( \log_2{\log_2{3}} \gt 0 \)
İfadenin değeri pozitiftir.
III. öncül:
\( 0 \lt \log_3{2} \lt 1 \)
\( \log_{\frac{1}{2}}{\log_3{2}} \gt 0 \)
İfadenin değeri pozitiftir.
IV. öncül:
\( \log_2{3} \gt 1 \)
\( \log_{\frac{1}{2}}{\log_2{3}} \lt 0 \)
İfadenin değeri negatiftir.
Buna göre I. ve IV. öncüllerdeki ifadelerin değeri negatiftir.
\( 0 \lt x \lt y \lt 1 \lt z \) olduğuna göre,
Aşağıdaki ifadeleri küçükten büyüğe doğru sıralayın.
\( a = \log_x{2}, \quad b = \log_y{4}, \quad c = \log_z{8} \)
Çözümü GösterLogaritma grafiklerini de düşünerek ifadelerin değerlerini karşılaştıralım.
\( a \) ve \( b \) ifadelerini karşılaştıralım.
\( a = \log_x{2} \)
\( b = \log_y{4} = 2\log_y{2} \)
Taban \( (0, 1) \) aralığında ve logaritma içi birden büyükse logaritma değeri negatif olur. Aynı \( x = 2 \) değeri için daha küçük tabanlı logaritma ifadesinin (\( a = \log_x{2} \)) grafiği daha üsttedir, dolayısıyla değeri daha büyüktür.
\( b = 2\log_y{2} \) olduğu için daha küçük negatif değeri \( a \)'ya göre daha da küçük olur.
\( b \lt a \)
Taban ve logaritma içi birden büyükse logaritma değeri pozitif olur, dolayısıyla \( c \) ifadesi diğer iki ifadeden büyüktür.
\( b \lt a \lt c \)
Aşağıdaki ifadelerden hangisinin değeri en büyüktür?
\( \cos{e^3}, \ln{\dfrac{\pi}{2}}, \log{11}, (\sqrt{3} - 1)^2 \)
Çözümü Göster1. ifade:
\( \cos{e^3} \)
Kosinüs değerleri tüm reel sayılarda \( [-1, 1] \) aralığındadır.
2. ifade:
\( \ln{\dfrac{\pi}{2}} \)
\( \frac{\pi}{2} \lt e \) olduğu için \( \ln{\frac{\pi}{2}} \lt 1\) olur.
3. ifade:
\( \log{11} \)
\( \log{10} = 1 \) olduğu için \( \log{11} \gt 1 \) olur.
4. ifade:
\( (\sqrt{3} - 1)^{10} \)
\( 1 \lt \sqrt{3} \lt 2 \) olduğu için \( 0 \lt \sqrt{3} - 1 \lt 1 \) ve \( (\sqrt{3} - 1)^2 \lt 1 \) olur.
Buna göre 3. ifadenin değeri en büyüktür.
Aşağıdaki ifadelerden hangisinin değeri en büyüktür?
\( \sin^2{\dfrac{4\pi}{3}}, \cot^2{\dfrac{4\pi}{3}}, \log{\dfrac{4\pi}{3}}, \ln{\dfrac{4\pi}{3}} \)
Çözümü Göster1. ifade:
\( \sin{\dfrac{4\pi}{3}} = -\sin{\dfrac{\pi}{3}} \)
\( \sin^2{\dfrac{4\pi}{3}} = (-\dfrac{\sqrt{3}}{2})^2 = \dfrac{3}{4} \)
2. ifade:
\( \cot{\dfrac{4\pi}{3}} = \cot{\dfrac{\pi}{3}} \)
\( \cot^2{\dfrac{4\pi}{3}} = (\dfrac{\sqrt{3}}{3})^2 = \dfrac{1}{3} \)
3. ifade:
\( \dfrac{4\pi}{3} \) ifadesinin yaklaşık değerini bulmak için \( \pi = 3,14 \) alalım.
\( 4 \lt \dfrac{4\pi}{3} \lt 5 \)
10 tabanında logaritması alınan değer 1 ve 10 aralığında olduğu için logaritma sonucu 0 ve 1 aralığında olur.
\( 0 \lt \log{\dfrac{4\pi}{3}} \lt 1 \)
4. ifade:
\( e = 2,71 \)
\( e \) tabanında logaritması alınan değer \( e \) sayısından büyük olduğu için doğal logaritma sonucu 1'den büyük olur.
\( e \lt \dfrac{4\pi}{3} \)
\( 1 \lt \ln{\dfrac{4\pi}{3}} \)
Buna göre 4. ifadenin değeri en büyüktür.
Aşağıdaki ifadelerden hangisinin değeri en küçüktür?
\( \log{e}, \sqrt{\log{e^2}}, \) \( {\left( \dfrac{1}{\log{e}} \right)}^2 , \) \( \dfrac{1}{\log{\sqrt{e}}} \)
Çözümü Göster1. ifade:
\( \log{e} \) ifadesinde logaritma içi (\( e \approxeq 2,7182... \)) 1'den büyük ve logaritma tabanı olan 10'dan küçük olduğu için ifadenin değer \( (0, 1) \) aralığında olur.
\( a \in (0, 1) \)
Diğer ifadeleri \( a \) cinsinden yazalım.
2. ifade:
\( \sqrt{\log{e^2}} = \sqrt{2\log{e}} = \sqrt{2a} \)
\( a \lt 1 \) olduğu için aynı zamanda \( a \lt 2 \) olur.
\( \sqrt{2a} \gt \sqrt{a \cdot a} = a \)
3. ifade:
\( {\left( \dfrac{1}{\log{e}} \right)}^2 = \dfrac{1}{a^2} \)
\( a \in (0, 1) \) olduğu için \( \frac{1}{a^2} \gt 1 \) olur.
\( \dfrac{1}{a^2} \gt a \)
4. ifade:
\( \dfrac{1}{\log{\sqrt{e}}} = \dfrac{1}{\log{e^{\frac{1}{2}}}} = \dfrac{2}{a} \)
\( a \lt 1 \) olduğu için \( \dfrac{2}{a} \gt 1 \) olur.
\( \dfrac{2}{a} \gt a \)
İfadeleri \( a \) cinsinden yazdığımızda en küçük değerin \( \log{e} \) ifadesine ait olduğunu görürüz.
Logaritma Grafiklerinde Simetri
Çarpmaya göre birbirinin tersi olan tabanların logaritma grafikleri \( x \) eksenine göre simetriktir.
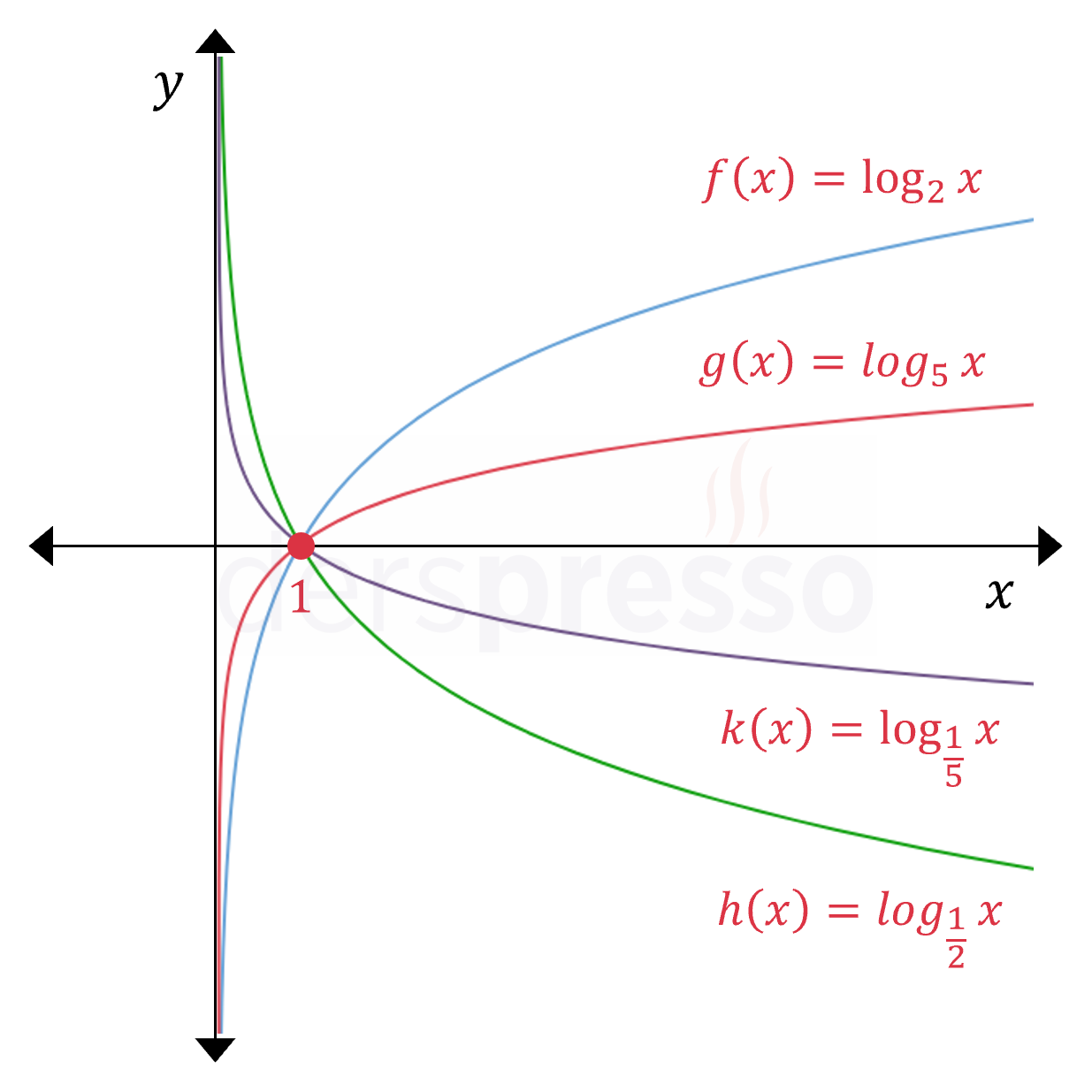
Grafikteki \( f \) ve \( h \) fonksiyonlarının simetrisini aşağıdaki gibi gösterebiliriz.
\( f(x) = \log_2{x} \)
\( h(x) = \log_{\frac{1}{2}}{x} = \log_{2^{-1}}{x} = -\log_2{x} \)
\( h(x) = -f(x) \) olduğu için bu iki fonksiyon \( x \) eksenine göre simetriktir.
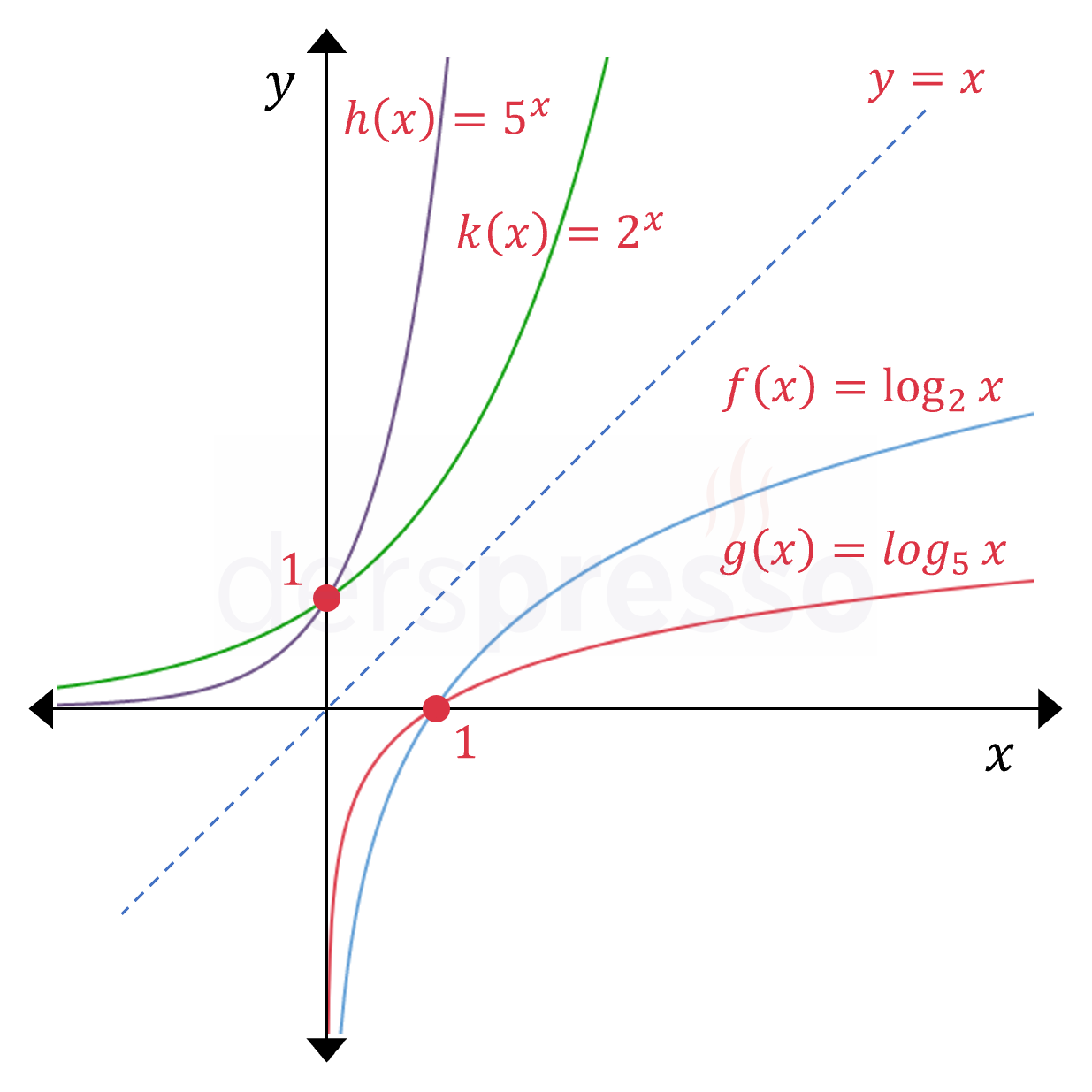
Logaritma ve Üstel Fonksiyon Grafikleri Arası Simetri
Bir fonksiyonun ve ters fonksiyonunun grafiği her zaman \( y = x \) doğrusuna göre simetriktir. Logaritma ve üstel fonksiyonlar birbirinin tersi oldukları için, belirli bir taban için bu iki fonksiyonun grafikleri de \( y = x \) doğrusuna göre simetrik olur.
Aşağıdaki iki farklı taban için logaritma ve üstel fonksiyon grafikleri verilmiştir. Bu grafiklerde aynı tabanlı grafiklerin \( y = x \) doğrusuna göre simetrik olduklarını görebiliriz (mavi grafik yeşil ile, kırmızı grafik mor ile simetrik).
\( f(x) = 2^{x + 3} - 4 \)
fonksiyonunun grafiğinin \( y = x \) doğrusuna göre simetriğini bulunuz.
Çözümü GösterBir fonksiyonun tersinin grafiği orijinal fonksiyonun grafiğinin \( y = x \) doğrusuna göre simetriğidir.
Bir fonksiyonun ters fonksiyonunu bulmak için önce \( x \) yalnız kalacak şekilde fonksiyon düzenlenir.
\( y = 2^{x + 3} - 4 \)
\( 2^{x + 3} = y + 4 \)
\( x + 3 = \log_2(y + 4) \)
\( x = \log_2(y + 4) - 3 \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirildiğinde elde edilen yeni fonksiyon, \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = \log_2(x + 4) - 3 \)
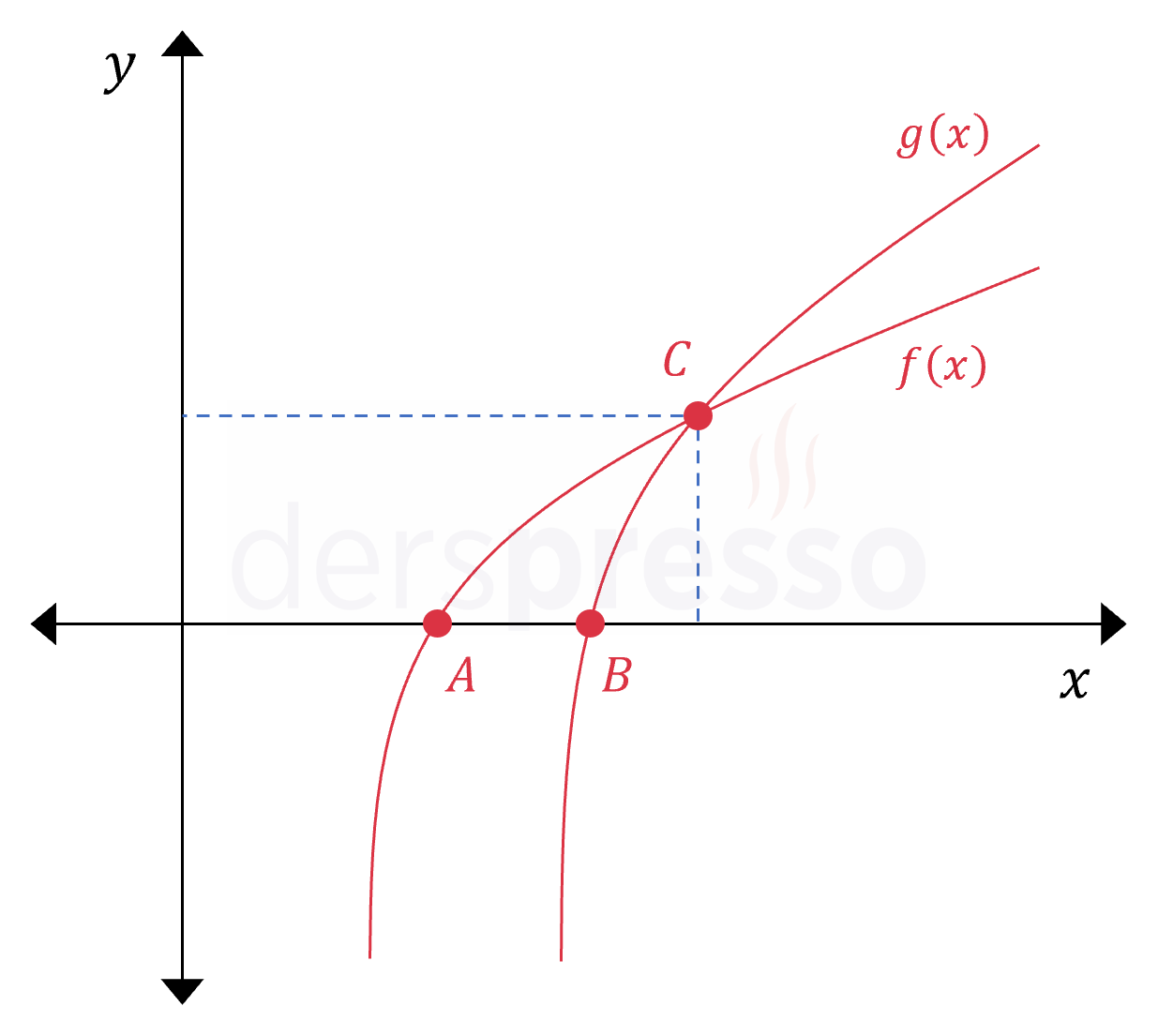
Yukarıda \( f(x) = \ln(x - 2) \) ve \( g(x) = 2\ln(x - 4) \) fonksiyonlarının grafikleri verilmiştir.
(a) \( A \) ve \( B \) noktalarının apsis değerlerini bulunuz.
(b) İki fonksiyonun kesiştiği \( C \) noktasının koordinatlarını bulunuz.
Çözümü Göster(a) seçeneği:
Fonksiyonların \( x \) eksenini kestikleri noktaları bulmak için denklemlerde \( y = 0 \) yazalım.
\( f(x) = \ln(x - 2) = 0 \)
\( x - 2 = e^0 = 1 \)
\( x = 3 \)
\( A(3, 0) \)
\( g(x) = 2\ln(x - 4) = 0 \)
\( x - 4 = e^0 = 1 \)
\( x = 5 \)
\( B(5, 0) \)
(b) seçeneği:
Fonksiyonların kesişim noktasını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( \ln(x - 2) = 2\ln(x - 4) \)
\( \ln(x - 2) = \ln(x - 4)^2 \)
Tabanları aynı iki logaritma ifadesinin eşitliğinde logaritma içleri birbirine eşittir.
\( x - 2 = (x - 4)^2 \)
\( x - 2 = x^2 - 8x + 16 \)
\( x^2 - 9x + 18 = 0 \)
\( (x - 3)(x - 6) = 0 \)
Logaritma tanımına göre logaritma ifadelerinin içleri pozitif olmalıdır.
\( x \gt 2 \) ve \( x \gt 4 \)
Buna göre \( x = 3 \) geçerli bir çözüm değildir ve fonksiyonların kesişim noktası \( x = 6 \) apsisli noktadır.
Verilen denklemlerden herhangi birinde \( x = 6 \) yazalım.
\( f(6) = \ln(6 - 2) \)
\( = \ln{4} = 2\ln{2} \)
\( C(6, 2\ln{2}) \)
\( f(x) = \ln{x} + 8x \)
\( A(\frac{1}{8}, m) \) ve \( B(\frac{1}{4}, n) \) noktaları bu fonksiyonun grafiği üzerindeki iki nokta olduğuna göre, \( [AB] \) doğru parçasının eğimini bulunuz.
Çözümü GösterVerilen noktaların apsis değerlerini fonksiyon tanımında yerine koyarak ordinat değerlerini bulalım.
\( f\left( \dfrac{1}{8} \right) = \ln{\dfrac{1}{8}} + 8 \cdot \dfrac{1}{8} = m \)
\( m = \ln{2^{-3}} + 1 \)
\( = 1 - 3\ln{2} \)
\( A(\frac{1}{8}, 1 - 3\ln{2}) \)
\( f\left( \dfrac{1}{4} \right) = \ln{\dfrac{1}{4}} + 8 \cdot \dfrac{1}{4} = n \)
\( n = \ln{2^{-2}} + 2 \)
\( = 2 - 2\ln{2} \)
\( B(\frac{1}{4}, 2 - 2\ln{2}) \)
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( m_{AB} = \dfrac{(2 - 2\ln{2}) - (1 - 3\ln{2})}{\frac{1}{4} - \frac{1}{8}} \)
\( = \dfrac{1 + \ln{2}}{\frac{1}{8}} \)
\( = 8 + 8\ln{2} \) bulunur.
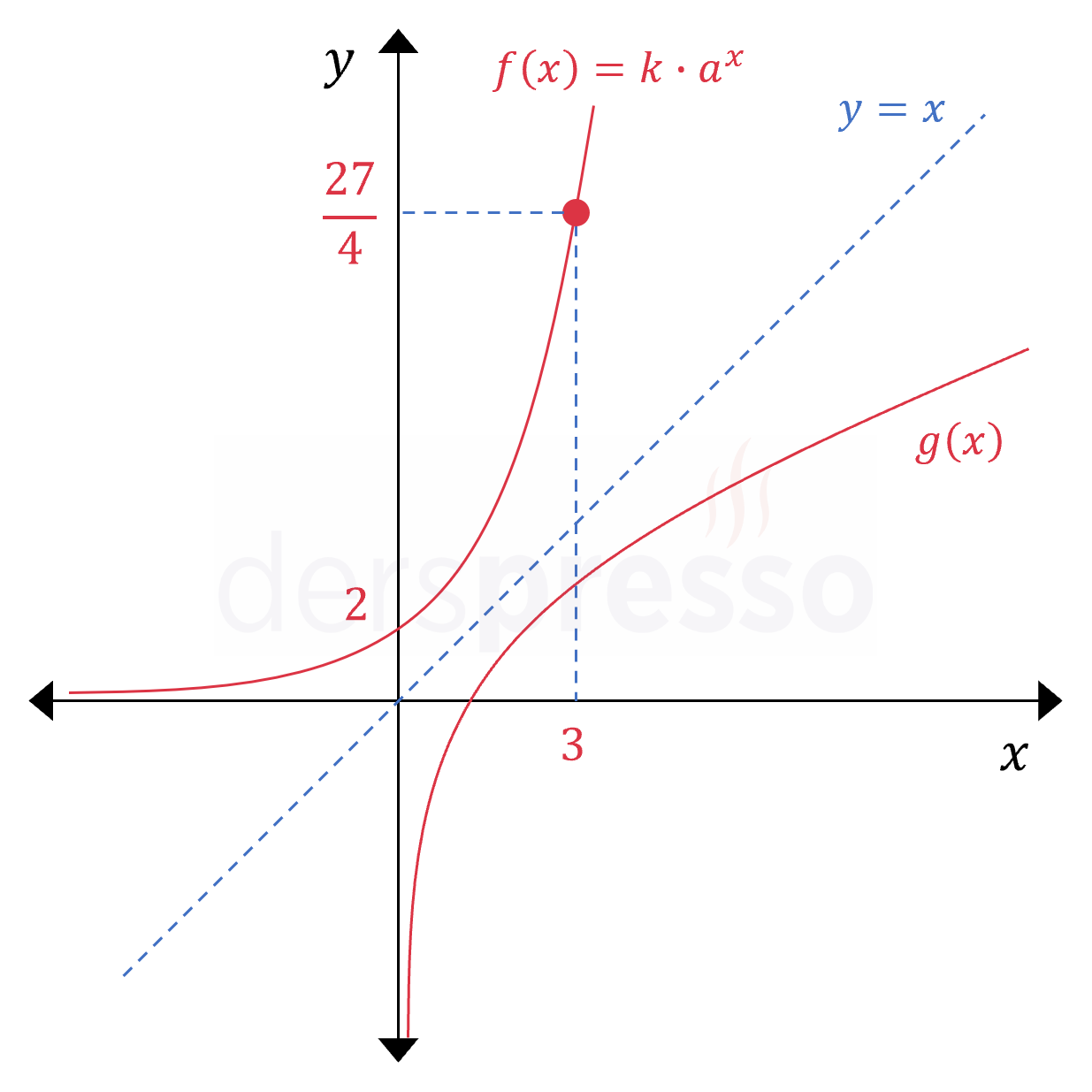
Yukarıda \( f(x) \) üstel fonksiyonunun ve \( g(x) \) logaritma fonksiyonunun grafikleri verilmiştir.
Bu iki grafik \( y = x \) doğrusuna göre simetrik olduğuna göre, \( g(\frac{9}{2}) \) kaçtır?
Çözümü Göster\( f(x) \) grafiği üzerinde verilen iki noktayı yerine koyarak fonksiyon tanımını bulalım.
\( f(0) = k \cdot a^0 = 2 \)
\( k = 2 \)
\( f(3) = 2 \cdot a^3 = \dfrac{27}{4} \)
\( a^3 = \dfrac{27}{8} \)
\( a = \dfrac{3}{2} \)
Buna göre \( f(x) \) fonksiyon tanımı aşağıdaki gibidir.
\( f(x) = 2\left( \dfrac{3}{2} \right)^x \)
Verilen iki grafik \( y = x \) doğrusuna göre simetrik ise bu iki fonksiyon birbirinin tersidir.
Bir fonksiyonun ters fonksiyonunu bulmak için önce \( x \) yalnız kalacak şekilde fonksiyon düzenlenir.
\( y = 2\left( \dfrac{3}{2} \right)^x \)
\( \left( \dfrac{3}{2} \right)^x = \dfrac{y}{2} \)
\( x = \log_{\frac{3}{2}}{\dfrac{y}{2}} \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirildiğinde elde edilen yeni fonksiyon, \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = g(x) = \log_{\frac{3}{2}}{\dfrac{x}{2}} \)
\( g(\frac{9}{2}) \) değerini bulmak için \( x = \frac{9}{2} \) koyalım.
\( g\left( \dfrac{9}{2} \right) = \log_{\frac{3}{2}}{\dfrac{\frac{9}{2}}{2}} \)
\( = \log_{\frac{3}{2}}{\dfrac{9}{4}} = \log_{\frac{3}{2}}\left( \dfrac{3}{2} \right)^2 \)
\( = 2 \) bulunur.
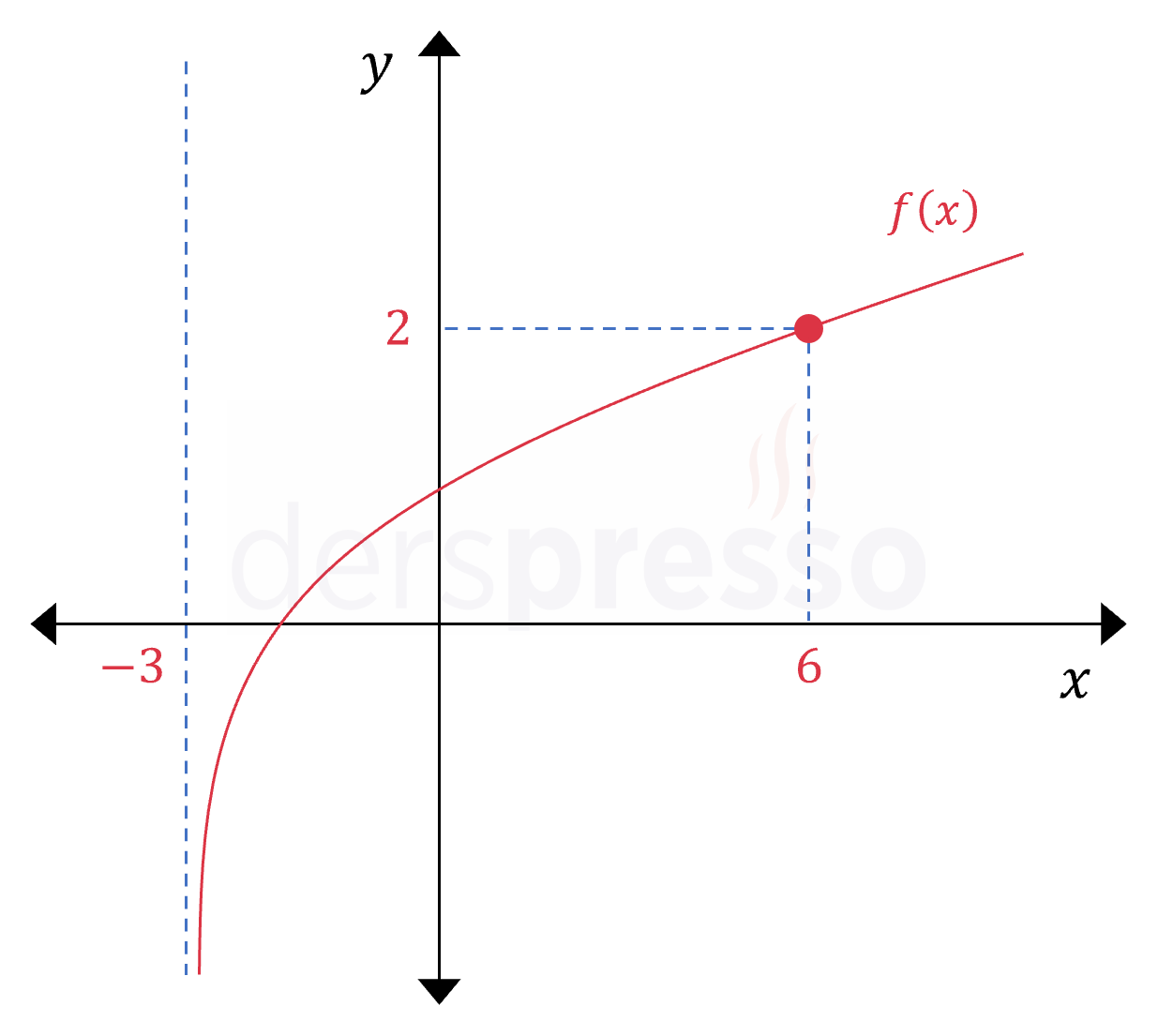
Yukarıdaki \( f(x) = \log_a(x + b) \) grafiğine göre, \( f(240) \) kaçtır?
Çözümü Göster\( x = -3 \) logaritma fonksiyonunun dikey asimptotu olup, logaritma içini sıfır, dolayısıyla logaritma ifadesini tanımsız yapan değerdir.
\( x + b = -3 + b = 0 \)
\( b = 3 \)
Verilen \( (6, 2) \) noktasını fonksiyonda yerine koyalım.
\( f(6) = \log_a(6 + 3) = 2 \)
\( a^2 = 9 \)
Logaritma tabanı negatif olamaz.
\( a = 3 \)
Fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \log_3(x + 3) \)
\( f(240) \) değerini bulmak için \( x = 240 \) yazalım.
\( f(240) = \log_3(240 + 3) \)
\( = \log_3{3^5} = 5 \) bulunur.
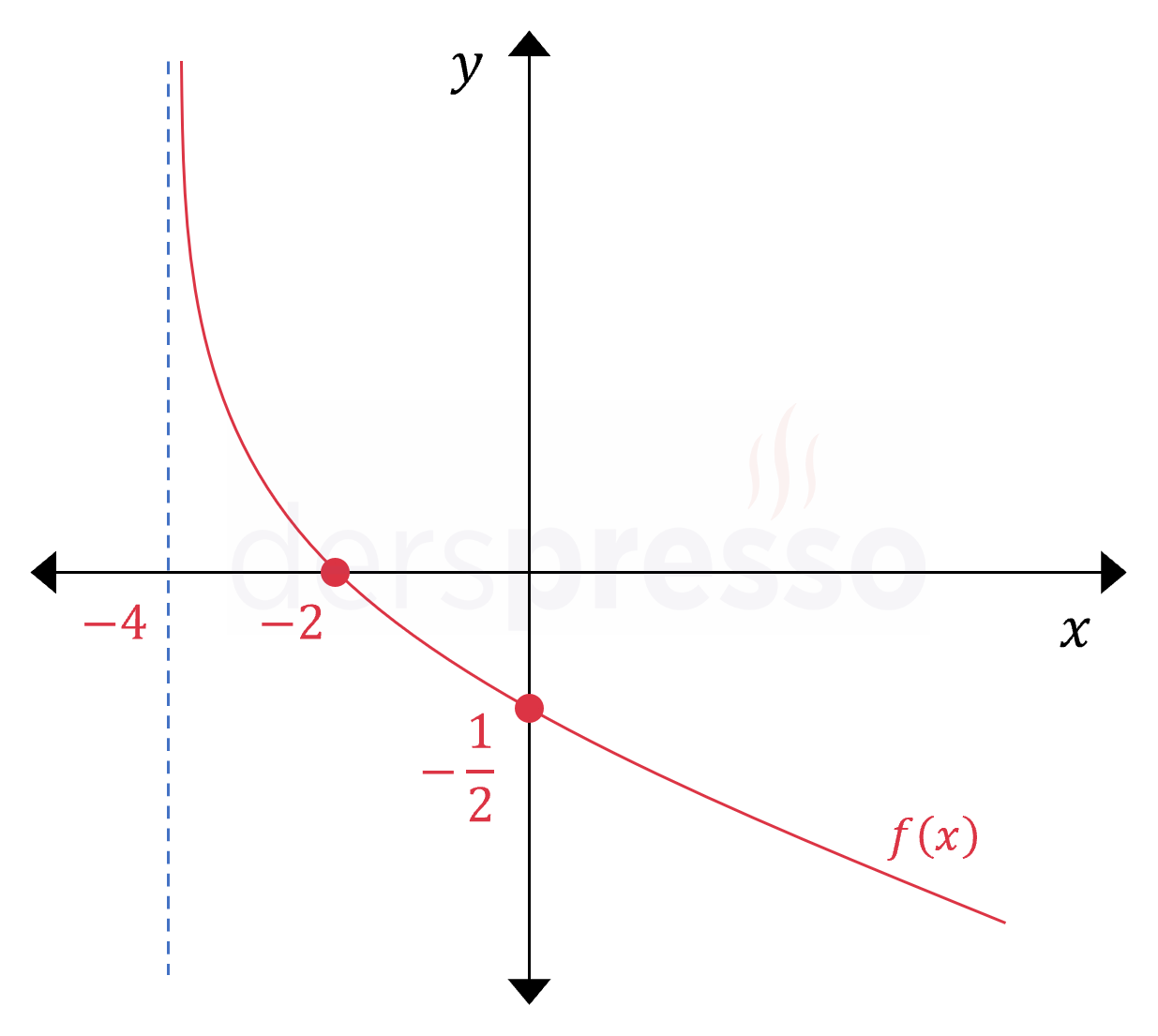
Yukarıdaki grafik \( y = \log_a(bx + c) \) fonksiyonuna aittir.
Buna göre \( abc \) çarpımı kaçtır?
Çözümü Göster\( x = -4 \) logaritma fonksiyonunun dikey asimptotu olup, logaritma içini sıfır, dolayısıyla logaritma ifadesini tanımsız yapan değerdir.
\( bx + c = 0 \)
\( -4b + c = 0 \)
\( c = 4b \)
Grafik \( (-2, 0) \) noktasından geçmektedir.
\( f(-2) = \log_a(b(-2) + c) = 0 \)
\( -2b + c = a^0 = 1 \)
\( -2b + 4b = 1 \)
\( b = \dfrac{1}{2} \)
\( c = 4b = 2 \)
Grafik \( (0, -\frac{1}{2}) \) noktasından geçmektedir.
\( f(0) = \log_a\left( \dfrac{1}{2}(0) + 2 \right) = -\dfrac{1}{2} \)
\( a^{-\frac{1}{2}} = 2 \)
\( a = \dfrac{1}{4} \)
\( abc = \dfrac{1}{4} \cdot \dfrac{1}{2} \cdot 2 = \dfrac{1}{4} \) bulunur.
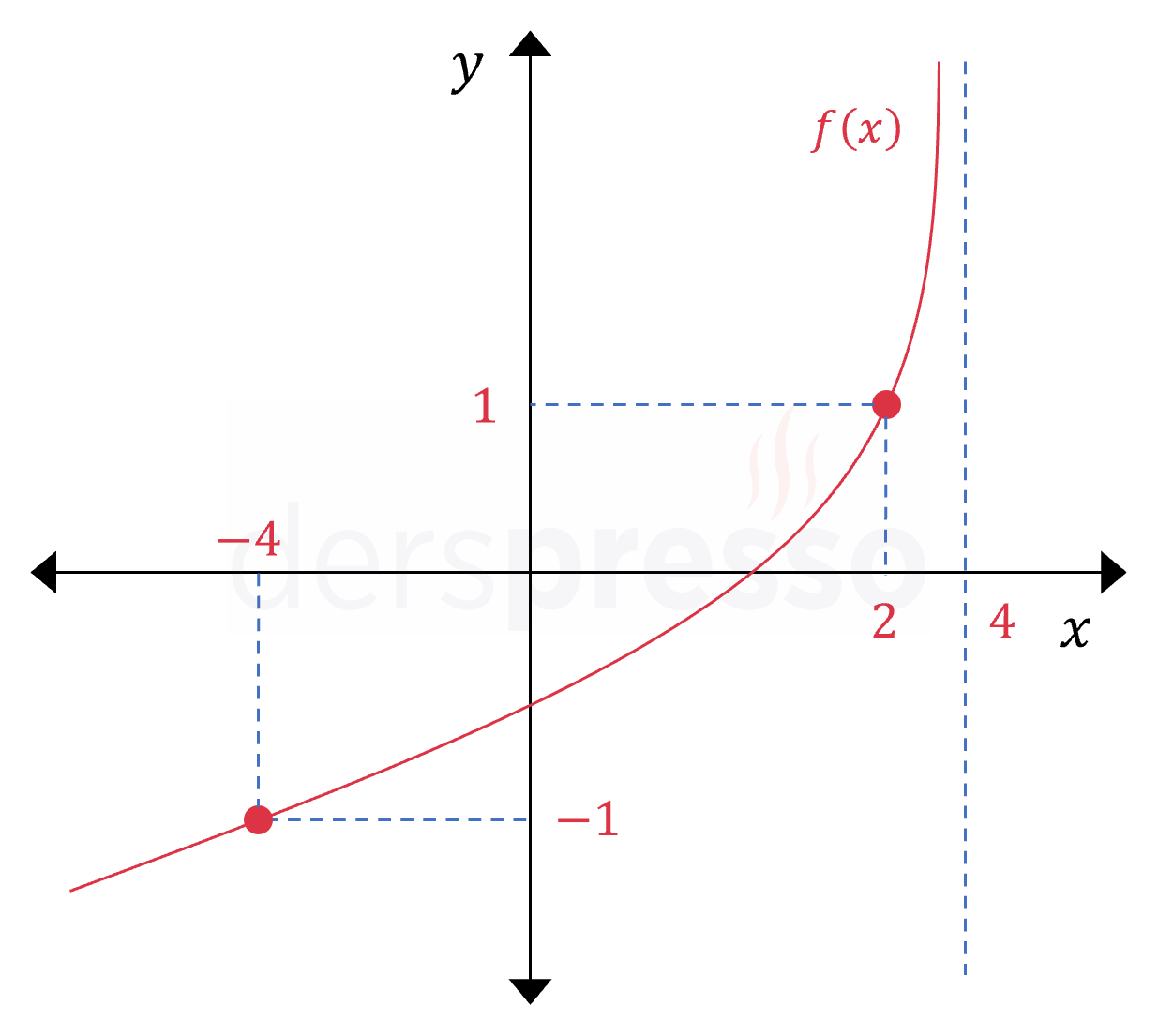
Yukarıdaki grafik \( y = \log_a(n - x) + m \) fonksiyonuna aittir.
Buna göre \( amn \) çarpımı kaçtır?
Çözümü Göster\( x = 4 \) logaritma fonksiyonunun dikey asimptotu olup, logaritma içini sıfır, dolayısıyla logaritma ifadesini tanımsız yapan değerdir.
\( n - x = n - 4 = 0 \)
\( n = 4 \)
Diğer bilinmeyenleri bulmak için grafikte verilen noktaları fonksiyon tanımında yerine koyalım.
\( (2, 1) \) noktası:
\( f(2) = \log_a(4 - 2) + m = 1 \)
\( \log_a{2} = 1 - m \)
\( (-4, -1) \) noktası:
\( f(-4) = \log_a(4 - (-4)) + m = -1 \)
\( \log_a{8} = -1 - m \)
\( 3\log_a{2} = -1 - m \)
\( \log_a{2} = \dfrac{-1 - m}{3} \)
Bulduğumuz iki \( \log_a{2} \) değerini birbirine eşitleyelim.
\( 1 - m = \dfrac{-1 - m}{3} \)
\( 3 - 3m = -1 - m \)
\( m = 2 \)
\( m \) değerini denklemlerden birinde yerine koyarak \( a \) değerini bulalım.
\( \log_a{2} = 1 - m = 1 - 2 = -1 \)
\( a^{-1} = 2 \)
\( a = \dfrac{1}{2} \)
\( amn = \dfrac{1}{2} \cdot 2 \cdot 4 = 4 \) bulunur.
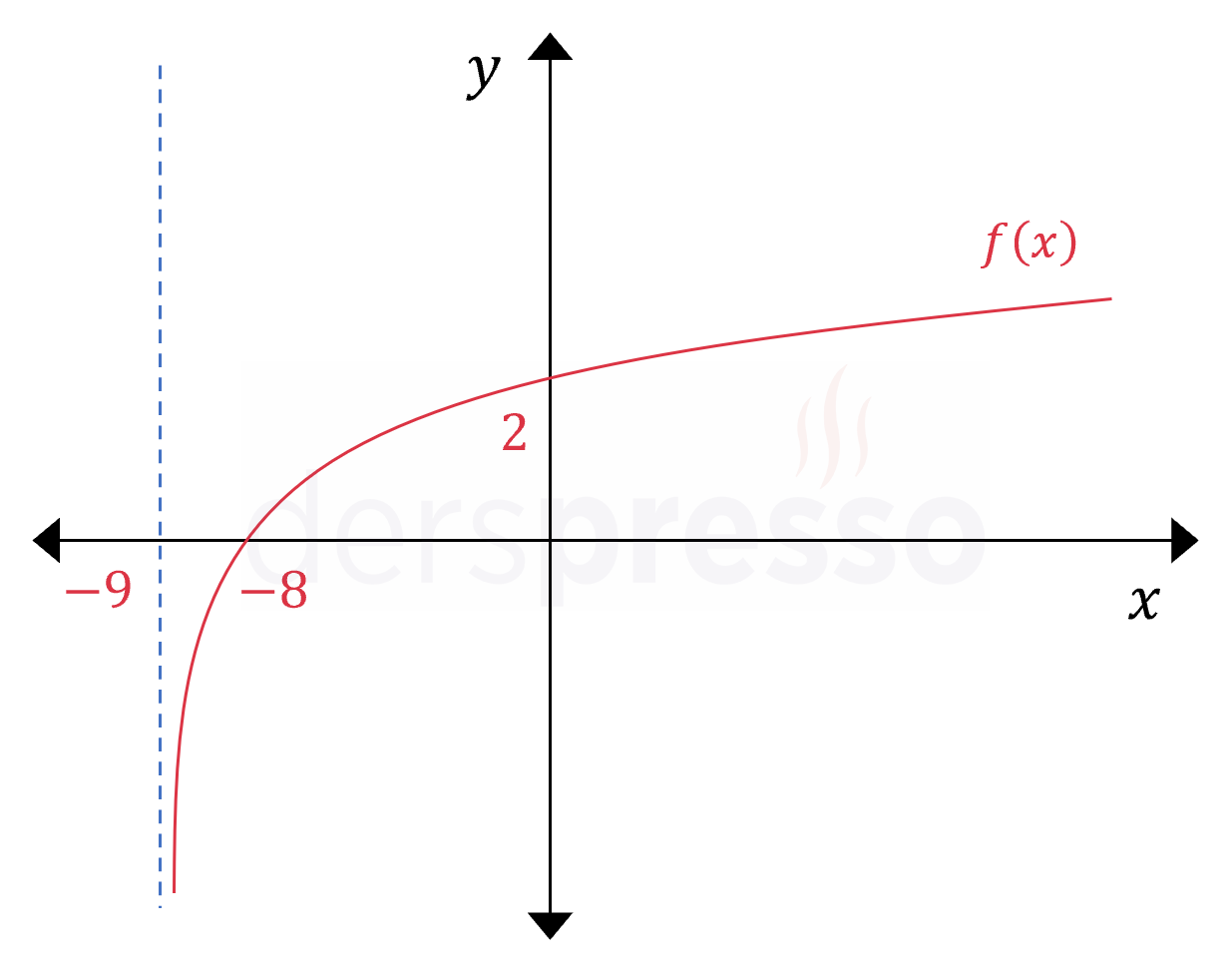
Yukarıda \( f(x) = \log_a(x + b) \) fonksiyonunun grafiği verilmiştir.
Buna göre, \( f(72) + f^{-1}(a) \) toplamı kaçtır?
Çözümü Göster\( x = -9 \) logaritma fonksiyonunun dikey asimptotu olup, logaritma içini sıfır, dolayısıyla logaritma ifadesini tanımsız yapan değerdir.
\( x + b = -9 + b = 0 \)
\( b = 9 \)
\( f(x) = \log_a(x + 9) \)
\( (0, 2) \) noktasını fonksiyonda yerine koyalım.
\( f(0) = \log_a(0 + 9) = 2 \)
Logaritma tabanı negatif olamaz.
\( a = 3 \)
\( f(x) = \log_3(x + 9) \)
\( f(72) \) değerini bulmak için \( x = 72 \) yazalım.
\( f(72) = \log_3(72 + 9) = \log_3{81} = 4 \)
\( f^{-1}(a) = f^{-1}(3) \)
\( f^{-1}(3) \) değerini bulmak için fonksiyon değerini 3 yapan \( x \) değerini bulalım.
\( \log_3(x + 9) = 3 \)
\( x + 9 = 27 \)
\( x = 18 \)
Buna göre \( f(72) + f^{-1}(a) = 4 + 18 = 22 \) bulunur.
Aşağıdaki sayılardan hangisi en büyüktür?
\( \log_9{27}, \quad \log_5{12} \)
Çözümü GösterLogaritma içinin üssünün kendisi, logaritma tabanının üssünün de çarpmaya göre tersi logaritma işleminin önüne katsayı olarak alınabilir.
\( \log_9{27} = \log_{3^2}{3^3} = \dfrac{3}{2}\log_3{3} = \dfrac{3}{2} \)
\( \log_5{12} \) ifadesinde logaritma içi logaritma tabanı olan 5'ten büyük olduğu için ifadenin sonucu 1'den büyüktür.
\( \log_5{12} \) ifadesinin \( \log_9{27} = \frac{3}{2} \) ifadesinden büyük olup olmadığını inceleyelim.
\( \log_5{12} \stackrel{?}{<>} \frac{3}{2} \)
Logaritma ifadesini üstel ifade şeklinde yazalım.
Logaritma tabanı 1'den büyük olduğu için eşitsizliğin yönü değişmez.
\( 12 \stackrel{?}{<>} 5^\frac{3}{2} \)
İki tarafın karesini alalım.
\( 144 \stackrel{?}{<>} 5^3 \)
\( 144 \gt 125 \)
Buna göre verilen sayılardan \( \log_5{12} \) daha büyüktür.
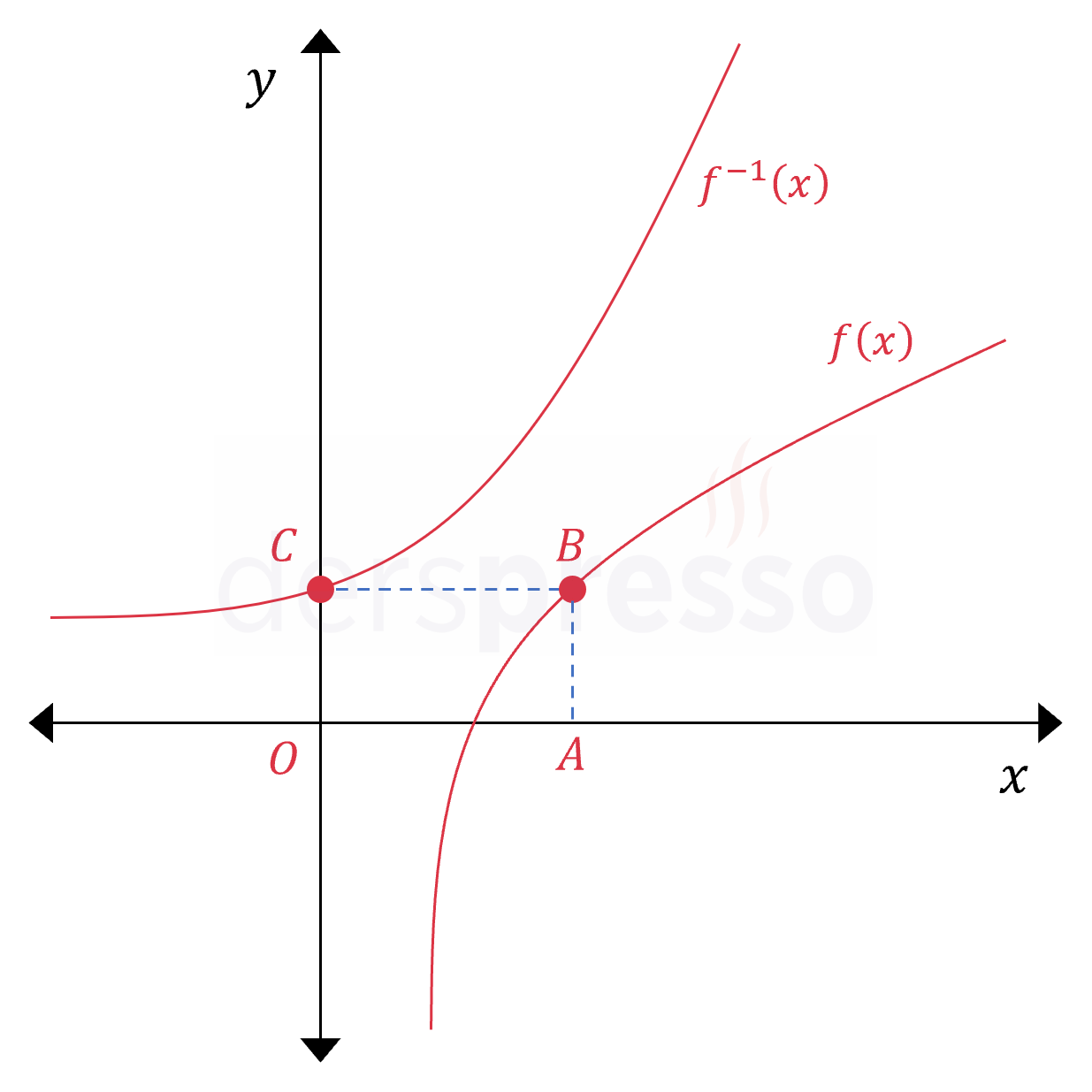
Şekilde \( f(x) = \log_2{\frac{x}{4}} \) ve \( f^{-1}(x) \) fonksiyonlarının grafikleri verilmiştir.
Buna göre, \( 0ABC \) dikdörtgeninin alanını bulunuz.
Çözümü Göster\( f \) fonksiyonunun ters fonksiyonunu bulalım.
Bir fonksiyonun ters fonksiyonunu bulmak için önce \( x \) yalnız kalacak şekilde fonksiyon düzenlenir.
\( y = \log_2{\dfrac{x}{4}} \)
\( \dfrac{x}{4} = 2^y \)
\( x = 4 \cdot 2^y = 2^{y+2} \)
\( x \) ve \( y \) değişkenlerinin yerleri değiştirildiğinde elde edilen yeni fonksiyon, \( y = f(x) \) fonksiyonunun ters fonksiyonu olan \( y = f^{-1}(x) \) fonksiyonudur.
\( y = f^{-1}(x) = 2^{x + 2} \)
\( C \) noktasının ordinat değerini bulmak için \( f^{-1}(x) \) fonksiyonunda \( x = 0 \) verelim.
\( f^{-1}(0) = 2^{0 + 2} = 4 \)
\( C(0, 4) \)
Buna göre \( B \) noktasının ordinat değeri de \( y = 4 \) olur.
\( B \) noktasının apsis değerini bulmak için \( f(x) \) fonksiyonunda \( y = 4 \) verelim.
\( f(x) = \log_2{\dfrac{x}{4}} = 4 \)
\( 2^4 = \dfrac{x}{4} \)
\( x = 64 \)
\( B(64, 4) \)
Buna göre dikdörtgenin yüksekliği 4, genişliği 64 olur.
\( A(OABC) = 4 \cdot 64 = 256 \) olarak bulunur.
\( y = \log_2{x} \) fonksiyonunun grafiğine ayrı ayrı 5 birim aşağı öteleme ve \( a \) çarpanı kadar yatay daralma dönüşümleri uygulandığında aynı grafik elde edildiğine göre, \( a \) kaçtır?
Çözümü Göster\( y = f(x) \) fonksiyonunun grafiğinde 5 birim aşağı yönde ötelemeye yol açan dönüşüm \( y = f(x) - 5 \) olur.
\( y = f(x) \) fonksiyonunun grafiğinde \( a \) çarpanı kadar yatay daralmaya yol açan dönüşüm \( y = f(ax) \) olur.
Fonksiyona bu iki dönüşüm uygulandığında aynı fonksiyon elde ediliyor.
\( \log_2{x} - 5 = \log_2(ax) \)
\( \log_2{x} - 5 = \log_2{a} + \log_2{x} \)
\( \log_2{a} = -5 \)
\( a = 2^{-5} = \dfrac{1}{32} \) bulunur.
\( f(x) = \log{\abs{x}} + 3 \) fonksiyonunun grafiği \( y = x \) doğrusu ile kaç noktada kesişir?
Çözümü GösterÖnce \( \log{x} \) fonksiyonuna iki dönüşüm uygulayarak sorudaki fonksiyonu elde edelim.
Fonksiyonun girdisinin mutlak değeri alındığında \( y \) ekseninin solunda kalan noktalar (varsa) silinir ve \( y \) ekseninin sağında kalan noktaların \( y \) eksenine göre yansıması oluşur.
\( f(x) \longmapsto f(\abs{x}) \)
\( f(\abs{x}) = \log{\abs{x}} \)
Bir fonksiyonun çıktısına 3 birim eklendiğinde grafiği 3 birim yukarı ötelenir.
\( f(\abs{x}) \longmapsto f(\abs{x}) + 3 \)
\( f(\abs{x}) + 3 = \log{\abs{x}} + 3 \)
Aşağıda bu iki dönüşüm sonucunda oluşan fonksiyonun ve \( y = x \) doğrusunun grafikleri verilmiştir.
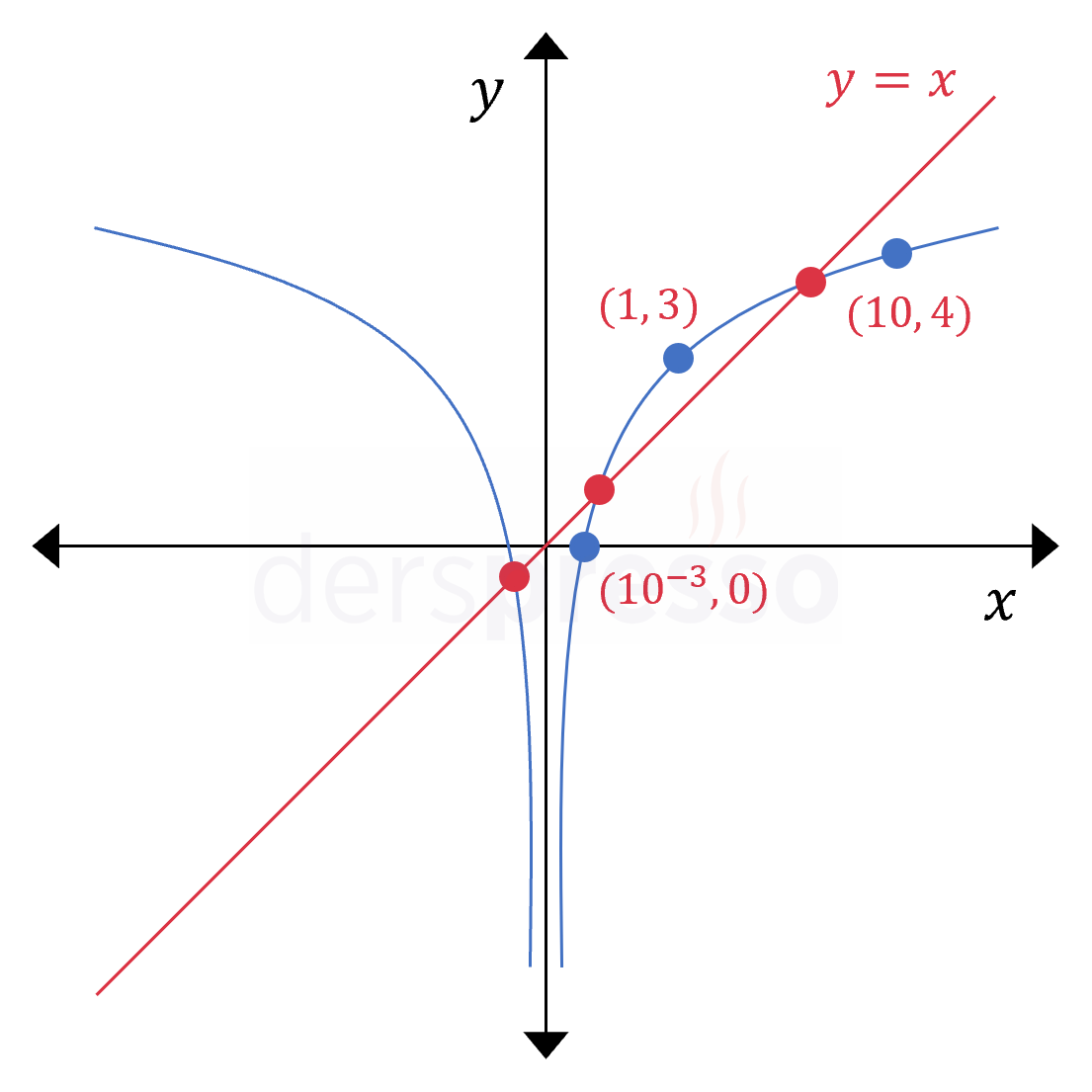
\( y = x \) doğrusunun fonksiyonun \( y \) ekseninin solunda kalan kısmını tek noktada kestiğinden emin olabiliriz, \( y \) ekseninin sağında kalan kısmını kesip kesmediğinden ya da kesiyorsa kaç noktada kestiğinden emin olmak için ya bir programla grafiğini çizmeliyiz ya da iki denklemi ortak çözmeliyiz.
Alternatif olarak \( y = x \) doğrusunun fonksiyonun \( y \) ekseninin sağında kalan kısmını 2 noktada kestiğini daha pratik bir yöntemle bulabiliriz.
Verilen logaritma fonksiyonunda \( y = 0 \) verip \( x \) değerini ve \( x = 1 \) ve \( x = 10 \) verip \( y \) değerlerini hesapladığımızda fonksiyonun aşağıdaki noktalardan geçtiğini buluruz.
\( (10^{-3}, 0), (1, 3), (10, 4) \)
Bu noktalardan 1. ve 3.sünün ordinat değerleri apsis değerlerinden küçük olduğu için \( y = x \) doğrusunun altında kalır, 2. noktanın ise ordinat değeri daha büyük olduğu için \( y = x \) doğrusunun üstünde kalır.
Buna göre fonksiyon grafiğinin doğrunun altındayken doğruyu kesip üstüne geçtiği, sonra tekrar kesip altına indiği sonucuna varabiliriz.
Buna göre verilen fonksiyon ve doğru 3 noktada kesişirler.