Köklü İfade Tanımı
\( n \) birden büyük bir tam sayı olmak üzere, \( y^n = x \) eşitliğini sağlayan \( y \) sayısına \( x \)'in \( n \). dereceden kökü denir ve \( y = \sqrt[n]{x} \) şeklinde gösterilir. Bir diğer ifadeyle; \( x \) sayısının \( n \). dereceden kökü, kendisiyle \( n \) kez çarpımının sonucu \( x \) olan sayıdır.
\( x, y \in \mathbb{R}, \quad n \in \mathbb{Z^+}, \quad n \ge 2 \) olmak üzere,
\( y^n = x \Longrightarrow y = \sqrt[n]{x} \)
\( \sqrt[2]{25} = \sqrt[2]{5 \cdot 5} = 5 \)
\( \sqrt[3]{-8} = \sqrt[3]{(-2)(-2)(-2)} = -2 \)
\( \sqrt[4]{81} = \sqrt[4]{3 \cdot 3 \cdot 3 \cdot 3} = 3 \)
Çıkarma işleminin toplamanın tersi olması gibi, kök işlemini de üs işleminin tersi olarak düşünebiliriz.
Bir köklü ifadenin bileşenleri kökün derecesi, kök içi ve bu ikisini ayıran kök işaretidir.
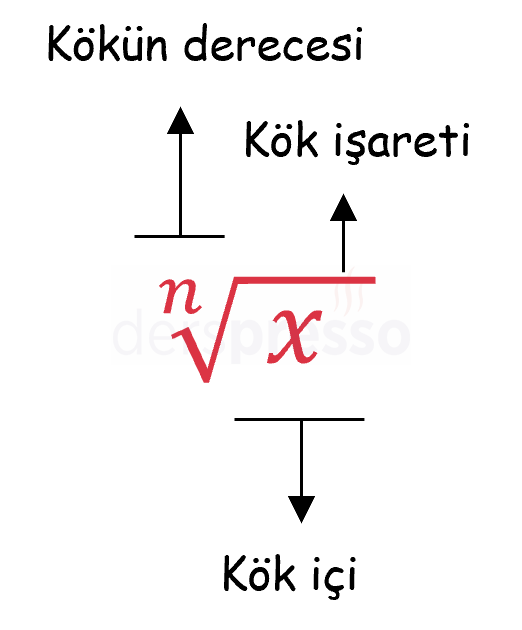
Bir köklü ifadenin derecesi belirtilmemişse derece 2 olarak alınır.
\( \sqrt{25} = \sqrt[2]{25} = 5 \)
Köklü ifadeler derecelerine göre okunurlar.
\( \sqrt{x} \): \( x \)'in karekökü (ikinci dereceden kökü)
\( \sqrt[3]{x} \): \( x \)'in küpkökü (üçüncü dereceden kökü)
\( \sqrt[4]{x} \): \( x \)'in dördüncü dereceden kökü
\( \sqrt[n]{x} \): \( x \)'in \( n \). dereceden kökü
Köklü ifadelerin standart yazılışında kök içindeki ifade en sade şekliyle bırakılır. Kök içindeki çarpanların kök dışına alınması ile ilgili kuralları önümüzdeki bölümlerde inceleyeceğiz.
\( \sqrt{18} = \sqrt{3^2 \cdot 2} = 3\sqrt{2} \)
\( \sqrt[3]{40} = \sqrt[3]{2^3 \cdot 5} = 2\sqrt[3]{5} \)
Ondalık sayıların karekökü, sayı kesirli ifadeye çevrilerek bulunabilir.
\( \sqrt{0,64} = \sqrt{\dfrac{64}{100}} \)
\( = \dfrac{8}{10} = 0,8 \)
\( \sqrt{2,25} = \sqrt{\dfrac{225}{100}} \)
\( = \dfrac{15}{10} = 1,5 \)
\( \sqrt{1,44} - \sqrt {0,49} + \sqrt{0,81} \) ifadesinin sonucu kaçtır?
Çözümü GösterOndalıklı sayıları kesre çevirelim.
\( \sqrt{\dfrac{144}{100}} - \sqrt{\dfrac{49}{100}} + \sqrt{\dfrac{81}{100}} \)
\( = \sqrt{\left( \dfrac{12}{10} \right)^2} - \sqrt{\left( \dfrac{7}{10} \right)^2} + \sqrt{\left( \dfrac{9}{10} \right)^2} \)
\( = \dfrac{12}{10} - \dfrac{7}{10} + \dfrac{9}{10} \)
\( = \dfrac{12 - 7 + 9}{10} \)
\( = \dfrac{14}{10} = \dfrac{7}{5} \) bulunur.
Bazı Sayıların Kök Değerleri
1000'e kadar olan sayılardan kök işlem sonucu tam sayı olanlar aşağıdaki tabloda verilmiştir.
| Sonuç | 2. Derece | 3. Derece | 4. Derece | 5. Derece |
|---|---|---|---|---|
| \( 1 \) | \( \sqrt{1} = \sqrt{1^2} = 1 \) | \( \sqrt[3]{1} = \sqrt[3]{1^3} = 1 \) | \( \sqrt[4]{1} = \sqrt[4]{1^4} = 1 \) | \( \sqrt[5]{1} = \sqrt[5]{1^5} = 1 \) |
| \( 2 \) | \( \sqrt{4} = \sqrt{2^2} = 2 \) | \( \sqrt[3]{8} = \sqrt[3]{2^3} = 2 \) | \( \sqrt[4]{16} = \sqrt[4]{2^4} = 2 \) | \( \sqrt[5]{32} = \sqrt[5]{2^5} = 2 \) |
| \( 3 \) | \( \sqrt{9} = \sqrt{3^2} = 3 \) | \( \sqrt[3]{27} = \sqrt[3]{3^3} = 3 \) | \( \sqrt[4]{81} = \sqrt[4]{3^4} = 3 \) | \( \sqrt[5]{243} = \sqrt[5]{3^5} = 3 \) |
| \( 4 \) | \( \sqrt{16} = \sqrt{4^2} = 4 \) | \( \sqrt[3]{64} = \sqrt[3]{4^3} = 4 \) | \( \sqrt[4]{256} = \sqrt[4]{4^4} = 4 \) | |
| \( 5 \) | \( \sqrt{25} = \sqrt{5^2} = 5 \) | \( \sqrt[3]{125} = \sqrt[3]{5^3} = 5 \) | \( \sqrt[4]{625} = \sqrt[4]{5^4} = 5 \) | |
| \( 6 \) | \( \sqrt{36} = \sqrt{6^2} = 6 \) | \( \sqrt[3]{216} = \sqrt[3]{6^3} = 6 \) | ||
| \( 7 \) | \( \sqrt{49} = \sqrt{7^2} = 7 \) | \( \sqrt[3]{343} = \sqrt[3]{7^3} = 7 \) | ||
| \( 8 \) | \( \sqrt{64} = \sqrt{8^2} = 8 \) | \( \sqrt[3]{512} = \sqrt[3]{8^3} = 8 \) | ||
| \( 9 \) | \( \sqrt{81} = \sqrt{9^2} = 9 \) | \( \sqrt[3]{729} = \sqrt[3]{9^3} = 9 \) | ||
| \( 10 \) | \( \sqrt{100} = \sqrt{10^2} = 10 \) | \( \sqrt[3]{1000} = \sqrt[3]{10^3} = 10 \) |
10'a kadar olan tam sayıların karekök değerleri aşağıdaki tabloda verilmiştir.
| \( x \) | \( \sqrt{x} \) |
|---|---|
| 2 | 1,4142... |
| 3 | 1,7320... |
| 5 | 2,2360... |
| 6 | 2,4494... |
| 7 | 2,6457... |
| 8 | 2,8284... |
| 10 | 3,1622... |
\( \sqrt[3]{0,000001331} \) ifadesinin değeri kaçtır?
Çözümü Göster\( 1331 = 11^3 \)
\( \sqrt[3]{0,000001331} = \sqrt[3]{1331 \cdot 10^{-9}} \)
\( = \sqrt[3]{11^3 \cdot 10^{-9}} \)
\( = 11 \cdot 10^{-3} = 0,011 \) bulunur.
\( \dfrac{\sqrt{147} - \sqrt{48}}{\sqrt{12}} \)
ifadesinin değeri kaçtır?
Çözümü Göster\( \sqrt{147} =\sqrt{49 \cdot 3} \)
\( = 7\sqrt{3} \)
\( \sqrt{48} = \sqrt{16 \cdot 3} \)
\( = 4\sqrt{3} \)
\( \sqrt{12} = \sqrt{4 \cdot 3} \)
\( = 2\sqrt{3} \)
Bu değerleri verilen ifadede yerlerine koyalım.
\( \dfrac{\sqrt{147} - \sqrt{48}}{\sqrt{12}} = \dfrac{7\sqrt{3} - 4\sqrt{3}}{2\sqrt{3}} \)
\( = \dfrac{3\sqrt{3}}{2\sqrt{3}} = \dfrac{3}{2} \) bulunur.
\( \sqrt[3]{24 + \sqrt{7 + \sqrt[4]{13 + \sqrt{9}}}} \) işleminin sonucu kaçtır?
Çözümü GösterEn içteki köklü ifadeden başlayarak köklü ifadelerin değerini bulalım.
\( \sqrt[3]{24 + \sqrt{7 + \sqrt[4]{13 + 3}}} \)
\( = \sqrt[3]{24 + \sqrt{7 + \sqrt[4]{16}}} \)
\( = \sqrt[3]{24 + \sqrt{7 + 2}}\)
\( = \sqrt[3]{24 + 3}\)
\( = \sqrt[3]{27} = 3\) bulunur.
\( \sqrt{7} + \sqrt{5} \) ifadesi \( \sqrt{28} + \sqrt{45} \) ifadesinden ne kadar eksiktir?
Çözümü Göster\( \sqrt{28} + \sqrt{45}\) ifadesini düzenleyelim.
\( \sqrt{28} + \sqrt{45} = \sqrt{4 \cdot 7} + \sqrt{9 \cdot 5} \)
\( = 2\sqrt{7} + 3\sqrt{5} \)
\( 2\sqrt{7} + 3\sqrt{5} \) ifadesinden \( \sqrt{7} + \sqrt{5} \) ifadesini çıkararak ikinci ifadenin birinciden ne kadar eksik olduğunu bulabiliriz.
\( 2\sqrt{7} + 3\sqrt{5} - (\sqrt{7} + \sqrt{5}) \)
\( = 2\sqrt{7} + 3\sqrt{5} - \sqrt{7} - \sqrt{5} \)
\( = \sqrt{7} + 2\sqrt{5} \) bulunur.
\( \dfrac{\sqrt{3}}{\sqrt{3} + \dfrac{1}{\sqrt{3} - \dfrac{1}{\sqrt{3}}}} \) işleminin sonucu kaçtır?
Çözümü Gösterİşleme en alttaki bölme işleminden başlayalım.
\( \dfrac{\sqrt{3}}{\sqrt{3} + \dfrac{1}{\dfrac{3}{\sqrt{3}} - \dfrac{1}{\sqrt{3}}}} \)
\( = \dfrac{\sqrt{3}}{\sqrt{3} + \dfrac{1}{\dfrac{2}{\sqrt{3}}}} \)
\( = \dfrac{\sqrt{3}}{\sqrt{3} + \dfrac{\sqrt{3}}{2}} \)
\( = \dfrac{\sqrt{3}}{\dfrac{2\sqrt{3}}{2} + \dfrac{\sqrt{3}}{2}} \)
\( = \dfrac{\sqrt{3}}{\dfrac{3\sqrt{3}}{2}} \)
\( = \dfrac{2\sqrt{3}}{3\sqrt{3}} = \dfrac{2}{3} \) bulunur.
\( \sqrt{4 + 7\sqrt{1 + 2\sqrt{6 + 2\sqrt{x}}}} = 5 \) eşitliğini sağlayan \( x \) değeri kaçtır?
Çözümü GösterSonucun 5 olması için en dıştaki köklü ifadenin içi 25 olmalıdır.
\( 4 + 7\sqrt{1 + 2\sqrt{6 + 2\sqrt{x}}} = 25 \)
\( \sqrt{1 + 2\sqrt{6 + 2\sqrt{x}}} = 3 \)
Sonucun 3 olması için en dıştaki köklü ifadenin içi 9 olmalıdır.
\( 1 + 2\sqrt{6 + 2\sqrt{x}} = 9 \)
\( \sqrt{6 + 2\sqrt{x}} = 4 \)
Sonucun 4 olması için en dıştaki köklü ifadenin içi 16 olmalıdır.
\( 6 + 2\sqrt{x} = 16 \)
\( \sqrt{x} = 5 \)
\( x = 25 \) bulunur.
\( \sqrt{\dfrac{25}{49} + \dfrac{49}{121} - \dfrac{10}{11}} \) işleminin sonucu kaçtır?
Çözümü GösterKöklü ifadeden kurtulmak için kök içini bir ifadenin parantez karesi şeklinde yazalım.
\( \sqrt{(\dfrac{5}{7})^2 + (\dfrac{7}{11})^2 - \dfrac{10}{11}} \)
Kök içindeki üçüncü terim parantez karesi açılımındaki ikinci terime karşılık gelir.
\( \dfrac{10}{11} = 2 \cdot \dfrac{5}{7} \cdot \dfrac{7}{11} \)
\( = \sqrt{(\dfrac{5}{7} - \dfrac{7}{11})^2} = \dfrac{5}{7} - \dfrac{7}{11} \)
\( = \dfrac{55}{77} - \dfrac{49}{77} = \dfrac{6}{77} \) bulunur.
\( \sqrt{204 \cdot 196 - 195 \cdot 205} \) işleminin sonucu kaçtır?
Çözümü GösterSoru verilen işlemleri yaparak çözülebilecek olsa da, daha hızlı bir çözüm için sayıları sadeleşecek bir forma getirmeye çalışalım.
Kök içindeki sayıları ortalamaları olan 200 sayısı cinsinden yazalım.
\( \sqrt{(200 + 4)(200 - 4) - (200 - 5)(200 + 5)} \)
\( a = 200 \) diyelim.
\( \sqrt{(a + 4)(a - 4) - (a - 5)(a + 5)} \)
Kare farkı özdeşliğini kullanalım.
\( \sqrt{(a^2 - 16) - (a^2 - 25)} \)
\( \sqrt{ a^2 - 16 - a^2 + 25} \)
\( = \sqrt{9} = 3 \) bulunur.
\( \sqrt{1457 \cdot 1469 - 1453 \cdot 1473} \) işleminin sonucu kaçtır?
Çözümü GösterSoru verilen işlemleri yaparak çözülebilecek olsa da, daha hızlı bir çözüm için sayıları sadeleşecek bir forma getirmeye çalışalım.
Kök içindeki sayılardan herhangi birine \( a \) diyelim. Biz burada \( a = 1453 \) olarak seçelim.
\( \sqrt{(a + 4)(a + 16) - a(a + 20)} \)
Parantez içindeki ifadeleri genişletelim.
\( = \sqrt{a^2 + 20a + 64 - (a^2 + 20a)} \)
\( = \sqrt{64} = 8 \) bulunur.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( \sqrt{1}, \sqrt{2}, \sqrt{3}, \ldots, \sqrt{a} \) sayı dizisinin 15 tam sayı terimi vardır.
Buna göre \( a \)'nın alabileceği en büyük değer kaçtır?
Çözümü GösterBir karekök ifadesinin sonucu tam sayı ise kök içindeki sayı bir tam sayının karesidir.
Buna göre sonucu tam sayı olan 15 terim, 1'den 15'e kadar olan tam sayıların karelerinin kareköküdür.
\( \sqrt{1}, \sqrt{4}, \sqrt{9}, \ldots, \sqrt{225} \)
Sayı dizisi \( \sqrt{15^2} = \sqrt{225} \) terimini içermeli, sonraki tam kare ifade olan \( \sqrt{16^2} = \sqrt{256} \) terimini içermemelidir.
Buna göre \( a \)'nın alabileceği en büyük değer 255 olur.
\( (ab) \) ve \( (ba) \) iki basamaklı sayılardır.
\( \sqrt{(ab) + (ba)} \) işleminin sonucu bir tam sayı olduğuna göre, \( (a, b) \) sıralı ikilisinin alabileceği kaç değer vardır?
Çözümü Gösterİki basamaklı sayıların çözümlemesini yapalım.
\( \sqrt{(ab) + (ba)} = \sqrt{(10a + b) + (10b + a)} \)
\( = \sqrt{11(a + b)} \)
\( a \) ve \( b\) birer rakam olduğu için, bu ifade \( a + b = 11 \) olduğunda tam sayı olur.
\( a + b = 11 \)
Toplamı 11 olan \( (a, b) \) rakam ikililerini bulalım.
\( (a, b) \in \{(2, 9), (3, 8), (4, 7), \ldots, (8, 3), (9, 2)\} \)
Buna göre verilen ifadeyi tam sayı yapan 8 tane \( (a, b) \) ikilisi vardır.
\( x \) bir tam kare sayı olduğuna göre, bu sayıdan iki sonraki tam kare sayı \( x \) cinsinden \( x \)'ten kaç fazladır?
Çözümü Göster\( x \) bir tam kare sayı olduğuna göre, bir doğal sayının karesi şeklinde yazılabilir.
\( n \in \mathbb{N} \) olmak üzere,
\( x = n^2 \)
İki sonraki tam kare sayı, \( n + 2 \) doğal sayısının karesidir.
\( (n + 2)^2 = n^2 + 4n + 4 \)
İki sonraki tam kare sayının ilk sayıdan ne kadar fazla olduğunu bulmak için iki ifadenin farkını alalım.
\( n^2 + 4n + 4 - n^2 \)
\( = 4n + 4 \)
Bu ifadeyi \( x \) cinsinden ifade edelim.
\( x = n^2 \Longrightarrow n = \sqrt{x} \)
\( 4n + 4 = 4\sqrt{x} + 4 \) bulunur.
Bulduğumuz ifadenin sağlamasını bir örnek üzerinden yapalım.
\( x = 100 = 10^2 \) bir tam kare sayıdır.
\( x \)'ten iki sonraki tam kare sayı 144'tür.
\( 4\sqrt{x} + 4 = 4\sqrt{100} + 4 = 44 \)
\( a \), \( b \) ve \( c \) her birinin pozitif tam bölen sayısı 3 olan farklı sayılardır.
Buna göre \( \sqrt{a} + \sqrt{b} + \sqrt{c} \) ifadesinin en küçük değeri kaçtır?
Çözümü GösterBir sayının pozitif tam bölen sayısını bulmak için sayı asal çarpanlarının üsleri biçiminde yazılır. Üslerin bir fazlasının çarpımı pozitif tam bölen sayısını verir.
Örneğin, \( 24 = 2^3 \cdot 3^1 \) sayısının pozitif tam bölen sayısı \( (3 + 1)(1 + 1) = 8 \) olur.
Bir sayının pozitif tam bölen sayısı 3 ise o sayının tek bir asal çarpanı vardır ve üssü 2'dir (\( A = x^2 \)), bu da o sayının bir asal sayının karesi olduğu anlamına gelir.
Bu yüzden \( \sqrt{a} + \sqrt{b} + \sqrt{c} \) ifadesinin sonucunun en küçük olması için \( a \), \( b \) ve \( c \) sayılarını karekök değerleri birer asal sayı olan en küçük tam kare sayılardan seçmeliyiz.
\( a = 2^2 = 4 \)
\( b = 3^2 = 9 \)
\( c = 5^2 = 25 \)
Buna göre verilen ifadenin en küçük değeri \( \sqrt{4} + \sqrt{9} + \sqrt{25} = 10 \) olur.
Kaç tane \( a \) tam sayısı için \( \sqrt{195 - \sqrt{a}} \) ifadesi bir tam sayıdır?
Çözümü Göster\( \sqrt{ 195 - \sqrt{a}} \) ifadesinin tam sayı olabilmesi için \( 195 - \sqrt{a} \) ifadesi bir tam kare sayıya eşit olmalıdır.
\( \sqrt{195} \approx 13,96 \)
Buna göre aşağıdaki koşulu sağlayan her \( m \) tam sayısı için \( 195 - \sqrt{a} \) ifadesi bir tam kare sayı olur.
\( m \in \mathbb{Z} \) ve \( 0 \le m \le 13 \) olmak üzere,
\( m^2 = 195 - \sqrt{a} \)
\( \sqrt{a} = 195 - m^2 \)
Bu aralıktaki her \( m \) tam sayısı için tek bir \( \sqrt{a} \) ve \( a \) tam sayı değeri vardır.
Buna göre verilen ifadeyi tam sayı yapan 14 tam sayı \( a \) değeri vardır.
\( \sqrt[4]{(9! + 10! + 11!) \cdot A} \) işleminin sonucunu tam sayı yapan en küçük \( A \) tam sayısı kaçtır?
Çözümü GösterKök içindeki ifadeyi çarpanlarına ayıralım.
\( \sqrt[4]{(9! + 10 \cdot 9! + 11 \cdot 10 \cdot 9!) \cdot A} \)
\( = \sqrt[4]{9!(1 + 10 + 110) \cdot A} = \sqrt[4]{9!\ 121 \cdot A} \)
Kök içindeki ifadeyi asal çarpanlarına ayıralım.
\( = \sqrt[4]{2^7 \cdot 3^4 \cdot 5^1 \cdot 7^1 \cdot 11^2 \cdot A} \)
Köklü ifadenin derecesi 4 olduğu için, ifadenin sonucunun tam sayı olabilmesi tüm asal çarpanların üsleri 4 ya da 4'ün bir tam sayı katı olmalıdır.
Buna göre olabilecek en küçük \( A \) sayısı içinde 2 çarpanı 1 kez, 5 ve 7 çarpanları 3'er kez, 11 çarpanı da 2 kez bulunmalıdır.
\( A = 2^1 \cdot 5^3 \cdot 7^3 \cdot 11^2 \) bulunur.