Paydayı Rasyonel Hale Getirme
Kesirli ifadelerin paydalarında köklü ifadeler bulunmasında matematiksel açıdan bir yanlışlık olmasa da, birkaç sebeple paydada sadece rasyonel ifadelerin bulunması tercih edilir.
- Tutarlılık: Bir sayının (örneğin bir problemin doğru cevabının) farklı gösterimleri bu şekilde standart bir forma getirilir (\( \frac{1}{\sqrt{2}} \) yerine \( \frac{\sqrt{2}}{2} \)).
- İşlem kolaylığı: Paydaları eşitlemek \( \frac{\sqrt{5}}{5} + \frac{\sqrt{5} + \sqrt{3}}{2} \) işlemi için \( \frac{1}{\sqrt{5}} + \frac{1}{\sqrt{5} - \sqrt{3}} \) işlemine göre daha kolaydır.
- Yaklaşık değer ile hesaplama: \( \sqrt{3} \) ifadesinin yaklaşık değerini kullanarak \( \frac{\sqrt{3}}{3} \) ifadesini hesaplamak ya da sonucunu tahmin etmek \( \frac{1}{\sqrt{3}} \) ifadesini hesaplamaktan daha kolaydır.
Paydayı rasyonel hale getirme, bir diğer ifadeyle paydayı kökten kurtarma işlemi paydanın farklı formları için farklı şekillerde gerçekleştirilebilir.
Paydada Tek Terimli İfade
Paydada \( \sqrt{a} \) şeklinde tek terimli ve 2. dereceden köklü bir ifade varsa pay ve payda bu ifadeyle çarpılarak payda kökten kurtarılabilir ve rasyonel hale getirilebilir.
\( \dfrac{\sqrt{2}}{\sqrt{3}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( \textcolor{red}{\sqrt{3}} \) ifadesi ile çarparak paydayı kökten kurtarabiliriz.
\( \dfrac{\sqrt{2}}{\sqrt{3}} \cdot \dfrac{\textcolor{red}{\sqrt{3}}}{\textcolor{red}{\sqrt{3}}} = \dfrac{\sqrt{6}}{3} \)
\( \dfrac{2}{\sqrt{125}} \) ifadesinin paydasını rasyonel hale getirelim.
Önce paydadaki ifadede kök içini sadeleştirelim.
\( \dfrac{2}{\sqrt{125}} = \dfrac{2}{5\sqrt{5}} \)
Payı ve paydayı paydadaki \( \textcolor{red}{\sqrt{5}} \) ifadesi ile çarparak paydayı kökten kurtarabiliriz.
\( = \dfrac{2}{5\sqrt{5}} \cdot \dfrac{\textcolor{red}{\sqrt{5}}}{\textcolor{red}{\sqrt{5}}} = \dfrac{2\sqrt{5}}{25} \)
Alternatif olarak, sadeleştirme yapmadan ve payı/paydayı \( \sqrt{125} \) ile çarparak da paydayı rasyonel hale getirebiliriz.
\( \dfrac{1}{\sqrt{a + 2}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( \textcolor{red}{\sqrt{a + 2}} \) ifadesi ile çarparak paydayı kökten kurtarabiliriz.
\( \dfrac{1}{\sqrt{a + 2}} \cdot \dfrac{\textcolor{red}{\sqrt{a + 2}}}{\textcolor{red}{\sqrt{a + 2}}} = \dfrac{\sqrt{a + 2}}{a + 2} \)
Paydada \( \sqrt[n]{a} \) şeklinde tek terimli ve n. dereceden köklü bir ifade varsa pay ve payda bu ifadenin kök içinin üssünü köklü ifadenin derecesine eşitleyecek ya da bu derecenin bir tam sayı katına getirecek bir ifade ile çarpılarak payda kökten kurtarılabilir ve rasyonel hale getirilebilir.
\( \dfrac{1}{\sqrt[3]{5}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( \sqrt[3]{5} \) ifadesinin içinin üssünü ifadenin derecesine eşitleyecek şekilde \( \textcolor{red}{\sqrt[3]{5^2}} \) ile çarparak paydayı kökten kurtarabiliriz.
\( \dfrac{1}{\sqrt[3]{5}} \cdot \dfrac{\textcolor{red}{\sqrt[3]{5^2}}}{\textcolor{red}{\sqrt[3]{5^2}}} = \dfrac{\sqrt[3]{5^2}}{\sqrt[3]{5^3}} = \dfrac{\sqrt[3]{5^2}}{5} \)
\( \dfrac{1}{\sqrt[4]{32}} \) ifadesinin paydasını rasyonel hale getirelim.
\( \dfrac{1}{\sqrt[4]{32}} = \dfrac{1}{\sqrt[4]{2^5}} \)
Payı ve paydayı paydadaki \( \sqrt[4]{2^5} \) ifadesinin içinin üssünü ifadenin derecesinin bir tam sayı katına getirecek şekilde \( \textcolor{red}{\sqrt[4]{2^3}} \) ile çarparak paydayı kökten kurtarabiliriz.
\( = \dfrac{1}{\sqrt[4]{2^5}} \cdot \dfrac{\textcolor{red}{\sqrt[4]{2^3}}}{\textcolor{red}{\sqrt[4]{2^3}}} = \dfrac{\sqrt[4]{2^3}}{\sqrt[4]{2^8}} = \dfrac{\sqrt[4]{2^3}}{2^2} \)
\( \dfrac{1}{\sqrt[5]{8b^2}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( \sqrt[5]{8b^2} \) ifadesinin içindeki çarpanların üssünü ifadenin derecesine eşitleyecek ya da bu derecenin bir tam sayı katına getirecek şekilde \( \textcolor{red}{\sqrt[5]{4b^3}} \) ile çarparak paydayı kökten kurtarabiliriz.
\( \dfrac{1}{\sqrt[5]{8b^2}} \cdot \dfrac{\textcolor{red}{\sqrt[5]{4b^3}}}{\textcolor{red}{\sqrt[5]{4b^3}}} = \dfrac{\sqrt[5]{4b^3}}{\sqrt[5]{32b^5}} = \dfrac{\sqrt[5]{4b^3}}{2b} \)
Paydada İki Terimli İfade
İki terimli ifadeleri rasyonel hale getirmek için kullanılabilecek özdeşlikler için özdeşlikler sayfasını inceleyebilirsiniz.
Paydada biri ya da ikisi karekök içinde olan iki terimli bir ifade varsa pay ve payda paydadaki ifadenin eşleniği ile çarpılarak \( a^2 - b^2 \) özdeşliği elde edilebilir ve paydada kök içindeki terimler kökten kurtarılabilir.
\( \dfrac{1}{\sqrt{5} - \sqrt{2}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( \sqrt{5} - \sqrt{2} \) ifadesinin eşleniği olan \( \textcolor{red}{\sqrt{5} + \sqrt{2}} \) ile çarparak paydada kök içindeki terimleri kökten kurtarabiliriz.
\( \dfrac{1}{\sqrt{5} - \sqrt{2}} \cdot \dfrac{\textcolor{red}{\sqrt{5} + \sqrt{2}}}{\textcolor{red}{\sqrt{5} + \sqrt{2}}} \)
\( = \dfrac{\sqrt{5} + \sqrt{2}}{(\sqrt{5})^2 - (\sqrt{2})^2} \)
\( = \dfrac{\sqrt{5} + \sqrt{2}}{3} \)
\( \dfrac{6}{3 + \sqrt{7}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı paydadaki \( 3 + \sqrt{7} \) ifadesinin eşleniği olan \( \textcolor{red}{3 - \sqrt{7}} \) ile çarparak paydada kök içindeki terimleri kökten kurtarabiliriz.
\( \dfrac{6}{3 + \sqrt{7}} \cdot \dfrac{\textcolor{red}{3 - \sqrt{7}}}{\textcolor{red}{3 - \sqrt{7}}} \)
\( = \dfrac{6(3 - \sqrt{7})}{3^2 - (\sqrt{7})^2} \)
\( = 3(3 - \sqrt{7}) \)
Paydada biri ya da ikisi küpkök içinde olan iki terimli bir ifade varsa pay ve payda \( a^3 - b^3 \) ya da \( a^3 + b^3 \) özdeşliği elde edilebilecek bir çarpan ile çarpılarak paydada kök içindeki terimler kökten kurtarılabilir.
Bu iki özdeşlik aşağıda hatırlatma olarak verilmiştir.
\( a - b = (\sqrt[3]{a})^3 - (\sqrt[3]{b})^3 \)
\( = (\sqrt[3]{a} - \sqrt[3]{b})((\sqrt[3]{a})^2 + \sqrt[3]{ab} + (\sqrt[3]{b})^2) \)
\( a + b = (\sqrt[3]{a})^3 + (\sqrt[3]{b})^3 \)
\( = (\sqrt[3]{a} + \sqrt[3]{b})((\sqrt[3]{a})^2 - \sqrt[3]{ab} + (\sqrt[3]{b})^2) \)
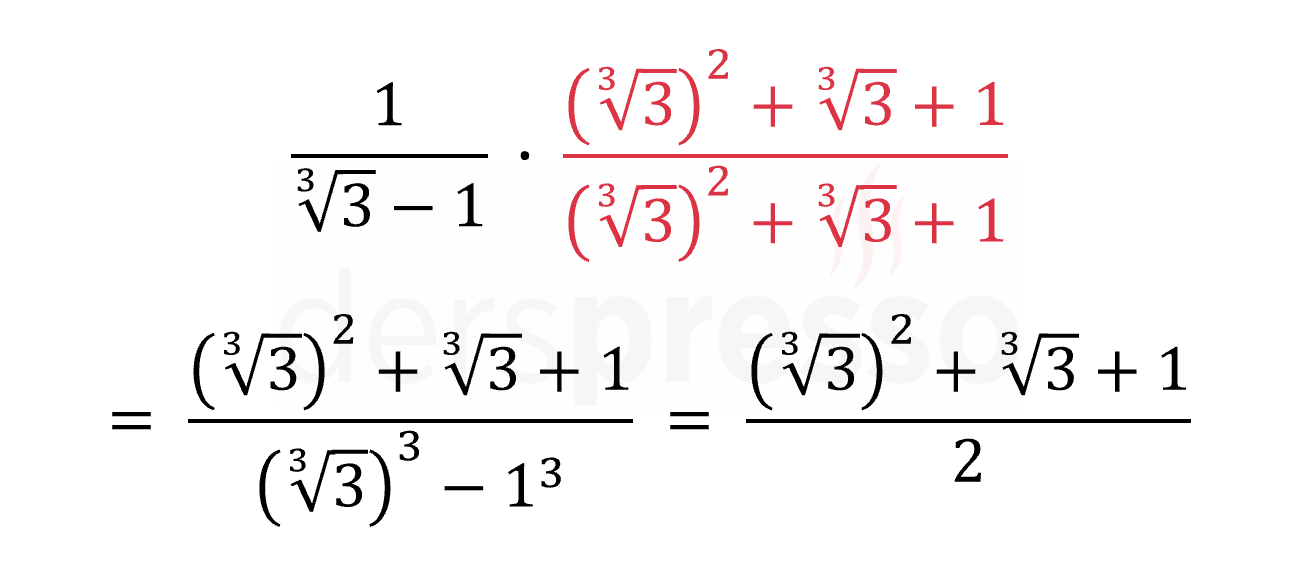
\( \dfrac{1}{\sqrt[3]{5} + \sqrt[3]{3}} \) ifadesinin paydasını rasyonel hale getirelim.
Payı ve paydayı \( \textcolor{red}{(\sqrt[3]{5})^2 - \sqrt[3]{5} \cdot \sqrt[3]{3} + (\sqrt[3]{3})^2} \) ile çarparak paydada kök içindeki terimleri kökten kurtarabiliriz.
\( \dfrac{1}{\sqrt[3]{5} + \sqrt[3]{3}} \cdot \dfrac{\textcolor{red}{(\sqrt[3]{5})^2 - \sqrt[3]{5} \cdot \sqrt[3]{3} + (\sqrt[3]{3})^2}}{\textcolor{red}{(\sqrt[3]{5})^2 - \sqrt[3]{5} \cdot \sqrt[3]{3} + (\sqrt[3]{3})^2}} \)
\( = \dfrac{(\sqrt[3]{5})^2 - \sqrt[3]{5} \cdot \sqrt[3]{3} + (\sqrt[3]{3})^2}{(\sqrt[3]{5})^3 + (\sqrt[3]{3})^3} \)
\( = \dfrac{(\sqrt[3]{5})^2 - \sqrt[3]{5} \cdot \sqrt[3]{3} + (\sqrt[3]{3})^2}{8} \)
Ahmet \( \sqrt{15} - \sqrt{10} \) ifadesini eşleniği ile çarpmak yerine yanlışlıkla bölmüştür.
Buna göre Ahmet'in bulması gereken sayı bulduğu sayıdan kaç fazladır?
Çözümü Gösterİlk olarak Ahmet'in eşleniği ile bölerek bulduğu sayıyı bulalım.
\( \dfrac{\sqrt{15} - \sqrt{10}}{\sqrt{15} + \sqrt{10}} \)
Paydadaki köklü ifadelerden kurtulmak için pay ve paydayı paydanın eşleniği ile çarpalım.
\( = \dfrac{(\sqrt{15} - \sqrt{10})(\sqrt{15} - \sqrt{10} )}{(\sqrt{15} + \sqrt{10})(\sqrt{15} - \sqrt{10}) } \)
\( = \dfrac{(\sqrt{15} - \sqrt{10})^2 }{(\sqrt{15})^2 - (\sqrt{10})^2} \)
\( = \dfrac{(\sqrt{15})^2 - 2\sqrt{15}\sqrt{10} + (\sqrt{10})^2}{15 - 10} \)
\( = \dfrac{15 - 2\sqrt{150} + 10}{5} \)
\( = \dfrac{25 - 2 \cdot 5\sqrt{6}}{5} \)
Buna göre Ahmet'in yanlış şekilde bulduğu sayı aşağıdaki gibidir.
\( = 5 - 2\sqrt{6} \)
Şimdi Ahmet'in bulması gereken sayıyı bulalım.
\( (\sqrt{15} - \sqrt{10})(\sqrt{15} + \sqrt{10})\)
Buna göre Ahmet'in bulması gereken sayı aşağıdaki gibidir.
\( = (\sqrt{15})^2 - (\sqrt{10})^2 = 5 \)
Ahmet'in bulması gereken sayıdan bulduğu sayıyı çıkaralım.
\( 5 - (5 - 2\sqrt{6}) = 2\sqrt{6} \) bulunur.
\( \dfrac{\sqrt{3} + 1}{\sqrt{5} - 1} = A \) olduğuna göre,
\( \dfrac{\sqrt{5} + 1}{\sqrt{3} - 1} = B \) ifadesinin \( A \) cinsinden değeri kaçtır?
Çözümü Göster\( A \) ifadesinin payını ve paydasını paydanın eşleniği ile çarpalım.
\( A = \dfrac{(\sqrt{3} + 1)(\sqrt{5} + 1)}{(\sqrt{5} - 1)(\sqrt{5} + 1)} \)
\( = \dfrac{(\sqrt{3} + 1)(\sqrt{5} + 1)}{(\sqrt{5})^2 - 1^2} \)
\( = \dfrac{(\sqrt{3} + 1)(\sqrt{5} + 1)}{4} \)
\( (\sqrt{3} + 1)(\sqrt{5} + 1) = 4A \)
\( B \) ifadesinin payını ve paydasını paydanın eşleniği ile çarpalım.
\( B = \dfrac{(\sqrt{5} + 1)(\sqrt{3} + 1)}{(\sqrt{3} - 1)(\sqrt{3} + 1)} \)
\( = \dfrac{(\sqrt{5} + 1)(\sqrt{3} + 1)}{(\sqrt{3})^2 - 1^2} \)
\( = \dfrac{(\sqrt{5} + 1)(\sqrt{3} + 1)}{2} \)
Bulduğumuz ifadenin payı \( 4A \)'ya eşittir.
\( B = \dfrac{4A}{2} = 2A \) bulunur.
\( \dfrac{1}{1 - \sqrt[3]{3} + \sqrt[3]{9}} \) ifadesini paydası rasyonel olacak şekilde en sade biçimde yazınız.
Çözümü GösterPaydadaki ifadeyi düzenleyelim.
\( \dfrac{1}{1 - \sqrt[3]{3} + \sqrt[3]{9}} = \dfrac{1}{\sqrt[3]{3^2} - \sqrt[3]{3} + 1} \)
Paydayı rasyonel hale getirmek için payı ve paydayı \( \sqrt[3]{3} + 1 \) ile çarpalım.
\( = \dfrac{\sqrt[3]{3} + 1}{(\sqrt[3]{3^2} - \sqrt[3]{3} + 1)(\sqrt[3]{3} + 1)} \)
Paydada iki küpün toplamı özdeşliğini kullanabiliriz.
\( a^3 + b^3 = (a + b)(a^2 - ab + b^2) \)
\( = \dfrac{\sqrt[3]{3} + 1}{(\sqrt[3]{3})^3 + 1^3} \)
\( = \dfrac{\sqrt[3]{3} + 1}{4} \) bulunur.
\( \dfrac{1}{\sqrt[3]{4} + \sqrt[3]{9} + \sqrt[3]{6}} \) ifadesini paydası rasyonel olacak şekilde en sade biçimde yazınız.
Çözümü GösterPaydadaki ifadeyi düzenleyelim.
\( \dfrac{1}{\sqrt[3]{4} + \sqrt[3]{9} + \sqrt[3]{6}} = \dfrac{1}{\sqrt[3]{3^2} + \sqrt[3]{6} + \sqrt[3]{2^2}} \)
Paydayı rasyonel hale getirmek için payı ve paydayı \( \sqrt[3]{3} - \sqrt[3]{2} \) ile çarpalım.
\( = \dfrac{\sqrt[3]{3} - \sqrt[3]{2}}{(\sqrt[3]{3} - \sqrt[3]{2})(\sqrt[3]{3^2} + \sqrt[3]{6} + \sqrt[3]{2^2})} \)
Paydada iki küpün farkı özdeşliğini kullanabiliriz.
\( a^3 - b^3 = (a - b)(a^2 + ab + b^2) \)
\( = \dfrac{\sqrt[3]{3} - \sqrt[3]{2}}{(\sqrt[3]{3})^3 - (\sqrt[3]{2})^3} \)
\( = \dfrac{\sqrt[3]{3} - \sqrt[3]{2}}{3 - 2} \)
\( = \sqrt[3]{3} - \sqrt[3]{2} \) bulunur.
\( \dfrac{\sqrt{3}}{\sqrt{5} + \sqrt{7} - 2\sqrt{3}} \) ifadesini paydası rasyonel olacak şekilde en sade biçimde yazınız.
Çözümü Göster\( a = \sqrt{5} + \sqrt{7} \) diyelim.
\( \dfrac{\sqrt{3}}{\sqrt{5} + \sqrt{7} - 2\sqrt{3}} = \dfrac{\sqrt{3}}{a - 2\sqrt{3}} \)
Payı ve paydayı payın eşleniği ile çarpalım.
\( = \dfrac{\sqrt{3}(a + 2\sqrt{3})}{(a - 2\sqrt{3})(a + 2\sqrt{3})} \)
\( = \dfrac{\sqrt{3}(a + 2\sqrt{3})}{a^2 - (2\sqrt{3})^2} \)
\( = \dfrac{\sqrt{3}(a + 2\sqrt{3})}{a^2 - 12} \)
\( a \) değerini yerine koyalım.
\( = \dfrac{\sqrt{3}(\sqrt{5} + \sqrt{7} + 2\sqrt{3})}{(\sqrt{5} + \sqrt{7})^2 - 12} \)
\( = \dfrac{\sqrt{15} + \sqrt{21} + 6}{5 + 2\sqrt{35} + 7 - 12} \)
\( = \dfrac{\sqrt{15} + \sqrt{21} + 6}{2\sqrt{35}} \)
Payı ve paydayı \( \sqrt{35} \) ile çarpalım.
\( = \dfrac{\sqrt{35}(\sqrt{15} + \sqrt{21} + 6)}{70} \)
\( = \dfrac{\sqrt{35 \cdot 15} + \sqrt{35 \cdot 21} + 6\sqrt{35})}{70} \)
\( = \dfrac{5\sqrt{21} + 7\sqrt{15} + 6\sqrt{35}}{70} \) bulunur.
\( \dfrac{1}{\sqrt{400} + \sqrt{401}} + \dfrac{1}{\sqrt{401} + \sqrt{402}} \) \( + \dfrac{1}{\sqrt{402} + \sqrt{403}} + \ldots \) \( + \dfrac{1}{\sqrt{899} + \sqrt{900}} \)
ifadesinin sonucu kaçtır?
Çözümü GösterHer bir terimin payını ve paydasını paydanın eşleniği ile çarpalım.
\( \dfrac{\sqrt{400} - \sqrt{401}}{(\sqrt{400} + \sqrt{401})(\sqrt{400} - \sqrt{401})} \) \( + \dfrac{\sqrt{401} - \sqrt{402}}{(\sqrt{401} + \sqrt{402})(\sqrt{401} - \sqrt{402})} + \ldots \)
\( = \dfrac{\sqrt{400} - \sqrt{401}}{(\sqrt{400})^2 - (\sqrt{401})^2} \) \( + \dfrac{\sqrt{401} - \sqrt{402}}{(\sqrt{401})^2 - (\sqrt{402})^2} + \ldots \)
Tüm paydalar \( -1 \) olarak sadeleşir.
\( = \dfrac{\sqrt{400} - \sqrt{401}}{-1} \) \( + \dfrac{\sqrt{401} - \sqrt{402}}{-1} + \ldots \)
\( = \dfrac{\sqrt{400} - \sqrt{401} + \sqrt{401} - \sqrt{402} + \sqrt{402} - \sqrt{403} - \ldots + \sqrt{899} - \sqrt{900}}{-1} \)
Paydaki ilk ve son terimler dışındaki terimler birbirini götürür.
\( = \dfrac{\sqrt{400} - \sqrt{900}}{-1} = \dfrac{20 - 30}{-1} \)
\( = 10 \) bulunur.