Dizi Tipleri ve Özellikleri
Sabit Dizi
Tüm terimleri birbirine eşit olan dizilere sabit dizi denir.
\( k \in \mathbb{R} \) olmak üzere,
\( a_n = k \) dizisi sabit dizidir.
\( a_n = 3 \)
\( (b_n) = (5, 5, 5, \ldots) \)
\( c_n = \sin(n\pi) \)
\( (c_n) = (0, 0, 0, \ldots) \)
Genel terimi rasyonel bir ifade şeklinde yazılan bir dizinin sabit dizi olması için aşağıdaki koşul sağlanmalıdır.
\( a_n = \dfrac{an + b}{cn + d} \)
\( \dfrac{a}{c} = \dfrac{b}{d} \) ise \( (a_n) \) bir sabit dizidir.
\( a_n = \dfrac{9n + 6}{3n + a} \) bir sabit dizi ise,
\( \dfrac{9}{3} = \dfrac{6}{a} \)
\( a = 2 \)
İSPATI GÖSTER
\( a_n = \dfrac{an + b}{cn + d} \)
\( (a_n) \) dizisi için aşağıdaki koşulun sağlandığını varsayalım ve bu orantının sabitine \( k \) diyelim.
\( k \in \mathbb{R} \) olmak üzere,
\( \dfrac{a}{c} = \dfrac{b}{d} = k \)
\( a = kc, \quad b = kd \)
Bu iki değeri dizinin genel teriminde yerine koyalım.
\( a_n = \dfrac{(kc)n + kd}{cn + d} \)
Paydaki ifadeyi \( k \) parantezine alalım.
\( = \dfrac{k(cn + d)}{cn + d} = k \)
Buna göre genel terimi verilen koşulu sağlayan bir dizi sabit dizidir.
Bir dizi hem aritmetik hem de geometrik dizi ise bu dizi sabit dizidir. Sabit bir dizinin aritmetik dizi olarak ortak farkı 0, geometrik dizi olarak ortak oranı 1 olur. Aritmetik ve geometrik dizileri önümüzdeki bölümde inceleyeceğiz.
Sonlu ve Sonsuz Diziler
Sonsuz sayıda terimden oluşan dizilere sonsuz dizi denir. Sonsuz dizilerde her \( a_n \) terimi için bir \( a_{n+1} \) terimi bulunur.
Sınırlı sayıda terimden oluşan dizilere sonlu dizi denir.
Bir dizinin sonlu olduğu belirtilmediği durumda sonsuz bir dizi olduğu anlaşılmalıdır.
Sonsuz dizilerin yakınsaklığını sonsuz seriler konusunun giriş bölümünde inceleyeceğiz.
Sınırlı Diziler
Eğer her \( n \) için \( a_n \le M \) koşulunu sağlayan bir \( M \) sayısı varsa \( (a_n) \) dizisi üstten sınırlı bir dizidir ve bu \( M \) sayısı dizinin bir üst sınırıdır.
Eğer her \( n \) için \( m \le a_n \) koşulunu sağlayan bir \( m \) sayısı varsa \( (a_n) \) dizisi alttan sınırlı bir dizidir ve bu \( m \) sayısı dizinin bir alt sınırıdır.
Bir dizinin üstten (alttan) sınırlı olması, dizinin grafiğinde tüm noktaların altında (üstünde) kaldığı yatay bir çizgi çizilebilmesi anlamına gelir.
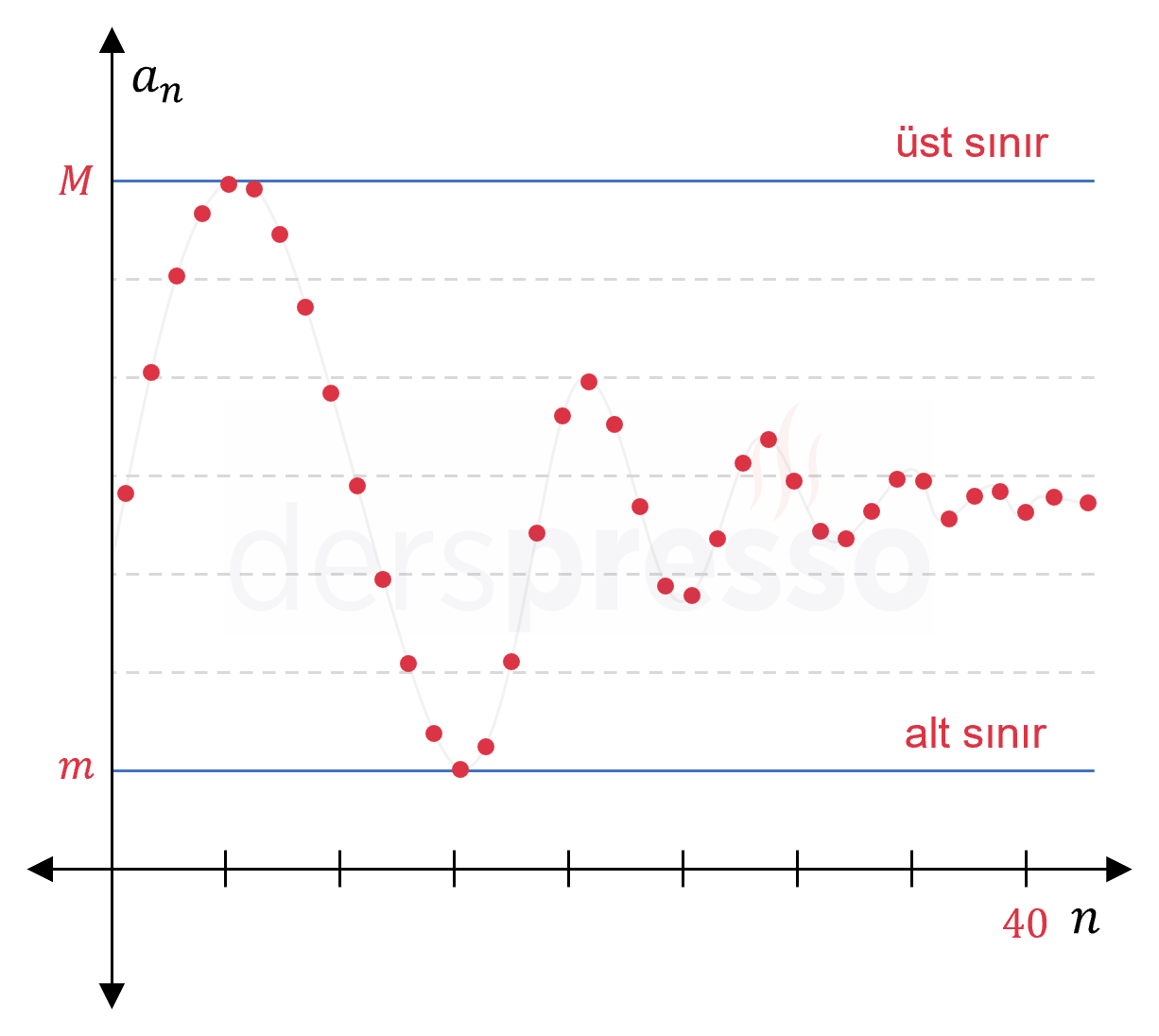
Hem üstten hem alttan sınırlı olan dizilere sınırlı dizi denir. Bu iki yönden en az birinde sınırlı olmayan dizilere sınırsız dizi denir.
Artan ve Azalan Diziler
Terimleri sürekli artan ya da sabit kalan (\( a_k \le a_{k + 1} \)) dizilere artan dizi denir.
Terimleri sürekli artan (\( a_k \lt a_{k + 1} \)) dizilere kesin artan dizi denir.
Terimleri sürekli azalan ya da sabit kalan (\( a_k \ge a_{k + 1} \)) dizilere azalan dizi denir.
Terimleri sürekli azalan (\( a_k \gt a_{k + 1} \)) dizilere kesin azalan dizi denir.
Yukarıdaki dört durumdan herhangi birine uyan dizilere monoton dizi denir. Buna göre monoton bir dizi tanım kümesindeki bir aralıkta artan bir diğer aralıkta azalan olamaz.
Alterne Diziler
Ardışık terimlerinin işaretleri farklı olan dizilere alterne dizi denir.
\( a_n = (-1)^n \)
\( (a_n) = (-1, 1, -1, 1, -1, 1, \ldots) \)
\( b_n = (-1)^{n+1}n^2 \)
\( (b_n) = (1, -4, 9, -16, 25, -36, \ldots) \)
\( c_n = \cos(\pi n)n! \)
\( (c_n) = (-1, 2, -6, 24, -120, 720, \ldots) \)
Yukarıdaki örneklerde görülebileceği gibi, ardışık terimlerin işaretlerindeki değişim \( (-1)^n \) çarpanı ya da trigonometrik fonksiyonlarla sağlanabilir.
Periyodik Diziler
Belirli sayıda terimde bir kendisini tekrarlayan dizilere periyodik dizi denir.
\( T \in \mathbb{Z^+} \) olmak üzere,
Her \( n \) için \( a_n = a_{n + T} \) ise,
\( (a_n) \) bir periyodik dizidir.
\( a_n = (-1)^n \) periyodu \( T = 2 \) olan bir periyodik dizidir.
\( a_1 = (-1)^1 = -1 \)
\( a_2 = (-1)^2 = 1 \)
\( a_3 = (-1)^3 = -1 \)
\( a_4 = (-1)^4 = 1 \)
\( a_n = \cos{\dfrac{2\pi n}{3}} \) periyodu \( T = 3 \) olan bir periyodik dizidir.
\( a_1 = \cos{\dfrac{2\pi}{3}} = -\dfrac{1}{2} \)
\( a_2 = \cos{\dfrac{4\pi}{3}} = -\dfrac{1}{2} \)
\( a_3 = \cos{\dfrac{6\pi}{3}} = 1 \)
\( a_4 = \cos{\dfrac{8\pi}{3}} = -\dfrac{1}{2} \)
\( a_5 = \cos{\dfrac{10\pi}{3}} = -\dfrac{1}{2} \)
\( a_6 = \cos{\dfrac{12\pi}{3}} = 1 \)
Periyodu \( T \) olan bir dizi için yukarıdaki eşitlik \( T \)'nin tüm tam sayı katları için de sağlanacağı için \( k \in \mathbb{Z^+} \) olmak üzere tüm \( kT \) değerleri de dizinin periyodu olur. Genellikle tüm bu değerler içinde en küçük değer dizinin periyodu olarak ifade edilir.
Sabit bir dizi aynı zamanda periyodu 1 olan bir periyodik dizidir.
\( a_n = (m - 2)n^3 + (k + 1)n + 2m - k \) dizisi bir sabit dizi olduğuna göre,
\( a_{71} + a_{72} + ... + a_{201} \) ifadesinin değeri kaçtır?
Çözümü GösterDizinin sabit dizi olması için genel terim \( n \) değişkenine bağlı olmamalı, dolayısıyla \( n \)'li terimlerin katsayıları sıfır olmalıdır.
\( m - 2 = 0 \Longrightarrow m = 2 \)
\( k + 1 = 0 \Longrightarrow k = -1 \)
Bu durumda dizi tanımı aşağıdaki gibi olur.
\( a_n = 2m - k = 2(2) - (-1) = 5 \)
Değeri sorulan ifadeyi hesaplayalım.
\( a_{71} + a_{72} + ... + a_{201} \) ifadesindeki terim sayısı \( 201 - 71 + 1 = 131 \)'dir.
Buna göre toplam ifadesinin sonucu \( 131 \cdot 5 = 655 \) olur.
\( a_1 = 6 \) olmak üzere,
\( a_n = \sqrt{\abs{(a_{n-1})^2 - 37}} \) olduğuna göre, \( a_{237} \) kaçtır?
Çözümü GösterDizinin terimlerini sırayla hesaplayalım.
\( a_1 = 6 \)
\( a_2 = \sqrt{\abs{6^2 - 37}} = 1 \)
\( a_3 = \sqrt{\abs{1^2 - 37}} = 6 \)
\( a_4 = \sqrt{\abs{6^2 - 37}} = 1 \)
\( a_5 = \sqrt{\abs{1^2 - 37}} = 6 \)
Dizinin terimlerinin periyodik şekilde 1 ve 6 değerlerini aldığını görüyoruz. Buna göre indisi çift sayı olan terimler 1, tek sayı olan terimler 6 olmaktadır.
\( a_{237} = 6 \) bulunur.
\( (a_n) \) bir sabit dizidir.
\( a_n = (x + 1)n + n^y + 5x^y \)
olduğuna göre, \( a_2 \)'nin alabileceği değerler çarpımı kaçtır?
Çözümü GösterDizinin sabit dizi olması için genel terim \( n \) değişkenine bağlı olmamalı, dolayısıyla ifadede \( n \)'li terim bulunmamalıdır.
\( n \) değişkenine bağlı \( (x + 1)n + n^y \) ifadesi iki \( (x, y) \) değer ikilisi için sabit sayı olur.
Durum 1: \( x = -1, y = 0 \)
Bu durumda her iki terimde de \( n \) değişkenleri yok olur.
\( a_n = (-1 + 1)n + n^0 + 5(-1)^0 \)
\( = 0 + 1 + 5 = 6 \)
\( a_n = a_2 = 6 \)
Durum 2: \( x = -2, y = 1 \)
Bu durumda iki terimde \( n \) değişkenleri yok olmaz, ancak birbirini götürür.
\( a_n = (-2 + 1)n + n^1 + 5(-2)^1 = -10 \)
\( = -n + n + (-10) = -10 \)
\( a_n = a_2 = -10 \)
Buna göre \( a_2 \)'nin alabileceği değerler çarpımı \( 6 \cdot (-10) = -60 \) olarak bulunur.
\( B = \{1, 2, 3, \ldots, 50\} \) ve \( b_n: B \to \mathbb{R} \) olmak üzere,
\( b_n = \sin{\dfrac{n\pi}{2}} \) dizisinin terimlerinin toplamı kaçtır?
Çözümü GösterDizinin ilk birkaç terimini bulalım.
\( b_1 = \sin{\dfrac{1\pi}{2}} = 1 \)
\( b_2 = \sin{\dfrac{2\pi}{2}} = 0 \)
\( b_3 = \sin{\dfrac{3\pi}{2}} = -1 \)
\( b_4 = \sin{\dfrac{4\pi}{2}} = 0 \)
\( b_5 = \sin{\dfrac{5\pi}{2}} = 1 \)
\( b_6 = \sin{\dfrac{6\pi}{2}} = 0 \)
Buna göre dizinin periyodu 4 olur, yani dizinin her ardışık dört teriminin toplamı 0 olur.
50'nin 4'e bölümünden kalan 2 olduğu için son iki terim \( a_{49} = 1 \) ve \( a_{50} = 0 \) olur.
\( \underbrace{b_1 + b_2 + \ldots + b_{48}}_{0} + b_{49} + b_{50} = 1 + 0 = 1 \) bulunur.
\( (a_n) \) dizisinde \( a_1 = 24 \) ve \( a_2 = 8 \) olarak veriliyor.
\( a_{n+2} = \dfrac{a_{n+1}}{a_n} \) olduğuna göre, \( a_{718} \) kaçtır?
Çözümü GösterDizinin ilk birkaç terimini hesaplayalım.
\( a_3 = \dfrac{a_2}{a_1} = \dfrac{8}{24} = \dfrac{1}{3} \)
\( a_4 = \dfrac{a_3}{a_2} = \dfrac{\frac{1}{3}}{8} = \dfrac{1}{24} \)
\( a_5 = \dfrac{a_4}{a_3} = \dfrac{\frac{1}{24}}{\frac{1}{3}} = \dfrac{1}{8} \)
\( a_6 = \dfrac{a_5}{a_4} = \dfrac{\frac{1}{8}}{\frac{1}{24}} = 3 \)
\( a_7 = \dfrac{a_6}{a_5} = \dfrac{3}{\frac{1}{8}} = 24 \)
\( a_8 = \dfrac{a_7}{a_6} = \dfrac{24}{3} = 8 \)
\( (a_n) = \left( 24, 8, \dfrac{1}{3}, \dfrac{1}{24}, \dfrac{1}{8}, 3, 24, 8, \ldots \right) \)
Dizinin bir teriminin değeri öncesindeki iki terimin değerine göre belirlenmektedir.
\( a_7 = a_1 \) ve \( a_8 = a_2 \) olduğu için dizinin periyodik olduğunu ve her 6 terimde bir terimlerin tekrar ettiğini söyleyebiliriz.
\( 718 \bmod{6} = 4 \) olduğuna göre \( a_{718} = a_4 \) olur.
\( a_{718} = \dfrac{1}{24} \) olarak bulunur.
\( a_n = n^3 - 24n^2 + 144n + 777 \)
dizisinde \( a_n \gt a_{n+1} \) koşulunu sağlayan en büyük \( n \) değeri kaçtır?
Çözümü GösterBir dizi aynı zamanda tanım kümesi pozitif tam sayılar olan bir fonksiyondur.
\( f: \mathbb{Z^+} \to \mathbb{R} \) olmak üzere,
\( f(x) = x^3 - 24x^2 + 144x + 777 \)
\( a_n \gt a_{n+1} \) eşitsizliği fonksiyonun azalan olduğu aralıkta sağlanır.
Fonksiyonun türevini alarak hangi aralıklarda azalan olduğunu bulalım.
\( f'(x) = 3x^2 - 48x + 144 \lt 0 \)
\( 3(x - 4)(x - 12) \lt 0 \)
Eşitsizliğin sol tarafı her iki çarpanı sıfır yapan \( x \) değerleri arasında negatif değer alır.
Buna göre fonksiyon \( x \in (4, 12) \) aralığında azalandır.
Fonksiyonu tekrar dizi olarak düşünürsek dizinin azalan olduğu en büyük \( n \) değeri \( n = 11 \) olarak bulunur.
\( a_{11} \gt a_{12} \)
\( (a_n) \) dizisinde \( a_1 = 3 \) ve \( a_{99} = 10 \) olarak veriliyor.
\( a_n + a_{n + 1} + a_{n+2} = 22 \) olduğuna göre, \( a_{35} \) kaçtır?
Çözümü GösterVerilen eşitliğe göre dizinin herhangi ardışık üç teriminin toplamı 22'dir.
Ardışık iki toplam durumunu yazalım.
\( a_n + a_{n + 1} + a_{n+2} = 22 \)
\( a_{n + 1} + a_{n+2} + a_{n + 3} = 22 \)
İkinci denklemi \( -1 \) ile çarpalım ve denklemleri taraf tarafa toplayalım.
\( a_n - a_{n + 3} = 0 \)
\( a_n = a_{n + 3} \)
Buna göre, \( (a_n) \) periyodik bir dizidir ve her 3 terimde bir terimleri tekrar eder.
99 sayısı 3'ün bir tam sayı katı olduğuna göre \( a_{99} = a_3 \) olur.
\( a_3 = a_{99} = 10 \)
Dizinin ilk üç teriminin toplamı 22 olmalıdır.
\( a_1 + a_2 + a_3 = 22 \)
\( 3 + a_2 + 10 = 22 \)
\( a_2 = 9 \)
\( 35 - 2 = 33 \) sayısı 3'ün bir tam sayı katı olduğuna göre \( a_{35} = a_2 \) olur.
\( a_{35} = a_2 = 9 \) bulunur.