Aritmetik Dizi
Ardışık terimleri arasındaki fark tüm dizi boyunca sabit olan dizilere aritmetik dizi denir. Aritmetik dizilerde ardışık terimler arasındaki bu sabit farka ortak fark denir ve \( d \) ile gösterilir.
\( d \in \mathbb{R} \) olmak üzere, her \( n \) için,
\( a_{n + 1} - a_n = d \) ise,
\( (a_n) \) bir aritmetik dizidir.
Aritmetik dizilerin genel terimi aşağıdaki gibidir. Bu formüle göre, aritmetik dizilerde \( n \). terim ortak farkın \( (n - 1) \) kez 1. terime eklenmesiyle bulunur.
\( (a_n) = a_1 + (n - 1)d \)
\( = (a_1, a_1 + d, a_1 + 2d, \) \( a_1 + 3d, \ldots) \)
Ortak farkı 5 olan bir aritmetik dizi:
\( (a_n) = 5n - 3 \)
\( = (2, 7, 12, 17, \ldots) \)
Aşağıda genel terimleri verilen bazı dizilerin aritmetik dizi olup olmadığı belirtilmiştir.
| Genel Terim | Terimler | Aritmetik Dizi? |
|---|---|---|
| \( (a_n) = 2n \) | \( (2, 4, 6, 8, \ldots) \) | Aritmetik dizi (\( d = 2 \)) |
| \( (b_n) = 3n + 1 \) | \( (4, 7, 10, 13, \ldots) \) | Aritmetik dizi (\( d = 3 \)) |
| \( (c_n) = -5n + 10 \) | \( (5, 0, -5, -10, \ldots) \) | Aritmetik dizi (\( d = -5 \)) |
| \( (d_n) = 5 \) | \( (5, 5, 5, 5, \ldots) \) | Aritmetik dizi (\( d = 0 \)) |
| \( (e_n) = n^2 \) | \( (1, 4, 9, 16, \ldots) \) | Aritmetik dizi değil |
| \( (f_n) = 2^n - 1 \) | \( (1, 3, 7, 15, \ldots) \) | Aritmetik dizi değil |
| \( (g_n) = \dfrac{n + 1}{n + 2} \) | \( (\frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots) \) | Aritmetik dizi değil |
Tablodaki ilk dört diziyi incelersek aritmetik dizilerin genel terimi \( n \)'nin katsayısının ortak farka eşit olduğu bir doğrusal fonksiyon formundadır (\( f(x) = dx + c \)).
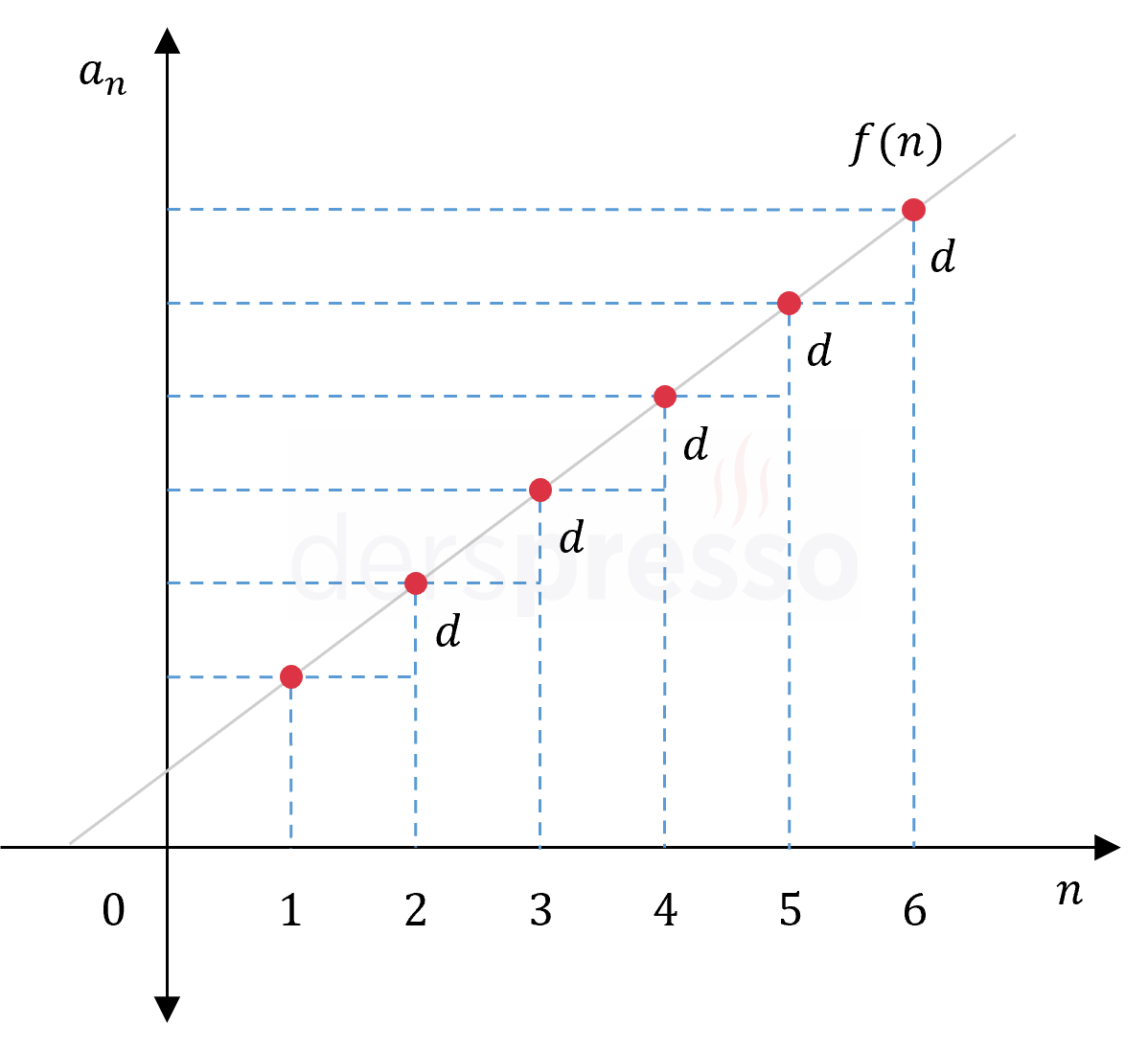
Bir aritmetik dizide ortak farkın işaretine göre dizi artan, azalan ya da sabit dizi olur.
\( d \gt 0 \): Artan dizi
\( d = 0 \): Sabit dizi
\( d \lt 0 \): Azalan dizi
Aritmetik diziler indirgemeli dizi olarak aşağıdaki şekilde ifade edilebilir.
\( a_n = a_{n - 1} + d \)
\( (a_n) = 5n - 3 \) dizisinin indirgemeli dizi olarak tanımı:
\( a_1 = 2 \)
\( a_n = a_{n - 1} + 5 \)
Bir aritmetik dizide \( n \). terim, birinci ya da herhangi diğer bir terim cinsinden aşağıdaki şekilde ifade edilebilir.
\( a_n = a_1 + (n - 1)d \)
\( a_n = a_p + (n - p)d \)
1. terimi 6 ve ortak farkı 2 olan bir aritmetik dizinin 12. terimi:
\( a_{12} = 6 + (12 - 1)2 = 28 \)
5. terimi 27 ve ortak farkı -3 olan bir aritmetik dizinin 10. terimi:
\( a_{10} = 27 + (10 - 5)(-3) = 12 \)
Yukarıdaki formül \( p \). ve \( q \). terimler cinsinden yazılıp ortak fark yalnız bırakıldığında, ortak farkın dizinin herhangi iki teriminin farkının bu iki terimin indislerinin farkına oranına eşit olduğu bulunur.
\( a_q = a_p + (q - p)d \)
\( d = \dfrac{a_q - a_p}{q - p} \)
4. terimi 12 ve 44. terimi 72 olan bir aritmetik dizinin ortak farkı:
\( d = \dfrac{72 - 12}{44 - 4} = \dfrac{3}{2} \)
Bir aritmetik dizide bir terim, kendisinden eşit uzaklıktaki iki terimin aritmetik ortalamasına (toplamlarının yarısına) eşittir.
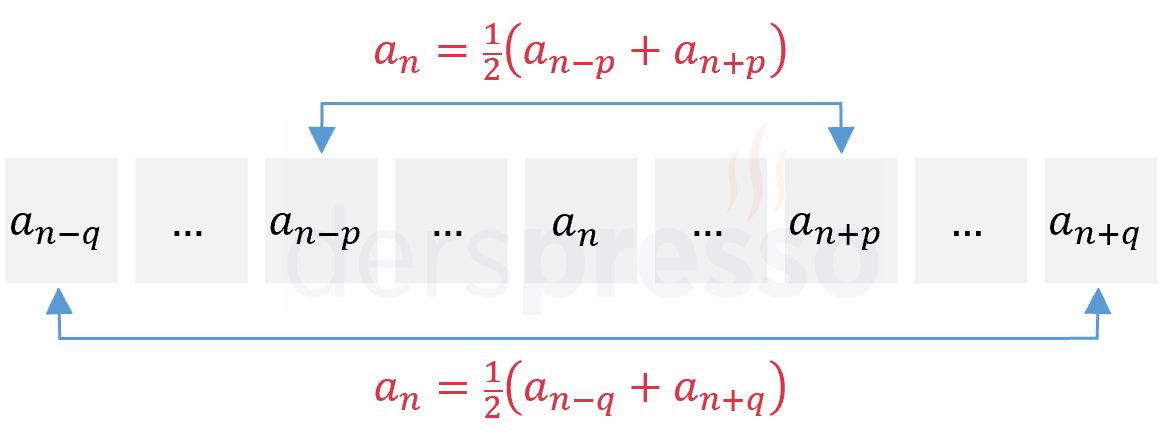
\( a_n = \frac{1}{2}(a_{n - p} + a_{n + p}) \) \( = \frac{1}{2}(a_{n - q} + a_{n + q}) \)
Bu kuralın bir sonucu olarak, bir terimden eşit uzaklıktaki terimlerin toplamı birbirine eşittir.
\( 2a_n = a_{n - p} + a_{n + p} = a_{n - q} + a_{n + q} \)
\( (a_n) = 2n + 5 \) olmak üzere,
\( a_{20} = 2 \cdot 20 + 5 = 45 \)
20. terime 5 terim uzaklıktaki iki terimin toplamı:
\( a_{15} + a_{25} = 35 + 55 = 2a_{20} = 90 \)
20. terime 10 terim uzaklıktaki iki terimin toplamı:
\( a_{10} + a_{30} = 25 + 65 = 2a_{20} = 90 \)
Aynı kuralın ikinci bir sonucu olarak, bir aritmetik dizinin ardışık üç teriminde ortadaki terim diğer iki terimin aritmetik ortalamasına eşittir.
\( a_n = \dfrac{a_{n - 1} + a_{n + 1}}{2} \)
Aynı kuralın üçüncü bir sonucu olarak, bir aritmetik dizide indisleri toplamı birbirine eşit olan terimlerin toplamları birbirine eşittir.
\( p + q = r + s \) ise,
\( a_p + a_q = a_r + a_s \)
\( a_7 + a_8 = a_3 + a_{12} \)
Aynı kuralın dördüncü bir sonucu olarak, sonlu bir aritmetik dizide baştan ve sondan eşit uzaklıkta bulunan terimlerin toplamı birbirine eşittir.
\( a \) ve \( b \) sayılarının arasına \( n \) tane terim yerleştirerek oluşturulan bir aritmetik dizinin ortak farkı aşağıdaki formülle bulunur.
\( d = \dfrac{b - a}{n + 1} \)
12 ve 60 sayıları arasına 5 terim ekleyerek oluşturulan aritmetik dizinin ortak farkı:
\( d = \dfrac{60 - 12}{5 + 1} = 8 \)
\( (a_n) = (12, \textcolor{red}{20, 28, 36, 44, 52}, 60) \)
Aritmetik dizilerde ilk \( n \) terimin toplamı \( S_n \) ile gösterilir ve aşağıdaki formülle hesaplanır.
\( (a_n) = a_1 + (n - 1)d \)
\( S_n = a_1 + a_2 + a_3 + \ldots + a_n \) olmak üzere,
\( S_n = \dfrac{n}{2}[2a_1 + (n - 1)d] \)
\( S_n = \dfrac{n}{2}[a_1 + a_n] \)
1. terimi 3 ve ortak farkı 2 olan bir aritmetik dizinin ilk 20 teriminin toplamı:
\( S_n = \dfrac{20}{2}[2 \cdot 3 + (20 - 1)2] \)
\( = 10 \cdot 44 = 440 \)
İSPATI GÖSTER
Dizinin ilk terimine \( a_1 \), dizideki terim sayısına \( n \) diyelim.
Aritmetik dizilerde dizinin son terimi aşağıdaki formülle hesaplanır.
\( a_n = a_1 + (n - 1)d \)
Ardışık sayılarda terimler toplamı formülü ile terimlerin toplamını bulalım
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \) \( \cdot \text{Terim sayısı} \)
\( S_n = \dfrac{a_1 + a_n}{2} \cdot n \)
\( = \dfrac{a_1 + a_1 + (n - 1)d}{2} \cdot n \)
\( = \dfrac{n}{2}[2a_1 + (n - 1)d] \)
Bir dizi hem aritmetik hem de geometrik dizi ise bu dizi sabit dizidir. Sabit bir dizinin aritmetik dizi olarak ortak farkı 0, geometrik dizi olarak ortak çarpanı 1'dir.
\( (a_n) \) bir aritmetik dizidir.
\( a_1 = 8 \)
\( \displaystyle\sum_{n = 1}^{10}{a_n} = 215 \)
olduğuna göre, \( a_7 - a_2 \) farkı kaçtır?
Çözümü GösterVerilen toplam sembolü dizinin ilk 10 teriminin toplamını ifade etmektedir.
Aritmetik dizinin ilk \( n \) teriminin toplamı formülünü yazalım.
\( S_n = \dfrac{n}{2}[2a_1 + (n - 1)d] \)
\( S_{10} = \dfrac{10}{2}(2(8) + 9d) \)
\( 215 = 5(16 + 9d) \)
\( 16 + 9d = 43 \)
\( d = 3 \)
2. ve 7. terimlerin farkı 5 ortak fark kadardır.
\( a_7 - a_2 = (7 - 2)d = 15 \) bulunur.
Aşağıdaki dizilerden hangileri bir aritmetik dizinin genel terimidir?
I. \( (a_n) = 3 \)
II. \( (b_n) = \tan(n\pi) \)
III. \( (c_n) = 5n - 3 \)
IV. \( (d_n) = n^2 - n \)
V. \( (e_n) = \log{2^n} \)
Çözümü GösterArdışık terimleri arasındaki fark eşit olan dizilere aritmetik dizi denir.
I. öncül:
\( (a_n) = 3 \)
\( = (3, 3, 3, \ldots) \)
Dizi ardışık terimleri arasındaki fark 0 olduğu için bir aritmetik dizidir.
II. öncül:
\( (b_n) = \tan(n\pi) \)
\( = (\tan{\pi}, \tan(2\pi), \tan(3\pi), \tan(4\pi), \ldots) \)
\( = (0, 0, 0, 0, \ldots) \)
Dizi ardışık terimleri arasındaki fark 0 olduğu için bir aritmetik dizidir.
III. öncül:
\( (c_n) = 5n - 3 \)
\( = (2, 7, 12, 17, \ldots) \)
Dizi ardışık terimleri arasındaki fark 5 olduğu için bir aritmetik dizidir.
IV. öncül:
\( (d_n) = n^2 - n \)
\( = (0, 2, 6, 12, \ldots) \)
Dizi ardışık terimleri arasındaki fark eşit olmadığı için bir aritmetik dizi değildir.
V. öncül:
\( (e_n) = \log{2^n} = n\log{2} \)
\( = (\log{2}, 2\log{2}, 3\log{2}, 4\log{2}, \ldots) \)
Dizi ardışık terimleri arasındaki fark \( \log{2} \) olduğu için bir aritmetik dizidir.
Buna göre I., II., III. ve V. öncüllerdeki diziler birer aritmetik dizidir.
\( (a_n) \) bir aritmetik dizidir.
\( 4a_3 = 5a_7 \)
olduğuna göre, \( (a_n) \) dizisinin kaçıncı terimi sıfırdır?
Çözümü GösterVerilen eşitlikteki terimleri birinci terim cinsinden yazalım.
\( 4(a_1 + 2d) = 5(a_1 + 6d) \)
\( 4a_1 + 8d = 5a_1 + 30d \)
\( a_1 + 22d = 0 \)
Eşitliğin sol tarafı dizinin 23. terimine eşittir.
\( a_{23} = 0 \)
Buna göre dizinin 23. terimi 0'dır.
\( (a_n) \) bir aritmetik dizidir.
\( x = 3a_1 - 4a_3 \)
\( y = 3a_5 - 2a_3 \)
olduğuna göre, \( x + y \) toplamı kaçtır?
Çözümü GösterVerilen eşitliklerdeki terimleri birinci terim cinsinden yazalım.
\( x = 3a_1 - 4(a_1 + 2d) \)
\( = 3a_1 - 4a_1 - 8d \)
\( = -a_1 - 8d \)
\( y = 3(a_1 + 4d) - 2(a_1 + 2d) \)
\( = 3a_1 + 12d - 2a_1 - 4d \)
\( = a_1 + 8d \)
İki ifadenin toplamını alalım.
\( x + y = -a_1 - 8d + a_1 + 8d \)
\( = 0 \) bulunur.
\( (a_n) \) bir aritmetik dizidir.
\( a_3 = \dfrac{7x + 5}{2} \)
\( a_9 = 4x + 15 \)
\( a_{12} = 8x + \dfrac{5}{2} \)
olduğuna göre, \( a_1 + a_7 \) toplamı kaçtır?
Çözümü Göster\( a_9 \)'u \( a_3 \) cinsinden yazalım.
\( a_9 = a_3 + 6d \)
\( \dfrac{7x + 5}{2} + 6d = 4x + 15 \)
\( 7x + 5 + 12d = 8x + 30 \)
\( x + 25 = 12d \)
\( a_{12} \)'yi \( a_3 \) cinsinden yazalım.
\( a_{12} = a_3 + 9d \)
\( \dfrac{7x + 5}{2} + 9d = 8x + \dfrac{5}{2} \)
\( 7x + 5 + 18d = 16x + 5 \)
\( 9x = 18d \)
\( x = 2d \)
Elde ettiğimiz iki denklemi ortak çözelim.
\( 2d + 25 = 12d \)
\( d = \dfrac{5}{2} \)
\( x = 5 \)
\( a_3 \) değerini kullanarak \( a_1 \) değerini bulalım.
\( a_3 = a_1 + 2d \)
\( \dfrac{7 \cdot 5 + 5}{2} = a_1 + 2 \cdot \dfrac{5}{2} \)
\( a_1 = 15 \)
\( a_3 \) değerini kullanarak \( a_7 \) değerini bulalım.
\( a_7 = a_3 + 4d \)
\( a_7 = \dfrac{7 \cdot 5 + 5}{2} + 4 \cdot \dfrac{5}{2} \)
\( a_7 = 30 \)
\( a_1 + a_7 \) toplamını bulalım.
\( a_1 + a_7 = 15 + 30 = 45 \) bulunur.
\( y \gt x \) olmak üzere, bir aritmetik dizide,
\( a_x = 2y, \quad a_y = 2x \)
olduğuna göre, \( a_{x + y} \) kaçtır?
Çözümü GösterAritmetik dizinin ortak farkına \( d \) diyelim.
\( (x + y) \). terimi \( x \). terim cinsinden yazalım.
\( a_{x + y} = a_x + dy = 2y + dy \)
\( (x + y) \). terimi \( y \). terim cinsinden yazalım.
\( a_{x + y} = a_y + dx = 2x + dx \)
Birinci denklemden ikinci denklemi taraf tarafa çıkaralım.
\( 0 = 2y - 2x + d(y - x)\)
\( y \gt x \) olduğu için ikinci çarpanları sadeleştirebiliriz.
\( -2(y - x) = d(y - x) \)
\( d = -2 \)
\( a_{x + y} = 2y + dy \)
\( = 2y + (-2)y = 0 \) bulunur.
Bir aritmetik dizinin ilk 5 terimi sırasıyla \( a, (2a + b), 32, (6a - b), (6a + 2b) \) olduğuna göre, dizinin 111. terimi kaçtır?
Çözümü GösterAritmetik diziye \( (a_n) \), dizinin ortak farkına \( d \) diyelim.
\( a_1 = a \)
\( a_2 = 2a + b \)
\( a_3 = 32 \)
\( a_4 = 6a - b \)
\( a_5 = 6a + 2b \)
\( a_4 \) ve \( a_5 \) terimleri arasındaki farkı bulalım.
\( d = a_5 - a_4 \)
\( = 6a + 2b - (6a - b) = 3b \)
Bu eşitliği kullanarak dizinin terimlerini birbirleri cinsinden yazalım.
\( a_2 = a_1 + d \)
\( 2a + b = a + 3b \)
\( a = 2b \)
\( a_3 = a_2 + d \)
\( 32 = 2a + b + 3b \)
\( 32 = 2a + 4b \)
\( 32 = 2 \cdot 2b + 4b \)
\( 32 = 8b \Longrightarrow b = 4 \)
\( a = 2b \Longrightarrow a = 8 \)
\( d = 3b \Longrightarrow d = 12 \)
\( a_1 = a = 8 \)
Bulduğumuz değerleri kullanarak \( a_{111} \) değerini bulalım.
\( a_n = a_1 + (n - 1)d \)
\( a_{111} = a_1 + (111 - 1)d \)
\( = 8 + 110(12) \)
\( = 1328 \) bulunur.
Bir aritmetik dizide ilk 7 terimin toplamı, ilk 17 terimin toplamına eşittir.
Buna göre, ilk 24 terimin toplamı kaçtır?
Çözümü GösterAritmetik dizinin ilk terimine \( a \), dizinin ortak farkına \( d \) diyelim.
Aritmetik dizi terimler toplamı formülü ile ilk 7 terimin toplamını bulalım.
\( S_n = \dfrac{n}{2}[a_1 + a_n] \)
\( S_7 = \dfrac{7}{2}[a + (a + 6d)] \)
\( = 7(a + 3d) \)
Aynı formül ile ilk 17 terimin toplamını bulalım.
\( S_{17} = \dfrac{17}{2}[a + (a + 16d)] \)
\( = 17(a + 8d) \)
İki toplam birbirine eşittir.
\( 7(a + 3d) = 17(a + 8d) \)
\( 7a + 21d = 17a + 136d \)
\( 10a = -115d \)
\( 2a = -23d \)
İlk 24 terimin toplamını bulalım.
\( S_{24} = \dfrac{24}{2}[a + (a + 23d)] \)
\( = 12(2a + 23d) \)
\( 2a = -23d \) ifadesini \( 2a \) yerine kullanalım.
\( = 12(-23d + 23d) = 0 \)
Buna göre aritmetik dizinin ilk 24 teriminin toplamı 0'a eşittir.
İlk terimi \( \log_3{2} \) olan bir aritmetik dizinin ortak farkı ilk teriminin iki katına eşittir.
Buna göre bu dizinin 5. terimi nedir?
Çözümü Göster\( a_1 = \log_3{2} \)
\( d = 2a_1 = 2\log_3{2} \)
Dizinin 5. terimini 1. terim cinsinden yazalım.
\( a_5 = a_1 + 4d \)
\( = \log_3{2} + 4 \cdot 2\log_3{2} \)
\( = 9\log_3{2} \) bulunur.
\( (a_n) \) aritmetik dizisinin ortak farkı \( d \)'dir.
Bu aritmetik dizinin ilk 7 teriminin toplamı ilk 12 teriminin toplamına eşit olduğuna göre, 6. terimin \( d \) cinsinden eşiti nedir?
Çözümü GösterDizinin genel terimini ve ilk \( n \) teriminin toplam formülünü yazalım.
\( (a_n) = a_1 + (n - 1)d \)
\( S_n = \dfrac{n}{2}[2a_1 + (n - 1)d] \)
Aritmetik dizinin ilk 7 teriminin toplamı ilk 12 teriminin toplamına eşittir.
\( S_7 = S_{12} \)
\( \dfrac{7}{2}(2a_1 + 6d) = \dfrac{12}{2}(2a_1 + 11d) \)
\( 14a_1 + 42d = 24a_1 + 132d \)
\( 10a_1 = -90d \)
\( a_1 = -9d \)
Bu eşitliği kullanarak dizinin 6. terimini bulalım.
\( a_6 = a_1 + (6 - 1)d \)
\( = a_1 + 5d \)
\( a_1 \) yerine bulduğumuz eşitini yazalım.
\( = -9d + 5d = -4d \) bulunur.
Bir aritmetik dizinin ilk beş elemanı \( a, x, b, c, 3x \) olduğuna göre, \( \frac{a}{c} \) oranı kaçtır?
Çözümü GösterDizinin ikinci ve beşinci terimleri aynı değişken cinsinden olduğu için bu terimleri kullanarak dizinin ortak farkını bulalım.
Bir aritmetik dizinin \( q \). terimi \( p \). terim cinsinden aşağıdaki şekilde yazılır.
\( a_q = a_p + (q - p)d \)
\( a_5 = a_2 + (5 - 2)d \)
\( 3x = x + 3d \)
\( d = \dfrac{2x}{3} \)
Bu ortak fark değerini kullanarak \( a \) ve \( c \) değerlerini \( x \) cinsinden yazalım.
\( a_2 = a_1 + d \)
\( x = a + \dfrac{2x}{3} \)
\( a = \dfrac{x}{3} \)
\( a_5 = a_4 + d \)
\( 3x = c + \dfrac{2x}{3} \)
\( c = \dfrac{7x}{3} \)
\( \frac{a}{c} \) oranını bulalım.
\( \dfrac{a}{c} = \dfrac{\frac{x}{3}}{\frac{7x}{3}} \)
\( = \dfrac{1}{7} \) bulunur.
\( (a_n) \) bir aritmetik dizidir.
\( a_5 + a_{13} = 22 \)
olduğuna göre, dizinin ilk 17 teriminin toplamı kaçtır?
Çözümü GösterBir aritmetik dizinin ilk \( n \) teriminin toplamı aşağıdaki formülle hesaplanır.
\( S_n = \dfrac{n}{2}(a_1 + a_n) \)
\( S_{17} = \dfrac{17}{2}(a_1 + a_{17}) \)
Bir aritmetik dizide indisleri toplamı birbirine eşit olan terimlerin toplamları birbirine eşittir.
\( 5 + 13 = 1 + 17 = 18 \) olduğu için,
\( a_5 + a_{13} = a_1 + a_{17} = 22 \)
Buna göre ilk 17 terimin toplamını aşağıdaki şekilde de yazabiliriz.
\( S_{17} = \dfrac{17}{2}(a_5 + a_{13}) \)
\( = \dfrac{17}{2}(22) = 187 \) bulunur.
Bir aritmetik dizinin ardışık üç teriminin toplamı 33, çarpımı 440'tır.
Bu terimlerden en büyük olanı kaçtır?
Çözümü GösterAritmetik dizinin ortak farkına \( d \) diyelim.
Bu üç terimi aşağıdaki şekilde yazabiliriz.
\( (a - d), a, (a + d) \)
Üç terimin toplamını yazalım.
\( a - d + a + a + d = 33 \)
\( 3a = 33 \)
\( a = 11 \)
Buna göre terimler aşağıdaki gibi olur.
\( (11 - d), 11, (11 + d) \)
Üç terimin çarpımını yazalım.
\( (11 - d) \cdot 11 \cdot (11 + d) = 440 \)
\( 121 - d^2 = 40 \)
\( 81 = d^2 \)
\( d = \pm 9 \)
Aritmetik dizinin artan ya da azalan olduğu bilgisi verilmemiş olsa da her iki durumda da terimlerden en büyük olanın değeri aynı olacaktır.
\( d = 9 \) olarak kabul edelim.
Bu durumda terimler aşağıdaki gibi olur.
\( 2, 11, 20 \)
Terimlerden en büyüğü 20 olarak bulunur.
Bir aritmetik dizinin 2. ve 13. terimlerinin çarpımı, 5. ve 11. terimlerinin çarpımına eşittir.
Dizinin ortak terimi sıfırdan farklı olduğuna göre, bu dizideki kaçıncı terim sıfıra eşittir?
Çözümü GösterBu dizinin 2. terimine \( a_2 \), ortak farkına \( d \) diyelim.
5., 11. ve 13. terimleri 2. terim cinsinden yazalım.
\( a_{13} = a_2 + 11d \)
\( a_5 = a_2 + 3d \)
\( a_{11} = a_2 + 9d \)
Dizinin 2. ve 13. terimlerinin çarpımı, 5. ve 11. terimlerinin çarpımına eşittir.
\( a_2 \cdot a_{13} = a_5 \cdot a_{11} \)
\( a_2(a_2 + 11d) = (a_2 + 3d)(a_2 + 9d) \)
\( a_2^2 + 11da_2 = a_2^2 + 3da_2 + 9da_2 + 27d^2 \)
\( da_2 = -27d^2 \)
Dizinin ortak terimi sıfırdan farklı olduğu için \( d \) çarpanlarını sadeleştirebiliriz.
\( a_2 = -27d \)
Sıfıra eşit olan terime \( k \). terim diyelim.
\( a_k = a_2 + (k - 2)d = 0 \)
\( -27d + (k - 2)d = 0 \)
\( 27d = (k - 2)d \)
\( k = 29 \)
Buna göre dizinin 29. terimi sıfıra eşittir.
\( (a_n) \) ve \( (b_n) \) aritmetik dizilerdir.
\( a_1 = 15, \quad b_1 = 65 \)
\( a_{80} + b_{80} = 80 \)
olduğuna göre, \( (a_n + b_n) \) aritmetik dizisinin ilk 80 teriminin toplamı kaçtır?
Çözümü GösterVerilen dizilerin genel terimini yazalım.
\( a_n \) dizisinin ortak farkına \( d_1 \), \( b_n \) dizisinin ortak farkına \( d_2 \) diyelim.
\( a_{80} = a_1 + 79d_1 = 15 + 79d_1 \)
\( b_{80} = b_1 + 79d_2 = 65 + 79d_2 \)
\( a_{80} + b_{80} = 80 \) veriliyor.
\( 15 + 79d_1 + 65 + 79d_2 = 80 \)
\( 80 + 79(d_1 + d_2) = 80 \)
\( 79(d_1 + d_2) = 0 \)
\( d_1 + d_2 = 0 \)
Bir aritmetik dizinin ilk \( n \) teriminin toplamı formülü aşağıdaki gibidir.
\( S_n = \dfrac{n}{2}[2a_1 + (n - 1)d] \)
Dizilerin ilk 80 terimi için toplam formüllerini yazalım.
\( \displaystyle\sum_{n = 1}^{80}{(a_n + b_n)} = \displaystyle\sum_{n = 1}^{80}{a_n} + \displaystyle\sum_{n = 1}^{80}{b_n} \)
\( = \dfrac{80}{2}[2 \cdot 15 + 79d_1] + \dfrac{80}{2}[2 \cdot 65 + 79d_2] \)
\( = 40(30 + 79d_1) + 40(130 + 79d_2) \)
\( = 1200 + 40 \cdot 79d_1 + 5200 + 40 \cdot 79d_2 \)
\( = 6400 + 40 \cdot 79(d_1 + d_2) \)
\( = 6400 + 40 \cdot 79(0) \)
\( = 6400 \) bulunur.
\( (a_n) \) bir aritmetik dizidir.
\( a_1 + a_3 + a_5 + a_7 = a_2 + a_4 + a_6 + 4 \)
\( a_{10} = 4a_8 \)
olduğuna göre, \( a_1 \) kaçtır?
Çözümü GösterBirinci eşitlikte \( a_2, a_4, a_6 \) terimlerini \( a_1, a_3, a_5 \) cinsinden yazalım.
\( a_1 + a_3 + a_5 + a_7 = a_1 + d + a_3 + d + a_5 + d + 4 \)
\( a_7 = 3d + 4 \)
İkinci eşitlikte \( a_8 \) ve \( a_{10} \) terimlerini \( a_7 \) cinsinden yazalım.
\( a_7 + 3d = 4(a_7 + d) \)
\( a_7 + 3d = 4a_7 + 4d \)
\( 3a_7 = -d \)
\( a_7 = -\dfrac{d}{3} \)
\( a_7 \) ve \( d \) arasında bulduğumuz iki eşitliği ortak çözelim.
\( 3d + 4 = -\dfrac{d}{3} \)
\( d = -\dfrac{6}{5} \)
\( d \) değerini kullanarak \( a_7 \) değerini bulalım.
\( a_7 = 3d + 4 = 3(-\dfrac{6}{5}) + 4 \)
\( a_7 = \dfrac{2}{5} \)
\( a_7 \) değerini kullanarak \( a_1 \) değerini bulalım.
\( a_7 = a_1 + 6d \)
\( \dfrac{2}{5} = a_1 + 6(-\dfrac{6}{5}) \)
\( a_1 = \dfrac{2}{5} + \dfrac{36}{5} \)
\( = \dfrac{38}{5} \) bulunur.
\( (a_n) \) dizisinin ilk \( n \) teriminin toplamı \( S_n \) olmak üzere,
\( S_{35} = S_{46} \) olduğuna göre,
I. \( (a_n) \) aritmetik dizi ise \( a_{41} = 0 \)'dır.
II. \( (a_n) \) sabit dizidir.
III. \( S_{15} = S_{66} \)
ifadelerinden kaçı her zaman doğrudur?
Çözümü Göster\( (a_n) \) aritmetik dizi ise,
\( S_{46} = S_{35} + a_{36} + \ldots + a_{46} = S_{35} \)
\( a_{36} + \ldots + a_{46} = 0 \)
Bir aritmetik dizinin belirli sayıda teriminin toplamı terim sayısı ile ortanca terimin çarpımına eşittir.
\( a_{36} \) ve \( a_{46} \) arası terimlerin ortanca terimi \( a_{41} \)'dir.
\( 11 \cdot a_{41} = 0 \Longrightarrow a_{41} = 0 \)
Buna göre I. öncül her zaman doğrudur.
Dizi sabit olmayan bir aritmetik dizi de olabileceği için II. öncül her zaman doğru değildir.
III. öncül aritmetik ya da sabit dizi için doğrudur, ancak dizi farklı bir tipte de olabileceği için her zaman doğru olmayabilir.
Buna göre sadece I. öncül her zaman doğrudur.
\( 37, 61, 85, \ldots \) aritmetik dizisindeki 3 basamaklı terimlerin ortalaması kaçtır?
Çözümü GösterDizinin genel terimini bulalım.
\( (a_n) = a_1 + (n - 1)d \)
Dizinin ilk terimi \( a_1 = 37 \) ve ortak farkı \( d = 61 - 37 = 24 \)'tür.
\( (a_n) = 37 + (n - 1)24 \)
\( (a_n) = 24n + 13 \)
3 basamaklı terimler aşağıdaki aralıkta bulunur.
\( 100 \le 24n + 13 \le 999 \)
\( 87 \le 24n \le 986 \)
\( \dfrac{87}{24} \le n \le \dfrac{986}{24} \)
Eşitsizliğin sınır değerlerinin yaklaşık değerlerini yazalım.
\( 3,6 \le n \le 41,08 \)
\( n \) tam sayı olduğu için aralığı aşağıdaki şekilde yazabiliriz.
\( 4 \le n \le 41 \)
Dizinin 4. terimini bulalım
\( a_4 = a_1 + (4 - 1)24 \)
\( = 37 + 3(24) = 109 \)
Dizinin 41. terimini bulalım
\( a_{41} = a_1 + (41 - 1)24 \)
\( = 37 + 40(24) = 997 \)
Bir aritmetik dizide belirli bir aralıktaki terimlerin ortalaması bu aralıktaki ilk ve son terimlerin ortalamasına eşittir.
3 basamaklı terimlerin ortalaması \( = \dfrac{109 + 997}{2} = 553 \) bulunur.
Bir çift fonksiyon olan \( f(x) \) fonksiyonunun reel sayı kökleri, aynı zamanda \( (a_n) \) aritmetik dizisinin birbirinden farklı ilk dört terimidir.
\( a_{10} = 30 \) olduğuna göre, \( a_{30} \) değeri kaçtır?
Çözümü Göster\( f(x) \) bir çift fonksiyon olduğu için kökleri \( y \) eksenine göre simetriktir. Kökler arası ortak fark eşit olacağı için, bu kökleri aritmetik dizinin ortak farkı \( d \) cinsinden aşağıdaki şekilde yazabiliriz.
\( (a_n) = (-\frac{3d}{2}, -\frac{d}{2}, \frac{d}{2}, \frac{3d}{2}, ...) \)
Bir aritmetik dizinin genel terimi aşağıdaki gibidir.
\( (a_n) = a_1 + (n - 1)d \)
\( (a_n) = -\dfrac{3d}{2} + (n - 1)d \)
\( a_{10} = 30 \) değerini kullanarak ortak farkı bulalım.
\( a_{10} = -\dfrac{3d}{2} + (10 - 1)d = 30 \)
\( d = 4 \)
\( a_1 = -\dfrac{3d}{2} = -6 \)
\( (a_n) = -6 + (n - 1)d \)
Genel terimi kullanarak \( a_{30} \) değerini bulalım.
\( a_{30} = -6 + (30 - 1)4 \)
\( = 110 \) bulunur.
\( (a_n) \) ilk terimi 8 ve ortak farkı 5 olan, \( (b_n) \) ise ilk terimi 1 ve ortak farkı 7 olan aritmetik dizilerdir.
İki dizinin ortak elemanlarından oluşan dizinin 15. terimi kaçtır?
Çözümü Göster\( (a_n) \) dizisinin ilk terimini ve ortak farkını kullanarak dizinin terimlerini yazalım.
\( (a_n) = (8, 13, 18, 23, 28, 33, 38, 43, 48, \ldots) \)
Aynı şekilde \( (b_n) \) dizisinin ilk terimini ve ortak farkını kullanarak dizinin terimlerini yazalım.
\( (b_n) = (1, 8, 15, 22, 29, 36, 43, 50, 57, \ldots) \)
İki dizinin ortak elemanlarından oluşan bir \( (c_n) \) dizisi tanımlayalım.
\( (c_n) \) dizisinin ilk elemanının 8 olduğunu yukarıdaki dizi tanımlarından görebiliriz. Ayrıca dizinin ortak farkı iki dizinin ortak farklarının EKOK'u olur.
\( EKOK(5, 7) = 35 \)
\( (c_n) = (8, 43, 78, \ldots) \)
Bu bilgilerle \( (c_n) \) dizisinin genel terimini yazalım.
\( (c_n) = 8 + (n - 1)35 \)
\( = 35n - 27 \)
\( (c_n) \) dizisinin 15. terimini bulalım.
\( c_{15} = 35(15) - 27 = 498 \) bulunur.
\( (a_n) \) ve \( (b_n) \) aritmetik dizilerdir.
\( (a_n) = (142, 147, 152, 157, \ldots) \)
\( (b_n) = (119, 130, 141, 152, \ldots) \)
Bu iki dizinin ortak terimlerinden oluşan \( c_n \) dizisinin beşinci terimi kaçtır?
Çözümü GösterDizilerin ortak farklarına sırasıyla \( d_a, d_b, d_c \) diyelim.
\( d_a = 147 - 142 = 5 \)
\( d_b = 130 - 119 = 11 \)
Bu iki dizinin ortak terimlerinden oluşan \( c_n \) dizisi de bir aritmetik dizidir ve ortak farkı dizilerin ortak farklarının EKOK'una eşittir.
\( d_c = EKOK(5, 11) = 55 \)
\( a_n \) ve \( b_n \) dizilerinin ilk ortak teriminin 152 olduğu görülüyor, buna göre \( c_n \) dizisinin ilk terimi de 152 olur.
\( c_n \) aritmetik dizisinin 5. terimini bulalım.
\( c_5 = 152 + (5 - 1)55 \)
\( = 372 \) bulunur.
\( (a_n) \) ve \( (b_n) \) aritmetik dizilerdir.
\( (a_n) = (8, 16, \ldots, 368) \)
\( (b_n) = (13, 16, \ldots, 352) \)
Bu iki dizinin ortak terim sayısı kaçtır?
Çözümü Göster\( (a_n) \) dizisinin ortak farkına \( d_a \) diyelim ve genel terimini bulalım.
\( (a_n) = a_1 + (n - 1)d_a \)
Dizinin ilk terimi \( a_1 = 8 \) ve ortak farkı \( d_a = 16 - 8 = 8 \)'dir.
\( (a_n) = 8 + (n - 1)8 \)
\( = 8n \)
\( (b_n) \) dizisinin ortak farkına \( d_b \) diyelim ve genel terimini bulalım.
\( (b_n) = b_1 + (n - 1)d_b \)
Dizinin ilk terimi \( b_1 = 13 \) ve ortak farkı \( d_b = 16 - 13 = 3 \)'tür.
\( (b_n) = 13 + (n - 1)3 \)
\( = 3n + 10 \)
Dizilerin ilk ortak terimi 16'dır. Buna göre dizilerin ortak terimleri ortak farkları olan 3 ve 8'in ortak katlarının 16 fazlasıdır.
\( EKOK(3, 8) = 24 \)
Verilen diziler sonlu olduğu için en büyük ortak terim son terimlerden küçük olandan, yani 352'den küçük ya da 352'ye eşit olmalıdır.
Dizilerin ortak terim sayılarına \( x \) dersek, 16 hariç \( x - 1 \) ortak terim vardır.
\( 16 + 24(x - 1) \le 352 \)
\( 24x \le 360 \)
\( x \le 15 \)
\( x \)'in alabileceği en büyük tam sayı değeri 15 olduğuna göre, dizilerin ortak terim sayısı 15 olarak bulunur.
\( S = \{4, 5, 6, \ldots, 500\} \) kümesinin elemanlarıyla ilk terimi 4 ve son terimi 500 olan kaç aritmetik dizi oluşturulabilir?
Çözümü GösterOluşturabileceğimiz dizilerin genel terimini yazalım.
\( (a_n) = a_1 + (n - 1)d \)
Dizilerin ilk terimi \( a_1 = 4 \)'tür ve terim sayısı kaç olursa olsun \( n \)'nin alabileceği en yüksek değer \( a_n = 500 \)'dür.
\( (a_n) = (4, \ldots, 500) \)
\( 500 = 4 + (n - 1)d \)
\( 496 = (n - 1)d \)
\( S \) kümesi tam sayılardan oluştuğu için \( d \) tam sayı olmalıdır.
496 sayısını asal çarpanlarının kuvvetleri biçiminde yazıp pozitif tam bölenlerinin sayısını bularak \( d \) sayısının kaç farklı değer alabileceğini bulalım.
\( 496 = 2^4 \cdot 31^1 \)
Pozitif tam bölen sayısı \( = (4 + 1)(1 + 1) = 10 \)
\( d \) sayısı 10 farklı pozitif tam sayı değer alabildiğine göre yazabileceğimiz farklı aritmetik dizi sayısı 10 olur.
\( (a_n) \) ve \( (b_n) \) aritmetik dizilerdir.
\( (a_n) = 7n + 25 \)
\( (b_n) = 10n + 13 \)
olduğuna göre, bu dizilerin ortak terimlerinden en küçük üçünün toplamı kaçtır?
Çözümü GösterOrtak terimlerin indislerine \( i \) ve \( j \) diyelim.
\( a_i = b_j = A \)
\( 7i + 25 = 10j + 13 = A \)
Eşitliğin taraflarını aralarında asal 7 ve 10 parantezine alabilecek şekilde eşitliğin taraflarına 17 ekleyelim.
\( 7i + 42 = 10j + 30 = A + 17 \)
\( 7(i + 6) = 10(j + 3) = A + 17 \)
Buna göre dizilerin her bir ortak teriminin 17 fazlası 7 ve 10'un bir ortak katıdır.
\( EKOK(7, 10) = 70 \)
\( A + 17 \in \{70, 140, 210, \ldots\} \)
\( A \in \{53, 123, 193, \ldots\} \)
Buna göre dizilerin ortak terimlerinden en küçük üçünün toplamı \( 53 + 123 + 193 = 369 \) olarak bulunur.