Karmaşık Sayıların Modülü (Mutlak Değeri)
Bir karmaşık sayının karmaşık düzlemde karşılık geldiği noktanın başlangıç noktasına olan uzaklığına o sayının modülü ya da mutlak değeri denir. Bir karmaşık sayının modülü \( \abs{z} \) şeklinde gösterilir.
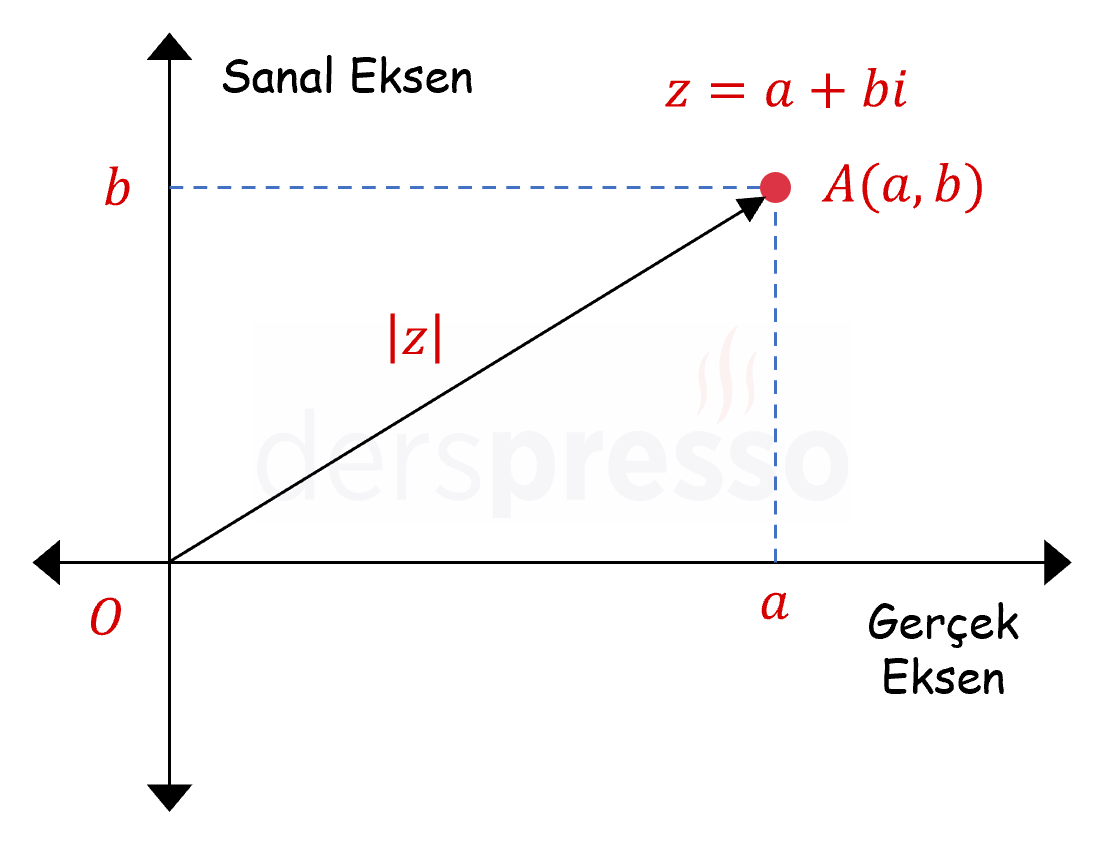
\( \abs{z} = \abs{a + bi} = \sqrt{a^2 + b^2} \)
\( z = -3 + 4i \) olmak üzere,
\( \abs{z} = \abs{-3 + 4i} = \sqrt{(-3)^2 + 4^2} = 5 \)
Modül İşlem Özellikleri
Bir karmaşık sayının modülü sıfırsa karmaşık sayının kendisi de sıfırdır. Bunun karşıtı da doğrudur, yani karmaşık sayı sıfıra eşitse modülü de sıfırdır.
\( \abs{z} = 0 \Longleftrightarrow z = 0 \)
Bir karmaşık sayının, eşleniğinin, negatifinin ve negatifinin eşleniğinin modülleri birbirine eşittir.
\( \abs{z} = \abs{\overline{z}} = \abs{-z} = \abs{-\overline{z}} \)
\( z = -3 + 4i \) olmak üzere,
\( \abs{z} = \abs{-3 + 4i} = \sqrt{(-3)^2 + 4^2} = 5 \)
\( \abs{\overline{z}} = \abs{-3 - 4i} = \sqrt{(-3)^2 + (-4)^2} = 5 \)
\( \abs{-z} = \abs{3 - 4i} = \sqrt{3^2 + (-4)^2} = 5 \)
\( \abs{-\overline{z}} = \abs{3 + 4i} = \sqrt{3^2 + 4^2} = 5 \)
Bir karmaşık sayının modülü ayrı ayrı reel ve sanal kısımlarının mutlak değerlerine eşittir ya da onlardan büyüktür.
\( \abs{z} \ge \abs{Re(z)} \ge Re(z) \)
\( \abs{z} \ge \abs{Im(z)} \ge Im(z) \)
Bir karmaşık sayının eşleniği ile çarpımı modülünün karesini verir.
\( z \cdot \overline{z} = {\abs{z}}^2 = a^2 + b^2 \)
\( z = 5 - 2i \) olmak üzere,
\( z \cdot \overline{z} = (5 - 2i)(5 + 2i) = 25 + 10i - 10i - 4i^2 = \textcolor{red}{29} \)
\( {\abs{z}}^2 = 5^2 + (-2)^2 = \textcolor{red}{29} \)
İki karmaşık sayının çarpımının modülü, modüllerinin çarpımına eşittir.
\( \abs{z_1 \cdot z_2} = \abs{z_1} \cdot \abs{z_2} \)
\( z_1 = 2 + i, \quad z_2 = 1 - 7i \)
\( \abs{z_1 \cdot z_2} = \abs{(2 + i)(1 - 7i)} \)
\( = \abs{2 - 14i + i - 7i^2} = \abs{9 - 13i} = \sqrt{9^2 + (-13)^2} = \textcolor{red}{5\sqrt{10}} \)
\( \abs{z_1} \cdot \abs{z_2} = \abs{2 + i} \cdot \abs{1 - 7i} \)
\( = \sqrt{2^2 + 1^2} \cdot \sqrt{1^2 + (-7)^2} = \sqrt{5} \cdot \sqrt{50} = \textcolor{red}{5\sqrt{10}} \)
İki karmaşık sayının bölümünün modülü, modüllerinin bölümüne eşittir.
\( z_2 \ne 0 \) olmak üzere,
\( \abs{\dfrac{z_1}{z_2}} = \dfrac{\abs{z_1}}{\abs{z_2}} \)
\( z_1 = 7 - i, \quad z_2 = -1 + 2i \)
\( \abs{\dfrac{z_1}{z_2}} = \abs{\dfrac{7 - i}{-1 + 2i}} \)
\( = \abs{\dfrac{7 - i}{-1 + 2i} \cdot \dfrac{-1 - 2i}{-1 - 2i}} \)
\( = \abs{\dfrac{-7 - 14i + i + 2i^2}{1 + 2i - 2i - 4i^2}} \)
\( = \abs{\dfrac{-9 - 13i}{5}} = \abs{-\dfrac{9}{5} - \dfrac{13}{5}i} \)
\( = \sqrt{(-\dfrac{9}{5})^2 + (-\dfrac{13}{5})^2} = \textcolor{red}{\sqrt{10}} \)
\( \dfrac{\abs{z_1}}{\abs{z_2}} = \dfrac{\abs{7 - i}}{\abs{-1 + 2i}} \)
\( = \dfrac{\sqrt{7^2 + (-1)^2}}{\sqrt{(-1)^2 + 2^2}} = \dfrac{\sqrt{50}}{\sqrt{5}} = \textcolor{red}{\sqrt{10}} \)
Bir karmaşık sayının üssünün modülü, modülünün üssüne eşittir.
\( \abs{z_1^{n}} = {\abs{z_1}}^n \)
\( z_1 = 4 - 3i \) olmak üzere,
\( \abs{z_1^2} = \abs{(4 - 3i)^2} \)
\( = \abs{4^2 - 24i + (3i)^2} = \abs{7 - 24i} \)
\( = \sqrt{7^2 + (-24)^2} = \textcolor{red}{25} \)
\( {\abs{z_1}}^2 = {\abs{4 - 3i}}^2 \)
\( = \sqrt{4^2 + (-3)^2}^2 = \textcolor{red}{25} \)
Aşağıdaki üçgen eşitsizlikleri karmaşık sayılar için de geçerlidir.
\( \abs{\abs{z_1} - \abs{z_2}} \le \abs{z_1 - z_2} \)
\( \abs{\abs{z_1} - \abs{z_2}} \le \abs{z_1 + z_2} \le \abs{z_1} + \abs{z_2} \)
\( \abs{z_1} - \abs{z_2} \le \abs{z_1 - z_2} \le \abs{z_1} + \abs{z_2} \)
İki Karmaşık Sayı Arasındaki Uzaklık
Karmaşık düzlemdeki iki nokta arasındaki uzaklık aşağıdaki formülle bulunur. Bu uzaklık aynı zamanda iki sayının farkının modülüne eşittir.
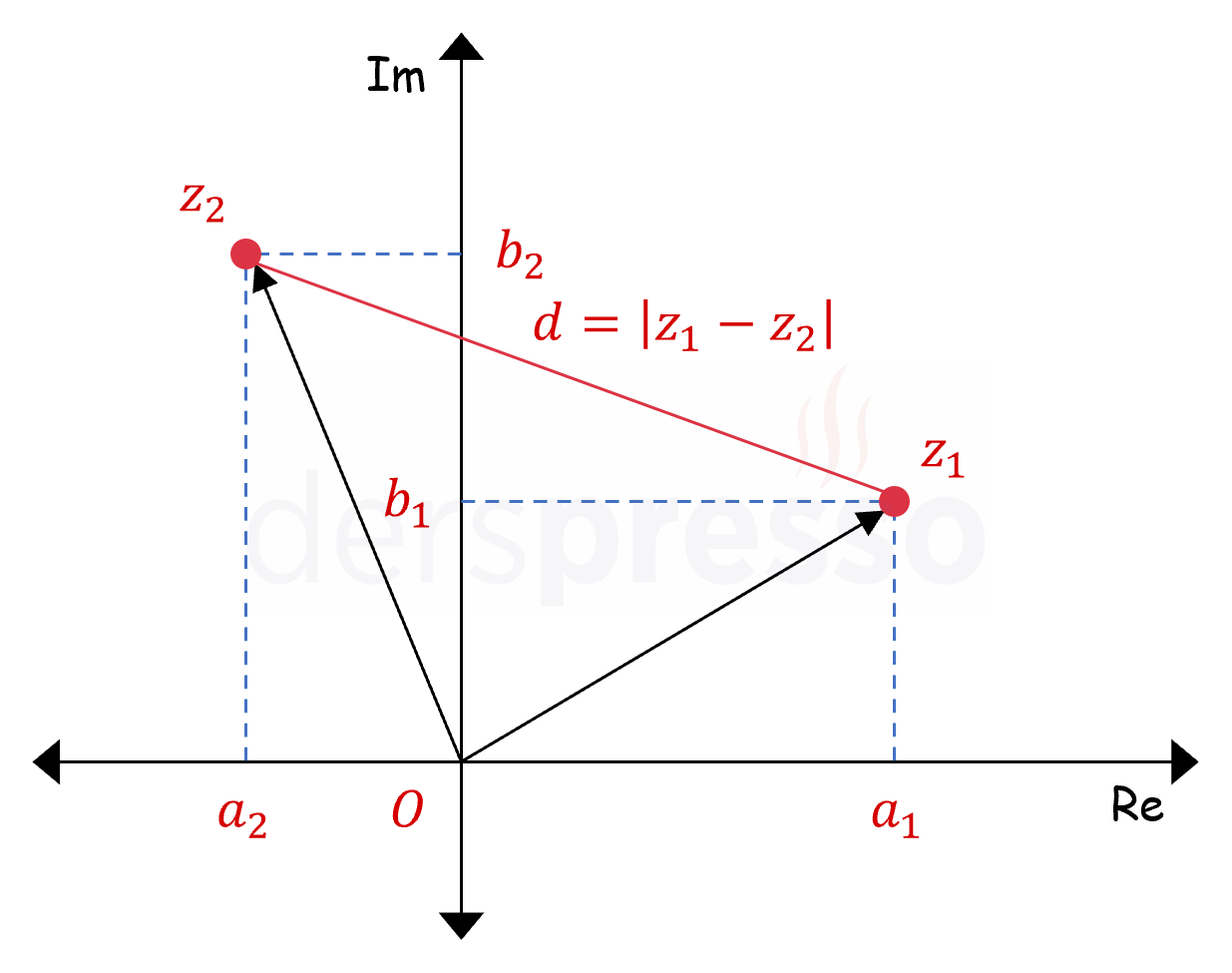
\( z_1 = a_1 + b_1i \)
\( z_2 = a_2 + b_2i \) olmak üzere,
\( d = \abs{z_1 - z_2} \)
\( d = \sqrt{(a_1 - a_2)^2 + (b_1 - b_2)^2} \)
\( z_1 = 4 \)
\( z_2 = -2 - 8i \) olmak üzere,
\( d = \sqrt{(4 - (-2))^2 + (0 - (-8))^2} \)
\( = \sqrt{36 + 64} = 10 \)
\( a \in \mathbb{R} \) olmak üzere,
\( z_1 = 2 + 3i \) ve \( z_2 = a + i \) karmaşık sayıları için,
\( \abs{z_1 - z_2} = \sqrt{53} \) koşulu sağlandığına göre, \( a \)'nın alabileceği değerlerin toplamı nedir?
Çözümü Göster\( z_1 - z_2 = (2 + 3i) - (a + i) \)
\( = (2 - a) + (3 - 1)i \)
\( = (2 - a) + 2i \)
\( \abs{z_1 - z_2} = \sqrt{53} = \sqrt{(2 - a)^2 + 2^2} \)
Eşitliğin taraflarının karesini alalım.
\( 53 = (2 - a)^2 + 4 \)
\( (2 - a)^2 = 49 \)
\( 2 - a = 7 \) ya da \( 2 - a = -7 \)
\( 2 - a = 7 \Longrightarrow a = -5 \)
\( 2 - a = -7 \Longrightarrow a = 9 \)
\( a \)'nın alabileceği değerlerin toplamı \( -5 + 9 = 4 \) olur.
\( z = \dfrac{(5 + 12i)(1 + 2i)(3 - 5i)}{(5 + 3i)(2 - i)} \)
olduğuna göre, \( \abs{z} \) kaçtır?
Çözümü Göster\( z = \dfrac{(5 + 12i)(3 - 5i + 6i - 10i^2)}{(10 - 5i + 6i - 3i^2)} \)
\( = \dfrac{(5 + 12i)(13 + i)}{13 + i} \)
\( = 5 + 12i \)
\( z \) karmaşık sayısının modülünü bulalım.
\( \abs{z} = \sqrt{5^2 + 12^2} \)
\( = \sqrt{169} = 13 \) bulunur.
\( z_1 = (k + 4) + 6i \)
\( z_2 = 5 + (5 - k)i \)
karmaşık sayıları arasındaki uzaklık \( \sqrt{10} \) birim olduğuna göre, \( k \)'nın pozitif değeri nedir?
Çözümü Göster\( a, b, c, d \in \mathbb{R} \) olmak üzere,
\( z_1 = a + bi \)
\( z_2 = c + di \) diyelim.
İki karmaşık sayı arasındaki uzaklık aşağıdaki formülle bulunur.
\( \abs{z_1 - z_2} = \sqrt{(a - c)^2 + (b - d)^2} \)
\( = \sqrt{(k + 4 - 5)^2 + (6 - (5 - k))^2} = \sqrt{10} \)
\( \sqrt{(k - 1)^2 + (k + 1)^2} = \sqrt{10} \)
\( \sqrt{k^2 - 2k + 1 + k^2 + 2k + 1} = \sqrt{10} \)
\( \sqrt{2k^2 + 2} = \sqrt{10} \)
Eşitliğin taraflarının karesini alalım.
\( 2k^2 + 2 = 10 \)
\( k^2 = 4 \)
\( k = \pm 2 \)
\( k \)'nın her iki değeri de yukarıdaki köklü denklemi sağlar.
\( k \)'nın pozitif değeri 2 olarak bulunur.
\( \abs{-z} + iz - 2 = 4i \)
eşitliğini sağlayan \( z \) karmaşık sayısı nedir?
Çözümü Göster\( z = ai + b \) diyelim.
Bir karmaşık sayının, eşleniğinin, negatifinin ve negatifinin eşleniğinin modülleri birbirine eşittir.
\( \abs{-z} = \abs{z} = \sqrt{a^2 + b^2} \)
Verilen eşitlikte yerlerine yazalım.
\( \sqrt{a^2 + b^2} + i(ai + b) - 2 = 4i \)
\( \sqrt{a^2 + b^2} + ai^2 + bi - 2 = 4i \)
\( \sqrt{a^2 + b^2} - a + bi - 2 = 4i \)
\( (\sqrt{a^2 + b^2} - a - 2) + bi = 4i \)
İki karmaşık sayının eşitliğinde sayıların reel ve sanal kısımları ayrı ayrı birbirine eşittir.
\( b = 4 \)
\( \sqrt{a^2 + b^2} - a - 2 = 0 \)
\( \sqrt{a^2 + 4^2} = a + 2 \)
Eşitliğin taraflarının karesini alalım.
\( a^2 + 16 = a^2 + 4a + 4 \)
\( 16 = 4a + 4 \)
\( a = 3 \)
\( z \) karmaşık sayısını yazalım.
\( z = ai + b = 3i + 4 \) bulunur.
\( z = \dfrac{(i - \sqrt{7})^4(2 + 2i)^2}{\sqrt{2} - \sqrt{2}i} \)
olduğuna göre, \( \abs{z^2} + \abs{z}^2 \) kaçtır?
Çözümü Göster\( \abs{z} = \abs{\dfrac{(i - \sqrt{7})^4(2 + 2i)^2}{\sqrt{2} - \sqrt{2}i}} \)
İki karmaşık sayının bölümünün modülü, modüllerinin bölümüne eşittir.
\( = \dfrac{\abs{(i - \sqrt{7})^4(2 + 2i)^2}}{\abs{\sqrt{2} - \sqrt{2}i}} \)
İki karmaşık sayının çarpımının modülü, modüllerinin çarpımına eşittir.
\( = \dfrac{\abs{(i - \sqrt{7})^4}\abs{(2 + 2i)^2}}{\abs{\sqrt{2} - \sqrt{2}i}} \)
Bir karmaşık sayının üssünün modülü, modülünün üssüne eşittir.
\( = \dfrac{\abs{(i - \sqrt{7})}^4\abs{(2 + 2i)}^2}{\abs{\sqrt{2} - \sqrt{2}i}} \)
\( = \dfrac{(\sqrt{(-\sqrt{7})^2 + 1^2})^4(\sqrt{2^2 + 2^2})^2}{\sqrt{(\sqrt{2})^2 + (\sqrt{2})^2}} \)
\( = \dfrac{(\sqrt{8})^4(\sqrt{8})^2}{\sqrt{4}} \)
\( = \dfrac{64 \cdot 8}{2} \)
\( = 256 = 2^8 \)
Bir karmaşık sayının üssünün modülü, modülünün üssüne eşittir.
\( \abs{z^2} = \abs{z}^2 \)
\( = (2^8)^2 = 2^{16} \)
\( \abs{z^2} + \abs{z}^2 = 2^{16} + 2^{16} \)
\( = 2 \cdot 2^{16} = 2^{17} \) bulunur.
\( \abs{-\overline{z}} + z = \dfrac{12}{1 + \sqrt{2}i} \)
olduğuna göre, \( Re(z) \) kaçtır?
Çözümü GösterBir karmaşık sayının, eşleniğinin, negatifinin ve negatifinin eşleniğinin modülleri birbirine eşittir.
\( x, y \in \mathbb{R} \) olmak üzere,
\( z = x + yi \) diyelim.
\( \abs{-\overline{z}} = \abs{z} = \sqrt{x^2 + y^2} \)
Bulduğumuz ifadeleri yerine yazalım.
\( \sqrt{x^2 + y^2} + x + yi = \dfrac{12}{1 + \sqrt{2}i} \)
Rasyonel ifadenin payını ve paydasını paydanın eşleniği ile çarpalım.
\( \sqrt{x^2 + y^2} + x + yi = \dfrac{12(1 - \sqrt{2}i)}{(1 + \sqrt{2}i)(1 - \sqrt{2}i)} \)
\( \sqrt{x^2 + y^2} + x + yi = \dfrac{12 - 12\sqrt{2}i}{1^2 - (\sqrt{2}i)^2} \)
\( \sqrt{x^2 + y^2} + x + yi = \dfrac{12 - 12\sqrt{2}i}{3} \)
\( \sqrt{x^2 + y^2} + x + yi = 4 - 4\sqrt{2}i \)
İki karmaşık sayının eşitliğinde sayıların reel ve sanal kısımları ayrı ayrı birbirine eşittir.
\( y = -4\sqrt{2} \)
\( \sqrt{x^2 + y^2} + x = 4 \)
\( \sqrt{x^2 + (-4\sqrt{2})^2} + x = 4 \)
\( \sqrt{x^2 + 32} + x = 4 \)
\( \sqrt{x^2 + 32} = 4 - x \)
Eşitliğin taraflarının karesini alalım.
\( x^2 + 32 = 16 - 8x + x^2 \)
\( 8x = -16 \)
\( x = -2 \)
Bulduğumuz değer yukarıda karesini aldığımız eşitliği sağlar.
\( z \) karmaşık sayısını yazalım.
\( z = x + yi = -2 - 4\sqrt{2}i \)
\( Re(z) = -2 \) bulunur.
\( a \in \mathbb{R} \) ve \( a \gt 1 \) olmak üzere,
\( z = \sqrt{2a + 3} + \sqrt{1 - a} \) karmaşık sayısının modülü 3 olduğuna göre, \( a \) değeri kaçtır?
Çözümü Göster\( a \gt 1 \) olduğuna göre, \( 2a + 3 \) pozitif ve \( 1 - a \) negatif olur.
\( z = \sqrt{2a + 3} + \sqrt{-(a - 1)} \)
\( = \sqrt{2a + 3} + \sqrt{a - 1}\sqrt{-1} \)
\( = \sqrt{2a + 3} + \sqrt{a - 1}i \)
Karmaşık sayının modülünü bulalım.
\( \abs{z} = \sqrt{(\sqrt{2a + 3})^2 + (\sqrt{a - 1})^2} \)
\( \sqrt{2a + 3 + a - 1} = 3 \)
\( \sqrt{3a + 2} = 3 \)
Eşitliğin taraflarının karesini alalım.
\( 3a + 2 = 9 \)
\( a = \dfrac{7}{3} \) bulunur.