Bir Karmaşık Sayının Argümenti
Bir karmaşık sayının analitik düzlemde gerçek eksenin pozitif tarafıyla yaptığı açıya o sayının argümenti denir ve \( \arg(z) \) şeklinde gösterilir. Argüment radyan cinsinden ifade edilir.
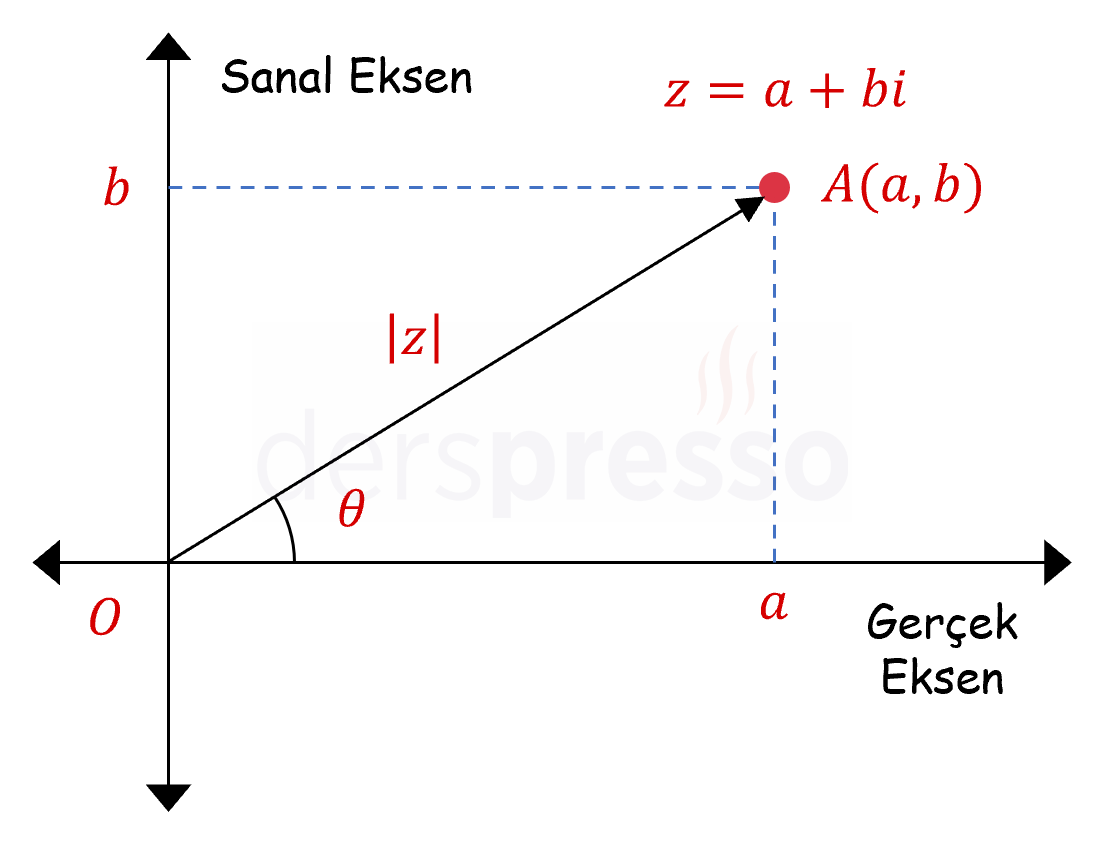
\( \Theta = \arg(z) \)
\( \sin{\Theta} = \dfrac{b}{\abs{z}} = \dfrac{b}{\sqrt{a^2 + b^2}} \)
\( \cos{\Theta} = \dfrac{a}{\abs{z}} = \dfrac{a}{\sqrt{a^2 + b^2}} \)
\( \tan{\Theta} = \dfrac{b}{a} \)
\( z = 2\sqrt{3} + 2i \)
\( \abs{z} = \sqrt{a^2 + b^2} = \sqrt{(2\sqrt{3})^2 + 2^2} = 4 \)
\( \sin{\Theta} = \dfrac{b}{\abs{z}} = \dfrac{2}{4} = \dfrac{1}{2} \)
\( \Theta = \arg(z) = \dfrac{\pi}{6} \)
Bu doğrultuda bir karmaşık sayıyı aşağıdaki şekilde de ifade edebiliriz.
\( z = a + bi \)
\( a = \abs{z} \cdot \cos{\Theta} \)
\( b = \abs{z} \cdot \sin{\Theta} \)
Yukarıdaki \( a \) ve \( b \) değerlerini \( z \) ifadesinde yerine koyalım.
\( z = \abs{z} \cdot \cos{\Theta} + (\abs{z} \cdot \sin{\Theta}) \cdot i \)
\( z = \abs{z} \cdot (\cos{\Theta} + i \cdot \sin{\Theta}) \)