Doğrunun Simetriği
Konu tekrarı için: Simetri Tipleri | Noktanın Simetriği
Bir doğrunun eksenlere, bir doğruya ya da bir noktaya göre simetriğini bulmak için o doğrunun denklemindeki değişkenlere belirli dönüşümler uygulanır.
Bir doğrunun bir noktaya göre simetriği doğrunun üzerindeki her noktanın simetri noktasına göre simetriği olan noktalardan oluşur. Benzer şekilde, bir doğrunun diğer bir doğruya göre simetriği doğrunun üzerindeki her noktanın simetri doğrusuna göre simetriği olan noktalardan oluşur.
Bir doğrunun farklı simetrileri için uygulanması gereken dönüşümler aşağıda belirtilmiştir.
\( x \) Eksenine Göre
Bir \( d \) doğrusunun \( x \) eksenine göre simetriği alınırken denklemde \( y \) işaret değiştirir.

\( d: ax + by + c = 0 \)
\( y \longmapsto -y \)
\( d': ax - by + c = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d' \) doğrusunun denklemi:
\( x - 2(-y) - 2 = 0 \)
\( x + 2y - 2 = 0 \)
\( d \) doğrusunun \( x \) eksenini kestiği noktanın bu eksene göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( x \) eksenini aynı noktada keser.
\( y \) Eksenine Göre
Bir \( d \) doğrusunun \( y \) eksenine göre simetriği alınırken denklemde \( x \) işaret değiştirir.

\( d: ax + by + c = 0 \)
\( x \longmapsto -x \)
\( d': -ax + by + c = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d' \) doğrusunun denklemi:
\( (-x) - 2y - 2 = 0 \)
\( -x - 2y - 2 = 0 \)
\( d \) doğrusunun \( y \) eksenini kestiği noktanın bu eksene göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( y \) eksenini aynı noktada keser.
Orijine Göre
Bir \( d \) doğrusunun orijine göre simetriği alınırken denklemde \( x \) ve \( y \) işaret değiştirir.
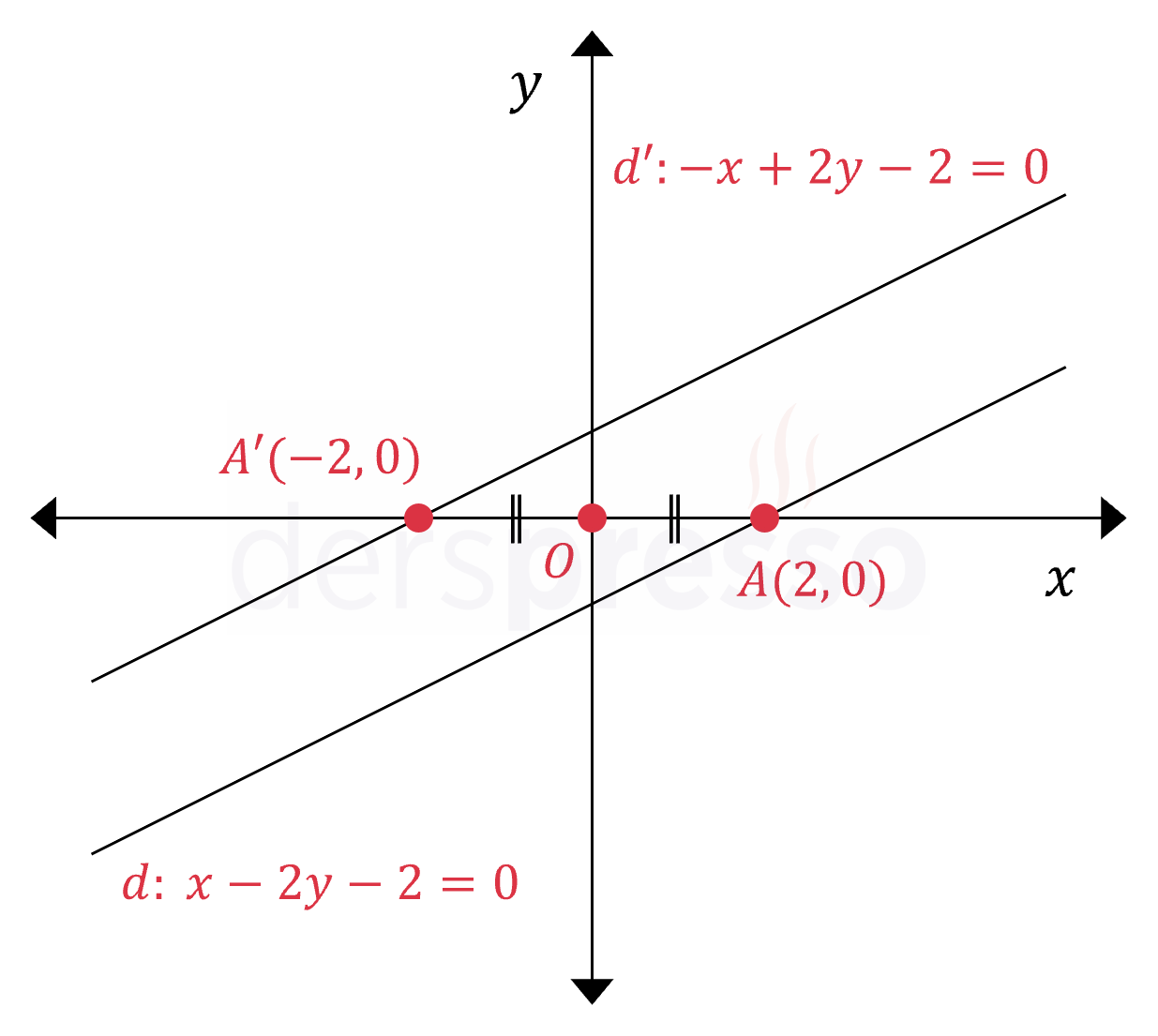
\( d: ax + by + c = 0 \)
\( x \longmapsto -x, \quad y \longmapsto -y \)
\( d': -ax - by + c = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d' \) doğrusunun denklemi:
\( (-x) - 2(-y) - 2 = 0 \)
\( -x + 2y - 2 = 0 \)
\( x \) ve \( y \) değişkenlerinin katsayılarının oranı değişmediği için, doğrunun kendisinin ve simetriğinin eğimleri aynı olur (doğrular paralel olur).
\( y = x \) Doğrusuna Göre
Bir \( d \) doğrusunun \( y = x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) yer değiştirir.
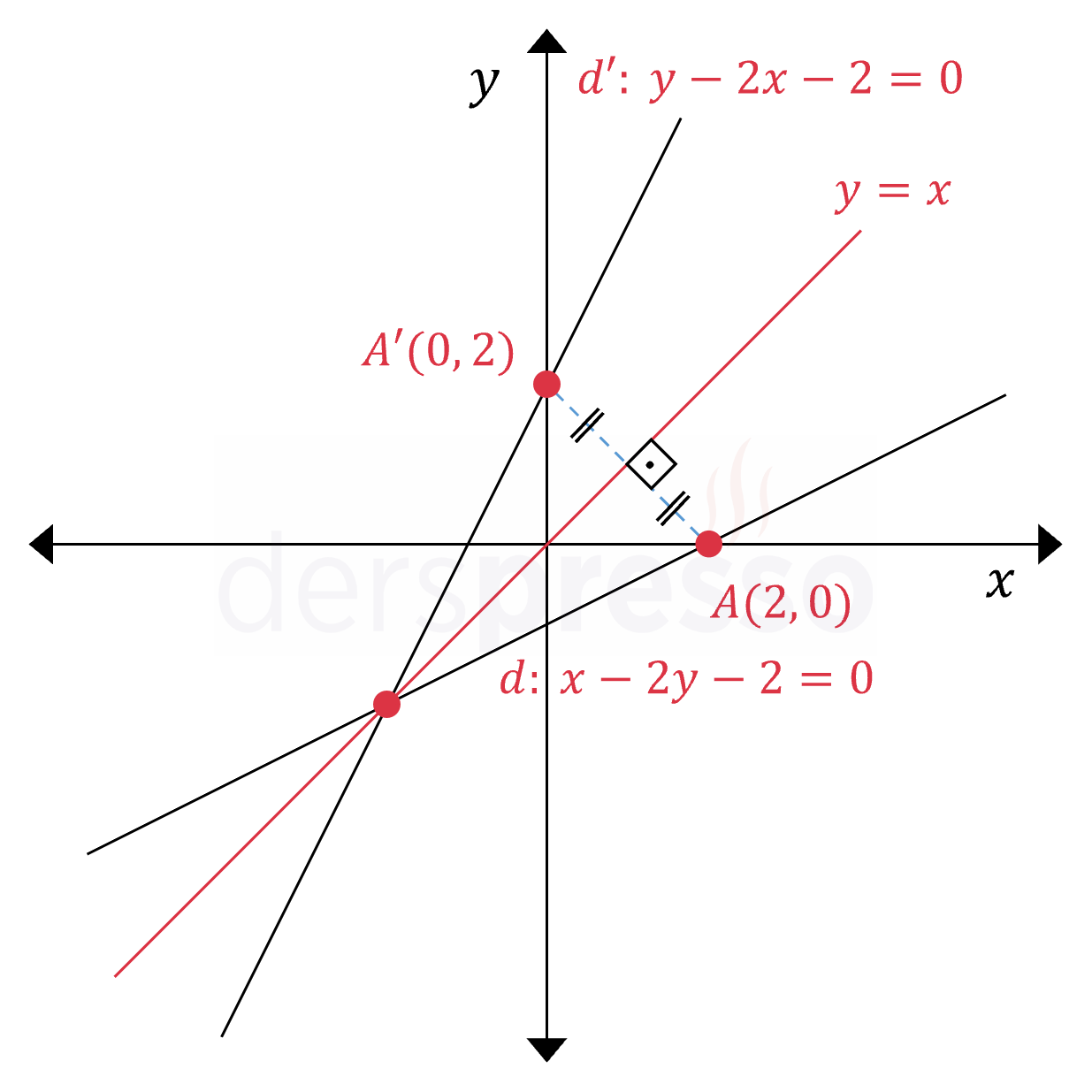
\( d: ax + by + c = 0 \)
\( x \longmapsto y, \quad y \longmapsto x \)
\( d': ay + bx + c = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d': y - 2x - 2 = 0 \)
\( d \) doğrusunun \( y = x \) doğrusunu kestiği noktanın bu doğruya göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( y = x \) doğrusunu aynı noktada keser.
\( y = -x \) Doğrusuna Göre
Bir \( d \) doğrusunun \( y = -x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) işaret ve yer değiştirir.

\( d: ax + by + c = 0 \)
\( x \longmapsto -y, \quad y \longmapsto -x \)
\( d': -ay - bx + c = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d' \) doğrusunun denklemi:
\( (-y) - 2(-x) - 2 = 0 \)
\( -y + 2x - 2 = 0 \)
\( d \) doğrusunun \( y = -x \) doğrusunu kestiği noktanın bu doğruya göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( y = -x \) doğrusunu aynı noktada keser.
Bir Noktaya Göre
Bir \( d \) doğrusunun \( S(m, n) \) noktasına göre simetriği alınırken denklemde \( x \) yerine \( 2m - x \), \( y \) yerine \( 2n - y \) yazılır.
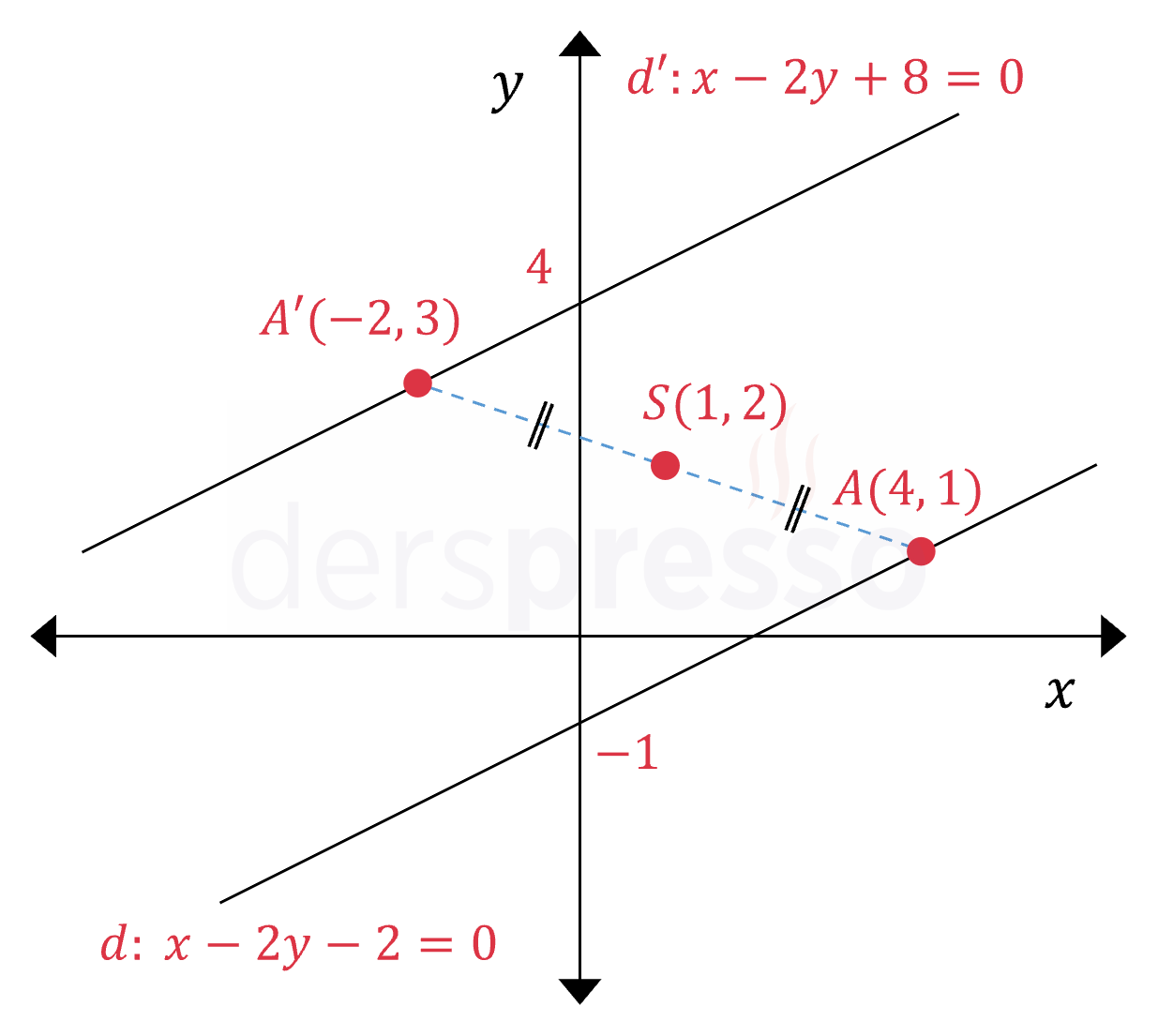
\( d: ax + by + c = 0 \)
Simetri noktası: \( S(m, n) \)
\( x \longmapsto 2m - x, \quad y \longmapsto 2n - y \)
\( d': a(2m - x) + b(2n - y) + c = 0 \)
\( d: x - 2y - 2 = 0 \)
Simetri noktası: \( S(1, 2) \)
\( d' \) doğrusunun denklemi:
\( (2(1) - x) - 2(2(2) - y) - 2 = 0 \)
\( 2 - x - 8 + 2y - 2 = 0 \)
\( x - 2y + 8 = 0 \)
\( d \) ve \( d' \) doğrularının eğimi aynı olur, \( d' \) doğrusunun denkleminde \( d \) doğrusuna göre sadece sabit terim değişir.
Alternatif bir yöntem olarak, \( d \) doğrusu üzerindeki bir noktanın \( S \) noktasına göre simetriği olan nokta bulunur. Daha sonra bu noktadan geçen ve eğimi \( d \) doğrusunun eğimi ile aynı olan doğrunun denklemi yazılır.
Paralel Bir Doğruya Göre
Bir \( d \) doğrusunun kendisine paralel olan bir \( d_s \) doğrusuna göre simetriği alınırken denklemde sadece sabit terime dönüşüm uygulanır.
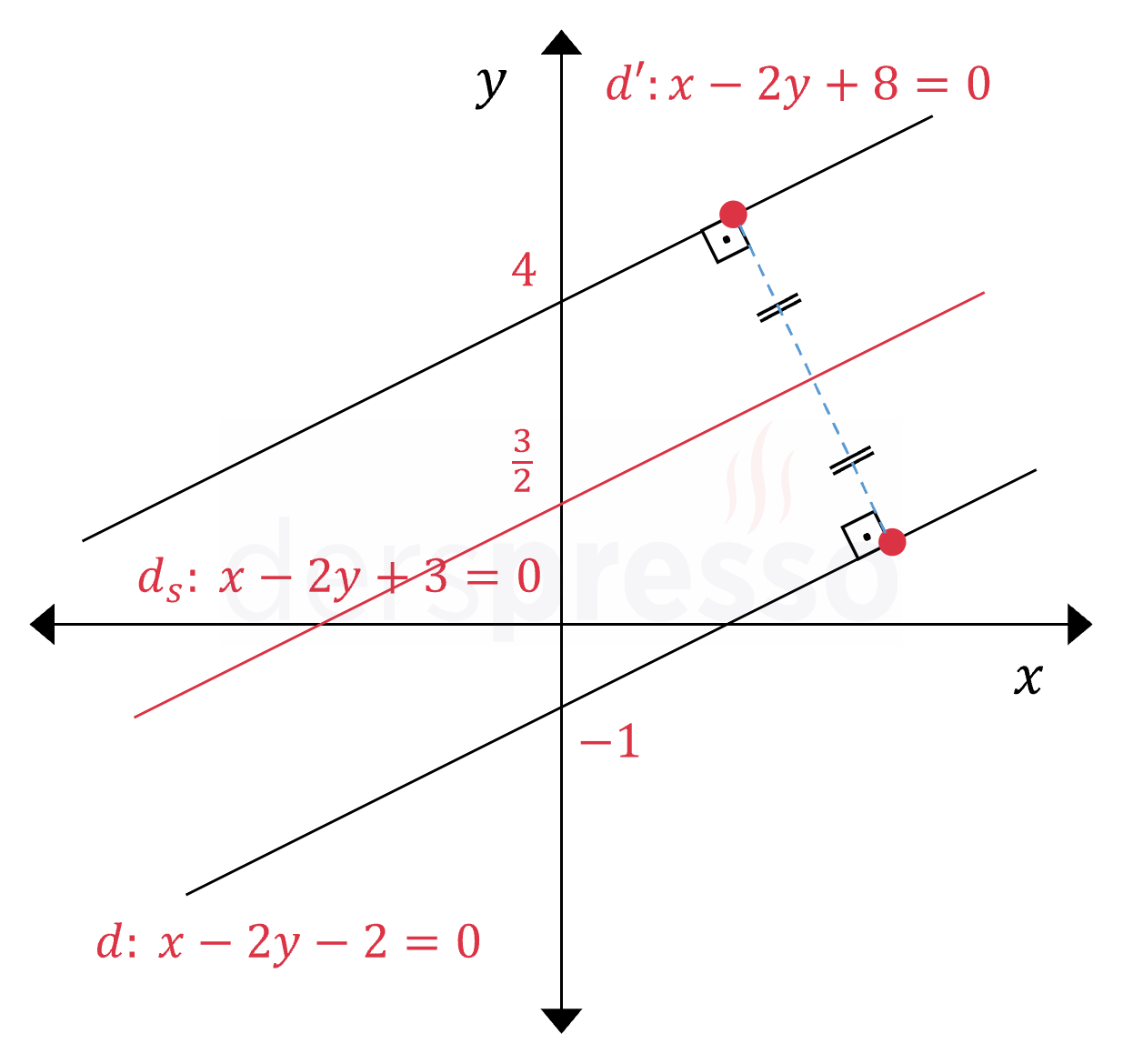
\( d: ax + by + c = 0 \)
\( d_s: ax + by + c_s = 0 \)
\( c' \longmapsto 2c_s - c \)
\( d': ax + by + c' = 0 \)
\( d: x - 2y - 2 = 0 \)
\( d_s: x - 2y + 3 = 0 \)
\( d' \) doğrusunun denklemi:
\( c' = 2(3) - (-2) = 8 \)
\( x - 2y + 8 = 0 \)
\( d \) ve \( d' \) doğrularının eğimi aynı olur, \( d' \) doğrusunun denkleminde \( d \) ve \( d_s \) doğrularına göre sadece sabit terim değişir.
\( y = n \) Doğrusuna Göre
Bir \( d \) doğrusunun yatay bir \( y = n \) doğrusuna göre simetriği alınırken denklemde \( y \) yerine \( 2n - y \) yazılır.
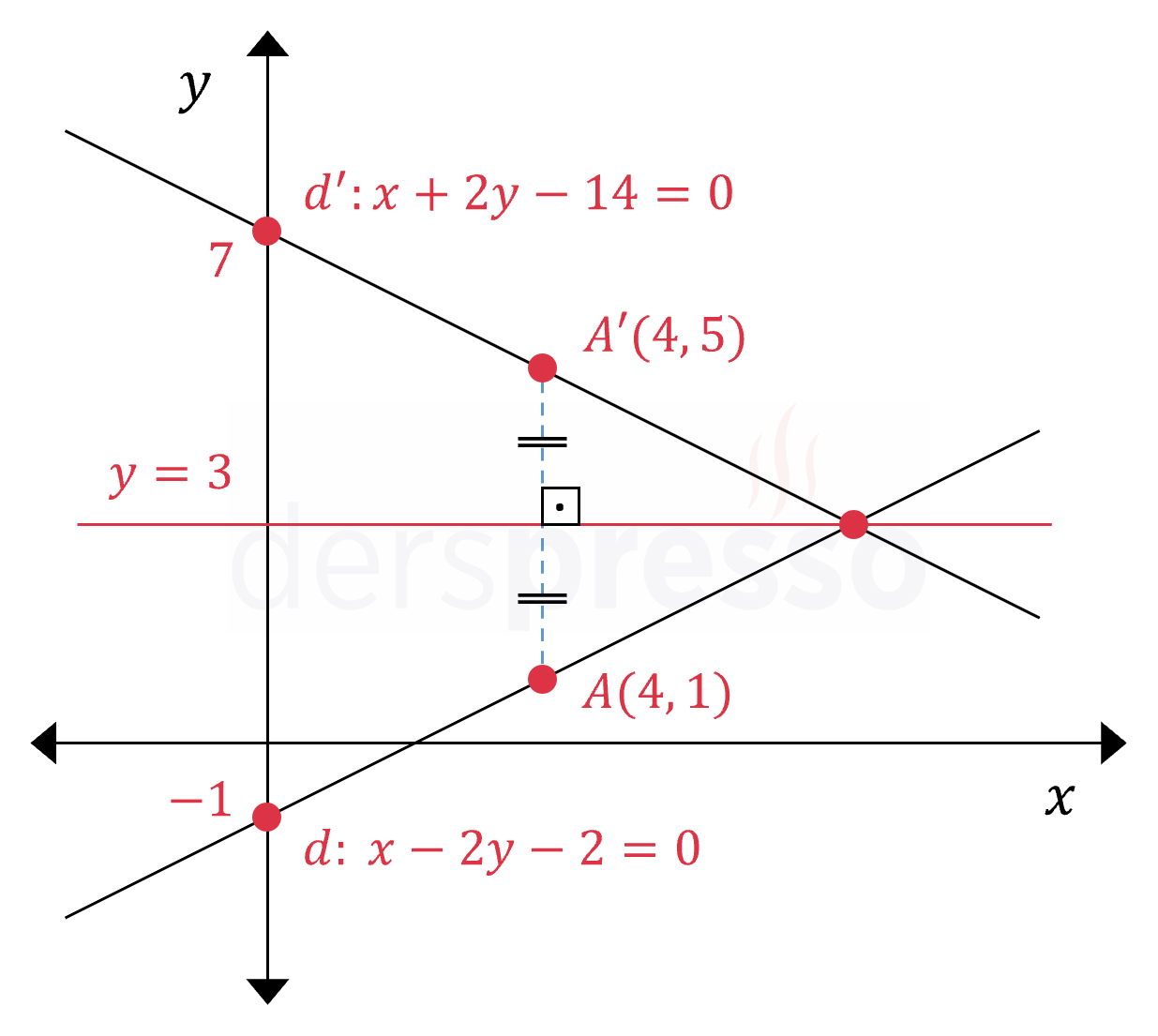
\( d: ax + by + c = 0 \)
Simetri doğrusu: \( y = n \)
\( y \longmapsto 2n - y \)
\( d': ax + b(2n - y) + c = 0 \)
\( d: x - 2y - 2 = 0 \)
Simetri doğrusu: \( y = 3 \)
\( d' \) doğrusunun denklemi:
\( x - 2(2(3) - y) - 2 = 0 \)
\( x - 12 + 2y - 2 = 0 \)
\( x + 2y - 14 = 0 \)
\( d \) doğrusunun \( y = n \) doğrusunu kestiği noktanın bu doğruya göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( y = n \) doğrusunu aynı noktada keser.
\( x = m \) Doğrusuna Göre
Bir \( d \) doğrusunun dikey bir \( x = m \) doğrusuna göre simetriği alınırken denklemde \( x \) yerine \( 2m - x \) yazılır.

\( d: ax + by + c = 0 \)
Simetri doğrusu: \( x = m \)
\( x \longmapsto 2m - x \)
\( d': a(2m - x) + by + c = 0 \)
\( d: x - 2y - 2 = 0 \)
Simetri doğrusu: \( x = 4 \)
\( d' \) doğrusunun denklemi:
\( (2(4) - x) - 2y - 2 = 0 \)
\( 8 - x - 2y - 2 = 0 \)
\( x + 2y - 6 = 0 \)
\( d \) doğrusunun \( x = m \) doğrusunu kestiği noktanın bu doğruya göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği \( x = m \) doğrusunu aynı noktada keser.
\( d: 2x + y + 1 = 0 \) doğrusunun aşağıdaki eksenler ve doğrulara göre simetriğini bulunuz.
(a) \( x \) eksenine göre
(b) \( y \) eksenine göre
(c) orijine göre
(d) \( y = x \) doğrusuna göre
(e) \( y = -x \) doğrusuna göre
(f) \( S(-4, 1) \) noktasına göre
(g) \( y = 3 \) doğrusuna göre
(h) \( x = -7 \) doğrusuna göre
Çözümü Göster(a) seçeneği:
Bir doğrunun \( x \) eksenine göre simetriği alınırken denklemde \( y \) işaret değiştirir.
\( d: 2x + y + 1 = 0 \)
\( y \longmapsto -y \)
\( d': 2x + (-y) + 1 = 0 \)
\( d': 2x - y + 1 = 0 \)
(b) seçeneği:
Bir doğrunun \( y \) eksenine göre simetriği alınırken denklemde \( x \) işaret değiştirir.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto -x \)
\( d': 2(-x) + y + 1 = 0 \)
\( d': -2x + y + 1 = 0 \)
(c) seçeneği:
Bir doğrunun orijine göre simetriği alınırken denklemde \( x \) ve \( y \) işaret değiştirir.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto -x, \quad y \longmapsto -y \)
\( d': 2(-x) + (-y) + 1 = 0 \)
\( d': -2x - y + 1 = 0 \)
(d) seçeneği:
Bir doğrunun \( y = x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) yer değiştirir.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto y, \quad y \longmapsto x \)
\( d': 2y + x + 1 = 0 \)
(e) seçeneği:
Bir doğrunun \( y = -x \) doğrusuna göre simetriği alınırken denklemde \( x \) ve \( y \) işaret ve yer değiştirir.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto -y, \quad y \longmapsto -x \)
\( d': 2(-y) + (-x) + 1 = 0 \)
\( d': -2y - x + 1 = 0 \)
(f) seçeneği:
Bir doğrunun \( S(m, n) \) noktasına göre simetriği alınırken aşağıdaki dönüşüm uygulanır.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto 2m - x, \quad y \longmapsto 2n - y \)
Simetri noktası \( S(-4, 1) \) olmak üzere,
\( d': 2(2(-4) - x) + (2(1) - y) + 1 = 0 \)
\( d': -2x - y - 13 = 0 \)
(g) seçeneği:
Bir doğrunun yatay bir \( y = n \) doğrusuna göre simetriği alınırken aşağıdaki dönüşüm uygulanır.
\( d: 2x + y + 1 = 0 \)
\( y \longmapsto 2n - y \)
Simetri doğrusu \( y = 3 \) olmak üzere,
\( d': 2x + (2(3) - y) + 1 = 0 \)
\( d': 2x - y + 7 = 0 \)
(h) seçeneği:
Bir doğrunun dikey bir \( x = m \) doğrusuna göre simetriği alınırken aşağıdaki dönüşüm uygulanır.
\( d: 2x + y + 1 = 0 \)
\( x \longmapsto 2m - x \)
Simetri doğrusu \( x = -7 \) olmak üzere,
\( d': 2(2(-7) - x) + y + 1 = 0 \)
\( d': -2x + y - 27 = 0 \)