İki Doğrunun Kesişimi
İki doğrunun (ya da eğrinin) kesişim noktaları, her iki doğru denklemini de sağlayan \( (x, y) \) ikilileridir. Aynı düzlemde bulunan iki doğrunun kesişimi üç farklı şekilde olabilir.
- Kesişen doğrular: Doğrular tek bir noktada kesişirler, dolayısıyla iki doğrunun da denklemini sağlayan tek bir \( (x, y) \) ikilisi vardır.
- Paralel doğrular: Doğrular kesişmezler, dolayısıyla iki doğrunun da denklemini sağlayan \( (x, y) \) ikilisi yoktur.
- Çakışık doğrular: Doğruların sonsuz sayıda ortak noktaları vardır, dolayısıyla iki doğrunun da denklemini sağlayan sonsuz sayıda \( (x, y) \) ikilisi vardır.
İki doğrunun kesişim noktasını bulmak için denklemler denklem sistemleri bölümünde gördüğümüz yöntemlerden biri kullanılarak ortak çözülür.
- Bulunan \( x \) çözüm değeri doğruların kesişim noktasının apsisini verir. Bu değer iki doğru denkleminden herhangi birinde yerine konarak kesişim noktasının ordinatı bulunur.
- Eğer çözüm kümesi boş küme ise doğrular kesişmez (paraleldir).
- Eğer iki denklemi de sağlayan sonsuz sayıda \( x \) değeri bulunuyorsa doğrular çakışıktır.
Her durumu birer örnek üzerinde gösterelim.
Eğimleri farklı iki doğru tek bir noktada kesişir.
\( d_1: 3x - y - 1 = 0 \)
\( d_2: -x - y + 3 = 0 \) doğrularının kesişim noktasını bulalım.
Eğimleri farklı iki doğru tek bir noktada kesişir.
\( -\dfrac{3}{-1} \ne -\dfrac{-1}{-1} \)
Denklemleri ortak çözerek doğruların kesişim noktasını bulalım.
Birinci doğrunun açık denklemini yazalım.
\( y = 3x - 1 \)
Bu \( y \) değerini ikinci denklemde yerine yazalım.
\( -x - (3x - 1) + 3 = 0 \)
\( x = 1 \)
Kesişim noktasının apsisi \( x = 1 \) olarak bulunur.
Bu değeri birinci denklemde yerine koyarak kesişim noktasının ordinatını bulalım.
\( y = 3x - 1 = 3(1) - 1 = 2 \)
Buna göre iki doğrunun kesişim noktası \( (1, 2) \) olarak bulunur.

Paralel doğrular kesişmez.
\( d_1: 2x - y + 2 = 0 \)
\( d_2: 4x - 2y - 8 = 0 \) doğrularının (varsa) kesişim noktasını bulalım.
Kapalı denklemlerinde \( x \) ve \( y \) katsayılarının oranları birbirine eşit, sabit terimlerin oranı birbirinden farklı olan iki doğru birbirine paraleldir.
\( \dfrac{2}{4} = \dfrac{-1}{-2} \ne \dfrac{2}{-8} \)
Denklemleri ortak çözerek doğruların kesişmediğini teyit edelim.
Birinci denklemin taraflarını \( -2 \) ile çarpalım.
\( -4x + 2y - 4 = 0 \)
Bu denklemi ikinci denklemle taraf tarafa toplayalım.
\( -12 = 0 \)
\( x \) değişkeninden bağımsız ve hiçbir \( x \) değeri için sağlanmayan bir eşitlik elde etmemiz, iki denklemi de sağlayan bir çözüm bulunmadığını gösterir.
Buna göre iki doğru paraleldir ve hiçbir noktada kesişmez.
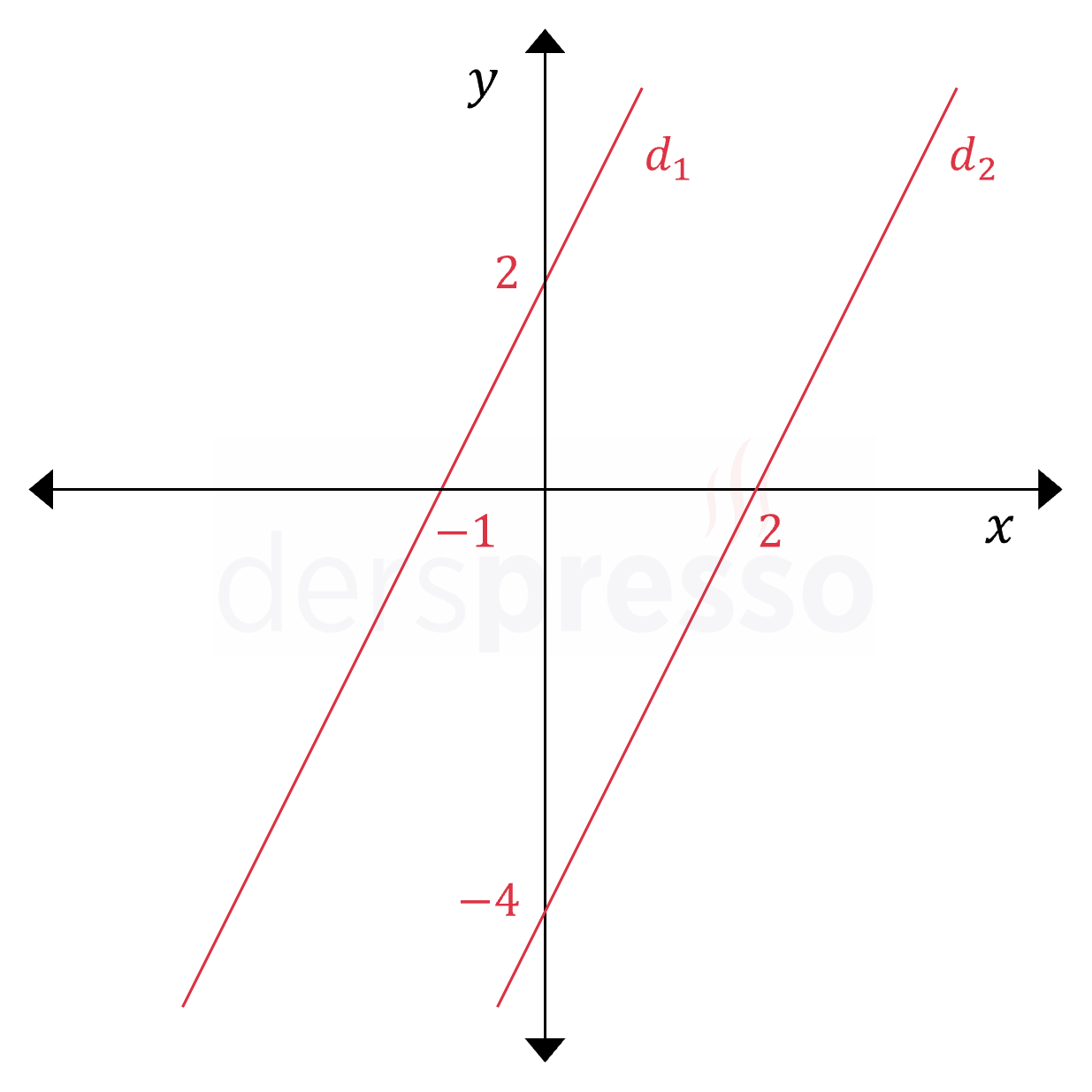
Çakışık doğruların sonsuz sayıda ortak noktaları vardır.
\( d_1: 2x - y + 2 = 0 \)
\( d_2: 4x - 2y + 4 = 0 \) doğrularının kesişim noktasını bulalım.
Kapalı denklemlerinde tüm katsayılarının oranları birbirine eşit olan iki doğru çakışıktır.
\( \dfrac{2}{4} = \dfrac{-1}{-2} = \dfrac{2}{4} \)
Denklemleri ortak çözerek doğruların çakışık olduğunu teyit edelim.
Birinci denklemin taraflarını \( -2 \) ile çarpalım.
\( -4x + 2y - 4 = 0 \)
Bu denklemi ikinci denklemle taraf tarafa toplayalım.
\( 0 = 0 \)
\( x \) değişkeninden bağımsız ve her \( x \) değeri için sağlanan bir eşitlik elde etmemiz, iki denklemi de sağlayan sonsuz sayıda çözüm bulunduğunu gösterir.
Buna göre iki doğru çakışıktır.

Koordinat düzleminde \( y = 3x + 2a \) ve \( y = 4 \) doğrularının kesişim noktasının apsisi \( -2 \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster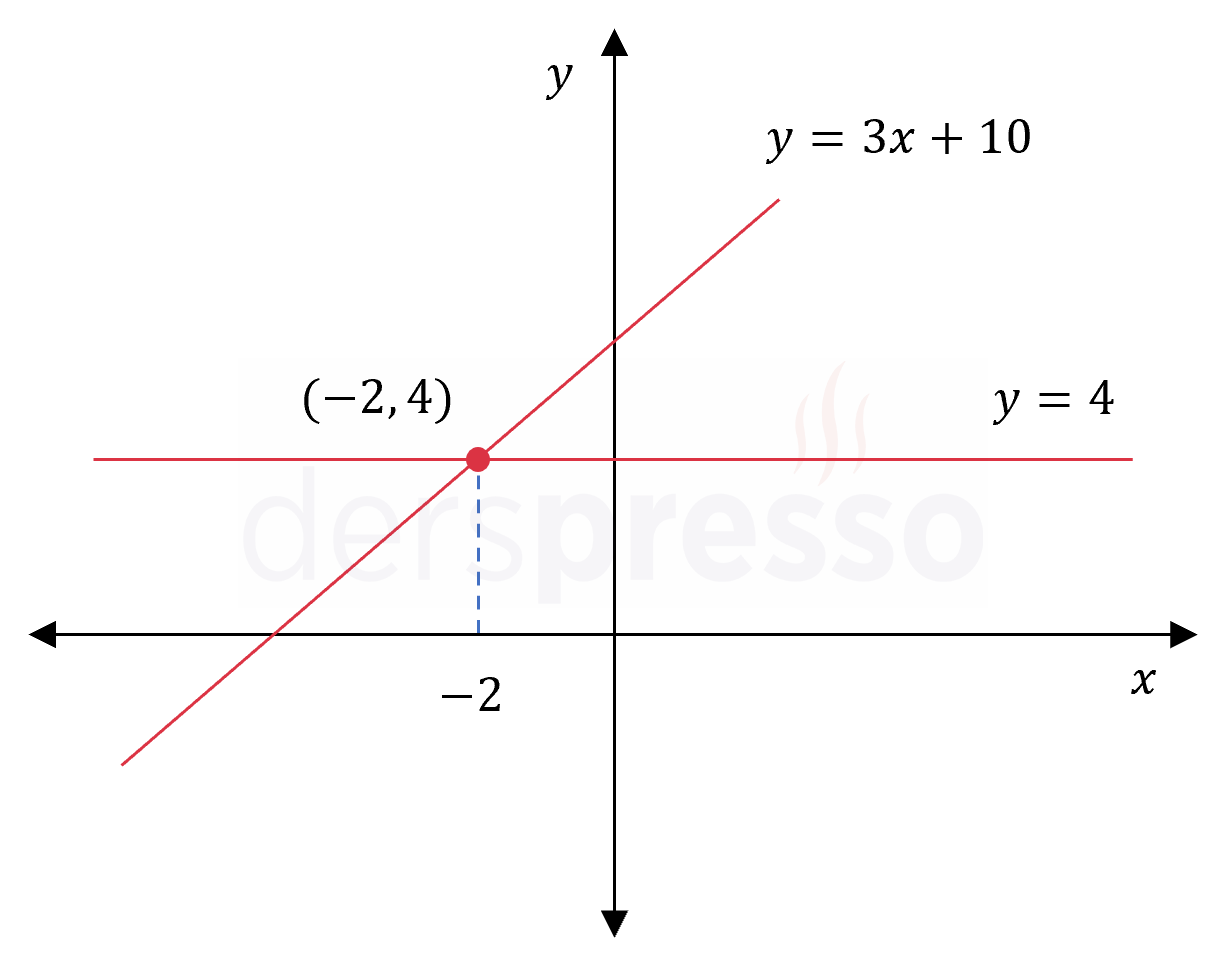
Doğruların kesişim noktalarında \( y \) değerleri eşittir.
\( 3x + 2a = 4 \)
Bu noktanın apsis değeri \( -2 \) olarak veriliyor.
\( 3(-2) + 2a = 4 \)
\( a = 5 \) bulunur.
\( y = x \), \( x = 0 \) ve \( y = 4 \) doğruları ile sınırlı bölgenin alanı kaç birimkaredir?
Çözümü GösterVerilen üç doğruyu koordinat düzleminde çizelim.

Şekilde oluşan taralı bölge bir dik üçgendir.
\( y = x \) ve \( y = 4 \) doğrularının kesişim noktasını bulmak için iki denklemi ortak çözdüğümüzde \( A \) noktasının koordinatlarını \( A(4, 4) \) olarak buluruz.
\( A(OAB) = \dfrac{\abs{OB} \cdot \abs{BA}}{2} \)
\( = \dfrac{4 \cdot 4}{2} = 8 \) birimkare bulunur.
\( d_1: x + 2y = 6 \) ve \( d_2: x + my = 12 \) doğruları \( y = -x \) doğrusu üzerinde kesiştiklerine göre, \( m \) kaçtır?
Çözümü GösterVerilen bilgiye göre üç doğru aynı noktada kesişirler.
\( d_1 \) ve \( y = -x \) doğrularının kesişim noktasını bulmak için birinci denklemde \( y = -x \) yazalım.
\( x + 2(-x) = 6 \)
\( x = -6, \quad y = 6 \)
Üç doğru \( (-6, 6) \) noktasında kesiştiğine göre, \( d_2 \) doğrusu bu noktadan geçer, dolayısıyla noktanın koordinatları doğrunun denklemini sağlar.
\( -6 + m(6) = 12 \)
\( m = 3 \) bulunur.

Koordinat düzleminde \( 2x + 6y - 12 = 0 \) ve \( \frac{x}{2} + 4y = 8 \) doğruları \( y \) ekseni üzerinde kesişmektedir.
Buna göre şekildeki taralı bölgenin alanı kaçtır?
Çözümü GösterVerilen doğrular \( y \) eksenini \( A \) noktasında kesmektedir.
Doğru denklemlerinden birinde \( x = 0 \) yazarak \( A \) noktasının ordinatını bulalım.
\( 2(0) + 6y - 12 = 0 \)
\( y = 2 \)
\( A(0, 2) \)
\( B \) noktasının apsisini bulmak için \( 2x + 6y - 12 = 0 \) denkleminde \( y = 0 \) yazalım.
\( 2x + 6(0) - 12 = 0 \)
\( x = 6 \)
\( B(6, 0) \)
\( C \) noktasının apsisini bulmak için \( \frac{x}{2} + 4y = 8 \) denkleminde \( y = 0 \) yazalım.
\( \dfrac{x}{2} + 4(0) = 8 \)
\( x = 16 \)
\( C(16, 0) \)

Taralı \( ABC \) üçgeninin alanını, \( [BC] \) doğru parçasını taban ve \( [AO] \) doğru parçasını yükseklik olarak kabul ederek hesaplayalım.
\( A(ABC) = \dfrac{\abs{BC}\abs{AO}}{2} \)
\( = \dfrac{10 \cdot 2}{2} = 10 \) bulunur.
Eğimleri \( 3 \) ve \( -6 \) olan iki doğru \( (0, k) \) noktasında kesişiyor.
Bu doğruların \( x \) eksenini kesen noktaları arasındaki uzaklık 3 birim olduğuna göre, \( k \)'nin alabileceği değerlerin çarpımı kaçtır?
Çözümü GösterDoğrular \( (0, k) \) noktasında, yani \( y \) ekseni üzerinde kesiştiklerine göre sabit terimleri \( k \) olur.
Doğrulara ait denklemler aşağıdaki gibidir.
\( d_1: y = 3x + k \)
\( d_2: y = -6x + k \)
Her bir doğrunun \( x \) eksenini kestiği noktayı bulmak için denklemde \( y = 0 \) yazalım.
\( 0 = 3x + k \Longrightarrow x = -\frac{k}{3} \)
\( 0 = -6x + k \Longrightarrow x = \frac{k}{6} \)
\( x \) ekseni üzerindeki bu iki nokta arasındaki uzaklık 3 birim olarak veriliyor.
\( \abs{\dfrac{k}{6} - (-\dfrac{k}{3})} = 3 \)
\( \abs{\dfrac{k}{2}} = 3 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( \dfrac{k}{2} = 3 \)
\( k = 6 \)
Durum 2:
\( \dfrac{k}{2} = -3 \)
\( k = -6 \)
\( k \)'nin alabileceği değerlerin çarpımı \( 6 \cdot (-6) = -36 \) olarak bulunur.
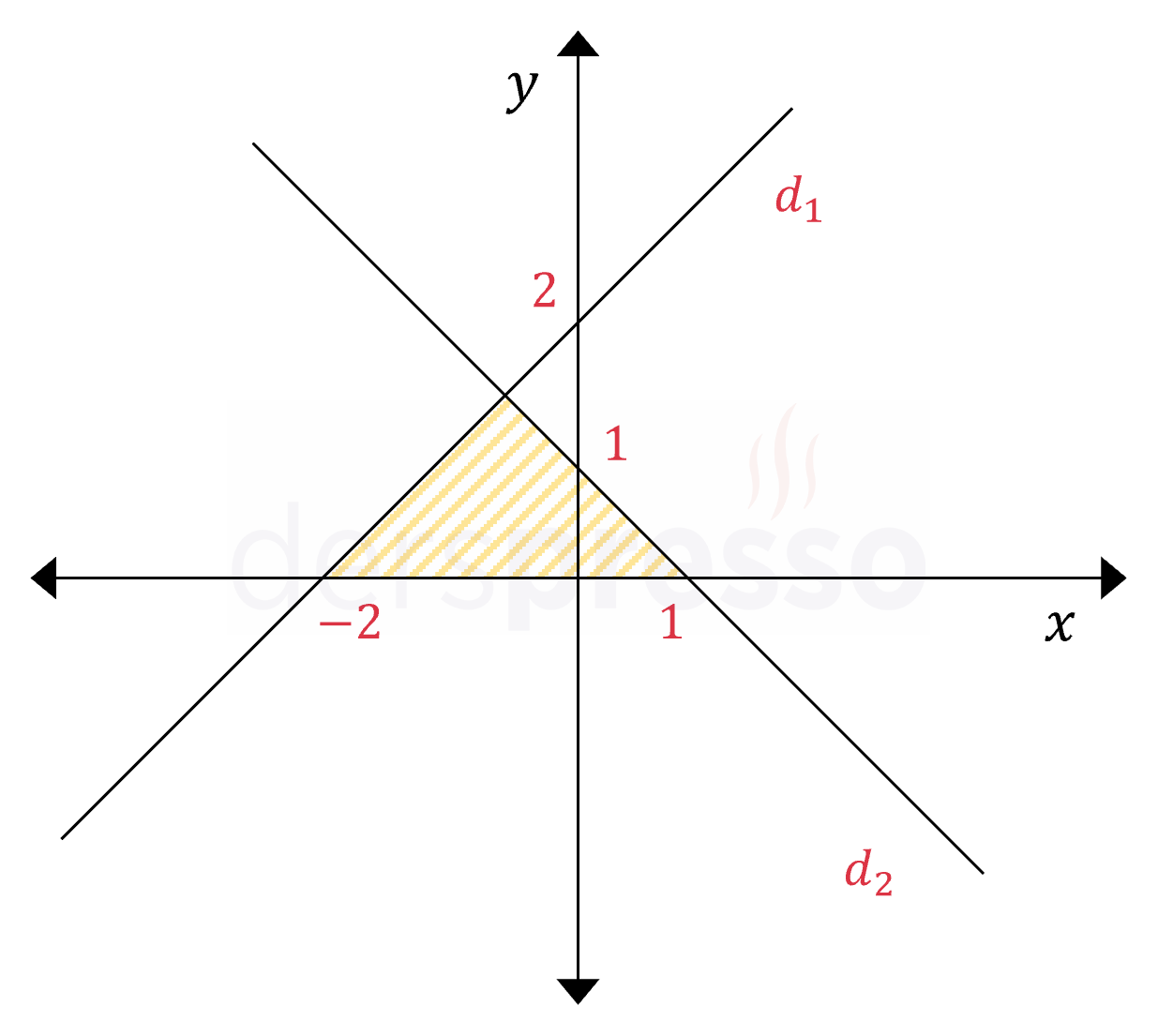
Şekildeki taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterEksenleri \( (a, 0) \) ve \( (0, b) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{a} + \dfrac{y}{b} = 1 \)
\( d_1 \) doğrusunun denklemini bulalım.
\( \dfrac{x}{-2} + \dfrac{y}{2} = 1 \)
\( y = x + 2 \)
\( d_2 \) doğrusunun denklemini bulalım.
\( \dfrac{x}{1} + \dfrac{y}{1} = 1 \)
\( y = -x + 1 \)
İki doğrunun kesişim noktasını bulmak için denklemleri ortak çözelim.
\( y = x + 2 = -x + 1 \)
\( x = -\dfrac{1}{2} \)
\( y = \dfrac{3}{2} \)
Buna göre taralı alan taban uzunluğu \( 1 - (-2) = 3 \) birim ve yüksekliği \( y = \frac{3}{2} \) birim olan üçgenin alanıdır.
\( A = \dfrac{3 \cdot \frac{3}{2}}{2} = \dfrac{9}{4} \) birimkare bulunur.
\( d_1: 3x + y + 6 = 0 \) ve \( d_2 \) doğruları \( y = -x \) doğrusu üzerinde bir noktada ve dik kesişiyorlar.
Buna göre \( d_1 \) ve \( d_2 \) doğruları ile \( x \) ekseninin oluşturduğu bölgenin alanı kaçtır?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının kesişim noktasına \( A \) diyelim.
\( d_2 \) doğrusunun denklemini bulmak için \( d_1 \) doğrusu ile kesiştiği noktanın koordinatlarını bulalım.
\( d_1 \) doğrusu \( y = -x \) doğrusu ile kesiştiğine göre doğru denkleminde \( y = -x \) yazalım.
\( 3x + y + 6 = 0 \)
\( 3x - x + 6 = 0 \)
\( x = -3 \)
\( A(-3, 3) \)

\( d_1 \) doğrusunun eğimine \( m_1 \), \( d_2 \) doğrusunun eğimine \( m_2 \) diyelim.
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m_1 = -\dfrac{3}{1} = -3 \)
\( d_1 \perp d_2 \) olduğuna göre, doğruların eğimleri çarpımı \( -1 \) olur.
\( m_1 \cdot m_2 = -1 \)
\( m_2 = \dfrac{1}{3} \)
\( (x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y - y_1 = m(x - x_1) \)
\( y - 3 = \dfrac{1}{3}(x - (-3)) \)
\( d_2: 3y - x - 12 = 0 \)
\( d_1 \) doğrusunun eksenleri kestiği noktaları bulalım.
\( x = 0 \) için denklemi çözelim.
\( 3(0) + y + 6 = 0 \)
\( y = -6 \)
\( y = 0 \) için denklemi çözelim.
\( 3x + 0 + 6 = 0 \)
\( x = -2 \)
\( d_1 \) doğrusu eksenleri \( (0, -6) \) ve \( (-2, 0) \) noktalarında keser.
\( d_2 \) doğrusunun eksenleri kestiği noktaları bulalım.
\( x = 0 \) için denklemi çözelim.
\( 3y - 0 - 12 = 0 \)
\( y = 4 \)
\( y = 0 \) için denklemi çözelim.
\( 3(0) - x - 12 = 0 \)
\( x = -12 \)
\( d_2 \) doğrusu eksenleri \( (0, 4) \) ve \( (-12, 0) \) noktalarında keser.
\( d_1 \) ve \( d_2 \) doğruları ile \( x \) ekseninin oluşturduğu bölge bir üçgendir.
Taralı \( ABC \) üçgeninin alanını, \( [BC] \) doğru parçasını taban ve \( [AD] \) doğru parçasını yükseklik olarak kabul ederek hesaplayalım.
\( A(ABC) = \dfrac{\abs{BC}\abs{AD}}{2} \)
\( = \dfrac{10 \cdot 3}{2} = 15 \) bulunur.

Koordinat düzleminde verilen \( d_1: y = 3x + 9 \) ve \( d_2 \) doğruları \( y \) ekseni üzerinde kesişmektedir.
Buna göre \( d_2 \) doğrusunun eksenleri kestiği noktaların koordinatları toplamı kaçtır?
Çözümü Göster\( d_1 \) doğrusunun eksenleri kestiği noktaların koordinatlarını bulalım.
\( x = 0 \) için denklemi çözelim.
\( y = 3(0) + 9 \)
\( y = 9 \)
\( A(0, 9) \)
\( y = 0 \) için denklemi çözelim.
\( 0 = 3x + 9 \)
\( x = -3 \)
\( C(-3, 0) \)
\( \abs{OC} = 3 \)
\( \abs{OA} = 9 \)
\( OAB \) üçgeninde \( [AC] \) doğru parçası \( A \) köşesine ait iç açıortay olup aşağıdaki oran sağlanır.
\( \dfrac{\abs{OA}}{\abs{OC}} = \dfrac{\abs{AB}}{\abs{BC}} = \dfrac{9}{3} = 3 \)
\( \abs{BC} = a \) diyelim.

\( \abs{AB} = 3a \) olur.
\( OAB \) dik üçgende Pisagor teoremini uygulayalım.
\( \abs{OA}^2 + \abs{OB}^2 = \abs{AB}^2 \)
\( 9^2 + (a + 3)^2 = (3a)^2 \)
\( 81 + a^2 + 6a + 9 = 9a^2 \)
\( 8a^2 - 6a - 90 = 0 \)
\( 4a^2 - 3a - 45 = 0 \)
\( (4a - 15)(a + 3) \)
\( a \) değeri \( \abs{BC} \) uzunluğuna karşılık geldiğinden dolayı negatif olamaz.
\( a = \dfrac{15}{4} \)
\( d_2 \) doğrusu \( x \) eksenini \( B \) noktasında keser.
\( \abs{OB} = a + 3 = \dfrac{15}{4} + 3 = \dfrac{27}{4} \)
\( B(-\frac{27}{4}, 0) \)
\( d_2 \) doğrusunun eksenleri kestiği noktaların koordinatları toplamını bulalım.
\( -\dfrac{27}{4} + 9 = \dfrac{9}{4} \) bulunur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( d_1: 5y = 4x + a \)
\( d_2: by = -5x + 20 \)
Koordinat düzleminde dik kesişen \( d_1 \) ve \( d_2 \) doğrularının kesişim noktası \( x \) ekseni üzerinde olduğuna göre, \( \frac{a}{b} \) oranı kaçtır?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının eğimlerine sırasıyla \( m_1 \) ve \( m_2 \) diyelim.
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m_1 = \dfrac{4}{5} \)
\( m_2 = -\dfrac{5}{b} \)
Doğrular dik kesiştiğine göre eğimleri çarpımı -1 olmalıdır.
\( m_1 \cdot m_2 = -1 \)
\( m_1 \cdot m_2 = \dfrac{4}{5} \cdot \left( -\dfrac{5}{b} \right) = -1 \)
\( b = 4 \)
Doğrular \( x \) ekseni üzerinde kesiştiği için \( y \) koordinatı 0'dır.
Doğruların kesiştiği noktaya \( C(x_0, 0) \) diyelim.
\( d_2: 4y = -5x + 20 \) doğrusu \( C(x_0, 0) \) noktasından geçtiğine göre noktanın koordinatları doğru denklemini sağlar.
\( 4(0) = -5x_0 + 20 \)
\( x_0 = 4 \)
\( C(4, 0) \)
\( C(4, 0) \) noktasının koordinatları \( d_1 \) doğru denklemini de sağlar.
\( 5(0) = 4(4) + a \)
\( a = -16 \)
\( \dfrac{a}{b} = \dfrac{-16}{4} = -4 \) bulunur.
\( ABCD \) paralelkenarında karşılıklı \( B \) ve \( D \) köşeleri \( d: 2x + ky + 3 = 0 \) doğrusu üzerindedir.
\( A(4, 6) \) ve \( C(-2, 4) \) olduğuna göre, \( k \) kaçtır?
Çözümü GösterParalelkenarda köşegenlerin kesişim noktası her iki köşegenin de orta noktasıdır.
Buna göre \( [AC] \) köşegeninin orta noktası ile \( [BD] \) köşegeninin orta noktası aynıdır.
İlk olarak \( [AC] \) köşegeninin orta noktasını bulalım.
\( [AC] \) köşegeninin orta noktasına \( K \) diyelim.
\( K\left( \dfrac{4 + (-2)}{2}, \dfrac{6 + 4}{2} \right) = K(1, 5) \)
\( K(1, 5) \) noktası \( [BD] \) köşegeninin de orta noktası olduğu için \( d \) doğrusunun üzerindedir, dolayısıyla koordinatları doğru denklemini sağlar.
\( 2(1) + k(5) + 3 = 0 \)
\( k = -1 \) bulunur.

Koordinat düzlemindeki \( d_1: x - 2y + 5 = 0 \), \( d_2: y = 3x \) ve \( d_3: y = -2x \) doğruları şekildeki gibidir.
\( d_1 \) ve \( d_2 \) doğruları \( A \) noktasında, \( d_1 \) ve \( d_3 \) doğruları \( B \) noktasında, \( d_2 \) ve \( d_3 \) doğruları orijinde kesiştiğine göre, \( ABO \) üçgeninin çevresi kaç birimdir?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının kesişimi olan \( A \) noktasının koordinatlarını bulmak için iki denklemi ortak çözelim.
\( d_1 \) doğrusunun denkleminde \( y = 3x \) yazalım.
\( x - 2(3x) + 5 = 0 \)
\( x = 1 \)
\( A \) noktasının ordinatını bulmak için \( d_2 \) doğrusunun denklemini kullanalım.
\( y = 3(1) = 3 \)
\( A(1, 3) \)
\( d_1 \) ve \( d_3 \) doğrularının kesişimi olan \( B \) noktasının koordinatlarını bulmak için iki denklemi ortak çözelim.
\( d_1 \) doğrusunun denkleminde \( y = -2x \) yazalım.
\( x - 2(-2x) + 5 = 0 \)
\( x = -1 \)
\( B \) noktasının ordinatını bulmak için \( d_3 \) doğrusunun denklemini kullanalım.
\( y = -2(-1) = 2 \)
\( B(-1, 2) \)
\( \abs{AB} \) uzunluğunu bulmak için iki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{AB} = \sqrt{(-1 - 1)^2 + (2 - 3)^2} \)
\( = \sqrt{5} \)
\( A \) noktasının orjine olan uzaklığını bulalım.
\( \abs{AO} = \sqrt{1^2 + 3^2} = \sqrt{10} \)
\( B \) noktasının orjine olan uzaklığını bulalım.
\( \abs{BO} = \sqrt{(-1)^2 + 2^2} = \sqrt{5} \)
\( ABO \) üçgeninin çevresini bulalım.
\( \text{Ç}(ABO) = \abs{AB} + \abs{AO} + \abs{BO} \)
\( = \sqrt{5} + \sqrt{10} + \sqrt{5} \)
\( = 2\sqrt{5} + \sqrt{10} \) bulunur.
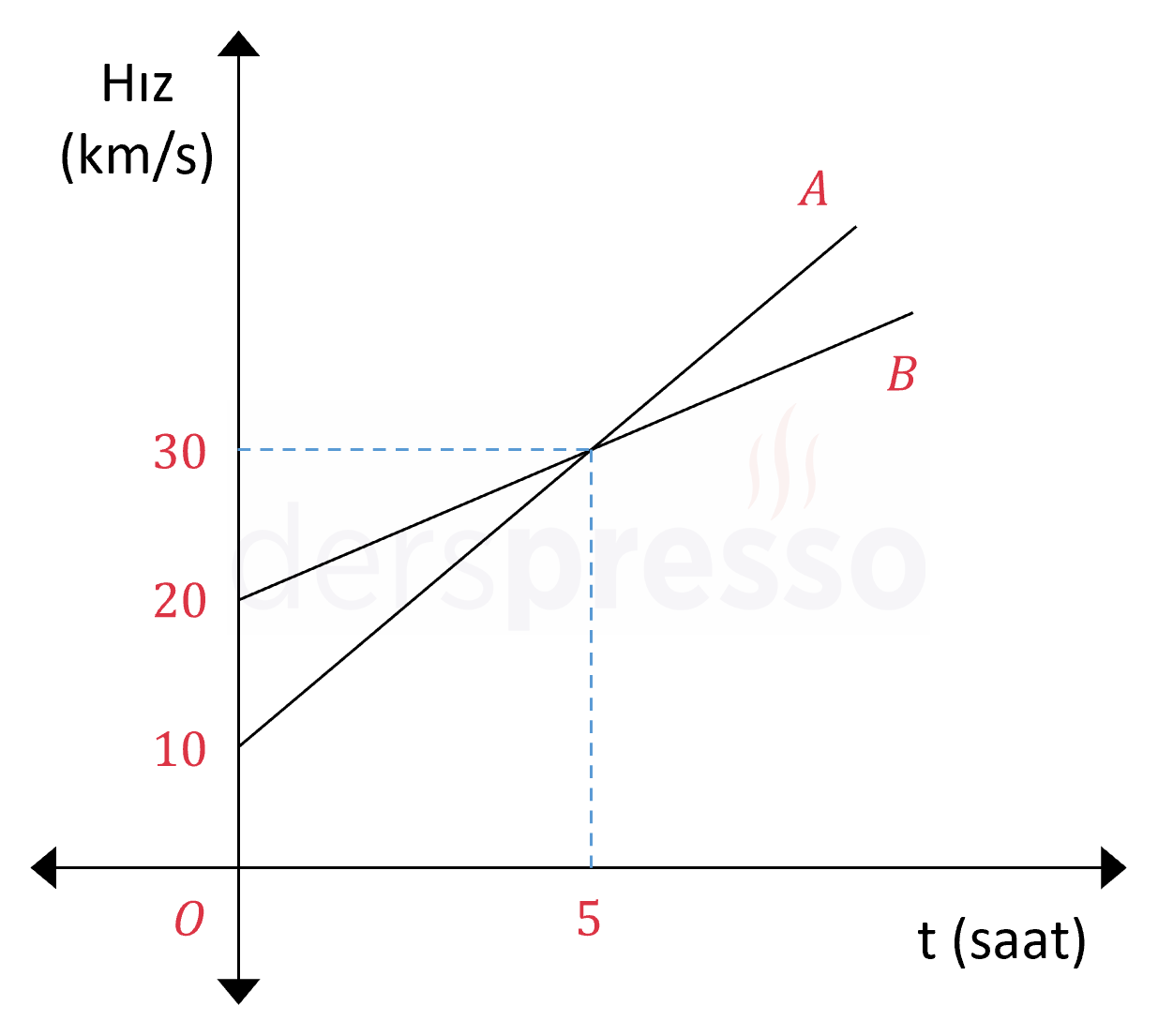
Yukarıda iki aracın hız - zaman grafikleri verilmiştir. Buna göre bu araçların kaçıncı dakikada hızlarının farkı 40 km/sa olur?
Çözümü Göster\( (0, 10) \) ve \( (5, 30) \) noktalarından geçen \( A \) aracının hız denklemini bulalım.
\( \dfrac{y - 30}{x - 5} = \dfrac{30 - 10}{5 - 0} = 4 \)
\( y - 30 = 4(x - 5) \)
\( y = 4x + 10 \)
\( (0, 20) \) ve \( (5, 30) \) noktalarından geçen \( B \) aracının hız denklemini bulalım.
\( \dfrac{y - 30}{x - 5} = \dfrac{30 - 20}{5 - 0} = 2 \)
\( y - 30 = 2(x - 5) \)
\( y = 2x + 20 \)
İki aracın hızları farkının 40 km/sa olduğu ana \( t \) dersek araçların \( t \) anındaki hızları aşağıdaki gibi olur.
\( y_A = 4t + 10 \)
\( y_B = 2t + 20 \)
Bu \( t \) anındaki hız farkını 40'a eşitleyelim.
\( y_A - y_B = (4t + 10) - (2t + 20) = 40 \)
\( 2t - 10 = 40 \)
\( t = 25 \) dakika bulunur.
Koordinat düzleminde \( (5, 3) \) noktasından geçen ve eksenleri kestiği noktaların koordinatları toplamı 16 olan doğruların denklemini bulunuz.
Çözümü Gösterİstenen doğruların \( x \) eksenini kestiği noktanın apsisine \( a \), \( y \) eksenini kestiği noktanın ordinatına \( b \) diyelim.
Eksenleri \( (a, 0) \) ve \( (0, b) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{a} + \dfrac{y}{b} = 1 \)
Doğruların eksenleri kestiği noktaların koordinatları toplamı 16 olarak veriliyor.
\( a + b = 16 \)
\( (5, 3) \) noktası bu doğru üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( \dfrac{5}{a} + \dfrac{3}{b} = 1 \)
Bulduğumuz iki denklemi ortak çözelim.
\( b \) değerini birinci denklemde yalnız bırakarak ikinci denklemde yerine koyalım.
\( b = 16 - a \)
\( \dfrac{5}{a} + \dfrac{3}{16 - a} = 1 \)
\( \dfrac{5(16 - a) + 3a}{a(16 - a)} = 1 \)
\( \dfrac{80 - 5a + 3a}{16a - a^2} = 1 \)
\( 80 - 2a = 16a - a^2 \)
\( a^2 - 18a + 80 = 0 \)
\( (a - 8)(a - 10) = 0 \)
\( a = 8 \) ya da \( a = 10 \)
\( a = 8 \) değerini birinci denklemde yerine koyarak \( b \) değerini bulalım.
\( 8 + b = 16 \)
\( b = 8 \)
\( a = 10 \) değerini birinci denklemde yerine koyarak \( b \) değerini bulalım.
\( 10 + b = 16 \)
\( b = 6 \)
\( (a, b) = (8, 8) \) için doğru denklemini bulalım.
\( \dfrac{x}{8} + \dfrac{y}{8} = 1 \)
\( x + y - 8 = 0 \)
\( (a, b) = (10, 6) \) için doğru denklemini bulalım.
\( \dfrac{x}{10} + \dfrac{y}{6} = 1 \)
\( 3x + 5y - 30 = 0 \)
Buna göre verilen koşulları sağlayan iki doğru vardır ve denklemleri aşağıdaki gibidir.
\( d_1: x + y - 8 = 0 \)
\( d_2: 3x + 5y - 30 = 0 \)
Koordinat düzleminde \( 2x + 3y = 0 \), \( x = 3 \), \( x = -\frac{3k}{2} \) ve \( y = 0 \) doğrularının sınırlandırdığı yamuğun alanı 24 birimkare olduğuna göre, \( k \) kaçtır?
Çözümü GösterVerilen doğruları koordinat düzleminde çizelim.
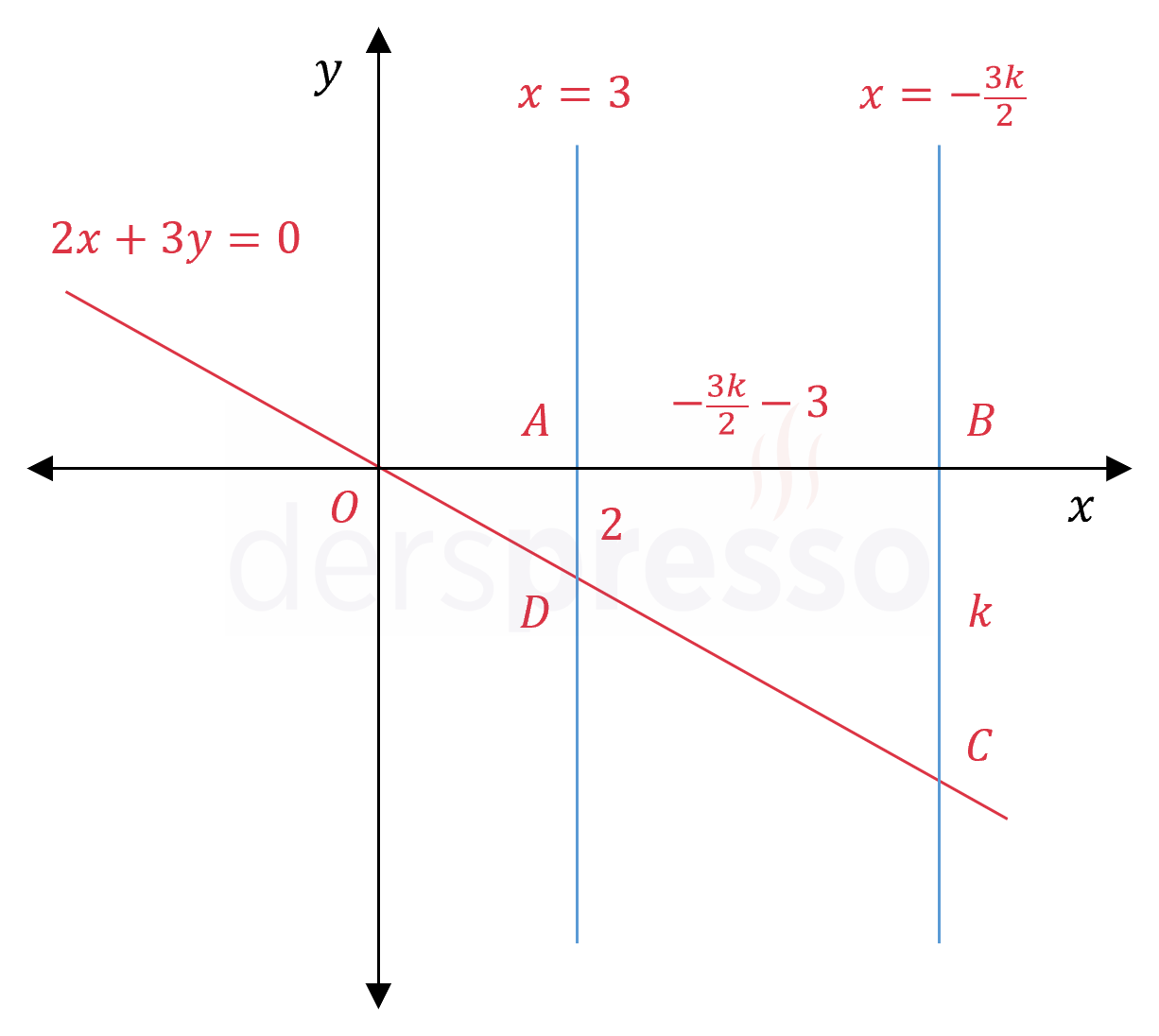
Her ne kadar \( x = -\frac{3k}{2} \) doğrusunun denklemi doğrunun \( y \) ekseninin solunda kaldığını düşündürtse de, verilen doğruların bir yamuk oluşturması için doğru \( y \) ekseninin sağında yer almalı, dolayısıyla \( k \) negatif olmalıdır.
Ayrıca yamuğun alanının 24 birimkare olabilmesi için bu doğru \( x = 3 \) doğrusunun da sağında yer almalıdır.
Oluşan yamuğun köşe noktalarına \( A, B, C, D \) diyelim.
\( A(3, 0) \)
\( B(-\frac{3k}{2}, 0) \)
\( D \) noktasının ordinatını bulmak için \( 2x + 3y = 0 \) doğru denkleminde \( x = 3 \) yazalım.
\( 2(3) + 3y = 0 \)
\( y = -2 \)
\( D(3, -2) \)
\( C \) noktasının ordinatını bulmak için \( 2x + 3y = 0 \) doğru denkleminde \( x = -\frac{3k}{2} \) yazalım.
\( 2(-\dfrac{3k}{2}) + 3y = 0 \)
\( y = k \)
\( C(-\frac{3k}{2}, k) \)
\( ABCD \) yamuğunun alanını hesaplamak için taban uzunluklarını ve yüksekliğini bulalım.
\( \abs{AD} = 2 \)
\( x = -\frac{3k}{2} \) doğrusunun apsis değerinden \( k \)'nın negatif olduğunu biliyoruz.
\( \abs{BC} = \abs{k} = -k \)
Yamuğun yüksekliği olan \( \abs{AB} \) uzunluğunu bulalım.
Ordinatı sıfır olan iki nokta arası uzaklık, apsislerinin farkına eşittir.
\( \abs{AB} = -\dfrac{3k}{2} - 3 \)
\( ABCD \) yamuğunun alanını bulalım.
\( A(ABCD) = \dfrac{(\abs{AD} + \abs{BC}) \cdot \abs{AB}}{2} \)
\( 24 = \dfrac{(2 - k)(-\frac{3k}{2} - 3)}{2} \)
\( 48 = -3k - 6 + \dfrac{3k^2}{2} + 3k \)
\( \dfrac{3k^2}{2} = 54 \)
\( k^2 = 36 \)
\( k \) negatif bir büyüklüktür.
\( k = -6 \) bulunur.
\( c \in \mathbb{R} \) olmak üzere,
\( x - y = 3 \)
\( cx + y = 2 \)
doğruları koordinat düzleminin III. bölgesinde kesiştiklerine göre, \( c \) hangi aralıktadır?
Çözümü Gösterİki doğru denklemini ortak çözerek kesişim noktalarını bulalım.
\( y \) değişkeninden kurtulmak için denklemleri taraf tarafa toplayalım.
\( x + cx = 3 + 2 \)
\( x = \dfrac{5}{c + 1} \)
Bu değeri birinci denklemde yerine koyalım.
\( x - y = 3 \)
\( \dfrac{5}{c + 1} - y = 3 \)
\( 5 - y(c + 1) = 3(c + 1) \)
\( y = \dfrac{2 - 3c}{c + 1} \)
Kesişim noktası III. bölgede ise noktanın apsis ve ordinatının işaretleri \( (-, -) \) olur.
\( x = \dfrac{5}{c + 1} \lt 0 \)
Pay pozitif olduğu için bu eşitsizlik payda negatif olduğunda sağlanır.
\( c + 1 \lt 0 \)
\( c \lt -1 \)
\( y = \dfrac{2 - 3c}{c + 1} \lt 0 \)
Eşitsizliğin kritik noktaları payı ve paydayı sıfır yapan \( c \in \{ -1, \frac{2}{3} \} \) değerleridir.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -1) \), \( (-1, \frac{2}{3}) \) ve \( (\frac{2}{3}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
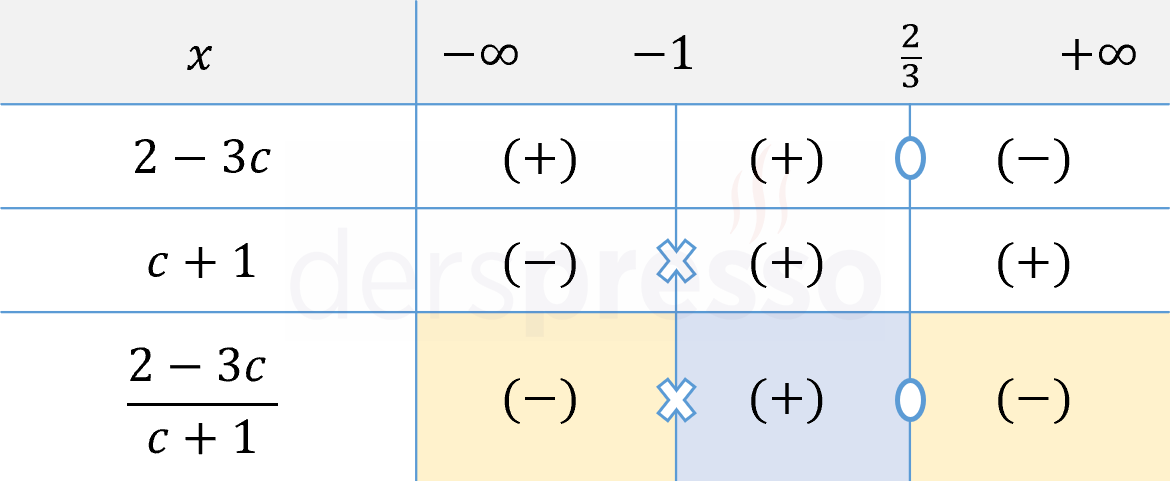
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için rasyonel ifadenin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( c \in (-\infty, -1) \cup (\frac{2}{3}, \infty) \)
Hem apsisi hem de ordinatı negatif yapan \( c \) aralığı bulduğumuz iki aralığın kesişim kümesidir.
Çözüm kümesi: \( c \in (-\infty, -1) \)