Doğrunun Eğimi
İnteraktif uygulama: Doğrunun Katsayıları
Eğimin Tanımı
Eğim bir doğrunun ne kadar dik olduğunu ve dikliğinin yönünü ifade eder. Bir doğrunun eğimi genellikle \( m \) ile gösterilir.
Bir doğrunun eğimi, doğru üzerinde bulunan iki nokta arasındaki dikey değişimin yatay değişime oranına eşittir. Bir doğrunun eğim açısı doğrunun \( x \) ekseni ile pozitif yönde yaptığı açıdır. Aşağıdaki şekil incelendiğinde, doğrunun eğiminin (ve bu değişim oranının) aynı zamanda eğim açısının tanjant değerine eşit olduğu görülebilir.
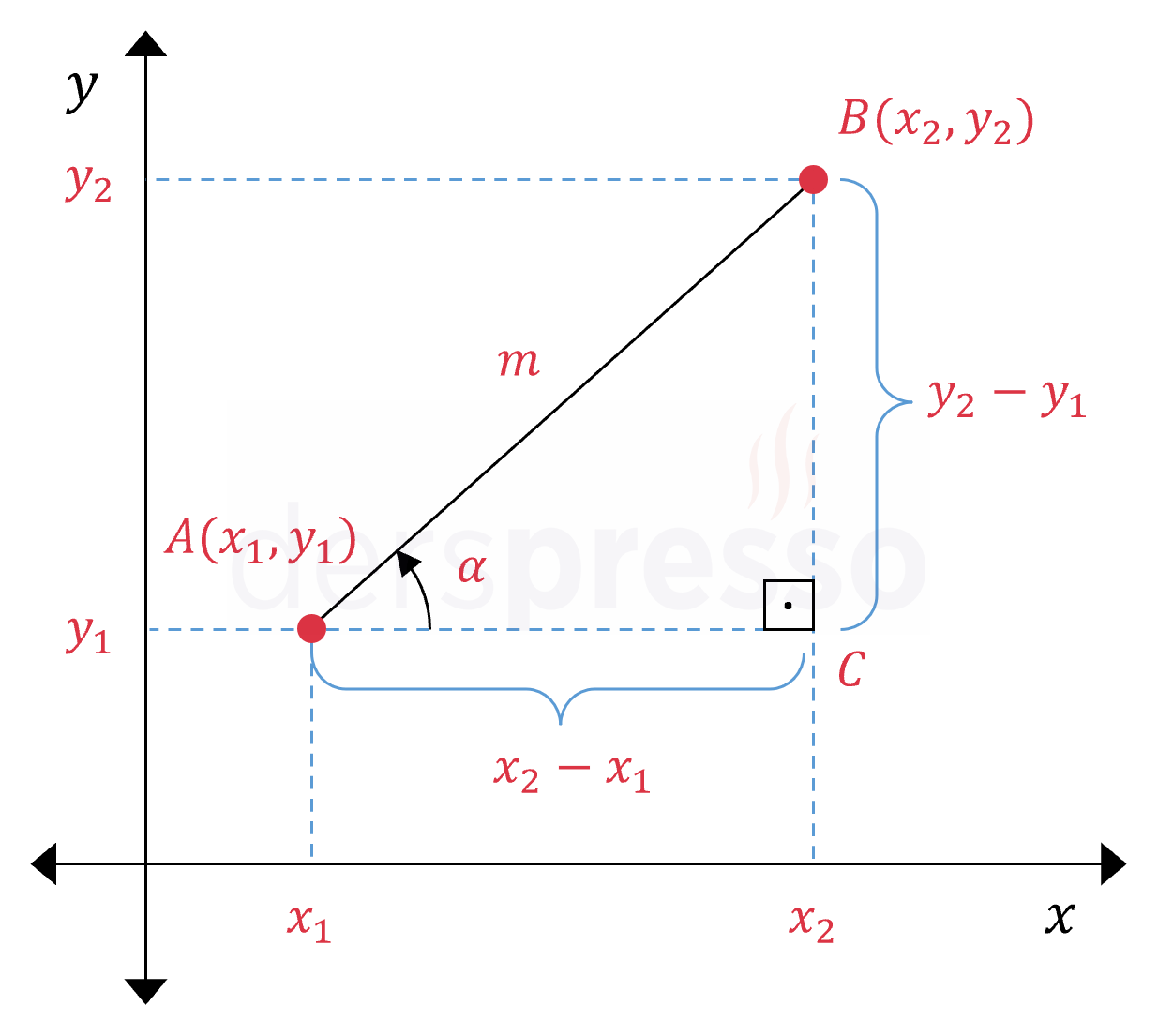
\( m = \tan{\alpha} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( A(1, -2) \) ve \( B(5, 6) \) noktalarından geçen doğrunun eğimini hesaplayalım.
Noktaları analitik düzlemde işaretleyelim ve bu iki noktadan geçen doğrunun grafiğini çizelim.

\( m = \dfrac{6 - (-2)}{5 - 1} = \dfrac{8}{4} = 2 \)
Bu değer aynı zamanda grafikte işaretli \( \alpha \) açısının tanjant değerine eşittir.
\( \tan{\alpha} = 2 \)
Eğim hesaplanırken hangi noktanın koordinatlarından hangi noktanın koordinatlarının çıkarıldığı önemli değildir, önemli olan noktaların koordinatlarının pay ve paydada aynı sırada birbirinden çıkarılmasıdır.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{y_1 - y_2}{x_1 - x_2} \)
\( \dfrac{6 - (-2)}{5 - 1} = \dfrac{-2 - 6}{1 - 5} = 2 \)
Eğim değeri \( x \) değişkenindeki her birim artış için \( y \) değişkenindeki artış ya da azalış miktarını verir ve \( y \) değişkeninin hangi hızda arttığını ya da azaldığını gösterir. Yukarıdaki örnekte \( A \) ve \( B \) noktaları arasında \( x \) 4 birim artarken \( y \) 8 birim artmıştır, yani \( x \)'in her birim artışı için \( y \) 2 birim artmıştır, bu da hesapladığımız eğim değerine eşittir.
Aşağıda farklı doğruların \( x \) değerlerindeki belirli miktar artış için \( y \) değerlerindeki artış/azalış miktarları ve bu doğrultuda oluşan eğim değerleri gösterilmiştir. Bu şekildeki her doğru için dikey ve yatay değişimlerin oranı alınarak eğim değeri ile karşılaştırılabilir.

Doğrunun açık denkleminde \( x \)'in katsayısı aynı zamanda doğrunun eğimini verir. Bu da \( x \) değerindeki her 1 birimlik artış için \( y \) değerinin \( m \) birim artması ya da azalması anlamına gelir.
\( y = \textcolor{red}{m}x + c \)
Aşağıdaki doğruların eğimi sırasıyla 2 ve -3'tür.
\( y = \textcolor{red}{2}x - 5 \)
\( y = \textcolor{red}{-3}x + 7 \)
Doğrunun kapalı denkleminde eğim aşağıdaki formülle bulunabilir.
\( ax + by + c = 0 \)
\( m = -\dfrac{a}{b} \)
\( 3x - 4y + 2 = 0 \) doğrusunun eğimi:
\( a = 3, \quad b = -4 \)
\( m = -\dfrac{3}{-4} = \dfrac{3}{4} \)
Aşağıdaki nokta ikililerinden geçen doğruların eğimlerini bulunuz.
(a) \( A(5, 3), B(-4, 0) \)
(b) \( A(5, 7), B(2, 3) \)
(c) \( A(-1, -4), B(3, -4) \)
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
(a) seçeneği:
\( A(5, 3), B(-4, 0) \)
\( m = \dfrac{0 - 3}{-4 - 5} = \dfrac{1}{3} \)
(b) seçeneği:
\( A(5, 7), B(2, 3) \)
\( m = \dfrac{3 - 7}{2 - 5} = \dfrac{4}{3} \)
(c) seçeneği:
\( A(-1, -4), B(3, -4) \)
\( m = \dfrac{-4 - (-4)}{3 - (-1)} = 0 \)
Aşağıdaki doğruların eğimlerini bulunuz.
(a) \( 3x - 5y - 4 = 0 \)
(b) \( y = \dfrac{-x + 4}{3} \)
(c) \( 2y - 4x = 7 \)
Çözümü Göster(a) seçeneği:
\( 3x - 5y - 4 = 0 \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m = -\dfrac{3}{-5} = \dfrac{3}{5} \)
(b) seçeneği:
\( y = \dfrac{-x + 4}{3} \)
Denklemi düzenleyelim.
\( y = -\dfrac{1}{3}x + \dfrac{4}{3} \)
\( y = mx + c \) şeklinde açık denklemi verilen bir doğrunun eğimi \( m \) olur.
\( m = -\dfrac{1}{3} \)
(c) seçeneği:
\( 2y - 4x = 7 \)
Denklemi düzenleyelim.
\( -4x + 2y - 7 = 0 \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m = -\dfrac{-4}{2} = 2 \)
Aşağıdaki doğruların eğimlerini bulunuz.
(a) \( -3y = 5x - 4 \)
(b) \( x = 4y + 6 \)
(c) \( \dfrac{5x - 4y}{3} = -1 \)
Çözümü Göster(a) seçeneği:
\( -3y = 5x - 4 \)
Denklemi düzenleyelim.
\( y = -\dfrac{5}{3}x + \dfrac{4}{3} \)
\( y = mx + c \) şeklinde açık denklemi verilen bir doğrunun eğimi \( m \) olur.
\( m = -\dfrac{5}{3} \)
(b) seçeneği:
\( x = 4y + 6 \)
Denklemi düzenleyelim.
\( x - 4y - 6 = 0 \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m = -\dfrac{1}{-4} = \dfrac{1}{4} \)
(c) seçeneği:
\( \dfrac{5x - 4y}{3} = -1 \)
Denklemi düzenleyelim.
\( 5x - 4y = -3 \)
\( 5x - 4y + 3 = 0 \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m = -\dfrac{5}{-4} = \dfrac{5}{4} \)
\( A(-2, 4) \) ve \( B(a, 2) \) noktalarından geçen doğrunun eğimi \( \frac{2}{7} \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{2}{7} = \dfrac{2 - 4}{a - (-2)} = \dfrac{-2}{a + 2} \)
İçler - dışlar çarpımı yapalım.
\( 2a + 4 = -14 \)
\( a = -9 \) bulunur.
Analitik düzlemde \( A(2p, 7p - 2) \) ve \( B(4, 4p + 4) \) noktalarından geçen doğrunun eğimi kaçtır?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{4p + 4 - (7p - 2)}{4 - 2p} \)
\( = \dfrac{6 - 3p}{4 - 2p} = \dfrac{3(2 - p)}{2(2 - p)} \)
\( = \dfrac{3}{2} \) bulunur.

Şekildeki \( d_1 \), \( d_2 \) ve \( d_3 \) doğrularının eğimlerinin toplamı kaçtır?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( d_1 \) doğrusu \( (0, 7) \) ve \( (3, 0) \) noktalarından geçmektedir.
\( m_1 = \dfrac{0 - 7}{3 - 0} = -\dfrac{7}{3} \)
\( d_2 \) doğrusu \( (-3, 0) \) ve \( (0, 4) \) noktalarından geçmektedir.
\( m_2 = \dfrac{4 - 0}{0 - (-3)} = \dfrac{4}{3} \)
\( d_3 \) doğrusu \( (0, -5) \) ve \( (6, 0) \) noktalarından geçmektedir.
\( m_3 = \dfrac{0 - (-5)}{6 - 0} = \dfrac{5}{6} \)
Eğimlerin toplamını bulalım.
\( m_1 + m_2 + m_3 = -\dfrac{7}{3} + \dfrac{4}{3} + \dfrac{5}{6} \)
\( = -\dfrac{1}{6} \) bulunur.
Eğim Açısı ve Değeri
Bir doğrunun eğim açısı, doğrunun \( x \) ekseni ile pozitif yönde yaptığı açıdır ve doğrunun eğimi bu eğim açısının tanjant değerine eşittir. Aşağıdaki grafikte bazı doğruların eğim açıları verilmiştir.

Bu doğruların eğim açıları doğrultusunda eğim değerleri aşağıdaki gibi olur.
\( d_1 \) doğrusunun eğim açısı \( 45° \)'dir.
\( m_1 = \tan{45°} = 1 \)
\( d_2 \) doğrusunun eğim açısı \( 135° \)'dir.
\( m_2 = \tan{135°} = -1 \)
\( d_3 \) doğrusunun eğim açısı \( 0° \)'dır.
\( m_3 = \tan{0°} = 0 \)
\( d_4 \) doğrusunun eğim açısı \( 90° \)'dir.
\( m_4 = \tan{90°} \Longrightarrow \) Tanımsız
Görülebileceği gibi, \( y \) eksenine göre sağa yatık (eğim açısı dar açı) olan doğruların eğimi pozitif, sola yatık (eğim açısı geniş açı) olan doğruların eğimi negatiftir.
Eğim açısı \( [0°, 180°) \) aralığında değer alabilir. Eğimin alabileceği değerler ise tanjant fonksiyonu ile aynı şekilde tüm reel sayılardır.
\( 0° \le \alpha \lt 180° \)
\( -\infty \lt m \lt \infty \)
Farklı eğim açısı aralıkları için eğim değer aralıkları aşağıdaki gibi olur.
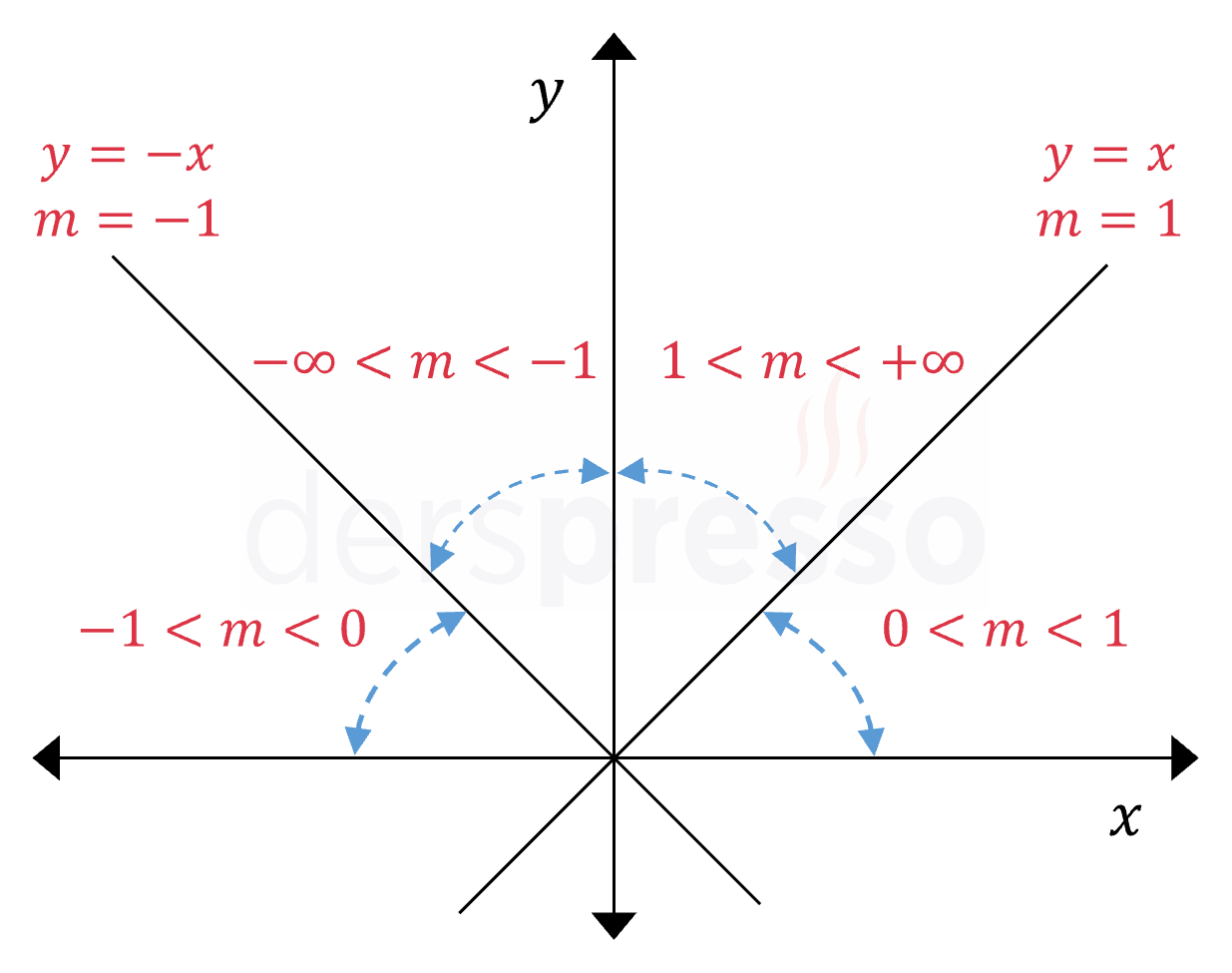
\( \tan{90°} \) tanımsız olduğu için \( \alpha = 90° \) için eğim tanımsızdır. Bu aynı zamanda, eğim açısının \( 90° \) olduğu dikey doğrular için \( x \) değişkenindeki birim artış için \( y \) değişkenindeki değişimin tanımsız olduğuna işaret eder.
Aşağıdaki nokta ikililerinden geçen doğruların eğim açılarının ölçüsü kaç derecedir?
(a) \( A(3, -1), B(-4, 6) \)
(b) \( A(\sqrt{3}, 3), B(0, 2) \)
(c) \( A(-2, -3), B(5, -3) \)
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
Bir doğrunun eğimi aynı zamanda doğrunun eğim açısının (\( \alpha \)) tanjant değerine eşittir.
\( m = \tan{\alpha} \)
(a) seçeneği:
\( A(3, -1), B(-4, 6) \)
\( m = \dfrac{6 - (-1)}{-4 - 3} = -1 \)
\( [0°, 180°) \) aralığında \( \tan{135°} = -1 \) olduğu için doğrunun eğim açısının ölçüsü \( 135° \) olur.
(b) seçeneği:
\( A(\sqrt{3}, 3), B(0, 2) \)
\( m = \dfrac{2 - 3}{0 - \sqrt{3}} = \dfrac{1}{\sqrt{3}} \)
\( [0°, 180°) \) aralığında \( \tan{30°} = \frac{1}{\sqrt{3}} \) olduğu için doğrunun eğim açısının ölçüsü \( 30° \) olur.
(c) seçeneği:
\( A(-2, -3), B(5, -3) \)
\( m = \dfrac{-3 - (-3)}{5 - (-2)} = 0 \)
\( [0°, 180°) \) aralığında \( \tan{0°} = 0 \) olduğu için doğrunun eğim açısının ölçüsü \( 0° \) olur.
Aşağıdaki doğruların eğimlerini bulunuz.
(a) \( y - 5 = 0 \)
(b) \( x + 4 = 0 \)
(c) \( x = 2y \)
Çözümü Göster(a) seçeneği:
\( y - 5 = 0 \)
\( y = 5 = 0x + 5 \)
Bu doğru \( x \) eksenine paralel (yatay) bir doğrudur ve eğim açısı 0°'dir.
Yatay doğruların ordinatı doğru boyunca sabit olduğu için eğimleri sıfırdır.
\( m = \tan{0°} = 0 \)
(b) seçeneği:
\( x + 4 = 0 \)
\( x = -4 \)
Bu doğru \( y \) eksenine paralel (dikey) bir doğrudur ve eğim açısı 90°'dir.
Yatay doğruların apsisi doğru boyunca sabit olduğu için eğimleri tanımsızdır.
\( m = \tan{90°} \): Tanımsız
(c) seçeneği:
\( x = 2y \)
\( y = \dfrac{1}{2}x \)
\( y = mx + c \) şeklinde açık denklemi verilen bir doğrunun eğimi \( m \) olur.
\( m = \dfrac{1}{2} \)
\( A(4, -1) \) ve \( B(-1, a) \) noktalarından geçen doğru \( x \) ekseni ile pozitif yönde 135°'lik açı yaptığına göre, \( a \) kaçtır?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1 }{x_2 - x_1} \)
\( = \dfrac{a - (-1)}{-1 - 4} = \dfrac{a + 1}{-5} \)
Bir doğrunun eğimi aynı zamanda doğrunun eğim açısının tanjant değerine eşittir.
Doğru \( x \) ekseni ile pozitif yönde 135°'lik açı yapıyorsa eğim açısı 135° olur.
\( m = \tan{135°} \)
\( \dfrac{a + 1}{-5} = -1 \)
\( a = 4 \) bulunur.
\( \dfrac{n+3}{\sqrt{3}}y - (\sqrt{3} + 1)x + 11 = 0 \) doğrusunun eğim açısı 30° olduğuna göre, \( n \) kaçtır?
Çözümü GösterBir doğrunun eğimi aynı zamanda doğrunun eğim açısının tanjant değerine eşittir.
\( m = \tan{30°} = \dfrac{\sqrt{3}}{3} \)
Denklemi \( ax + by + c = 0 \) formunda olan bir doğrunun eğimi aşağıdaki formülle bulunur.
\( m = -\dfrac{a}{b} \)
Verilen doğru denklemindeki katsayıları kullanarak eğim formülünü yazalım ve \( \frac{\sqrt{3}}{3} \) değerine eşitleyelim.
\( -\dfrac{-(\sqrt{3} + 1)}{\frac{n + 3}{\sqrt{3}}} = \dfrac{\sqrt{3}}{3} \)
\( \dfrac{\sqrt{3}(\sqrt{3} + 1)}{n + 3} = \dfrac{\sqrt{3}}{3} \)
\( \dfrac{\sqrt{3} + 1}{n + 3} = \dfrac{1}{3} \)
İçler - dışlar çarpımı yapalım.
\( 3\sqrt{3} + 3 = n + 3 \)
\( n = 3\sqrt{3} \) bulunur.
\( A(0, 9) \) noktasından geçen ve eğim açısı 60° olan doğrunun \( x \) eksenini kestiği noktanın apsisi kaçtır?
Çözümü GösterDoğrunun \( x \) eksenini kestiği noktaya \( B \) diyelim.

Doğrunun eğim açısı 60°'dir.
\( m(\widehat{ABO}) = 60° \)
\( ABO \) üçgeni 30-60-90° özel üçgenidir.
30-60-90° özel üçgeninde 60° açının gördüğü kenarın uzunluğu 30° açının gördüğü kenarın uzunluğunun \( \sqrt{3} \) katıdır.
\( \abs{AO} = 9 \)
\( \abs{BO} = \dfrac{9}{\sqrt{3}} = 3\sqrt{3} \)
Buna göre \( B \) noktasının koordinatları \( B(-3\sqrt{3}, 0) \) ve apsisi \( -3\sqrt{3} \) olarak bulunur.
\( 2x - 2y + 3 = 0 \) ve \( \sqrt{3}x + y + 2 = 0 \) doğrularının eğim açıları toplamı kaç derecedir?
Çözümü GösterBir doğrunun açık denkleminde \( x \)'in katsayısı doğrunun eğimini verir.
Birinci doğrunun eğim değerine \( m_1 \) ve eğim açısına \( \alpha \), ikinci doğrunun eğim değerine \( m_2 \) ve eğim açısına \( \beta \) diyelim.
\( 2x - 2y + 3 = 0 \) doğrusunun açık denklemini yazalım.
\( y = x + \dfrac{3}{2} \)
\( m_1 = 1 \)
\( [0°, 180°) \) aralığında tanjant değeri \( 1 \) olan açı \( 45° \)'dir.
\( \alpha = 45° \)
\( \sqrt{3}x + y + 2 = 0 \) doğrusunun açık denklemini yazalım.
\( y = -\sqrt{3}x - 2 \)
\( m_2 = -\sqrt{3} \)
\( [0°, 180°) \) aralığında tanjant değeri \( -\sqrt{3} \) olan açı \( 120° \)'dir.
\( \beta = 120° \)
Doğruların eğim açılarının toplamını bulalım.
\( \alpha + \beta = 45° + 120° = 165° \) bulunur.
Analitik düzlemdeki \( (2a, -8) \) ve \( (-3, 3a) \) noktaları, eğim açısı dar açı ve eğimi \( -a \) olan bir doğru üzerindedir.
Buna göre, \( a \) kaçtır?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( -a = \dfrac{3a - (-8)}{-3 - 2a} \)
\( 3a + 2a^2 = 3a + 8 \)
\( a^2 = 4 \)
Doğrunun eğim açısı dar açı ise \( (0°, 90°) \) aralığındadır, dolayısıyla \( -a \) olan eğim değeri pozitif, yani \( a \lt 0 \) olmalıdır.
\( a = -2 \) bulunur.
\( A(3, 3k + 1) \) ve \( B(2, 5k - 7) \) noktalarından geçen doğrunun eğim açısı geniş açı olduğuna göre, \( k \)'nın alabileceği en küçük tam sayı değeri kaçtır?
Çözümü GösterDoğrunun eğim açısı geniş açı olduğuna göre eğimi negatiftir.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{5k - 7 - (3k + 1)}{2 - 3} \lt 0 \)
\( \dfrac{2k - 8}{-1} \lt 0 \)
\( -2k + 8 \lt 0 \)
\( k \gt 4 \)
\( k \)'nın alabileceği en küçük tam sayı değeri 5'tir.
\( (2a - 12)x + (a + 5)y + 12 = 0 \) doğrusu \( x \) eksenine paralel olduğuna göre, \( y \) eksenini hangi noktada keser?
Çözümü Göster\( x \) eksenine paralel olan bir doğrunun eğimi sıfır olur.
Denklemi verilen doğrunun eğimini bulalım.
\( m = -\dfrac{2a - 12}{a + 5} \)
Eğimi sıfır yapan \( a \) değerini bulalım.
\( -\dfrac{2a - 12}{a + 5} = 0 \)
\( 2a - 12 = 0 \)
\( a = 6 \)
\( a = 6 \) değerini kullanarak doğrunun denklemini yazalım.
\( (2(6) - 12)x + (6 + 5)y + 12 = 0 \)
\( 11y + 12 = 0 \)
\( y = -\dfrac{12}{11} \)
Bu doğru \( y \) eksenini \( (0, -\frac{12}{11}) \) noktasında keser.

Yukarıdaki şekildeki \( d_1 \) ve \( d_2 \) doğruları dik kesiştiğine göre, \( \frac{m}{n} \) kaçtır?
Çözümü Göster\( d_1 \) ve \( d_2 \) doğrularının eğimlerine sırasıyla \( m_1 \) ve \( m_2 \) diyelim.
Doğruların eksenleri kestikleri noktaları kullanarak eğimlerini bulalım.
\( m_1 = \dfrac{4 - 0}{0 - m} = -\dfrac{4}{m} \)
\( m_2 = \dfrac{n - 0}{0 - (-3)} = \dfrac{n}{3} \)
\( d_1 \) ve \( d_2 \) doğruları dik kesiştiğine göre eğimleri çarpımı -1 olur.
\( m_1m_2 = -1 \)
\( -\dfrac{4}{m} \cdot \dfrac{n}{3} = -1 \)
\( \dfrac{n}{m} = \dfrac{3}{4} \)
\( \dfrac{m}{n} = \dfrac{4}{3} \) bulunur.
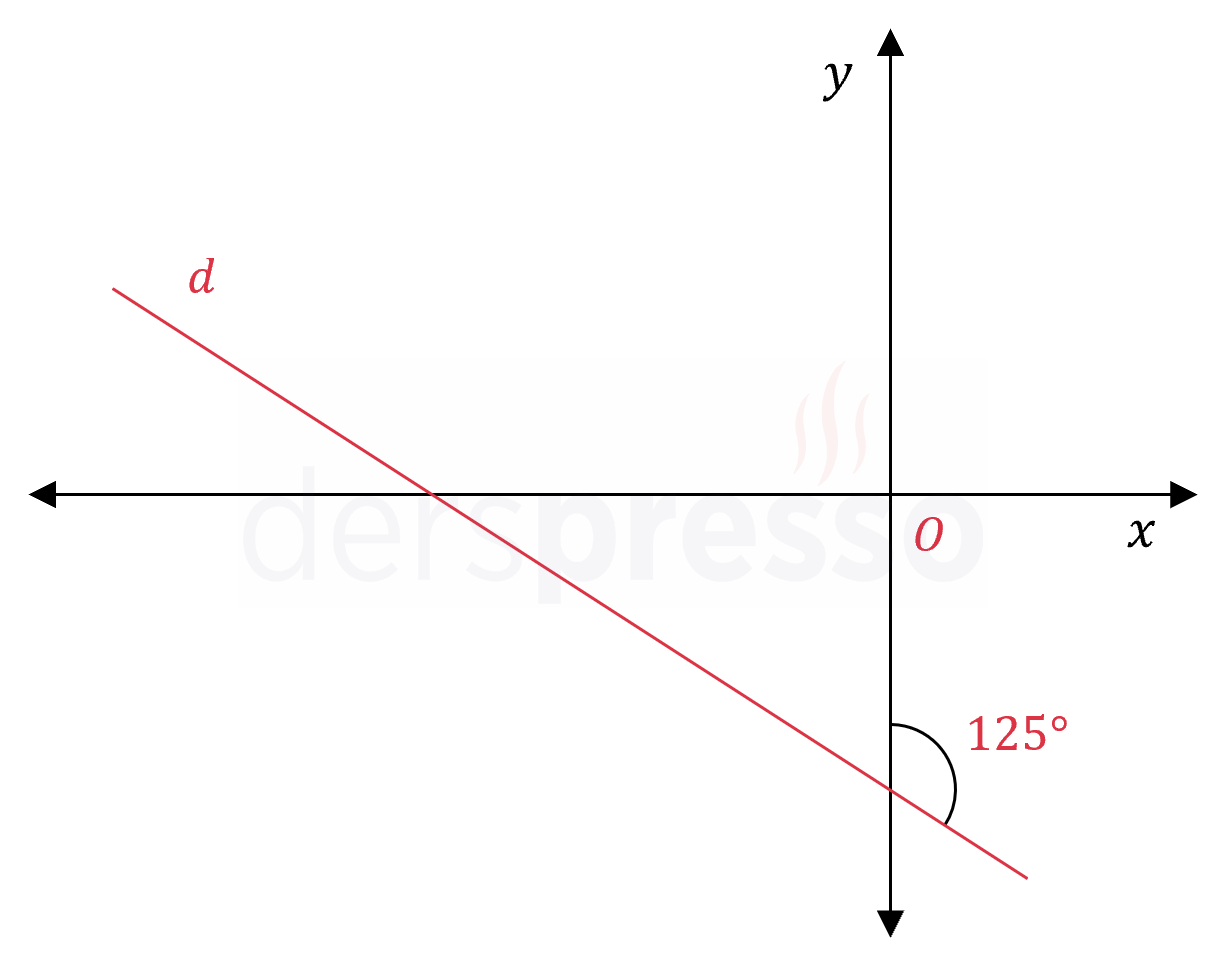
Yukarıdaki şekildeki \( d \) doğrusunun eğim açısı kaçtır?
Çözümü GösterBir doğrunun eğim açısı, doğrunun \( x \) ekseni ile pozitif yönde yaptığı açıdır.
Aşağıdaki şekle göre \( d \) doğrusunun \( x \) ekseni ile yaptığı pozitif yönlü açı 145° olur.
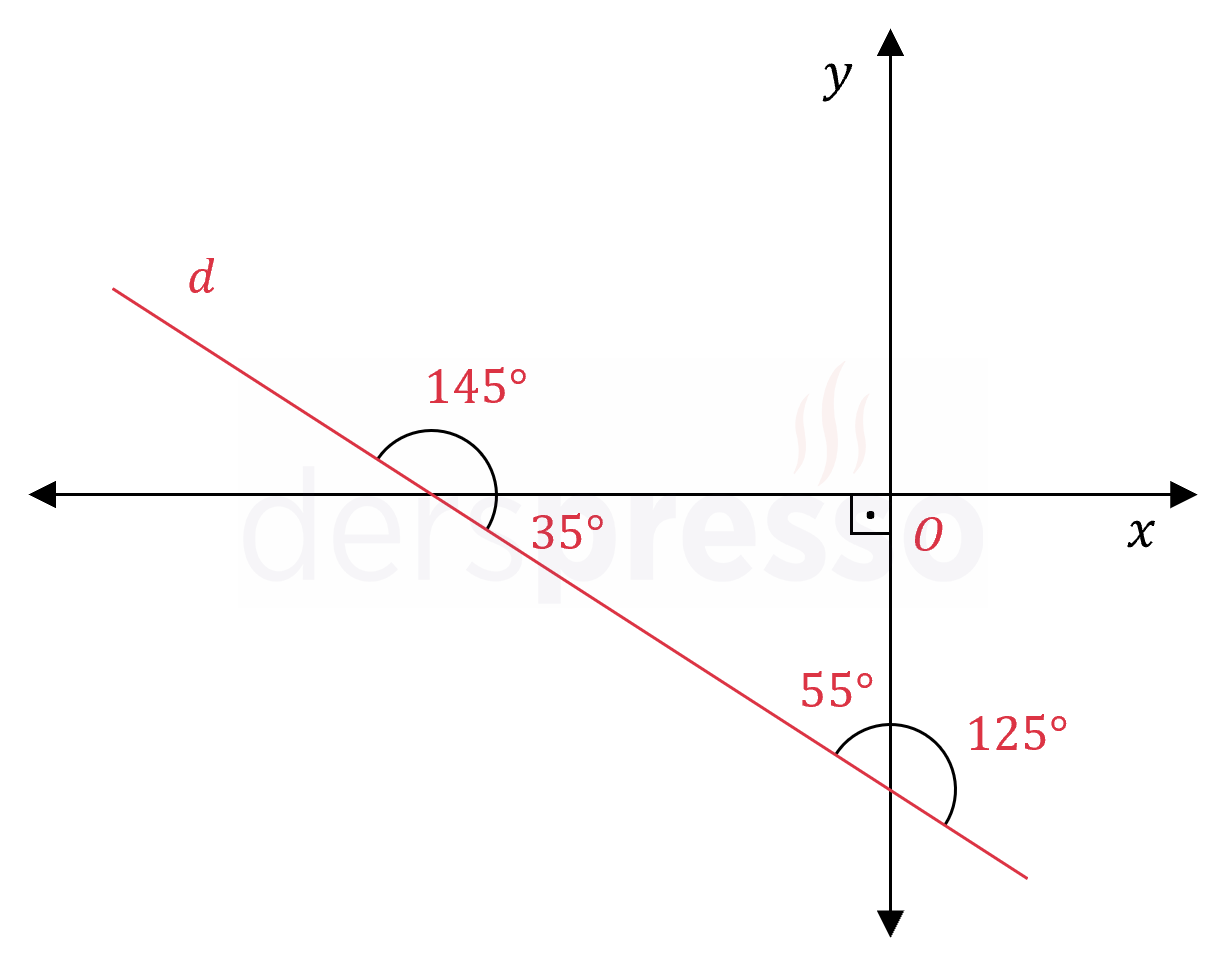
\( d \) doğrusunun eğim açısı 145° olarak bulunur.
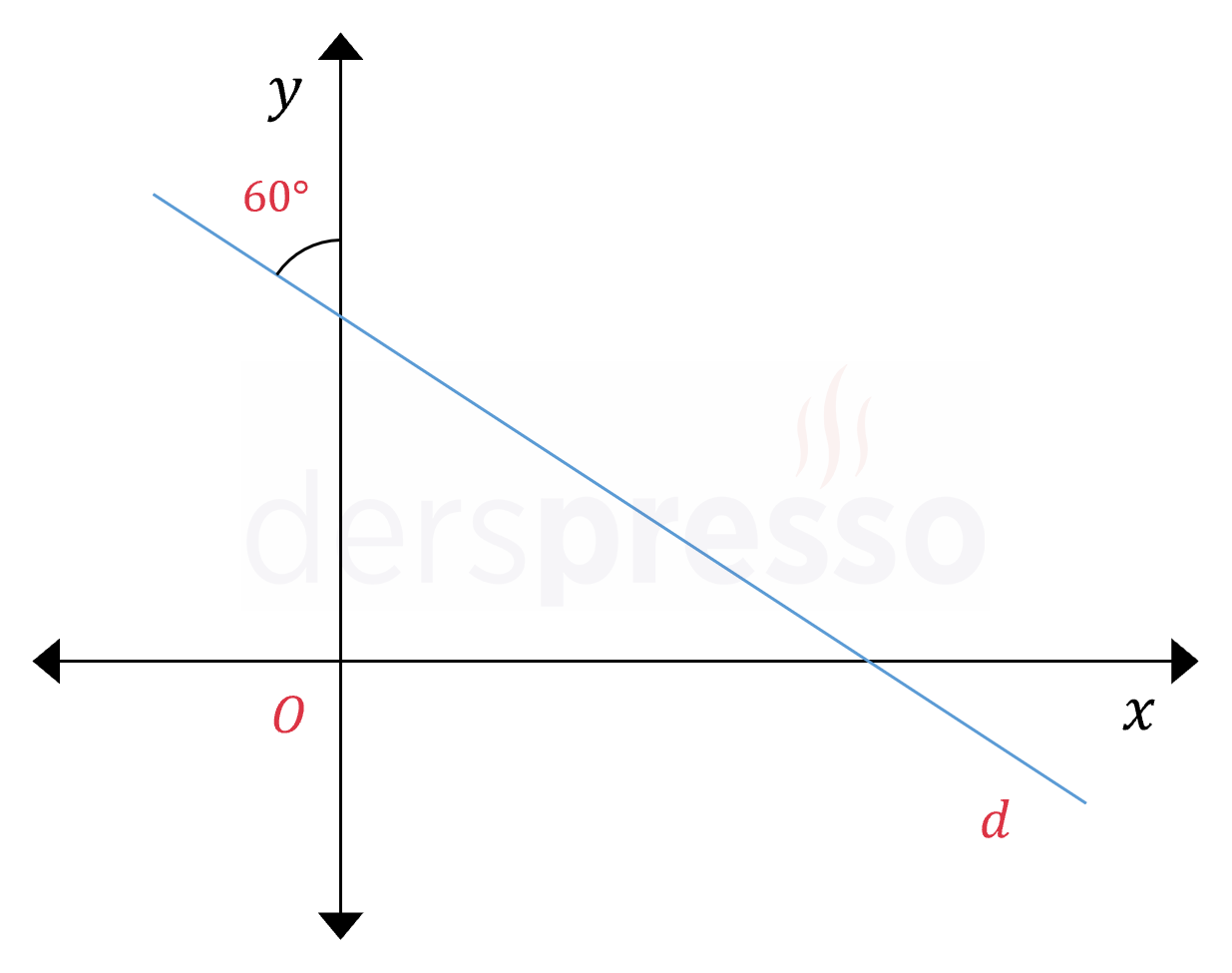
Şekildeki \( d \) doğrusunun eğimi kaçtır?
Çözümü GösterBir doğrunun eğimi o doğrunun \( x \) ekseni ile yaptığı pozitif yönlü açının tanjant değerine eşittir.
Aşağıdaki şekle göre \( d \) doğrusunun \( x \) ekseni ile yaptığı pozitif yönlü açı 150° olur.
\( m = \tan{150°} = -\tan{30°} \)
\( = -\dfrac{\sqrt{3}}{3} \) bulunur.

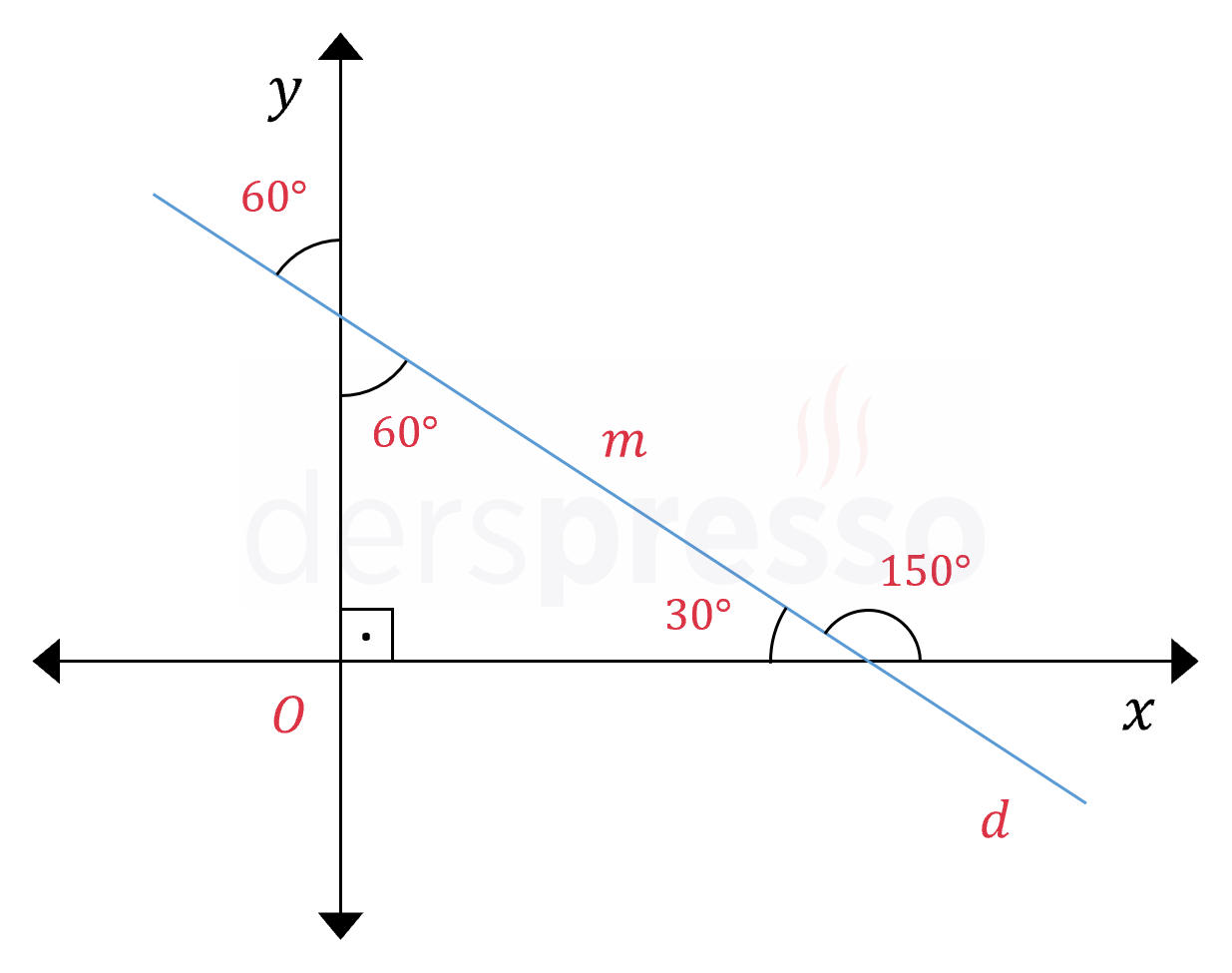
Yukarıdaki şekildeki \( d_1, d_2, d_3 \) doğrularının eğimleri sırasıyla \( m_1, m_2, m_3 \) olarak veriliyor.
Buna göre bu doğruların eğimlerini küçükten büyüğe doğru sıralayınız.
Çözümü GösterYöntem 1:
Eğim açısı dar açı olan (sağa yatık) doğruların eğimi pozitif, geniş açı olan (sola yatık) doğruların eğimi negatif olur.
\( d_1 \) doğrusunun eğim açısı geniş açı olduğu için eğimi negatiftir.
\( d_2 \) ve \( d_3 \) doğrularının eğim açıları dar açı olduğu için eğimleri pozitiftir.
Bir doğrunun eğimi doğrunun eğim açısının tanjant değerine eşittir.
\( d_2 \) doğrusunun eğim açısı \( d_3 \) doğrusundan daha büyük olduğu için tanjant değeri, dolayısıyla eğimi daha büyüktür.
Buna göre doğruların eğimlerinin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( m_1 \lt m_3 \lt m_2 \)
Yöntem 2:
Alternatif olarak, \( d_2 \) ve \( d_3 \) doğrularının eğimlerini eğim formülünü kullanarak bulalım.
\( d_2 \) ve \( d_3 \) doğrularını kesen \( y = 3 \) doğrusu çizelim ve doğruların bu doğruyu kestiği noktaların apsis değerlerine sırasıyla \( x_2 \) ve \( x_3 \) diyelim.
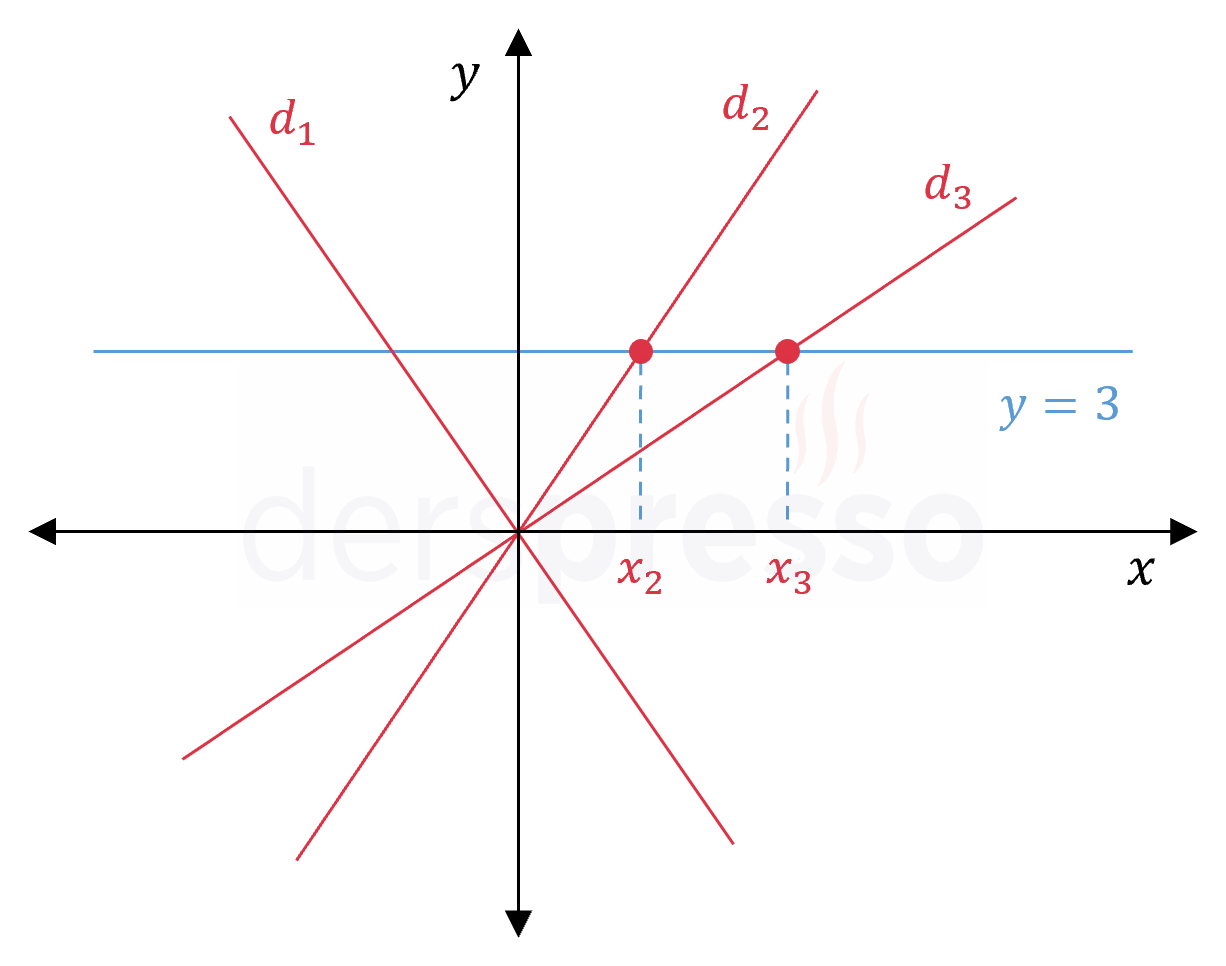
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
İki doğrunun orijin ve \( y = 3 \) doğrusunu kestikleri noktaları kullanarak eğimlerini hesaplayalım
\( m_{d_2} = \dfrac{3 - 0}{x_2 - 0} = \dfrac{3}{x_2} \)
\( m_{d_3} = \dfrac{3 - 0}{x_3 - 0} = \dfrac{3}{x_3} \)
\( 0 \lt x_2 \lt x_3 \) olduğu için \( m_3 \lt m_2 \) olur.
Buna göre doğruların eğimlerinin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( m_1 \lt m_3 \lt m_2 \)
\( d_1, d_2, d_3, d_4 \) doğrularının eğimleri sırasıyla \( m_1 = -3 \), \( m_2 = 2 \), \( m_3 = -5 \) ve \( m_4 = 4 \) olarak veriliyor.
Bu doğruların eğim açılarını küçükten büyüğe doğru sıralayınız.
Çözümü GösterVerilen doğruların eğim açılarına sırasıyla \( \alpha_1, \alpha_2, \alpha_3, \alpha_4 \) diyelim.
Verilen eğim değerlerini kullanarak göre analitik düzlemde örnek doğrular çizelim.
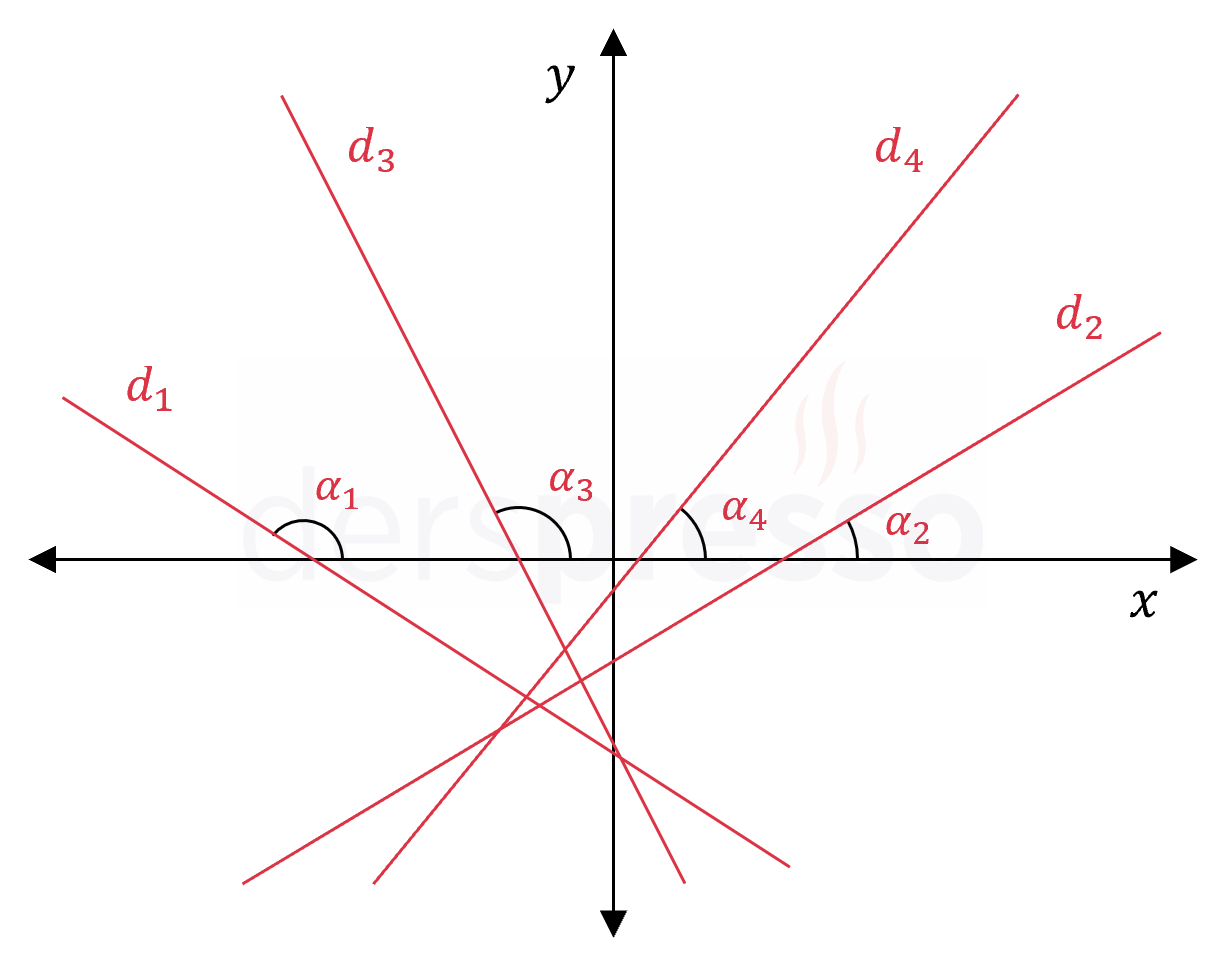
Pozitif eğime sahip doğrular \( x \) ekseni ile pozitif yönde dar açı, negatif eğime sahip doğrular \( x \) ekseni ile pozitif yönde geniş açı yapar.
Pozitif eğimli doğrularda eğim açısı arttıkça eğim değeri artar.
Negatif eğimli doğrularda eğim açısı arttıkça eğim değeri artar (mutlak değer olarak azalır).
Buna göre doğruların eğim açılarının sıralaması aşağıdaki gibi olur.
\( \alpha_2 \lt \alpha_4 \lt \alpha_3 \lt \alpha_1 \)
Eğim açısı 60° olan ve \( A(p, 3p) \) noktasından geçen doğrunun denklemi \( 2y = -mx + n \) olduğuna göre, \( \frac{mn}{p} \) oranı kaçtır?
Çözümü GösterBir doğrunun eğimi aynı zamanda doğrunun eğim açısının tanjant değerine eşittir.
\( \tan{60°} = \sqrt{3} \)
Doğrunun açık denklemini yazalım.
\( y = -\dfrac{m}{2}x + \dfrac{n}{2} \)
Bir doğrunun eğimi doğrunun açık denkleminde \( x \)'in katsayısına eşittir.
Buna göre verilen doğrunun eğimi \( m \) değil, \( -\frac{m}{2} \) değeridir.
\( y = \sqrt{3}x + \dfrac{n}{2} \)
\( m \) değerini bulalım.
\( -\dfrac{m}{2} = \sqrt{3} \)
\( m = -2\sqrt{3} \)
\( A(p, 3p) \) noktası doğrunun üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( 3p = \sqrt{3}p + \dfrac{n}{2} \)
\( 6p = 2\sqrt{3}p + n \)
\( n = (6 - 2\sqrt{3})p \)
\( \frac{mn}{p} \) oranını bulalım.
\( \dfrac{mn}{p} = \dfrac{-2\sqrt{3} \cdot (6 - 2\sqrt{3})p}{p} \)
\( = 12 - 12\sqrt{3} \) bulunur.
\( K(2, n + 12) \) ve \( L(2n, n^2) \) noktalarından geçen doğrunun eğim açısı geniş açı olduğuna göre, \( n \) doğal sayısının alabileceği değerler toplamı kaçtır?
Çözümü GösterDoğru parçasının eğim açısı geniş açı olduğuna göre eğimi negatiftir.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{n^2 - (n + 12)}{2n - 2} \)
Bu eğim değeri negatiftir.
\( \dfrac{n^2 - n - 12}{2n - 2} \lt 0 \)
\( \dfrac{(n + 3)(n - 4)}{2(n - 1)} \lt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{ -3, 1, 4 \} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -3) \), \( (-3, 1) \), \( (1, 4) \) ve \( (4, +\infty) \) aralıklarını oluşturur.
Bir işaret tablosu oluşturalım.
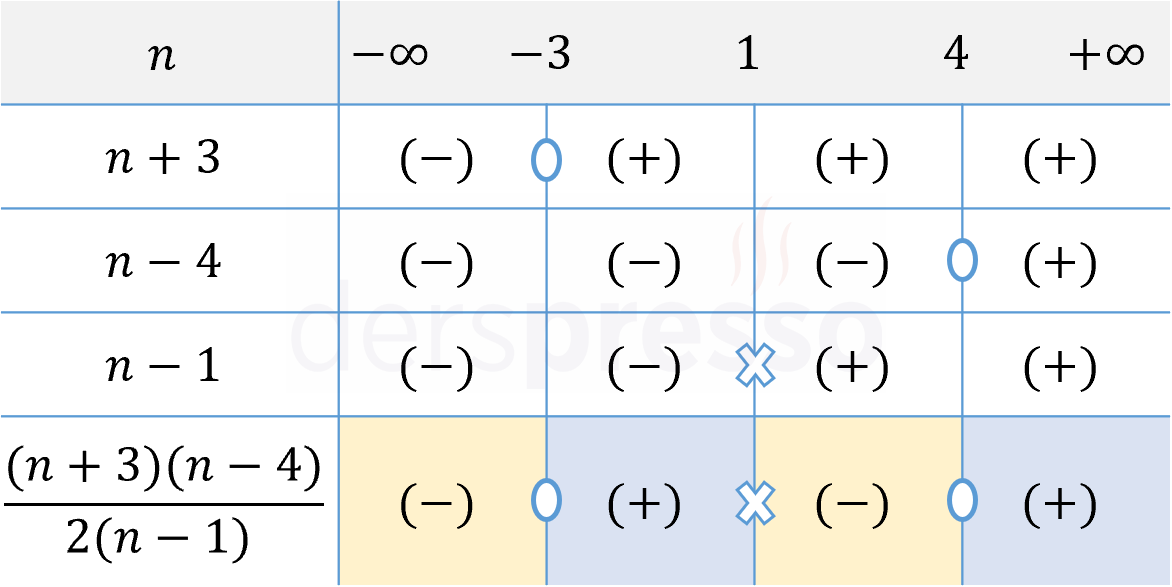
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( n = 1 \) değerinde tanımsız, payı sıfır yapan \( \{ -3, 4 \} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için rasyonel ifadenin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -3) \cup (1, 4) \)
\( n \) ifadesi doğal sayı olduğuna göre \( n \)'nin alabileceği değerler \( (1, 4) \) açık aralığındadır.
\( n \)'nin alabileceği değerlerin toplamı \( 2 + 3 = 5 \) olarak bulunur.
Analitik düzlemde \( OCDE \) bir karedir.
\( \abs{AO} = 7\sqrt{3}, \quad \abs{CO} = 4 \)
Buna göre \( d_1 \) ve \( d_2 \) doğrularının eğimleri çarpımı kaçtır?
Çözümü Göster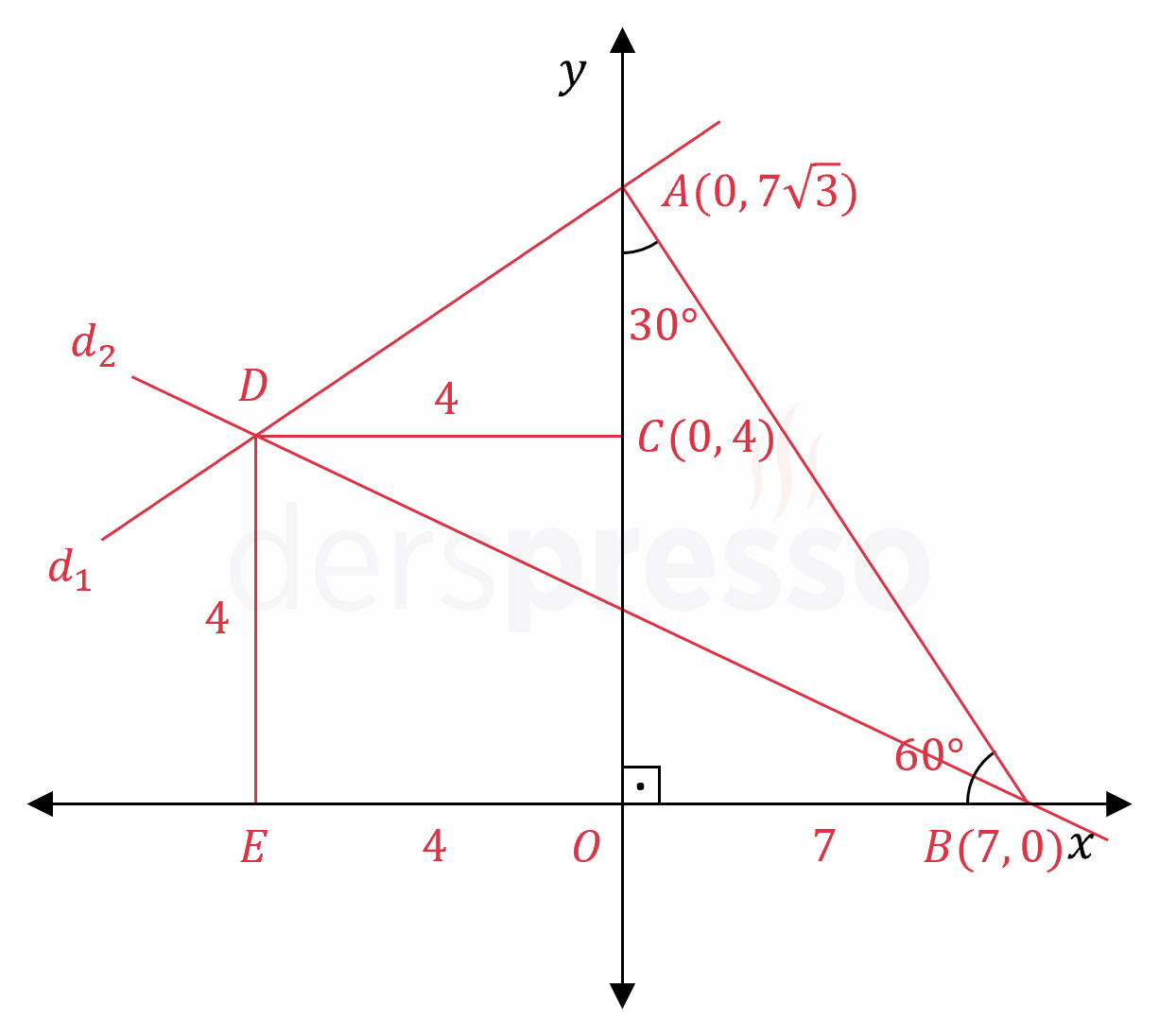
\( A(0, 7\sqrt{3}) \)
\( C(0, 4) \)
\( AOB \) bir dik üçgendir.
\( m(\widehat{ABO}) = 60° \)
30-60-90° özel üçgeninde 60°'lik açının gördüğü kenarın uzunluğu 30°'lik açının gördüğü kenarın uzunluğunun \( \sqrt{3} \) katıdır.
\( \abs{OB} = 7 \)
\( B(7, 0) \)
\( OCDE \) bir karedir.
\( \abs{OC} = \abs{OE} = 4 \)
\( D(-4, 4) \)
Karenin \( D \) köşesinden geçen \( d_1 \) ve \( d_2 \) doğrularının eğimlerini iki noktası bilinen doğrunun eğimi formülü ile bulalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( d_1 \) doğrusunun eğimi için \( D \) ve \( A \) noktalarını, \( d_2 \) doğrusunun eğimi için \( D \) ve \( B \) noktalarını kullanalım.
\( d_1 \) ve \( d_2 \) doğrularının eğimlerine sırasıyla \( m_1 \) ve \( m_2 \) diyelim.
\( m_1 = \dfrac{7\sqrt{3} - 4}{0 - (-4)} \)
\( = \dfrac{7\sqrt{3} - 4}{4} \)
\( m_2 = \dfrac{0 - 4}{7 - (-4)} \)
\( = \dfrac{-4}{11} \)
İki doğrunun eğimlerinin çarpımını bulalım.
\( m_{1} \cdot m_{2} = \dfrac{7\sqrt{3} - 4}{4} \cdot \dfrac{-4}{11} \)
\( = \dfrac{4 - 7\sqrt{3}}{11} \) bulunur.
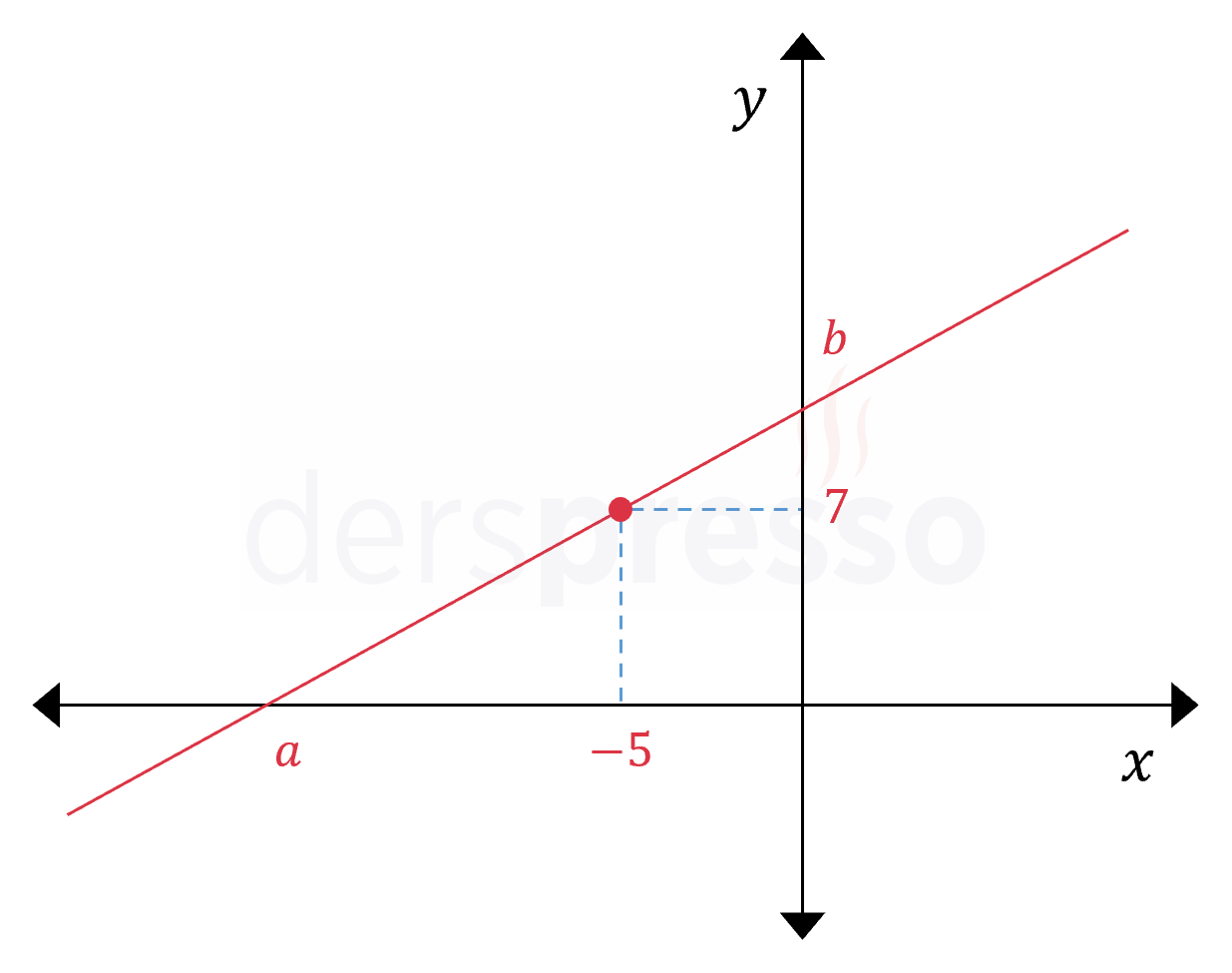
Yukarıdaki şekle göre \( (a - 5)(b - 7) \) çarpımının sonucu kaçtır?
Çözümü Göster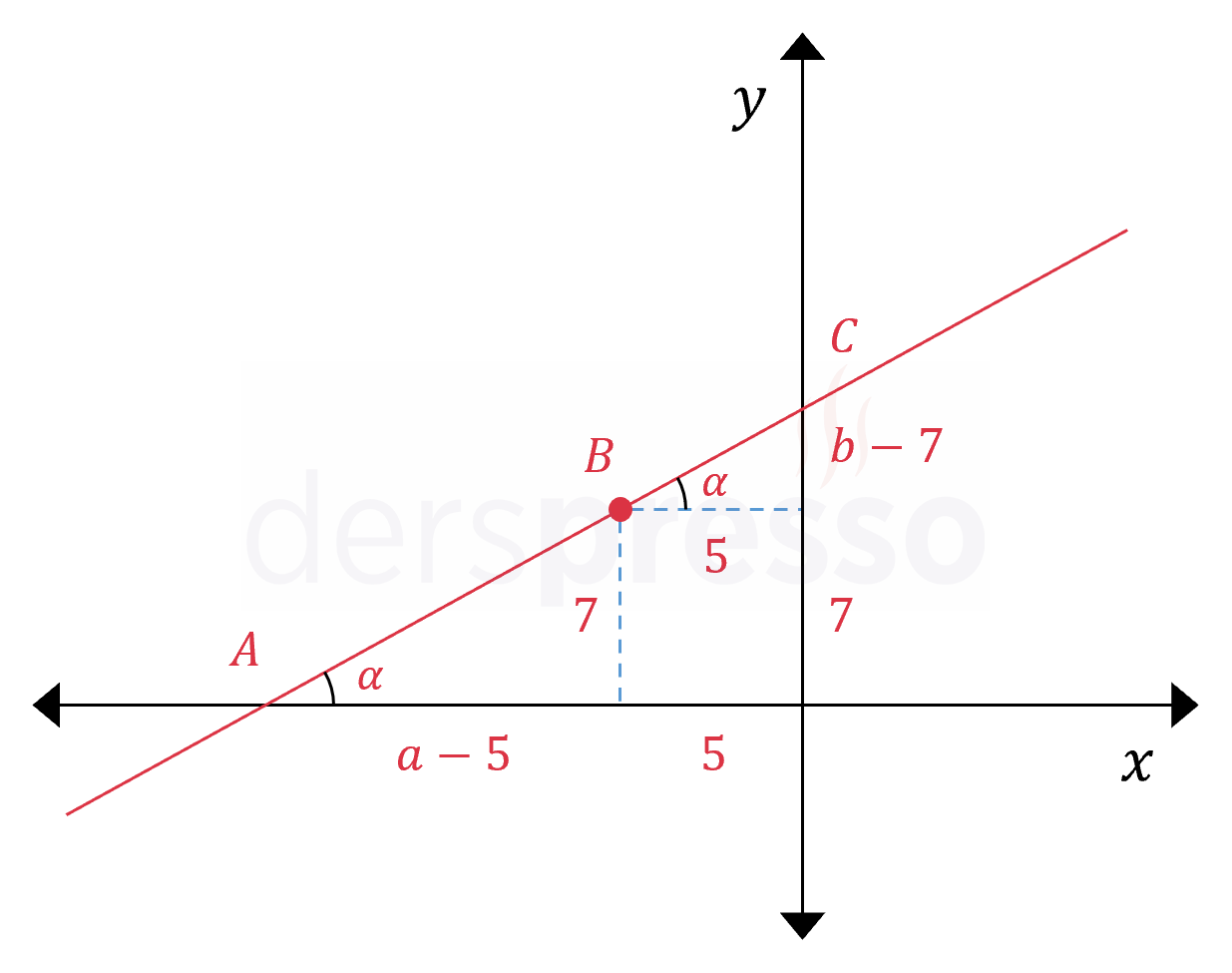
\( A \) ve \( B \) noktalarını kullanarak doğrunun eğimini hesaplayalım.
\( m_{AB} = \dfrac{7}{a - 5} \)
\( B \) ve \( C \) noktalarını kullanarak doğrunun eğimini hesaplayalım.
\( m_{BC} = \dfrac{b - 7}{5} \)
Doğrunun eğimi tüm doğru boyunca sabittir.
\( m_{AB} = m_{BC} \)
\( \dfrac{7}{a - 5} = \dfrac{b - 7}{5} \)
İçler - dışlar çarpımı yapalım.
\( (a - 5)(b - 7) = 35 \) bulunur.
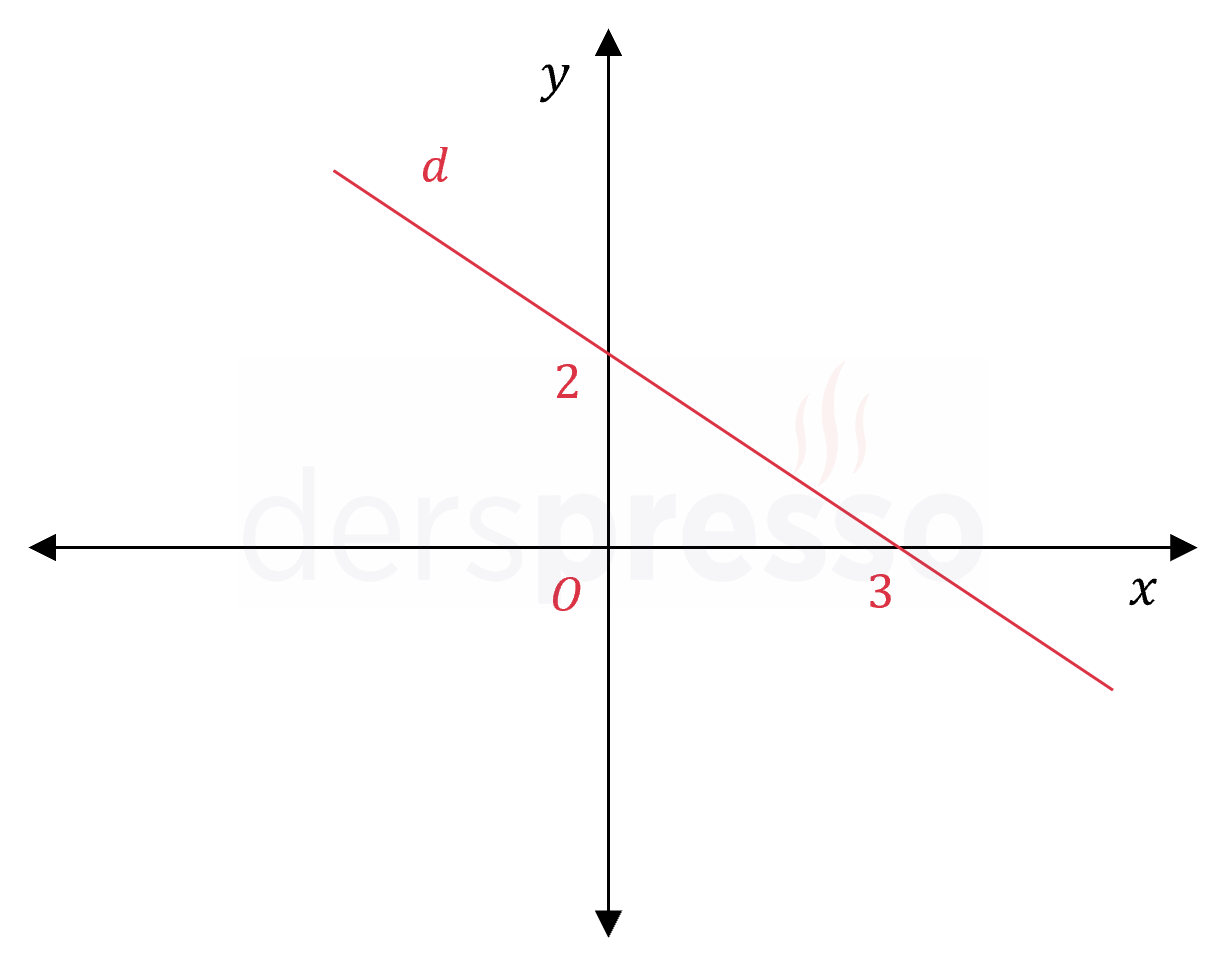
Yukarıdaki \( d \) doğrusu 9 birim sola ötelendiğinde elde edilen doğru \( y \) eksenini hangi noktada keser?
Çözümü GösterÖteleme sonrası oluşan doğruya \( d' \) diyelim.
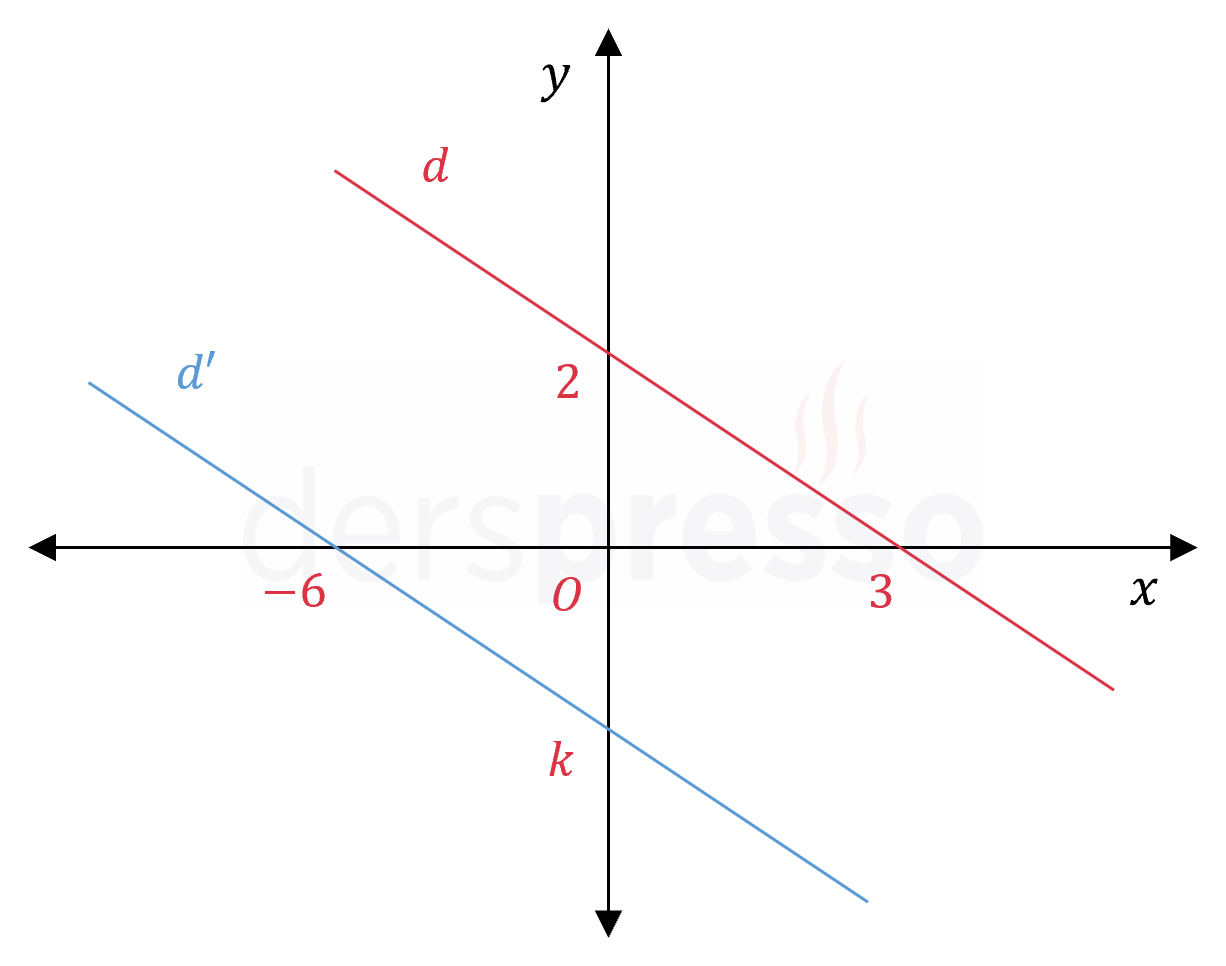
\( d \) doğrusu 9 birim sola ötelendiğinde oluşan \( d' \) doğrusu \( x \) eksenini \( 3 - 9 = -6 \) apsisli noktada keser.
\( d' \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğruların eğimini kullanalım.
Bir doğru \( x \) ya da \( y \) ekseni boyunca ötelendiğinde eğimi değişmez.
\( m_d = m_{d'} \)
\( d' \) doğrusunun \( y \) eksenini kestiği noktanın ordinat değerine \( k \) diyelim.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( m_d = \dfrac{0 - 2}{3 - 0} = -\dfrac{2}{3} \)
\( m_{d'} = \dfrac{k - 0}{0 - (-6)} = \dfrac{k}{6} \)
İki eğim birbirine eşittir.
\( -\dfrac{2}{3} = \dfrac{k}{6} \)
\( 3k = -12 \)
\( k = -4 \)
Buna göre \( d' \) doğrusu \( y \) eksenini \( (0, -4) \) noktasında keser.
\( d: 2x + y - 7 = 0 \) doğrusu 4 birim sağa ve 4 birim aşağı ötelendiğinde elde edilen doğrunun denklemi nedir?
Çözümü GösterÖteleme sonrası oluşan doğruya \( d' \) diyelim.
Bir doğru \( x \) ya da \( y \) ekseni boyunca ötelendiğinde eğimi değişmez, dolayısıyla \( d' \) doğrusunun denklemi aşağıdaki formda olur.
\( d': 2x + y + c = 0 \)
\( d \) doğrusunu sağlayan bir nokta seçelim.
\( x = 0 \) için:
\( 2(0) + y - 7 = 0 \)
\( y = 7 \)
Buna göre \( (0, 7) \) noktası \( d \) doğrusu üzerindedir.
Bir nokta 4 birim sağa ötelendiğinde apsisi 4 birim artar, 4 birim aşağı ötelendiğinde ordinatı 4 birim azalır.
\( (0, 7) \longmapsto (4, 3) \)
Bir doğru ötelendiğinde üzerindeki tüm noktalar da ötelendiği için \( (4, 3) \) noktası \( d' \) doğrusu üzerindedir ve bu doğrunun denklemini sağlar.
\( d': 2x + y + c = 0 \)
\( 2(4) + 3 + c = 0 \)
\( c = -11 \)
\( d': 2x + y - 11 = 0 \) bulunur.
\( A \) ve \( B \) noktaları II. bölgede yer alıp \( O \) noktası orijindir.
\( m_{OA} = -1, \quad m_{OB} = -3 \)
\( \abs{OA} = \abs{OB} \)
olduğuna göre, \( [AB] \) doğrusunun eğimi kaçtır?
Çözümü Göster\( a, b \in \mathbb{R^+} \) olmak üzere,
\( m_{OA} = -1 \) olduğuna göre, \( A \) noktasının koordinatlarına \( A(-a, a) \) diyebiliriz.
\( m_{OA} = \dfrac{a - 0}{-a - 0} = -1 \)
\( m_{OB} = -3 \) olduğuna göre, \( B \) noktasının koordinatlarına \( A(-b, 3b) \) diyebiliriz.
\( m_{OB} = \dfrac{3b - 0}{-b - 0} = -3 \)
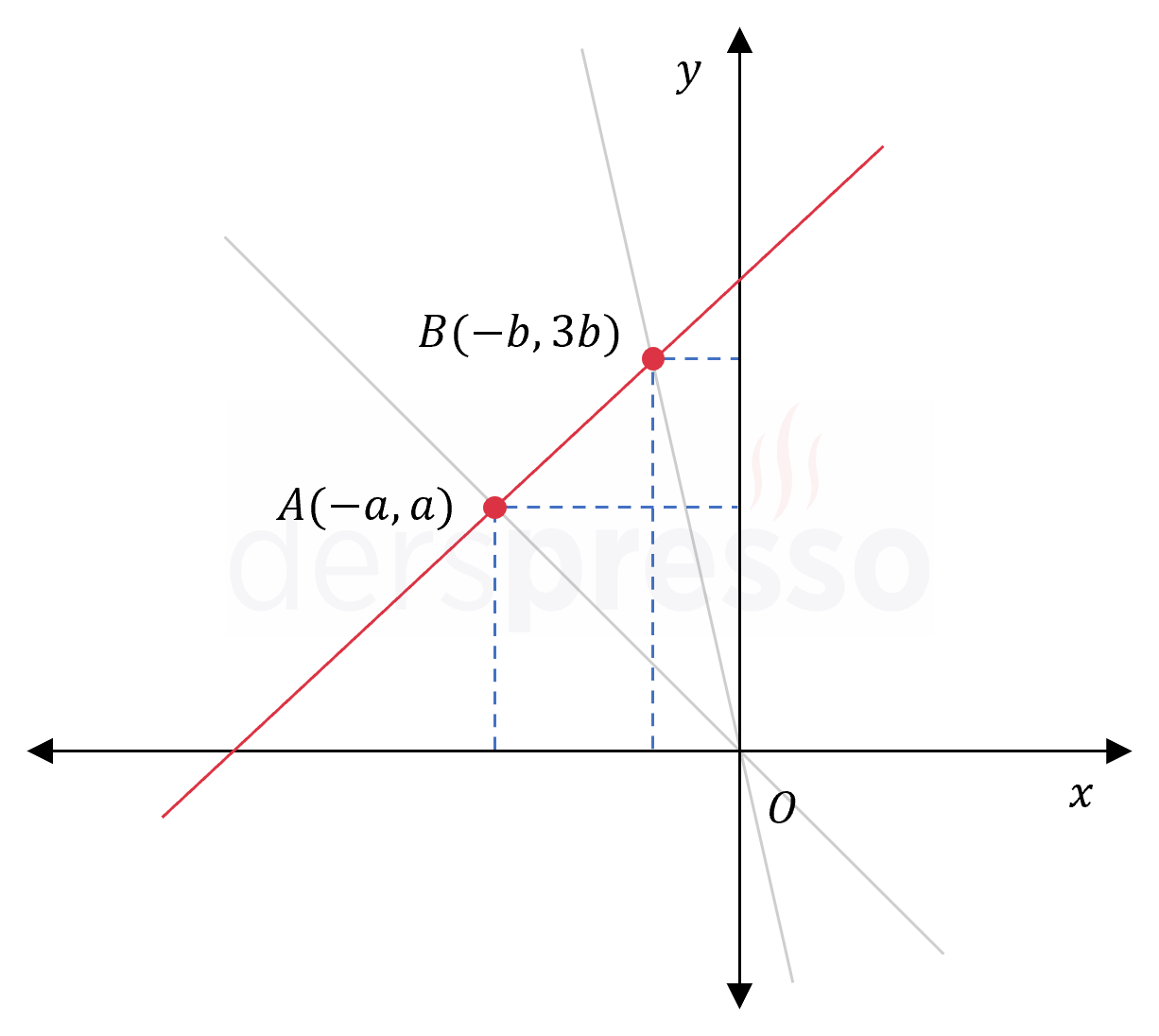
\( \abs{OA} \) ve \( \abs{OB} \) doğrularının uzunluklarını hesaplayalım.
\( \abs{OA} = \sqrt{(-a - 0)^2 + (a - 0)^2} = \sqrt{2}a \)
\( \abs{OB} = \sqrt{(-b - 0)^2 + (3b - 0)^2} = \sqrt{10}b \)
İki doğru parçasının uzunlukları birbirine eşittir.
\( \sqrt{2}a = \sqrt{10}b \)
\( a = \sqrt{5}b \)
\( A(-a, a) = A(-\sqrt{5}b , \sqrt{5}b) \)
\( B(-b, 3b) \)
Bu değerleri kullanarak \( [AB] \) doğru parçasının eğimini bulalım.
\( m_{AB} = \dfrac{3b - \sqrt{5}b}{-b - (-\sqrt{5}b)} \)
\( = \dfrac{b(3 - \sqrt{5})}{b(\sqrt{5} - 1)} \)
\(= \dfrac{3 - \sqrt{5}}{\sqrt{5} - 1} \)
Paydayı rasyonel hale getirmek için eşleniği ile çarpalım.
\(= \dfrac{(3 - \sqrt{5})(\sqrt{5} + 1)}{(\sqrt{5} - 1)(\sqrt{5} + 1)} \)
\(= \dfrac{3\sqrt{5} + 3 - 5 - \sqrt{5}}{(\sqrt{5})^2 - 1^2} \)
\(= \dfrac{\sqrt{5} - 1}{2} \) bulunur.
Eğim ve Değişim Oranı
Eğimin bir tanımı da iki nokta arasındaki dikey değişimin yatay değişime oranı, bir diğer ifadeyle \( y \) değişkenindeki değişim oranıdır. Aşağıda bunun yorumuna dönük iki örnek verilmiştir.
Ağacın Boyunun Büyüme Hızı
Aşağıdaki grafikte bir ağacın boyunun yıllara göre değişim grafiği ve denklemi verilmiştir. Buna göre ağacın \( t = 0 \) anındaki boyu 3 metredir ve doğrunun eğimi \( m = 0,5 \) olduğuna göre ağacın boyu her yıl \( 0,5 \) metre uzamaktadır.
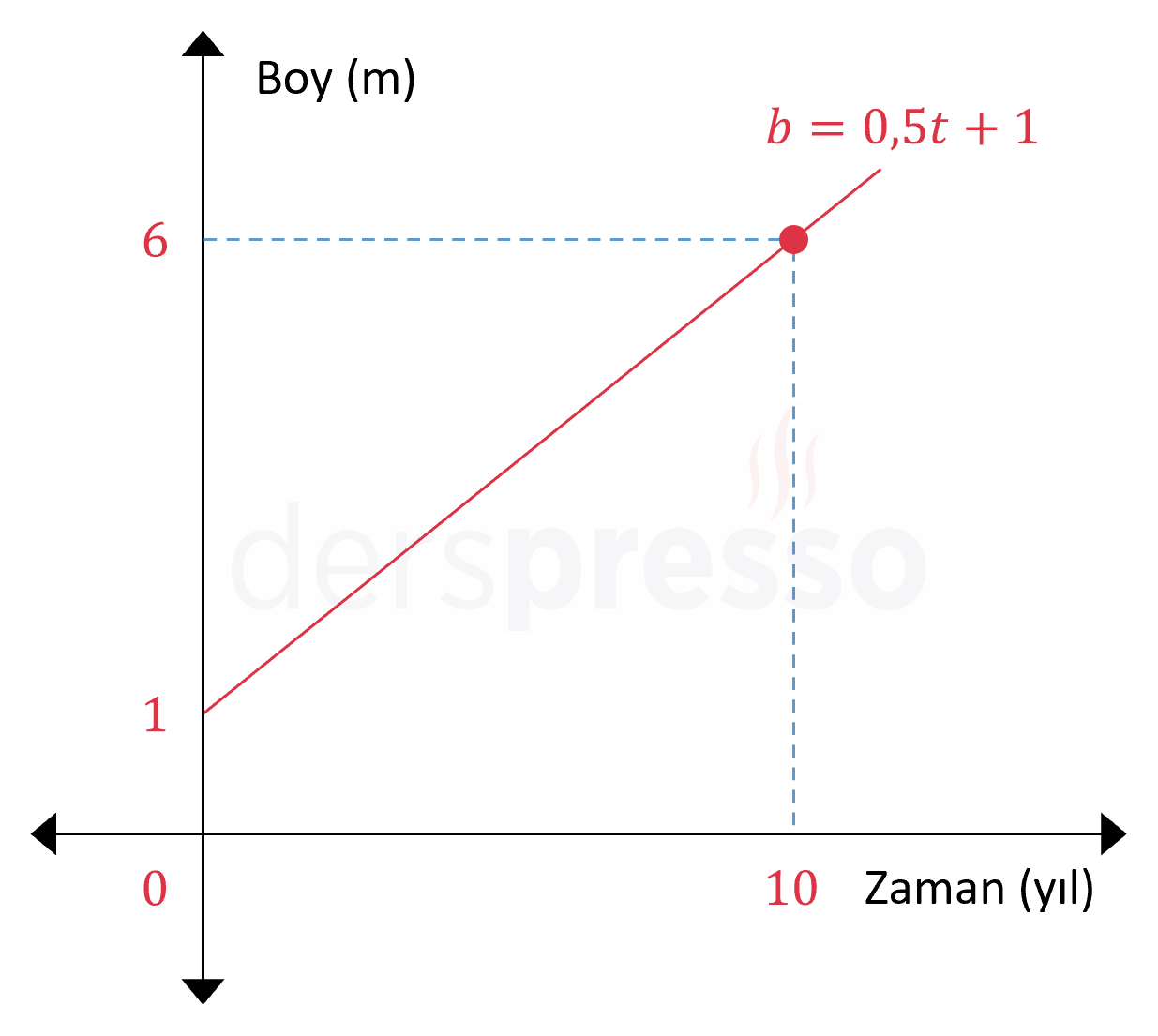
Ağacın 8. yıl sonundaki boyunu hesaplamak istiyor olalım. Ağacın boyu her yıl 0,5 metre uzadığına göre 8 yıl boyunca toplam \( 0,5 \cdot 8 = 4 \) metre uzar. Ağacın ilk boyu 3 metre olduğu için bu süre sonunda boyu 7 metre olur. Denklemde \( t = 8 \) değerini koyduğumuzda da aynı sonucu elde ederiz.
Ağacın yıllara göre boy değerleri aşağıdaki tabloda listelenmiştir. Görülebileceği gibi, ağacın her yıl boyundaki değişim miktarı sabittir ve doğrunun eğimine eşittir.
| Yıl | Boy (m) | Bir Önceki Yıla Göre Değişim |
|---|---|---|
| \( 0 \) | \( 3,0 \) | \( \) |
| \( 1 \) | \( 3,5 \) | \( 0,5 \) |
| \( 2 \) | \( 4,0 \) | \( 0,5 \) |
| \( 3 \) | \( 4,5 \) | \( 0,5 \) |
| \( 4 \) | \( 5,0 \) | \( 0,5 \) |
| \( 5 \) | \( 5,5 \) | \( 0,5 \) |
| \( 6 \) | \( 6,0 \) | \( 0,5 \) |
| \( 7 \) | \( 6,5 \) | \( 0,5 \) |
| \( 8 \) | \( 7,0 \) | \( 0,5 \) |
Aracın Hızı
Aşağıdaki grafikte ise sabit hızla giden bir aracın konum - zaman grafiği verilmiştir. Buna göre araç \( t = 0 \) anında başlangıç noktasındadır ve doğrunun eğimi \( m = 75 \) olduğuna göre araç her saatte \( 75 \) km yol almaktadır.
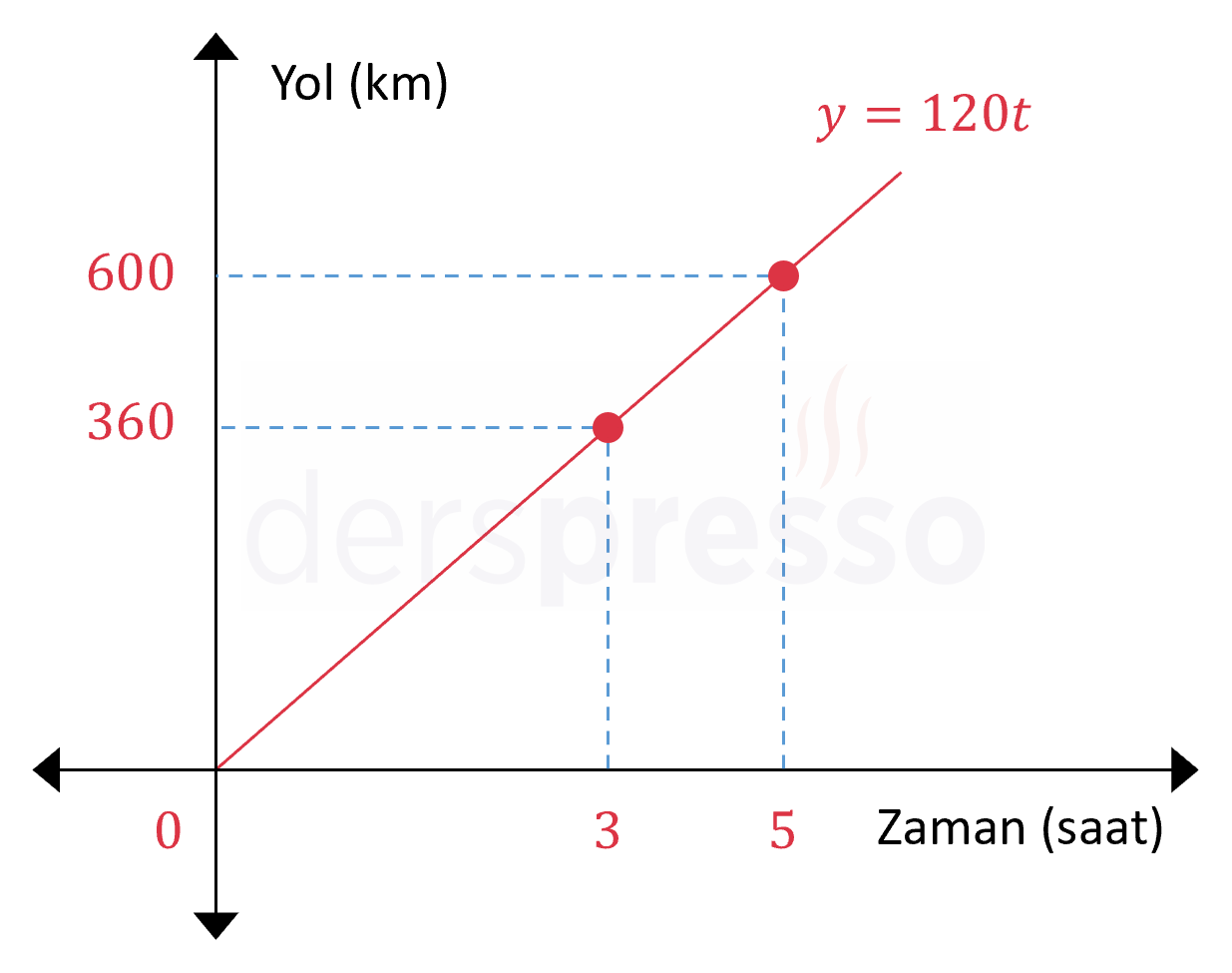
Bu eğim değerine göre araç \( t = 4 \) anında toplam \( 75 \cdot 4 = 300 \) km, \( t = 8 \) anında da toplam \( 75 \cdot 8 = 600 \) km yol almış olur.
Aracın zamana göre konumu aşağıdaki tabloda listelenmiştir. Görülebileceği gibi, aracın her saatte aldığı yol miktarı sabittir ve doğrunun eğimine (aracın sabit hızına) eşittir.
| Zaman | Konum | 1 Saatte Konumdaki Değişiklik |
|---|---|---|
| \( 0 \) | \( 0 \) | \( \) |
| \( 1 \) | \( 75 \) | \( 75 \) |
| \( 2 \) | \( 150 \) | \( 75 \) |
| \( 3 \) | \( 225 \) | \( 75 \) |
| \( 4 \) | \( 300 \) | \( 75 \) |
| \( 5 \) | \( 375 \) | \( 75 \) |
| \( 6 \) | \( 450 \) | \( 75 \) |
| \( 7 \) | \( 525 \) | \( 75 \) |
| \( 8 \) | \( 600 \) | \( 75 \) |
Özetle, bir doğrunun eğimi \( x \) ekseninin temsil ettiği değişkendeki bir birimlik artış için \( y \) ekseninin temsil ettiği değişkenin kaç birim arttığını ya da azaldığını gösterir.