İzdüşüm
Bir Noktanın Bir Doğru Üzerindeki İzdüşümü
Bir \( A \) noktasının bir doğru üzerindeki izdüşümü, o doğru üzerinde \( A \) noktasına en yakın olan noktadır. Bu nokta aynı zamanda \( A \) noktasından doğruya çizilen dikmenin doğruyu kestiği noktadır.
Aşağıdaki grafikteki \( A \) noktasının \( x \) ekseni, \( y \) ekseni ve \( d \) doğrusu üzerindeki izdüşümleri sırasıyla \( A_1 \), \( A_2 \) ve \( A_3 \) noktalarıdır.

Bir Doğru Parçasının Bir Doğru Üzerindeki İzdüşümü
Bir \( [AB] \) doğru parçasının bir doğru üzerindeki izdüşümü, \( [AB] \) üzerindeki tüm noktaların o doğru üzerindeki izdüşümlerinin oluşturduğu doğru parçasıdır. Bu izdüşüm aynı zamanda \( [AB] \)'nin uç noktalarının izdüşümlerini birleştiren doğru parçasıdır.
Aşağıdaki grafikteki \( [AB] \) doğru parçasının \( x \) ve \( y \) eksenleri üzerindeki izdüşümleri sırasıyla \( [A_1B_1] \) ve \( [A_2B_2] \) doğru parçalarıdır.
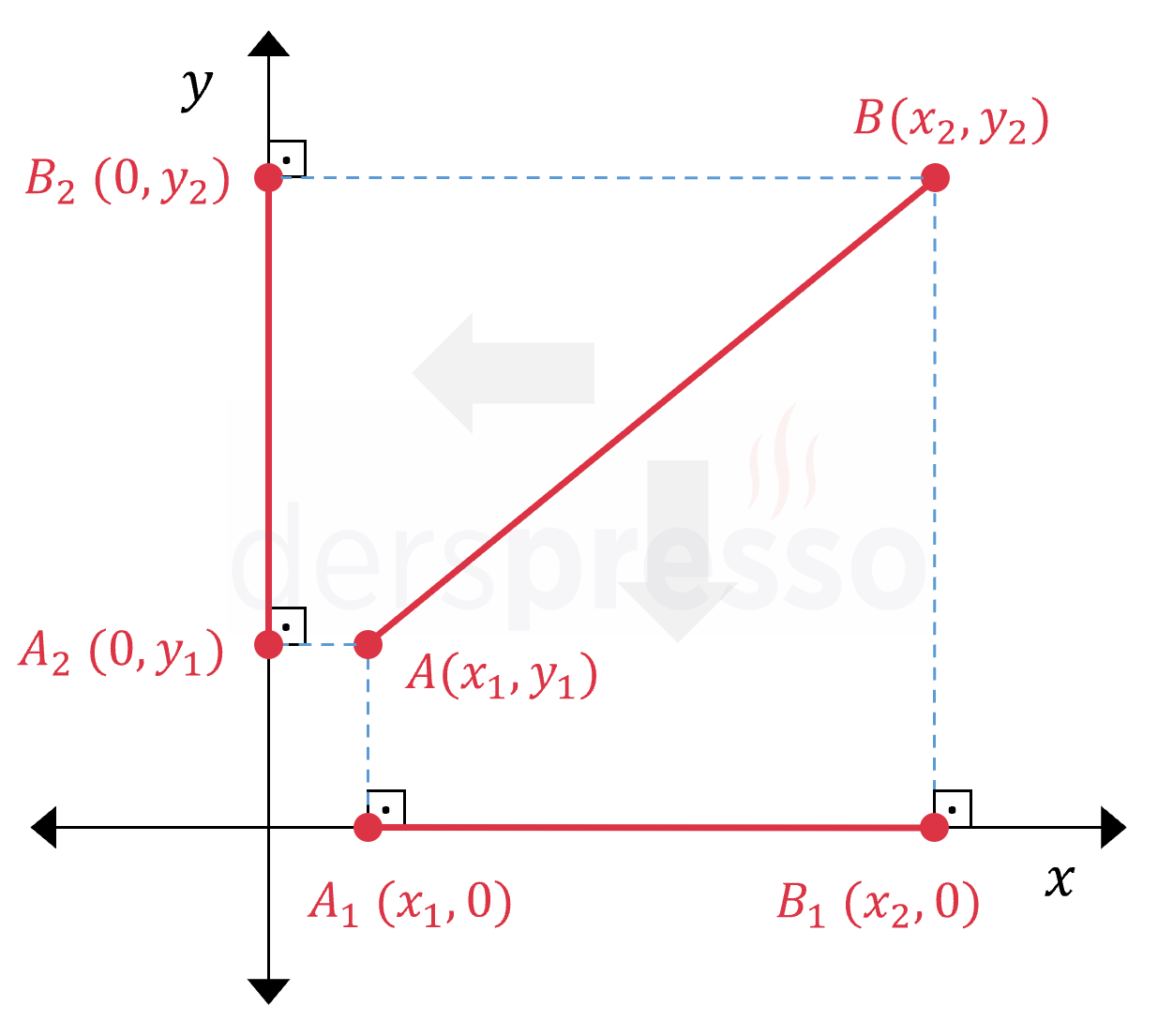
Bir doğru parçasının \( x \) ekseni üzerindeki izdüşümünün uzunluğu doğru parçasının uç noktalarının apsis değerleri arasındaki farka eşittir. Benzer şekilde, doğru parçasının \( y \) ekseni üzerindeki izdüşümünün uzunluğu doğru parçasının uç noktalarının ordinat değerleri arasındaki farka eşittir.
\( \abs{A_1B_1} = \abs{x_2 - x_1} \)
\( \abs{A_2B_2} = \abs{y_2 - y_1} \)
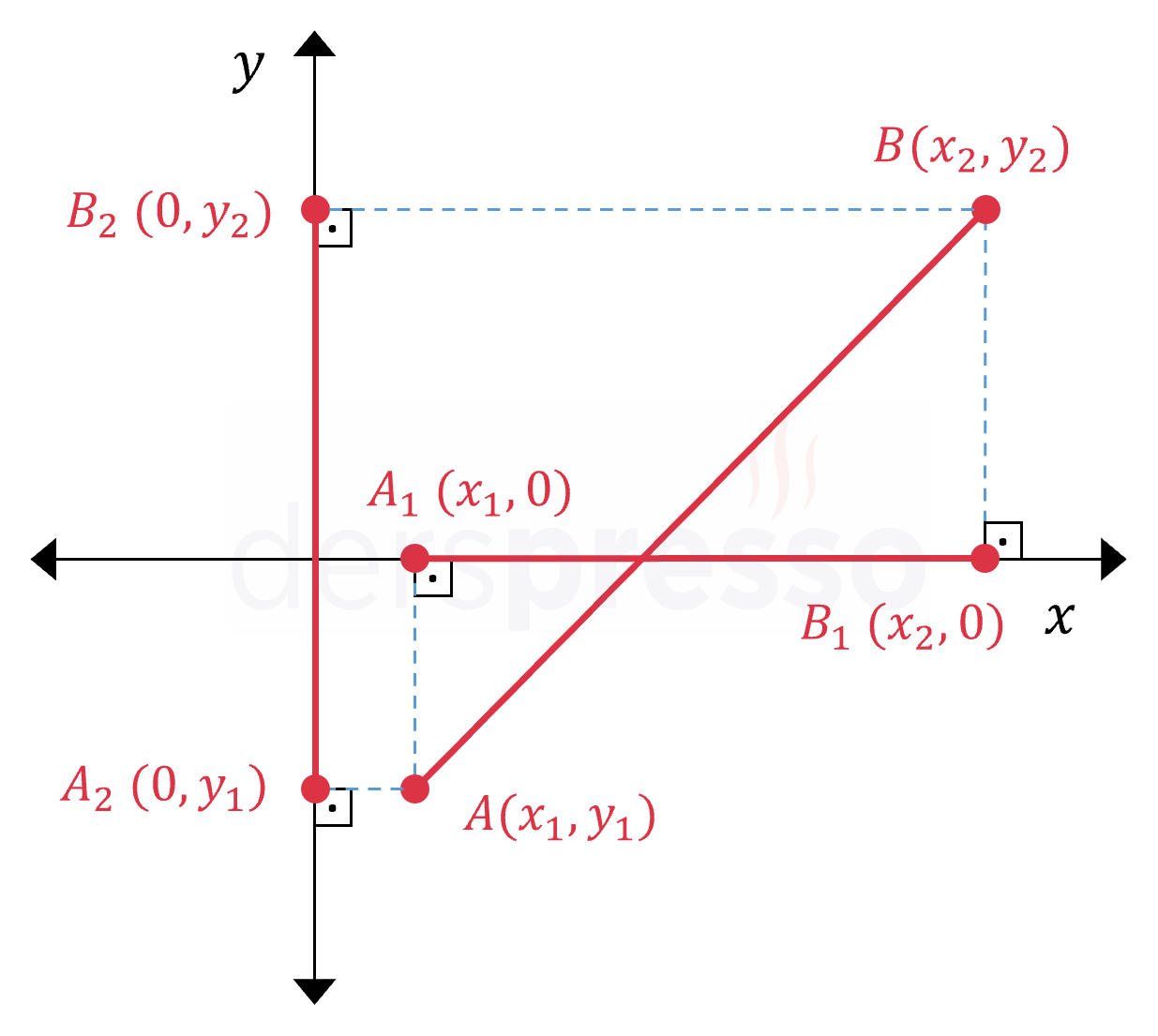
\( x \) eksenini kesen bir \( [AB] \) doğru parçasının eksenler üzerindeki izdüşümleri aşağıdaki şekilde oluşur.

Analitik düzlemde \( A(3, 6) \) ve \( B(7, 4) \) noktaları veriliyor.
Buna göre \( [AB] \) doğru parçasının \( x \) ve \( y \) eksenleri üzerindeki izdüşümlerinin uzunlukları toplamı kaçtır?
Çözümü Göster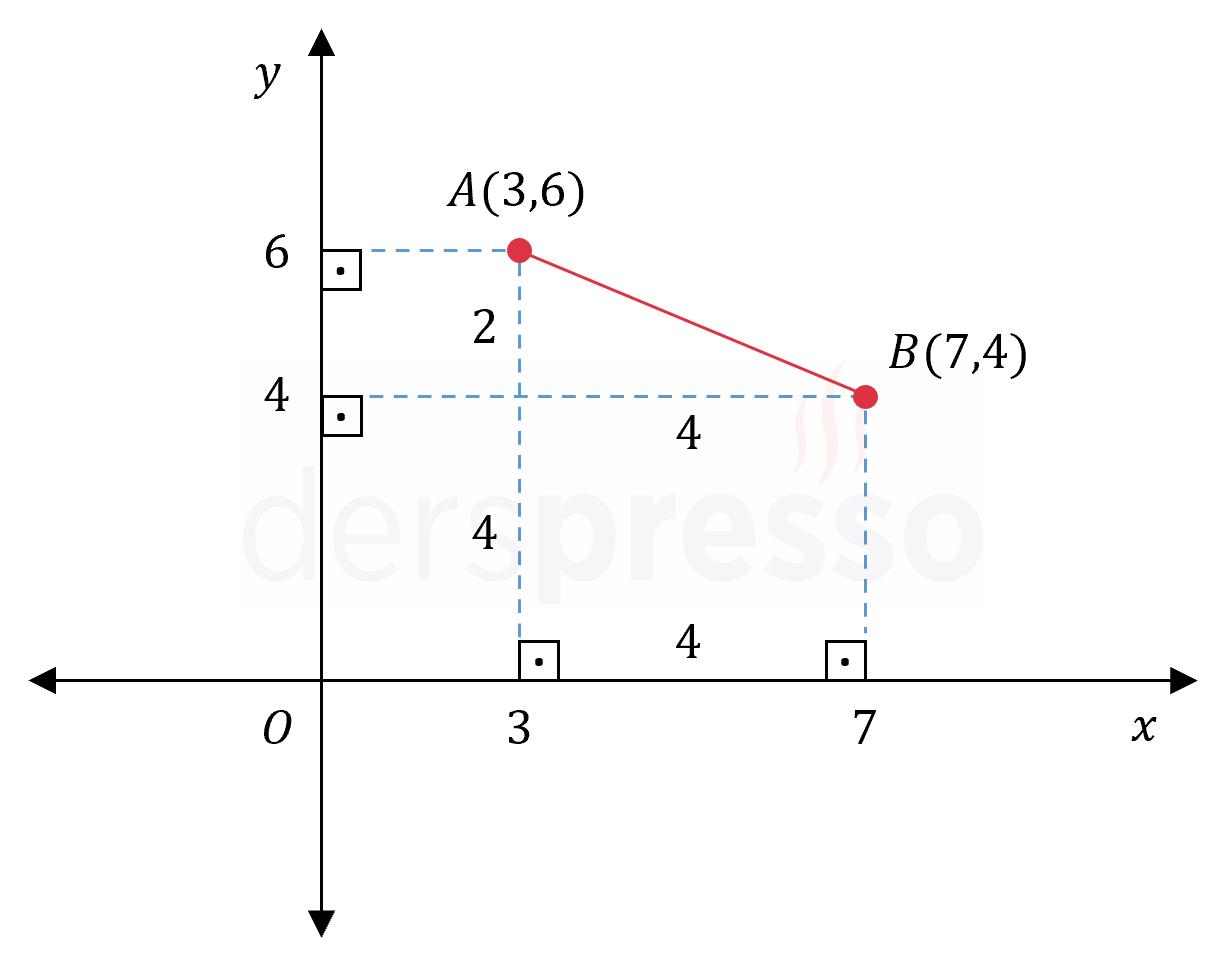
\( [AB] \) doğru parçasının \( x \) ekseni üzerindeki dik izdüşümünün uzunluğu, \( A \) ve \( B \) noktalarının apsisleri farkının mutlak değerine eşittir.
\( \abs{x_2 - x_1} = \abs{7 - 3} = 4 \)
\( [AB] \) doğru parçasının \( y \) ekseni üzerindeki dik izdüşümünün uzunluğu, \( A \) ve \( B \) noktalarının ordinatları farkının mutlak değerine eşittir.
\( \abs{y_2 - y_1} = \abs{6 - 4} = 2 \)
İzdüşümlerin uzunluklarının toplamı \( 4 + 2 = 6 \) olarak bulunur.