Yüzde, Kar ve Zarar Problemleri
%40'ı 150 olan sayının %12'si kaçtır?
Çözümü GösterSayıya \( x \) diyelim.
Sayının %40'ı 150'dir.
\( x \cdot \dfrac{40}{100} = 150 \)
\( x = \dfrac{150 \cdot 100}{40} = 375 \)
Bu sayının %12'sini bulalım.
\( 375 \cdot \dfrac{12}{100} = 45 \) bulunur.
Bir sayının %30 eksiği 126 ise bu sayı kaçtır?
Çözümü GösterAradığımız sayıya \( x \) diyelim.
Bu sayının %30 eksiğini bulalım.
\( x - x \cdot \dfrac{30}{100} = \dfrac{7x}{10} \)
Bu sayı 126'ya eşittir.
\( \dfrac{7x}{10} = 126 \)
\( x = \dfrac{1260}{7} = 180 \) bulunur.
\( 3x - y \) sayısının %70'i, \( 3y - x \) sayısının %40'ına eşittir.
Buna göre \( x \) sayısı \( y \) sayısının yüzde kaçına eşittir?
Çözümü Göster\( 3x - y \) sayısının %70'ini, \( 3y - x \) sayısının %40'ına eşitleyelim.
\( (3x - y) \cdot \dfrac{70}{100} = (3y - x) \cdot \dfrac{40}{100} \)
\( 70(3x - y) = 40(3y - x) \)
\( 7(3x - y) = 4(3y - x) \)
\( 21x - 7y = 12y - 4x \)
\( 25x = 19y \)
Bilinmeyenleri \( k \) değişkeni cinsinden aşağıdaki şekilde yazabiliriz.
\( x = 19k, \quad y = 25k \)
\( x \) sayısına \( y \) sayısının yüzde \( a \)'sı diyelim.
\( 25k \cdot \dfrac{a}{100} = 19k \)
\( 25a = 1900 \)
\( a = 76 \)
\( x \) sayısı \( y \) sayısının %76'sına eşittir.
\( x \) sayısı \( y \) sayısının %80'i, \( y \) sayısı \( z \) sayısının %5'idir.
Buna göre \( x \) sayısı \( z \) sayısının yüzde kaçıdır?
Çözümü Göster\( x \) sayısı \( y \) sayısının %80'idir.
\( x = y \cdot \dfrac{80}{100} = \dfrac{4y}{5} \)
\( y \) sayısı \( z \) sayısının %5'idir.
\( y = z \cdot \dfrac{5}{100} = \dfrac{z}{20} \)
Bulduğumuz \( y \) değerini ilk denklemde yerine yazalım.
\( x = \dfrac{4y}{5} = \dfrac{4 \cdot \frac{z}{20}}{5} \)
\( = z \cdot \dfrac{4}{100} \)
Buna göre \( x \) sayısı \( z \) sayısının %4'üdür.
\( a \) sayısı \( b \) sayısının yüzde kaçıdır?
Çözümü Göster\( a \) sayısı \( b \) sayısının yüzde \( x \)'i olsun.
\( a = b \cdot \dfrac{x}{100} \)
\( x = \dfrac{100a}{b} \) bulunur.
Bir sayının %10 eksiği ile %40 fazlasının toplamı 207 ediyorsa bu sayı kaçtır?
Çözümü GösterAradığımız sayıya \( 100x \) diyelim.
Bu sayının %10 eksiğini bulalım.
\( 100x - 100x \cdot \dfrac{10}{100} = 90x \)
Bu sayının %40 fazlasını bulalım.
\( 100x + 100x \cdot \dfrac{40}{100} = 140x \)
İki sayının toplamı 207'ye eşittir.
\( 90x + 140x = 207 \)
\( 230x = 207 \)
\( x = \dfrac{207}{230} = \dfrac{9}{10} \)
Aradığımız sayı \( 100x = 100 \cdot \frac{9}{10} = 90 \) olarak bulunur.
\( x = 3k + 8 \)
\( y = 2k + 4 \)
olmak üzere, \( k \) sayısı \( x \) sayısının %30'udur.
Buna göre, \( y \) sayısı \( x \) sayısının yüzde kaçıdır?
Çözümü Göster\( k \) sayısı \( x \) sayısının %30'udur.
\( k = x \cdot \dfrac{30}{100} = \dfrac{3x}{10} \)
Bu \( k \) değerini ilk denklemde yerine yazalım.
\( x = 3(\dfrac{3x}{10}) + 8 \)
\( x = \dfrac{9x}{10} + 8 \)
\( \dfrac{x}{10} = 8 \)
\( x = 80 \)
Bulduğumuz \( x \) değerini ilk denklemde yerine koyarak \( k \) değerini bulalım.
\( k = \dfrac{3(80)}{10} = 24 \)
Bulduğumuz \( k \) değerini ikinci denklemde yerine koyalım.
\( y = 2(24) + 4 = 52 \)
\( y \) sayısı \( x \) sayısının \( \%a \)'sı olsun.
\( y = x \cdot \dfrac{a}{100} \)
\( 52 = 80 \cdot \dfrac{a}{100} \)
\( 52 = 4 \cdot \dfrac{a}{5} \)
\( a = \dfrac{5 \cdot 52}{4} = 65 \)
Buna göre \( y \) sayısı \( x \) sayısının %65'idir.
Berra'ya bir doğum günü sürprizi yapmak isteyen arkadaşları bir pasta almış ve pastanın fiyatını aralarında eşit bölüşmüşlerdir. Daha sonra bu sürprize bir arkadaşları daha dahil olmuş ve pasta fiyatını tekrar eşit bölüşmüşlerdir.
Bu durumda kişi başına düşen tutar %10 azaldığına göre, Berra'ya pasta alan kaç arkadaşı vardır?
Çözümü GösterBerra'ya ilk durumda pasta alan arkadaşların sayısına \( x \), bir kişinin ödediği tutara \( 10y \) diyelim.
Sürprize bir arkadaşları daha dahil olduğunda Berra'ya pasta alan arkadaşların sayısı \( x + 1 \) olur.
Yeni durumda kişi başına düşen tutar \( 10y - 10y \cdot \frac{10}{100} = 9y \) olur.
Her iki durumda pasta için ödenen toplam tutar aynıdır.
\( x \cdot 10y = (x + 1) \cdot 9y \)
\( 10x = 9(x + 1) \)
\( 10x = 9x + 9 \)
\( x = 9 \)
Berra'ya pasta alan arkadaşların sayısı sonradan katılan arkadaşı da dahil ettiğimizde \( x + 1 = 10 \) olur.
Bir iş yerindeki kadın çalışan sayısı %14 artırılıp erkek çalışan sayısı %42 azaltıldığında toplam çalışan sayısının değişmeyeceği hesaplanıyor.
Buna göre bu iş yerindeki kadın çalışan sayısının erkek çalışan sayısına oranı kaçtır?
Çözümü Gösterİş yerindeki kadın çalışan sayısına \( k \), erkek çalışan sayısına \( e \) diyelim.
Kadın çalışanların %14'ü \( k \cdot \frac{14}{100} \) olur.
Erkek çalışanların %42'si \( e \cdot \frac{42}{100} \) olur.
Kadın çalışanların sayısı \( k \cdot \frac{14}{100} \) kadar artırılıp erkek çalışanların sayısı \( e \cdot \frac{42}{100} \) kadar azaltıldığında toplam çalışan sayısı değişmiyorsa bu iki değer birbirine eşittir.
\( k \cdot \dfrac{14}{100} = e \cdot \dfrac{42}{100} \)
\( 14k = 42e \)
\( \dfrac{k}{e} = \dfrac{42}{14} = 3 \) bulunur.
Fadime cüzdanındaki parayla 8 ekmek alabilmektedir. Ekmeğe %60 zam yapılırsa Fadime cüzdanındaki parayla kaç ekmek alabilir?
Çözümü GösterEkmeğin fiyatına \( 10x \) diyelim.
Ekmeğe %60 zam yapıldığında ekmeğin yeni fiyatı \( 10x + 10x \cdot \frac{60}{100} = 16x \) olur.
Fadime zamsız fiyatıyla 8 ekmek alabildiğine göre cüzdanındaki para \( 10x \cdot 8 \) TL'dir.
Ekmeğe zam yapıldığında Fadime'nin alabileceği ekmek sayısına \( y \) diyelim.
\( 10x \cdot 8 = 16x \cdot y \)
\( y = 5 \) bulunur.
Bir kavanozda çilekli, elmalı, portakallı ve orman meyveli 200 adet şeker bulunmaktadır.
%3 olan elmalı şeker oranını %4'e çıkarmak için kavanozdan en az kaç şeker çıkarmak gerekir?
Çözümü GösterBaşlangıçta kavanozdaki 200 şekerden \( 200 \cdot \frac{3}{100} = 6 \) tanesi elmalıdır.
6 elmalı şekerin kavanozdaki şekerlerin %4'ü olması için toplam şeker sayısı \( \frac{6}{\%4} = 6 \cdot \frac{100}{4} = 150 \) olmalıdır.
Buna göre kutudan \( 200 - 150 = 50 \) tane elmalı olmayan şeker çıkarılmalıdır.
Yapılacak bir geziye A şubesindeki öğrencilerin %30'u, B şubesindeki öğrencilerin %45'i katılacaktır. Bu iki şubedeki öğrencilerin tamamının %35'inin geziye katılacağı biliniyor.
Buna göre, B şubesindeki öğrenci sayısı A şubesindeki öğrenci sayısının yüzde kaçıdır?
Çözümü Gösterİşlem kolaylığı açısından A şubesindeki öğrenci sayısına \( 100a \), B şubesindeki öğrenci sayısında \( 100b \) diyelim.
A şubesindeki öğrencilerin %30'u yani \( 100a \cdot \frac{30}{100} = 30a \) öğrenci, B şubesindeki öğrencilerin %45'i yani \( 100b \cdot \frac{45}{100} = 45b \) öğrenci geziye katılacaktır.
Bu iki şubedeki öğrencilerin tamamının ise %35'i yani \( (100a + 100b) \cdot \dfrac{35}{100} = 35a + 35b \) öğrenci geziye katılacaktır.
Her iki şekilde bulduğumuz geziye katılacak toplam öğrenci sayısı birbirine eşittir.
\( 30a + 45b = 35a + 35b \)
\( 5a = 10b \)
\( a = 2b \)
B şubesindeki öğrenci sayısının A şubesindeki öğrenci sayısına oranını bulalım.
\( \dfrac{100b}{100a} = \dfrac{100b}{200b} = \dfrac{1}{2} = \%50 \)
Buna göre, B şubesindeki öğrenci sayısı A şubesindeki öğrenci sayısının %50'sidir.
Bir bahçede beyaz ve turuncu renkte tavşanlar vardır. Beyaz tavşan sayısı %28 oranında artıp turuncu tavşan sayısı %28 oranında azaldığında beyaz ve turuncu tavşan sayılarının oranı tam tersine dönüyor.
Buna göre bahçedeki toplam tavşan sayısı yüzde kaç değişmiştir?
Çözümü GösterBaşlangıçtaki beyaz tavşan sayısına \( b \), turuncu tavşan sayısına \( t \) diyelim.
%28 oranında artış sonucunda beyaz tavşan sayısı \( 1,28b \), %28 oranında azalma sonucunda turuncu tavşan sayısı \( 0,72t \) olur.
Bu değişim sonucunda tavşan sayılarının oranı tersine dönüyor.
\( \dfrac{b}{t} = \dfrac{0,72t}{1,28b} \)
\( \dfrac{b^2}{t^2} = \dfrac{72}{128} = \dfrac{9}{16} \)
Eşitliğin iki tarafının karekökünü alalım.
\( \dfrac{b}{t} = \dfrac{3}{4} \)
\( t \)'yi \( b \) cinsinden yazalım.
\( t = \dfrac{4b}{3} \)
Başlangıçtaki toplam tavşan sayısını \( b \) cinsinden bulalım.
\( t + b = \dfrac{4b}{3} + b = \dfrac{7b}{3} \)
Sondaki toplam tavşan sayısını \( b \) cinsinden bulalım.
\( 1,28b + 0,72t = 1,28b + 0,72 \cdot \dfrac{4b}{3} \)
\( = 1,28b + 0,96b = 2,24b = \dfrac{56b}{25} \)
Toplam tavşan sayısındaki değişim yüzdesini bulalım.
\( \dfrac{\frac{56b}{25} - \frac{7b}{3}}{\frac{7b}{3}} \cdot 100 \)
\( = \dfrac{\frac{168b}{75} - \frac{175b}{75}}{\frac{7b}{3}} \cdot 100 \)
\( = \dfrac{-\frac{7b}{75}}{\frac{7b}{3}} \cdot 100 \)
\( = -\dfrac{3}{75} \cdot 100 = -\% 4 \)
Buna göre, bahçedeki toplam tavşan sayısı %4 oranında azalmıştır.
Bir üçgenin bir kenarının uzunluğu %30 azaltılıyor. Bu üçgenin alanının değişmemesi için bu kenara ait yüksekliğin uzunluğu yüzde kaç artırılmalıdır?
Çözümü GösterÜçgenin kenar uzunluğuna işlem kolaylığı açısından \( 100x \) diyelim.
Kenar uzunluğu %30 azaltıldığında yeni uzunluk \( 100x - 100x \cdot \frac{30}{100} = 70x \) olur.
Üçgenin bu kenarına ait yüksekliğin uzunluğuna \( h \) diyelim.
Alanın değişmemesi için yüksekliği \( \%a \) artıralım.
Yüksekliği \( \%a \) artırdığımızda yeni yükseklik \( h + h \cdot \frac{a}{100} = h \cdot (1 + \frac{a}{100}) \) olur.
Üçgenin önceki ve sonraki alanları birbirine eşittir.
\( A = \dfrac{100x \cdot h}{2} = \dfrac{70x \cdot h \cdot (1 + \frac{a}{100})}{2} \)
Eşitliğin iki tarafındaki \( x \) ve \( h \) değişkenleri sadeleşir.
\( 10 = 7(1 + \dfrac{a}{100}) \)
\( 1 + \dfrac{a}{100} = \dfrac{10}{7} \)
\( \dfrac{a}{100} = \dfrac{3}{7} \)
\( a = \dfrac{300}{7} \)
Buna göre alanın değişmemesi için yüksekliğin uzunluğu \( \%\frac{300}{7} \) artırılmalıdır.
Daire şeklindeki tarlasının alanını %69 büyütmek isteyen Mehmet amca tarlasının yarıçapını yüzde kaç büyütmelidir?
Çözümü GösterMehmet amcanın tarlasının yarıçapına \( r = 10 \) birim diyelim.
Bu durumda tarlanın alanı \( \pi r^2 = 100\pi \) birimkare olur.
Tarlanın alanı %69 artırıldığında alan \( 100\pi \cdot \dfrac{169}{100} = 169\pi \) birimkareye çıkar.
Alan artırıldığında oluşan tarlanın yarıçapına \( x \) birim diyelim.
\( \pi x^2 = 169\pi \)
\( x = 13 \)
Tarlanın yarıçapındaki artış yüzdesine \( \%a \) diyelim.
\( 13 = 10 \cdot (1 + \dfrac{a}{100}) \)
\( 1 + \dfrac{a}{100} = \dfrac{13}{10} \)
\( \dfrac{a}{100} = \dfrac{3}{10} \)
\( a = 30 \)
Buna göre Mehmet amca tarlasının yarıçapını \( \%30 \) büyütmelidir.
Eren'in eviyle okulunun arası 720 metredir. Ev ile okul arasında bulunan Eren'in eve uzaklığı 180 metredir.
Okula doğru yürüyen Eren'in ev ile arasındaki mesafe %15 arttığına göre, okula olan uzaklığı yüzde kaç azalmıştır?
Çözümü GösterEren'in ilk durumda eve olan uzaklığı 180 metre ise okula olan uzaklığı \( 720 - 180 = 540 \) metredir.
Eren'in ev ile arasındaki mesafe %15 arttığında okula doğru \( 180 \cdot \frac{15}{100} = 27 \) metre daha yürümüştür.
Okula doğru 27 metre yürüdüğünde okul ile arasındaki mesafe \( \%a \) azalmış olsun.
\( 540 \cdot \dfrac{a}{100} = 27 \)
\( a = \dfrac{2700}{540} = 5 \)
Buna göre Eren'in okula olan uzaklığı \( \%5 \) azalmıştır.
Bir grup arkadaş bir kafede buluşuyorlar ve \( x \) adet çay ve \( y \) adet kahve içiyorlar. Bu kafede kahvenin fiyatı çayın fiyatından %75 daha pahalıdır.
Arkadaşlar \( y \) adet çay ve \( x \) adet kahve içmiş olsalardı %20 daha az hesap ödeyeceklerdi.
Buna göre, \( x \) ve \( y \) arasındaki bağıntıyı bulunuz.
Çözümü GösterBir çay fiyatına işlem kolaylığı açısından \( 100k \) diyelim. Bu durumda bir kahve fiyatı \( 100k \cdot (1 + \frac{75}{100}) = 175k \) olur.
Buna göre toplam hesap \( 100kx + 175ky \) olur.
\( y \) adet çay ve \( x \) adet kahve içmeleri durumunda ise toplam hesap \( 100ky + 175kx \) olurdu.
İkinci durumda hesap %20 daha az olduğuna göre, ikinci durumda ödenecek tutar birinci durumun %80'idır.
\( (100kx + 175ky) \cdot \dfrac{80}{100} = 100ky + 175kx \)
\( 25k(4x + 7y) \cdot \dfrac{4}{5} = 25k(4y + 7x) \)
\( 4(4x + 7y) = 5(4y + 7x) \)
\( 16x + 28y = 20y + 35x \)
\( 8y = 19x \) bulunur.
Serdar yeni aldığı kitabı her gün bir önceki gün okuduğunun %50'sini okuyarak 4 günde bitiriyor. Sevde ise aynı kitabın %40'ını ilk gün okuyor, daha sonra hergün 75 sayfa okuyarak kitabı toplam 10 günde bitiriyor.
Buna göre, Serdar üçüncü gün kaç sayfa kitap okumuştur?
Çözümü GösterSerdar'ın birinci gün okuduğu sayfa sayısına işlem kolaylığı açısından \( 200x \) diyelim.
Serdar ikinci gün \( 200x \cdot \frac{50}{100} = 100x \) sayfa okur.
Serdar üçüncü gün \( 100x \cdot \frac{50}{100} = 50x \) sayfa okur.
Serdar dördüncü gün \( 50x \cdot \frac{50}{100} = 25x \) sayfa okur.
Serdar dördüncü gün sonunda kitabı bitirdiğine göre, kitap toplam \( 200x + 100x + 50x + 25x = 375x \) sayfadır.
Sevde ilk gün kitabın %40'ını okuduysa \( 375x \cdot \frac{40}{100} = 150x \) sayfa okumuştur. Geriye \( 375x - 150x = 225x \) sayfa kalır.
Sevde kitabı her gün 75 sayfa okuyarak toplamda 10 günde bitirdiğine göre, kalan \( 225x \) sayfayı 9 günde okumuştur.
\( 225x = 9 \cdot 75 \)
\( x = 3 \)
Buna göre Serdar üçüncü gün \( 50x = 50 \cdot 3 = 150 \) sayfa kitap okumuştur.
Aşağıda bir ailenin aylık giderleri ve toplam giderler içindeki paylarının bulunduğu bir tablo verilmiştir.
| Tutar | Yüzde | |
|---|---|---|
| Kira | 12000 TL | |
| Elektrik | 1000 TL | %5 |
| Doğalgaz | ||
| Mutfak | 4500 TL |
Bu tabloya göre ailenin giderlerinin yüzde kaçını doğalgaz faturası oluşturmaktadır?
Çözümü GösterAilenin aylık toplam giderine \( x \) TL diyelim.
Elektrik harcamasına baktığımızda, aylık toplam giderin %5'i 1000 TL'ye karşılık gelmektedir.
\( x \cdot \dfrac{5}{100} = 1000 \)
\( x = 20000 \) TL
Buna göre ailenin aylık toplam gideri 20.000 TL'dir.
Tablodaki doğalgaz hariç harcamalar \( 12000 + 1000 + 4500 = 17500 \) TL'dir.
Buna göre doğalgaz faturası \( 20000 - 17500 = 2500 \) TL'dir.
Doğalgaz faturasının toplam giderler içindeki payına yüzde \( a \) diyelim.
\( 20000 \cdot \dfrac{a}{100} = 2500 \)
\( 200a = 2500 \)
\( a = 12,5 \) bulunur.
Bir iş yerinde çalışanların %20'si asgari ücretle çalışmaktayken %30'u asgari ücretli olmak üzere 150 yeni çalışan işe alınmıştır.
Son durumda çalışanların %23'ü asgari ücretli olduğuna göre, bu iş yerinde toplam kaç çalışan vardır?
Çözümü Gösterİşe alım öncesinde iş yerindeki çalışan sayısına \( 100x \) diyelim.
Bunların %20'si yani \( 100x \cdot \frac{20}{100} = 20x \)'i asgari ücretle çalışmaktadır.
İşe yeni alınan 150 çalışanın %30'u yani \( 150 \cdot \frac{30}{100} = 45 \)'i asgari ücretlidir.
Bu bilgileri bir tabloda özetleyelim.
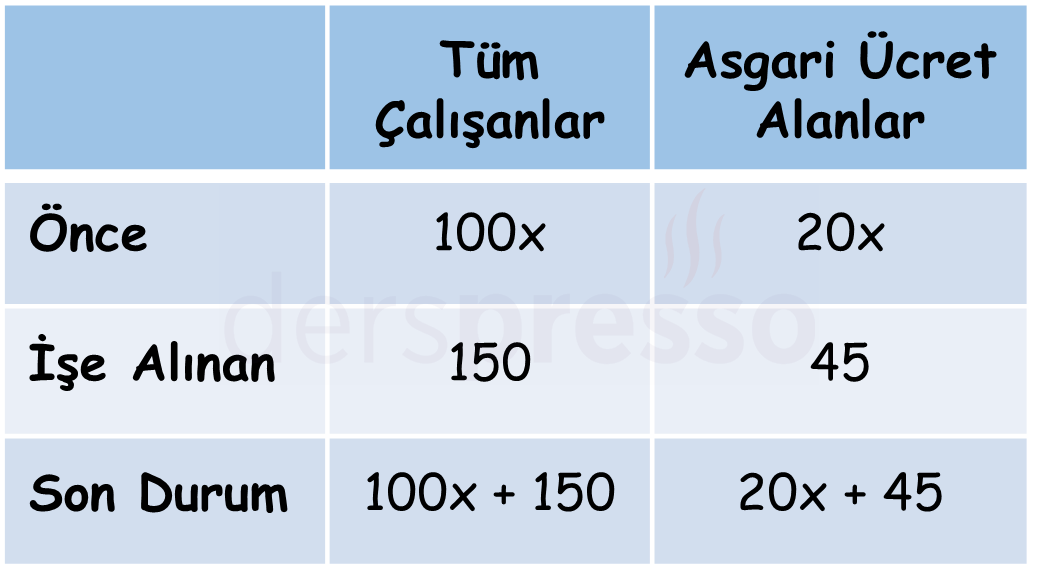
Son durumda asgari ücret alanlar tüm çalışanların %23'ü olduğuna göre aşağıdaki orantıyı kurabiliriz.
\( \dfrac{20x + 45}{100x + 150} = \dfrac{23}{100} \)
\( \dfrac{20x + 45}{2x + 3} = \dfrac{23}{2} \)
İçler - dışlar çarpımı yapalım.
\( 40x + 90 = 46x + 69 \)
\( 6x = 21 \)
\( 2x = 7 \)
Şirketteki toplam çalışan sayısını bulalım.
\( 100x + 150 = 50(2x) + 150 \)
\( = 50(7) + 150 = 500 \) kişi bulunur.
Süheyla kurutmak için 25 kg domates almıştır. Kurutmadan önce %40'ı su olan domatesler bir süre kurutulduktan sonra su oranları %16 olmuştur.
Son durumda Süheyla'nın elinde kaç kilo domates kalmıştır?
Çözümü GösterBaşlangıçta domateslerin %40'ı suysa kalan %60'ı katı kısmıdır.
Domateslerin katı kısmı \( 25 \cdot \frac{60}{100} = 15 \) kg'dır.
Bir süre kurutulduktan sonra %16'sı su kalıyorsa %84'ü katı kısmı olur.
Domateslerin katı kısmı kurutma öncesi ve sonrası değişmeyeceği için iki durum için katı kısmın ağırlıklarını eşitleyebiliriz.
Bir süre kurutulduktan sonra domateslerin toplam ağırlığına \( x \) kg diyelim.
\( x \cdot \dfrac{84}{100} = 15 \)
\( x \cdot \dfrac{7}{25} = 5 \)
\( x = \dfrac{125}{7} \) kg domates kalmıştır.
Bir sınıftaki öğrenciler kahverengi ya da mavi gözlüdür. Bu sınıftaki öğrencilerin %60'ı kızdır.
Sınıftaki öğrencilerin %46'sı mavi gözlü olduğuna göre, kız öğrencilerin en az yüzde kaçı mavi gözlüdür?
Çözümü GösterSınıftaki öğrenci sayısına işlem kolaylığı açısından 100 diyelim.
Sınıftaki öğrencilerin %60'ı kız olduğuna göre, kız öğrenci sayısı 60, erkek öğrenci sayısı 40 olur.
Sınıftaki öğrencilerin %46'sı mavi gözlü olduğuna göre, mavi gözlü öğrenci sayısı 46, kahverengi gözlü öğrenci sayısı 54 olur.
Mavi gözlü kız öğrenci sayısını en az olması için tüm erkek öğrencilerin mavi gözlü olduğunu kabul edelim.
Erkek öğrencilerin 40'ı da mavi gözlü olduğu durumda kız öğrencilerin \( 46 - 40 = 6 \)'sı mavi gözlü olur.
60 kız öğrenciden 6'sı mavi gözlü ise \( \frac{6}{60} \cdot 100 = \%10 \)'u mavi gözlü olur.
Bir atlet olan Derya kısa ve uzun mesafe koşulara katılmaktadır ve bu yarışmaların %40'ı kısa mesafedir.
Derya katıldığı kısa mesafe koşularının %30'unu, uzun mesafe koşularının %40'ını kazandığına göre, en az kaç koşuya katılmış olabilir?
Çözümü GösterDerya'nın katıldığı yarışma sayısına tam sayı sonuç elde ettiğimizden emin olmak için \( 1000 \) diyelim.
Bu yarışmaların %40'ı yani \( 1000 \cdot \frac{40}{100} = 400 \)'ü kısa mesafe, %60'ı yani \( 1000 \cdot \frac{60}{100} = 600 \)'ü uzun mesafe koşularıdır.
Derya katıldığı kısa mesafe koşularının %30'unu yani \( 400 \cdot \frac{30}{100} = 120 \)'sini, uzun mesafe koşularının da %40'ını yani \( 600 \cdot \frac{40}{100} = 240 \)'ını kazanmıştır.
Bu bilgileri bir tabloda özetleyelim.
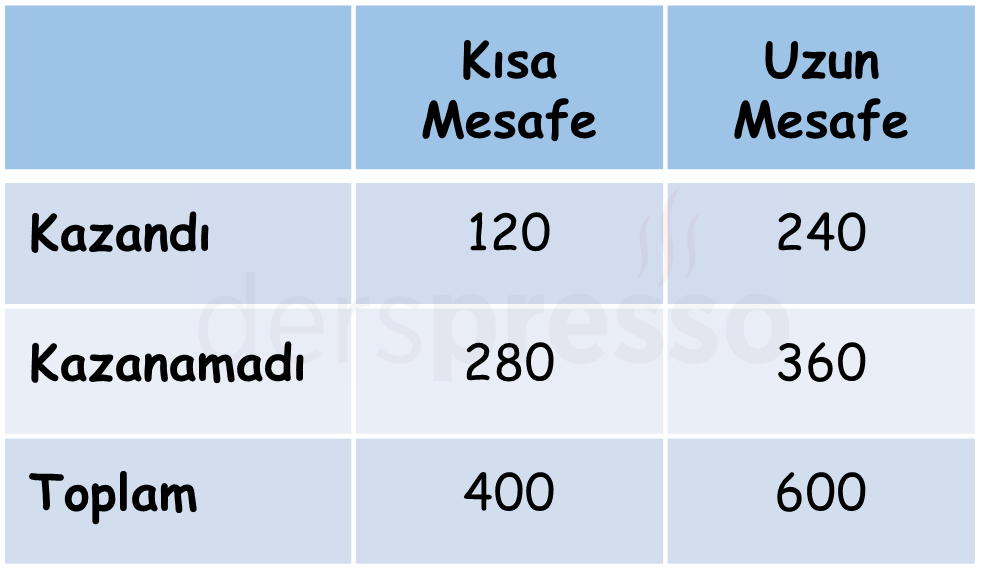
Tablodaki sayıların EBOB'u 40'tır.
EBOB(120, 280, 240, 360) = 40
Buna göre tablodaki tüm sayıları 40'a böldüğümüzde soruda verilen yüzdeler sağlanacak şekilde birer tam sayı değer elde ederiz.
Buna göre Derya en az \( \frac{1000}{40} = 25 \) koşuya katılmış olabilir.
Bir kafede aynı kahve türü küçük ve büyük olmak üzere iki farklı boyda satılmaktadır ve büyük boy kahvenin fiyatı küçük boy kahvenin fiyatının 2 katıdır.
Küçük boy kahvenin mililitre fiyatı büyük boy kahvenin mililitre fiyatından %16 daha fazla olduğuna göre, büyük boy kahve küçük boy kahveden mililitre olarak yüzde kaç daha fazladır?
Çözümü GösterKüçük boy kahvenin fiyatına \( k \) diyelim. Bu durumda büyük boy kahvenin fiyatı \( 2k \) olur.
Küçük boy kahve \( a \) ml, büyük boy kahve \( b \) ml olsun.
Küçük ve büyük boy kahvenin birim fiyatları sırasıyla \( \frac{k}{a} \) ve \( \frac{2k}{b} \) olarak yazılabilir.
Küçük boy kahvenin mililitre fiyatı büyük boy kahvenin mililitre fiyatından %16 fazladır.
\( \dfrac{2k}{b} \cdot (1 + \dfrac{16}{100}) = \dfrac{k}{a} \)
\( \dfrac{b}{a} = 2 \cdot \dfrac{116}{100} = \dfrac{232}{100} \)
Buna göre büyük boy kahve küçük boy kahveden mililitre olarak \( (\dfrac{232}{100} - 1) \cdot 100 = \%132 \) daha fazladır.
Barış bir satranç turnuvasında belirli sayıda maçı tamamlamış ve 12 maçı kalmıştır. Barış'ın turnuvadaki kazanma oranı kalan maçlardan 6'sını kazanırsa %40, 7'sini kazanırsa %45 olacaktır.
Buna göre Barış turnuvada şu ana kadar kaç maç oynamıştır?
Çözümü GösterBarış'ın turnuvada tamamladığı maç sayısına \( x \), kazandığı maç sayısına \( y \) diyelim.
Kalan 12 maçı oynadıktan sonra toplam \( x + 12 \) maç oynamış olacaktır. Kalan maçlardan 6'ını kazanırsa toplam \( y + 6 \) maç kazanmış olur. Bu durumda kazanma oranı %40 olacağından aşağıdaki denklemi yazabiliriz.
\( \dfrac{y + 6}{x + 12} = \dfrac{40}{100} \)
Kalan maçlardan 7'sini kazanırsa toplam \( y + 7 \) maç kazanmış olur. Bu durumda kazanma oranı %45 olacağından aşağıdaki denklemi yazabiliriz.
\( \dfrac{y + 7}{x + 12} = \dfrac{45}{100} \)
Bulduğumuz iki denklemi taraf tarafa bölelim.
\( \dfrac{y + 6}{y + 7} = \dfrac{40}{45} = \dfrac{8}{9} \)
İçler - dışlar çarpımı yapalım.
\( 9y + 54 = 8y + 56 \)
\( y = 2 \)
Bulduğumuz \( y \) değerini denklemlerden birinde yerine koyalım.
\( \dfrac{2 + 6}{x + 12} = \dfrac{40}{100} \)
\( x = 8 \)
Buna göre Barış turnuvada şu ana kadar 8 maç oynamıştır.
Bir quidditch takımı bu sezonda şu ana kadar 30 maç yapmış, bu maçların %60'ını kazanmıştır. Sezonda kalan maçlardan %90'ını kazanırlarsa takımın tüm sezon için kazanma oranı %80 olacaktır.
Bu quidditch takımı bu sezon kalan maçlarının %60'ını kazanırsa tüm sezonda toplam kaç maç kazanmış olur?
Çözümü GösterTakım bu sezonda \( 30 \cdot \frac{60}{100} = 18 \) maç kazanmıştır.
Kalan maç sayısına işlem kolaylığı açısından \( 10x \) diyelim.
Bu maçların \( 10x \cdot \frac{90}{100} = 9x \) tanesini kazanırlarsa sezondaki \( 30 + 10x \) tane maçın \( 18 + 9x \) tanesini kazanmış olurlar.
Bu durumda tüm sezon için kazanma oranı %80 olmaktadır.
\( \dfrac{18 + 9x}{30 + 10x} = \dfrac{80}{100} \)
\( \dfrac{18 + 9x}{3 + x} = 8 \)
\( 18 + 9x = 24 + 8x \)
\( x = 6 \)
Buna göre takımın bu sezonda oynayacağı \( 10x = 60 \) maçı kalmıştır.
Bu maçlardan %60'ını kazanırlarsa \( 60 \cdot \frac{60}{100} = 36 \) maç daha kazanmış olurlar.
Bu durumda tüm sezonda kazandıkları toplam maç sayısı \( 18 + 36 = 54 \) olur.

Bir spor salonunda üyelik süresi arttıkça üyelik ücretine uygulanan indirim oranı yukarıdaki grafikteki gibidir.
Spor salonunun indirimsiz üyelik ücreti aylık 1200 TL olduğuna göre, ayda en fazla 750 TL ödemek isteyen bir kişi kaç aylık üyelik yaptırmalıdır?
Çözümü Gösterİndirimli üyelik ücretinin en fazla 750 TL olabilmesi için gerekli üyelik süresine \( t \) ay diyelim.
Aylık üyelik ücretinin en fazla 750 TL olduğu \( t \) süresini bulalım.
\( 1200 \cdot (1 - \dfrac{50t + 20}{100(t + 4)}) \le 750 \)
\( 1 - \dfrac{50t + 20}{100(t + 4)} \le \dfrac{5}{8} \)
\( \dfrac{50t + 20}{100(t + 4)} \ge \dfrac{3}{8} \)
\( 400t + 160 \ge 300t + 1200 \)
\( 100t \ge 1040 \)
\( t \ge 10,4 \)
Buna göre, üyelik ücretinin en fazla 750 TL olması için 11 aylık üyelik yaptırılmalıdır.
Tabletinin şarjı %30 dolu olan Cem kalan şarjı ile 1 saat oyun oynayabileceğini ya da 1 saat 20 dk film izleyebileceğini hesaplıyor.
Cem bu andan itibaren 16 dk film izliyor ve daha sonra tabletini 11 dakika şarj ediyor.
Şarjdan sonra Cem 1 saat 10 dk oyun oynayınca şarj tamamen bittiğine göre, tabletin şarjı %0'da iken kaç dakika boyunca şarj edilirse %100 dolu olur?
Çözümü GösterVerilen bilgilere göre %30 şarj 60 dk oyuna ya da 80 dk filme denktir.
80 dk film %30 şarja denkse 16 dk film %6 şarja denktir, dolayısıyla Cem 16 dk film izlediğinde şarj %6 azalır ve %24 olur.
60 dk oyun %30 şarja denkse 70 dk oyun %35 şarja denktir, dolayısıyla Cem tableti 11 dk şarj ettikten sonra şarj %35'e çıkmıştır.
Buna göre 11 dakika şarj tabletin pilini %24'ten %35'e çıkarmış, yani %11 artırmıştır.
Tabletin şarjı 11 dakikada %11 arttığına göre, %100 dolması için 100 dakika şarj edilmelidir.
Gökhan satış temsilciliğini yaptığı ürünün aylık toplam satışı üzerinden aşağıdaki şekilde prim alıyor.
- Satışların 100.000 TL'ye kadar olan kısmından %3
- Satışların 100.000 TL'yi aşan, ama 250.000 TL'nin altında kalan kısmından %4
- Satışların 250.000 TL'yi aşan kısmından %5
Gökhan Ekim ayında toplam satış üzerinden %4,5 prim aldığına göre, bu ayda ne kadar satış yapılmıştır?
Çözümü GösterAylık satış tutarına \( x \) diyelim.
Ay sonunda hesaplanan prim yüzdesi %4,5 olduğu için aylık satışlar 250.000 TL'nin üzerine çıkmıştır.
\( x \gt 250000 \)
Satışların 100.000 TL'ye kadar olan kısmından \( 100000 \cdot \frac{3}{100} = 3000 \) TL prim alınır.
Satışların 100.000 TL - 250.000 TL arasındaki kısmından \( (250000 - 100000) \cdot \frac{4}{100} = 6000 \) TL prim alınır.
Satışların 250.000 TL'yi aşan kısmından \( (x - 250000) \cdot \frac{5}{100} \) TL prim alınır.
Toplam hesaplanan prim toplam satışın %4,5'udur.
\( \dfrac{3000 + 6000 + (x - 250000) \cdot \frac{5}{100}}{x} = \dfrac{4,5}{100} \)
İçler - dışlar çarpımı yapalım.
\( 300000 + 600000 + (x - 250000) \cdot 5 = 4,5x \)
\( 900000 + 5x - 1250000 = 4,5x \)
\( 0,5x = 350000 \)
\( x = 700.000 \) TL bulunur.
Kar ve Zarar Problemleri
Bir kırtasiye toptancıdan 40 kutu kalem alıyor ve bu kalemlerin kutusunu %60 karla satıyor.
Buna göre, kırtasiye kaç kutu kalem sattığında kalemleri almak için ödediği parayı kazanmış olur?
Çözümü GösterBir kutu kalemin toptancıdan alış fiyatına işlem kolaylığı açısından 100 lira diyelim.
Kırtasiye bu kalemleri %60 karla \( 100 + 100 \cdot \frac{60}{100} = 160 \) liraya satmaktadır.
Kırtasiye 40 kutu kalemi almak için toplam \( 40 \cdot 100 \) lira ödemiştir. Bu parayı geri kazanmak için satması gereken kutu sayısına \( x \) diyelim.
\( x \cdot 160 = 40 \cdot 100 \)
\( x = 25 \)
Buna göre kırtasiye 25 kutu kalem sattığında toptancıya ödediği parayı kazanmış olur.
Menüsündeki pizzaların fiyatında %30'luk indirim yapan bir restoranın günlük sipariş sayısı %30 artmıştır.
Buna göre bu restoranın pizza satışlarından bir günde elde ettiği gelirdeki değişim hakkında ne söylenebilir?
Çözümü GösterBir pizzanın fiyatına işlem kolaylığı açısından 100 TL diyelim.
Restoran her gün 100 adet pizza siparişi alıyor olsun.
Yapılan %30'luk indirim sonrasında pizzaların fiyatı \( 100 - 100 \cdot \frac{30}{100} = 70 \) TL olur.
İndirim sonrası pizza satışları %30 arttıysa günlük satış adedi \( 100 + 100 \cdot \frac{30}{100} = 130 \) adet olmuştur.
Restoran indirimden önce pizza satışlarından günde \( 100 \cdot 100 = 10000 \) lira kazanmaktayken indirim sonrası günde \( 130 \cdot 70 = 9100 \) lira kazanmaya başlar.
Buna göre indirim sonrası restoranın pizza satışlarından elde ettiği gelir günlük \( \frac{10000 - 9100}{10000} \cdot 100 = \%9 \) azalmıştır.
Bir restoran sahibi ikinci bir şube açmaya karar veriyor. Yeni şubeyle birlikte restoranların aylık geliri 60000 lira artacak, aylık kira giderleri de 40000 liradan 60000 liraya çıkacaktır.
Yeni durumda restoranların aylık kira giderlerinin aylık gelirlere oranı %10 azalacağına göre, birinci şubenin aylık geliri kaç liradır?
Çözümü GösterYeni şubeyle birlikte aylık kira giderlerinin aylık gelirlere oranı %10 azalacaksa eski oranın %90'ı olur.
Birinci şubenin aylık gelirine \( x \) diyelim.
Yeni şube açılınca aylık gelir \( x + 60000 \) lira olur.
\( \dfrac{40000}{x} \cdot \dfrac{90}{100} = \dfrac{60000}{x + 60000} \)
\( \dfrac{3}{5x} = \dfrac{1}{x + 60000} \)
İçler - dışlar çarpımı yapalım.
\( 3x + 180000 = 5x \)
\( 2x = 180000 \)
\( x = 90000 \) TL bulunur.
Bir manav sattığı limonların 5 tanesini 8 liraya alıp 6 tanesini 10,8 liraya satıyor. Bu manavın limon satışındaki kar ya da zarar yüzdesi nedir?
Çözümü GösterKar - zarar durumunu görmek için 1 tane limonun alış ve satış fiyatlarını inceleyelim.
1 limonun maliyetine \( m \), satış fiyatına \( s \) diyelim.
Manav limonların 5 tanesini 8 liraya alıyor.
\( 5m = 8 \)
\( m = \dfrac{8}{5} = 1,6 \)
Manav limonların 6 tanesini 10,8 liraya satıyor.
\( 6s = 10,8 \)
\( s = \dfrac{10,8}{6} = 1,8 \)
Birim satış fiyatı maliyetten yüksek olduğuna göre satıcı kar etmektedir.
\( \text{Kar %} = \dfrac{\text{Satış fiyatı} - \text{Maliyet}}{\text{Maliyet}} \cdot 100 \)
\( = \dfrac{1,8 - 1,6}{1,6} \cdot 100 \)
\( = \dfrac{0,2}{1,6} \cdot 100 \)
\( = \dfrac{1}{8} \cdot 100 = 12,5 \)
Buna göre satıcı \( \%12,5 \) kar etmektedir.
Bir çömlek ustası yaptığı çömleklerin maliyetine %25 kar ekleyerek satış fiyatını belirlemektedir.
Satışların azalması üzerine dükkanını kapatmaya karar veren usta, elinde kalan çömlekleri satış fiyatı üzerinden 42 lira indirim yaparak satmaya başlıyor. Usta bu çömlek satışında maliyet üzerinden %25 zarar ettiğine göre, bir çömleğin maliyeti kaç liradır?
Çözümü GösterUstanın yaptığı çömleklerin maliyetine işlem kolaylığı açısından \( 100x \) lira diyelim.
Usta maliyete %25 kar ekliyorsa çömleklerin satış fiyatı \( 100x \cdot \frac{125}{100} = 125x \) lira olur.
42 lira indirim sonrasında çömleklerin indirimli satış fiyatı \( 125x - 42 \) lira olur. Bu fiyat düzeyinde usta maliyet üzerinden %25 zarar etmektedir.
\( \dfrac{125x - 42}{100x} = \dfrac{75}{100} \)
\( \dfrac{125x - 42}{x} = 75 \)
\( 125x - 42 = 75x \)
\( 50x = 42 \)
\( 100x = 84 \)
Buna göre bir çömleğin maliyeti 84 liradır.
Bir çiftçiden toplu marul alımı yapan bir manav toplam marul bedelini %20 indirimli ödemiştir.
Bu marulları çiftçinin normal satış fiyatının %40 üzerinde satan manavın kar oranı yüzde kaç olur?
Çözümü GösterKar oranı sorulduğu için fiyatın bir önemi yoktur. Çiftçinin 1 kg marul için normal satış fiyatına 100 lira diyelim.
Manav bu marulları %20 indirimli olarak kilosu \( 100 - 100 \cdot \frac{20}{100} = 80 \) liradan alıyor, çiftçinin normal satış fiyatının %40 üzerinde, yani \( 100 + 100 \cdot \frac{40}{100} = 140 \) liradan satıyor.
Marulun kilosunu 80 TL'den alıp 140 TL'den satan manav kilo başına 60 lira kar etmektedir.
Buna göre manavın kar oranı \( \frac{60}{80} \cdot 100 = \%75 \) olur.
Kar oranını %35 olarak belirleyen bir manifaturacı elindeki kumaşları sattıktan sonra çırağının kumaşları ölçmek için kullandığı metrenin olması gerekenden %10 daha kısa ölçtüğünü fark ediyor.
Buna göre, manifaturacının bu kumaş satışından elde ettiği gerçek kar oranı kaçtır?
Çözümü GösterKumaşların metre alış fiyatına (maliyetine) işlem kolaylığı açısından 100 TL diyelim.
1 metre kumaş satarken %10 daha kısa ölçen metre kullanan çırak müşteriye \( 100 - 100 \cdot \frac{10}{100} = 90 \) cm kumaş vermektedir. Bu 90 cm kumaşın maliyeti de manifaturacıya 90 TL olmaktadır.
Manifaturacı bu 90 cm kumaşı 1 metre olduğunu düşünerek %35 karla \( 100 \cdot \frac{135}{100} = 135 \) TL'ye satmaktadır.
Maliyeti 90 TL, satış fiyatı 135 TL olan kumaştan elde edilen kar oranını bulalım.
\( \dfrac{135 - 90}{90} \cdot 100 = \%50 \) bulunur.
Ahsen tarlasında yetiştirdiği domatesleri toplarken bir kısmını çürük çıktığı için atıyor.
Bu durumda domateslerin kilogram başına maliyeti %25 oranında arttığına göre, toplanan domateslerin ağırlıkça yüzde kaçı çürük çıkmıştır?
Çözümü GösterAhsen'in topladığı domates miktarına işlem kolaylığı açısından 100 kg, çürük çıkan domates miktarına da \( a \) kg diyelim.
Toplam maliyete \( x \) dersek kilogram başına maliyetteki artış yüzdesini aşağıdaki formülle hesaplayabiliriz.
\( \dfrac{x}{100} \cdot (1 + \dfrac{25}{100}) = \dfrac{x}{100 - a} \)
\( \dfrac{x}{100} \cdot \dfrac{125}{100} = \dfrac{x}{100 - a} \)
\( \dfrac{1}{100} \cdot \dfrac{5}{4} = \dfrac{1}{100 - a} \)
\( \dfrac{1}{80} = \dfrac{1}{100 - a} \)
İçler - dışlar çarpımı yapalım.
\( 100 - a = 80 \)
\( a = 20 \)
Buna göre toplanan domateslerin \( \frac{20}{100} = \%20 \)'si çürük çıkmıştır.
Bir pastanede her birinin maliyeti 40 lira olan 70 pastanın bir kısmı bir gün önce, diğerleri bugün yapılmıştır. Bu pastane bir gün önce yapılmış olan pastaları %30 zararına, bugün yapılanları ise %40 karla satmaktadır.
Pastane elindeki tüm pastaları sattığında ne kar ne de zarar ettiğine göre, pastaların kaçı bir gün önce yapılmıştır?
Çözümü GösterBir gün önce yapılan pastaların sayısına \( x \) diyelim, bu durumda bugün yapılan pastaların sayısı \( 70 - x \) olur.
Pastane pastaların tümünü üretmek için toplam \( 40 \cdot 70 = 2800 \) lira harcamıştır. Tüm pastaları sattıktan sonra ne kar ne de zarar ettiklerine göre, pastaların satışından toplam 2800 lira kazanmışlardır.
Bir gün önce yapılan pastalar %30 zararla satıldıysa bu pastalar \( 40 - 40 \cdot \frac{30}{100} = 28 \) liradan satılmıştır.
Bugün yapılan pastalar %40 karla satıldıysa bu pastalar \( 40 + 40 \cdot \frac{40}{100} = 56 \) liradan satılmıştır.
Tüm pastalardan elde edilen geliri hesaplayalım.
\( 28x + 56(70 - x) = 2800 \)
\( x + 2(70 - x) = 100 \)
\( x + 140 - 2x = 100 \)
\( x = 40 \)
Buna göre pastaların 40 tanesi bir gün önce yapılmıştır.
Piyasa fiyatı 2500 TL olan bir ürünü iki adet kuponu arka arkaya kullanarak satın alan bir müşteri son durumda 1995 TL ödemiştir.
İlk kupon %16 indirim sağladığına göre, ikinci kuponun indirim yüzdesi kaçtır?
Çözümü GösterKuponlar arka arkaya uygulandığı için ikinci kupon ilk kupon uygulanmış indirimli fiyata uygulanacaktır.
İlk kupon %16 indirim sağlıyor.
\( 2500 \cdot \dfrac{16}{100} = 400 \) TL indirim sağlar.
Buna göre ilk indirim sonrası ürün fiyatı \( 2500 - 400 = 2100 \) TL olur.
Ürünün indirimli fiyatı ile ödenen tutar arasındaki fark ikinci kuponun indirim tutarını verir.
\( 2100 - 1995 = 105 \)
İkinci kuponun indirim oranını indirim tutarının indirimli ürün fiyatına oranı şeklinde ifade edebiliriz.
\( \text{İndirim oranı} = \dfrac{105}{2100} \)
\( = \dfrac{5}{100} = \%5 \)
Buna göre ikinci kupon %5 oranında indirim sağlar.
Bir mağazadaki indirim oranları %12 ile %28 arasında değişmektedir. Bu mağazadan alınan bir ürüne 792 TL ödendiğine göre, bu ürünün indirimsiz fiyatının alabileceği en yüksek ve en düşük değerler arasındaki fark kaçtır?
Çözümü Gösterİndirim oranının %12 olduğu durumdaki indirimsiz satış fiyatını bulalım.
\( x \cdot \dfrac{88}{100} = 792 \)
\( x = 900 \) TL
İndirim oranının %28 olduğu durumdaki indirimsiz satış fiyatını bulalım.
\( y \cdot \dfrac{72}{100} = 792 \)
\( y = 1100 \) TL
Buna göre ürünün indirimsiz fiyatının alabileceği en yüksek ve en düşük değerler arasındaki fark \( 1100 - 900 = 200 \) TL'dir.
Bir ev hanımı evinde yaptığı mezeleri bir şarküteriye %44 karla satıyor. Şarküteri mezeleri bir restorana %25 karla satıyor. Restoran da mezeleri müşterilerine %40 karla 630 TL'ye satıyor.
Buna göre mezelerin ev hanımına maliyeti ne kadardır?
Çözümü GösterMezelerin ev hanımına maliyetine \( x \) TL diyelim.
Şarküterinin mezelere ödediği tutar \( x \cdot \frac{144}{100} \) TL olur.
Restoranın mezelere ödediği tutar \( x \cdot \frac{144}{100} \cdot \frac{125}{100} \) TL olur.
Restoran müşterilerinin ödediği tutar \( x \cdot \frac{144}{100} \cdot \frac{125}{100} \cdot \frac{140}{100} \) TL olur.
Restoran müşterilerinin ödediği tutar 630 TL'dir.
\( x \cdot \dfrac{144}{100} \cdot \dfrac{125}{100} \cdot \dfrac{140}{100} = 630 \)
\( x \cdot \dfrac{36}{25} \cdot \dfrac{5}{4} \cdot \dfrac{7}{5} = 630 \)
Sadeleştirmeler yapıldığında \( x = 250 \) TL bulunur.
Bir çiçekçi 8 tanesi 28 TL'den çiçekler satın alıyor. Bu çiçeklerin 10 tanesini 56 TL'ye satan çiçekçinin karı yüzde kaçtır?
Çözümü GösterÇiçekçi 8 çiçeği 28 TL'ye alıyorsa 1 çiçeğin alış fiyatı \( \frac{28}{8} = \frac{7}{2} \) TL olur.
Çiçekçi 10 çiçeği 56 TL'ye satıyorsa 1 çiçeğin satış fiyatı \( \frac{56}{10} = \frac{28}{5} \) TL olur.
\( \text{Kar %} = \dfrac{\text{Satış} - \text{Maliyet}}{\text{Maliyet}} \cdot 100 \)
\( = \dfrac{\frac{28}{5} - \frac{7}{2}}{\frac{7}{2}} \cdot 100 \)
\( = \dfrac{2 \cdot 28 - 5 \cdot 7}{10} \cdot \dfrac{2}{7} \cdot 100 \)
\( = \dfrac{21}{10} \cdot \dfrac{200}{7} \)
\( = \%60 \) olarak bulunur.
Zuhal biriktirdiği parayı bileşik faize yatırıyor. 4 yılın sonunda parası iki katına çıkacağına göre, Zuhal parasının 8 katına çıkması için kaç yıl beklemelidir?
Çözümü GösterZuhal'in yatırdığı para miktarına \( x \) diyelim.
4 yıl sonunda bu para 2 katına çıkacaktır.
\( x \Longrightarrow 2x \)
Sonraki 4 yılın sonunda yine aynı durum gerçekleşecek ve ilk 4 yıl sonundaki tutar iki katına çıkacaktır.
\( 2x \Longrightarrow 4x \)
Sonraki 4 yılın sonunda da yine aynı durum gerçekleşecek ve ilk 8 yıl sonundaki tutar iki katına çıkacaktır.
\( 4x \Longrightarrow 8x \)
Buna göre 3 adet 4 yıllık süreler sonunda, yani 12 yılda Zuhal'in parası 8 katına çıkacaktır.
Bir kafenin sahibi içeceklerde %30 indirim yaptığında bir gün içinde gelen müşteri sayısının %120 arttığını gözlemlemiştir.
Buna göre kafenin günlük cirosu yüzde kaç artmıştır?
Çözümü Gösterİşlem kolaylığı açısından normal bir günde kafeye 10 müşteri geldiğini ve bir içecek fiyatının 10 lira olduğunu varsayalım.
Bu durumda kafenin günlük cirosu \( 10 \cdot 10 = 100 \) lira olur.
İçeceklere %30 indirim yapıldığında bir içeceğin fiyatı \( 10 - 10 \frac{30}{100} = 7 \) lira olmuştur.
Müşteri sayısı %120 arttığında bir günde \( 10 + 10 \cdot \frac{120}{100} = 22 \) müşteri gelmiştir.
Kafenin indirim sonrası günlük cirosu \( 22 \cdot 7 = 154 \) lira olur.
Cirodaki artış yüzdesini bulalım.
\( \dfrac{154 - 100}{100} = \%54 \) bulunur.
Bir fırıncının ekmeklerinin \( \frac{3}{8} \)'ü bayattır.
Fırıncı taze ekmekleri %40 kârla, bayat ekmekleri %10 zararla sattığına göre, tüm ekmeklerden elde ettiği kâr oranı yüzde kaçtır?
Çözümü GösterTüm ekmeklerin sayısına işlem kolaylığı açısından \( 8x \) diyelim.
Bu ekmeklerden \( 5x \) tanesi taze, \( 3x \) tanesi bayattır.
Bir ekmeğin maliyetine işlem kolaylığı açısından 10 lira diyelim.
Tüm ekmekler \( 8x \) tane olduğundan ekmeklerin toplam maliyeti \( 8x \cdot 10 = 80x \) liradır.
Taze ekmeklerin kârlı satış fiyatını bulalım.
\( 10 + 10 \cdot \dfrac{40}{100} = 14 \) lira
Bayat ekmeklerin zararına satış fiyatını bulalım.
\( 10 - 10 \cdot \dfrac{10}{100} = 9 \) lira
Toplamda satıştan kaç lira gelir edildiğini bulalım.
\( 5x \cdot 14 + 3x \cdot 9 = 97x \) lira
Ekmeklerin satışından elde edilen kâr \( 97x - 80x = 17x \) liradır.
Satıştan elde edilen kâr oranını bulalım.
\( \text{Kar %} = \dfrac{\text{Satış} - \text{Maliyet}}{\text{Maliyet}} \)
\( = \dfrac{97x - 80x}{80x} \)
\( = \% 21,25 \) bulunur.
Kuru üzüm ticareti yapan Ferhat çiftçilerden üzümün kilosunu 12 TL'ye alıyor. Kurutma aşaması sonrasında üzümlerin ağırlığı %40 oranında azalmaktadır.
Ferhat kuru üzümleri birer kiloluk paketlere koyup satmaktadır. Bu paketlerin tanesine 5 TL veren Ferhat %44 kar elde etmek için bir paket kuru üzümü kaç TL'ye satmalıdır?
Çözümü Göster1 kg kuru üzümün kurutulmadan önceki ağırlığına \( x \) kg diyelim.
Kurutma aşaması sonrasında üzümlerin ağırlığı %40 oranında azalmaktadır.
\( x - x \cdot \dfrac{40}{100} = 1 \)
\( x \cdot \dfrac{60}{100} = 1 \)
\( x = \dfrac{5}{3} \) kg
Buna göre \( \frac{5}{3} \) kg üzüm kurutma aşaması sonrasında 1 kg olmaktadır.
1 kg üzümün alış fiyatı 12 TL olduğuna göre, \( \frac{5}{3} \) kg üzümün alış fiyatı \( \frac{5}{3} \cdot 12 = 20 \) TL olur.
Paket ücretini de eklediğimizde bir paket kuru üzümün maliyeti \( 20 + 5 = 25 \) TL olur.
Ferhat %44 kar elde etmek için kuru üzümün paketini \( 25 \cdot \frac{144}{100} = 36 \) TL'ye satmalıdır.
Gönül mağazasındaki iki farklı üründen birincisini %60 karla, ikincisini %60 zararla 480 TL'ye satıyor.
Gönül'ün bu satıştan net karı ya da zararı yüzde kaçtır?
Çözümü GösterBirinci ürünün maliyetine \( a \), ikinci ürünün maliyetine \( b \) diyelim.
%60 karla satılan birinci ürünün maliyeti \( a \), edilen kar \( 480 - a \) olur.
\( \dfrac{480 - a}{a} = \dfrac{60}{100} \)
\( \dfrac{480 - a}{a} = \dfrac{3}{5} \)
İçler - dışlar çarpımı yapalım.
\( 5 \cdot 480 - 5a = 3a \)
\( 8a = 5 \cdot 480 \)
\( a = 300 \) TL
%60 zararla satılan ikinci ürünün maliyeti \( b \), edilen zarar \( b - 480 \) olur.
\( \dfrac{b - 480}{b} = \dfrac{60}{100} \)
\( \dfrac{b - 480}{b} = \dfrac{3}{5} \)
İçler - dışlar çarpımı yapalım.
\( 5b - 5 \cdot 480 = 3b \)
\( 2b = 5 \cdot 480 \)
\( b = 1200 \) TL
İki ürünün maliyetlerinin toplamını alalım.
\( a + b = 300 + 1200 = 1500 \) TL
İki ürünün satış fiyatlarının toplamını alalım.
\( 480 + 480 = 960 \) TL
Satış fiyatı maliyetin altında kaldığı için iki ürünün satışından zarar edilmiştir.
\( \text{Zarar %} = \dfrac{\text{Satış fiyatı} - \text{Maliyet}}{\text{Maliyet}} \cdot 100 \)
\( = \dfrac{960 - 1500}{1500} \cdot 100 \)
\( = -\dfrac{540}{1500} \cdot 100 = -\%36 \)
Buna göre bu iki ürünün satışından toplamda %36 zarar edilmiştir.
Aylin mağazası için toplam 760 TL'ye 2 adet gömlek alıyor. Birinci gömleği %30 kar ile satışa koyuyor.
Mağazaya ilk gelen müşteriye birinci gömleği alması durumunda ikinci gömleğe maliyeti üzerinden %18 indirim yapacağını söylüyor.
Bu müşteriye iki gömleği de satan Aylin'in bu satış için net karı ya da zararı olmadığına göre, bu iki ürünün alış fiyatlarının farkı kaçtır?
Çözümü GösterBirinci ürünün alış fiyatına \( x \) diyelim. Bu durumda ikinci ürünün alış fiyatı \( 760 - x \) olur.
Birinci üründen edilen kar ikinci üründen edilen zarara eşit olacaktır.
\( x \cdot \dfrac{30}{100} = (760 - x) \cdot \dfrac{18}{100} \)
\( 30x = 18 \cdot 760 - 18x \)
\( 48x = 18 \cdot 760 \)
\( x = 285 \) TL
Bu durumda ikinci ürünün alış fiyatı \( 760 - x = 475 \) TL olur.
Ürünlerin fiyatlarının farkı \( 475 - 285 = 190 \) TL olarak bulunur.
İki farklı ürüne 10'ar TL indirim yapıldığında fiyatlarının oranı \( \frac{5}{8} \), birincisine %10 ikincisine %30 zam yapıldığında fiyatlarının oranı \( \frac{187}{351} \) olmaktadır.
Buna göre bu ürünlerin başlangıçtaki fiyatlarının toplamı kaçtır?
Çözümü Gösterİşlem kolaylığı açısından birinci ürünün fiyatına \( 10a \), ikinci ürünün fiyatına \( 10b \) diyelim.
Ürünlere 10'ar TL indirim yapıldığında fiyatlarının oranı \( \frac{5}{8} \) oluyor.
\( \dfrac{10a - 10}{10b - 10} = \dfrac{5}{8} \)
İçler - dışlar çarpımı yapalım.
\( 80a - 80 = 50b - 50 \)
\( 8a = 5b + 3 \)
Birinci ürüne %10 ikinci ürüne %30 zam yapıldığında fiyatlarının oranı \( \frac{187}{351} \) oluyor.
Birinci ürüne %10 zam yapıldığında fiyatı \( 10a \cdot \frac{110}{100} = 11a \), ikinci ürüne %30 zam yapıldığında fiyatı \( 10b \cdot \frac{130}{100} = 13b \) olur.
\( \dfrac{11a}{13b} = \dfrac{187}{351} = \dfrac{11 \cdot 17}{13 \cdot 27} \)
\( \dfrac{a}{b} = \dfrac{17}{27} \)
\( a = 17k, \quad b = 27k \) diyelim.
Bu değerleri ilk denklemde yerine yazalım.
\( 8 \cdot 17k = 5 \cdot 27k + 3 \)
\( 136k = 135k + 3 \)
\( k = 3 \)
Ürünlerin başlangıçtaki fiyatlarının toplamını bulalım.
\( 10a + 10b = 10 \cdot 17k + 10 \cdot 27k \)
\( = 440k = 440 \cdot 3 = 1320 \) bulunur.
Bir bakkal sattığı una talaş katarak maliyetine satış yaptığını söylemesine rağmen gerçekte %12 kar elde etmektedir.
Unun kilogram maliyeti talaşın kilogram maliyetinin 4 katı olduğuna göre, bakkal un ile talaşı hangi oranda karıştırmıştır?
Çözümü GösterSatılan karışımdaki un miktarına \( x \) kg, talaş miktarına \( y \) kg diyelim.
Talaşın kilogram maliyeti \( m \) ise unun kilogram maliyeti \( 4m \) olur.
Buna göre satıcının \( x + y \) kilogramlık satış için maliyeti aşağıdaki gibi olur.
\( x \cdot 4m + y \cdot m \)
Satıcı maliyetine satış yaptığını söylediğine göre ürünü kilogramı \( 4m \) liradan satmaktadır, buna göre satıştan eline geçen tutar aşağıdaki gibi olur.
\( (x + y) \cdot 4m \)
Bu satıştan elde ettiği kar oranını bulalım.
\( \text{Kar %} = \dfrac{\text{Satış} - \text{Maliyet}}{\text{Maliyet}} \cdot 100 \)
\( 12 = \dfrac{(4mx + 4my) - (4mx + my)}{4mx + my} \cdot 100 \)
\( 3 = \dfrac{3y}{4x + y} \cdot 25 \)
İçler - dışlar çarpımı yapalım.
\( 12x + 3y = 75y \)
\( 12x = 72y \)
\( x = 6y \)
Üründeki un - talaş oranını bulalım.
\( \dfrac{x}{y} = 6 \) olarak bulunur.
Ananasları tezgaha indirimsiz fiyatıyla koyan bir manav, 9 ananas alana 1 ananas hediye veriyor.
Manav 12 ananas alan müşterisine kaç ananas hediye ederse ek %15 indirim yapmış olur?
Çözümü GösterManav ilk durumda 10 ananası 9 ananas fiyatına veriyor.
10 ananas için verilen indirim yüzdesini bulalım.
\( \dfrac{1}{10} \cdot 100 = 10 \)
12 ananas alındığı durumdaki hediye ananas sayısına \( a \) diyelim.
12 ananas alan müşteriye %10 indirim üzerine ek %15 indirim yapıldığında indirim oranı %25 olur.
\( \dfrac{a}{12 + a} \cdot 100 = 25 \)
\( 4a = 12 + a \)
\( a = 4 \) bulunur.
Mehmet %36 indirimle satılan bir ürün alıyor ve bu ürün için bir satış fiyatı belirleyip bu fiyat üzerinden %20 indirimle satıyor.
Mehmet'in bu satıştan kârı alış fiyatının %10'u olduğuna göre, Mehmet'in ürün için belirlediği indirimsiz satış fiyatı, ürünün indirimsiz alış fiyatının yüzde kaçıdır?
Çözümü GösterÜrünün indirimsiz alış fiyatına \( 1000x \) TL diyelim.
Mehmet ürünü %36 indirimle \( 1000x - 1000x \cdot \frac{36}{100} = 640x \) TL'ye alıyor.
Mehmet daha sonra ürünü %10 kârla \( 640x + 640x \cdot \dfrac{10}{100} = 704x \) TL'ye satıyor.
Mehmet'in ürün için belirlediği indirimsiz satış fiyatına \( y \) diyelim.
Ürünün indirimli satış fiyatı indirimsiz satış fiyatının %20'sidir.
\( y \cdot \dfrac{80}{100} = 704x \)
\( y = 880x \)
Mehmet'in ürün için belirlediği indirimsiz satış fiyatının ürünün indirimsiz alış fiyatının yüzde kaçı olduğunu bulalım.
\( \dfrac{\text{İndirimsiz satış fiyatı}}{\text{İndirimsiz alış fiyatı}} \cdot 100 = \dfrac{880x}{1000x} \cdot 100 = 88 \)
%88 olarak bulunur.
Bir butik açan Serkan sermayesinin;
- %40'ıyla pantolon alıp %60 karla satmıştır.
- %20'siyle elbise alıp %50 karla satmıştır.
- Kalan kısmı olan 35000 lirayla kira ve faturaları ödemiştir.
Serkan bu butik işinden toplamda %20 kar ettiğine göre, pantolonlardan toplam kaç lira kar etmiştir?
Çözümü GösterSerkan'ın sermayesine \( 100x \) diyelim.
Serkan sermayesinin %40'ı olan \( 100x \cdot \frac{40}{100} = 40x \) liralık kısımla %60 kar elde etmişse bu kısımdan \( 40x \cdot \frac{60}{100} = 24x \) lira kar etmiştir.
Serkan sermayesinin %20'si olan \( 100x \cdot \frac{20}{100} = 20x \) liralık kısımla %50 kar elde etmişse bu kısımdan \( 20x \cdot \frac{50}{100} = 10x \) lira kar etmiştir.
Serkan'ın toplam geliri pantolon ve elbiseden gelirlerinin toplamı olur.
\( (40x + 24x) + (20x + 10x) = 94x \)
Serkan'ın toplam gideri pantolon ve elbise alış fiyatları ile kira ve faturalara ödediği tutarın toplamı olur.
\( 40x + 20x + 35000 = 60x + 35000 \)
Kar gelir ve giderin farkına eşittir.
\( 94x - (60x + 35000) = 34x - 35000 \)
Serkan toplamda %20 kar etmişse karı \( 100x \cdot \frac{20}{100} = 20x \) olur.
\( 34x - 35000 = 20x \)
\( 14x = 35000 \)
\( x = 2500 \)
Buna göre Serkan pantalonlardan \( 24x = 24 \cdot 2500 = 60000 \) lira kar elde etmiştir.
Bir telefon mağazası iki farklı telefonun her birini 9900 TL'ye satarsa ne kar ne de zarar ediyor.
Bu mağaza telefonlardan birini %12,5 karla sattığına göre, diğer telefondan yüzde kaç zarar etmiştir?
Çözümü GösterKarla satılan telefonun maliyetine işlem kolaylığı açısından \( 200k \) diyelim.
\( \text{Kar} = 200k \cdot \dfrac{12,5}{100} = 25k \)
\( \text{Satış fiyatı} = 200k + 25k = 225k \)
İki telefon da 9900 TL'ye satılmıştır.
\( 9900 = 225k \)
\( k = 44 \)
Mağaza birinci telefondan \( 25k = 25 \cdot 44 = 1100 \) TL kar etmiştir.
Bu iki satıştan toplamda kar ya da zarar edilmediğine göre, birinci telefondan edilen kar ikinci telefondan edilen zarara eşit olmalıdır.
Buna göre ikinci telefondan 1100 TL zarar edilmiştir.
İkinci telefonun maliyeti \( 9900 + 1100 = 11000 \) TL olur.
Zarar yüzdesini bulalım.
\( \text{Zarar %} = \dfrac{\text{Maliyet} - \text{Satış tutarı}}{\text{Maliyet}} \cdot 100 \)
\( = \dfrac{11000 - 9900}{11000} \cdot 100 \)
\( = 10 \) olarak bulunur.
| A operatörü | B operatörü | |
|---|---|---|
| İnternet | 2 GB | 3 GB |
| Konuşma | 100 dk | 100 dk |
| Sabit ücret | 60 TL | 80 TL |
A ve B operatörlerinin aylık fiyat tarifeleri tablodaki gibidir. Bu operatörler belirledikleri kullanım miktarı aşıldığında aşım miktarına bağlı olarak sabit ücretin üzerine ekleme yaparak fatura tutarını belirlemektedir.
A operatörü aşılan her 1 GB internet için 8 TL, her 1 saatlik konuşma için 5 TL faturaya yansıtmaktadır. B operatörü ise aşılan her 1 GB internet için 7 TL, her 1 saatlik konuşma için 3 TL faturaya yansıtmaktadır.
Ekim ayında 5 GB internet kullanan bir B operatörü müşterisi en az kaç dakika konuşursa A operatörüyle kıyaslandığında zarar etmemiş olur?
Çözümü GösterAy sonunda A operatöründe ödenecek faturaya \( a \), B operatöründe ödenecek faturaya \( b \) diyelim.
Müşterinin zarar etmemesi için \( a \ge b \) olmalıdır.
A operatörünün planına göre 3 GB, B operatörünün planına göre 2 GB internet aşımı olmuştur.
Saat cinsinden konuşma aşım miktarına \( x \) diyelim.
A ve B operatörleri için sabit ücret, internet ve konuşma aşım ücretlerini toplayarak fatura tutarlarını bulalım.
\( a = 60 + 3 \cdot 8 + 5x \)
\( b = 80 + 2 \cdot 7 + 3x \)
\( 84 + 5x \ge 94 + 3x \)
\( x \ge 5 \)
Aşım miktarı 5 saat olduğunda kullanıcı zarar etmemiş olur. Aşım miktarını dakikaya çevirip sabit ücrete dahil olan 100 dakikayı ekleyelim.
\( 5 \cdot 60 + 100 = 400 \) dakika bulunur.
Bir market sahibi halden aldığı elmaları marketinde satıyor. Elmaları halde aldığı kişinin tartısı arızalı olduğu için elmaları gerçek ağırlığından %10 daha ağır tartıyor. Market sahibinin tartısı da arızalı olduğu için elmaları satarken gerçek ağırlığından %5 daha hafif tartıyor.
Bu arızalar hakkında bilgisi olmayan market sahibi elmalara ödediği tutar üzerine %60 kar eklediğine göre, market sahibinin gerçek kar oranı kaçtır?
Çözümü GösterElmanın kilogram alış fiyatına \( 100x \) diyelim.
Haldeki tartı %10 daha ağır tarttığı için market sahibi \( 100x \) ödeyerek 1 kg elma aldığını düşünürken aslında \( \frac{1}{1 + \%10} = \frac{10}{11} \) kg elma almıştır.
Elmanın market sahibine kilogram başına gerçek maliyetini bulalım.
Maliyet \( = \dfrac{100x}{\frac{10}{11}} = 110x \)
Market sahibi elmaların maliyetini \( 100x \) olarak düşünerek %60 karla \( 160x \)'e satmaktadır.
Marketteki tartı %5 daha hafif tarttığı için market sahibi 1 kg elma sattığını düşünürken aslında \( \frac{1}{1 - \%5} = \frac{20}{19} \) kg elma satmaktadır.
Elmanın kilogram başına gerçek satış fiyatını bulalım.
Satış fiyatı \( = \dfrac{160x}{\frac{20}{19}} = 152x \)
Buna göre elmaların kilogram başına gerçek maliyeti \( 110x \), gerçek satış fiyatı da \( 152x \) olmaktadır.
Gerçek kar \( = \dfrac{152x - 110x}{110x} \cdot 100 \)
\( = \%38,18... \) bulunur.