Hareket (Yol/Hız/Zaman) Problemleri
Hareket problemlerinde hareket halindeki araç ya da kişilerin katettikleri mesafeler, hızları ve hareket süreleri arasındaki ilişkileri kullanarak verilen problemi denkleme dönüştürmemiz ve çözmemiz beklenir. Bu tip problemlerde araç ve kişilerin belirli aralıklarda sabit hızlarla hareket ettikleri varsayılır.
Bir aracın katettiği mesafe ortalama hızı ile geçen sürenin çarpımına eşittir.
\( x \): Katedilen mesafe
\( v \): Ortalama hız
\( t \): Süre
Mesafe: \( x = v \cdot t \)
Ortalama hız: \( v = \dfrac{x}{t} \)
Süre: \( t = \dfrac{x}{v} \)
Aynı anda \( A \) ve \( B \) noktalarından birbirine doğru hareket eden iki araç \( t \) süre sonra \( C \) noktasında karşılaşıyorlarsa:
\( \abs{AB} = x \) olmak üzere,
\( x = (v_1 + v_2) \cdot t \)
Aynı anda \( A \) ve \( B \) noktalarından aynı yönde hareket eden iki araç \( t \) süre sonra \( C \) noktasında karşılaşıyorlarsa:
\( \abs{AB} = x \) olmak üzere,
\( x = (v_1 - v_2) \cdot t \)
Hızı 110 km/saat olan A aracı, önündeki 95 km/saat hızla giden B aracına 6 saat sonra yetişiyor.
Araçlar sabit hızla hareket ettiğine göre, başlangıçta aralarındaki mesafe kaç km'dir?
Çözümü GösterA aracı önündeki B aracına yetişmeye çalışırken aralarındaki mesafe saatte \( 110 - 95 = 15 \) km azalır.
Aralarındaki mesafe 6 saat sonra kapandığına göre, başlangıçta aralarında \( 15 \cdot 6 = 90 \) km mesafe vardır.
Bir adımının uzunluğu 45 cm olan Ahmet okula yürüyerek giderken dakikada 80 adım atıyor ve yol 15 dakika sürüyor.
Bir adımının uzunluğu 30 cm olan kardeşi Esma ise aynı yolu yürüyerek giderken dakikada 90 adım atıyor.
Buna göre Esma'nın okula varması kaç dakika sürer?
Çözümü GösterEsma'nın yürüme süresine \( t \) diyelim.
Bir adımın uzunluğu, dakika atılan adım sayısı ve toplam sürenin çarpımı yürünen toplam mesafeyi verir.
Ahmet'in yürüdüğü mesafe \(= 45 \cdot 80 \cdot 15 \)
Esma'nın yürüdüğü mesafe \(= 30 \cdot 90 \cdot t \)
İki kardeşin yürüdükleri mesafe eşittir.
\( 45 \cdot 80 \cdot 15 = 30 \cdot 90 \cdot t \)
\( 1 \cdot 80 \cdot 1 = 2 \cdot 2 \cdot t \)
\( t = 20 \) dk bulunur.
Sabit hızla hareket eden Salih yola çıktıktan 6 saat sonra kilometre sayacı 18700 km gösterirken 13 saat sonra 19575 km gösteriyor.
Buna göre Salih'in hızı saatte kaç kilometredir?
Çözümü GösterSalih \( 13 - 6 = 7 \) saatte \( 19575 - 18700 = 875 \) kilometre yol gitmiştir.
Ortalama hız (\( v \)), gidilen mesafenin süreye bölümüne eşittir.
\( v = \dfrac{875}{7} = 125 \) km/sa bulunur.
Bir araç belli bir mesafeyi sabit bir hızla 20 saatte, saatteki hızını 36 km arttırdığında ise aynı yolu 16 saatte gidebiliyor.
Buna göre bu mesafe kaç kilometredir?
Çözümü GösterAracın gittiği mesafeye \( x \), en baştaki sabit hızına \( v \) diyelim.
Toplam mesafe, ortalama hız ile sürenin çarpımına eşittir.
\( x = vt \)
Araç verilen mesafeyi sabit hızla 20 saatte gidiyor.
\( x = 20v \)
Araç saatteki hızını 36 km arttırırsa aynı yolu 16 saatte gidiyor.
\( x = 16(v + 36) \)
Her iki durumdaki mesafeler eşittir.
\( x = 20v = 16(v + 36) \)
\( 5v = 4(v + 36) \)
\( v = 144 \) km/sa
144 kilometre hızla giden aracın 20 saatte gittiği mesafeyi bulalım.
\( x = 20 \cdot 144 = 2880 \) km bulunur.
\( B \) şehri \( A \) şehrinin 23 km kuzeyinde,
\( C \) şehri \( B \) şehrinin 30 km doğusunda,
\( D \) şehri \( C \) şehrinin 48 km güneyinde,
\( E \) şehri \( D \) şehrinin 90 km batısında yer almaktadır.
Buna göre, \( A \) ve \( E \) şehirleri arasındaki kuş uçuşu mesafe kaç km'dir?
Çözümü GösterVerilen bilgileri bir şekil üzerinde gösterelim.
İstenen uzaklığa \( x \) km diyelim.
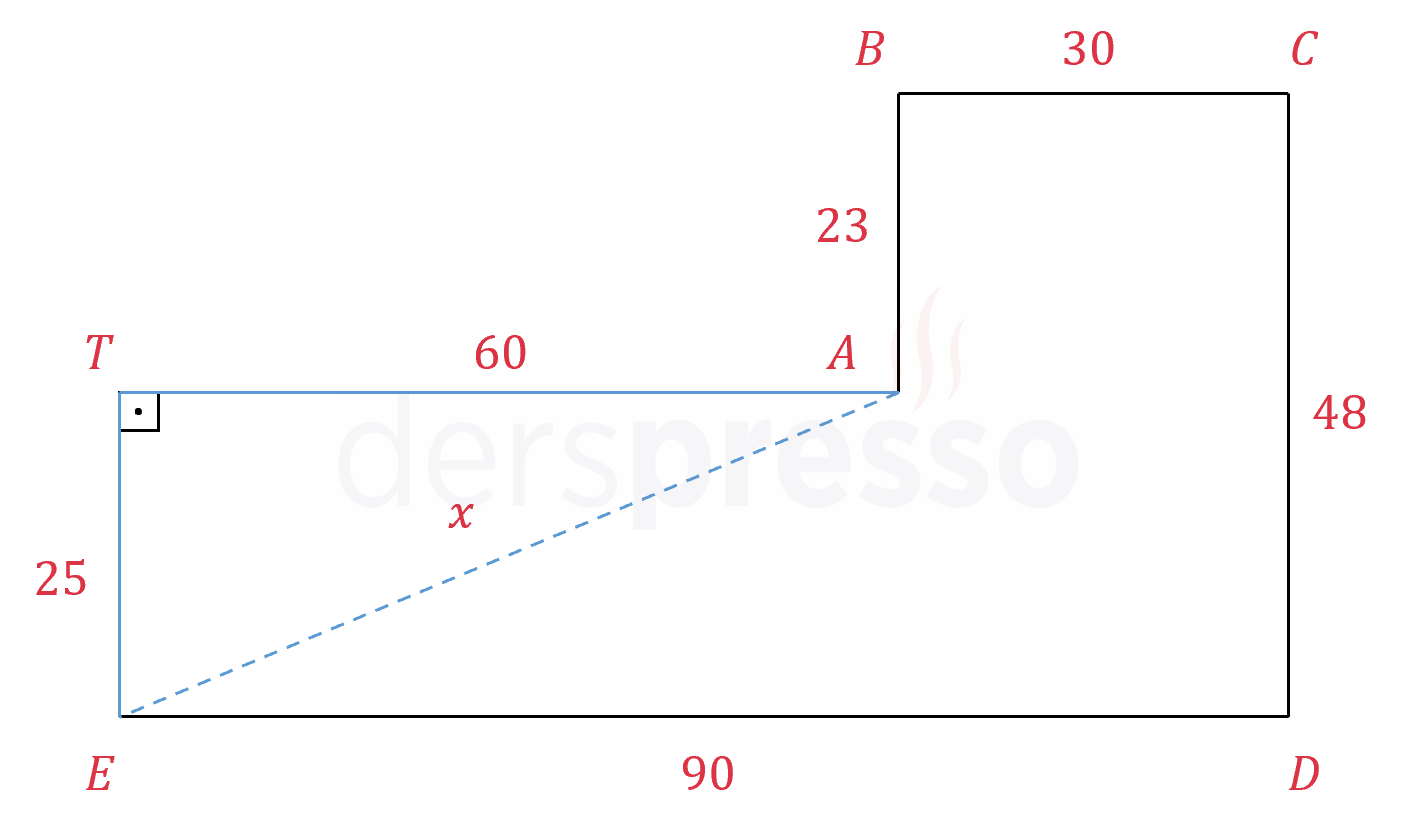
\( \abs{TA} \) uzaklığını bulalım.
\( \abs{TA} = \abs{ED} - \abs{BC} \)
\( = 90 - 30 = 60 \) km
\( \abs{TE} \) uzaklığını bulalım.
\( \abs{TE} = \abs{CD} - \abs{BA} \)
\( = 48 - 23 = 25 \) km
\( ETA \) dik üçgeninde Pisagor teoremini uygulayalım.
\( \abs{TE}^2 + \abs{TA}^2 = \abs{AE}^2 \)
\( 25^2 + 60^2 = x^2 \)
\( x = 65 \) km
\( A \) ve \( E \) şehirleri arasındaki kuş uçuşu mesafe 65 km bulunur.
A kentinden B kentine 30 km/saat sabit hızla gidip B kentinden A kentine 20 km/saat sabit hızla dönen bir aracın gidiş dönüş ortalama hızı kaç km/saat olur?
Çözümü GösterA kentiyle B kenti arası mesafeye \( x \) km diyelim.
Aracın gidiş dönüşte gittiği toplam yol \( 2x \) km olur.
Süre (\( t \)), toplam mesafenin (\( x \)) ortalama hıza (\( v \)) bölümüne eşittir.
\( t = \dfrac{x}{v} \)
Buna göre araç A kentinden B kentine \( \frac{x}{30} \) saatte gidip, B kentinden A kentine \( \frac{x}{20} \) saatte dönmüştür.
Aracın gidiş dönüşte harcadığı toplam süreyi bulalım.
\( \dfrac{x}{30} + \dfrac{x}{20} = \dfrac{2x}{60} + \dfrac{3x}{60} \)
\( = \dfrac{5x}{60} = \dfrac{x}{12} \) saat
Ortalama hız (\( v \)), toplam mesafenin (\( x \)) toplam süreye (\( t \)) bölümüne eşittir.
\( v = \dfrac{2x}{\frac{x}{12}} = 2x \cdot \dfrac{12}{x} = 24 \) km/saat bulunur.
160 km'lik bir yolu 2 saatte giden bir araç, aynı yolu 45 dk daha kısa sürede alabilmesi için ortalama hızını kaç km/saat arttırmalıdır?
Çözümü Göster160 km'lik yolu 2 saatte giden bir aracın ortalama hızı \( \frac{160}{2} = 80 \) km/saat'tir.
45 dakika \( = \frac{45}{60} = \frac{3}{4} \) saat
Aracın bu yolu \( \frac{3}{4} \) saat daha kısa sürede alması için \( 2 - \frac{3}{4} = \frac{5}{4} \) saatte alması gerekir.
Aracın 160 km'lik yolu \( \frac{5}{4} \) saatte alması için gerekli ortalama hızı bulalım.
\( v = \dfrac{160}{\frac{5}{4}} = 160 \cdot \dfrac{4}{5} = 128 \) km/saat
Buna göre, araç hızını \( 128 - 80 = 48 \) km/saat artırmalıdır.
Bir araç molalar hariç tutulduğunda bir yolu ortalama 150 km/saat hızla 4 saatte gidiyor.
Aracın yol boyunca verdiği molalar da dikkate alındığında ortalama hızı 125 km/saate düştüğüne göre, aracın mola verdiği toplam süre kaç dakikadır?
Çözümü GösterMolalar hariç tutulduğundaki ortalama hız ile yolculuk süresinin çarpımı toplam mesafeyi verir.
\( 150 \cdot 4 = 600 \) km
Molalar dahil edildiğindeki yolculuk süresine \( t \) diyelim.
\( 125 \cdot t = 600 \)
\( t = 4,8 \) saat
Aradaki zaman farkı toplam mola süresine denk gelir.
Buna göre araç \( 4,8 - 4 = 0,8 \) saat, yani \( 0,8 \cdot 60 = 48 \) dakika mola vermiştir.
Bir araç saniyede \( 3a \) metre hızla 10 saniyede aldığı yolu, saniyede \( 2a - 6 \) metre hızla 24 saniyede alabiliyor.
Bu araç saniyede \( a \) metre hızla 320 metrelik bir yolu kaç saniyede alır?
Çözümü GösterAraç bir yolu \( 3a \) m/sn hızla 10 saniyede alıyorsa yol \( 10 \cdot 3a = 30a \) metredir.
Araç aynı yolu \( 2a - 6 \) m/sn hızla 24 saniyede alıyorsa yol aynı zamanda \( 24(2a - 6) \) metredir.
Her iki durumda yol uzunluğu birbirine eşitttir.
\( 30a = 24(2a - 6) \)
\( 5a = 4(2a - 6) \)
\( 5a = 8a - 24 \)
\( 3a = 24 \)
\( a = 8 \)
Aracın \( a = 8 \) m/sn hızla 320 metrelik yolu alacağı süreyi bulalım.
\( t = \dfrac{320}{8} = 40 \) saniye bulunur.
Saatte 240 km/sa sabit hızla giden bir yüksek hızlı trende seyahat eden Kerem, trenin en arka noktasından en ön noktasına doğru sabit hızla 3 dakikada yürürken kolundaki akıllı saat Kerem'in hızını 245 km/sa olarak ölçüyor.
Buna göre, trenin uzunluğu kaç metredir?
Çözümü Göster3 dakika \( = \dfrac{3}{60} = \dfrac{1}{20} \) saat
Kerem'in yürüme hızına \( v \) km/sa, trenin uzunluğuna \( x \) km diyelim.
Tren hareket halindeyken Kerem yürüdüğünde toplam hızı trenin hızı ile yürüme hızının toplamına eşit olur.
\( 240 + v = 245 \)
\( v = 5 \) km/sa
Kerem trenin en arkasından en önüne yürüdüğünde trenin boyu kadar mesafe katetmiştir.
Buna göre Kerem, \( x \) km uzunluğunda mesafeyi 5 km/sa hızla \( \frac{1}{20} \) saatte katetmiştir.
\( x = 5 \cdot \dfrac{1}{20} = \dfrac{1}{4} \) km
Buna göre trenin uzunluğu \( \frac{1}{4} \cdot 1000 = 250 \) metredir.
Ahmet evinden işine motosikletle gidip gelmektedir. Giderken işe 45 dakikada varırken dönüşte aynı yolu 1 saat 15 dakikada almaktadır.
Ahmet'in dönerkenki ortalama hızı giderkenki ortalama hızından 24 km/saat az olduğuna göre, Ahmet'in evi ile işi arasındaki mesafe kaç km'dir?
Çözümü Göster45 dakika \( = \dfrac{45}{60} = \dfrac{3}{4} \) saat
1 saat 15 dakika \( = \dfrac{75}{60} = \dfrac{5}{4} \) saat
Ahmet'in işe giderkenki hızına \( v \) diyelim. Giderken \( \frac{3}{4} \) saatte işe vardığına göre evle iş arası \( \frac{3v}{4} \) km'dir.
Dönerkenki hızı \( v - 24 \) ve dönüş süresi \( \frac{5}{4} \) saat olduğuna göre, evle iş arası aynı zamanda \( \frac{5}{4}(v - 24) = \frac{5v - 120}{4} \) km'dir.
Gidiş ve dönüşteki yol uzunlukları birbirine eşittir.
\( \dfrac{3v}{4} = \dfrac{5v - 120}{4} \)
\( 3v = 5v - 120 \)
\( 2v = 120 \)
\( v = 60 \) km/saat
Ahmet evden işe \( v = 60 \) km/saat hızla \( \frac{3}{4} \) saatte gittiğine göre, bu yol \( 60 \cdot \frac{3}{4} = 45 \) km'dir.
A şehrinden B şehrine ortalama 90 km/saat hızla giden Seray, dönüşte ortalama 50 km/saat hızla dönmüştür.
Yolculuk sırasında hiç mola vermeyen Seray yolda toplam 14 saat geçirdiğine göre, A ve B şehirleri arası kaç km'dir?
Çözümü GösterSeray'ın gidişte harcadığı süreye \( t \) saat diyelim. Gidiş ve dönüş için harcadığı toplam süre 14 saat olduğuna göre, dönüşte harcadığı süre \( 14 - t \) saat olur.
Seray gidişte 90 km/saat hızla \( t \) saatte \( 90t \) km yol almıştır. Aynı yolu dönüşte 50 km/saat hızla \( 14 - t \) saatte almıştır.
Gidiş ve dönüşteki yol uzunlukları birbirine eşittir.
\( 90t = 50(14 - t) \)
\( 90t = 700 - 50t \)
\( 140t = 700 \)
\( t = 5 \) saat
Seray A ve B şehirleri arasını 90 km/saat hızla 5 saatte aldığına göre, iki şehir arası \( 5 \cdot 90 = 450 \) km'dir.
Ali ve Ahmet \( x \) metre uzunluğundaki bir havuzun karşılıklı iki tarafından sabit hızla ve aynı anda yüzmeye başlıyorlar ve 1 dakika sonra ilk kez buluşuyorlar.
İkinci kez buluştuklarında toplamda \( 3x \) metre gittiklerine göre, ikinci buluşmaları yüzmeye başladıktan kaç dakika sonra olmuştur?
Çözümü GösterAli'nin dakikada \( a \), Ahmet'in dakikada \( b \) metre yüzdüğünü varsayalım.
İkinci kez buluşma sürelerine \( t \) diyelim.
\( t \) dakikada yüzülen toplam mesafeyi ikisinin hızlarının toplamından bulalım.
\( (a + b) \cdot 1 = x \)
\( (a + b) \cdot t = 3x \)
\( t = 3 \) dk olarak bulunur.
Bir aracın yarıçapı 42 cm olan tekerlekleri yarıçapı 40 cm olan tekerleklerle değiştiriliyor.
Buna göre, araç belirli bir mesafeyi katederken her bir tekerleğin yapacağı dönüş sayısı ilk duruma göre yüzde kaç artar?
Çözümü GösterBir tekerleğin ilk durumda \( x \) km gitmek için yapacağı dönüş sayısına \( n \), ikinci durumda \( x \) km gitmek için yapacağı dönüş sayısına \( n' \) diyelim.
Tekerleğin her iki durumda katettiği toplam mesafe birbirine eşit ve \( x \) km'dir.
\( 2\pi \cdot 42 \cdot n = 2\pi \cdot 40 \cdot n' \)
\( n' = \dfrac{42n}{40} \)
\( = \dfrac{21n}{20} = \dfrac{105n}{100} \)
Buna göre, yeni durumda bir tekerleğin dönüş sayısı ilk duruma göre yüzde 5 artar.
Gizem eşkenar üçgen şeklindeki bir pistin ilk kenarını saatte 6 km, ikinci kenarını saatte 12 km, üçüncü kenarını saatte 8 km ile koşuyor.
Buna göre, Gizem'in ortalama hızı saatte kaç kilometredir?
Çözümü GösterÜçgenin bir kenarının uzunluğuna \( x \) km, Gizem'in tüm pisti koşma süresine \( t \) saat diyelim.
\( t = \dfrac{x}{6} + \dfrac{x}{8} + \dfrac{x}{12} \)
\( = \dfrac{4x}{24} + \dfrac{3x}{24} + \dfrac{2x}{24} \)
\( = \dfrac{9x}{24} = \dfrac{3x}{8} \) saat
Gizem'in ortalama hızı, pistin toplam uzunluğunun tüm pisti koşma süresine eşittir.
Ortalama hız \( = \dfrac{3x}{\frac{3x}{8}} = 8 \) km/saat bulunur.
Yeliz sabit hızla yürüyüş yaptığı yolun dörtte birini gittikten sonra hızını 2 katına çıkararak mola vermeden yolu tamamlıyor.
Yeliz yürüyüş için toplam 5 saat harcadığına göre, kaç saat yürüdükten sonra hızını iki katına çıkarmıştır?
Çözümü GösterYeliz'in yürüdüğü yolun uzunluğuna işlem kolaylığı açısından 8 birim diyelim.
Bu yolun ilk kısmı \( 8 \cdot \frac{1}{4} = 2 \) birim, kalan kısmı \( 8 - 2 = 6 \) birimdir.
Yeliz'in yolun ilk kısmındaki hızına \( v \) diyelim, bu durumda yolun ikinci kısmındaki hızı \( 2v \) olur.
Yeliz 2 birimlik yolu \( \frac{2}{v} \) saatte, 6 birimlik kalan yolu \( \frac{6}{2v} = \frac{3}{v} \) saatte yürür.
Toplam yürüyüş süresini bulalım.
\( \dfrac{2}{v} + \dfrac{3}{v} = \dfrac{5}{v} \) saat
Yeliz yürüyüş için toplam 5 saat harcamıştır.
\( \dfrac{5}{v} = 5 \)
\( v = 1 \) birim/saat
Buna göre yürüyüşün ilk kısmı \( \frac{2}{v} = 2 \) saat sürmüştür, yani Yeliz 2 saat yürüdükten sonra hızını 2 katına çıkarmıştır.
Bir koşu pistinin uzunluğu 720 metredir. Pistin başından aynı anda aynı yöne doğru sabit hızlarla koşmaya başlayan Arın ve Barlas'ın koşuları ile ilgili aşağıdakiler bilinmektedir.
- Arın Barlas'tan dakikada 60 metre daha hızlı koşmaktadır.
- Arın pistin diğer ucuna ulaştığında Barlas'ın Arın'a olan uzaklığı 120 metredir.
Buna göre Barlas pisti toplam kaç dakikada koşar?
Çözümü GösterBarlas'ın hızına \( v \), Arın'ın hızına \( v + 60 \) diyelim.
Arın pisti tamamladığında \( 720 \) metre koşmuş olur. Barlas bu noktada \( 720 - 120 = 600 \) metre koşmuş olur.
İkisi aynı süre koştukları için koştukları mesafelerin hızlarına oranları birbirine eşittir.
\( \dfrac{720}{v + 60} = \dfrac{600}{v} \)
İçler - dışlar çarpımı yapalım.
\( 720v = 600v + 36000 \)
\( 120v = 36000 \)
\( v = 300 \) m/dk
Buna göre Barlas pisti toplam \( \frac{720}{300} = 2,4 \) dakikada koşar.
Aralarında 720 km mesafe olan bir otobüs ile bir motosiklet birbirlerine doğru aynı anda sabit hızlarla yola çıkıyorlar.
Otobüs 480 km yol aldıktan sonra saatte 40 km/saat hızla hareket eden motosikletle karşılaşıyor. Buna göre otobüs karşılaştıkları ana kadar kaç km/saat hızla ilerlemiştir?
Çözümü GösterAralarında 720 km olan yolda otobüs 480 km gittiğinde motosikletli ile karşılaşıyorsa motosiklet bu noktaya kadar \( 720 - 480 = 240 \) km yol gitmiştir.
Motosikletlinin saatteki hızı 40 km/saat olduğuna göre, bu yolu \( \frac{240}{40} = 6 \) saatte gitmiştir.
Otobüs de 480 km'yi aynı sürede gittiğine göre, bu yoldaki sabit hızı \( \frac{480}{6} = 80 \) km/saat olur.
Aralarında 360 km mesafe bulunan iki araç birbirine doğru sabit hızlarla hareket ediyor ve araçlar 1,5 saat sonra karşılaşıyor.
Bu araçlardan birinin hızı aynı tutulurken diğerinin hızı saatte kaç km azaltılırsa karşılaşma süreleri 2 saat olur?
Çözümü GösterBu araçlar birbirlerine doğru hareket ettikleri için bir saatte hızlarının toplamı kadar yaklaşırlar.
Buna göre 1,5 saatte aralarındaki 360 km'lik mesafe kapanıyorsa hızları toplamı \( \frac{360}{1,5} = 360 \cdot \frac{2}{3} = 240 \) km/saat'tir.
Bu iki aracın 1,5 saat yerine 2 saatte karşılaşmaları için hızları toplamı \( \frac{360}{2} = 180 \) km/saat olmalıdır.
Araçlardan birinin hızını değiştirmeden hızları toplamını 240 km/saat'ten 180 km/saat'e düşürmek için araçlardan birinin hızı saatte \( 240 - 180 = 60 \) km/saat azaltılmalıdır.
Aynı noktadan zıt yönlere sabit hızlarla hareket eden iki araçtan biri diğerinden 20 km/saat daha hızlıdır.
Aynı anda harekete başladıktan 2 saat sonra aralarındaki uzaklık 220 km olduğuna göre, hızlı giden aracın hızı saatte kaç km'dir?
Çözümü Gösterİki araçtan yavaş olanın hızına \( v \) km/saat diyelim. Hızlı olanın hızı bu durumda \( v + 20 \) km/saat olur.
İki saat sonra yavaş olan araç başlangıç noktasına \( 2v \) km, hızlı olan araç ise \( 2(v + 20) = 2v + 40 \) km uzaklıkta olur.
2 saat sonra aralarındaki uzaklık 220 km'dir.
\( 2v + (2v + 40) = 220 \)
\( 4v + 40 = 220 \)
\( 4v = 180 \)
\( v = 45 \) km/saat
Buna göre, hızlı giden aracın hızı \( v + 20 = 45 + 20 = 65 \) km/saat'tir.
Saatte \( 2v \) km sabit hızla hareket eden bir at arabası ile saatte \( 5v \) km sabit hızla hareket eden bir traktör A kentinden B kentine doğru aynı anda hareket ediyorlar.
At arabası A kenti ile B kenti arasındaki C kentine vardığında; traktör B kentine varmış, hiç mola vermeden geri dönmeye başlamış ve dönerken C kentine ulaşmıştır.
Buna göre, C ve B kentleri arası mesafenin A ve B kentleri arası mesafeye oranı kaçtır?
Çözümü GösterAnlatılan durumu aşağıdaki gibi çizebiliriz.
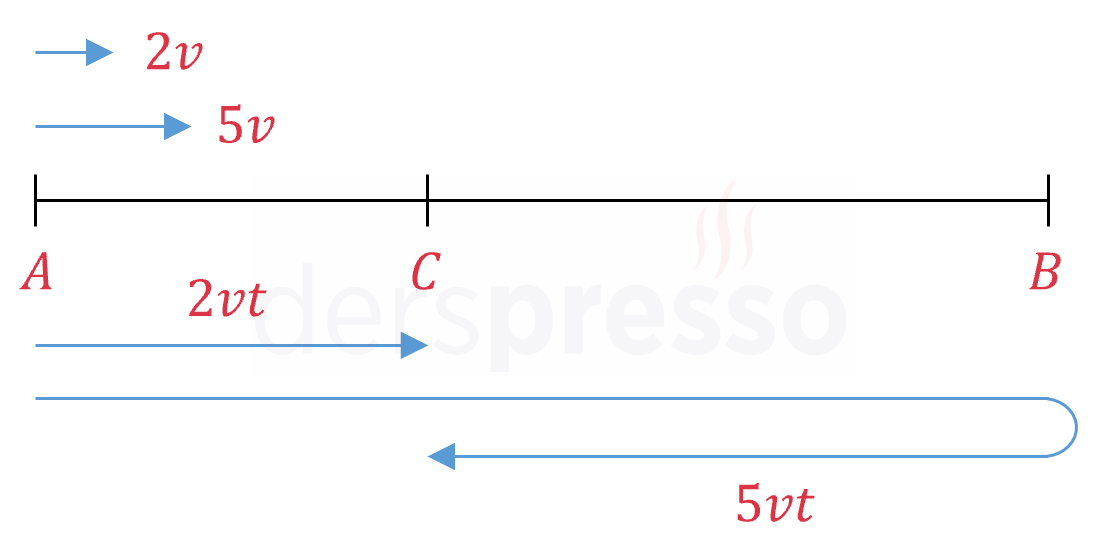
At arabasının C kentine varış süresine \( t \) diyelim. Bu durumda A ve C kentleri arası mesafe \( 2v \cdot t = 2vt \) olur.
Aynı sürede traktör A kentinden B kentine varıp geri dönmüş ve C kentine ulamıştır. Traktör bu sürede toplam \( 5v \cdot t = 5vt \) yol almıştır.
Traktör giderken A kentinden C kentine varana kadar \( 2vt \) yol gitmiştir. Toplamda \( 5vt \) yol giden traktör B ve C kentleri arasında gidiş - dönüş toplam \( 5vt - 2vt = 3vt \) yol almıştır. Bu durumda B ve C kentleri arası mesafe \( \frac{3vt}{2} \) olur.
A ve C kentleri arası mesafe \( 2vt \), C ve B kentleri arası mesafe \( \frac{3vt}{2} \) olduğuna göre, A ve B kentleri arası mesafe \( 2vt + \frac{3vt}{2} = \frac{7vt}{2} \) olur.
C ve B kentleri arasındaki mesafenin A ve B kentleri arasındaki mesafeye oranını bulalım.
\( \dfrac{\frac{3vt}{2}}{\frac{7vt}{2}} = \dfrac{3}{7} \) bulunur.
Cemre okula yetişmek için evden çıkıp sabit hızla koşmaya başlıyor. Koşmaya başladıktan 4 dakika sonra okula 240 metre, 10 dakika sonra 24 metre kalıyor.
Buna göre Cemre'nin eviyle okulu arası kaç metredir?
Çözümü GösterCemre koşmaya başladıktan 4 dakika sonra okula 240 metre, 10 dakika sonra 24 metre kalıyorsa Cemre \( 10 - 4 = 6 \) dakikada \( 240 - 24 = 216 \) metre koşmaktadır.
Bu durumda Cemre'nin hızı dakikada \( \frac{216}{6} = 36 \) metredir.
Buna göre Cemre'nin eviyle okulu arası uzaklığı aşağıdaki iki hesaplamadan biri ile bulabiliriz.
Koşmaya başladıktan 4 dakika sonra okula 240 metre kalıyor.
\( 4 \cdot 36 + 240 = 384 \) metre
Koşmaya başladıktan 10 dakika sonra okula 24 metre kalıyor.
\( 10 \cdot 36 + 24 = 384 \) metre
Semih ve Kübra A kentinden 480 km uzaklıktaki B kentine doğru aynı anda farklı araçlarla ve sabit hızlarla yola çıkıyorlar. Semih 160 km yol aldığında, Kübra Semih'in yarım saat önce bulunduğu noktaya geliyor.
Semih yola çıktıktan 6 saat sonra B kentine ulaştığına göre, Kübra B kentine Semih'ten kaç saat sonra ulaşır?
Çözümü GösterSemih 480 km'lik yolu 6 saatte alıyorsa hızı saatte \( \frac{480}{6} = 80 \) km'dir.
Semih 160 km yol aldığında yola çıkmasının üzerinden \( \frac{160}{80} = 2 \) saat geçmiştir.
Kübra bu sürenin sonunda Semih'in yarım saat önce bulunduğu (yani 1,5 saatte vardığı) noktaya gelmiş olduğuna göre, 2 saatte \( 80 \cdot 1,5 = 120 \) km yol almıştır.
Buna göre Kübra'nın hızı saatte \( \frac{120}{2} = 60 \) km'dir.
Kübra A kentinden B kentine \( \frac{480}{60} = 8 \) saatte, yani Semih'ten \( 8 - 6 = 2 \) saat sonra varır.
Çevresi 6 km olan dairesel bir pistte aynı noktada bulunan iki bisikletli zıt yönlerde aynı anda harekete başlıyor.
Bisikletlerden biri dakikada 300 metre diğeri 200 metre sabit hızla hareket ettiğine göre, bu iki bisikletli kaç dakika sonra karşılaşır?
Çözümü GösterBisikletlerin hızları metre\dakika cinsinden verildiği için pistin uzunluğunu metreye çevirelim.
6 km = 6000 metre
Bu bisikletliler birbirine dakikada \( 300 + 200 = 500 \) metre yakınlaşır.
Buna göre iki bisiklet \( \frac{6000}{500} = 12 \) dakika sonra karşılaşır.
Dairesel bir parkurda A noktasında bulunan iki koşucudan birinin sabit hızı 9 km/saat, diğerinin sabit hızı 12 km/saat'tir.
Aynı anda zıt yönlere doğru harekete başlayan bu koşucular 3 saat sonra B noktasında karşılaşıyor. Bu koşuculardan yavaş olan karşılaşmadan kaç saat sonra tekrar A noktasına varır?
Çözümü Göster9 km/saat hızla koşan koşucu 3 saatte \( 3 \cdot 9 = 27 \) km, 12 km/saat hızla koşan koşucu 3 saatte \( 3 \cdot 12 = 36 \) km yol alır.
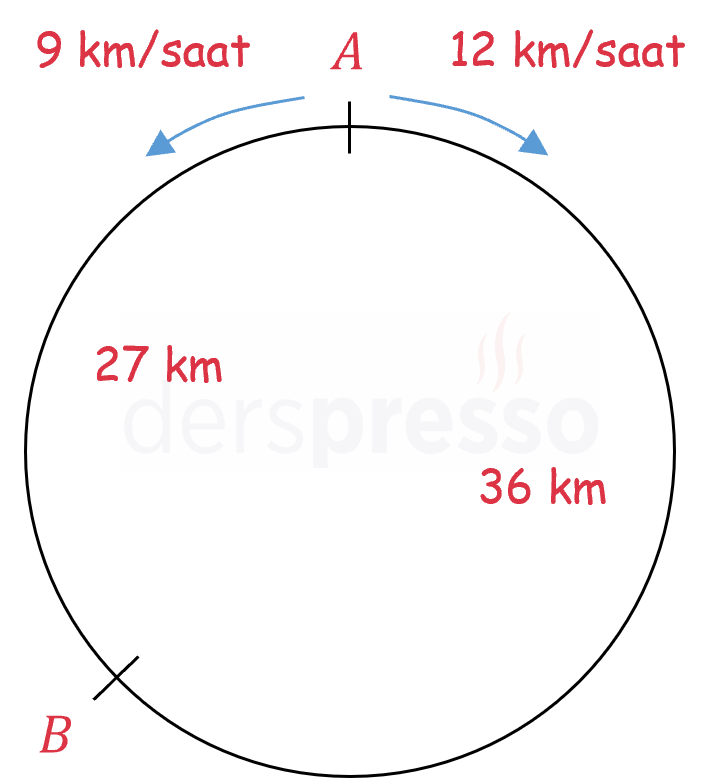
Yavaş olan yani 9 km/saat hızla koşan koşucunun A noktasına varması için, hızlı koşucunun katettiği mesafe olan 36 km daha yol alması gerekir.
Buna göre yavaş olan koşucu karşılaşmadan \( \frac{36}{9} = 4 \) saat sonra tekrar A noktasına varır.
İki gemi 20 km/sa hızla birbirine doğru ilerliyor. Gemiler arasındaki uzaklık 360 km iken birinci gemideki bir mürettebat sürat botuna atlıyor ve 100 km/sa hızla ikinci gemiye doğru hareket ediyor. İkinci gemiye varır varmaz geri dönüyor ve tekrar birinci gemiye doğru 40 km/sa hızla yola çıkıyor.
Mürettebat birinci gemiye vardığında iki gemi arasındaki mesafe kaç km olur?
Çözümü GösterSoruyu iki adımda inceleyelim.
1. adım:
Sürat botu ile ikinci geminin nerede ve ne zaman karşılaştığını bulalım.
Sürat botu ve ikinci gemi birbirine \( 100 + 20 = 120 \) km/sa hızla yaklaşır.
Aralarında 360 km mesafe olduğuna göre bot ve gemi \( \frac{360}{120} = 3 \) saat sonra karşılaşırlar.
3 saatin sonunda iki gemi arasındaki mesafeyi bulalım.
İki gemi birbirine saatte \( 20 + 20 = 40 \) km/sa hızla yaklaşır.
Gemiler 3 saatin sonunda birbirlerine \( 40 \cdot 3 = 120 \) km yaklaşır, dolayısıyla sürat botu ikinci gemiye vardığında aralarındaki mesafe \( 360 - 120 = 240 \) km olur.
2. adım:
Sürat botu ile birinci geminin tekrar nerede ve ne zaman karşılaştığını bulalım.
Sürat botu ve birinci gemi birbirine \( 40 + 20 = 60 \) km/sa hızla yaklaşır.
Aralarında 240 km mesafe olduğuna göre bot ve gemi \( \frac{240}{60} = 4 \) saat sonra karşılaşırlar.
4 saatin sonunda iki gemi arasındaki mesafeyi bulalım.
İki gemi birbirine saatte \( 20 + 20 = 40 \) km/sa hızla yaklaşır.
Gemiler 4 saatin sonunda birbirlerine \( 40 \cdot 4 = 160 \) km yaklaşır, dolayısıyla aralarındaki mesafe \( 240 - 160 = 80 \) km olur.
Ali ile Mehmet dairesel bir pistte aynı noktadan ters yönde sabit hızlarla koşmaya başlıyorlar ve 36 saniye sonra pistin belirli bir noktasında ilk kez buluşuyorlar.
Ali bu pisti tek başına 90 saniyede koştuğuna göre, Mehmet bu pisti tek başına kaç saniyede koşar?
Çözümü GösterAli'nin saniyedeki hızına \( x \) metre, Mehmet'in saniyedeki hızına \( y \) metre diyelim.
Ali bu pisti tek başına 90 saniyede koştuğuna göre, pistin uzunluğu \( 90x \) metre olur.
Ali ve Mehmet koşmaya başladıktan 36 saniye sonra pistin belirli bir noktasında ilk kez buluşuyorlar.
İlk buluşma noktasına kadar ikisinin koştukları mesafelerin toplamı pistin uzunluğuna eşit olur.
\( 36(x + y) = 90x \)
\( y = \dfrac{3x}{2} \)
Mehmet'in pisti tek başına koştuğu süreye \( t \) saniye diyelim.
\( y \cdot t = 90x \)
\( \dfrac{3x}{2} \cdot t = 90x \)
\( t = 60 \) saniye bulunur.
Aynı noktadan zıt yönlere doğru hareket eden iki araçtan birincisinin sabit hızı 80 km/saat, ikincisinin sabit hızı 120 km/saat'tir.
70 km'lik dairesel bir yol üzerinde hareket eden bu iki araç kaç dakika sonra ilk kez karşılaşıp aralarında 30 km olacak kadar uzaklaşırlar?
Çözümü Gösterİki araç birbirine saatte \( 80 + 120 = 200 \) km hızla yaklaşır.
Araçlar 70 km'lik dairesel yolda \( \frac{70}{200} = \frac{7}{20} = 0,35 \) saat sonra karşılaşırlar.
Araçlar karşılaştıktan sonra yine saatte 200 km hızla birbirinden uzaklaşırlar. 30 km uzaklaşmak için \( \frac{30}{200} = \frac{3}{20} = 0,15 \) saat daha hareket ederler.
Buna göre başlangıçtan itibaren \( 0,35 + 0,15 = 0,5 \) saat, yani 30 dakika sonra aralarında 30 km olacak kadar uzaklaşmış olurlar.

Yukarıda bir aracın hızının zamana bağlı değişimi gösterilmiştir.
Buna göre aracın yol boyunca ortalama hızı saatte kaç kilometredir?
Çözümü GösterAracın gittiği toplam mesafeye \( x \), ortalama hızına \( v \) diyelim.
Araç ilk 2 saat boyunca saatte 40 km hızla giderek \( 2 \cdot 40 = 80 \) km yol gitmiştir.
Araç sonraki 1 saat boyunca saatte 60 km hızla giderek \( 1 \cdot 60 = 60 \) km yol gitmiştir.
Araç sonraki 3 saat boyunca saatte 120 km hızla giderek \( 3 \cdot 120 = 360 \) km yol gitmiştir.
Araç sonraki 2 saat boyunca saatte 160 km hızla giderek \( 2 \cdot 160 = 320 \) km yol gitmiştir.
Aracın gittiği toplam mesafeyi bulalım.
\( x = 80 + 60 + 360 + 320 = 820 \) km
Araç bu yolu 8 saatte gitmiştir.
Ortalama hız, toplam mesafenin toplam süreye bölümüne eşittir.
\( v = \dfrac{820}{8} = 102,5 \) km/sa bulunur.

Yukarıda hızları doğrusal olarak değişen \( A \) ve \( B \) araçlarının hız - zaman grafiği verilmiştir.
\( A \) aracının hızı 50 m/s olduğunda \( B \) aracının hızı kaç m/s olur?
Çözümü GösterAraçların birim zamanda hızlarındaki değişim (artış ya da azalış) miktarlarını bulalım.
\( A \) aracının hızı 4 saatte 140 m/s'den 80 m/s'ye düşüyor.
\( \dfrac{80 - 140}{4} = -15 \) m/s
\( B \) aracının hızı 10 saatte 0 m/s'den 120 m/s'ye çıkıyor.
\( \dfrac{120 - 0}{10} = 12 \) m/s
\( A \) aracının hızının 50 m/s olduğu zamana \( t \) diyelim.
\( A \) aracının hızı saniyede 15 m/s azalmaktadır.
\( 140 - 15t = 50 \)
\( t = 6 \)
\( A \) aracının hızı 6. saniyede 50 m/s olur.
\( B \) aracının 6. saniyedeki hızını bulalım.
\( B \) aracının hızı saniyede 12 m/s artmaktadır.
\( 0 + 12 \cdot 6 = 72 \) m/s bulunur.
Berkay sabah işe gitmek için bisikletiyle evden çıktıktan bir süre sonra arkadaşıyla karşılaşıyor ve biraz sohbet ettikten sonra tekrar yola devam ediyor. Berkay arkadaşıyla karşılaştıktan sonra hızını artırmasına rağmen işe 5 dakika geç kalıyor.
Aşağıda Berkay'ın evden işe varana kadarki konum - zaman grafiği verilmiştir.
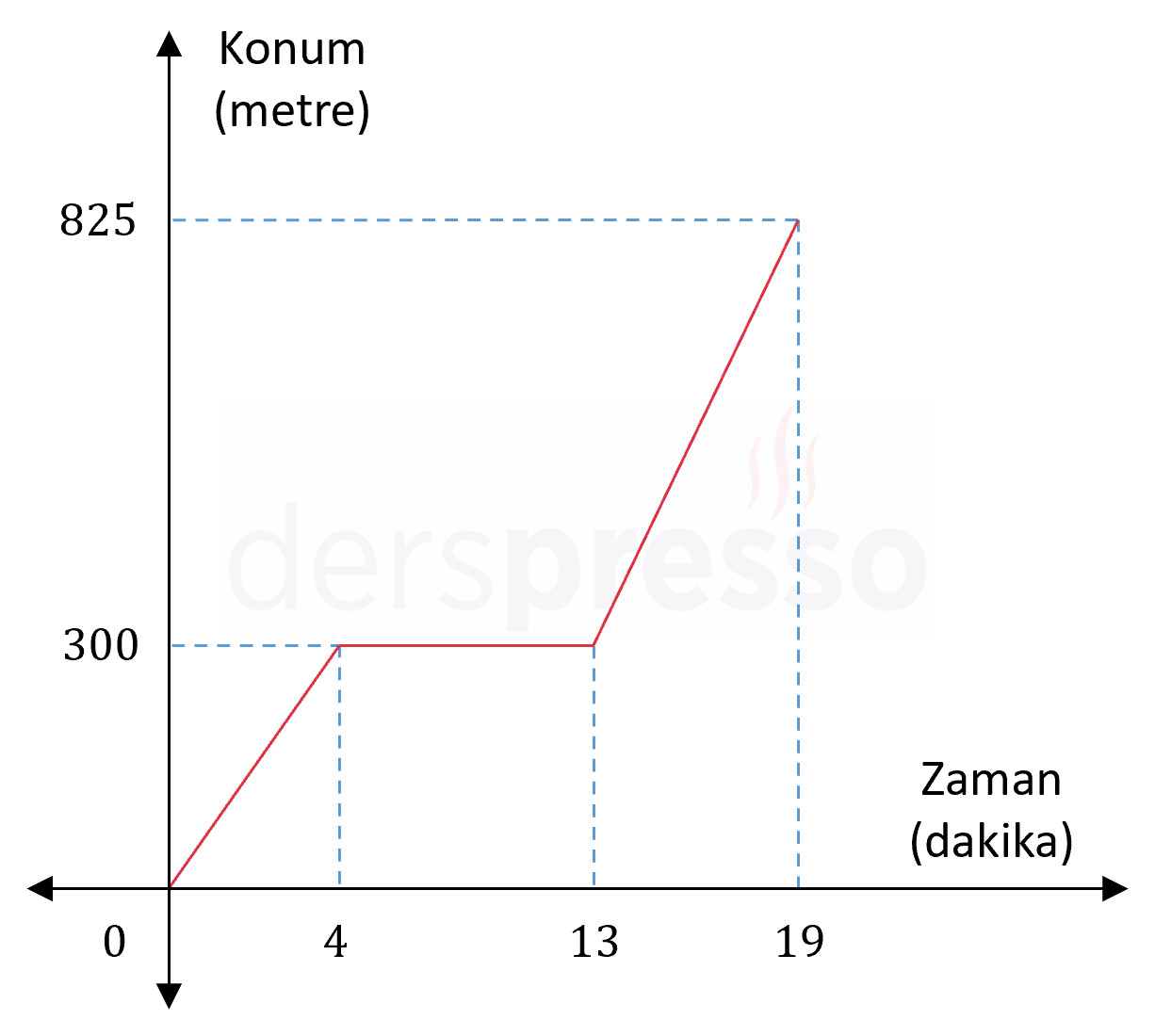
Buna göre Berkay, arkadaşı ile karşılaşmamış ve evden çıktığı ilk hızla işe gitmiş olsaydı işe kaç dakika erken varırdı?
Çözümü GösterBerkay'ın evden çıktıktan sonraki (arkadaşıyla karşılaşıncaya kadarki) ilk hızına \( v_1 \) diyelim.
\( x = v_1 \cdot t \)
\( 300 = v_1 \cdot 4 \)
\( v_1 = 75 \) m/dk
Berkay bu ilk hızıyla işe gitmiş olsaydı işe kaç dakikada varacağını bulalım.
Berkay'ın eviyle işi arası 825 metredir.
\( 825 = 75 \cdot t \)
\( t = 11 \) dakika
Berkay arkadaşıyla hiç karşılaşmamış ve ilk hızıyla işe gitmiş olsaydı 11 dakikada işe varmış olacaktı.
Grafiğe göre Berkay 19 dakika sonunda işe 5 dakika geç kaldığına göre, işe \( 19 - 5 = 14 \) dakika sonra varmış olsaydı işe tam zamanında yetişmiş olacaktı.
Berkay ilk hızıyla 11 dakikada işe varacağına göre, işe \( 14 - 11 = 3 \) dakika erken varmış olurdu.
Ali ve Berk, birlikte kahve içtikten sonra aynı cadde üzerindeki evlerine doğru zıt yönlerde ve sabit hızlarla koşmaya başlıyorlar.
İki arkadaşın koşmaya başladıktan sonra aralarındaki mesafenin zamana bağlı değişimi aşağıdaki grafikte gösterilmiştir.

Berk evine daha önce vardığına göre, Berk'in evi kaç metre uzaklıktadır?
Çözümü GösterAli ve Berk sabit hızlarla koştuklarına göre, grafikteki 6. dakikadaki değişim Berk'in evine vardığı zamana karşılık gelir.
Ali'nin hızına \( v_A \), Berk'in hızına \( v_B \) diyelim.
Ali ve Berk zıt yönlerde koştuklarına göre, hızlarının toplamı 6. dakikada aralarındaki mesafenin geçen süreye bölünmesiyle elde edilir.
\( v_A + v_B = \dfrac{x}{t} \)
\( = \dfrac{1500}{6} = 250 \) m/dk
6. dakikadan sonra sadece Ali koşmaktadır.
\( v_A = \dfrac{2100 - 1500}{10 - 6} = 150 \) m/dk
Berk'in hızını bulalım.
\( v_A + v_B = 150 + v_B = 250 \)
\( v_B = 100 \) m/dk
Berk evine 6 dakikada vardığına göre, evinin uzaklığını bulalım.
\( x = v \cdot t \)
\( = 100 \cdot 6 = 600 \) metre bulunur.
Bir araç sabit bir hızla yola çıkıp her saatin sonunda hızını %50 artırarak gideceği yere 4 saatte varıyor.
Bu aracın yolculuk boyunca ortalama hızı 130 km/sa olduğuna göre, araç tüm yolu ilk hızıyla gitseydi yolculuk kaç saat sürerdi?
Çözümü GösterAracın ilk hızına işlem kolaylığı açısından \( 40v \) diyelim.
Aracın ikinci saatteki hızı \( 40v + 40v \cdot \frac{50}{100} = 60v \) olur.
Aracın üçüncü saatteki hızı \( 60v + 60v \cdot \frac{50}{100} = 90v \) olur.
Aracın dördüncü saatteki hızı \( 90v + 90v \cdot \frac{50}{100} = 135v \) olur.
Katedilen mesafe ortalama hız ile sürenin çarpımına eşittir.
Buna göre araç her saatte sırasıyla \( 40v, 60v, 90v, 135v \) yol gitmiştir.
Aracın gittiği toplam mesafeyi bulalım.
\( 40v + 60v + 90v + 135v = 325v \) km
Ortalama hız toplam mesafenin toplam süreye bölümüne eşittir.
\( \dfrac{325v}{4} = 130 \) km/sa
\( v = \dfrac{520}{325} = \dfrac{8}{5} \) km/sa
Tüm yolun uzunluğunu bulalım.
\( 325v = 325 \cdot \dfrac{8}{5} = 520 \) km
Aracın ilk hızını bulalım.
\( 40 \cdot \dfrac{8}{5} = 64 \) km/sa
Araç tüm yolu ilk hızıyla gitseydi yolculuğun kaç saat süreceğini bulalım.
Yolculuk süresi gidilen mesafenin ortalama hıza bölümüne eşittir.
\( t = \dfrac{520}{64} \)
\( = \dfrac{65}{8} = 8,125 \) saat bulunur.
Ters yönlerde saniyede 5 metre sabit hızla giden ve aynı uzunluktaki iki trenin baş tarafları aynı hizada buluştuğu anda, Çağrı bu noktadan trenlere paralel bir şekilde sabit hıza koşmaya başlıyor.
Çağrı'yla aynı yönde giden tren Çağrı'yı 13 saniyede, ters yönde giden tren 7 saniyede geçtiğine göre, Çağrı saniyede kaç metre hızla koşmaktadır?
Çözümü GösterÇağrı'nın saniyedeki hızına \( v \) metre, trenlerin boyuna \( x \) metre diyelim.
Çağrı ile aynı yönde giden tren Çağrı'yı 13 saniyede geçiyor.
\( x = 13(5 - v) \)
Çağrı ile ters yönde giden tren Çağrı'yı 7 saniyede geçiyor.
\( x = 7(5 + v) \)
Her iki trenin boyu birbirine eşittir.
\( 13(5 - v) = 7(5 + v) \)
\( 65 - 13v = 35 + 7v \)
\( 20v = 30 \)
\( v = \dfrac{3}{2} \) metre/saniye olarak bulunur.
Aralarındaki mesafe 540 km olan A ve C noktalarında bulunan iki araç aynı anda ve sabit hızlarla birbirine doğru harekete başlıyorlar ve 6 saat sonra iki nokta arasındaki B noktasında karşılaşıyorlar.
A noktasından yola çıkan araç daha sonra C noktasına 4 saatte vardığına göre, C noktasından yola çıkan aracın hızı saatte kaç km'dir?
Çözümü GösterA noktasından yola çıkan aracın hızına \( a \), C noktasından yola çıkan aracın hızına \( c \) diyelim.

Araçlar birlikte toplam 540 km'lik mesafeyi 6 saatte aldıklarına göre, hızları toplamı \( \frac{540}{6} = 90 \) km/saat'tir.
\( a + c = 90 \)
A ve B noktaları arası mesafe \( 6a \), B ve C noktaları arası mesafe \( 6c \) km'dir.
A noktasından yola çıkan araç B ve C noktaları arası mesafeyi 4 saatte gittiğine göre, bu mesafeye \( 4a \) km de diyebiliriz.
\( 6c = 4a \)
\( a = \dfrac{3c}{2} \)
Bu değeri yukarıdaki denklemde yerine koyalım.
\( a + c = 90 \)
\( \dfrac{3c}{2} + c = 90 \)
\( \dfrac{5c}{2} = 90 \)
\( c = 36 \) km/saat
Buna göre, C noktasından hareket eden aracın hızı 36 km/saat'tir.

Şekildeki çevresi 600 m ve çapı \( [AB] \) olan dairesel pistin A ve B noktalarında iki atlet vardır.
Sabit hızla koşan atletlerden birinin hızı 300 m/dk, diğerinin hızı 240 m/dk olduğuna göre, hızlı olan atlet kaç dakika sonra yavaş olanı 3. kez geçer?
Çözümü GösterAtletler çemberin çapının iki ucunda bulunduklarına göre aralarındaki mesafe çemberin çevresinin yarısı, yani \( \frac{600}{2} = 300 \) m olur.
Hızlı koşan atletle yavaş koşan arasında \( 300 - 240 = 60 \) m/dk hız farkı olduğuna göre, aralarındaki mesafe dakikada 60 m azalacaktır.
Hızlı koşan atlet yavaş koşan atletten 300 m (pistin çevresinin yarısı) fazla koştuğunda yavaş koşan atlete ilk kez yetişecektir.
Hızlı koşan atlet o noktadan itibaren yavaş koşan atletten 600 m (pistin çevresi) fazla koştuğunda yavaş koşan atleti 2. kez geçecektir.
Hızlı koşan atlet o noktadan itibaren yavaş koşan atletten 600 m (pistin çevresi) fazla koştuğunda yavaş koşan atleti 3. kez geçecektir.
Buna göre hızlı koşan atlet yavaş koşan atletten toplamda \( 300 + 600 + 600 = 1500 \) m fazla koştuğunda yavaş koşan atleti 3. kez geçecektir.
Hızlı koşan atlet yavaş koşan atletten dakikada 60 m fazla koştuğuna göre yavaş koşan atleti \( \frac{1500}{60} = 25 \) dakika sonra 3. kez geçer.
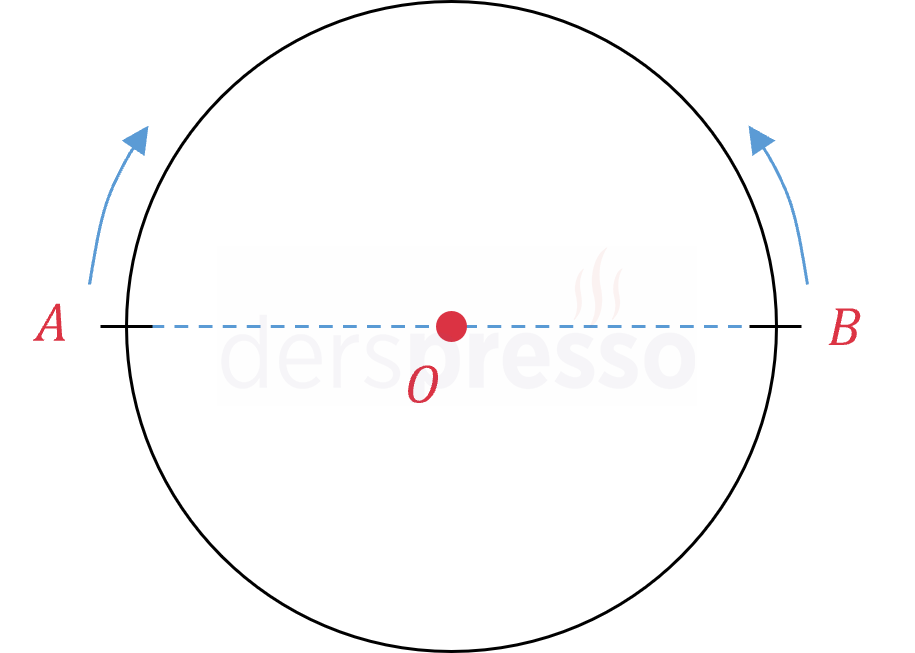
Şekildeki çevresi 1,5 km ve çapı \( [AB] \) olan çember şeklindeki koşu parkurunda Ahmet ve Beril sırasıyla A ve B noktalarından aynı anda sabit hızlarla koşmaya başlıyorlar.
Ahmet ve Beril 50 dakika sonra üçüncü kez karşılaşıyorlar. Ahmet'in hızı dakikada 40 metre olduğuna göre, Beril'in hızı dakikada kaç metredir?
Çözümü Gösterİlk karşılaşmaları harekete başladıktan \( t \) dakika sonra oluyor diyelim.
İlk karşılaşma için aralarındaki yarım çemberlik mesafeyi kapatmaları gerekir. İlk karşılaşma anından sonra ikinci karşılaşmaya kadar ise tam çemberlik bir mesafeyi kapatmaları gerekir, bunun için de \( 2t \) dakika geçer.
İkinci kez karşılaştıktan sonra üçüncü karşılaşmaya kadar yine tam çemberlik bir mesafeyi kapatmaları gerektiği için \( 2t \) dakika daha geçer.
Buna göre harekete başladıktan \( t + 2t + 2t = 5t \) dakika sonra üçüncü kez karşılaşırlar.
\( 5t = 50 \Longrightarrow t = 10 \) dk
Çemberin çevresi 1,5 km yani 1500 metredir. Yarım çemberin uzunluğu \( \frac{1500}{2} = 750 \) metredir.
Aralarındaki 750 metrelik mesafeyi 10 dakikada kapatıyorlarsa hızları toplamı dakikada \( \frac{750}{10} = 75 \) metredir.
Ahmet'in hızı dakikada 40 metre olduğuna göre, Beril'in hızı dakikada \( 75 - 40 = 35 \) metredir.
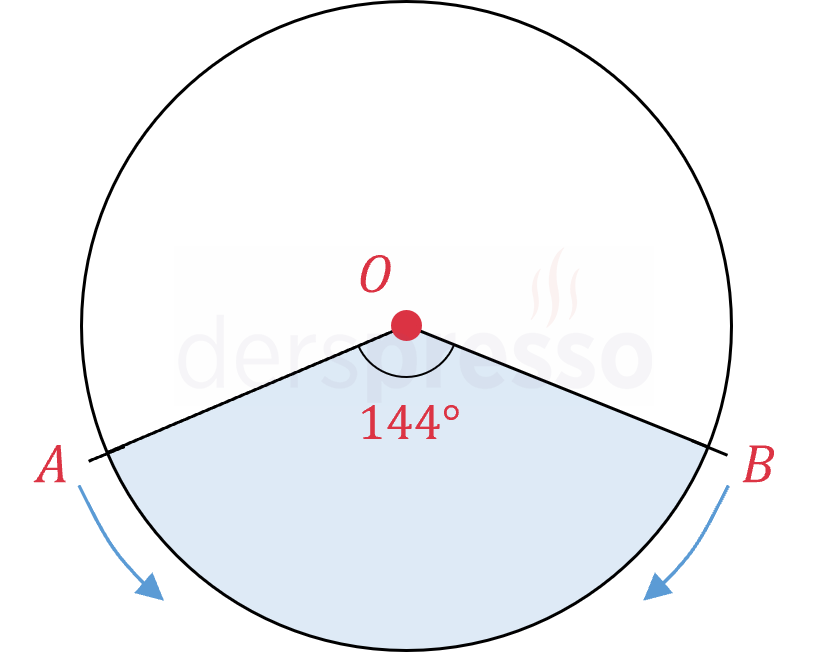
Merkezi \( O \) noktası olan yukarıdaki çemberde A ve B noktalarındaki iki cisim ok yönünde aynı anda sabit hızlarla harekete başladıktan 14 dakika sonra karşılaşıyorlar.
İki cisim ilk kez karşılaştıktan kaç dakika sonra tekrar karşılaşırlar?
Çözümü Gösterİki cisim karşılaşmadan önce 144 derecelik çember yayı kadar yol alırlar. Bu noktadan sonra 360 derecelik (tam) çember yayı kadar daha yol aldıklarında ikinci kez karşılaşırlar.
Çember yaylarının uzunluğu onları gören merkez açı ile doğru orantılı olduğu için en başta aralarındaki mesafenin tam çember yay uzunluğuna oranı \( \frac{144}{360} = \frac{2}{5} \)'tir.
İlk kez karşılaşıncaya kadar 14 dakikada \( 2x \) kadar yol katettiklerine göre ne kadar sürede \( 5x \) kadar yol katedeceklerini bulalım.
\( \dfrac{2x}{5x} = \dfrac{14}{t} \)
\( t = 7 \cdot 5 = 35 \) dakika bulunur.
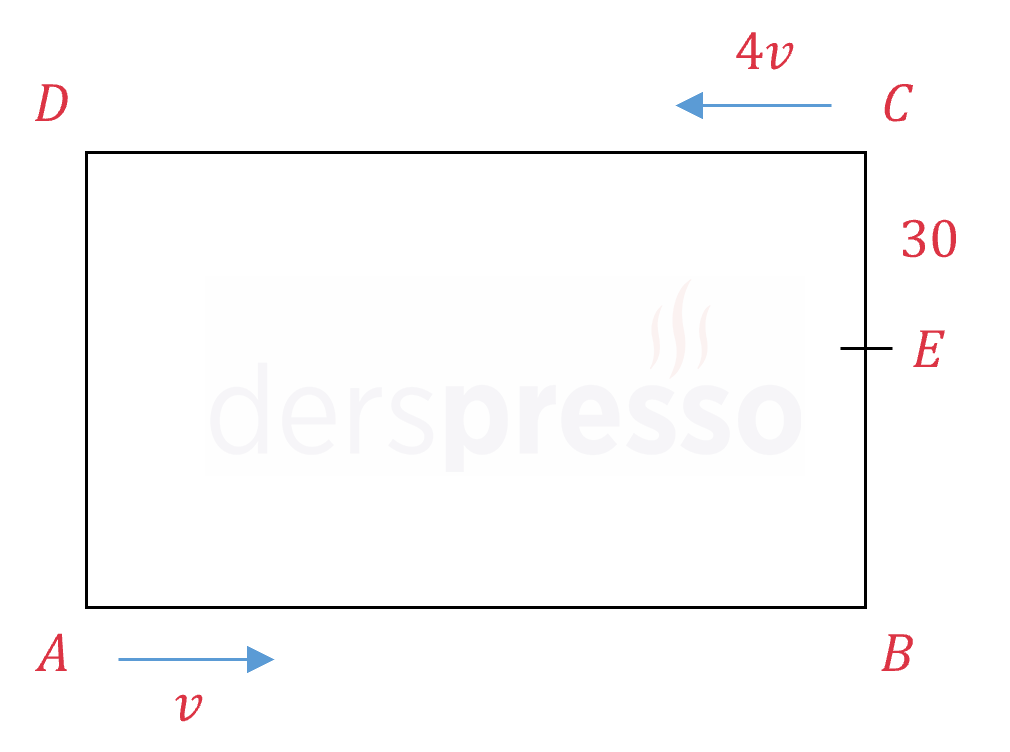
Dikdörtgen şeklindeki bir parkurda \( A \) noktasındaki araç sabit \( v \) hızıyla \( B \) noktasına doğru, \( C \) noktasındaki araç sabit \( 4v \) hızıyla \( D \) noktasına doğru hareket etmektedir.
Bu iki araç aynı anda harekete başladıktan sonra ilk kez \( E \) noktasında karşılaşıyorlar.
\( \abs{CE} = 30 \) km olduğuna göre, bu parkur toplam kaç km'dir?
Çözümü Göster\( \abs{AB} = \abs{DC} = x \) km ve \( \abs{BE} = y \) km diyelim.
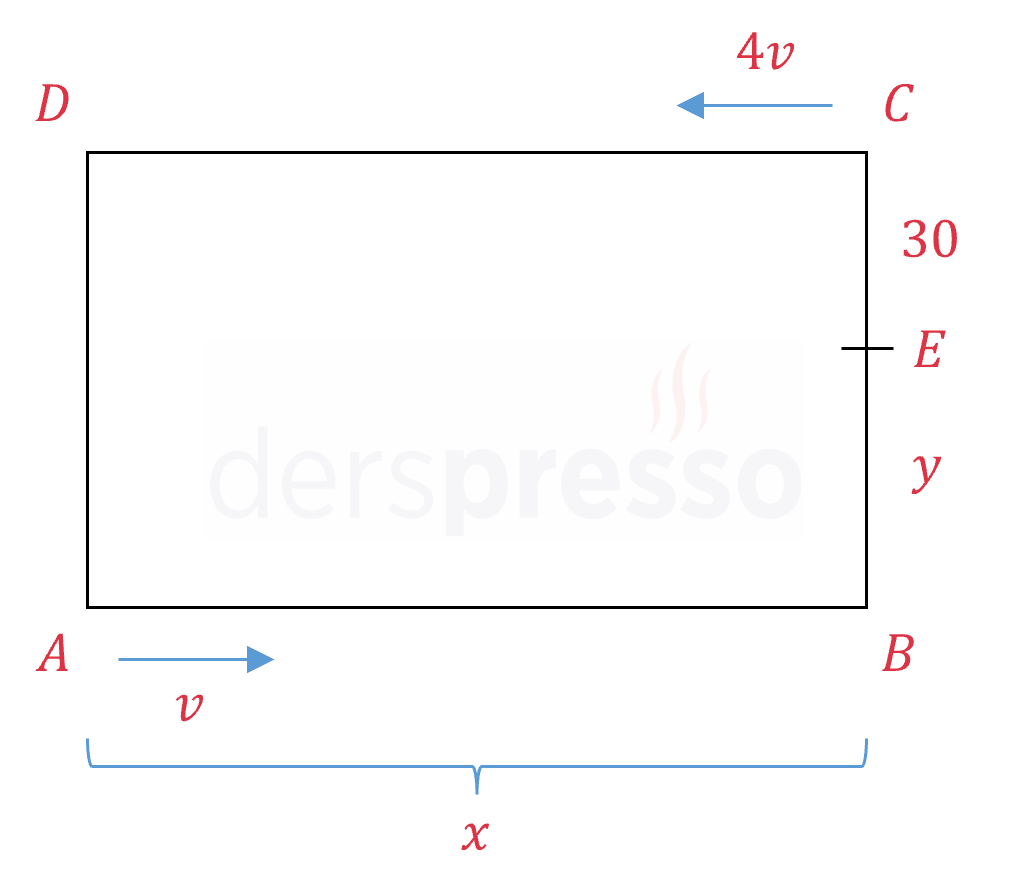
\( C \) noktasından yola çıkan aracın \( E \) noktasına kadar aldığı yolu bulalım.
\( x + (y + 30) + x + y = 2(x + y) + 30 \) km
Aynı sürede \( A \) noktasından yola çıkan aracın \( E \) noktasına kadar aldığı yolu bulalım.
\( x + y \) km
\( C \) noktasından yola çıkan aracın hızı \( A \) noktasından yola çıkan aracın hızının 4 katı olduğundan aynı sürede aldığı yol da 4 katı olur.
\( 2(x + y) + 30 = 4(x + y) \)
\( 2x + 2y + 30 = 4x + 4y \)
\( 2x + 2y = 30 \)
\( x + y = 15 \)
Parkurun çevresini hesaplayalım.
\( 2(x + y + 30) = 2(15 + 30) = 90 \) km bulunur.
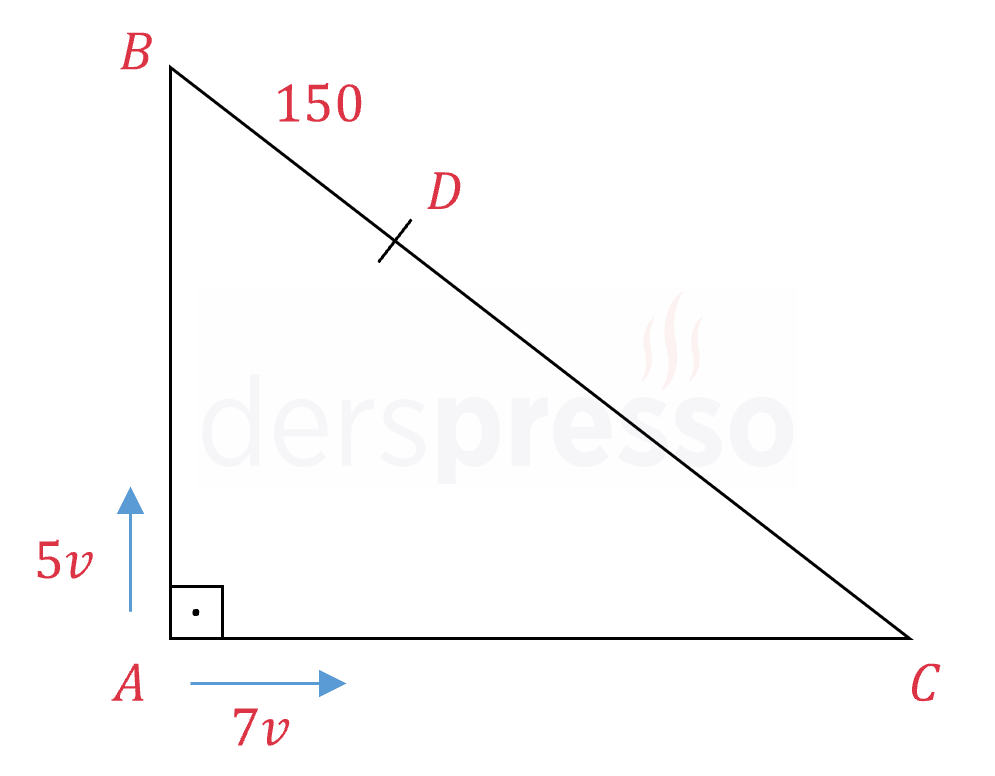
Şekilde verilen dik üçgen şeklindeki koşu parkurunda \( 12\abs{AB} = 5\abs{AC} \) ve \( \abs{BD} = 150 \) metredir.
\( A \) noktasında bulunan Ahsen sabit \( 5v \) hızıyla \( B \) noktasına doğru, aynı noktada bulunan Büşra da aynı anda sabit \( 7v \) hızıyla \( C \) noktasına doğru koşmaya başlıyor.
Ahsen ile Büşra ilk kez \( D \) noktasında karşılaştıklarına göre, \( \abs{DC} \) kaç metredir?
Çözümü Göster\( 12\abs{AB} = 5\abs{AC} \) olduğuna göre, \( \abs{AB} = 5k \) ve \( \abs{AC} = 12k \) diyelim.
Parkur dik üçgen şeklinde olduğu için \( \abs{BC} \) uzunluğunu Pisagor teoremi ile bulabiliriz.
\( \abs{BC} = \sqrt{(5k)^2 + (12k)^2} = 13k \)
\( \abs{BD} = 150 \) metre verildiğinden \( \abs{DC} = 13k - 150 \) metre olur.
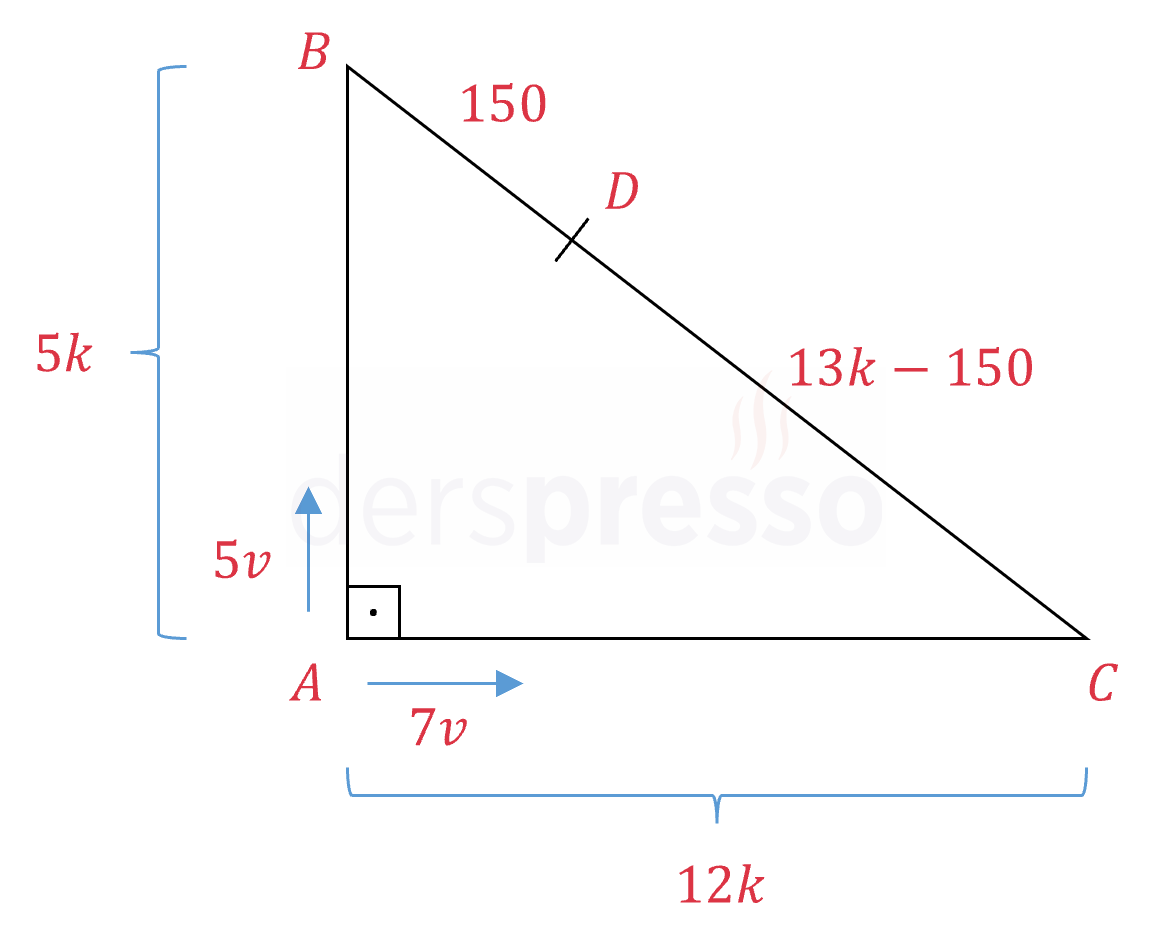
Ahsen \( D \) noktasına gelene kadar toplam \( 5k + 150 \) metre, Büşra ise \( 12k + (13k - 150) = 25k - 150 \) metre yol almış olur.
Ahsen ve Büşra'nın aynı sürede aldıkları yolların oranı hızlarının oranına eşittir.
\( \dfrac{5k + 150}{25k - 150} = \dfrac{5v}{7v} \)
\( \dfrac{k + 30}{5k - 30} = \dfrac{5}{7} \)
İçler - dışlar çarpımı yapalım.
\( 7(k + 30) = 5(5k - 30) \)
\( 7k + 210 = 25k - 150 \)
\( 18k = 360 \)
\( k = 20 \)
Buna göre \( \abs{DC} = 13(20) - 150 = 110 \) metre bulunur.

Caner arkadaşı Melike'yle buluşmak için bulunduğu noktadan yürüyerek, Melike ise bulunduğu noktadan arabasıyla buluşacakları kafeye gidecektir.
Caner A ya da B kafelerinden hangisine doğru yürürse yürüsün aynı anda buluşacakları noktaya varmaktadırlar. Caner'in A kafesine olan uzaklığı B kafesine olan uzaklığının \( \frac{4}{5} \) katıdır.
Melike arabayla 45 km/saat sabit hızla hareket ettiğine göre, Caner saatte kaç km/saat hızla yürümektedir?
Çözümü GösterMelike'nin A kafesine olan uzaklığına \( x \) km diyelim.
Caner'in A kafesine olan uzaklığı B kafesine olan uzaklığının \( \frac{4}{5} \) katı olduğuna göre, A kafesine olan uzaklığına \( 4k \), B kafesine olan uzaklığına \( 5k \) diyebiliriz.
Caner hangi kafeye yürürse yürüsün aynı anda vardıklarına göre, iki durumda katetttikleri yolun hızlarına oranları eşit olmalıdır.
Caner'in yürüme hızına \( v \) diyelim.
Önce A kafesinde buluştukları durum için yolculuk sürelerini eşitleyelim.
\( \dfrac{x}{45} = \dfrac{4k}{v} \)
Şimdi B kafesinde buluştukları durum için yolculuk sürelerini eşitleyelim.
\( \dfrac{x + 9k}{45} = \dfrac{5k}{v} \)
İki orantıyı taraf tarafa bölelim.
\( \dfrac{\frac{x}{45}}{\frac{x + 9k}{45}} = \dfrac{\frac{4k}{v}}{\frac{5k}{v}} \)
\( \dfrac{x}{x + 9k} = \dfrac{4}{5} \)
İçler - dışlar çarpımı yapalım.
\( 5x = 4(x + 9k) \)
\( 5x = 4x + 36k \)
\( x = 36k \)
İlk denklemde \( x \) yerine bulduğumuz değeri yazalım.
\( \dfrac{x}{45} = \dfrac{4k}{v} \)
\( \dfrac{36k}{45} = \dfrac{4k}{v} \)
\( v = 5 \) km/saat bulunur.
Alper ön tekerleğinin yarıçağı 35 cm, arka tekerleğinin yarıçapı 50 cm olan bisikletiyle bir yarışa katılıyor.
Yarış bittiğinde iki tekerlek toplamda 15300 devir yaptığına göre, Alper kaç metre yol gitmiştir?
Çözümü GösterTekerleklerin dönüş sayısı; çevreleri, dolayısıyla yarıçapları ile ters orantılıdır.
Buna göre ön tekerleğin toplam dönüş sayısına \( 10k \) dersek arka tekerleğin toplam dönüş sayısı \( 7k \) olur.
\( 10k \cdot 35 = 7k \cdot 50 \)
Bu durumda tekerleklerin yaptığı toplam dönüş sayısı \( 17k \) olur.
\( 17k = 15300 \)
\( k = 900 \)
Arka tekerlek toplamda \( 7 \cdot 900 = 6300 \) dönüş yapmıştır.
Alper'in gittiği toplam mesafeyi bulmak için arka tekerleğin çevresi ile toplam dönüş sayısını çarpalım.
\( 2\pi r = 2\pi \cdot 50 \) cm
\( = 100\pi \) cm \( = \pi \) metre
Alper'in gittiği toplam mesafeyi bulalım.
\( \pi \cdot 6300 = 6300\pi \) metre olarak bulunur.
Sabit hızla koşan iki koşucu arasındaki yarışta yavaş olan koşucu parkurun \( \frac{1}{3} \)'ünü koştuğunda hızlı olan koşucu 800 metre koşmuştur. Hızlı olan koşucu parkurun \( \frac{2}{3} \)'ünü koştuğunda ise yavaş olan koşucu 900 metre koşmuştur.
Buna göre yarış parkuru kaç km'dir?
Çözümü GösterParkurun uzunluğuna işlem kolaylığı açısından \( 3x \) metre diyelim.
Yavaş olan koşucu parkurun \( 3x \cdot \frac{1}{3} = x \) kadarını koştuğunda hızlı olan koşucu 800 metre koştuğuna göre, hızları oranı \( \frac{x}{800} \) olur.
Hızlı olan koşucu bu parkurun \( 3x \cdot \frac{2}{3} = 2x \) kadarını koştuğunda yavaş olan koşucu 900 metre koştuğuna göre, hızları oranı aynı zamanda \( \frac{900}{2x} \) olur.
Her iki durumda koşucuların hızları oranı birbirine eşittir.
\( \dfrac{x}{800} = \dfrac{900}{2x} \)
İçler - dışlar çarpımı yapalım.
\( 2x^2 = 800 \cdot 900 \)
\( x^2 = 400 \cdot 900 \)
\( x = 20 \cdot 30 = 600 \) metre
Buna göre parkurun toplam uzunluğu \( 3x = 3 \cdot 600 = 1800 \) metredir.
Cevap \( 1,8 \) km bulunur.
200 metrelik bir koşu pistinde Nisa ve Miray sabit hızlarla yarışıyorlar. Miray yarışı bitirdiğinde Nisa'nın yarışı bitirmesine daha 60 metre vardır.
İkinci kez aynı sabit hızlarla yarıştıklarında Miray pistin başlangıç noktasından 60 metre daha geride yarışa başladığına göre, Miray yarışı bitirdiğinde Nisa'nın yarışı bitirmesine kaç metre vardır?
Çözümü GösterMiray'ın ilk yarışı tamamlama süresine \( t \) saniye diyelim.
Buna göre Miray'ın hızı \( \frac{200}{t} \) m/s, Nisa'nın hızı \( \frac{140}{t} \) m/s olur.
Miray ikinci yarışta 260 metre koştuğuna göre, ikinci yarışı bitirme süresini bulalım.
\( \dfrac{260}{\frac{200}{t}} = \dfrac{13t}{10} \) saniye
Nisa'nın ikinci yarışta bu sürede koştuğu mesafeyi bulalım.
\( \dfrac{140}{t} \cdot \dfrac{13t}{10} = 182 \) metre
Buna göre, Miray yarışı bitirdiğinde Nisa'nın yarışı bitirmesine \( 200 - 182 = 18 \) metre vardır.
Bir pistte sabit hızlarla ilerleyen A, B ve C araçları yarışmaktadır. C aracı yarışı bitirdiğinde A aracının yarışı bitirmesine 480 metre, B aracının ise yarışı bitirmesine 625 metre vardır.
A aracı yarışı bitirdiğinde B aracının yarışı bitirmesine 225 metre kaldığına göre, bu pistin uzunluğu kaç metredir?
Çözümü GösterPistin uzunluğuna \( x \) metre diyelim.
C aracı yarışı bitirdiğinde araçların durumu aşağıdaki gibidir.
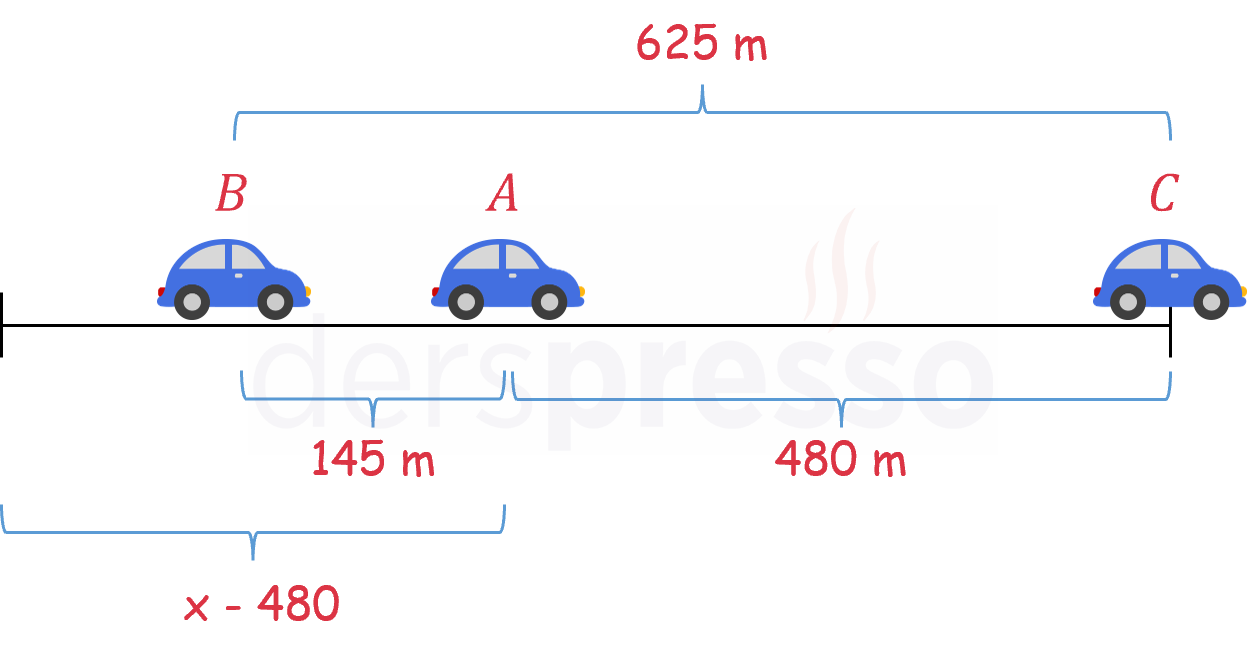
A aracı yarışı bitirdiğinde ise araçların durumu aşağıdaki gibidir.

Buna göre A aracı \( x - 480 \) metre gittiğinde B aracı ile arasındaki mesafe \( 625 - 480 = 145 \) metre açılmıştır. Daha sonra A aracı 480 metre daha gittiğinde B aracı ile arasındaki mesafe \( 225 - 145 = 80 \) metre daha açılmıştır.
Araçların hızı sabit olduğuna göre, A aracının aldığı yolla B aracı ile arasındaki mesafe arasında doğru orantı vardır.
\( \dfrac{x - 480}{145} = \dfrac{480}{80} \)
\( \dfrac{x - 480}{145} = 6 \)
\( x - 480 = 870 \)
\( x = 1350 \) metre bulunur.
Doğrusal bir pistin iki ucundaki A ve B koşucuları aynı anda sabit hızlarla birbirlerine doğru koşmaya başladığında A'nın hızı B'nin hızının \( \frac{2}{3} \) katıdır.
Bu iki koşucu karşılaştıktan sonra A hızını yarıya düşürürken B hızını 2 katına çıkarıyor ve koşmaya devam ediyorlar. B karşılaşmadan 15 dakika sonra pistin başına vardığına göre, A kaç dakika sonra pistin sonunda olur?
Çözümü GösterA'nın hızı B'nin hızının \( \frac{2}{3} \) katı olduğundan B'nin hızına \( 3v \), A'nın hızına \( 3v \cdot \frac{2}{3} = 2v \) diyelim.
Aynı anda koşmaya başladıktan sonra karşılaştıkları süreye \( t \) diyelim.
A \( t \) dakikada \( 2v \cdot t = 2vt \), B ise \( 3v \cdot t = 3vt \) yol almış olur.

Karşılaştıktan sonra A \( 2v \cdot \frac{1}{2} = v \) hızıyla, B ise \( 3v \cdot 2 = 6v \) hızıyla koşmaya devam ediyor.
15 dakika sonra pistin başına varan B karşılaşma sonrasında \( 6v \cdot 15 = 90v \) yol alır.
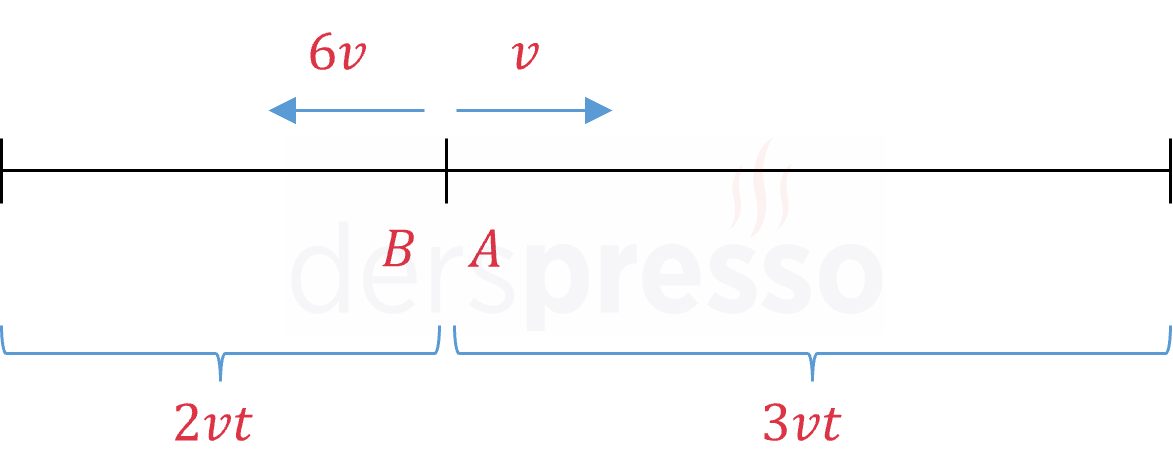
\( 90v \) aynı zamanda A'nın karşılaşma öncesinde aldığı yola eşittir.
\( 2vt = 90v \)
\( t = 45 \) dakika
Buna göre A'nın karşılaşma sonrası pistin sonuna kadar alacağı yol \( 3vt = 3v \cdot 45 = 135v \) olur.
A bu yolu \( v \) hızıyla gideceği için geçireceği süre \( \dfrac{135v}{v} = 135 \) dakika olur.
İşe vardığında bilgisayarını evde unuttuğunu farkeden Kerem, bilgisayarını almak için eve doğru sabit hızla yola çıkıyor. İşten çıktıktan 1 saat sonra toplantısına 1,5 saat kaldığını farkeden Kerem, hızını \( \frac{3}{2} \) katına çıkarıyor ve eve 20 dakika sonra varıyor.
Evde bir süre vakit geçirip tekrar aynı hızla yola çıkan Kerem tam zamanında işe vardığına göre, evde ne kadar vakit geçirmiştir?
Çözümü GösterKerem'in ilk hızına \( v \) diyelim.
Ev ile ofis arası mesafeyi hesaplayalım.
\( v \cdot 1 + \dfrac{3v}{2} \cdot \dfrac{20}{60} = \dfrac{3v}{2} \)
Evden ofise dönüş süresine \( t \) diyelim.
Evden ofise ne kadar sürede döndüğünü bulalım.
\( \dfrac{3v}{2} \cdot t = \dfrac{3v}{2} \)
\( t = 1 \) saat
Kerem toplantıya 1,5 saat kaldığı andan itibaren 20 dakikayı eve varmak için, 1 saati de evden ofise dönmek için harcamıştır.
Buna göre Kerem'in evde geçirdiği süre 10 dakikadır.
Sabit hızlarla koşan üç atletin katıldığı bir yarışta; birinci atlet yarışı tamamladığında ikinci atlete 50 metre, üçüncü atlete 60 metre fark atmış oluyor.
İkinci atlet yarışı tamamladığında üçüncü atlete 15 metre fark atmış oluyor.
Buna göre pistin toplam uzunluğu kaç metredir?
Çözümü GösterBirinci atlet yarışı tamamladığında, ikinci ve üçüncü atletler arasındaki mesafe \( 60 - 50 = 10 \) metredir.
İkinci atlet 50 metre daha koşarak yarışı tamamladığında ise ikinci ve üçüncü atletler arasındaki mesafe 15 metre oluyor.
Yani ikinci atlet 50 metre koştuğunda üçüncü atlete 5 metre daha fark atmıştır.
İkinci ve üçüncü atletlerin arasındaki mesafeler arasında doğru orantı kuralım.
İkinci atlet üçüncü atlete 5 metre farkı 50 metrede atıyorsa 15 metre farkı 150 metrede atar.
Buna göre pistin toplam uzunluğu 150 metredir.
Bir bisikletli kare şeklindeki bir parkın etrafında bir tur atıyor. Bisikletli parkın üç kenarı boyunca ortalama hızını sırasıyla 8 m/s, 4 m/s ve 12 m/s olarak ölçüyor.
Bisikletlinin tur boyunca ortalama hızı 6,4 m/s olduğuna göre, parkın dördüncü kenarı boyunca hızı kaç m/s'dir?
Çözümü GösterParkın bir kenar uzunluğuna \( x \) m, bisikletin dördüncü kenar boyunca hızına \( v \) m/s diyelim.
Ortalama hız toplam mesafenin toplam zamana bölümüne eşittir.
\( \dfrac{4x}{\frac{x}{8} + \frac{x}{4} + \frac{x}{12} + \frac{x}{v}} = 6,4 \)
\( \dfrac{x}{x(\frac{1}{8} + \frac{1}{4} + \frac{1}{12} + \frac{1}{v})} = 1,6 \)
İçler - dışlar çarpımı yapalım.
\( \dfrac{1}{8} + \dfrac{1}{4} + \dfrac{1}{12} + \dfrac{1}{v} = \dfrac{10}{16} \)
\( \dfrac{3 + 6 + 2}{24} + \dfrac{1}{v} = \dfrac{5}{8} \)
\( \dfrac{1}{v} = \dfrac{5}{8} - \dfrac{11}{24} \)
\( \dfrac{1}{v} = \dfrac{4}{24} = \dfrac{1}{6} \)
\( v = 6 \) m/s bulunur.
Şeyma bir toplantı için evden toplantı yerine doğru yola çıkıyor ve 75 km/saat sabit hızla giderse 20 dakika geç, 100 km/saat sabit hızla giderse 15 dakika erken varacağını hesaplıyor.
Buna göre, evle toplantı yeri arası uzaklık kaç km'dir?
Çözümü GösterEvle toplantı yeri arası uzaklığa \( x \) km, evden çıktığı anda toplantı saatine olan süreye \( t \) saat diyelim.
75 km/saat hızla gittiğinde 20 dk geç varıyor.
\( x = 75(t + \dfrac{20}{60}) \)
100 km/saat hızla gittiğinde 15 dk erken varıyor.
\( x = 100(t - \dfrac{15}{60}) \)
Her iki durumda mesafeler birbirine eşittir.
\( x = 75(t + \dfrac{20}{60}) = 100(t - \dfrac{15}{60}) \)
\( 75t + 75 \cdot \dfrac{1}{3} = 100t - 100 \cdot \dfrac{1}{4} \)
\( 25t = 25 + 25 \)
\( t = 2 \) saat
Evle toplantı yeri arası mesafeyi bulalım.
\( x = 75(2 + \dfrac{20}{60}) \)
\( = 75 \cdot \dfrac{7}{3} = 175 \) km bulunur.
Ali A şehrinden B şehrine doğru, Cem de B şehrinden A şehrine doğru aynı anda ve sabit hızlarla yola çıkıyor.
İki kişi birbirini geçtikten 2 saat 50 dakika sonra Ali B şehrine, ondan 1 saat 25 dakika sonra da Cem A şehrine ulaşıyor.
Ali'nin hızı saatte \( 35\sqrt{6} \) km olduğuna göre, Cem'in hızı saatte kaç km'dir?
Çözümü GösterCem'in hızına \( v \), karşılaşana kadar geçen süreye \( t \) diyelim.
Cem'in \( t \) sürede aldığı yolu Ali 2 saat 50 dakikada alıyor.
2 saat 50 dakika = 170 dakika
\( 35\sqrt{6} \cdot \dfrac{170}{60} = vt \)
\( t = \dfrac{35\sqrt{6} \cdot 170}{60v} \)
Ali'nin \( t \) sürede aldığı yolu ise Cem Ali'den 1 saat 25 dakika daha uzun sürede, yani 4 saat 15 dakikada alıyor.
4 saat 15 dakika = 255 dakika
\( v\dfrac{255}{60} = 35\sqrt{6}t \)
\( t = \dfrac{255v}{60 \cdot 35\sqrt{6}} \)
Bulduğumuz iki \( t \) değerini birbirine eşitleyelim.
\( \dfrac{35\sqrt{6} \cdot 170}{60v} = \dfrac{255v}{60 \cdot 35\sqrt{6}} \)
\( v^2 = \dfrac{35\sqrt{6} \cdot 35\sqrt{6} \cdot 170}{255} \)
\( = \dfrac{35^2 \cdot 6 \cdot 17 \cdot 5 \cdot 2}{17 \cdot 3 \cdot 5} \)
\( = 35^2 \cdot 2^2 \)
\( = 70^2 \)
\( v = 70 \) km/saat olarak bulunur.
Sabit hızla seyreden bir tren uzunlukları 550 m ve 750 m olan iki köprüyü sırasıyla 35 ve 45 saniyede geçiyor.
Buna göre treninin uzunluğunun metre, hızının da m/sn cinsinden değerleri toplamı kaçtır?
Çözümü GösterTrenin uzunluğuna \( x \) metre, hızına \( v \) m/sn diyelim.
Tren bir köprüyü geçerken kendi uzunluğu artı köprünün uzunluğu kadar yol kateder.
\( v = \dfrac{x + 550}{35} \) m/sn
\( v = \dfrac{x + 750}{45} \) m/sn
Trenin her iki köprüyü geçerkenki hızları birbirine eşittir.
\( \dfrac{x + 550}{35} = \dfrac{x + 750}{45} \)
İçler - dışlar çarpımı yapalım.
\( 45(x + 550) = 35(x + 750) \)
\( 9(x + 550) = 7(x + 750) \)
\( 9x + 4950 = 7x + 5250 \)
\( 2x = 300 \)
\( x = 150 \) m
Trenin hızını bulmak için bu değeri hız denklemlerinden birinde yerine koyalım.
\( v = \dfrac{150 + 550}{35} = 20 \) m/sn
Buna göre trenin uzunluğu ve hızının toplamları \( 150 + 20 = 170 \) olarak bulunur.
57 km/s sabit hızla giden bir arabada yolculuk yapan Esra ters yönde sabit hızla giden trenin kendisini 8 saniyede geçtiğini görüyor.
Trenin uzunluğu 200 metre olduğuna göre, hızı kaç km/s'tir?
Çözümü GösterTrenin hızına \( v \) diyelim.
200 metre = 0,2 km
8 saniye = 8 / 3600 saat
Trenin uzunluğu, ters yönde ilerleyen tren ve arabanın hızları toplamı ile geçen sürenin çarpımına eşittir.
\( 0,2 = (v + 57) \cdot \dfrac{8}{3600} \)
\( v + 57 = \dfrac{720}{8} = 90 \)
\( v = 33 \) km/s olarak bulunur.
Hızı sabit ve 60 km/saat olan 400 m uzunluğundaki bir tren bir tüneli 2 dakikada geçiyor.
Bu tüneli \( \frac{1}{20000} \) ölçekli haritada çizmek isteyen Aslı, harita üzerinde tüneli kaç cm olarak çizer?
Bilgi: Ölçek, harita üzerinde iki nokta arasındaki uzunluğun gerçek uzunluğa bölümü ile bulunur.
Çözümü GösterTren saatte 60 km hızla gidiyorsa 2 dakikada 2 km, yani 2000 m yol gider.
2000 m tünelin ve trenin uzunlukları toplamına eşittir.
Trenin uzunluğu 400 m olduğundan tünelin uzunluğu 1600 m'dir.
1600 m uzunluğun \( \frac{1}{20000} \) ölçekli haritada karşılık geldiği uzunluğu bulalım.
1600 m = 160000 cm
\( \dfrac{160000}{20000} = 8 \) cm olarak bulunur.
Bir yolcu gemisi bir kıyıya paralel ve doğrusal şekilde seyahat ederken 700 metre uzunluğundaki bir limanı 10 dakikada, 1000 metre uzunluğundaki tatil köyünü 13 dakikada geçiyor.
Geminin hızı sabit olduğuna göre, uzunluğu kaç metredir?
Çözümü GösterGeminin hızına \( v \) metre/dk, uzunluğuna \( x \) metre diyelim.
Gemi limanı ve tatil köyünü geçerken liman ve tatil köyünün uzunluklarına ek olarak kendi uzunluğu kadar da mesafe kateder.
Geminin hızı alınan yolun süreye oranına eşittir.
\( v = \dfrac{700 + x}{10} = \dfrac{1000 + x}{13} \)
İçler - dışlar çarpımı yapalım.
\( 13(700 + x) = 10(1000 + x) \)
\( 13 \cdot 700 + 13x = 10 \cdot 1000 + 10x \)
\( 3x = 900 \)
\( x = 300 \) metre olarak bulunur.
Sabit hızlarla hareket eden A ve B trenleri aynı yönde ilerlerken 12 saniyede, zıt yönlerde ilerlerken 4 saniyede birbirlerini geçiyorlar.
A treninin uzunluğu 115 metre, B treninin uzunluğu 155 metre olduğuna göre, bu trenlerden hızlı olan yavaş olanı bir istasyonda durmaktayken kaç saniyede geçer?
Çözümü GösterA treninin hızına \( a \) m/sn, B treninin hızına \( b \) m/sn diyelim.
Trenler aynı yönde de zıt yönlerde de ilerlerken birbirlerini geçerken aldıkları yol trenlerin uzunluklarının toplamı kadardır.
Trenler aynı yönde ilerlerken birbirlerini geçme hızı:
\( a - b = \dfrac{115 + 155}{12} = 22,5 \)
Trenler zıt yönlerde ilerlerken birbirlerini geçme hızı:
\( a + b = \dfrac{115 + 155}{4} = 67,5 \)
Eşitlikleri taraf tarafa toplayalım.
\( 2a = 90 \)
\( a = 45 \) m/s
\( b = 22,5 \) m/s
Hızlı olan trenin yavaş olan treni istasyonda dururken kaç saniyede geçeceğini bulalım.
\( \dfrac{115 + 155}{45} = 6 \) saniye
Ahmet arabasıyla 68 km/saat sabit hızla işine giderken yan şeritte aynı yönde 44 km/saat sabit hızla gitmekte olan bir tırı tam olarak geçmesi 3 saniye sürmüştür.
Tırın uzunluğu Ahmet'in arabasının uzunluğunun 4 katı olduğuna göre, tır aynı hızla 204 metrelik bir tüneli kaç saniyede geçer?
Çözümü GösterAhmet'in arabasının uzunluğuna \( x \) diyelim. Bu durumda tırın uzunluğu \( 4x \) olur.
Ahmet'in tırı geçmek için katetmesi gereken yol arabasının uzunluğuyla tırın uzunluğunun toplamına eşittir.
\( 4x + x = 5x \)
Ahmet'in hızıyla tırın hızının farkı \( 68 - 44 = 24 \) km/saat'tir. Bu hızı metre/saniyeye çevirelim.
\( 24 \cdot \dfrac{1000}{60 \cdot 60} = \dfrac{20}{3} \) m/sn
Ahmet tırı 3 saniyede geçerken katettiği toplam yolu bulalım.
\( 3 \cdot \dfrac{20}{3} = 20 \) metre
Bu mesafe araba ve tırın uzunlukları toplamı olan \( 5x \)'e eşittir.
\( 5x = 20 \Longrightarrow x = 4 \)
Tırın uzunluğu \( 4x = 4 \cdot 4 = 16 \) metredir.
Tırın tüneli geçmesi için katetmesi gereken mesafe \( 204 + 16 = 220 \) metredir.
Tırın hızını metre/saniyeye çevirelim.
\( 44 \cdot \dfrac{1000}{60 \cdot 60} = \dfrac{110}{9} \) m/sn
Tırın tüneli geçme süresini bulalım.
\( \dfrac{220}{\frac{110}{9}} = 18 \) saniye bulunur.
Bir koşu yarışına katılan Demet ve Dilara aynı anda yarışa başladıktan \( t \) saniye sonra Demet 15 adım, Dilara 18 adım atmıştır.
Demet'in 11 adımının uzunluğu Dilara'nın 13 adımının uzunluğuna eşit olduğuna göre, Demet'in ortalama hızının Dilara'nın ortalama hızına oranı kaçtır?
Çözümü GösterDemet'in bir adımının uzunluğuna \( x \) metre, Dilara'nın bir adımının uzunluğuna \( y \) metre diyelim.
\( 11x = 13y \)
Buna göre Demet'in bir adımının uzunluğuna \( 13k \), Dilara'nın bir adımının uzunluğuna \( 11k \) diyebiliriz.
Demet \( t \) saniyede \( 15 \cdot 13k = 195k \) metre, Dilara aynı sürede \( 18 \cdot 11k = 198k \) metre koşar.
Süreler aynı olduğu için koştukları mesafelerin oranı hızlarının oranını verir.
\( \dfrac{195k}{198k} = \dfrac{65}{66} \) olarak bulunur.
A ve B gemileri aynı anda sırasıyla X ve Y limanlarından birbirlerine doğru sabit hızlarla hareket ediyorlar. B gemisi X limanına 24 dakikada, A gemisi Y limanına B gemisi ile karşılaştıktan 4 dakika sonra varıyor.
Buna göre A gemisi X limanından Y limanına toplam kaç dakikada varmıştır?
Çözümü Gösterİki geminin karşılaştığı noktaya K noktası diyelim.
X ve Y limanları arasındaki uzaklığa \( m \), Y limanı ve K noktası arasındaki uzaklığa \( n \) diyelim.
Bu durumda X limanı ve K noktası arasındaki uzaklık \( m - n \) olur.
Bu uzaklıklar aşağıdaki şekilde gösterilmiştir.

A gemisinin hızına \( a \), B gemisinin hızına \( b \) diyelim.
A gemisi \( n \) mesafesini 4 dakikada, B gemisi \( m \) mesafesini 24 dakikada alıyor.
\( a = \dfrac{n}{4} \)
\( b = \dfrac{m}{24} \)
A ve B gemileri aynı anda hareket edip K noktasına aynı anda varıyor. Bu yüzden A ve B gemilerinin K noktasına gelme süreleri eşittir.
\( \dfrac{m - n}{a} = \dfrac{n}{b} \)
Bulduğumuz \( a \) ve \( b \) değerlerini bu eşitlikte yerine yazalım.
\( \dfrac{m - n}{\frac{n}{4}} = \dfrac{n}{\frac{m}{24}} \)
\( \dfrac{4(m - n)}{n} = \dfrac{24n}{m} \)
İçler - dışlar çarpımı yapalım.
\( 24n^2 = 4m^2 - 4mn \)
\( 6n^2 + mn - m^2 = 0 \)
\( (3n - m)(2n + m) = 0 \)
\( 3n - m = 0 \Longrightarrow m = 3n \)
\( 2n + m = 0 \Longrightarrow m = -2n \)
Uzunluk değerleri negatif olamayacağı için ikinci çözüm geçerli değildir.
\( m = 3n \Longrightarrow n = \dfrac{m}{3} \)
Bu değeri \( a \) hız formülünde yerine koyalım.
\( a = \dfrac{n}{4} = \dfrac{\frac{m}{3}}{4} = \dfrac{m}{12} \)
\( a \) değeri A gemisinin hızına, \( m \) değeri de X - Y limanları arası uzaklığa eşit olduğu için, bu eşitlikten A gemisinin X limanından Y limanına 12 dakikada vardığı sonucunu çıkarabiliriz.
Sabit hızlarla uçan iki drone A noktasında karşılaşıyor. Karşılaştıktan sonra biri kuzeye doğru diğeri doğuya doğru uçmaya devam eden iki drone'un 3 saat sonra aralarındaki uzaklık 78 km oluyor.
Drone'lardan birinin hızı diğerinden 14 km/sa fazla olduğuna göre, hızlı olan drone'un hızı kaç km/sa'tir?
Çözümü GösterYavaş olan drone'un hızına \( x \) km/sa, hızlı olan drone'un hızına \( x + 14 \) km/sa diyelim.
Buna göre 3 saatte yavaş drone \( 3x \) km, hızlı drone \( 3(x + 14) = 3x + 42 \) km yol alır.
Drone'lardan biri kuzeye doğru diğeri doğuya doğru uçtuğu için aralarında 90 derecelik açı vardır.
Drone'ların birbirine göre konumları aşağıdaki şekildeki gibi olur.
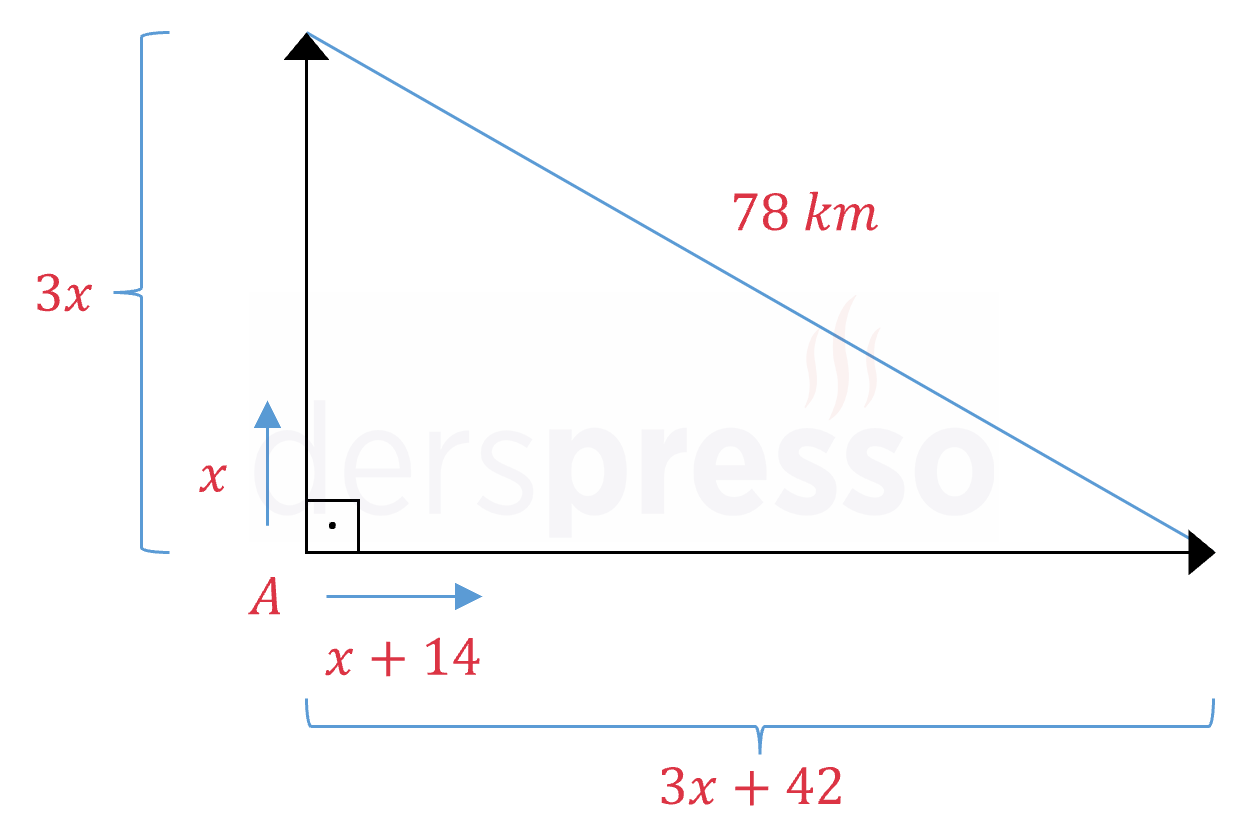
Oluşan dik üçgende Pisagor teoremini kullanalım.
\( (3x)^2 + (3x + 42)^2 = 78^2 \)
\( 9x^2 + 9x^2 + 2 \cdot 3x \cdot 42 + 42^2 = 78^2 \)
Eşitliğin taraflarını 9 ile sadeleştirelim.
\( 2x^2 + 28x + 196 = 676 \)
\( 2x^2 + 28x - 480 = 0 \)
\( x^2 + 14x - 240 = 0 \)
\( (x + 24)(x - 10) = 0 \)
\( x = -24 \) ya da \( x = 10 \)
Drone'ların hızı negatif olamaz.
\( x = 10 \)
Buna göre hızlı olan drone'un hızı \( x + 14 = 24 \) km/sa olur.
Nehirde A noktasından B noktasına akıntı ile aynı yönde yüzen bir kişi sabit \( m \) hızıyla yüzdüğünde B noktasına 60 saniyede, sabit \( 2m \) hızıyla yüzdüğünde ise 48 saniyede ulaşıyor.
Bu kişi yüzmeden sadece akıntı ile A noktasından B noktasına kaç saniyede ulaşır?
Çözümü GösterA ve B noktaları arası mesafeye \( x \) metre, akıntının hızına \( n \) m/sn diyelim.
Kişi akıntı ile aynı yönde yüzdüğü için bileşke hızı akıntının hızı ile kendi hızının toplamına eşit olur.
İki durumda alınan yollar birbirine eşittir.
\( 60(m + n) = 48(2m + n) \)
\( 60m + 60n = 96m + 48n \)
\( 12n = 36m \)
\( n = 3m \)
Bu eşitliği kullanarak \( x \)'in \( m \) cinsinden değerini bulalım.
\( x = 60(m + n) \)
\( = 60(m + 3m) = 240m \)
Bu kişinin sadece akıntının hızıyla \( x \) yolunu aldığı zamana \( t \) saniye diyelim.
\( x = nt \)
\( 240m = 3m \cdot t \)
\( t = 80 \) saniye bulunur.
Aynı tarlada çalışan X ve Y traktörlerinin tekerlerinin çapları sırasıyla 50 ve 60 cm'dir. X traktörünün bu tarlayı uzunluğu boyunca katedebilmesi için tekerlerin yapması gereken devir sayısı Y traktöründen 800 fazladır.
Y traktörü bu tarlayı 1,5 saatte katedebildiğine göre, ortalama hızı kaç km/saattir?
Çözümü GösterBir traktörün tekerlerinin 1 devrinde traktörün katettiği mesafe 1 tekerin çevresine eşittir.
X ve Y traktörlerinin tekerlerinin yarıçapları sırasıyla 25 ve 30 cm'dir.
X traktörünün 1 tekerinin çevresini bulalım.
\( 2 \pi \cdot 25 = 50 \pi \)
Y traktörünün 1 tekerinin çevresini bulalım.
\( 2 \pi \cdot 30 = 60 \pi \)
Tekerlerin çevre uzunluğunun devir sayısı ile çarpımı tarlanın uzunluğunu verir. İki traktör de aynı tarlada çalıştığı için bulunan uzunluklar birbirine eşittir.
Y traktörünün yaptığı devir sayısına \( n \) dersek X traktörünün yaptığı devir sayısı \( n + 800 \) olur.
\( 50\pi(n + 800) = 60\pi n \)
\( 50n + 40000 = 60n \)
\( n = 4.000 \) devir
Y traktörünün teker çevresini ve devir sayısını kullanarak tarlanın uzunluğunu bulalım.
\( 60\pi \cdot 4000 = 240.000\pi \) cm
1 km = 100.000 cm
\( = \dfrac{240000\pi}{100000} = \dfrac{12\pi}{5} \) km
Y traktörü \( \frac{12\pi}{5} \) km yolu 1,5 saatte katedebildiğine göre hızını km/saat cinsinden bulalım.
Hız \( = \dfrac{\frac{12\pi}{5}}{\frac{3}{2}} = \dfrac{8\pi}{5} \) km/saat bulunur.
Bir koşucu saatte 9 km sabit hızla koştuğunda ulaşmak istediği yere saat 15:20'de varıyor. Aynı yolu saatte 12 km sabit hızla koştuğunda ise saat 14:35'te varıyor.
Bu koşucu saatte 15 km sabit hızla koşarsa ulaşmak istediği yere saat kaçta varır?
Çözümü GösterKoşucunun koştuğu mesafeye \( d \) km, saatte 9 km hızla koşarkenki koşu süresine \( t \) saat diyelim.
\( d = 9t \)
Koşucu saatte 12 km hızla koştuğunda aynı mesafeyi 45 dakika daha kısa sürede, yani \( t - \frac{3}{4} \) saatte alır.
\( d = 12(t - \dfrac{3}{4}) = 12t - 9 \)
Her iki durumda yol uzunlukları birbirine eşittir.
\( d = 9t = 12t - 9 \)
\( 3t = 9 \)
\( t = 3 \) saat
Bulduğumuz \( t \) değerini kullanarak \( d \) değerini bulalım.
\( d = 9t = 27 \) km
Koşucu saatte 15 km hızla koştuğunda 27 km'yi ne kadar sürede tamamlayacağını bulalım.
\( \dfrac{27}{15} = \dfrac{9}{5} \) saat
\( = 108 \) dakika
Koşu süresi 3 saat olduğunda koşucunun varış zamanı 15:20 olduğuna göre, 108 dakika olduğunda 72 dakika öncesi, yani saat 14:08 olur.
Motorlu bir tekne sabit bir akıntının olduğu bir nehirde gitmektedir.
Tekne \( A \) noktasından \( B \) noktasına 5 saatte giderken \( B \) noktasından \( A \) noktasına 7 saatte geri dönmektedir.
Tekne motorunu kapatırsa aynı akıntıda \( A \) noktasından \( B \) noktasına kaç saatte varır?
Çözümü GösterTeknenin nehre göre saatteki hızına \( v_s \), akıntının saatteki hızına \( v_a \) diyelim.
Tekne \( A \) noktasından \( B \) noktasına daha kısa sürede vardığına göre akıntı \( A \) noktasından \( B \) noktasına doğrudur.
Teknenin karaya göre hızı akıntı yönünde giderken \( v_s + v_a \), akıntıya ters yönde giderken \( v_s - v_a \) olur.
Teknenin \( A \) noktasından \( B \) noktasına katettiği mesafeyi bulalım.
\( x = 5(v_s + v_a) \)
Teknenin \( B \) noktasından \( A \) noktasına katettiği mesafeyi bulalım.
\( x = 7(v_s - v_a) \)
Her iki durumdaki mesafeler birbirine eşittir.
\( x = 5(v_s + v_a) = 7(v_s - v_a) \)
\( 5v_s + 5v_a = 7v_s - 7v_a \)
\( v_s = 6v_a \)
İki eşitlikten herhangi birinde \( v_s \) yerine \( 6v_a \) yazalım.
\( x = 7(v_s - v_a) \)
\( = 7(6v_a - v_a) = 35v_a \)
Buna göre \( A \) ve \( B \) noktaları arası mesafe akıntının hızının 35 katına eşittir.
Dolayısıyla tekne motorunu kapattığında sadece akıntının hızıyla \( A \) noktasından \( B \) noktasına 35 saatte varır.
Standart bir duvar saatinde, aynı konumda bulunan akrep ve yelkovan yaklaşık kaç dakika sonra tekrar aynı konuma gelir?
Çözümü GösterSoruyu iki farklı yöntemle çözelim.
1. yöntem:
Saat 12:00 ve 00:00'da akrep ve yelkovan aynı konumda bulunur.
Bu iki zaman arasındaki 12 saatlik sürede yelkovan akrebi 11 kez geçer.
Buna göre yelkovan akrebi her \( \frac{12}{11} \) saatte bir geçer.
Saat cinsinden süreyi dakikaya çevirelim.
\( \dfrac{12}{11} \cdot 60 = 65,45 \) dakika bulunur.
2. yöntem:
Saat üzerinde her 5 dakikalık bölüme bir yay diyelim.
Akrep 1 saatte 1 yay ilerlerken yelkovan 12 yay ilerler.
Akrep ve yelkovanın aynı konumda olduktan sonra yine aynı konuma geldikleri süreye \( t \) diyelim.
Akrep \( t \) saatte \( t \) yay ilerlerken yelkovan \( 12t \) yay ilerler.
\( 12t \) yelkovanın bir tam dönüşünü de içerdiği için bu tam dönüşü çıkardığımızda akrep ve yelkovanın aldıkları mesafeler birbirine eşit olur.
\( 12t - 12 = t \)
\( t = \dfrac{12}{11} \) saat
Saat cinsinden süreyi dakikaya çevirelim.
\( \dfrac{12}{11} \cdot 60 = 65,45 \) dakika bulunur.
Bir deprem aynı uzaklığı kateden birincil ve ikincil sismik dalgalar üretiyor. Bu deprem sonucu birincil dalgalar olan P dalgaları 10 saniyede, ikincil dalgalar olan S dalgaları 16 saniyede yeryüzüne ulaşıyor.
P dalgaları S dalgalarından 3000 m/s daha hızlı olduğuna göre, depremin merkez üssünün yeryüzüne uzaklığı kaç kilometredir?
Çözümü GösterDepremin merkez üssünün yeryüzüne olan uzaklığına \( d \) diyelim.
P dalgalarının hızına \( v_p \), S dalgalarının hızına \( v_s \) diyelim.
P dalgalarının yeryüzüne ulaşma süresi 10 saniye, S dalgalarının yeryüzüne ulaşma süresi 16 saniye olarak veriliyor.
P ve S dalgalarının ikisi de aynı \( d \) yolunu kateder.
\( d = 10v_p = 16v_s \)
\( v_p \) hızı \( v_s \) hızından 3000 m/s daha büyüktür.
\( v_p = v_s + 3000 \)
\( 10(v_s + 3000) = 16v_s\)
\( 10v_s + 30000 = 16v_s \)
\( v_s = 5000 \) m/s
Depremin merkez üssünün yeryüzüne olan uzaklığını bulalım.
\( d = 16v_s \)
\( = 16 \cdot 5000 = 80.000 \) m
\( = 80 \) km bulunur.
Bir metro durağının girişinde yan yana ve aynı uzunlukta yürüyen merdiven ve normal merdiven bulunmaktadır. Yürüyen merdivenin bir basamağının en üstten en alta inmesi 1 dakika sürüyor.
Asya normal merdivenden aşağı 40 saniyede indiğine göre, yürüyen merdivenden aynı hızla yürüyerek aşağı inmesi ne kadar sürer?
Çözümü GösterMerdivenlerin uzunluğuna \( d \) diyelim.
Asya'nın hızına \( v_a \), yürüyen merdivenin hızına \( v_b \) diyelim.
Asya yürüyen merdivenden \( v_a \) hızıyla yürüyerek indiğinde toplam hızı \( v_a + v_b \) olur.
Yürüyen merdiven \( d \) mesafesini 60 saniyede kateder.
\( d = 60v_b \)
\( v_b = \dfrac{d}{60} \)
Asya normal merdivende \( d \) mesafesini 40 saniyede kateder.
\( d = 40v_a \)
\( v_a = \dfrac{d}{40} \)
Asya yürüyen merdivenle yürüyerek indiğinde hızı \( v_a + v_b \) olur.
Asya'nın yürüyen merdivenle inme süresine \( t \) diyelim.
\( d = (v_a + v_b)t \)
\( t = \dfrac{d}{v_a + v_b} \)
\( v_a \) ve \( v_b \)'nin \( d \) cinsinden karşılıklarını yazalım.
\( = \dfrac{d}{\frac{d}{40} + \frac{d}{60}} \)
\( = \dfrac{d}{\frac{3d}{120} + \frac{2d}{120}} \)
\( = \dfrac{120d}{5d} = 24 \) saniye bulunur.
Bir alışveriş merkezindeki yürüyen merdiven hareket halindeyken; Fatih merdiveni yürüyerek 25 saniyede, koşarak 15 saniyede çıkıyor. Merdiven çalışmıyorken ise Fatih merdiveni koşarak 20 saniyede çıkıyor.
Buna göre yürüyen merdiven çalışmıyorken Fatih merdiveni yürüyerek kaç saniyede çıkar?
Çözümü GösterYürüyen merdivenin hızına \( v_m \), Fatih'in koşarkenki hızına \( v_k \), yürürkenki hızına \( v_y \) diyelim.
Merdivenin uzunluğuna \( x \) metre diyelim.
Merdiven hareket halindeyken Fatih koştuğunda toplam hızı merdivenin hızı ile koşma hızının toplamına eşit olur.
\( v_m + v_k = \dfrac{x}{15} \)
Merdiven hareket halindeyken Fatih yürüdüğünde toplam hızı merdivenin hızı ile yürüme hızının toplamına eşit olur.
\( v_m + v_y = \dfrac{x}{25} \)
Merdiven duruyorken Fatih koştuğunda hızı koşma hızına eşit olur.
\( v_k = \dfrac{x}{20} \)
Fatih'in koşma hızını birinci denklemde yerine koyarak merdivenin hızını bulalım.
\( v_m + \dfrac{x}{20} = \dfrac{x}{15} \)
\( v_m = \dfrac{x}{60} \)
Bu değeri ikinci denklemde yerine koyarak Fatih'in yürüme hızını bulalım.
\( \dfrac{x}{60} + v_y = \dfrac{x}{25} \)
\( v_y = \dfrac{7x}{300} \)
Merdiven duruyorken Fatih yürüdüğünde hızı yürüme hızına eşit olur. Bu durumda \( x \) mesafesini çıkma süresini bulalım.
\( \dfrac{x}{v_y} = \dfrac{x}{\frac{7x}{300}} \)
\( = \dfrac{300}{7} \) saniye bulunur.
Ahmet, A şehrinden B şehrine gitmek için arabasıyla yolculuğa çıkıyor. Ahmet sabit hızla gitmekte, ancak yolun radarlı kısımlarında hızını üçte bir oranında düşürmektedir.
Ahmet yol radarsız olsaydı B şehrine ulaşacağı sürede yolun dörtte üçünü tamamladığına göre, toplam yolculuk süresinin kaçta kaçı radarlı yolda geçmiştir?
Çözümü GösterAracın radarsız yoldaki hızına \( v \) diyelim. Bu durumda radarlı yoldaki hız \( \frac{2v}{3} \) olur.
İşlem kolaylığı açısından toplam yolculuk süresine 1 saat, yolculuğun radarlı kısmında geçen süreye \( t \) saat diyelim. Bu durumda yolculuğun radarsız kısmında geçen süre \( 1 - t \) saat olur.
Radarlı ve radarsız yolun tamamı, A ve B arası (radarsız yolda 1 saatte gidilebilecek) mesafenin dörtte üçünü eşittir.
\( \dfrac{2v}{3} \cdot t + v \cdot (1 - t) = \dfrac{3}{4} \cdot 1 \cdot v \)
\( v \) bilinmeyenleri sadeleşir.
\( \dfrac{2t}{3} + 1 - t = \dfrac{3}{4} \)
\( \dfrac{t}{3} = \dfrac{1}{4} \)
\( t = \dfrac{3}{4} \)
Buna göre, toplam yolculuk süresinin dörtte üçü radarlı yolda geçmiştir.
Adem'in dijital kol saati 24 saatlik zaman formatını kullanarak saat ve dakikayı göstermektedir (23:59 şeklinde).
Buna göre, Adem saatinin ekranında 3 rakamını bir günde toplam kaç dakika görür?
Çözümü GösterKol saatinin saat kısmı 03, 13 ve 23 olduğu zamanlarda ekranda 3 rakamı görülür.
\( 3 \times 60 = 180 \) dk
Geriye kalan 21 saat boyunca, saatin dakika kısmı 30 ile 39 (30 ve 39 dahil) arasında bir sayı gösterdiğinde ekranda 3 rakamı görülür.
\( 21 \times 10 = 210 \) dk
Geriye kalan 21 saat boyunca, saatin dakika kısmı 03, 13, 23, 43, 53 sayılarını gösterdiğinde de ekranda 3 rakamı görülür.
\( 21 \times 5 = 105 \) dk
Buna göre, Adem saatinin ekranında 3 rakamını günde \( 180 + 210 + 105 = 495 \) dakika görür.
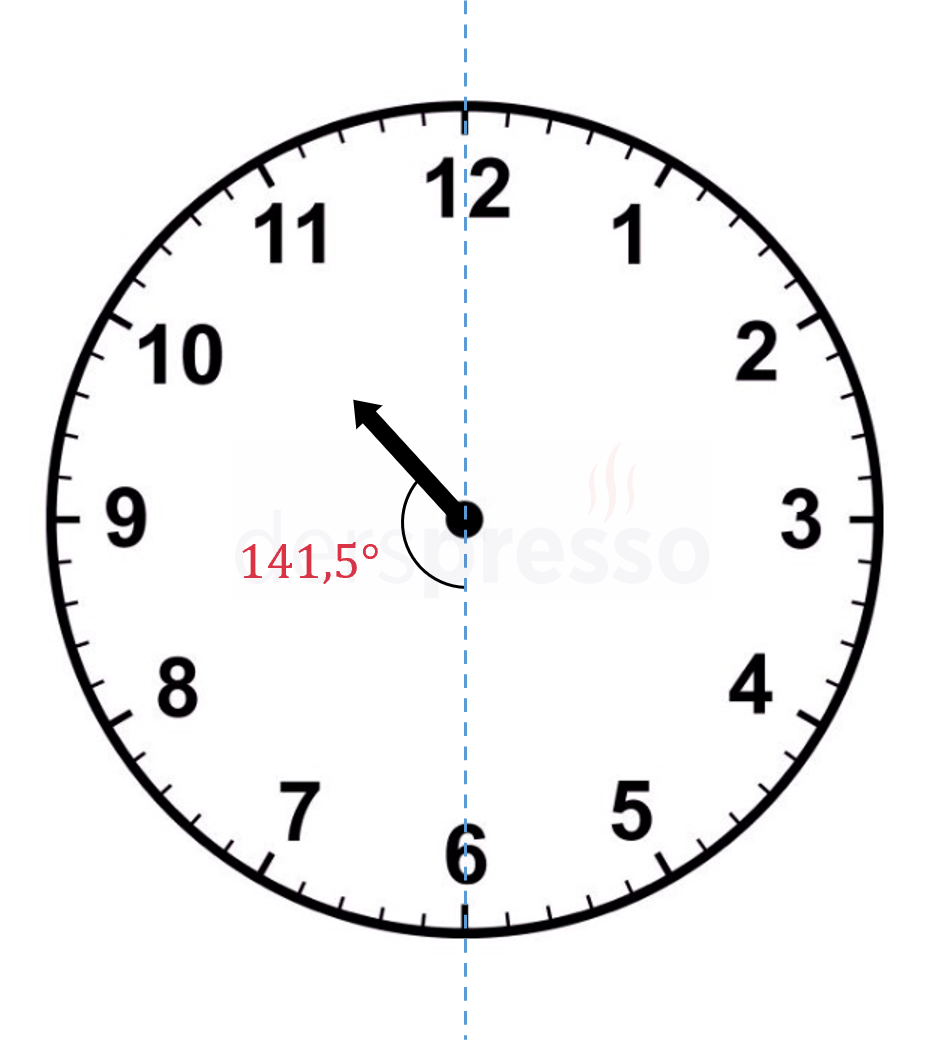
Mehtap okula giderken kol saatinin yelkovanının düştüğünü fark ediyor. Saatinin akrepi ile saat 6 arasında şekildeki gibi 141,5°'lik açı olduğuna göre, saat kaçtır?
Çözümü GösterAkrepin 1°'yi ne kadar sürede döndüğünü hesaplayalım.
Akrep 12 saatte 360° döndüğüne göre 1 saatte \( \frac{360}{12} = 30° \) döner.
Dolayısıyla akrep \( \frac{60}{30} = 2 \) dakikada 1° döner.
Akrep ile saat 6 arasında 141,5°'lik açı varsa son tam saat olan 10 ile arasında \( 141,5 - 120 = 21,5° \)'lik açı vardır.
Akrep 21,5 dereceyi \( 21,5 \times 2 = 43 \) dakikada döner.
Buna göre saat 10:43'tür.
Ada'nın annesi Ada'yı okuldan almak için her gün aynı saatte arabayla evden okula doğru yola çıkıyor.
Ada bir gün dersi 50 dk erken bittiği için okuldan eve yürümeye karar veriyor ve annesiyle yolda karşılaşarak eve arabayla birlikte gidiyorlar.
Eve normal zamandan 30 dk önce vardıklarına göre, Ada okuldan eve kaç dakika yürümüştür?
Çözümü GösterAda'nın eve doğru yürüdüğü süreye \( t \) dk diyelim ve normal bir günde annesinin Ada'yı saat 4:00'da aldığını varsayalım.
Eve normal zamandan 30 dk önce vardılarsa bu zaman kazancı annesinin yolda karşılaştıkları noktadan normal bir günde okula gidip aynı noktaya dönmesi için gerekli zamana karşılık gelir.
Buna göre yolda karşılaştıkları noktadan okula arabayla gidiş ve dönüş süresi 15'er dk'dır.
Buna göre annesi normal bir günde saat 3:45'te yolda karşılaştıkları noktada olur.
Ada'nın dersi 50 dk erken bittiğine göre saat 3:10'da eve doğru yürümeye başlamıştır.
Saat 3:10'da yürümeye başlayan Ada saat 3:45'te annesiyle yolda karşılaştığına göre, toplam 35 dk yürümüştür.
Bir lunaparktaki çocuk treni düz bir parkurda sabit hızla ilerlemektedir.
Trenin dışında duran Zeynep, tren hareket halindeyken trenin en arkasından en önüne doğru eşit uzunlukta adımlarla ve sabit hızla yürümeye başlıyor ve trenin en önüne 400 adımda ulaşıyor.
Tekrar trenin en arkasına dönmek isteyen Zeynep, tren hareket halindeyken trenin en önünden en arkasına 240 adımda ulaşıyor.
Buna göre, trenin uzunluğu Zeynep'in kaç adımına eşittir?
Çözümü GösterZeynep'in attığı toplam adım sayısını bulalım.
\( 400 + 240 = 640 \)
Zeynep'in ileriye doğru attığı adım sayısının geriye doğru attığı adım sayısından farkı, trenin bu sürede ilerlediği (adım cinsinden) mesafeye eşittir.
\( 400 - 240 = 160 \)
Buna göre, Zeynep 640 adım attığı sürede tren 160 adım ilerlemiştir.
Dolayısıyla, Zeynep'in 4 adım attığı sürede tren 1 adım ilerler.
Trenin uzunluğu, Zeynep'in geri dönüşte attığı adım sayısı ve bu sürede trenin ilerlediği adım sayısının toplamına eşittir.
Zeynep'in 240 adım attığı sürede tren \( \frac{240}{4} = 60 \) adım ilerler.
Buna göre, trenin uzunluğu Zeynep'in \( 240 + 60 = 300 \) adımına eşittir.

Atakan 16:00'da başlayan bir saatlik gitar dersi sırasında saate baktığında akrep ve yelkovanın şekildeki gibi dikeyle eşit açılar yaptığını fark ediyor.
Buna göre, dersin bitmesine kaç saniye kalmıştır?
Çözümü GösterHer ibrenin dikeyle yaptığı açıya \( x \) derece, saat 16:00'dan Atakan'ın saate baktığı ana kadar geçen süreye \( s \) saniye diyelim.
Bir saat \( 60 \times 60 = 3600 \) saniyedir.
Saat üzerindeki iki saat (örneğin 3 ve 4) arasındaki açı \( \frac{360}{12} = 30 \) derecedir.
Akrep bir saatte \( 360 \div 12 = 30° \) döner.
Akrepin \( s \) saniyede döndüğü açıyı bulalım.
\( 30° \cdot \dfrac{s}{3600} = \dfrac{s}{120} \) derece
Akrep için \( x \) açısı saat 4 ve 6 arasındaki açı ile \( s \) saniyede döndüğü açının farkına eşittir.
\( x = 2 \cdot 30 - \dfrac{s}{120} \)
\( = 60 - \dfrac{s}{120} \)
Yelkovan bir saatte 360° döner.
Yelkovanın \( s \) saniyede döndüğü açıyı bulalım.
\( 360° \cdot \dfrac{s}{3600} = \dfrac{s}{10} \) derece
Yelkovan için \( x \) açısı \( s \) saniyede döndüğü açı ile 180°'nin farkına eşittir.
\( x = \dfrac{s}{10} - 180 \)
Bulduğumuz iki \( x \) ifadesini eşitleyelim.
\( 60 - \dfrac{s}{120} = \dfrac{s}{10} - 180 \)
\( \dfrac{s}{10} + \dfrac{s}{120} = 180 + 60 \)
\( \dfrac{13s}{120} = 240 \)
\( s \approx 2215 \) saniye
Buna göre ders 2215 saniye önce başlamıştır.
Dolayısıyla dersin bitmesine \( 3600 - 2215 = 1385 \) saniye kalmıştır.
Alp ve Mert kare şeklindeki bir parkın etrafında scooter'larıyla aynı köşeden ters yönde ve sabit hızlarla ilerlemeye başlıyorlar.
Alp'in hızı saatte 54 km, Mert'in hızı ise saatte 36 km'dir ve Mert park etrafında bir turunu 3 dakikada tamamlamaktadır.
Alp ve Mert sadece karenin aynı kenarında olduklarında birbirilerini gördüklerine göre, 2. kez karşılaştıklarında birbirlerini kaç saniye görürler?
Çözümü GösterVerilen hızları metre/saniye cinsinden bulalım.
Alp'in hızı \( \frac{54 \cdot 1000}{3600} = 15 \) metre/saniyedir.
Mert'in hızı \( \frac{36 \cdot 1000}{3600} = 10 \) metre/saniyedir.
Mert bir turunu 3 dakikada, yani 180 saniyede tamamlamaktadır.
Buna göre, kare şeklindeki bahçenin çevresi \( 10 \cdot 180 = 1800 \) metre, bir kenarı 450 metredir.
Alp bir turu \( \frac{1800}{15} = 120 \) saniyede tamamlar.
120 saniyede Mert \( 120 \cdot 10 = 1200 \) metre ilerlemiştir.
Alp ilk turu tamamladığında ikisinin konumu şekildeki gibi olur.
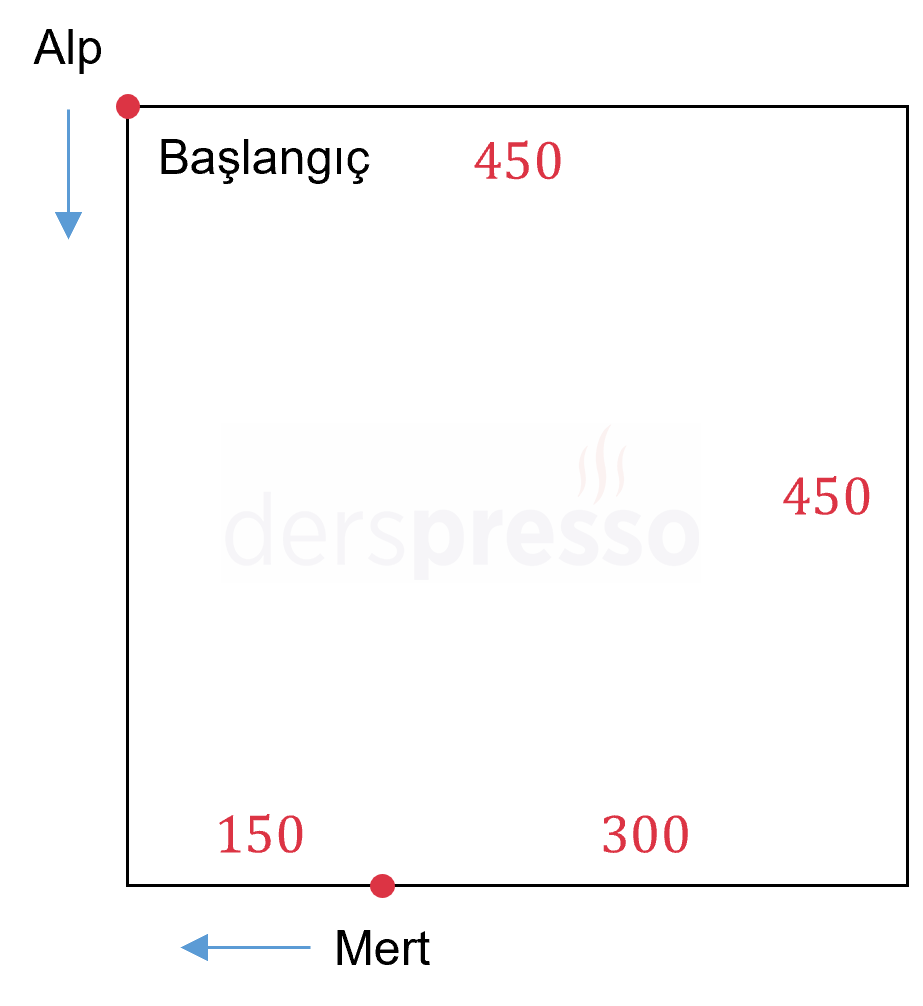
Mert 150 metre ilerlediğinde Alp'in görüş açısına gireceğine göre, Mert ilk kez görüş açısına girdiğinde aralarındaki mesafeyi bulalım.
Mert 150 metreyi 15 saniyede ilerler.
Alp 15 saniyede \( 15 \cdot 15 = 225 \) metre ilerler.
Buna göre, ikinci turda birbirlerini ilk kez gördüklerinde aralarında \( 450 - 225 = 225 \) metre olur.
İkinci kez karşılaştıklarında birbirlerini kaç saniye gördüklerini bulalım.
Birbirlerine doğru ilerledikleri için, buluşma süreleri aralarındaki mesafenin hızlarının toplamına oranına eşittir.
\( \dfrac{225}{15 + 10} = 9 \) saniye birbirlerini görürler.
Ali ve Mehmet daire şeklinde bir yarış pistinde aynı noktadan ve birbirlerine ters yönde koşmaya başlıyorlar.
İlk karşılaşmalarında Ali 250 metre koşmuş, ikinci karşılaşmalarında ise Mehmet ilk karşılaşmalarından sonra 350 metre daha koşmuştur.
Ali ve Mehmet sabit hızlarla koştuklarına göre, pistin uzunluğu kaç metredir?
Çözümü GösterPistin uzunluğuna \( x \) diyelim.
İlk karşılaşmada Ali 250, Mehmet \( x - 250 \) metre koşmuştur.
İkinci karşılaşmalarında Mehmet 350 metre koştuysa pistin kalan 250 metresini koştuktan sonra ilk başladıkları yerden 100 metre daha koşmuştur.
Buna göre, Ali ikinci karşılaşmada \( x - 250 - 100 = x - 350 \) metre daha koşmuştur.
Ali'nin hızına \( v_a \), Mehmet'in hızına \( v_m \) diyelim.
İlk karşılaşmaları için hızlarının oranını bulalım.
\( \dfrac{v_a}{v_m} = \dfrac{250}{x - 250} \)
İkinci karşılaşmaları için hızlarının oranını bulalım.
\( \dfrac{v_a}{v_m} = \dfrac{x - 350}{350} \)
İki oranı birbirine eşitleyelim.
\( \dfrac{v_a}{v_m} = \dfrac{250}{x - 250} = \dfrac{x - 350}{350} \)
\( (x - 350)(x - 250) = 250 \cdot 350 \)
\( x^2 - 600x + 250 \cdot 350 = 250 \cdot 350 \)
\( x^2 - 600x = 0 \)
\( x(x - 600) = 0 \)
\( x = 600 \) metre bulunur.
Eda, Los Angeles'dan yerel saatle 17:05'te kalkan uçağa biniyor ve Londra'ya ertesi gün yerel saatle 12:20'de varıyor. 14:35'te Londra'dan tekrar uçağa binen Eda, İstanbul'a yerel saatle 20:25'te iniyor.
Saat farkı Los Angles ve Londra arasındaki 8 saat, Londra ve İstanbul arasındaki 2 saat olduğuna göre, toplam uçuş süresi nedir?
Çözümü Gösterİlk uçuşun Los Angeles saatine göre kalkış saati 17:05'tir. Los Angeles ve Londra arasındaki saat farkı 8 saattir.
Londra, Los Angeles'tan daha doğuda olduğundan Los Angeles'tan 8 saat ileridedir.
Bu durumda ilk uçuşun Londra saatine göre kalkış saati \( 17:05 + 8 = 25:05 \), yani ertesi gün \( 01:05 \) olur.
İlk uçuşun Londra saatine göre iniş saati 12:20'dir. Aynı saat diliminde olan iniş saatinden kalkış saatini çıkararak ilk uçuşun süresini bulalım.
\( 12:20 - 01:05 = 11:15 \)
İlk uçuşun süresi 11 saat 15 dakikadır.
Eda, Londra saatine göre 14:35'te tekrar uçağa biniyor.
İstanbul, Londra'dan daha doğuda olduğundan Londra'dan 2 saat ileridedir.
Bu durumda ikinci uçuşun İstanbul saatine göre kalkış saati \( 14:35 + 2 = 16:35 \) olur.
İkinci uçuşun İstanbul saatine göre iniş saati 20:25'tir. Aynı saat diliminde olan iniş saatinden kalkış saatini çıkarak ikinci uçuşun süresini bulalım.
\( 20:25 - 16:35 = 03:50 \)
İkinci uçuşun süresi 3 saat 50 dakikadır.
İki uçuşun sürelerini toplayarak toplam uçuş süresini bulalım.
\( 11:15 + 03:50 = 14:65 \Longrightarrow 15:05 \)
Toplam uçuş süresi 15 saat 5 dakikadır.