Karışım Problemleri
39 litre suyla 21 litre alkol karıştırılırsa karşımın yüzde kaçı alkol olur?
Çözümü GösterKarışımın toplam hacmi \( 39 + 21 = 60 \) litre olur. Bu 60 litrenin 21 litresi alkoldür.
Alkol oranı \( = \dfrac{21}{60} = \dfrac{7}{20} = \dfrac{35}{100} \)
Buna göre karışımın %35'i alkol olur.
Tuz, un ve su kullanılırak yapılan bir hamurda tuz miktarı su miktarının \( \frac{1}{3} \)'ü, un miktarı ise su miktarının 2 katıdır.
Bu hamurdaki un oranı yüzde kaçtır?
Çözümü GösterHamurdaki tuz miktarına \( x \) gram diyelim.
Tuz miktarı su miktarının \( \frac{1}{3} \)'ü olduğuna göre su miktarı \( 3x \) gramdır.
Un miktarı su miktarının 2 katı olduğuna göre un miktarı \( 2 \cdot 3x = 6x \) gramdır.
Buna göre hamurun toplamı \( x + 3x + 6x = 10x \) gramdır.
Hamurdaki un oranı \( = \dfrac{6x}{10x} = \dfrac{60}{100} = \%60 \) olur.
Ali bahçesindeki çitleri boyamak için üç rengi karıştırarak istediği tonda kahverengi boya elde etmek istiyor.
Ali'nin hazırladığı karışımda sarı rengin %20 fazlası kadar mavi renk, mavi rengin %80 fazlası kadar da kırmızı renk vardır.
Karışım toplam 1417 kg olduğuna göre, karışımın kaç litresi mavi renktir?
Çözümü GösterAli'nin hazırladığı karışımdaki sarı renk miktarına işlem kolaylığı açısından \( 25x \) kg diyelim.
Karışımda sarı rengin %20 fazlası kadar mavi renk vardır.
\( 25x + 25x \cdot \dfrac{20}{100} = 25x + 5x \)
\( = 30x \) kg mavi renk
Karışımda mavi rengin %80 fazlası kadar kırmızı renk vardır.
\( 30x + 30x \cdot \dfrac{80}{100} = 30x + 24x \)
\( = 54x \) kg kırmızı renk
Tüm renklerin miktarlarını toplayarak 1417'ye eşitleyelim.
\( 25x + 30x + 54x = 1417 \)
\( x = 13 \)
Karışımdaki mavi renk miktarı \( 30x = 30 \cdot 13 = 390 \) kg'dır.
Bir kasap %15 yağlı kıyma ile %25 yağlı kıymayı karıştırarak %18 yağlı kıyma elde etmek istiyor.
Bu işlem için 100 kg kıyma kullanacağına göre, %15 yağlı kıymadan kaç kg kullanmalıdır?
Çözümü Göster100 kg kıyma içindeki %15 yağlı kıyma miktarına \( x \) kg, %25 yağlı kıyma miktarına \( 100 - x \) kg diyelim.
Karışımdaki toplam yağ miktarını hesaplayalım.
\( x \cdot \dfrac{15}{100} + (100 - x) \cdot \dfrac{25}{100} = 18 \)
\( 15x + 2500 - 25x = 1800 \)
\( x = 70 \)
Buna göre %15 yağlı kıymadan 70 kg kullanılmalıdır.
60 gramlık bir şeker - su karışımında %40 oranında şeker bulunmaktadır. Buna göre bu karışıma;
(a) 12 gram şeker, 28 gram su eklenirse yeni karışımın şeker yüzdesi kaç olur?
(b) %24'ü şeker olan 180 gramlık şeker - su karışımı eklenirse yeni karışımın şeker yüzdesi kaç olur?
Çözümü Göster60 gramlık karışımın \( 60 \cdot \frac{40}{100} = 24 \) gramı şekerdir, kalan \( 60 - 24 = 36 \) gramı sudur.
(a) seçeneği:
Bu karışıma 12 gram şeker eklendiğinde toplam şeker miktarı \( 24 + 12 = 36 \) gram, 28 gram su eklendiğinde karışımın toplam ağırlığı \( 60 + 12 + 28 = 100 \) gram olur.
Yeni karışımın şeker yüzdesi \( \frac{36}{100} = \%36 \) olur.
(b) seçeneği:
Eklenen 180 gramlık şeker - su karışımındaki şeker miktarı \( 180 \cdot \frac{24}{100} = 43,2 \) gramdır.
Yeni karışımdaki toplam şeker miktarı \( 24 + 43,2 = 67,2 \) gram, karışımın toplam ağırlığı \( 60 + 180 = 240 \) gram olur.
Yeni karışımın şeker yüzdesi \( \frac{67,2}{240} = \frac{672}{2400} = \frac{28}{100} = \%28 \) olur.
%30'u şeker olan 120 gram şekerli su karışımına 35 gram su ekleniyor.
Kaç gram daha su eklenirse yeni karışımın su oranı %80 olur?
Çözümü Göster120 gram şeker - su karışımının %30'u şeker ise karışımdaki şeker miktarı \( 120 \cdot \frac{30}{100} = 36 \) gram, su miktarı \( 120 - 36 = 84 \) gramdır.
Karışımın su oranın %80 olması için eklenmesi gereken toplam su miktarına \( x \) diyelim.
\( \dfrac{84 + x}{120 + x} = \dfrac{80}{100} \)
\( \dfrac{84 + x}{120 + x} = \dfrac{4}{5} \)
İçler - dışlar çarpımı yapalım.
\( 5(84 + x) = 4(120 + x) \)
\( 420 + 5x = 480 + 4x \)
\( x = 60 \)
Buna göre karışıma toplamda \( x = 60 \) gram su eklenmelidir.
35 gram su eklendiği belirtildiği için eklenmesi gereken su miktarı \( 60 - 35 = 25 \) gramdır.
Serhat %60 oranında alkol içeren 120 gramlık bir su - alkol karışımını seyrelterek %45'lik bir su - alkol karışımı elde etmek istiyor.
Serhat bu seyreltme işleminde kaç gram su kullanmalıdır?
Çözümü Gösterİlk durumda karışımda \( 120 \cdot \frac{60}{100} = 72 \) gram alkol bulunur.
Serhat'ın karışıma eklemesi gereken su miktarına \( x \) gram diyelim.
Seyreltme işlemi sonunda oluşacak karışım \( 120 + x \) gram olur, alkol miktarı ise yine 72 gram olarak kalır.
Seyreltme işlemi sonrasında elde edilmek istenen alkol oranı %45'tir.
\( \dfrac{72}{120 + x} = \dfrac{45}{100} \)
\( \dfrac{72}{120 + x} = \dfrac{9}{20} \)
İçler - dışlar çarpımı yapalım.
\( 1440 = 1080 + 9x \)
\( 9x = 360 \)
\( x = 40 \) gram su eklenmelidir.
Şeker ve su kullanarak tatlı şerbeti hazırlayan Neşe, %20'si şeker olan şerbeti ocakta ısıtmaktadır.
Neşe ocağı kapattığında şerbetten 300 ml su buharlaşmış ve şerbetteki şeker oranı %25 olmuştur. Buna göre başlangıçtaki şerbet miktarı kaç litredir?
Çözümü GösterŞerbetin başlangıçtaki hacmine işlem kolaylığı açısından \( 100x \) ml diyelim.
Bu şerbetin \( 100x \cdot \frac{20}{100} = 20x \) ml'si şeker, kalan \( 100x - 20x = 80x \) ml'si sudur.
Buharlaşma gerçekleşince kalan şerbetin hacmi \( 100x - 300 \) ml olur, şeker miktarı ise aynı kalır.
Buharlaşma sonrası şerbetteki şeker oranı %25'tir.
\( \dfrac{20x}{100x - 300} = \dfrac{25}{100} \)
\( \dfrac{20x}{100x - 300} = \dfrac{1}{4} \)
İçler - dışlar çarpımı yapalım.
\( 80x = 100x - 300 \)
\( 20x = 300 \)
\( x = 15 \)
Buna göre başlangıçtaki şerbet miktarı \( 100x = 1500 \) ml, yani 1,5 litredir.
480 gramlık alkol - su karışımına 20 gram alkol ve 150 gram su eklendiğinde karışımın alkol oranı %40 oluyor.
Buna göre, bu karışımın alkol oranı başlangıçta kaçtır?
Çözümü GösterKarışımda başlangıçtaki alkol miktarına \( x \) diyelim.
Bu durumda başlangıçtaki su miktarı \( 480 - x \) olur.
Karışıma 20 gram alkol ve 150 gram su eklendiğinde toplam alkol miktarı \( x + 20 \), toplam su miktarı \( 480 - x + 150 = 630 - x \) olur. Karışımın toplam ağırlığı ise \( 480 + 20 + 150 = 650 \) gram olur.
Son durumda karışımdaki alkol oranı %40'tır.
\( \dfrac{x + 20}{650} = \dfrac{40}{100} \)
\( \dfrac{x + 20}{650} = \dfrac{2}{5} \)
İçler - dışlar çarpımı yapalım.
\( 5x + 100 = 1300 \)
\( x = 240 \)
Başlangıçtaki alkol oranını bulalım.
\( \frac{240}{480} \cdot 100 = \%50 \) bulunur.
Alkol oranı %60 olan 300 gramlık alkol - su karışımının dörtte biri dökülüp yerine aynı miktarda su ekleniyor.
Buna göre, elde edilen yeni karışımın alkol oranı yüzde kaçtır?
Çözümü Göster300 gramlık karışımın dörtte biri \( \frac{300}{4} = 75 \) gramdır. Bu miktar döküldüğünde geriye \( 300 - 75 = 225 \) gram kalır.
Karışımdan bir miktar döküldüğünde içindeki alkol oranı değişmez.
%60'ı alkol olan 225 gramlık karışımdaki alkol miktarı \( 225 \cdot \frac{60}{100} = 135 \) gramdır.
Dökülen miktar yerine yine 75 gram su eklendiğinde oluşan yeni karışımın alkol oranını bulalım.
\( \dfrac{135}{225 + 75} \cdot 100 = 45 \)
Buna göre, elde edilen yeni karışımın alkol oranı %45'tir.
%40'ı tuz olan 30 kilogramlık tuz - su karışımıyla %47'si alkol olan 120 kilogramlık alkol - su karışımı karıştırılıyor.
Buna göre, elde edilen karışımın tuz oranı yüzde kaçtır?
Çözümü GösterTuz - su karışımının \( 30 \cdot \frac{40}{100} = 12 \) kilogramı tuzdur.
Alkol - su karışımının 0 kilogramı tuzdur.
Elde edilen karışım toplam \( 30 + 120 = 150 \) kg olur. Bunun \( 12 + 0 = 12 \) kilogramı tuzdur.
Yeni karışımın tuz yüzdesini bulalım.
\( \dfrac{12}{150} = \dfrac{8}{100} = \%8 \) bulunur.
Şeker oranı %20 ve %60 olan iki şekerli su karışımı karıştırılıyor.
Bu işlem sonucunda şeker oranı %35 olan 120 kilogramlık yeni bir karışım elde edildiğinde göre, karışıma %20'lik şekerli su karışımından kaç kg eklenmiştir?
Çözümü Göster%20'lik şekerli su karışımının ağırlığına \( x \) kg diyelim.
Yeni karışım 120 kg olduğuna göre %60'lık şekerli su karışımı \( 120 - x \) kg olur.
%20'lik karışımla %60'lık karışım karıştırılınca %35'lik bir karışım oluşuyor.
\( 20x + 60(120 - x) = 35 \cdot 120 \)
\( x + 3(120 - x) = 35 \cdot 6 \)
\( x + 360 - 3x = 210 \)
\( 2x = 150 \)
\( x = 75 \)
Buna göre %20'lik şekerli su karışımından 75 kg alınmıştır.
Ağırlıkça %30'u alkol olan bir su - alkol karışımı ile ağırlıkça %55'i alkol olan bir su - alkol karışımı karıştırılıyor.
Bu iki karışımın birleşiminden ağırlıkça %40'ı alkol olan bir karışım elde edildiğine göre, %30'luk karışımın ağırlığının %55'lik karışımın ağırlığına oranı kaçtır?
Çözümü Göster%30'luk karışımın ağırlığına \( x \), %55'lik karışımın ağırlığına \( y \) diyelim.
İki karışım karıştırılınca oluşan karışımın ağırlığı \( x + y \) olur.
%30'luk karışımla %55'lik karışım karıştırılınca %40'lık bir karışım oluşuyor.
\( 30x + 55y = 40(x + y) \)
\( 30x + 55y = 40x + 40y \)
\( 10x = 15y \)
\( 2x = 3y \)
Soruda \( \frac{x}{y} \) oranı sorulmaktadır.
\( \dfrac{x}{y} = \dfrac{3}{2} \) bulunur.
Kuruyemişçide iki farklı kuru üzüm - leblebi karışımından birincisinde 4 kg kuru üzüm, 21 kg leblebi, ikincisinde 6 kg kuru üzüm, 9 kg leblebi vardır.
Bu karışımların homojen olarak dağıldığı düşünülürse birinci kaptaki kuruyemişin \( \frac{1}{5} \)'i, ikinci kaptaki kuruyemişin \( \frac{2}{3} \)'ü alınarak oluşturulan yeni karışımın leblebi oranı yüzde kaç olur?
Çözümü GösterBirinci karışımda \( 4 + 21 = 25 \) kg kuruyemiş vardır. Kuru üzüm oranı \( \frac{4}{25} = \frac{16}{100} \) yani %16'dır.
İkinci karışımda \( 6 + 9 = 15 \) kg kuruyemiş vardır. Kuru üzüm oranı \( \frac{6}{15} = \frac{40}{100} \) yani %40'tır.
Birinci karışımdan \( 25 \cdot \frac{1}{5} = 5 \) kg, ikinci karışımdan \( 15 \cdot \frac{2}{3} = 10 \) kg kuruyemiş alınarak oluşturulan yeni karışım toplam \( 5 + 10 = 15 \) kg olur.
Yeni karışımın kuru üzüm oranına \( x \) diyelim.
\( 5 \cdot 16 + 10 \cdot 40 = 15 \cdot x \)
\( 15x = 480 \)
\( x = 32 \)
Buna göre yeni karışımın kuru üzüm oranı %32, leblebi oranı ise %68 olur.
Ayşe evine oturmaya gelen arkadaşına kahve ve sütten oluşan bir içecek hazırlıyor. %40'ı kahve olan 300 mililitrelik içeceğin \( \frac{2}{5} \)'i taşırken dökülüyor.
Ayşe dökülen miktarın yarısı kadar süt yarısı kadar kahve ekleyip yine 300 mililitrelik bir içecek elde ediyor. Buna göre son durumda içecekteki kahve oranı yüzde kaçtır?
Çözümü Göster300 mililitrelik kahvenin \( 300 \cdot \frac{2}{5} = 120 \) mililitresi dökülmüştür.
Ayşe kalan %40'ı kahve olan \( 300 - 120 = 180 \) mililitrelik karışıma %50'si kahve olan 120 mililitre karışım ekliyor.
Yeni oluşan karışımın kahve oranına yüzde \( x \) diyelim.
\( 180 \cdot 40 + 120 \cdot 50 = 300 \cdot x \)
\( 3 \cdot 8 + 2 \cdot 10 = x \)
\( x = 44 \) bulunur.
%15'i antep fıstığı olan \( X \) gr karışık kuruyemiş paketine 20 gr daha antep fıstığı eklendiğinde paketteki kuruyemişlerin %25'i antep fıstığı olmuştur.
Buna göre, \( X \) kaçtır?
Çözümü GösterEklenen 20 gr kuruyemişi %100'ü antep fıstığı olan bir karışım gibi düşünerek karışımın denklemini kuralım.
\( X \cdot 15 + 20 \cdot 100 = (X + 20) \cdot 25 \)
\( 3X + 400 = 5X + 100 \)
\( 2X = 300 \)
\( X = 150 \) gr bulunur.
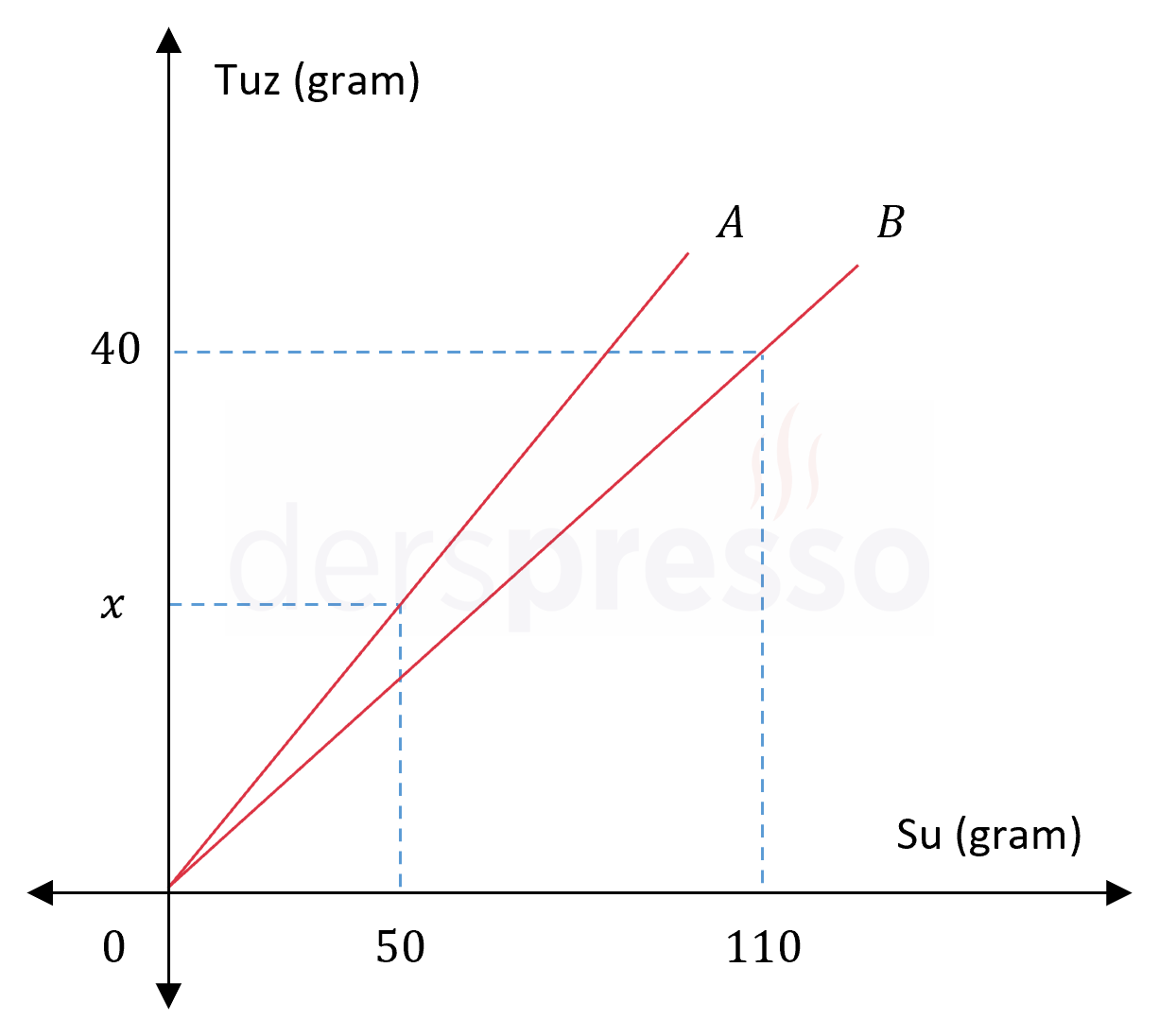
Yukarıdaki grafikte A ve B kaplarındaki karışımların içerdiği tuz ve su miktarları verilmiştir.
A kabından alınan 70 gramlık karışım ile B kabından alınan 30 gramlık karışımın karıştırılmasıyla elde edilen karışımdaki tuz oranı %28 olduğuna göre, \( x \) kaçtır?
Çözümü GösterA ve B kaplarındaki karışımların tuz oranlarını bulalım.
Her kaptaki tuz oranı, tuz miktarının toplam karışım miktarına bölümüyle bulunur.
A kabındaki tuz miktarı: \( \dfrac{x}{50 + x} \)
B kabındaki tuz miktarı: \( \dfrac{40}{40 + 110} \)
A kabından alınan 70 gram karışımdaki tuz miktarı \( 70 \cdot \frac{x}{50 + x} \) gram olur.
B kabından alınan 30 gram karışımdaki tuz miktarı \( 30 \cdot \frac{40}{150} = 8 \) gram olur.
A ve B kaplarından alınan karışımların toplamı 100 gramdır.
Oluşan karışımda %28'lik tuz oranı olduğuna göre, karışımda \( 100 \cdot \frac{28}{100} = 28 \) gram tuz vardır.
\( 70 \cdot \dfrac{x}{50 + x} + 8 = 28 \)
\( \dfrac{x}{50 + x} = \dfrac{2}{7} \)
\( 7x = 100 + 2x \)
\( x = 20 \) bulunur.
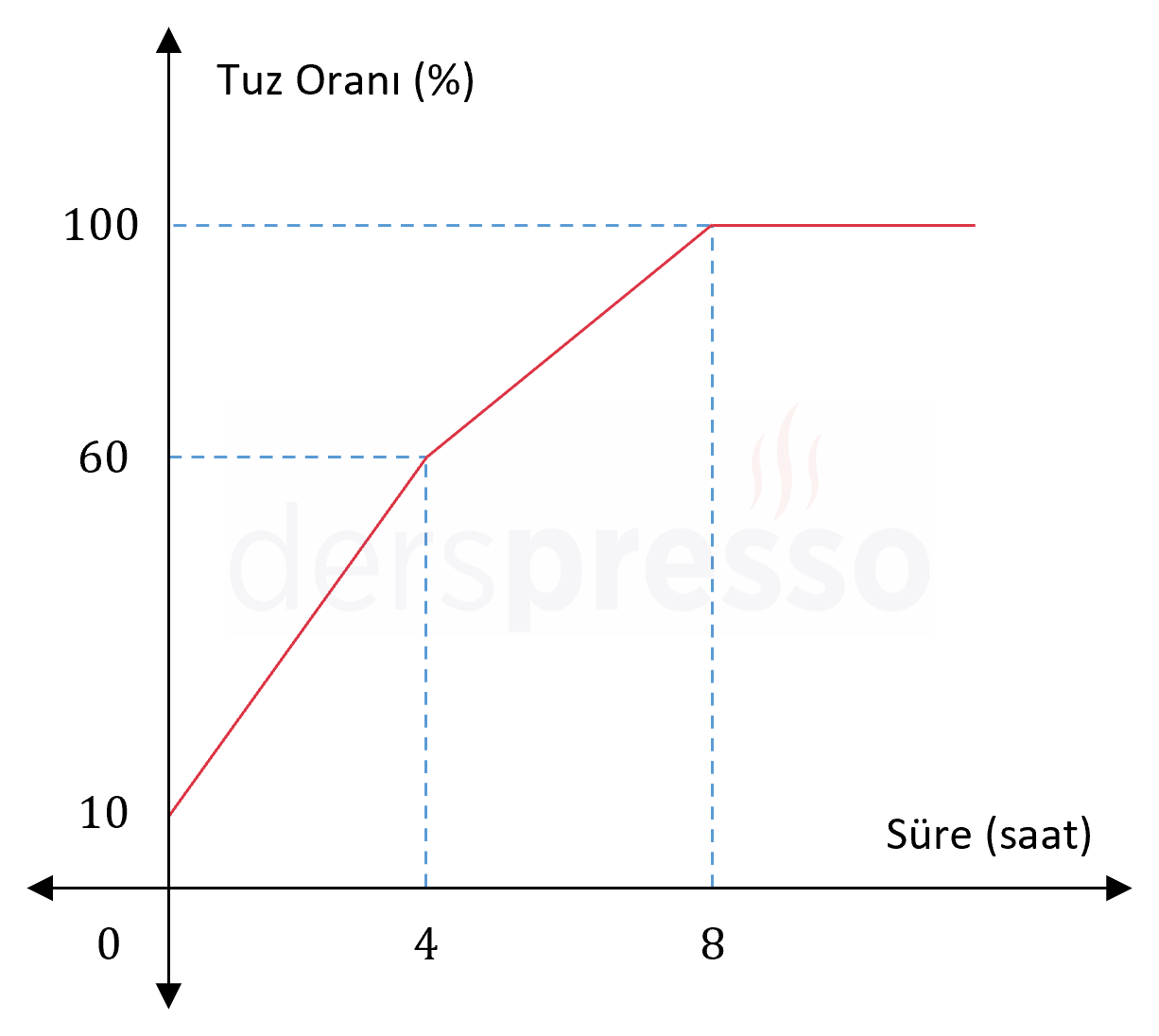
Yukarıda başlangıçta içerisinde 600 gramlık tuz - su karışımı bulunan bir kabın bir ısıtıcıyla ısıtılması sonucunda, kaptaki tuz oranındaki zamana göre değişimi gösteren grafik verilmiştir.
Isıtıcının derecesi ilk 4 saatin ardından kısılmış, daha sonra kaptaki buharlaşma tüm su buharlaşana (tuz oranı %100 olana) kadar devam etmiştir.
Buna göre ilk 4 saatte buharlaşan su miktarı ikinci 4 saatte buharlaşan su miktarının kaç katıdır?
Çözümü GösterBaşlangıçtaki tuz ve su miktarını bulalım.
Başlangıçtaki tuz oranı %10'dur.
\( 600 \cdot \dfrac{10}{100} = 60 \) gram
Buna göre başlangıçta karışımda 60 gram tuz ve 540 gram su bulunmaktadır.
İlk 4 saatte buharlaşan su miktarına \( x \) diyelim.
4 saat sonunda kaptaki tuz oranı %60'tır, tuz miktarı ise sabit kalır.
\( (600 - x) \cdot \dfrac{60}{100} = 60 \)
\( 600 - x = 100 \)
\( x = 500 \)
İlk 4 saatte buharlaşan su miktarı 500 gram olduğuna göre, kapta kalan karışım miktarı 100 gram olur.
Kaptaki tuz miktarı 60 gram olduğuna göre, kalan su miktarı (dolayısıyla ikinci 4 saatte buharlaşan su miktarı) 40 gram olur.
İlk 4 saatte buharlaşan su miktarının ikinci 4 saatte buharlaşan su miktarının kaç katı olduğunu bulalım.
\( \dfrac{500}{40} = \dfrac{25}{2} \) bulunur.
Bir market 800 gramlık paketler halinde bir günde toplam 500 kg fındık ve fıstık satmıştır. Satılan paketler sadece fındıktan, sadece fıstıktan ya da eşit oranda fındık ve fıstıktan oluşmaktadır.
Satılan kuruyemiş miktarının beşte biri fındık olduğuna ve karışık kuruyemiş paket sayısı 50 olduğuna göre, sadece fıstık içeren kaç paket vardır?
Çözümü Göster500 kg = 500000 gram
Satılan kuruyemişlerin beşte biri yani \( \frac{500000}{5} = 100000 \) gramı fındık, \( 500000 - 100000 = 400000 \) gramı fıstıktır.
50 paket karışık kuruyemiş toplam \( 50 \cdot 800 = 40000 \) gramdır.
Bu 40000 gram karışık kuruyemişin 20000 gramı fındık, 20000 gramı fıstıktır.
Tüm fıstıkların ağırlığından karışık kuruyemişte kullanılan fıstıkların ağırlığını çıkardığımızda sadece fıstık içeren paketlerdeki fıstık miktarını buluruz.
\( 400000 - 20000 = 380000 \) gram
Bu fıstık miktarının 800 gramlık kaç pakete karşılık geldiğini bulalım.
\( \dfrac{380000}{800} = 475 \) paket bulunur.
Bir şekerli su karışımında şeker oranı \( \%(2x + y) \), su oranı \( \%y \)'dir.
18 gramı tuz, 72 gramı şeker olan başka bir tuz - şeker karışımının tuz oranı \( \%(x - y) \) olduğuna göre, \( x \) kaçtır?
Çözümü GösterBir karışım iki bileşenden oluşuyorsa bu iki bileşenin yüzde olarak oranlarının toplamı 100 olmalıdır.
\( (2x + y) + y = 100 \)
\( 2x + 2y = 100 \)
\( x + y = 50 \)
İkinci tuz - şeker karışımı toplam \( 18 + 72 = 90 \) gramdır. Bu karışımdaki tuz oranı \( \frac{18}{90} = \frac{20}{100} = %20 \) olur.
\( x - y = 20 \)
İki denklemi ortak çözelim.
\( x = 35 \) bulunur.
Çiğ domates %94 oranında su içerirken kuru domateste bu oran %19'dur.
Buna göre 150 kilogram çiğ domatesten kaç kilogram kuru domates elde edilir?
Çözümü GösterÇiğ domatesteki su oranı %94 ise domates posası oranı %6 olur.
150 kg çiğ domatesteki posa miktarını bulalım.
Posa miktarı \( = 150 \cdot \dfrac{6}{100} = 9 \) kg
Bu durumda kuru domatesteki posa miktarı da 9 kg olacaktır.
Kuru domatesteki su oranı %19 ise domates posası oranı %81 olur.
Elde edilen kuru domates miktarına \( x \) kg diyelim.
\( 9 = \dfrac{81}{100} \cdot x \)
\( x = \dfrac{100}{9} \) kg olarak bulunur.
Domates kurutulduğunda içindeki likopenin %3'ünü kaybeder.
Ortalama 30 mg/kg likopen içeren orta boy domatesler ile ortalama 40 mg/kg likopen içeren büyük boy domatesler hangi oranda karıştırılırsa kurutulmuş domatesler ortalama 32,98 mg/kg likopen içerir? (Domatesler kurutulduğunda ağırlık kaybı yaşanmamıştır.)
Çözümü GösterOrta boy domateslerden \( x \) kg, büyük boy domateslerden \( y \) kg kullandığımızı varsayalım.
Kurutulmadan önce orta boy domatesler \( 30x \) mg, büyük boy domatesler \( 40y \) mg likopen içerir.
Domatesler kurutulduğunda içindeki likopenin %3'ünü kaybettiğine göre kurutma sonrası likopenin %97'si kalır.
Bu durumda kalan likopen miktarı \( (30x + 40y) \cdot \frac{97}{100} \) olur.
Toplam domates miktarı \( x + y \) kg'dır.
Tüm domatesler içindeki likopen oranını bulalım.
\( \dfrac{(30x + 40y) \cdot \frac{97}{100}}{x + y} = 32,98 \)
\( 2910x + 3880y = 3298x + 3298y \)
\( 388x = 582y \)
\( \dfrac{y}{x} = \dfrac{388}{582} = \dfrac{2}{3} \)
Buna göre domatesler \( \frac{2}{3} \) oranında karıştırılmalıdır.
Orijinal bal sattığını iddia eden bir satıcıdan şikayet üzerine alınan örnek analiz edildiğinde balın kimyasal içerdiği tespit edilmiştir.
Bu satıcı balı maliyetine sattığını öne sürmüş, ancak satışlardaki gerçek kar oranının %40 olduğu hesaplanmıştır. Buna göre satılan karışımdaki kimyasal yüzdesi kaçtır? (Satıcı kimyasallar için para harcamamıştır.)
Çözümü Göster100 kg bala katılan kimyasal miktarına \( x \) kg, 1 kg balın maliyetine \( m \) TL diyelim.
Satıcının 100 kg bal aldığını varsayarsak cebinden \( 100m \) TL çıkmıştır.
Bala \( x \) kg kimyasal kattığında elindeki kimyasallı bal miktarı \( 100 + x \) kg olur.
Satıcı balın tamamını sattığında \( (100 + x)m \) TL ciro elde eder.
Satıcının gerçek kar oranı %40'tır.
\( \text{Kar %} = \dfrac{\text{Satış} - \text{Maliyet}}{\text{Maliyet}} \cdot 100 \)
\( 40 = \dfrac{(100 + x)m - 100m}{100m} \cdot 100 \)
\( 40 = \dfrac{xm}{m} \)
\( x = 40 \)
Buna göre 140 kg olarak satılan kimyasallı bal 40 kg kimyasal içerir.
Karışımdaki kimyasal yüzdesini bulalım.
\( \dfrac{40}{140} \cdot 100 = \%\dfrac{200}{7} \) bulunur.
Tamamen dolu üç farklı kabın hacimleri sırasıyla 2, 5 ve 6 ile doğru orantılıdır. Bu kaplarda bulunan alkol - su karışımları sırasıyla \( 1:1 \), \( 2:3 \) ve \( 3:4 \) oranlarında alkol ve su içermektedir.
Bu üç karışım taşmayacak şekilde dördüncü bir kaba aktarılıyor. Buna göre son durumda dördüncü kapta oluşan karışımın su oranı kaçtır?
Çözümü Gösterİşlem kolaylığı açısından kapların hacimlerine sırasıyla \( 14k \), \( 35k \) ve \( 42k \) diyelim.
1. kapta \( 1:1 \) oranında alkol ve su bulunmaktadır, dolayısıyla kapta \( 7k \) alkol, \( 7k \) su bulunmaktadır.
2. kapta \( 2:3 \) oranında alkol ve su bulunmaktadır, dolayısıyla kapta \( 14k \) alkol, \( 21k \) su bulunmaktadır.
3. kapta \( 3:4 \) oranında alkol ve su bulunmaktadır, dolayısıyla kapta \( 18k \) alkol, \( 24k \) su bulunmaktadır.
Üç kap tek kapta birleştirildiğinde kapta \( 7k + 14k + 18k = 39k \) alkol, \( 7k + 21k + 24k = 52k \) su bulunur.
Son durumdaki su oranını bulalım.
\( \dfrac{52k}{52k + 39k} = \dfrac{52k}{91k} \)
\( = \dfrac{4}{7} \) bulunur.
195 mililitrelik homojen bir karışımdaki alkol/su oranı \( \frac{4}{9} \)'dur. Bu karışımdan bir miktar dökülerek yerine aynı miktarda alkol eklendiğinde karışımdaki oran \( \frac{2}{3} \)'e yükseliyor.
Buna göre karışımdan dökülen miktar kaç mililitredir?
Çözümü GösterDökülen miktara işlem kolaylığı açısından \( 13t \) diyelim.
Karışımdaki alkol/su oranı \( \frac{4}{9} \) olduğuna göre, alkol miktarının karışıma oranı \( \frac{4}{13} \), su miktarının karışım miktarına oranı \( \frac{9}{13} \) olur.
Buna göre 195 mililitrelik karışımda \( 195 \cdot \frac{4}{13} = 60 \) mL alkol, \( 195 \cdot \frac{9}{13} = 135 \) mL su bulunmaktadır.
Dökülen karışımın da \( 13t \cdot \frac{4}{13} = 4t \) mililitresi alkol, \( 13t \cdot \frac{9}{13} = 9t \) mililitresi sudur.
Karışımda son durumdaki alkol/su oranını bulalım.
\( \dfrac{60 - 4t + 13t}{135 - 9t} = \dfrac{2}{3} \)
İçler - dışlar çarpımı yapalım.
\( 3 \cdot 60 + 3 \cdot 9t = 2 \cdot 135 - 2 \cdot 9t \)
\( 180 + 27t = 270 - 18t \)
\( 45t = 90 \)
\( t = 2 \)
Karışımdan dökülen miktar \( 13t = 26 \) mL olarak bulunur.
Üç farklı kahve çeşidinin kafein oranları arasındaki ilişki aşağıdaki gibidir.
- 60 ml A kahvesinin içerdiği kafein miktarı ile 180 ml B kahvesinin içerdiği kafein miktarının toplamı, 480 ml C kahvesinin içerdiği kafein miktarına eşittir.
- 180 ml B kahvesinin içerdiği kafein miktarı ile 60 ml C kahvesinin içerdiği kafein miktarının toplamı, 60 ml A kahvesinin içerdiği kafein miktarına eşittir.
Buna göre, bu üç kahve çeşidinden kafein oranı en yüksek olanı hangisidir?
Çözümü GösterVerilen kahve miktarlarının EBOB'u 60 olduğu için karşılaştırmaları 60 ml üzerinden yapalım.
60 ml kahvede A, B ve C kahvelerinin içerdikleri kafein miktarlarına sırasıyla \( a \), \( b \) ve \( c \) diyelim.
Verilen bilgilere göre denklemleri yazalım.
\( a + 3b = 8c \)
\( 3b + c = a \)
Birinci denklemden ikinci denklemi çıkaralım.
\( a + 3b - (3b + c) = 8c - a \)
\( a - c = 8c - a \)
\( 2a = 9c \)
Kafein miktarlarına \( a = 9k \) ve \( c = 2k \) diyelim ve bu değerleri ikinci denklemde yerine koyalım.
\( 3b + 2k = 9k \)
\( b = \dfrac{7k}{3} \)
Buna göre aynı miktarda kahve içinde en çok kafein A kahvesinde bulunur.
Otomobil antifriz çözeltisi hazırlayan bir makine birebir oranda antifriz ve su karıştırması gerekirken \( \frac{2}{3} \) oranında karıştırıyor.
Bu sorun makine 120 litrelik karışım hazırladıktan sonra fark ediliyor. Sorunu çözmek için bir teknisyen yanlış hesaplama yaparak karışımdan bir miktar döküp yerine aynı miktarda antifriz ekliyor ve karışımdaki oran \( \frac{11}{9} \)'a çıkıyor.
Son durumda karışımdan hangi miktarda dökülüp yerine aynı miktarda su eklenirse sorun tamamen giderilir?
Karışım ilk hazırlandığında \( 120 \cdot \frac{2}{5} = 48 \) lt antifriz ve \( 120 \cdot \frac{3}{5} = 72 \) lt sudan oluşmaktadır.
İlk müdahale sonucunda dökülen miktara işlem kolaylığı açısından \( 5k \) lt diyelim. Bu miktarın \( 5k \cdot \frac{2}{5} = 2k \) litresi antifriz, \( 5k \cdot \frac{3}{5} = 3k \) litresi su olur.
Bu durumda yeni karışımdaki antifriz/su oranı aşağıdaki gibi olur.
\( \dfrac{48 - 2k + 5k}{72 - 3k} = \dfrac{11}{9} \)
İçler - dışlar çarpımı yapalım.
\( 9(48 + 3k) = 11(72 - 3k) \)
\( 432 + 27k = 792 - 33k \)
\( 60k = 360 \)
\( k = 6 \)
Buna göre ilk müdahale sonucunda \( 5k = 30 \) lt karışım dökülmüş, 30 litre antifriz eklenmiştir.
Sonuçta karışımda \( 48 - 2k + 30 = 66 \) lt antifriz, \( 72 - 3k = 54 \) lt su bulunur.
Sorunu tamamen gidermek için dökülmesi gereken miktara işlem kolaylığı açısından \( 20t \) diyelim.
Dökülen bu \( 20t \) litrelik karışımın \( 20t \cdot \frac{11}{20} = 11t \) litresi antifriz, \( 20t \cdot \frac{9}{20} = 9t \) litresi su olur.
Tekrar 20 lt su eklendiğinde karışımdaki antifriz/su oranı istendiği gibi birebir oranda olmalıdır.
\( \dfrac{66 - 11t}{54 - 9t + 20t} = 1 \)
\( 66 - 11t = 54 + 11t \)
\( 22t = 12 \)
\( t = \dfrac{6}{11} \)
\( 20t = 20 \cdot \dfrac{6}{11} = \dfrac{120}{11} \) lt bulunur.