Sayı ve Kesir Problemleri
Sayı ve kesir problemleri; verilen bir metni anlamamız, bir ya da daha fazla değişken tanımlamamız, bu değişkenler arasında verilen ilişkileri birer denkleme (ya da bazı durumlarda eşitsizliğe) dönüştürmemiz ve bu denklemleri çözmemiz beklenen en temel problemlerdir.
Bir sayının 6 katının 5 eksiği aynı sayının 4 katının 7 fazlasına eşittir. Buna göre bu sayı kaçtır?
Çözümü GösterDeğeri istenen sayıya \( x \) diyelim ve verilen bilgileri iki cebirsel ifadenin eşitliği şeklinde yazalım.
\( 6x - 5 = 4x + 7 \)
\( x \)'i yalnız bırakalım.
\( 2x - 5 = 7 \)
\( 2x = 12 \)
\( x = 6 \) bulunur.
Toplamları 84 olan 3 sayıdan birincisi ikincisinden 4 fazla, üçüncüsünden 7 eksiktir. Buna göre bu sayıların en büyüğü kaçtır?
Çözümü GösterBirinci sayıya \( x \) diyelim. Bu durumda ikinci sayı \( x - 4 \), üçüncü sayı \( x + 7 \) olur.
Bu üç sayının toplamı 84'tür.
\( x + (x - 4) + (x + 7) = 84 \)
\( 3x + 3 = 84 \)
\( x \)'i yalnız bırakalım.
\( 3x = 81 \)
\( x = 27 \)
Sayıların en büyüğü \( x + 7 = 34 \) olarak bulunur.
Doğan'ın oyuncak araba ve askerlerinin toplam sayısı 90'dır. Doğan oyuncak arabalarından ikisini kaybedince kalan arabaların sayısı askerlerin sayısının 3 katı oluyor.
Buna göre, Doğan'ın başlangıçta kaç oyuncak arabası vardır?
Çözümü GösterDoğan'ın başlangıçtaki oyuncak arabalarının sayısına \( x \), askerlerinin sayısına \( y \) diyelim.
Araba ve askerlerin toplam sayısı 90'dır.
\( x + y = 90 \)
Doğan arabalardan ikisini kaybedince araba sayısı asker sayısının 3 katı oluyor.
\( x - 2 = 3y \)
\( x \)'i \( y \) cinsinden yazalım.
\( x = 3y + 2 \)
Bu \( x \) değerini ilk denklemde yerine yazalım.
\( (3y + 2) + y = 90 \)
\( 4y + 2 = 90 \)
\( 4y = 88 \)
\( y = 22 \)
Başlangıçtaki araba sayısını bulmak için \( y \) değerini ilk denklemde yerine yazalım.
\( x + 22 = 90 \)
\( x = 68 \) bulunur.
Bir torbada belirli miktarda mavi ve kırmızı bilye bulunuyor.
Bu torbadan 10 kırmızı bilye çıkarılırsa mavi bilyelerin sayısı kırmızı bilyelerin sayısının 3 katı oluyor. Onun yerine 35 mavi bilye çıkarılırsa kırmızı bilyeler mavi bilyelerin iki katı oluyor.
Buna göre, en başta torbada kaç bilye vardır?
Çözümü GösterTorbadaki mavi bilyelerin sayısına \( x \), kırmızı bilyelerin sayısına \( y \) diyelim.
Torbadan 10 kırmızı bilye çıkarılırsa mavi bilyelerin sayısı kırmızı bilyelerin sayısının 3 katı oluyor.
\( x = 3(y - 10) \)
Torbadan 35 mavi bilye çıkarılırsa kırmızı bilyeler mavi bilyelerin iki katı oluyor.
\( y = 2(x - 35) = 2x - 70 \)
İlk eşitlikteki \( y \) yerine ikinci eşitlikteki karşılığı koyalım.
\( x = 3(y - 10) \)
\( x = 3(2x - 70 - 10) \)
\( x = 6x - 240 \)
\( x = 48 \)
\( y \) değerini bulmak için ikinci eşitlikte \( x = 48 \) koyalım.
\( y = 2(x - 35) \)
\( = 2(48 - 35) = 26 \)
Torbadaki toplam bilye sayısını bulalım.
\( x + y = 48 + 26 = 74 \) bulunur.
Kahve içmeye giden bir grup arkadaş gelen hesabı kişi sayısına böldüklerinde kişi başına 12 TL düşmektedir, ancak 4 kişinin yanında para olmadığı için kalanlar hesabı aralarında bölüşüyorlar.
Ödeme yapanlar ödemeleri gerekenden 6'şar TL fazla ödediklerine göre, bu grupta kaç kişi vardır?
Çözümü GösterGruptaki kişi sayısına \( x \) diyelim.
Buna göre toplam hesap \( 12x \) olur.
Ödeme yapan kişi sayısı 4 azalınca kişi başı yapılan ödeme \( 12 + 6 = 18 \) TL oluyor.
Her iki durumda toplam hesap tutarı eşittir.
\( 12x = 18(x - 4) \)
\( 12x = 18x - 72 \)
\( 6x = 72 \)
\( x = 12 \) bulunur.
Bir şirkette çalışan kadınların sayısı erkeklerin sayısından 6 fazladır. Kadın çalışanların yarısı, erkek çalışanların 3'te birinin 7 fazlası zam alacaktır.
Zam alacak olan toplam çalışan sayısı 30 olduğuna göre, şirkette kaç kadın çalışan vardır?
Çözümü GösterKadın çalışan sayısına işlem kolaylığı açısından \( 2x \), erkek çalışan sayısına \( 3y \) diyelim.
Kadın çalışan sayısı erkek çalışan sayısından 6 fazladır.
\( 2x = 3y + 6 \)
Şirkette 30 çalışan zam alacaktır.
\( (2x \cdot \dfrac{1}{2}) + (3y \cdot \dfrac{1}{3} + 7) = 30 \)
\( x + y + 7 = 30 \)
\( x \)'i \( y \) cinsinden yazalım.
\( x = 23 - y \)
İlk denklemde \( x \) yerine bulduğumuz değeri yazalım.
\( 2(23 - y) = 3y + 6 \)
\( 46 - 2y = 3y + 6 \)
\( 5y = 40 \)
\( y = 8 \)
Bu \( y \) değerini kullanarak \( x \)'i bulalım.
\( x = 23 - y \)
\( = 23 - 8 = 15 \)
Buna göre şirkette \( 2x = 2(15) = 30 \) kadın çalışan vardır.
Veli toptancıdan tanesi 3,75 TL olan su ve 6 TL olan ayrandan belirli bir sayıda alıyor. Veli'nin ödeyeceği toplam tutar aşağıdakilerden hangisi olabilir?
(a) 41 TL
(b) 41,50 TL
(c) 41,75 TL
(d) 42 TL
(e) 42,25 TL
Çözümü Göster3,75 ve 6 sayılarının ikisi de 0,75'in bir tam sayı katı olduğu için Veli'nin ödeyeceği toplam tutar 0,75'in bir tam sayı katı olmalıdır.
Seçeneklerde 0,75'in bir tam sayı katı olan tek sayı 42'dir.
Toplam tutarın 42 TL olabileceğini kontrol edelim.
8 tane su ve 2 tane ayranın fiyatı:
\( 8 \cdot 3,75 + 2 \cdot 6 = 42 \) TL
Doğru cevap (d) seçeneğidir.
Selin ve Seray para biriktirmeye çalışan iki kardeştir ve ikisinin de bir miktar birikmiş parası vardır.
Anneleri Selin'e Seray'ın birikmiş parasının çeyreği kadar para verince Selin'in parası Seray'ın parasının 3 katı oluyor.
Buna göre Selin'in başlangıçtaki parasını Seray'ın parası cinsinden yazın.
Çözümü GösterSelin'in başlangıçtaki parasına \( m \), Seray'ın parasına \( n \) diyelim.
Anneleri Selin'e Seray'ın birikmiş parasının çeyreği kadar para verince Selin'in parası Seray'ın parasının 3 katı oluyor.
\( m + \dfrac{n}{4} = 3n \)
\( m = 3n - \dfrac{n}{4} \)
\( m = \dfrac{11n}{4} \) bulunur.
Bir kuruyemişçide toplam 56 kg fıstık ve ceviz vardır. Fıstığın kilosu 40 TL, cevizin kilosu 30 TL'dir.
Fıstık ve cevizlerin toplam satış fiyatı 1990 TL olduğuna göre, kuruyemişçide kaç kg ceviz vardır?
Çözümü GösterToplam fıstık miktarına \( x \) kg, ceviz miktarına \( y \) kg diyelim.
Toplam miktar 56 kg'dır.
\( x + y = 56 \)
\( x = 56 - y \)
Toplam fiyat 1990 TL'dir.
\( 40x + 30y = 1990 \)
\( 4x + 3y = 199 \)
Yukarıda bulduğumuz \( x \) değerini bu denklemde yerine yazalım.
\( 4(56 - y) + 3y = 199 \)
\( 224 - 4y + 3y = 199 \)
\( y = 25 \) kg ceviz vardır.
Fatma teyze elindeki parayla 30 kg domates ve 25 kg patlıcan ya da 40 kg patlıcan alabilmektedir.
Buna göre Fatma teyze elindeki parayla kaç kg domates alabilir?
Çözümü GösterDomatesin kilogram fiyatına \( x \), patlıcanın kilogram fiyatına \( y \) diyelim.
Fatma teyze elindeki parayla 30 kg domates ve 25 kg patlıcan alabildiğine göre, para miktarına \( 30x + 25y \) diyebiliriz.
Fatma teyze aynı parayla 40 kg patlıcan alabiliyorsa para miktarına \( 40y \) de diyebiliriz.
Her iki durumdaki para miktarları birbirine eşittir.
\( 30x + 25y = 40y \)
\( 30x = 15y \)
\( 2x = y \)
Toplam para miktarı olan \( 40y \) ifadesinde \( y = 2x \) yazalım.
\( 40y = 40(2x) = 80x \)
Fatma teyzenin elindeki para \( 80x \) olduğuna göre, kilogram fiyatı \( x \) olan domatesten 80 kg alabilir.
Bir okul 2 yılda bir düzenlenen satranç turnuvasına 2020 ve 2022 yıllarında 4 kişilik bir takım gönderiyor. 2022 yılındaki takım, mezun olan bir oyuncunun yerine gelen yeni bir oyuncu dışında 2020 yılındaki takımla aynıdır.
Bu iki takımın yaş ortalamaları aynı olduğuna göre, mezun olan oyuncu ile yeni oyuncunun yaş farkı kaçtır?
Çözümü Göster2020 yılındaki oyuncuların yaşlarına \( a, b, c, d \) diyelim.
Mezun olan oyuncunun yaşı \( a \) olsun.
2022 yılında takıma yeni katılan oyuncunun yaşına \( e \) diyelim.
Aradan geçen 2 yılda değişmeyen 3 oyuncunun yaşı 2 yaş artacaktır.
Bu durumda 2022 yılındaki oyuncuların yaşları \( b + 2 \), \( c + 2 \), \( d + 2 \) ve \( e \) olur.
İki yıl için de takımın yaş ortalamasını yazalım ve takımın yaş ortalaması aynı kaldığı için iki ortalamayı birbirine eşitleyelim.
\( \dfrac{a + b + c + d}{4} = \dfrac{b + 2 + c + 2 + d + 2 + e}{4} \)
\( a + b + c + d = b + c + d + e + 6 \)
\( a = e + 6 \)
Mezun olan oyuncu ile yeni oyuncu arasındaki yaş farkı 6'dır.
Bir kırtasiye haftanın ilk günü elindeki defterlerin \( \frac{1}{8} \)'ini, ikinci günü kalan defterlerin \( \frac{4}{7} \)'sini satmıştır. Geriye kalan defterleri ise üçüncü gün satmıştır. Üçüncü gün defterlerden kazandığı para 330 TL ise sattığı tüm defterlerden toplam kaç TL para kazanmıştır?
Çözümü GösterBaşlangıçta kırtasiyenin elindeki defter sayısına \( a \) diyelim.
İlk gün satılan defter sayısı: \( a \cdot \dfrac{1}{8} = \dfrac{a}{8} \)
İlk gün sonunda kalan defter sayısı: \( a - \dfrac{a}{8} = \dfrac{7a}{8} \)
İkinci gün kalan defterlerin \( \frac{4}{7} \)'si satılmıştır.
İkinci gün satılan defter sayısı: \( \dfrac{7a}{8} \cdot \dfrac{4}{7} = \dfrac{a}{2} \)
İlk iki günde satılan defter sayısı: \( \dfrac{a}{8} + \dfrac{a}{2} = \dfrac{5a}{8} \)
Üçüncü gün kalan defterler satılmıştır.
Üçüncü gün satılan defter sayısı: \( a - \dfrac{5a}{8} = \dfrac{3a}{8} \)
Defterlerin \( \frac{3}{8} \)'i 330 TL'ye satıldıysa tümünün satış tutarını bulalım.
\( \dfrac{330}{\frac{3}{8}} = 330 \cdot \dfrac{8}{3} = 880 \) TL bulunur.
Bir dernek tarafından bir ortaokuldaki 8. sınıf öğrencilerine belirli sayıda defter dağıtılacaktır. Okuldaki 8. sınıflar A, B ve C şubelerinden oluşmaktadır.
Defterler tüm öğrencilere dağıtılırsa öğrenci başına 18 tane, sadece A şubesindeki öğrencilere dağıtılırsa öğrenci başına 60 tane, sadece B şubesindeki öğrencilere dağıtılırsa öğrenci başına 72 tane defter düşmektedir.
Buna göre, defterler sadece C şubesindeki öğrencilere dağıtılırsa öğrenci başına kaç tane defter düşer?
Çözümü GösterDağıtılacak toplam defter sayısına \( x \); A, B, C şubelerindeki öğrenci sayısına sırasıyla \( a, b, c \) diyelim.
Verilen bilgileri denklem şeklinde yazalım.
\( x = 18(a + b + c) \)
\( x = 60a = 72b \)
\( \frac{x}{c} \) oranı C şubesindeki öğrenci başına düşen defter sayısını verir.
\( a \) ve \( b \) bilinmeyenlerini \( x \) cinsinden yazalım.
\( 60a = x \)
\( a = \dfrac{x}{60} \)
\( 72b = x \)
\( b = \dfrac{x}{72} \)
Denklemde \( a \) ve \( b \) bilinmeyenlerini \( x \) cinsinden yazalım.
\( x = 18(\dfrac{x}{60} + \dfrac{x}{72} + c) \)
\( x = \dfrac{18x}{60} + \dfrac{18x}{72} + 18c \)
\( x = \dfrac{108x}{360} + \dfrac{90x}{360} + 18c \)
\( x = \dfrac{198x}{360} + 18c \)
\( \dfrac{162x}{360} = 18c \)
\( \dfrac{x}{c} = \dfrac{360 \cdot 18}{162} = 40 \) bulunur.
Efe, 1 ve 10 dahil olmak üzere 1'den 10'a kadar olan tam sayılardan ikisini seçiyor.
Efe'nin seçtiği iki tam sayının çarpımı, kalan 8 sayının toplamına eşit olduğuna göre, Efe'nin seçtiği tam sayılar nedir?
Çözümü GösterEfe'nin seçtiği sayılara \( a \) ve \( b \) diyelim.
1'den 10'a kadar olan tam sayıların toplamını bulalım.
\( \dfrac{10 \cdot 11}{2} = 55 \)
Verilen bilgileri denklem şeklinde yazalım.
\( ab = 55 - (a + b) \)
\( ab + a + b = 55 \)
Eşitliğin her iki tarafına 1 ekleyelim.
\( ab + a + b + 1 = 56 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( a(b + 1) + (b + 1) = 56 \)
\( (a + 1)(b + 1) = 56 \)
56'yı asal çarpanlarına ayıralım.
\( 56 = 2^3 \cdot 7 \)
56 sayısı aşağıdaki şekillerde iki farklı sayının çarpımı şeklinde yazılabilir.
\( 56 = 56 \cdot 1 = 28 \cdot 2 = 14 \cdot 4 = 8 \cdot 7 \)
\( a \) ve \( b \) sayılarının 1 ve 10 arasında olduğunu dikkate alırsak \( a + 1 \) ve \( b + 1 \) sayıları (sıradan bağımsız) 7 ve 8 olmalıdır.
Buna göre, Efe'nin seçtiği tam sayılar 6 ve 7 olarak bulunur.
Ayşe'nin evindeki iki kovadan küçük olanın hacmi büyük olanın hacminin üçte ikisidir. Bu kovalardan küçük olan tamamen dolu iken büyük olan boştur.
Ayşe ilk olarak küçük kovadaki suyun dörtte üçünü büyük kovaya boşaltıyor, daha sonra büyük kovadaki suyun üçte ikisini küçük kovaya boşaltıyor, son olarak küçük kovadaki suyun beşte dördünü büyük kovaya boşaltıyor.
Buna göre, bu işlemlerin sonunda büyük kovanın kaçta kaçı dolu olur?
Çözümü GösterBüyük kovanın hacmine \( 60x \) diyelim. Bu durumda küçük kovanın hacmi \( 60x \cdot \frac{2}{3} = 40x \) olur.
İşlemleri kovalara sırayla uygulayalım.
En başta küçük kovada \( 40x \) miktar su vardır, büyük kova ise boştur.
Birinci işlemde küçük kovadan büyük kovaya \( 40x \cdot \frac{3}{4} = 30x \) miktar su boşaltılır.
Birinci işlem sonunda küçük kovada \( 40x - 30x = 10x \), büyük kovada \( 30x \) miktar su olur.
İkinci işlemde büyük kovadan küçük kovaya \( 30x \cdot \frac{2}{3} = 20x \) miktar su boşaltılır.
İkinci işlem sonunda küçük kovada \( 10x + 20x = 30x \), büyük kovada \( 30x - 20x = 10x \) miktar su olur.
Üçüncü işlemde küçük kovadan büyük kovaya \( 30x \cdot \frac{4}{5} = 24x \) miktar su boşaltılır.
Üçüncü işlem sonunda küçük kovada \( 30x - 24x = 6x \), büyük kovada \( 10x + 24x = 34x \) miktar su olur.
Bu işlemler sonunda büyük kovanın kaçta kaçının dolu olduğunu bulalım.
\( \dfrac{34x}{60x} = \dfrac{17}{30} \) bulunur.
Bir satıcı ürünlerini elindeki kolilere beşerli koyduğunda 4 koli boş kalıyor.
Satıcı ürün sayısını 12 artırıp koli sayısını 6 eksiltip ürünleri kolilere yedişerli koyduğunda ise 2 ürün artıyor.
Buna göre satıcının en başta kaç adet ürünü vardır?
Çözümü GösterSatıcının en başta elindeki koli sayısına \( k \) diyelim.
Birinci durumdaki ürün sayısını bulalım.
\( 5(k - 4) \)
İkinci durumdaki ürün sayısını bulalım.
\( 7(k - 6) + 2 \)
İkinci durumdaki ürün sayısı birinci durumdakinden 12 fazladır.
\( 5(k - 4) + 12 = 7(k - 6) + 2 \)
\( 5k - 20 + 12 = 7k - 42 + 2 \)
\( k = 16 \)
Birinci durumdaki ürün sayısını bulalım.
\( 5(k - 4) = 5(16 - 4) \)
\( = 60 \) bulunur.
Aynı mağazada çalışan iki arkadaştan Ayşe'nin ekip arkadaşlarından kadın olanların sayısı erkek olanların sayısının 2 katından 4 fazladır.
Ali'nin ekip arkadaşlarından kadın olanların sayısı erkek olanların sayısının 3 katından 1 eksiktir.
Buna göre bu mağazada toplam kaç çalışan vardır?
Çözümü GösterAyşe'nin ekip arkadaşlarından erkek olanların sayısına \( x \) diyelim.
Bu durumda Ayşe'nin ekip arkadaşlarından kadın olanların sayısı \( 2x + 4 \) olur.
Ayşe de kadın olduğundan mağazadaki toplam kadın sayısı \( 2x + 4 + 1 = 2x + 5 \) olur.
Buna göre Ayşe'nin bakış açısıyla mağazada toplam \( x + (2x + 5) = 3x + 5 \) çalışan vardır.
Ali erkek olduğundan Ali'nin ekip arkadaşlarından erkek olanların sayısı \( x - 1 \) olur.
Bu durumda Ali'nin ekip arkadaşlarından kadın olanların sayısı \( 3(x - 1) - 1 = 3x - 4 \) olur.
Buna göre Ali'nin bakış açısıyla mağazada toplam \( x + 3x - 4 = 4x - 4 \) çalışan vardır.
Her iki durumda bulduğumuz toplam çalışan sayıları birbirine eşittir.
\( 3x + 5 = 4x - 4 \)
\( x = 9 \)
Ali ya da Ayşe için bulduğumuz toplam çalışan sayılarından herhangi birine bulduğumuz \( x \) değerini yazarak mağazadaki toplam çalışan sayısını bulalım.
\( 3x + 5 = 3(9) + 5 \)
\( = 32 \) bulunur.
Bir şehirde 2023 yılında toplam 49.005 ton atığın geri dönüşüm ile tekrar kullanılabildiği gözlemlenmiştir.
Bu atıkların dokuzda ikisi cam atıklardan, cam atıkların onbirde üçü kavanozlardan oluştuğuna göre, atıkların kaç tonu kavanozlardan oluşur?
Çözümü Göster49.005 ton atığın dokuzda ikisi cam atıklardan oluşuyor.
\( 49005 \cdot \dfrac{2}{9} = 10.890 \) ton cam atık
10.890 ton cam atığın onbirde üçü kavanozlardan oluşuyor.
\( 10890 \cdot \dfrac{3}{11} = 2.970 \) ton kavanoz
Buna göre, atıkların 2.970 tonu kavanozlardan oluşur.
Bir sınıftaki öğrencilerin bir kısmı 12 yaşında, bir kısmı 13 yaşındadır.
Sınıftaki öğrencilerin yaşları toplamı 188 olduğuna göre, bu sınıfta 12 yaşında kaç öğrenci vardır?
Çözümü Göster12 yaşındaki öğrencilerin sayısına \( x \), 13 yaşındaki öğrencilerin sayısına \( y \) diyelim.
Sınıftaki öğrencilerin yaşları toplamı 188'dir.
\( 12x + 13y = 188 \)
\( 12(x + y) + y = 188 \)
\( x + y \gt y \) ve \( y \gt 0 \) olmalıdır.
\( x + y \) toplamına değer vererek \( y \) değerlerini bulalım.
\( x + y = 12 \) verelim.
\( 12(12) + (44) = 188 \)
\( 12 \lt 44 \) olduğu için bu çözüm geçersizdir.
\( x + y = 13 \) verelim.
\( 12(13) + (32) = 188 \)
\( 13 \lt 32 \) olduğu için bu çözüm geçersizdir.
\( x + y = 14 \) verelim.
\( 12(14) + (20) = 188 \)
\( 14 \lt 20 \) olduğu için bu çözüm geçersizdir.
\( x + y = 15 \) verelim.
\( 12(15) + (8) = 188 \)
Bu çözüm geçerlidir.
\( x + y = 16 \) verelim.
\( 12(16) + (-4) = 188 \)
\( -4 \lt 0 \) olduğu için bu çözüm geçersizdir.
\( x + y = 15, \quad y = 8 \)
\( x = 7 \)
Buna göre, sınıfta 12 yaşında 7 öğrenci vardır.
Bir sepette sarı ve mavi mandallar bulunmaktadır.
Bu sepetten 5 tane sarı mandal çıkarınca sepette kalan sarı mandallar kalan tüm mandalların \( \frac{2}{5} \)'i kadar oluyor.
Sepetten 5 sarı yerine 3 mavi mandal çıkarınca kalan sarı mandallar kalan tüm mandalların yarısı kadar oluyor.
Buna göre, en başta sepetteki toplam mandal sayısı kaçtır?
Çözümü GösterSepette bulunan toplam mandal sayısına \( 5x + 5 \) diyelim.
Sepetten 5 sarı mandal çıkarınca sepette \( (5x + 5 - 5) \cdot \frac{2}{5} = 2x \) tane sarı mandal kalır.
Buna göre toplamda \( 2x + 5 \) sarı mandal vardır.
Sepetten 3 mavi mandal çıkarınca kalan mandalların yarısı sarı oluyor.
\( \dfrac{5x + 5 - 3}{2} = 2x + 5 \)
\( 5x + 2 = 4x + 10 \)
\( x = 8 \)
Başta sepette bulunan toplam mandal sayısını bulalım.
\( 5x + 5 = 5 \cdot 8 + 5 \)
\( = 45 \) bulunur.
Bir iş yerinde 1 amir 30 işçiyi yönetiyor. Bu iş yerine 5 amir alınıp 30 işçi çıkarıldığında her amir 21 işçiyi yönetmeye başlıyor.
Buna göre başlangıçta bu iş yerinde çalışan amir ve işçi sayısı toplam kaçtır?
Çözümü GösterBaşlangıçtaki amir sayısına \( x \) diyelim. Her amir 30 işçi yönettiğine göre işçi sayısı \( 30x \) olur.
İşe 5 amir alındığında amir sayısı \( x + 5 \), işten 30 işçi çıkarıldığında işçi sayısı \( 30x - 30 \) olur.
Son durumda her amir 21 işçiyi yönetiyor.
\( \dfrac{30x - 30}{x + 5} = 21 \)
\( 30x - 30 = 21(x + 5) \)
\( 30x - 30 = 21x + 105 \)
\( 9x = 135 \)
\( x = 15 \)
Başlangıçtaki amir sayısı 15 olduğuna göre, işçi sayısı \( 30x = 30(15) = 450 \) olur.
Başlangıçtaki toplam işçi ve amir sayısı \( 15 + 450 = 465 \) olarak bulunur.
Ayşe bir kitabı her gün 25 sayfa okuyarak \( n \) günde bitirebiliyor. Ayşe bu kitabı 1. gün 1 sayfa, 2. gün 2 sayfa, 3. gün 3 sayfa şeklinde devam ederek okuduğunda ise \( n \) günde bitiriyor.
Buna göre \( n \) kaçtır?
Çözümü GösterAyşe her gün 25 sayfa okuyarak kitabı \( n \) günde bitiriyorsa kitap \( 25n \) sayfadır.
Ayşe aynı kitabı 1. gün 1 sayfa, 2. gün 2 sayfa şeklinde devam ederek \( n \) günde bitiriyorsa kitabın sayfa sayısı \( 1 + 2 + 3 + \ldots + n \) olur.
Ardışık \( n \) sayının toplamını bulalım.
\( 1 + 2 + 3 + \ldots + n = \dfrac{n(n + 1)}{2} \)
Her iki durumda bulduğumuz sayfa sayıları birbirine eşittir.
\( 25n = \dfrac{n(n + 1)}{2} \)
\( n(n + 1) = 50n \)
\( n^2 + n = 50n \)
\( n^2 - 49n = 0 \)
\( n(n - 49) = 0 \)
\( n = 0 \) ya da \( n = 49 \)
\( n = 0 \) olamayacağı için \( n = 49 \) bulunur.
Bir baba 4 çocuğundan birinciye elindeki paranın yarısını, diğer çocuklarına ise sırasıyla bir önceki çocuğuna verdiği paranın yarısını veriyor.
Baba çocuklara paraları verdikten sonra elinde kalan para üçüncü çocuğuna verdiği paradan 50 lira eksiktir.
Buna göre, babanın elinde en başta kaç lira vardır?
Çözümü GösterBabanın elinde en başta \( n \) lira olduğunu varsayalım.
Çocuklarına sırasıyla verdiği paraları yazalım ve toplayalım.
\( \dfrac{n}{2} + \dfrac{n}{4} + \dfrac{n}{8} + \dfrac{n}{16} = \dfrac{15n}{16} \)
Babanın elinde en sonda \( \frac{n}{16} \) lira kalmıştır.
Babanın elinde kalan para, üçüncü çocuğuna verdiği paradan 50 lira eksiktir.
\( \dfrac{n}{8} = \dfrac{n}{16} + 50 \)
\( \dfrac{n}{16} = 50 \)
\( n = 800 \) lira olarak bulunur.
Sayfa numaralandırması 13. sayfadan başlayan bir kitabın sayfalarını numaralandırmak için toplam 630 rakam kullanıldığına göre, bu kitap kaç sayfadır?
Çözümü Göster13-99 arası kaç sayfa bulunduğunu bulalım.
Terim sayısı \( = 99 - 13 + 1 = 87 \)
13-99 arası sayfalarda her sayfada iki rakam bulunduğu için \( 87 \cdot 2 = 174 \) rakam kullanılır.
Buna göre 3 basamaklı sayfalarda \( 630 - 174 = 456 \) tane rakam kullanılmıştır.
Üç basamaklı bir sayıda üç rakam bulunduğu için bu sayıyı üçe bölerek kaç tane üç basamaklı sayfa numarası bulunduğunu bulalım.
\( \dfrac{456}{3} = 152 \)
Kitapta 100 dahil olmak üzere 100'den itibaren 152 tane sayfa bulunur.
Buna göre kitap 251 sayfadır.
Ahmet bir merdivenin basamaklarını altışar altışar çıkıp beşer beşer iniyor.
Ahmet inişte ve çıkışta toplam 77 adım attığına göre, bu merdiven kaç basamaklıdır?
Çözümü GösterMerdivendeki toplam basamak sayısına bölme kolaylığı açısından \( 30x \) diyelim.
Çıkarken atılan adım sayısı \( \frac{30x}{6} = 5x \), inerken atılan adım sayısı \( \frac{30x}{5} = 6x \) olur.
İnişte ve çıkışta atılan toplam adım sayısı 77'dir.
\( 5x + 6x = 77 \)
\( x = 7 \)
Buna göre merdivende toplam \( 30x = 30(7) = 210 \) basamak vardır.
Merve evinden 290 adım uzaktaki okuluna gitmek için evden çıkıyor.
Merve spor amaçlı 7 adım ileri 3 adım geri şeklinde yürüdüğüne göre, okula ulaşmak için kaç adım atmalıdır?
Çözümü GösterMerve attığı her \( 7 + 3 = 10 \) adımda \( 7 - 3 = 4 \) adım ilerlemektedir.
Merve bu döngüyü 71 kez tamamladığında \( 71 \cdot 10 = 710 \) adım atmış ve \( 71 \cdot 4 = 284 \) adım ilerlemiş olur.
Daha sonra 6 adım daha attığında 290 adım ilerlemiş ve okula varmış olur.
Buna göre Merve okula vardığında \( 710 + 6 = 716 \) adım atmış olur.
Bir yarışa katılacak olan Ali, parkta önce 3 adım geri sonra 6 adım ileri şeklinde yürüyerek hazırlanmaktadır.
Ali toplam 440 adım attığında başlangıç noktasından kaç adım ileri gitmiştir?
Çözümü GösterAli 3 adım geri 6 adım ileri giderek ilerliyorsa \( 3 + 6 = 9 \) adım attığında \( 6 - 3 = 3 \) adım ilerliyordur.
Ali 440 adımın 432'sini attığında \( \frac{432}{9} = 48 \) tur bu döngüyü tamamlamış, yani \( 48 \cdot 3 = 144 \) adım ileri gitmiş olur.
Geriye kalan 8 adımda önce 3 adım geri gider, sonra 5 adım ileri gider ve \( 5 - 3 = 2 \) adım daha ileri gitmiş olur.
Buna göre Ali 440 adım attığında başlangıç noktasından \( 144 + 2 = 146 \) adım ileri gitmiş olur.
Bir düğündeki davetliler masalara dörderli oturduklarında 23 kişi ayakta kalıyor. Davetliler masalara beşerli otursalardı 2 masa boş kalacak ve bir masada 4 kişi oturacaktı.
Buna göre bu düğünde kaç davetli vardır?
Çözümü GösterSalondaki toplam masa sayısına \( x \) diyelim.
Davetlilier masalara dörderli oturduklarında \( x \) masada toplam \( 4x \) kişi oturur, ayaktaki 23 kişi ile birlikte toplam davetli sayısı \( 4x + 23 \) olur.
Davetlilier masalara beşerli oturduklarında \( x - 3 \) tam dolu masada toplam \( 5(x - 3) \) kişi ve tam dolmayan 1 masada 4 kişi oturur, bu durumda toplam davetli sayısı \( 5(x - 3) + 4 \) kişi olur.
Davetli sayısı her iki durumda birbirine eşittir.
\( 4x + 23 = 5(x - 3) + 4 \)
\( 4x + 23 = 5x - 15 + 4 \)
\( x = 34 \)
Bulduğumuz \( x \) değerini davetli sayısı ifadelerinden birinde yerine koyup toplam davetli sayısını bulalım.
\( 4(34) + 23 = 136 + 23 = 159 \) davetli bulunur.
İnci yeni aldığı test kitabını, her gün bir önceki gün çözdüğünün 2 katı sayıda soru çözerek bir haftada bitiriyor.
İnci 7. gün bir önceki gün çözdüğünden 96 soru fazla çözdüğüne göre, bu kitapta toplam kaç soru vardır?
Çözümü Gösterİnci'nin 6. gün çözdüğü soru sayısına \( x \) diyelim.
İnci'nin 7. gün çözdüğü soru sayısı \( 2x \) olur.
\( x + 96 = 2x \)
\( x = 96 \)
İnci 6. gün 96 soru çözdüğüne göre, 7. gün 192, 5. gün 48, 4. gün 24, 3. gün 12, 2. gün 6, 1. gün 3 soru çözmüştür.
Kitapta toplam \( 3 + 6 + 12 + 24 + 48 + 96 + 192 = 381 \) soru vardır.
Ayşe teyze bayram yaklaşırken apartmandaki her çocuğa çocuk sayısı adedince verecek kadar şeker almıştır.
Çocuklardan 8'i 12'şer tane, diğerleri dokuzar tane şeker aldığında Ayşe teyzenin elinde apartmandaki çocuk sayısı kadar şeker kalmıştır.
Apartmandaki her çocuk Ayşe teyzeden şeker aldığına göre, apartmanda kaç çocuk vardır?
Çözümü GösterApartmandaki çocuk sayısına \( x \) diyelim. Ayşe teyzenin aldığı şeker sayısı \( x^2 \) olur.
Çocuklardan 8'i 12'şer şeker aldığında \( 8 \cdot 12 = 96 \) şeker, diğerleri dokuzar şeker aldığında \( (x - 8) \cdot 9 \) şeker alınmış olur.
Ayşe teyzede çocuk sayısı kadar şeker kaldığına göre, toplam şeker sayısını \( 96 + 9(x - 8) + x \) şeklinde ifade edebiliriz.
Her iki durumdaki toplam şeker sayısı birbirine eşittir.
\( x^2 = 96 + 9(x - 8) + x \)
\( x^2 = 96 + 9x - 72 + x \)
\( x^2 = 10x + 24 \)
\( x^2 - 10x - 24 = 0 \)
\( (x + 2)(x - 12) = 0 \)
\( x = -2 \) veya \( x = 12 \)
Çocuk sayısı -2 olamayacağı için \( x = 12 \) olur.
Sercan'ın odasındaki kavanozda 25 kuruşluk, 50 kuruşluk ve 1 TL'lik madeni paralardan oluşan 320 TL vardır. 25 kuruşların toplam değeri, 50 kuruş ve 1 TL'lerin toplam değerine eşittir. 1 TL'lerin sayısı ise 50 kuruşların sayısının yarısıdır.
Buna göre kavanozda kaç tane 25 kuruş vardır?
Çözümü GösterKavanozda bulunan 1 TL sayısına \( x \) diyelim. Bu durumda 50 kuruş sayısı \( 2x \) olur.
50 kuruş ve 1 TL'lerin toplam değeri \( 1(x) + 0,5(2x) = 2x \) olur.
25 kuruşların toplam değeri de \( 2x \) olduğu için kavanozdaki toplam para miktarı \( 2x + 2x = 4x \) TL olur.
\( 4x = 320 \)
\( x = 80 \)
25 kuruşların toplam değeri \( 2x \) olduğu için toplam \( \frac{2x}{0,25} = 8x \) tane 25 kuruş vardır.
Buna göre kavanozda \( 80 \cdot 8 = 640 \) tane 25 kuruş vardır.
Her netin 2 puan değerinde olduğu ve 4 yanlış cevabın bir doğruyu götürdüğü bir sınavda 50 soru vardır.
Bu sınavda 6 soruyu boş bırakan bir öğrenci 63 puan aldığına göre, kaç soruyu yanlış cevaplamıştır?
Çözümü GösterÖğrenci 63 puan aldığına göre \( \frac{63}{2} = 31,5 \) neti vardır.
Boş soru sayısı 6 olduğuna göre cevaplanan soru sayısı \( 50 - 6 = 44 \)'tür.
Öğrencinin yanlış cevapladığı soru sayısına \( 4x \) diyelim.
Cevaplanan 44 sorudan \( 4x \) soru yanlış ise yanlışlar \( \frac{4x}{4} = x \) tane doğruyu götürür, sonuç olarak net sayısı \( 44 - 4x - x = 44 - 5x \) olur.
\( 44 - 5x = 31,5 \)
\( 5x = 12,5 \)
\( x = 2,5 \)
Buna göre yanlış cevap sayısı \( 4x = 4(2,5) = 10 \) olarak bulunur.
50 soruluk bir testte her doğru cevap için 5 puan verilirken, her yanlış cevap için 2 puan düşürülüyor.
Bir öğrenci bu testte 8 soruyu boş bırakıp 133 puan aldığına göre, öğrencinin doğru cevap verdiği soru sayısı kaçtır?
Çözümü GösterÖğrenci \( 50 - 8 = 42 \) soruyu cevaplamıştır.
Doğru cevap sayısına \( a \) diyelim. Bu durumda yanlış cevap sayısı \( 42 - a \) olur.
Öğrencinin aldığı puanı hesaplayalım.
\( 5a - 2(42 - a) = 5a - 84 + 2a \)
\( = 7a - 84 \)
Öğrenci sınavdan 133 puan almıştır.
\( 7a - 84 = 133 \)
\( a = 31 \) bulunur.
Ceren bankadaki parasının üçte birini çekiyor ve cüzdanındaki 360 TL ile birleştirerek dörtte birini harcıyor.
Bu harcamadan sonra cüzdanında 330 TL kaldığına göre, Ceren'in banka hesabında kalan para kaç TL'dir?
Çözümü GösterBaşlangıçta Ceren'in banka hesabında bulunan paraya \( 12x \) diyelim.
Ceren bankadan \( 12x \cdot \frac{1}{3} = 4x \) TL çekiyor.
Parayı çektikten sonra cüzdanındaki para ile birlikte Ceren'in yanında \( 360 + 4x \) TL'si olur.
Bu tutarın dörtte biri olan \( \frac{360 + 4x}{4} = x + 90 \) TL'yi harcadıktan sonra elinde kalan tutarı bulalım.
\( (360 + 4x) - (x + 90) = 3x + 270 \)
Cüzdanında kalan bu tutar 330 TL olarak veriliyor.
\( 3x + 270 = 330 \)
\( 3x = 60 \)
\( x = 20 \)
Ceren'in banka hesabında kalan parayı bulalım.
\( 12x - 4x = 8x = 8(20) = 160 \) TL bulunur.
Bir dondurma markası 3 tane dondurma çubuğu getirene bir tane hediye dondurma kampanyası başlatmıştır.
Buna göre, elinde 62 tane çubuk olan bir çocuk toplam kaç tane hediye dondurma alabilir?
Çözümü GösterElindeki 62 çubuktan 60'ıyla \( \frac{60}{3} = 20 \) tane hediye dondurma alabilir.
Bunun sonucunda \( 20 + 2 = 22 \) çubuğu olur.
Bu çubukların 21'iyle \( \frac{21}{3} = 7 \) tane hediye dondurma alabilir.
Bunun sonucunda \( 7 + 1 = 8 \) çubuğu olur.
Bu çubukların 6'sıyla \( \frac{6}{3} = 2 \) tane hediye dondurma alabilir.
Bunun sonucunda \( 2 + 2 = 4 \) çubuğu olur.
Bu çubukların 3'üyle \( \frac{3}{3} = 1 \) tane hediye dondurma alabilir.
Bunun sonucunda \( 1 + 1 = 2 \) çubuğu olur, ama bu çubuklarla hediye dondurma alamaz.
Buna göre çocuk toplamda \( 20 + 7 + 2 + 1 = 30 \) tane hediye dondurma alabilir.
Hande 42 basamağı bulunan bir merdiveni üçer üçer çıkıp ikişer ikişer iniyor.
Hande'nin bu süreçte hiç ayak basmadığı basamak sayısı kaçtır?
Çözümü GösterHande çıkarken 3., 6., 9., ... , 42. basamaklara, yani \( \frac{42}{3} = 14 \) basamağa basmıştır.
İnerken ise 2., 4., 6., ... , 42. basamaklara, yani \( \frac{42}{2} = 21 \) basamağa basmıştır.
Hande'nin hem inerken hem çıkarken bastığı basamaklar 6'nın katı olanlardır, buna göre 6., 12., 18., ... , 42. basamaklara, yani \( \frac{42}{6} = 7 \) basamağa hem inerken hem çıkarken basmıştır.
Bu durumda Hande 7 basamağa hem inerken hem çıkarken bastığı için toplamda \( 14 + 21 - 7 = 28 \) farklı basamağa basmıştır.
Buna göre \( 42 - 28 = 14 \) basamağa hiç ayak basmamıştır.
Bora salça yapmak için pazardan 4 kasa domates almıştır. Kasalar ikişerli tartıldığında çıkan değerler 81, 76, 69, 82, 77 ve 65 kg oluyor.
Buna göre bu 4 kasanın toplam ağırlığı nedir?
Çözümü Göster4 kasanın ağırlıklarına sırasıyla \( a, b, c, d \) diyelim.
Bu kasalar ikişerli tartıldığında ortaya çıkan toplamları yazalım.
\( a + b = 81 \)
\( a + c = 76 \)
\( a + d = 69 \)
\( b + c = 82 \)
\( b + d = 77 \)
\( c + d = 65 \)
Toplamları incelediğimizde her kasanın tartıma 3 kere dahil olduğunu görürüz.
6 tartımın sonuçlarını taraf tarafa toplayalım.
\( 3a + 3b + 3c + 3d = 81 + 76 + 69 + 82 + 77 + 65 \)
\( 3(a + b + c + d) = 450 \)
\( a + b + c + d = 150 \)
4 kasa domatesin toplam ağırlığı 150 kg'dır.
Bir masada 3 farklı boyutta bardak bulunmaktadır. 1. bardak tamamen suyla dolu, diğer bardaklar ise boştur.
Önce 1. bardaktaki suyun bir kısmı ile 2. bardak tamamen, sonra 2. bardaktaki suyun bir kısmı ile 3. bardak tamamen dolduruluyor.
Bu işlem sonucunda tüm bardaklarda eşit miktarda su bulunduğuna göre, bardakların toplam hacmi 3. bardağın hacminin kaç katıdır?
Çözümü Göster3. bardağın hacmine \( x \) diyelim.
3. bardak tamamen dolduktan sonra tüm bardaklardaki su miktarı eşit oluyorsa toplam su miktarına \( 3x \) diyebiliriz.
Toplam su miktarı başlangıçta 1. bardağı tamamen doldurduğuna göre 1. bardağın hacmi \( 3x \) olur.
İkinci adımda 2. bardak tamamen doluyken 3. bardağa \( x \) kadar su aktarıldıktan sonra 2. bardakta \( x \) kadar su kaldığına göre, 2. bardağın hacmi \( 2x \) olur.
Bu durumda bardakların toplam hacmi \( x + 2x + 3x = 6x \), dolayısıyla 3. bardağın hacminin 6 katı olur.
Aşağıdaki tabloda bir konser için bilet tiplerine göre bilet fiyatları verilmiştir.
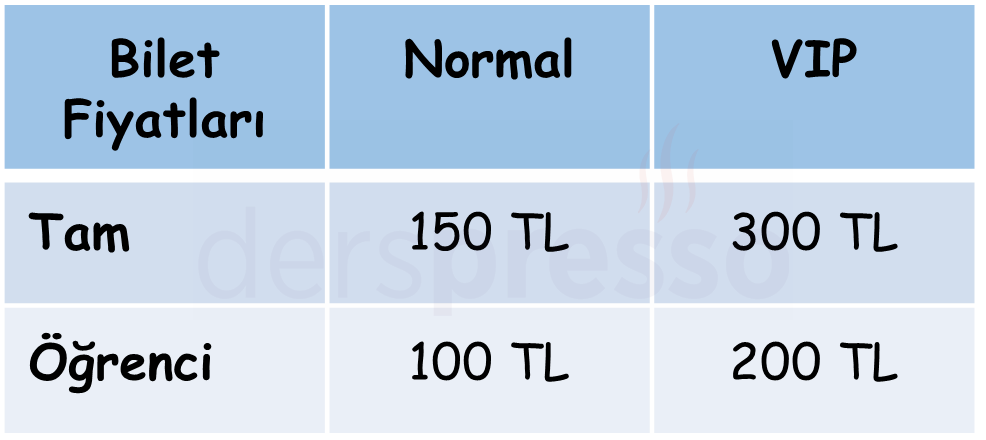
- VIP bilet alan öğrenci sayısı, tam VIP bilet alanların sayısından 15 eksiktir.
- Normal bilet alan öğrenci sayısı, VIP bilet alan öğrenci sayısının 3 katıdır.
- Tam biletlere ödenen toplam tutar, normal biletlere ödenen toplam tutarın iki katıdır.
- Biletlere ödenen toplam tutar 15.000 TL'dir.
Buna göre, bu konser için kaç öğrenci bileti alınmıştır?
Çözümü GösterSatılan tam normal bilet sayısına \( a \), tam VIP bilet sayısına \( b \) diyelim.
Aşağıdaki tabloya bilet tiplerine göre bilet satış adetlerini yerleştirelim.
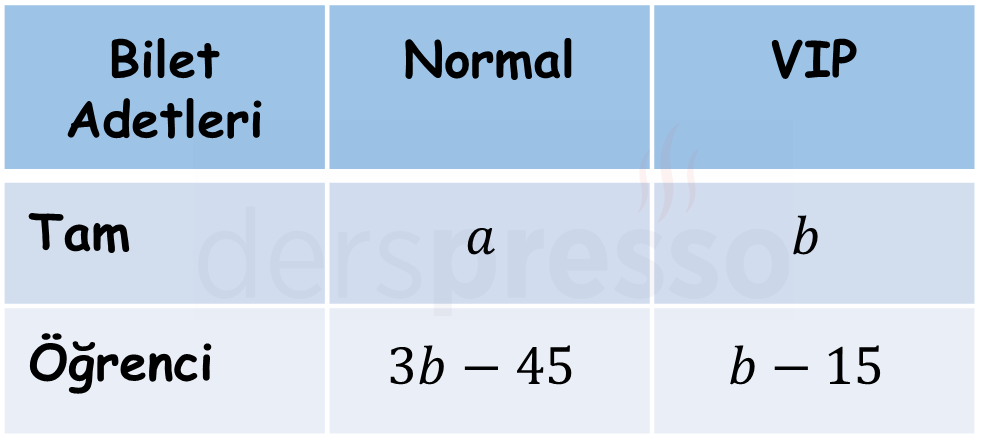
VIP bilet alan öğrenci sayısı, tam VIP bilet alanların sayısından 15 eksik olduğuna göre \( b - 15 \) olur.
Normal bilet alan öğrenci sayısı, VIP bilet alan öğrenci sayısının 3 katı olduğuna göre \( 3b - 45 \) olur.
Tam biletlere ödenen toplam tutar, normal biletlere ödenen toplam tutarın iki katıdır.
\( 150a + 300b = 2(150a + 100(3b - 45)) \)
\( 150a + 300b = 300a + 600b - 9000 \)
\( 150a + 300b = 9000 \)
\( a + 2b = 60 \)
Biletlere ödenen toplam tutar 15.000 TL'dir.
\( 150a + 300b + 100(3b - 45) + 200(b - 15) = 15000 \)
\( 150a + 300b + 300b - 4500 + 200b - 3000 = 15000 \)
\( 150a + 800b = 22500 \)
\( 3a + 16b = 450 \)
Bulduğumuz iki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 6, \quad b = 27 \)
Konser için bilet alan öğrenci sayısını bulalım.
\( (3b - 45) + (b - 15) = 4b - 60 \)
\( = 4(27) - 60 = 48 \) bulunur.
Bir hayvanat bahçesindeki pandaların beslenmeleri ile ilgili aşağıdakiler biliniyor.
- 5 yaş altı pandalara 3 saatte bir, 5 yaş ve üstü pandalara 6 saatte bir mama veriliyor.
- 5 yaş altı pandalara her seferinde 300 gram, 5 yaş ve üstü pandalara ise 500 gram mama veriliyor.
- Pandalara bir günde toplam 176 kez ve 72 kg mama veriliyor.
Buna göre, hayvanat bahçesinde 5 yaş ve üstü kaç panda vardır?
Çözümü Göster5 yaş altı panda sayısına \( x \), 5 yaş ve üstü panda sayısına \( y \) diyelim.
Bir günde verilen toplam mama sayısını bulalım.
5 yaş altı pandalara 3 saatte bir mama veriliyorsa bir günde \( \frac{24}{3} = 8 \) kez mama verilir.
5 yaş ve üstü pandalara 6 saatte bir mama veriliyorsa bir günde \( \frac{24}{6} = 4 \) kez mama verilir.
Pandalara bir günde toplam 176 kez mama verilmiştir.
\( 8x + 4y = 176 \)
Bir günde verilen toplam mama miktarını bulalım.
5 yaş altı bir pandaya her seferinde 300 gr mama veriliyorsa tümüne bir günde toplam \( 300 \cdot 8x = 2400x \) gr mama verilir.
5 yaş ve üstü bir pandaya her seferinde 500 gr mama veriliyorsa tümüne bir günde toplam \( 500 \cdot 4y = 2000y \) gr mama verilir.
Pandalara bir günde toplam 72 kg = 72000 gr mama veriliyor.
\( 2400x + 2000y = 72000 \)
\( 24x + 20y = 720 \)
Bulduğumuz iki denklemi ortak çözelim.
1. denklemin taraflarını -3 ile çarpıp denklemleri taraf tarafa toplayalım.
\( -24x - 12y = -528 \)
\( 24x + 20y = 720 \)
\( -24x + 24x - 12y + 20y = -528 + 720 \)
\( 8y = 192 \)
\( y = 24 \) bulunur.
100 cm uzunluğunda bir telin sol ucundan 18 cm uzunluğunda bir parça kesiliyor.
Bu telin orta noktası hangi yöne kaç santimetre kayar?
Çözümü Göster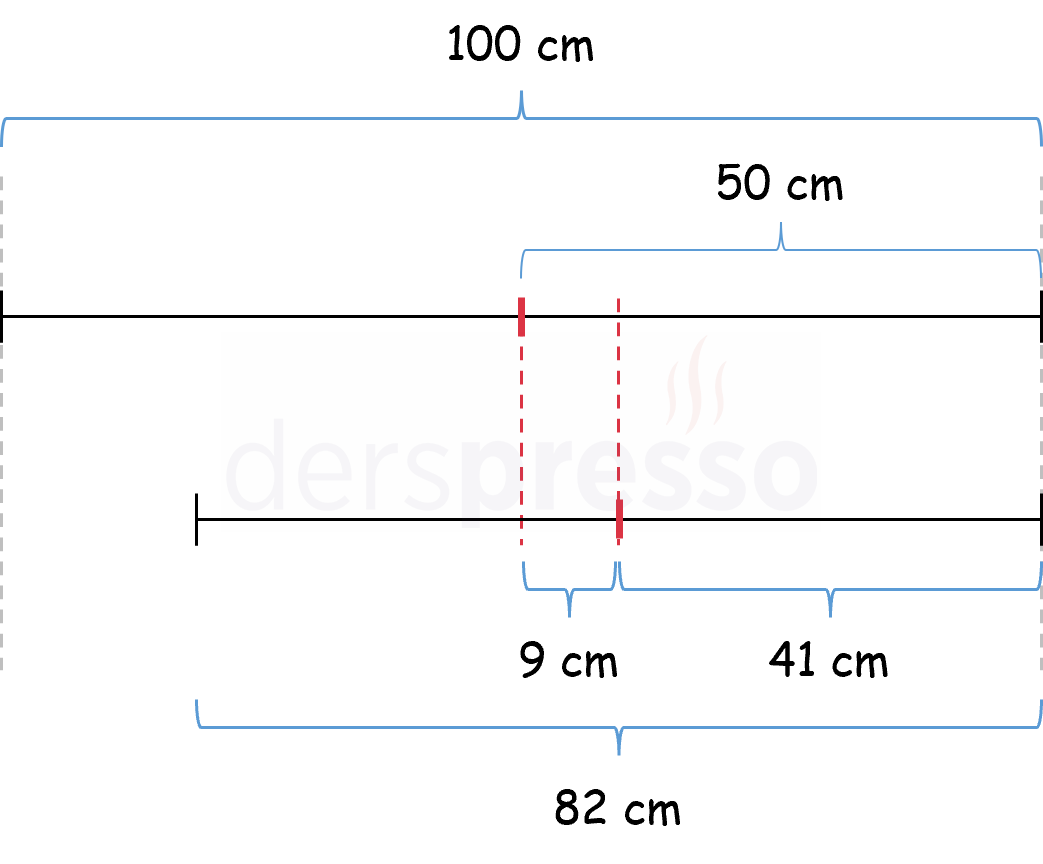
Şekilde de gösterildiği gibi bir tel sol ucundan kesildiğinde, orta noktası kesilen tarafın tersi yönde kesilen uzunluğun yarısı kadar kayar.
Buna göre sol ucundan 18 cm kesilen telin orta noktası sağa doğru 9 cm kayar.
Bir telin önce sol ucundan \( \frac{1}{4} \)'ü, sonra sağ ucundan \( \frac{1}{5} \)'i kesilince orta noktası ilk duruma göre 8 cm kaymaktadır.
Buna göre bu tel başlangıçta kaç cm'dir?
Çözümü GösterTelin uzunluğuna bölme kolaylığı açısından \( 40x \) cm diyelim.
Telin önce sol ucundan \( 40x \cdot \frac{1}{4} = 10x \) cm kesiliyor. Bu işlem sonucunda telin uzunluğu \( 40x - 10x = 30x \) cm olur.
Daha sonra kalan telin sağ ucundan \( 30x \cdot \frac{1}{5} = 6x \) cm kesiliyor.
Telin orta noktası sol ucundan \( 10x \) cm kesilince sağ tarafa \( \frac{10x}{2} = 5x \) cm, sağ ucundan \( 6x \) cm kesilince sol tarafa \( \frac{6x}{2} = 3x \) cm kayar.
Sonuç olarak telin orta noktası \( 5x - 3x = 2x \) kadar sağ tarafa kayar.
\( 2x = 8 \)
\( x = 4 \)
Telin başlangıçtaki uzunluğu \( 40x = 40 \cdot 4 = 160 \) cm olarak bulunur.
Belirli bir yükseklikten bırakılan bir top, yere çarptıktan sonra düştüğü yükseliğin \( \frac{2}{3} \)'ü kadar yükselmektedir.
Top üçüncü kez yere çarptıktan sonra 80 cm yükseldiğine göre, başlangıçta kaç cm yükseklikten bırakılmıştır?
Çözümü GösterTopun ilk bırakıldığı yüksekliğe işlem kolaylığı açısından \( 27x \) cm diyelim.
Top ilk kez yere çarptıktan sonra \( 27x \cdot \frac{2}{3} = 18x \) cm yükselir.
İkinci kez yere çarptıktan sonra \( 18x \cdot \frac{2}{3} = 12x \) cm yükselir.
Üçüncü kez yere çarptıktan sonra \( 12x \cdot \frac{2}{3} = 8x \) cm yükselir.
Top üçüncü kez yere çarptıktan sonra 80 cm yükselmiştir.
\( 8x = 80 \)
\( x = 10 \) cm
Buna göre topun ilk bırakıldığı yükseklik \( 27x = 27 \cdot 10 = 270 \) cm olarak bulunur.
Belirli bir yükseklikten bırakılan bir top, yere çarptıktan sonra düştüğü yüksekliğin \( \frac{1}{4} \)'ü kadar yükselmektedir.
Top üçüncü kez yere çarpana kadar toplamda 312 cm yol aldığına göre, birinci kez yere çarptıktan sonra kaç cm yükselmiştir?
Çözümü GösterTopun ilk bırakıldığı yüksekliğe işlem kolaylığı açısından \( 16x \) cm diyelim.
Top birinci kez yere çarptıktan sonra \( 16x \cdot \frac{1}{4} = 4x \) cm yükselir ve \( 4x \) cm düşer.
Top ikinci kez yere çarptıktan sonra \( 4x \cdot \frac{1}{4} = x \) cm yükselir ve \( x \) cm düşer.
Top üçüncü kez yere çarptığında toplam \( 16x + 4x + 4x + x + x = 26x \) cm yol almış olur.
\( 26x = 312 \)
\( x = 12 \) cm
Buna göre top birinci kez yere çarptıktan sonra \( 4x = 4 \cdot 12 = 48 \) cm yükselmiştir.
Bir okulda bağış toplama etkinliği yapılıyor. Bu okuldan mezun olan 24 öğrenci okula eşit miktarlarda bağış yapmak istiyor. Etkinlikte öğretmenler mezunların yapacağı toplam bağışın \( \frac{5}{3} \) katı, bir veli de öğretmenlerin yapacağı toplam bağışın \( \frac{7}{5} \) katı bağış yapacağını açıklıyor.
Toplanmak istenen bağış tutarı 228.000 TL olduğuna göre, her bir mezun kaç TL bağış yapmalıdır?
Çözümü GösterHer bir mezunun yapacağı bağış miktarına \( x \) diyelim.
24 mezunun her biri \( x \) TL bağış yaparsa tüm mezunlar toplamda \( 24x \) TL bağış yapar.
Öğretmenler mezunların \( \frac{5}{3} \) katı bağış yapacağına göre, toplam \( 24x \cdot \frac{5}{3} = 40x \) TL bağış yapar.
Bir veli öğretmenlerin yapacağı bağış miktarının \( \frac{7}{5} \) katı bağış yapacağına göre, toplam \( 40x \cdot \frac{7}{5} = 56x \) TL bağış yapar.
Toplam bağış miktarını bulalım.
\( 24x + 40x + 56x = 228000 \)
\( 120x = 228000 \)
\( x = 1900 \)
Hedeflenen tutarın toplanabilmesi için 24 mezunun her biri 1900 TL bağış yapmalıdır.
120 litre yağ 6 ve 10 litrelik tenekelere doldurulacaktır.
Hiç yağ artmayacak, tenekeler tam dolacak ve iki farklı boyuttaki tenekeden en az birer tane kullanılacak şekilde en az kaç teneke gerekir?
Çözümü GösterKullanılacak 6 litrelik teneke sayısına \( x \), 10 litrelik teneke sayısına \( y \) diyelim.
Toplam yağ miktarı 120 litredir.
\( 6x + 10y = 120 \)
\( 3x + 5y = 60 \)
Kullanılan toplam teneke sayısı \( x + y \) olur. Bunu en az yapabilmek için katsayısı daha büyük olan \( y \) için en büyük değer seçilmelidir.
Her iki tipteki tenekeden en az bir tane kullanılma şartından dolayı \( y = 12 \) olamaz.
\( y = 11 \) olursa \( x \) tam sayı olmaz.
\( y = 10 \) olursa \( x \) tam sayı olmaz.
\( y = 9 \) olursa \( x = 5 \) olur.
Buna göre toplam teneke sayısı en az \( x + y = 5 + 9 = 14 \) olur.
Bir dart turnuvasında oyuncular 15, 20, 25, 30 ya da 45 puan almışlardır. Bu puanların her biri en az dörder oyuncu tarafından alınmıştır.
Bu turnuvada 100 kişi yarıştığına göre, en çok kaç sporcu aynı puanı almış olabilir?
Çözümü GösterEn çok oyuncunun belirli bir puanı alması için, diğer puanları en az sayıda, yani dörder oyuncu almalıdır.
5 farklı puandan herhangi birini (örneğin 15) en çok oyuncunun aldığı puan olarak seçelim ve diğer 4 puanın her birini dörder oyuncunun aldığını varsayalım.
Buna göre toplamda \( 4 \cdot 4 = 16 \) oyuncu diğer dört puanı almış olur.
Bu durumda seçtiğimiz puanı alan oyuncu sayısı en çok \( 100 - 16 = 84 \) olabilir.
Ayaz, Bade ve Ceyda birlikte yemek yiyorlar. Hesap geldiğinde Ayaz ve Bade ayrı ayrı \( x \) TL, Ceyda ise Ayaz ve Bade'nin ödediğinden daha fazla olmak üzere \( y \) TL ödüyor.
Sonrasında hesabı eşit paylaşmaya karar verdiklerine göre, Ayaz Ceyda'ya ödemesi gereken tutar \( x \) ve \( y \) cinsinden nedir?
Çözümü GösterHer birinin ödediği tutarları toplayarak toplam hesabı bulalım.
\( x + x + y = 2x + y \)
Hesabı eşit ödemek istedikleri için kişi başına düşen tutar toplam hesabın üçte biri, yani \( \frac{2x + y}{3} \) olur.
Fazla ödeyen kişi Ceyda olduğundan Ayaz kişi başına düşen tutardan az ödemiştir.
Bu durumda kişi başına ödenmesi gereken tutardan Ayaz'ın ödediği tutarı çıkarırsak Ayaz'ın Ceyda'ya ödemesi gereken tutarı buluruz.
\( \dfrac{2x + y}{3} - x = \dfrac{2x + y - 3x}{3} \)
\( = \dfrac{y - x}{3} \) bulunur.
Ahu, Beril, Cemil ve Deren gittikleri restoranda 270 liralık hesabı bölüşüyorlar.
Beril diğerlerinin ödediği tutarın \( \frac{1}{5} \)'ini, Cemil diğerlerinin ödediği tutarın \( \frac{1}{2} \)'sini, Deren ise diğerlerinin ödediği tutarın \( \frac{1}{4} \)'ünü ödediğine göre, Ahu ne kadar ödemiştir?
Çözümü GösterHerkesin ödediği tutara sırasıyla \( a, b, c, d \) diyelim.
\( a + b + c + d = 270 \)
Beril diğerlerinin ödediği tutarın beşte birini ödüyor.
\( b = \dfrac{a + c + d}{5} \)
\( 5b = a + c + d \)
Toplam eşitliğini kullanarak \( a + c + d \) yerine \( 270 - b \) yazalım.
\( 5b = 270 - b \)
\( b = 45 \)
Aynı yöntemle diğerlerinin ödediği tutarları bulalım.
Cemil diğerlerinin ödediği tutarın yarısını ödüyor.
\( c = \dfrac{a + b + d}{2} \)
\( 2c = a + b + d \)
Toplam eşitliğini kullanarak \( a + b + d \) yerine \( 270 - c \) yazalım.
\( 2c = 270 - c \)
\( c = 90 \)
Deren diğerlerinin ödediği tutarın dörtte birini ödüyor.
\( d = \dfrac{a + b + c}{4} \)
\( 4d = a + b + c \)
Toplam eşitliğini kullanarak \( a + b + c \) yerine \( 270 - d \) yazalım.
\( 4d = 270 - d \)
\( d = 54 \)
Toplam hesap 270 liradır.
\( a + b + c + d = 270 \)
\( a + 45 + 90 + 54 = 270 \)
\( a = 81 \) lira bulunur.
Efe, Ata, Berke ve Ceren birlikte misket oyunu oynayacaklardır.
Efe'nin hiç misketi olmadığından Ata kendi misketlerinin \( \frac{1}{3} \)'ünü, Berke \( \frac{3}{8} \)'ini, Ceren de \( \frac{2}{7} \)'sini Efe'ye veriyor.
3 arkadaşın Efe'ye verdiği misket sayıları birbirine eşit olduğuna göre, son durumda Efe'nin misketlerinin sayısının toplam misket sayısına oranı kaç olur?
Çözümü GösterAta, Berke ve Ceren'in misket sayılarına işlem kolaylığı açısından sırasıyla \( 3a, 8b, 7c \) diyelim.
Üç arkadaşın Efe'ye verdikleri misket sayılarını bulalım.
\( 3a \cdot \dfrac{1}{3} = a \)
\( 8b \cdot \dfrac{3}{8} = 3b \)
\( 7c \cdot \dfrac{2}{7} = 2c \)
3 arkadaşın Efe'ye verdikleri misket sayıları birbirine eşittir.
\( a = 3b = 2c \)
Efe'nin yeni durumda misketlerinin toplam misket sayısına oranını bulalım.
\( \dfrac{a + 3b + 2c}{3a + 8b + 7c} \)
Tüm bilinmeyenleri \( b \) cinsinden yazalım.
\( = \dfrac{3b + 3b + 3b}{3(3b) + 8b + 7(\frac{3b}{2})} \)
\( = \dfrac{9b}{9b + 8b + \frac{21b}{2}} \)
\( = \dfrac{9b}{\frac{55b}{2}} \)
\( = \dfrac{18}{55} \) bulunur.
Tamamen su dolu olan bir varilin toplam ağırlığı \( x \) kg'dır. İçindeki suyun \( \frac{2}{3} \)'ü kullanıldığında varilin toplam ağırlığı \( y \) kg olmaktadır.
Buna göre boş varilin ağırlığı \( x \) ve \( y \) cinsinden nedir?
Çözümü GösterBoş varilin ağırlığına \( a \) kg diyelim.
Varil tamamen doluyken içindeki suyun ağırlığı \( x - a \) kg olur.
Kullanılan suyun ağırlığı \( (x - a) \cdot \frac{2}{3} \) olur.
İçindeki suyun \( \frac{2}{3} \)'ü kullanıldığında varilin toplam ağırlığı \( y \) kg olmaktadır.
\( x - (x - a) \cdot \dfrac{2}{3} = y \)
\( a \)'yı yalnız bırakalım.
\( 3x - 2(x - a) = 3y \)
\( 3x - 2x + 2a = 3y \)
\( 2a = 3y - x \)
\( a = \dfrac{3y - x}{2} \) bulunur.
Bir koşu yarışından Adnan baştan \( (x + 2) \)., sondan \( (x - 5) \). sırada yer almaktadır.
Bu koşu yarışında toplam 72 yarışçı olduğuna göre, Adnan birinci olmak için kaç kişiyi geçmelidir?
Çözümü GösterAdnan baştan \( (x + 2) \). olduğuna göre önünde \( x + 1 \) kişi vardır.
Adnan sondan \( (x - 5) \). olduğuna göre arkasında \( x - 6 \) kişi vardır.
Yarışa katılan Adnan dahil toplam kişi sayısını bulalım.
\( \underbrace{(x + 1)}_\text{önünde} + \underbrace{1}_\text{kendisi} + \underbrace{(x - 6)}_\text{arkasında} = 2x - 4 \)
Yarışa katılan kişi sayısı 72'dir.
\( 2x - 4 = 72 \)
\( 2x = 76 \)
\( x = 38 \)
Buna göre Adnan'ın önünde \( x + 1 = 39 \) kişi vardır.
Adnan'ın birinci olmak için önündeki herkesi geçmesi gerektiği için 39 kişiyi geçmelidir.
Bir yemekhane sırasındaki öğrencilerden Emre baştan \( a \)., Sıla sondan \( (a + 7) \). sırada yer almaktadır. Emre ile Sıla arasında 11 öğrenci vardır.
Emre Sıla'dan daha önde olduğuna ve sırada toplam 56 öğrenci bulunduğuna göre, Emre sondan kaçıncı sıradadır?
Çözümü GösterEmre baştan \( a \). öğrenci ise Emre'nin önünde \( a - 1 \) öğrenci vardır.
Sıla sondan \( (a + 7) \). öğrenci ise Sıla'nın arkasında \( a + 6 \) öğrenci vardır.
Emre ve Sıla arasında 11 kişi olduğuna göre sıradaki toplam öğrenci sayısı aşağıdaki gibi olur.
\( (a - 1) + 1 + 11 + 1 + (a + 6) = 2a + 18 \)
Sırada toplam 56 öğrenci vardır.
\( 2a + 18 = 56 \)
\( 2a = 38 \)
\( a = 19 \)
Buna göre sıra aşağıdaki gibi olur.
\( \underbrace{\ldots}_\text{25 kişi} \text{Sıla} \underbrace{\ldots}_\text{11 kişi} \text{Emre} \underbrace{\ldots}_\text{18 kişi} \)
Bu sıraya baktığımızda Emre'nin arkasında \( 25 + 1 + 11 = 37 \) öğrenci vardır, yani Emre sondan 38. sıradadır.
Bir gişe sırasında Cemile baştan 16., Ayşegül sondan 25. sıradadır.
Cemile ile Ayşegül arasında 13 kişi olduğuna göre, bu sırada en çok kaç kişi vardır?
Çözümü GösterBu gişe sırasını Cemile ya da Ayşegül'ün önde olmasına göre iki farklı şekilde düşünebiliriz.
Durum 1: Cemile önde
\( \underbrace{\ldots}_\text{24 kişi} \text{Ayşegül} \underbrace{\ldots}_\text{13 kişi} \text{Cemile} \underbrace{\ldots}_\text{15 kişi} \)
Bu durumda sırada toplam \( 24 + 1 + 13 + 1 + 15 = 54 \) kişi vardır.
Durum 2: Ayşegül önde
\( \underbrace{\ldots}_\text{10 kişi} \text{Cemile} \underbrace{\ldots}_\text{13 kişi} \text{Ayşegül} \underbrace{\ldots}_\text{1 kişi} \)
Bu durumda sırada toplam \( 10 + 1 + 13 + 1 + 1 = 26 \) kişi vardır.
Buna göre bu sırada en çok 54 kişi vardır.
Bir kutuda 3 mor, 6 sarı, 10 siyah top vardır. Çekilen toplar kutuya geri atılmamak üzere bu kutudan toplar çekilecektir.
(a) Bu kutudan en az bir siyah top çektiğimizden emin olmak için en az kaç top çekilmelidir?
(b) Bu kutudan her renkten en az bir top çektiğimizden emin olmak için en az kaç top çekilmelidir?
Çözümü Göster(a) En az bir siyah top çektiğimizden emin olmak için siyah toptan önce diğer renklerdeki tüm topları çekeceğimiz en kötü senaryo varsayılmalıdır. Buna göre ilk 9 çekilişte 3 mor ve 6 sarı topu çektikten sonra çekeceğimiz topun kesinlikle siyah olacağından emin olabiliriz.
Buna göre en az bir siyah top çektiğimizden emin olmak için en az \( 3 + 6 + 1 = 10 \) top çekilmelidir.
(b) Her renkten en az bir top çektiğimizden emin olmak için önce en çok sayıda top olan renkleri çekeceğimizi varsaymamız gerekir. Buna göre ilk 10 çekilişte 10 siyah top, sonraki 6 çekilişte 6 sarı top çektikten sonra çekeceğimiz topun mor olacağından ve tüm renklerden en az bir top çektiğimizden emin olabiliriz.
Buna göre her renkten en az bir top çektiğimizden emin olmak için en az \( 10 + 6 + 1 = 17 \) top çekilmelidir.
Başlangıçta her birinde 300'er adet misket olan 5 arkadaş bir oyun oynayacaktır. Bu oyuna göre her turda herkes birbirine belli miktarda misket verecek ve ilk kişinin misketi bittiği turda en fazla miskete sahip olan kişi oyunu kazanacaktır.
Her turda verilecek misket sayıları aşağıda verilmiştir.
1. kişi 2. kişiye her tur 15 misket,
3. kişi 1. kişiye her tur 14 misket,
2. kişi 5. kişiye her tur 21 misket,
4. kişi 1. kişiye her tur 25 misket,
5. kişi 3. kişiye her tur 29 misket,
2. kişi 4. kişiye her tur 24 misket,
5. kişi 4. kişiye her tur 18 misket verecektir.
Buna göre oyunun kaç turda bittiğini ve oyunu kazanan kişiyi bulunuz.
Çözümü GösterBir kişinin misketinin bitmesi için oynanması gereken tur sayısına \( k \) diyelim ve \( k \) tur sonunda herkesin elinde kalan misket sayısını bulalım.
1. kişinin \( k \) tur sonunda elinde kalan misket sayısı:
\( = 300 + 14k + 25k - 15k = 300 + 24k \)
2. kişinin \( k \) tur sonunda elinde kalan misket sayısı:
\( = 300 + 15k - 21k - 24k = 300 - 30k \)
3. kişinin \( k \) tur sonunda elinde kalan misket sayısı:
\( = 300 + 29k - 14k = 300 + 15k \)
4. kişinin \( k \) tur sonunda elinde kalan misket sayısı:
\( = 300 + 24k + 18k - 25k = 300 + 17k \)
5. kişinin \( k \) tur sonunda elinde kalan misket sayısı:
\( = 300 + 21k - 29k - 18k = 300 - 26k \)
\( k \) tur sonunda misketi biten ilk kişi, her turda misket sayısı en çok azalan 2. kişi olur.
\( k \) tur sonunda oyunu kazanan kişi, her turda misket sayısı en çok artan 1. kişi olur.
2. kişinin misketlerinin bittiği tur sayısını bulalım.
\( 300 - 30k = 0 \)
\( k = 10 \)
Buna göre oyun 10 turda bitmiştir ve oyunu 1. kişi kazanmıştır.
Aynı uzunluktaki iki mumdan biri 4, diğeri 7 saatte tamamen yanmaktadır.
Mumlar aynı anda yakıldığına göre, kaç saat sonra mumlardan birinin boyu diğerinin boyunun 3 katı olur?
Çözümü GösterHer bir mumun boyuna işlem kolaylığı açısından \( 28x \) cm diyelim (sayının hem 4'e hem 7'ye tam bölünmesi için).
7 saatte tamamen yanan mum saatte \( 4x \) cm, 4 saatte tamamen yanan mum saatte \( 7x \) cm yanar.
Mumlardan birinin boyunun diğerinin üç katı olduğu süreye \( t \) diyelim. 4 saatte tamamen yanan mum daha hızlı yandığı için boyu diğerinin 3 katı olan mum 7 saatte yanandır.
Mumlar yakıldıktan \( t \) saat sonraki mumların boyları arasındaki ilişkiyi yazalım.
\( 28x - 4xt = 3(28x - 7xt) \)
\( 28x - 4xt = 84x - 21xt \)
\( 17xt = 56x \)
\( t = \dfrac{56}{17} \) saat bulunur.
Farklı yapıdaki iki mumdan birinin boyu diğerinin boyunun 2 katıdır. Bu mumlardan uzun olan 4 saatte, kısa olan 10 saatte tamamen yanmaktadır.
Mumların saat 12:00'da eşit boyda olmaları için saat kaçta aynı anda yakılmaları gerekir?
Çözümü GösterKısa olan mumun boyuna \( 20x \) cm diyelim. Bu mum 10 saatte yandığına göre saatte \( 2x \) cm yanar.
Uzun olan mumun boyu \( 20x \cdot 2 = 40x \) cm olur. Bu mum 4 saatte yandığına göre, saatte \( 10x \) cm yanar.
Bu mumlar yakıldıktan sonra boylarının eşitlendiği süreye \( t \) diyelim.
Mumlar yakıldıktan \( t \) saat sonraki mumların boyları arasındaki ilişkiyi yazalım.
\( 20x - 2xt = 40x - 10xt \)
\( 8xt = 20x \)
\( t = \dfrac{5}{2} \) saat
Mumlar yakıldıktan 2,5 saat sonra boyları eşit olmaktadır.
Buna göre mumların saat 09:30'da yakılmaları gerekir.
Cenk, Kerem ve Bensu aralarında tenis maçı yapıyorlarlar. Aynı anda iki kişi maç yapabilmektedir.
12 maçla en az maçı yapan Cenk, 15 maçla en çok maçı yapan Bensu olduğuna göre, Kerem kaç maç yapmıştır?
Çözümü GösterCenk ve Kerem'in aralarında yaptıkları maç sayısına \( x \) diyelim.
Cenk toplam 12 maç yaptığından Bensu'yla yaptığı maç sayısı \( 12 - x \) olur.
Bensu toplam 15 maç yaptığına göre Kerem'le yaptığı maç sayısı \( 15 - (12 - x) = x + 3 \) olur.
Bu durumda Kerem toplam \( x + (x + 3) = 2x + 3 \) maç yapmış olur.
Kerem'in yaptığı maç sayısı Cenk'ten fazla, Bensu'dan az olmalıdır.
\( 12 \lt 2x + 3 \lt 15 \)
\( 9 \lt 2x \lt 12 \)
\( \dfrac{9}{2} \lt x \lt 6 \)
\( x \)'in alabileceği tek tam sayı değer 5 olur.
Buna göre Kerem \( 2x + 3 = 2(5) + 3 = 13 \) maç yapmıştır.
Saatleri yanlış ayarlanmış olan Ada, Beril, Cem ve Derya gün içinde süreleri aynı olan 3 toplantıya girecektir.
Bu 4 arkadaş iş yerine geldiklerinde elektronik saat 10:00'ı gösterirken Ada'nın saati 10:05'i, Beril'in saati 09:57'yi, Cem'in saati 10:02'yi ve Derya'nın saati 09:58'i gösteriyor.
İlk toplantı Cem'in saatine göre 11:03'te başlıyor ve Ada'nın saatine göre 12:28'de bitiyor.
Son toplantı Derya'nın saatine 15:40'ta başladığına göre Beril'in saatine göre kaçta biter?
Çözümü GösterCem'in saati 2 dk ileri olduğuna göre, ilk toplantının gerçek başlama saati 11:01'dir.
Ada'nın saati 5 dk ileri olduğuna göre, ilk toplantının gerçek bitiş saati 12:23'tür.
Dolayısıyla bir toplantının süresi 1 saat 22 dk'dır.
Derya'nın saati 2 dk geri olduğuna göre, son toplantının gerçek başlama saati 15:42'dir.
Bir toplantı 1 saat 22 dk sürdüğüne göre, son toplantının gerçek bitiş saati 17:04 olur.
Beril'in saati 3 dk geri olduğuna göre, son toplantı Beril'in saatine göre 17:01'de biter.
Ali gece yarısı saat 00:00'da, doğru olduğunu bildiği cep telefonunun saatine göre kol saatini ayarlıyor, gece uyandığında cep telefonu 02:30'u gösterirken kol saatinin 02:39'u gösterdiğini görüyor.
Ali sabah uyandığında kol saati 08:50'yi gösteriyorsa saat gerçekte kaçtır?
Çözümü Göster2 saat 30 dakika 150 dakika, 2 saat 39 dakika 159 dakikadır.
Buna göre kol saati 150 dakikada 9 dakika geç kalmaktadır.
Ali sabah uyandığında, kol saatine göre saat 00:00'dan itibaren 8 saat 50 dakika geçmiştir.
8 saat 50 dakika \( 60 \cdot 8 + 50 = 530 \) dakikadır.
Ali sabah uyandığında gece yarısından itibaren geçen gerçek süreye \( t \) diyelim ve ilk bulduğumuz gerçek - hatalı süre oranıyla karşılaştıralım.
\( \dfrac{t}{530} = \dfrac{150}{159} \)
\( t = \dfrac{530 \cdot 150}{159} \)
\( = 10 \cdot 50 \)
\( = 500 \) dakika
Buna göre, saat 00:00'dan Ali sabah uyanana kadar geçen gerçek süre 500 dakikadır.
\( 500 = 8 \cdot 60 + 20 \)
500 dakika, 8 saat 20 dakika yapar.
Buna göre, Ali sabah uyandığında gerçek saat 08:20'dir.
Ali, Şeyma, Canan ve Tülin isimli 4 kardeş bir ağaçtan elma topluyorlar. Ali 6, Şeyma 10, Canan 15, Tülin ise 1 elma toplamıştır.
Sonrasında Canan Ali'ye \( a \) tane, Tülin'e \( c \) tane elma veriyor. Şeyma ise Tülin'e \( b \) tane elma veriyor.
Bu işlemden sonra herkeste eşit sayıda elma olduğuna göre, Canan Tülin'e kaç elma vermiştir?
Çözümü GösterKardeşlerin ilk durumdaki elma sayıları aşağıdaki tabloda ilk satırda, son durumdaki elma sayıları ikinci satırda verilmiştir.
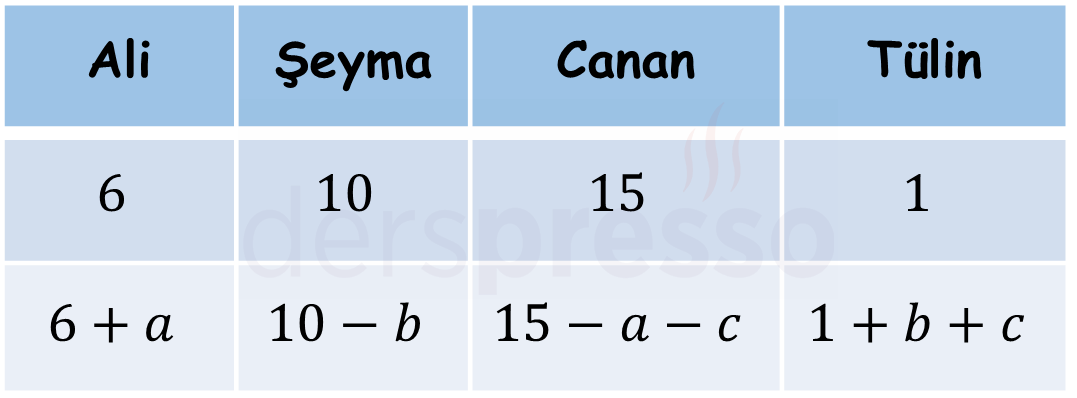
Son durumda dört kardeşin elma sayıları birbirine eşittir.
\( 6 + a = 10 - b \)
\( a + b = 4 \)
\( 15 - a - c = 1 + b + c \)
\( a + b + 2c = 14 \)
\( \underbrace{(a + b)}_{4} + 2c = 14 \)
\( 2c = 10 \)
\( c = 5 \)
Buna göre, Canan Tülin'e 5 elma vermiştir.
Ceren bir sayıya 3 ekleyip \( \frac{2}{5} \) ile çarpması gerekirken, sayıdan 3 çıkarıp \( \frac{2}{5} \)'e bölmüştür. Bulduğu sayı bulması gereken sayının 5 katı ise başlangıçtaki sayı kaçtır?
Çözümü GösterBaşlangıçtaki sayıya \( a \) diyelim.
Ceren'in yapması gereken işlem:
\( (a + 3) \cdot \dfrac{2}{5} = \dfrac{2a + 6}{5} \)
Ceren'in yaptığı işlem:
\( (a - 3) \div \dfrac{2}{5} = (a - 3) \cdot \dfrac{5}{2} \)
\( \dfrac{5a - 15}{2} \)
Bulduğu sayı bulması gereken sayının 5 katıdır.
\( \dfrac{5a - 15}{2} = 5 \cdot \dfrac{2a + 6}{5} \)
\( 5a - 15 = 4a + 12 \)
\( a = 27 \) bulunur.
İki basamaklı tüm doğal sayıları yazarken toplamda kaç tane tek sayı rakam kullanılır?
Çözümü Göster10'dan 19'a kadar olan sayılarda onlar basamağında 10 tane, birler basamağında 5 tane olmak üzere toplam 15 tane tek rakam vardır.
20'den 29'a kadar olan sayılarda tümü birler basamağında olmak üzere toplam 5 tane tek rakam vardır.
30'dan 39'a kadar olan sayılarda onlar basamağında 10 tane, birler basamağında 5 tane olmak üzere toplam 15 tane tek rakam vardır.
\( \vdots \)
90'dan 99'a kadar olan sayılarda onlar basamağında 10 tane, birler basamağında 5 tane olmak üzere toplam 15 tane tek rakam vardır.
Buna göre 1, 3, 5, 7 ve 9 ile başlayan iki basamaklı sayılarda 15'er adet tek rakam, 2, 4, 6 ve 8 ile başlayan iki basamaklı sayılarda ise 5'er adet tek rakam kullanılır.
Toplam tek rakam sayısı \( 5 \cdot 15 + 4 \cdot 5 = 95 \) olarak bulunur.
Bir kitapta bulunan sayfa numaraları toplam 2523 rakamdan oluşmaktadır.
Kitap 1. sayfadan başladığına göre, bu kitap kaç sayfadır?
Çözümü Gösterİlk 9 sayfada toplam 9 rakam bulunur.
İki basamaklı sayfa numaralarında (10'dan 99'a kadar) toplam \( (99 - 10 + 1) \cdot 2 = 180 \) rakam bulunur.
Buna göre 1 ve 2 basamaklı sayfa numaraları \( 180 + 9 = 189 \) rakamdan oluşur.
Geriye \( 2523 - 189 = 2334 \) rakam kalır.
Kalan sayfaların numaralarında 3 basamak bulunduğu için 2334'ü 3'e bölelim.
\( \dfrac{2334}{3} = 778 \)
Kitapta 778 sayfa daha olduğuna göre kitap \( 99 + 778 = 877 \) sayfadır.
Bir kitabın 1'den başlayarak tüm sayfa numaralarının toplamı alınıyor. Bu toplama işlemi sırasında bir sayfa numarası yanlışlıkla iki kez toplanıyor.
Toplama sonucu 540 olarak bulunduğuna göre, iki kez toplanan sayfa numarası kaçtır?
Çözümü GösterToplam sayfa sayısına \( n \), iki kez toplanan sayfa numarasına \( a \) diyelim.
Buna göre toplama işlemi aşağıdaki şekilde olur.
\( (1 + 2 + 3 + \ldots + n) + a = 540 \)
Ardışık sayıların terimler toplamı formülünü kullanalım.
\( \dfrac{n(n + 1)}{2} + a = 540 \)
\( 1 \le a \le n \) olacak şekilde yukarıdaki eşitliği sağlayan \( n \) sayısını deneyerek bulmamız gerekir.
Buna göre bu eşitsizliği sağlayan \( n \) değeri 32 olur.
\( n = 31 \) olduğunda \( a \gt n \) ve \( n = 33 \) olduğunda \( a \lt 0 \) olduğu denenerek görülebilir.
\( \dfrac{32(32 + 1)}{2} + a = 540 \)
\( 528 + a = 540 \)
\( a = 12 \)
İki kez toplanan sayfa numarası 12 olarak bulunur.
Emre tahtaya 1'den 50'ye kadar olan tam sayıları yazıyor ve toplamını alıyor.
Daha sonra Oya Emre'nin yazdığı sayılardaki 1 rakamlarını silip yerine 7 rakamını yazıyor ve sayıların toplamını alıyor.
Oya'nın toplamı ile Emre'nin toplamı arasındaki fark kaçtır?
Çözümü GösterBir sayının değeri; birler basamağındaki 1 yerine 7 yazıldığında 6, onlar basamağındaki 1 yerine 7 yazıldığında 60 artar.
\( \{1, 11, 21, 31, 41\} \) olmak üzere 5 tane sayının birler basamağında değişiklik yapılmıştır.
\( \{10, 11, 12, \ldots, 19\} \) olmak üzere 10 tane sayının onlar basamağında değişiklik yapılmıştır.
Buna göre, iki toplam arasındaki fark \( 5 \cdot 6 + 10 \cdot 60 = 630 \) olarak bulunur.
Uzun yola çıkacak olan bir tır sürücüsü 8.000 km yol almayı planlamaktadır. Takılı halde 10 lastiği bulunan tırın 6 da yedek lastiği vardır.
Sürücü lastikleri yolda her biri eşit derecede aşınacak şekilde değiştirdiğine göre, yolculuk sonunda her lastik kaç km yol almış olur?
Çözümü Göster8.000 km yol boyunca 10 lastik toplam 80.000 km yol alır.
Bu yol 16 lastiğe eşit şekilde dağıtıldığında her lastik \( \frac{80.000}{16} = 5.000 \) km yol almış olur.
Fahrenheit (F) ve derece (C) cinsinden sıcaklıklar arasında aşağıdaki ilişki vardır.
\( F = \dfrac{9}{5}C + 32 \)
Hissedilen sıcaklığın gerçek sıcaklıktan 5°C yüksek olduğu bir günde hissedilen sıcaklıkla gerçek sıcaklığın toplamı 145 Fahrenheit olduğuna göre, bu günde hissedilen sıcaklık kaç °C'dir?
Çözümü GösterHissedilen sıcaklığa \( x \) °C diyelim. Bu durumda gerçek sıcaklık \( (x - 5) \) °C olur.
Hissedilen sıcaklıkla gerçek sıcaklığın toplamını Fahrenheit cinsinden yazalım.
\( \dfrac{9}{5}x + 32 + \dfrac{9}{5}(x - 5) + 32 = 145 \)
\( \dfrac{9}{5}(x + x - 5) + 64 = 145 \)
\( \dfrac{9}{5}(2x - 5) = 81 \)
\( 2x - 5 = 45 \)
\( x = 25 \)°C bulunur.
Bir toplantıya katılan 6 kişiden 5'i sırasıyla diğer 1, 2, 3, 4, 5 kişiyi tanıyordur.
Buna göre, 6. kişi diğer kaç kişiyi tanıyordur?
Çözümü Göster6. kişinin tanıdığı kişi sayısına \( n \) diyelim.
Adım 1:
Her kişinin tanıdığı kişi sayılarını aşağıdaki tablonun birinci adımına girelim.
| Adım | 1. Kişi | 2. Kişi | 3. Kişi | 4. Kişi | 5. Kişi | 6. Kişi |
|---|---|---|---|---|---|---|
| Adım 1 | 1 | 2 | 3 | 4 | 5 | n |
| Adım 2 | 0 | 1 | 2 | 3 | - | n - 1 |
| Adım 3 | - | 0 | 1 | - | - | n - 2 |
Adım 2:
5 kişiyi tanıyan 5. kişi diğer kişilerin tümünü tanıyordur.
5. kişiyi bu gruptan çıkaralım ve diğerlerinin tanıdığı kişi sayılarını birer eksiltelim.
Tanıdığı kişi sayısı 0'a düştüğü için 1. kişiyi de gruptan çıkaralım.
Adım 3:
Kalan 4 kişi arasından 3 kişiyi tanıyan 4. kişi diğer kişilerin tümünü tanıyordur.
4. kişiyi gruptan çıkaralım ve diğerlerinin tanıdığı kişi sayılarını birer eksiltelim.
Tanıdığı kişi sayısı 0'a düştüğü için 2. kişiyi de gruptan çıkaralım.
Kalan 2 kişiden 3. kişi 1 kişiyi tanıdığına göre bu 6. kişidir, dolayısıyla 6. kişinin tanıdığı kişi sayısı da 1 olmalıdır.
\( n - 2 = 1 \)
\( n = 3 \)
Buna göre 6. kişi toplantıdaki 3 kişiyi tanıyordur.
Ela \( \{ 1, 2, 3, 4, 5, \ldots, 26 \} \) kümesinden iki tane sayı seçiyor.
Seçilen sayıların çarpımı diğer 24 sayının toplamına eşit olduğuna göre, seçilen sayıların farkının pozitif değeri nedir?
Çözümü GösterEla'nın seçtiği sayılara \( a \) ve \( b \) diyelim.
Kümedeki sayıların toplamını, ardışık sayıların terimler toplamı formülü ile bulalım.
\( \dfrac{26 \times 27}{2} = 351 \)
Seçilen iki sayının çarpımı diğer 24 sayının toplamına eşittir.
\( ab = 351 - a - b \)
\( a + b + ab = 351 \)
Eşitliğin sol tarafını çarpanlarına ayırabilmek için eşitliğin her iki tarafına 1 ekleyelim.
\( a + b + ab + 1 = 352 \)
\( a + ab + b + 1 = 352 \)
\( a(b + 1) + b + 1 = 352 \)
\( (a + 1)(b + 1) = 352 \)
\( a \) ve \( b \) 26'dan küçük olduğu için 352 sadece aşağıdaki şekilde çarpanlarına ayrılabilir.
\( (a + 1)(b + 1) = 16 \times 22 \)
\( a \) ve \( b \) sayıları sıradan bağımsız 15 ve 21 olur.
Ela'nın seçtiği sayıların farkının pozitif değeri \( 21 - 15 = 6 \) bulunur.
Samet'in katıldığı bir araba yarışında bulunduğu konumla ilgili aşağıdakiler bilinmektedir:
- Arkasındaki arabalardan 5'i Samet'i geçerse önündeki araba sayısı arkasındaki araba sayısının 3 katı olacaktır.
- Samet önündeki 5 arabayı geçerse önündeki ve arkasındaki araba sayısı eşit olacaktır.
Buna göre Samet bu yarışta baştan kaçıncı sıradadır?
Çözümü GösterArkasındaki arabalardan 5'i Samet'i geçerse sıralama aşağıdaki gibi olmaktadır.
\( \underbrace{\ldots}_\text{x araba} \text{Samet} \underbrace{\ldots}_\text{3x araba} \)
Buna göre mevcut durumda sıralama aşağıdaki gibidir.
\( \underbrace{\ldots}_\text{(x + 5) araba} \text{Samet} \underbrace{\ldots}_\text{(3x - 5) araba} \)
Samet önündeki 5 arabayı geçerse sıralama aşağıdaki gibi olacaktır.
\( \underbrace{\ldots}_\text{(x + 10) araba} \text{Samet} \underbrace{\ldots}_\text{(3x - 10) araba} \)
Bu durumda Samet'in önündeki ve arkasındaki araba sayıları eşit olacaktır.
\( x + 10 = 3x - 10 \)
\( 2x = 20 \)
\( x = 10 \)
Samet'in mevcut konumunda önünde \( 3x - 5 = 3(10) - 5 = 25 \) araba olduğuna göre baştan 26. sıradadır.
Fatih elindeki parayı yaşları birbirinden farklı 5 yeğenine dağıtmak istiyor.
İlk olarak elindeki paranın yarısına 800 TL ekleyerek bu parayı en büyük yeğenine veriyor. Daha sonra aynı işlemi her bir yeğeni için uygulayarak elindeki tüm parayı yeğenlerine dağıtıyor.
Buna göre Fatih ortanca yeğenine kaç lira vermiştir?
Çözümü GösterFatih'in elindeki paraya işlem kolaylığı açısından \( 64x \) diyelim.
En büyük yeğenin aldığı ve Fatih'in elinde kalan tutarı bulalım.
Verilen: \( 32x + 800 \)
Kalan: \( 64x - (32x + 800) = 32x - 800 \)
2. yeğenin aldığı ve Fatih'in elinde kalan tutarı bulalım.
Verilen: \( (16x - 400) + 800 = 16x + 400 \)
Kalan: \( 32x - 800 - (16x + 400) = 16x - 1200 \)
Ortanca yeğenin aldığı ve Fatih'in elinde kalan tutarı bulalım.
Verilen: \( (8x - 600) + 800 = 8x + 200 \)
Kalan: \( 16x - 1200 - (8x + 200) = 8x - 1400 \)
4. yeğenin aldığı ve Fatih'in elinde kalan tutarı bulalım.
Verilen: \( (4x - 700) + 800 = 4x + 100 \)
Kalan: \( 8x - 1400 - (4x + 100) = 4x - 1500 \)
En küçük yeğenin aldığı ve Fatih'in elinde kalan tutarı bulalım.
Verilen: \( (2x - 750) + 800 = 2x + 50 \)
Kalan: \( 4x - 1500 - (2x + 50) = 2x - 1550 \)
Soruda belirtildiği üzere, Fatih elinde kalan son parayı en küçük yeğenine vermiştir.
\( 2x - 1550 = 0 \)
\( x = 775 \)
Ortanca yeğenin aldığı parayı bulmak için bulduğumuz \( x \) değerini yerine koyalım.
\( 8x + 200 = 8(775) + 200 \)
\( = 6400 \)
Buna göre ortanca yeğen 6400 TL almıştır.
Yük kapasitesi 84 ton olan bir gemide bir grup fil taşınmaktadır. Gruptaki en ağır fil 6450 kg, en hafif fil 4850 kg'dır.
Buna göre, bu gemide en fazla kaç fil taşınıyor olabilir?
Çözümü GösterSoruda en hafif filin tek olduğu bilgisi verilmediği için en hafif fille aynı kiloda başka filler de olduğunu düşünebiliriz.
Fil sayısının en büyük değerini bulmak için en ağır fil dışındaki filleri en hafif kiloda almalıyız.
Toplam fil sayısına \( n \) diyelim.
\( 6450 + 4850(n - 1) = 84000 \)
\( 6450 + 4850n - 4850 = 84000 \)
\( 4850n = 82400 \)
\( n = \dfrac{82400}{4850} \approxeq 16,98 \)
Buna göre \( n \) sayısının alabileceği en büyük değer 16 olur. Fil sayısının 17 olması durumunda en ağır fil dışındaki tüm filler en hafif fille aynı ağırlıkta olsa bile geminin yük kapasitesi aşılacaktır.
Kare şeklindeki bir zemin özdeş kare fayanslarla kaplanacaktır.
Karenin en dıştaki kenarları ve köşegenleri döşenirken 81 tane fayans kullanıldığına göre, zeminin tamamen kaplanması için kaç tane daha fayansa ihtiyaç vardır?
Çözümü GösterKarenin bir kenarında kullanılan fayans sayısına \( x \) diyelim.
Kenarların köşeleri ortak olduğundan diğer kenarlara sırayla \( x - 1, x - 1, x - 2 \) tane fayans döşenir.
Buna göre, en dış kenarlara toplam \( 4x - 4 \) tane fayans döşenmiştir.
Köşegenlerlere döşenen fayans sayısı \( x \)'in tek ya da çift olmasına göre iki şekilde olabilir.
Kenarlar döşendikten sonra iki köşegene döşenen fayans sayısı:
\( = \begin{cases} 2(x - 2) & x \text{ çift ise} \\ 2(x - 2) - 1 & x \text{ tek ise} \end{cases} \)
Not: Bu denklemler 3x3 ve 4x4 karelerde değer verilerek kontrol edilebilir. \( x \)'in tek olduğu durumda 1 çıkarmamızın sebebi karenin en ortasında iki köşegenin kesişiminde bir fayansın ortak olmasıdır.
\( x \) çift sayı ise toplam döşenen fayans sayısı \( 4x - 4 + 2(x - 2) = 6x - 8 \) olur.
\( 6x - 8 = 81 \)
\( 6x = 89 \)
\( x \) tam sayı çıkmadığı için \( x \) çift sayı olamaz.
\( x \) tek sayı ise toplam döşenen fayans sayısı \( 4x - 4 + 2(x - 2) - 1 = 6x - 9 \) olur.
\( 6x - 9 = 81 \)
\( x = 15 \)
\( x \) tam ve tek sayı çıktığından \( x = 15 \) doğru cevaptır.
Buna göre daha döşenmesi gereken fayans sayısı \( 15^2 - 81 = 144 \) olarak bulunur.
Bir sınıftaki öğrencilerin bir kısmı 2 haftada bir, diğerleri 3 haftada bir nöbet tutmaktadır.
İlk 5 hafta nöbet tutan öğrenci sayısı sırasıyla 42, 36, 33, 40, 38 olduğuna göre, 6. hafta nöbet tutan toplam öğrenci sayısı kaçtır?
Çözümü Göster2 haftada bir nöbet tutan öğrencilerin izleyeceği periyotlar aşağıdaki gibi olur.
\( a \) sayıda öğrenci 1. hafta, 3. hafta ve 5. hafta nöbet tutar.
\( b \) sayıda öğrenci 2. hafta, 4. hafta ve 6. hafta nöbet tutar.
3 haftada bir nöbet tutan öğrencilerin izleyeceği periyotlar aşağıdaki gibi olur.
\( c \) sayıda öğrenci 1. hafta ve 4. hafta nöbet tutar.
\( d \) sayıda öğrenci 2. hafta ve 5. hafta nöbet tutar.
\( e \) sayıda öğrenci 3. hafta ve 6. hafta nöbet tutar.
Hafta bazında tutulan nöbet sayılarının toplamını alalım.
1. hafta: \( a + c = 42 \)
2. hafta: \( b + d = 36 \)
3. hafta: \( a + e = 33 \)
4. hafta: \( b + c = 40 \)
5. hafta: \( a + d = 38 \)
6. hafta: \( b + e = ? \)
2. ve 3. haftaları kendi aralarında toplayalım.
\( (b + d) + (a + e) = 36 + 33 = 69 \)
5. haftada \( a + d = 38 \) verildiği için \( b + e = 31 \) olarak bulunur.
3 aşamadan oluşan bir yarışmada 2. aşamada elenen yarışmacılara 10'ar altın, 3. aşamada elenen yarışmacılara 15'er altın, tüm aşamaları başarıyla tamamlayan yarışmacılara 30'ar altın verilirken 1. aşamada elenen yarışmacılara ödül verilmemektedir.
Yarışmacıların \( \% 20\)'si ilk aşamada elenmiş, \( \%30 \)'u 2. aşamayı geçmiş, \( \%10 \)'u ise 3. aşamayı tamamlayarak büyük ödülü kazanmıştır. Buna göre tüm yarışmada yarışmacı başına düşen ortalama altın sayısı kaçtır?
Çözümü Göster3. aşamayı geçen yarışmacılar aynı zamanda 1 ve 2. aşamaları, 2. aşamayı geçen yarışmacılar da aynı zamanda 1. aşamayı geçmiştir. Bu yarışmacılar aşamayı geçen yarışmacı sayısına dahil edilirken o aşamanın sonucunda dağıtılan ödüle dahil edilmezler.
Toplam yarışmacı sayısına işlem kolaylığı açısından \( 100x \) diyelim.
Özetlemek gerekirse, 1. aşamada elenen yarışmacılar ödül kazanmazken, 2. aşamada elenen yarışmacılar 10 altın, 3. aşamada elenen yarışmacılar 15 altın, 3. aşamayı tamamlayan yarışmacılar ise 30 altın kazanmaktadır.
\( 20x \) yarışmacı 1. aşamada eleniyor ve bir ödül kazanamıyor.
\( 10x \) yarışmacı 3. aşamayı tamamlayarak 30 altın kazanıyor.
Buna göre 2. aşamayı geçen \( 30x \) yarışmacıdan \( 30x - 10x = 20x \)'i 3. aşamada elendiği için 15 altın kazanır.
Geriye kalan \( 100x - 20x - 20x - 10x = 50x \) yarışmacı ise 2. aşamada elenen ve 10 altın kazanan yarışmacılardır.
Toplam dağıtılan altın sayısını hesaplayalım.
\( 50x \cdot 10 + 20x \cdot 15 + 10x \cdot 30 = 1100x \)
Toplam altın sayısını yarışmacı sayısına bölerek yarışmacı başına düşen ortalama altın sayısını bulalım.
\( \dfrac{1100x}{100x} = 11 \) altın bulunur.
Paralarının toplamı 720 TL olan üç kardeşin para miktarları ile ilgili aşağıdakiler biliniyor.
- Kardeşlerden birinin parası bir diğer kardeşin parasının 2 katıdır.
- Kardeşlerden birinin parası bir diğer kardeşin parasının 3 katıdır.
Buna göre bu kardeşlerden parası en çok olanın parası en çok kaç TL olabilir?
Çözümü GösterBirinci öncüle göre kardeşlerden ikisinin parasına \( 6x \) ve \( 12x \) diyelim.
\( \textcolor{red}{6x} - \textcolor{red}{12x} \)
İkinci öncüle göre üçüncü kardeşin parası (ilk iki kardeşten birinin 3 katı ya da 3'te biri olmak üzere) 4 farklı şekilde olabilir.
\( \textcolor{blue}{2x} - \textcolor{red}{6x} - \textcolor{red}{12x} \)
\( \textcolor{red}{6x} - \textcolor{red}{12x} - \textcolor{blue}{18x} \)
\( \textcolor{blue}{4x} - \textcolor{red}{6x} - \textcolor{red}{12x} \)
\( \textcolor{red}{6x} - \textcolor{red}{12x} - \textcolor{blue}{36x} \)
Her durum için kardeşlerin paraları toplamını ve en büyük para miktarını bulalım.
Durum 1:
\( 2x + 6x + 12x = 20x = 720 \)
\( x = 36 \)
\( 12x = 432 \)
Durum 2:
\( 6x + 12x + 18x = 36x = 720 \)
\( x = 20 \)
\( 18x = 360 \)
Durum 3:
\( 4x + 6x + 12x = 22x = 720 \)
\( x = \dfrac{360}{11} \)
\( 12x = \dfrac{4320}{11} \approx 392,72 \)
Durum 4:
\( 6x + 12x + 36x = 54x = 720 \)
\( x = \dfrac{40}{3} \)
\( 36x = 480 \)
Buna göre kardeşlerden parası en çok olanın parası, 4. durumda olmak üzere en çok 480 TL olabilir.