Ters Orantı
İki değişkenin değerleri değişirken çarpımları sabit kalıyorsa bu iki değişken birbiriyle ters orantılıdır. Ters orantılı iki değişkenin bu sabit çarpımına orantı sabiti denir ve genellikle \( k \) ile gösterilir.
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( xy = k \)
\( y = \dfrac{k}{x} \)
\( y \) değişkeni \( x \) değişkeni ile ters orantılı ise aynı zamanda \( \frac{1}{x} \) değişkeni ile doğru orantılıdır.
\( xy = k \) ise,
\( \dfrac{y}{\frac{1}{x}} = k \)
\( y = k\ \dfrac{1}{x} \)
Doğru ve ters orantı arasındaki temel fark değişkenlerden biri artarken diğerinin artması ya da azalması değildir. Doğru orantıda değişkenlerin oranı sabitken ters orantıda değişkenlerin çarpımı sabittir.
Aralarında ters orantı ilişkisi bulunan iki değişken için \( k \) orantı sabiti, değişkenlerin birbirine karşılık gelen tüm değerleri için sağlanır.
\( x_1y_1 = x_2y_2 = x_3y_3 = \ldots = k \)
Ayşegül cebindeki 400 TL ile annesine; (a) tanesi 80 TL olan güllerden kaç tane (\( x \)) alabilir? (b) 8 tane gül almak için tanesi kaç TL (\( y \)) olan güllerden almalıdır?
\( x \cdot 80 = 8 \cdot y = 400 \)
\( x = \dfrac{400}{80} = 5 \) tane
\( y = \dfrac{400}{8} = 50 \) TL
İki değişken arasındaki ters orantı ilişkisini bir örnek üzerinde gösterelim.
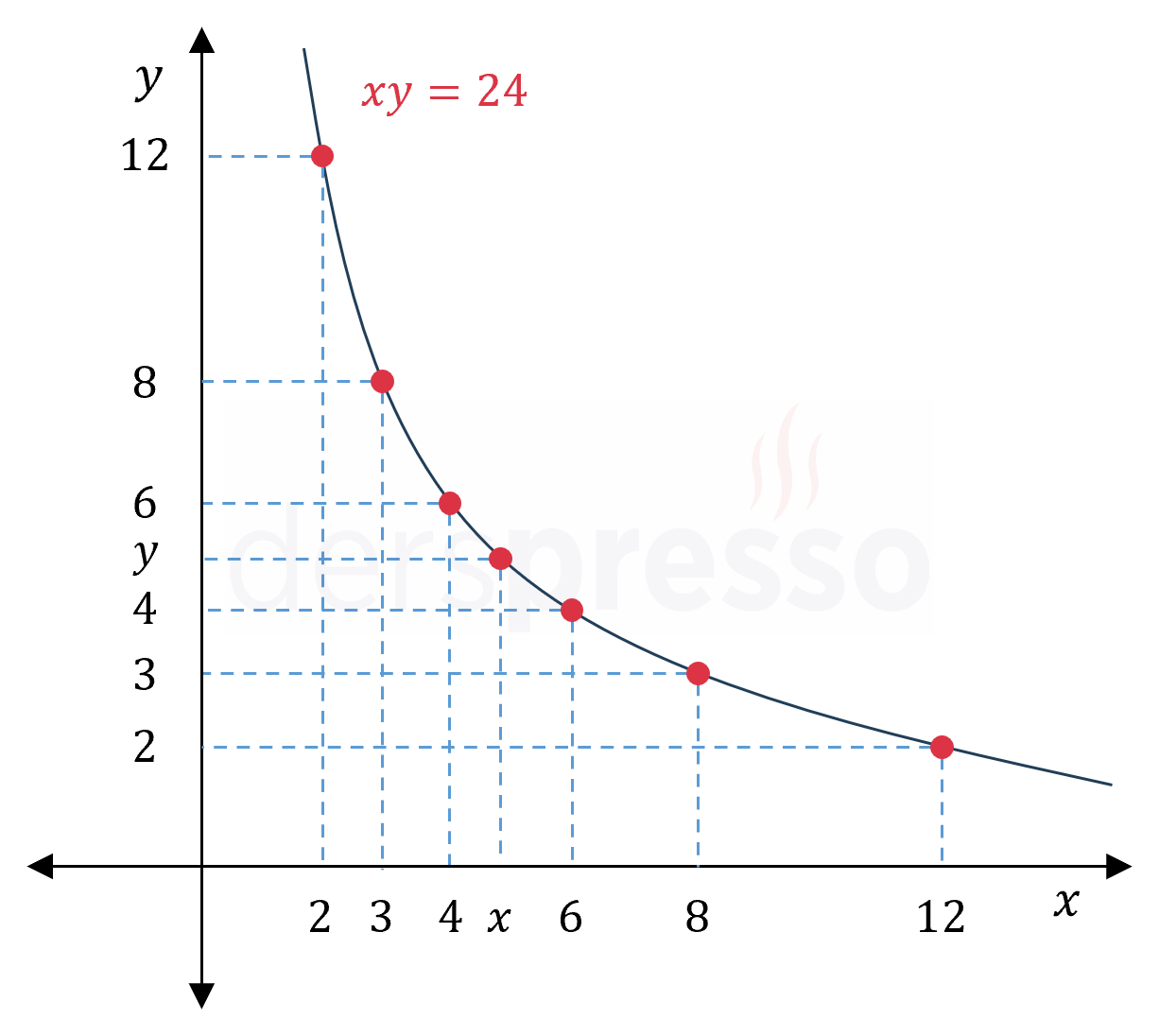
Birbiriyle ters orantılı ve çarpımları 24 olan \( x \) ve \( y \) değişkenlerinin farklı değerlerini tablo ve grafik üzerinde gösterelim.
Ters orantının orantı sabiti 24 ise iki değişkenin değerlerinin çarpımı her durumda sabit ve 24'e eşittir.
\( xy = 24 \)
Orantı sabiti sağlanacak şekilde değişkenlerin alabilecekleri farklı değerlerden bazılarını bir tabloda gösterelim.
| \( x \) | \( 2 \) | \( 3 \) | \( 4 \) | \( 6 \) | \( 8 \) | \( 12 \) |
| \( y \) | \( 12 \) | \( 8 \) | \( 6 \) | \( 4 \) | \( 3 \) | \( 2 \) |
| \( xy = k \) | \( 24 \) | \( 24 \) | \( 24 \) | \( 24 \) | \( 24 \) | \( 24 \) |
Değişkenlerin bu değerleri aşağıdaki grafikte işaretlenmiştir.
Ters orantıya gerçek hayattan aşağıdaki örnekler verilebilir.
- Bir aracın ortalama hızı ve belirli bir mesafeyi katetme süresi: Bu durumda orantı sabiti toplam mesafedir.
- Bir miktar parayı paylaşan kişi sayısı ve kişi başına düşen miktar: Bu durumda orantı sabiti toplam para miktarıdır.
- Bir işi tamamlamak için gerekli kişi sayısı ve kişi başına çalışma süresi: Bu durumda orantı sabiti toplam iş miktarıdır.
- Bant genişliği ve bir dosyayı indirmek için geçen süre: Bu durumda orantı sabiti indirilen dosyanın boyutudur.
İki değişken arasındaki ters orantı ilişkisini ikinci bir örnek üzerinde gösterelim.
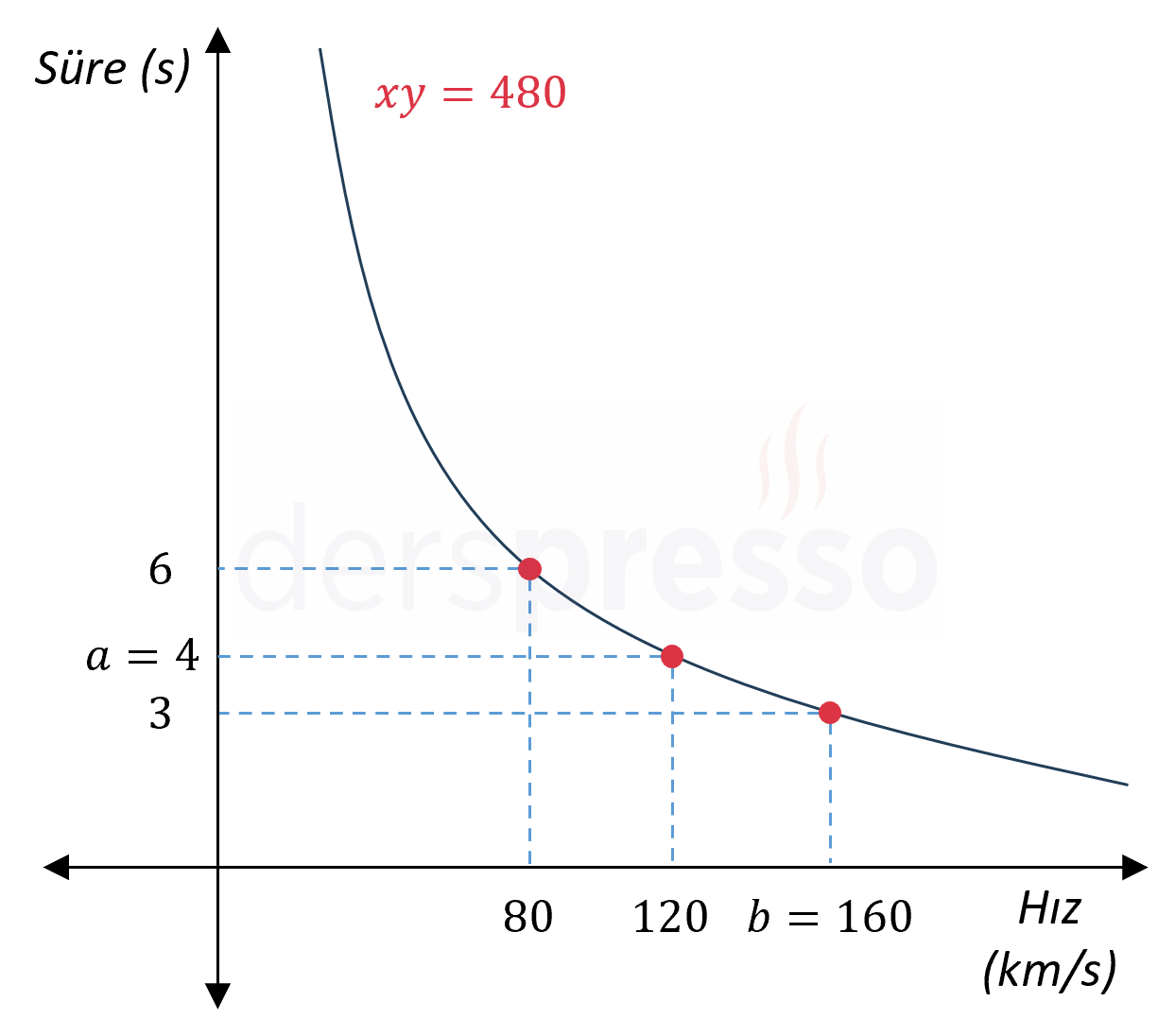
Bir araç sabit 80 km/s hızla gittiğinde 6 saatte aldığı bir yolu, sabit 120 km/s hızla gittiğinde kaç saatte alır?
Aracın hızına \( x \), yolculuk süresine \( y \) diyelim.
Aracın hızı arttıkça yolculuk süresi çarpımları toplam mesafeyi verecek şekilde azalacağı için, bu iki değişken arasında ters orantı olduğunu söyleyebiliriz.
\( xy = k \)
Verilen birinci durumda araç 80 km/s hızla yolu 6 saatte alıyor.
Verilen ikinci durumda araç 120 km/s hızla gittiğinde aynı yolu kaç saatte alacağı soruluyor. Bu süreye \( a \) saat diyelim.
\( a \) değerini bulmak için verilen değerleri ters orantı formülünde yerine koyalım.
\( x_1y_1 = x_2y_2 = k \)
\( 80 \cdot 6 = 120 \cdot a = k \)
\( a = \dfrac{480}{120} = 4 \) saat
Buna göre araç 120 km/s hızla gittiğinde aynı yolu 4 saatte alır.
Ters orantı formülünü kullanarak orantı sabitini bulalım.
\( k = 6 \cdot 80 = 480 \)
Bu değer aynı zamanda aracın katettiği toplam yola eşittir.
Yukarıdaki örnekteki aracın aynı yolu 3 saatte alması için hızı saatte kaç km olmalıdır?
Bulduğumuz orantı sabitini kullanarak hız ya da yolculuk süresi bilinen tüm durumlarda bilinmeyen değişken değerini bulabiliriz.
Aracın yolu 3 saatte alabilmesi için gerekli hıza saatte \( b \) km diyelim.
\( xy = 480 \)
\( b \cdot 3 = 480 \)
\( b = 160 \) km/s
Yukarıdaki iki örnekte bulduğumuz değerleri ters orantının grafiği üzerinde gösterelim.
Bir değişken diğer bir değişkenle ters orantılı olabileceği gibi, o değişkenin karesi, küpü, karekökü ya da herhangi bir fonksiyonu ile de ters orantılı olabilir. Bu durumlarda iki değişken arasındaki formül ve grafik ilişkisi aşağıdaki gibi olur.
| Grafik | Ters Orantı |
|---|---|
|
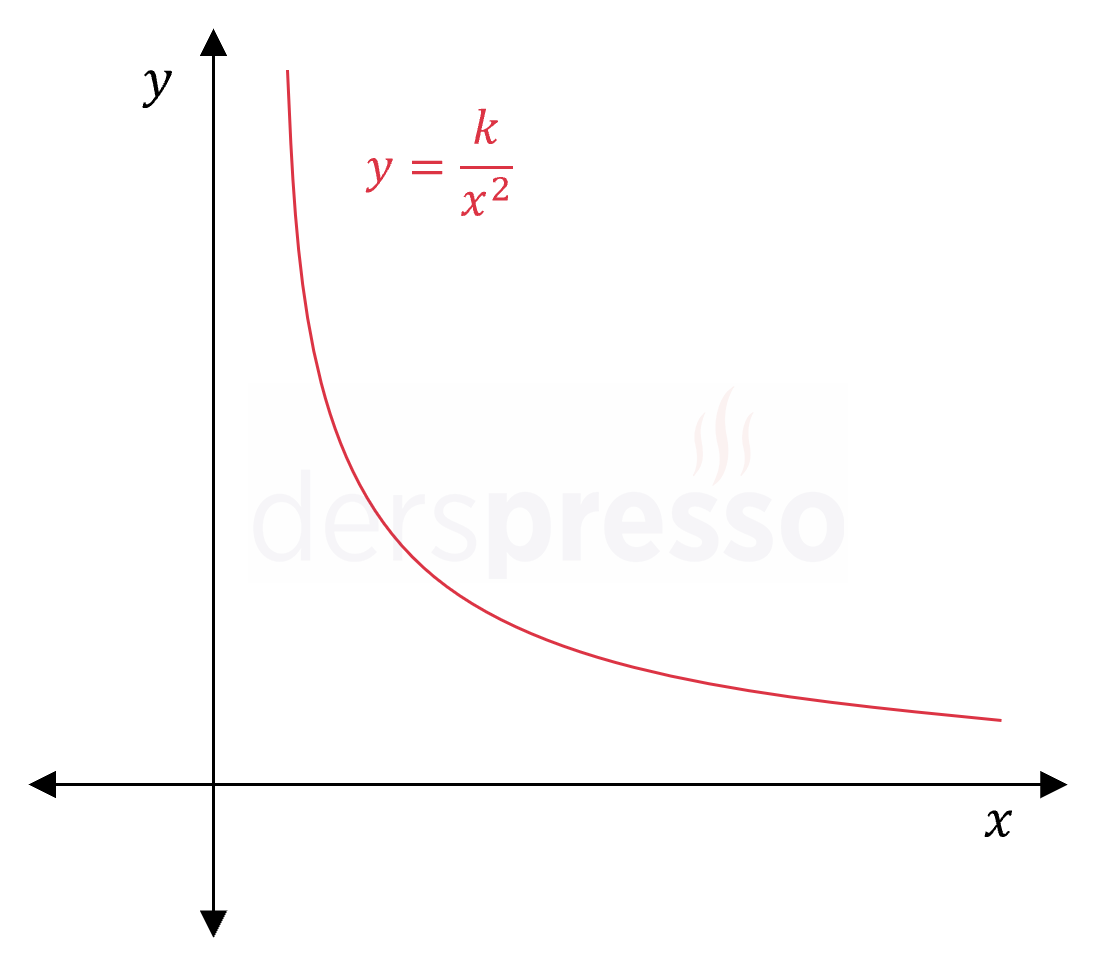
\( y = k\ \dfrac{1}{x^2} \) \( y \) değişkeni \( x \)'in karesi ile ters orantılıdır. |
|
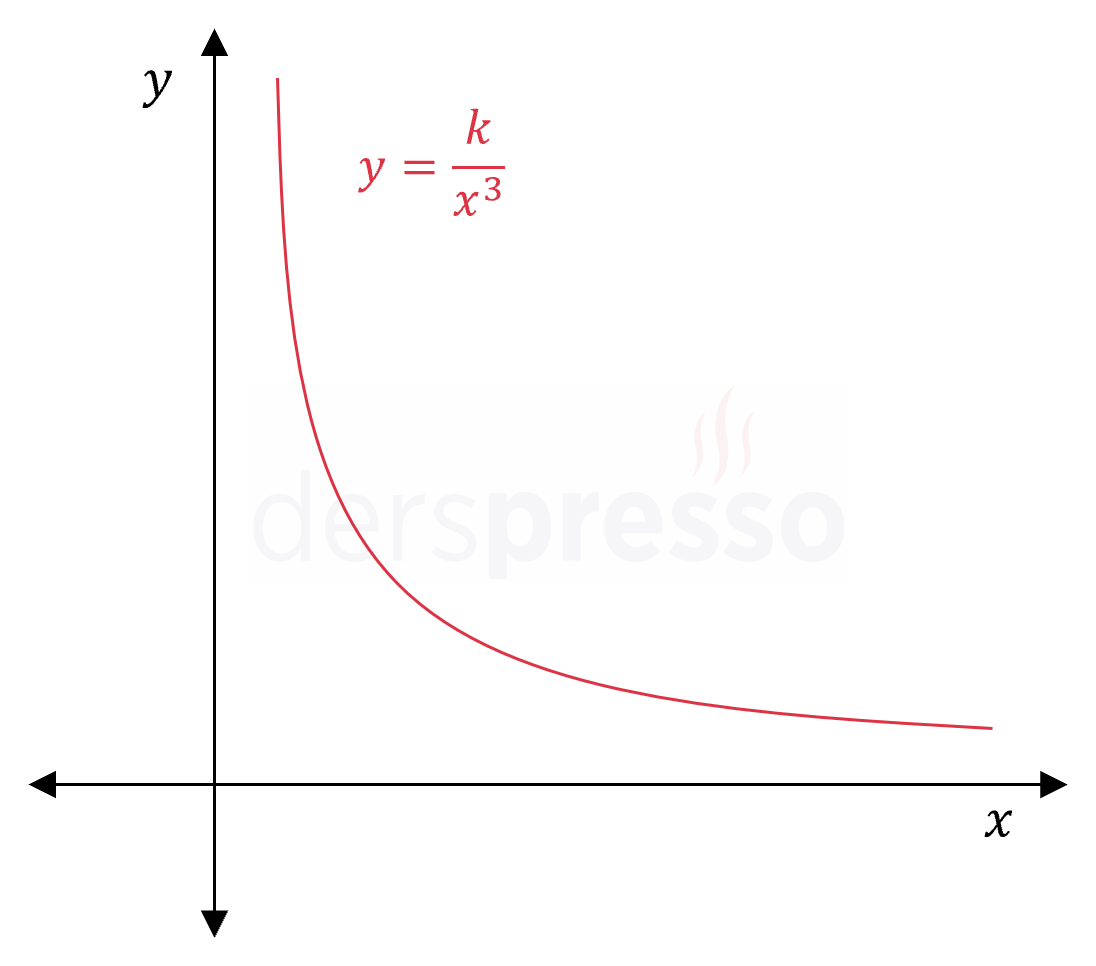
\( y = k\ \dfrac{1}{x^3} \) \( y \) değişkeni \( x \)'in küpü ile ters orantılıdır. |
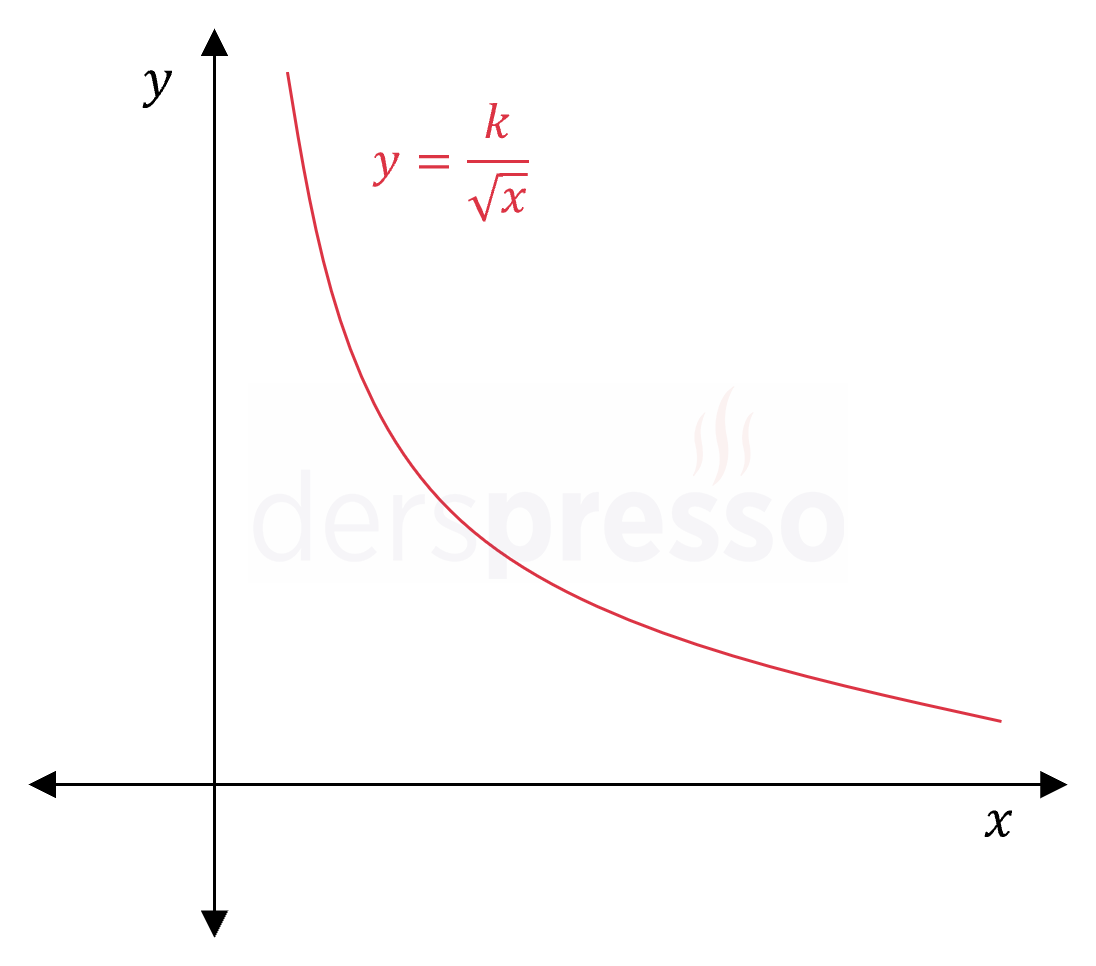
|
\( y = k\ \dfrac{1}{\sqrt{x}} \) \( y \) değişkeni \( x \)'in karekökü ile ters orantılıdır. |
\( 4a - 1 \) sayısı \( 3b - 7 \) sayısı ile ters orantılıdır.
\( a = 4 \) iken \( b = 5 \) ise \( b = 9 \) iken \( a \) kaçtır?
Çözümü Göster\( 4a - 1 \) sayısı \( 3b - 7 \) sayısı ile ters orantılı olduğuna göre çarpımları bir orantı sabitine eşittir.
\( (4a - 1)(3b - 7) = k \)
\( a = 4 \) iken \( b = 5 \) olarak veriliyor.
\( (4 \cdot 4 - 1)(3 \cdot 5 - 7) = k \)
\( 15 \cdot 8 = 120 = k \)
Bulduğumuz orantı sabitini kullanarak \( b = 9 \) iken \( a \) değerini bulalım.
\( (4a - 1)(3 \cdot 9 - 7) = 120 \)
\( (4a - 1) \cdot 20 = 120 \)
\( 4a - 1 = 6 \)
\( a = \dfrac{7}{4} \) bulunur.
\( a = \dfrac{b}{7}, \quad b = \dfrac{7}{4c}, \quad c = \dfrac{d}{12} \)
olduğuna göre, aşağıdakilerden hangileri doğrudur?
I. \( a \) ile \( b \) doğru orantılıdır.
II. \( a \) ile \( d \) ters orantılıdır.
III. \( b \) ile \( d \) doğru orantılıdır.
IV. \( a \) iki katına çıkarılırsa \( c \) yarıya iner.
Çözümü GösterI. öncül:
\( a = \dfrac{b}{7} \)
\( \dfrac{a}{b} = \dfrac{1}{7} \)
İki değişkenin değerleri değişirken oranları sabit kalıyorsa bu iki değişken birbiriyle doğru orantılıdır.
\( a \) ile \( b \) doğru orantılıdır.
I. öncül doğrudur.
II. öncül:
\( a = \dfrac{b}{7} \) eşitliğinde \( b = \dfrac{7}{4c} \) yazalım.
\( a = \dfrac{\frac{7}{4c}}{7} \)
\( a = \dfrac{1}{4c} \)
\( c = \dfrac{d}{12} \) yazalım.
\( a = \dfrac{1}{4(\frac{d}{12})} \)
\( a = \dfrac{3}{d} \)
\( ad = 3 \)
İki değişkenin değerleri değişirken çarpımları sabit kalıyorsa bu iki değişken birbiriyle ters orantılıdır.
\( a \) ile \( d \) ters orantılıdır.
II. öncül doğrudur.
III. öncül:
\( b = \dfrac{7}{4c} \)
\( c = \dfrac{d}{12} \) yazalım.
\( b = \dfrac{7}{4(\frac{d}{12})} \)
\( b = \dfrac{21}{d} \)
\( bd = 21 \)
İki değişkenin değerleri değişirken çarpımları sabit kalıyorsa bu iki değişken birbiriyle ters orantılıdır.
\( b \) ile \( d \) ters orantılıdır.
III. öncül yanlıştır.
IV. öncül:
\( a = \dfrac{b}{7} \)
\( b = \dfrac{7}{4c} \) yazalım.
\( a = \dfrac{\frac{7}{4c}}{7} \)
\( a = \dfrac{1}{4c} \)
\( ac = \dfrac{1}{4} \)
\( a \) iki katına çıktığında ve \( c \) yarıya indiğinde orantı sabiti değişmiyorsa bu öncül doğrudur.
\( (2a)(\frac{c}{2}) = \dfrac{1}{4} \)
\( ac = \dfrac{1}{4} \)
IV. öncül doğrudur.
Buna göre I., II ve IV. öncüller doğrudur.
\( x \) ve \( y \) pozitif sayılar olup birbiriyle ters orantılıdır.
Buna göre \( x \) \( \%a \) kadar artırılırsa \( y \) yüzde kaç azalır?
Çözümü Göster\( x \) ve \( y \) birbiriyle ters orantılı ise çarpımları bir orantı sabitine eşittir.
\( x \cdot y = k \)
\( x \) \( \%a \) kadar arttığında \( y \) \( \%b \) azalır diyelim.
\( x(1 + \dfrac{a}{100}) \cdot y(1 - \dfrac{b}{100}) = k \)
Her iki durumda orantı sabiti aynıdır.
\( x \cdot y = x(1 + \dfrac{a}{100}) \cdot y(1 - \dfrac{b}{100}) \)
\( 1 = (1 + \dfrac{a}{100})(1 - \dfrac{b}{100}) \)
\( (100 + a)(100 - b) = 10000 \)
\( 10000 + 100a - 100b - ab = 10000 \)
\( 100b + ab = 100a \)
\( b(100 + a) = 100a \)
\( b = \dfrac{100a}{100 + a} \) bulunur.
5 işçinin birlikte 4'er saat çalışarak tamamlayabildiği bir işi 8 işçi birlikte kaçar saat çalışarak tamamlayabilir?
Çözümü GösterBir işçinin çalışma süresine \( x \), işin tamamlanması için ihtiyaç duyulan işçi sayısına \( y \) diyelim.
Toplam iş miktarı bir işçinin çalışma süresi ile işçi sayısının çarpımına eşit olduğu için, iki değişken arasında ters orantı olduğunu söyleyebiliriz.
\( xy = k \)
Verilen birinci durumda 5 işçi 4'er saat çalışarak işi tamamlıyor.
Verilen ikinci durumda aynı işi 8 işçinin kaçar saat çalışarak tamamlayacağı soruluyor. Bu süreye \( a \) saat diyelim.
\( a \) değerini bulmak için verilen değerleri ters orantı formülünde yerine koyalım.
\( x_1y_1 = x_2y_2 = k \)
\( 4 \cdot 5 = a \cdot 8 = k \)
\( x = 2,5 \) saat
Buna göre 8 işçi aynı işi 2,5'ar saat çalışarak tamamlayabilir.
Ayşe 24 günde bir halı dokumaktadır. Ayşe iş kapasitesini %60 artırırsa bir halıyı kaç günde tamamlar?
Çözümü GösterAyşe'nin bir günde tamamladığı iş miktarına \( 100x \) diyelim.
Ayşe \( 100x \) kapasitede 24 günde 1 halı dokumaktadır.
Ayşe günlük iş kapasitesini %60 artırırsa iş kapasitesi \( 160x \) olur.
Ayşe'nin \( 160x \) kapasitede 1 halıyı dokuma süresine \( a \) gün diyelim.
İş kapasitesi artarsa bir halıyı dokumak için harcanan gün sayısı azalacağı için iki değişken arasında ters orantı olduğunu söyleyebiliriz.
\( 100x \cdot 24 = 160x \cdot a \)
\( a = \dfrac{100x \cdot 24}{160x} \)
\( = 15 \) gün bulunur.
Bir çitanın dakikada soluk alıp verme hızı vücudundaki yağ oranının karesi ile ters orantılıdır.
Yağ oranı %9 olan bir çitanın soluk alıp verme hızı dakikada 100 'dür. Buna göre, yağ oranı %10 olan bir çitanın dakikada soluk alıp verme hızı nedir?
Çözümü GösterÇitanın bir dakikada solup alıp verme hızına \( b \), vücudundaki yağ oranına yüzde \( f \) diyelim.
Solup alıp verme hızı ile yağ oranının karesi ters orantılı olduğu için bu değişkenlerin çarpımı sabittir.
\( b \cdot f^2 = k \)
İki çita için verilen bilgilere bu eşitliği uygulayalım. Bulmak istediğimiz solup alıp verme hızına \( x \) diyelim.
\( 100 \cdot \left( \dfrac{9}{100} \right)^2 = x \cdot \left( \dfrac{10}{100} \right)^2 = k \)
\( 100 \cdot \dfrac{9^2}{100^2} = x \cdot \dfrac{10^2}{100^2} = k \)
\( x = 81 \) solup alıp verme
Fidan'ın şarjı tam dolu olan telefonu 3 gün 20 saat dayanmaktadır.
Fidan bir saatteki telefon kullanımını %84 arttırırsa tam dolu olan telefonu kaç saat dayanır?
Çözümü GösterPilin toplam kapasitesi sabit olduğu için, telefon kullanımı ve şarjın dayanma süresi ters orantılıdır.
Telefon saatte 100x dakika kullanılıyorsa daha sonra 184x dakika kullanılmaktadır.
3 gün 20 saatin toplam kaç saat olduğunu bulalım.
\( 3 \cdot 24 + 20 = 92 \) saat
Kullanım arttıktan sonra şarjın dayanma süresine \( t \) diyelim.
\( 92 \cdot 100x = t \cdot 184x \)
\( t = 50 \) saat
Buna göre yeni kullanımda telefonun şarjı 50 saat dayanır.
Bir yürüyen merdivenin hareketini sağlayan birbirine temas eden iki dişli çarktan büyük olanın yarıçapının küçük olanın yarıçapına oranı \( \frac{39}{21} \)'dir.
Bu yürüyen merdiven belirli bir yol aldığında küçük dişli 78 devir yaptığına göre, büyük dişli kaç devir yapar?
Çözümü GösterSorudaki değişkenleri aşağıdaki şekilde tanımlayalım.
\( r_k, r_b \): Küçük ve büyük dişlilerin yarıçapları
\( d_k, d_b \): Küçük ve büyük dişlilerin devir sayıları
Dişlilerin yarıçapları arasındaki oran \( \frac{39}{21} \) olduğuna göre yarıçapları aşağıdaki şekilde yazabiliriz.
\( r_k = 21k, \quad r_b = 39k \)
Dişliler birbirine temas ettiği için belirli bir sürede aldıkları yollar birbirine eşittir. Bu eşitliği aşağıdaki formülle ifade edebiliriz.
Küçük dişlinin çevresi x küçük dişlinin devir sayısı = Büyük dişlinin çevresi x büyük dişlinin devir sayısı
\( 2\pi r_k \cdot d_k = 2\pi r_b \cdot d_b \)
Dişlilerin yarıçapları ve devir sayılarının çarpımı sabit olduğu için, bu formül bize iki değişken arasında ters orantı olduğunu göstermektedir.
Ortak çarpanları sadeleştirip yukarıda bulduğumuz değişkenleri denklemde yerine koyalım.
\( r_k \cdot d_k = r_b \cdot d_b \)
\( 21k \cdot 78 = 39k \cdot d_b \)
\( d_b = 42 \) devir
Ali'nin 60 adet tavuğu ve bu tavuklara 148 gün yetecek miktarda tavuk yemi vardır.
Ali 38 gün sonra bu tavuklardan 16'sını satıyor. Buna göre kalan yemler kalan tavuklara kaç gün yeter?
Çözümü GösterBaşlangıçta 60 adet tavuk ve 148 günlük yem vardır.
38 gün sonunda 60 adet tavuk ve \( 148 - 38 = 110 \) günlük yem kalmıştır.
60 tavuktan 16'sını satıldığında 44 tavuk kalır.
60 adet tavuğa 110 gün yetecek miktardaki yemin 44 tavuğa kaç gün yeteceğini bulalım.
Tavuk sayısı azaldıkça yem miktarı daha uzun süre yeteceği için çarpımları sabit kalacak şekilde tavuk sayısı ve günlük yem miktarı ters orantılıdır.
Kalan yem miktarının 44 tavuğa yeteceği gün sayısına \( x \) diyelim.
\( 60 \cdot 110 = 44 \cdot x \)
\( x = 150 \) gün bulunur.