Temel Satır İşlemleri
Bir matris üzerinde, matrisin temsil ettiği lineer denklem sisteminin çözüm kümesini değiştirmeden yapılabilecek işlemlere temel (elementer) satır işlemleri denir.
Örnek olarak, aşağıda sağda verilen denklem sistemi (bu bölümde inceleyeceğimiz) temel satır işlemleri ile soldaki denklem sisteminden türetilmiştir ve her iki denklem sisteminin tek çözümü \( (a, b, c) = (5, 2, -3) \) üçlüsüdür.

Soldaki denklem sisteminin çözümü üç değişkenli bir sistem için bile pek çok işlem gerektiriyor olsa da, sağdaki denklem sistemi aşağıdaki adımlarla kolayca çözülebilir.
Üçüncü denklemi kullanarak \( c \) değerini bulalım.
\( -5c = 15 \Longrightarrow c = -3 \)
İkinci denklemi ve bulduğumuz \( c \) değerini kullanarak \( b \) değerini bulalım.
\( 2b + 3c = -5 \Longrightarrow b = 2 \)
Birinci denklemi ve bulduğumuz \( b, c \) değerlerini kullanarak \( a \) değerini bulalım.
\( a - b + 2c = -3 \Longrightarrow a = 5 \)
Temel satır işlemlerini kullanmaktaki amaçlardan biri; bir lineer denklem sistemine denk, yani aynı çözüm kümesine sahip olan daha sade denklem sistemleri elde etmek ve bu şekilde denklem sisteminin çözümünü kolaylaştırmaktır.
Yer değiştirme, skaler çarpma ve toplama olmak üzere üç tip temel satır işlemi vardır.
Yer Değiştirme
Yer değiştirme satır işleminde matrisin iki satırı aralarında yer değiştirir.
Bir matrisin \( i \). ve \( j \). satırları arasındaki yer değiştirme işlemi aşağıdaki şekilde gösterilir.
\( i \ne j \) olmak üzere,
\( R_i \leftrightarrow R_j \)
Aşağıdaki şekilde matrisin birinci ve üçüncü satırları arasındaki yer değiştirme işlemi gösterilmiştir.
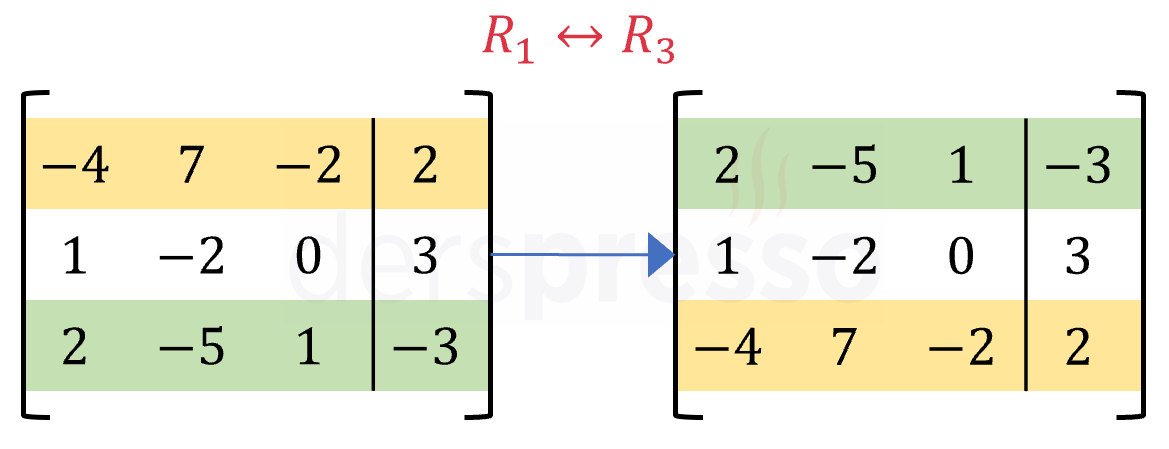
Yer değiştirme işleminin tersi kendisidir. Buna göre bir yer değiştirme işlemi ve tersi bir matrise arka arkaya uygulandığında matris ilk haline gelir.
\( R_i \leftrightarrow R_j \) işleminin tersi:
\( R_j \leftrightarrow R_i \)
Skaler Çarpma
Çarpma satır işleminde matrisin bir satırının her elemanı sıfırdan farklı bir reel sayı ile çarpılır.
Bir matrisin \( i \). satırının \( k \) sayısı ile çarpma işlemi aşağıdaki şekilde gösterilir.
\( k \in \mathbb{R}, \quad k \ne 0 \) olmak üzere,
\( kR_i \rightarrow R_i \)
Aşağıdaki şekilde matrisin ikinci satırına uygulanan 3 ile çarpma işlemi gösterilmiştir.
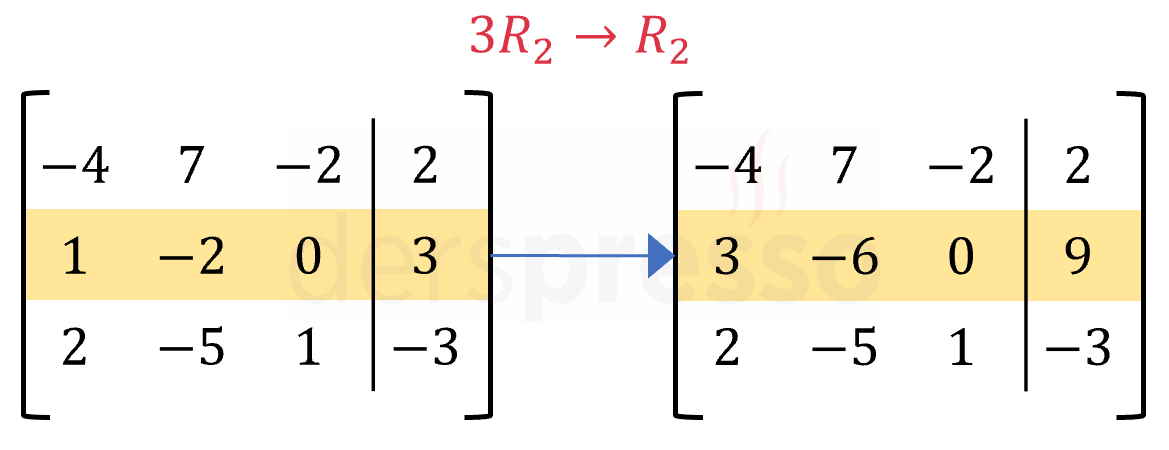
Skaler çarpma işleminin tersi skalerin çarpmaya göre tersi ile çarpma işlemidir. Buna göre bir skaler çarpma işlemi ve tersi bir matrise arka arkaya uygulandığında matris ilk haline gelir.
\( kR_i \rightarrow R_i \) işleminin tersi:
\( \dfrac{1}{k}R_i \rightarrow R_i \)
Toplama
Toplama satır işleminde matrisin bir satırının her elemanının belirli bir katı alınır ve ikinci bir satır ile toplanır. Bu işlemde sonuç ikinci satıra yazılır, birinci satır orijinal haliyle kalır.
Bir matrisin \( i \). satırının \( k \) katını \( j \). satırla toplama işlemi aşağıdaki şekilde gösterilir.
\( k \in \mathbb{R}, \quad i \ne j \) olmak üzere,
\( kR_i + R_j \rightarrow R_j \)
Aşağıdaki şekilde matrisin ikinci satırının -2 katının üçüncü satırla toplama işlemi gösterilmiştir.
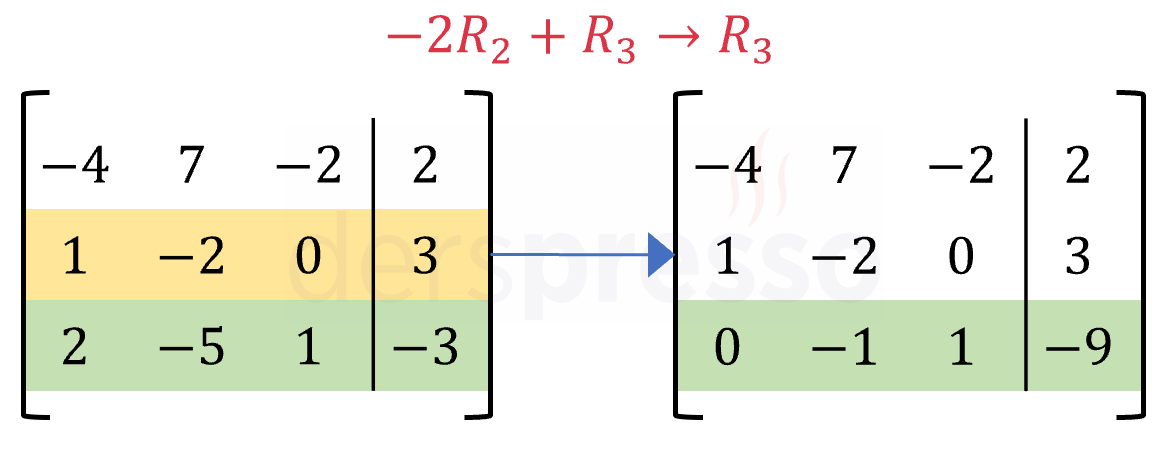
Toplama işleminin tersi \( i \). satırın \( -k \) katını \( j \). satırla toplama işlemidir. Buna göre bir toplama işlemi ve tersi bir matrise arka arkaya uygulandığında matris ilk haline gelir.
\( kR_i + R_j \rightarrow R_j \) işleminin tersi:
\( -kR_i + R_j \rightarrow R_j \)
Temel satır işlemleri bir matrise tekrarlı şekilde uygulanabilir. Bir \( A \) matrisine herhangi bir sayıda ve sırada uygulanan temel satır işlemleri sonucunda \( B \) matrisi elde ediliyorsa \( A \) ve \( B \) matrisleri satırca denk matrislerdir.
Satırca denk matrislerin karşılık geldikleri lineer denklem sistemlerinin çözüm kümeleri aynıdır. Bir diğer ifadeyle, bir denklem sistemine uygulanan temel satır işlemleri sistemin çözüm kümesini değiştirmez.
Temel satır işlemleri geri alınabilir işlemlerdir. Bir \( B \) matrisi satır işlemleri ile \( A \) matrisinden türetilebiliyorsa \( A \) matrisi de yukarıda her işlem için belirtilen ters işlemlerle \( B \) matrisinden türetilebilir.