Determinant Hesaplama
Bir matrisinin determinantını hesaplamak oldukça fazla işlem gerektirebilir.
- \( 3 \times 3 \) ve daha küçük boyutlu matrislerin determinantı, aşağıda bahsedeceğimiz yöntemlerle hesaplanabilir.
- Belirli koşulları sağlayan matrislerin determinantı determinant özellikleri kullanılarak hesaplanabilir.
- Kofaktör açılımı:
- Satır işlemleri: Bu yöntem ilk iki yöntemin kullanılamadığı durumlarda en hızlı çözümü sunar.
- Permütasyon: Bu yöntem işlem yoğunluğu açısından pratik olmasa da determinant özelliklerinin anlaşılmasında faydalı bir içgörü sağlar.
\( 3 \times 3 \) ve daha küçük boyutlu matrislerin determinantı aşağıdaki hatırlaması kolay formül ve yöntemler kullanılarak hesaplanabilir.
\( 1 \times 1 \) Matrisin Determinantı
\( 1 \times 1 \) bir matrisin determinantı matrisin tek elemanına eşittir.
\( A = \begin{bmatrix} a \end{bmatrix} \) olmak üzere,
\( det(A) = a \)
\( A = \begin{bmatrix} 3 \end{bmatrix} \) olmak üzere,
\( det(A) = 3 \)
\( 2 \times 2 \) Matrisin Determinantı
\( 2 \times 2 \) bir matrisin determinantı, aşağıdaki şekildeki yeşil ok üzerindeki iki elemanın çarpımı ile kırmızı ok üzerindeki iki elemanın çarpımının farkına eşittir.

\( det(A) = ad - cb \)
\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) olmak üzere,
\( det(A) = 1 \cdot 4 - 3 \cdot 2 = -2 \)
\( 3 \times 3 \) Matrisin Determinantı
Sarrus kuralı olarak bilinen yönteme göre, \( 3 \times 3 \) bir matrisin determinantını bulmak için önce ilk iki sütundaki elemanlar matrisin sağına \( 3 \times 5 \) bir matris oluşturacak şekilde kopyalanır. Matrisin determinantı, aşağıdaki şekildeki yeşil oklar üzerindeki elemanların çarpımlarının toplamı ile kırmızı oklar üzerindeki elemanların çarpımlarının toplamının farkına eşittir.
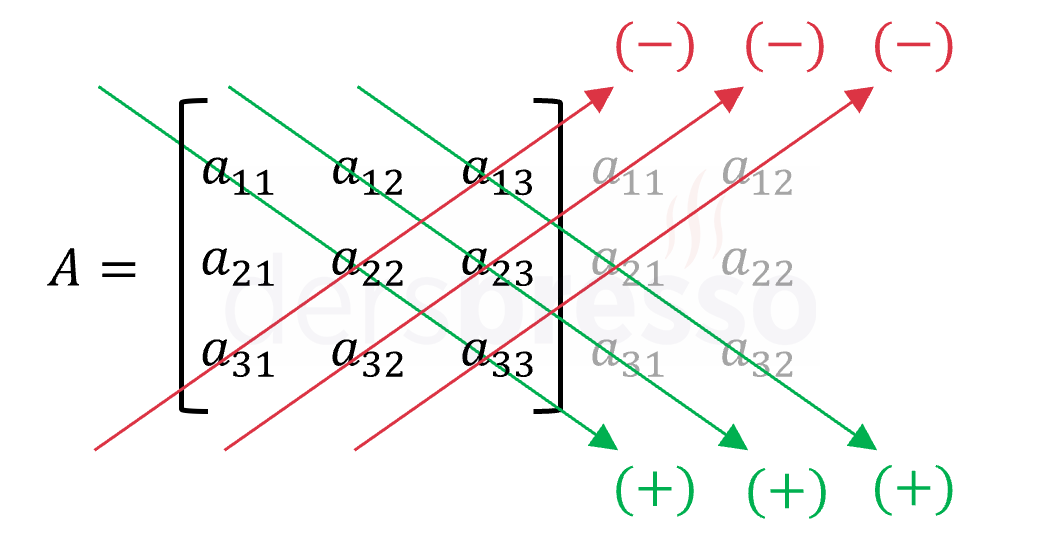
\( det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - (a_{31}a_{22}a_{13} + a_{32}a_{23}a_{11} + a_{33}a_{21}a_{12}) \)
\( A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \) olmak üzere,
\( det(A) = 1 \cdot 5 \cdot 9 + 2 \cdot 6 \cdot 7 + 3 \cdot 4 \cdot 8 - (7 \cdot 5 \cdot 3 + 8 \cdot 6 \cdot 1 + 9 \cdot 4 \cdot 2) \)
\( = 45 + 84 + 96 - 105 - 48 - 72 \)
\( = 0 \)
Sarrus kuralının sadece \( 3 \times 3 \) matrisler için geçerli olduğu unutulmamalıdır.
Aşağıdaki matrislerin determinantını bulunuz.
(a) \( A = \begin{bmatrix} 2 & -3 \\ 1 & -4 \end{bmatrix} \)
(b) \( B = \begin{bmatrix} 10 & 5 \\ 7 & 2 \end{bmatrix} \)
(c) \( C = \begin{bmatrix} -5 & 1 \\ 21 & -5 \end{bmatrix} \)
Çözümü Göster\( 2 \times 2 \) matris determinant formülünü kullanalım.
(a) seçeneği:
\( A = \begin{bmatrix} 2 & -3 \\ 1 & -4 \end{bmatrix} \)
\( det(A) = 2 \cdot (-4) - 1 \cdot (-3) = -5 \)
(b) seçeneği:
\( B = \begin{bmatrix} 10 & 5 \\ 7 & 2 \end{bmatrix} \)
\( det(B) = 10 \cdot 2 - 7 \cdot 5 = -15 \)
(c) seçeneği:
\( C = \begin{bmatrix} -5 & 1 \\ 21 & -5 \end{bmatrix} \)
\( det(C) = (-5) \cdot (-5) - 21 \cdot 1 = 4 \)
Aşağıdaki matrislerin determinantını bulunuz.
(a) \( A = \begin{bmatrix} 7 & 0 & 5 \\ -9 & 10 & 1 \\ 2 & -4 & 0 \end{bmatrix} \)
(b) \( B = \begin{bmatrix} 9 & 4 & 2 \\ 8 & -3 & 5 \\ 0 & 6 & 1 \end{bmatrix} \)
(c) \( C = \begin{bmatrix} -6 & 7 & 5 \\ -2 & 5 & 2 \\ 7 & 8 & -10 \end{bmatrix} \)
Çözümü Göster\( 3 \times 3 \) matris determinant formülünü (Sarrus kuralını) kullanalım.
(a) seçeneği:
\( A = \begin{bmatrix} 7 & 0 & 5 \\ -9 & 10 & 1 \\ 2 & -4 & 0 \end{bmatrix} \)
\( det(A) = 7 \cdot 10 \cdot 0 + 0 \cdot 1 \cdot 2 + 5 \cdot (-9) \cdot (-4) - (2 \cdot 10 \cdot 5 + (-4) \cdot 1 \cdot 7 + 0 \cdot (-9) \cdot 0) \)
\( = 0 + 0 + 180 - 100 + 28 - 0 \)
\( = 108 \)
(b) seçeneği:
\( B = \begin{bmatrix} 9 & 4 & 2 \\ 8 & -3 & 5 \\ 0 & 6 & 1 \end{bmatrix} \)
\( det(B) = 9 \cdot (-3) \cdot 1 + 4 \cdot 5 \cdot 0 + 2 \cdot 8 \cdot 6 - (0 \cdot (-3) \cdot 2 + 6 \cdot 5 \cdot 9 + 1 \cdot 8 \cdot 4) \)
\( = -27 + 0 + 96 - 0 - 270 - 32 \)
\( = -233 \)
(c) seçeneği:
\( C = \begin{bmatrix} -6 & 7 & 5 \\ -2 & 5 & 2 \\ 7 & 8 & -10 \end{bmatrix} \)
\( det(C) = (-6) \cdot 5 \cdot (-10) + 7 \cdot 2 \cdot 7 + 5 \cdot (-2) \cdot 8 - (7 \cdot 5 \cdot 5 + 8 \cdot 2 \cdot (-6) + (-10) \cdot (-2) \cdot 7) \)
\( = 300 + 98 - 80 - 175 + 96 - 140 \)
\( = 99 \)