10'un Kuvvetleri İle Gösterim
10'un kuvvetleri ile gösterim, çok büyük ve çok küçük sayıların ifadesini, okunabilirliğini, karşılaştırmasını ve bu sayılar arasındaki işlemleri kolaylaştırmak için kullanılan bir gösterimdir.
Aşağıdaki örneklerde çok büyük ve çok küçük bazı sayıların 10'un kuvvetleri ile gösterimi verilmiştir.
| Büyüklük | 10'un Kuvvetleri İle Gösterim | Sayı |
|---|---|---|
| Standart atmosfer basıncı | \( 1,013 \times 10^5 \) Pa | \( 101.325 \) Pa |
| Işığın bir yılda katettiği mesafe | \( 9,46 \times 10^{12} \) km | \( 9.460.000.000.000 \) km |
| Hidrojen atomunun yarıçapı | \( 5,3 \times 10^{-8} \) mm | \( 0,000000053 \) mm |
| Avogadro sayısı | \( 6,02214 \times 10^{23} \) g/mol | |
| Kütleçekim sabiti | \( 6,674 \times 10^{-11} \) Newton \( \cdot \) m\( ^2 \cdot \) kg\( ^2 \) |
Bu gösterim, katsayı ve 10'un kuvveti olmak üzere iki kısımdan oluşur.
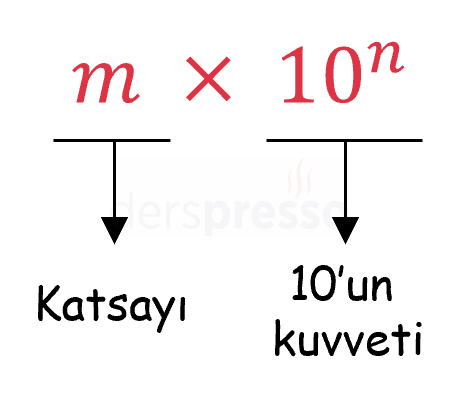
Bir sayıyı 10'un artan kuvvetleri şeklinde yazmak için sayının katsayısında ve kuvvetinde aşağıdaki değişiklikler yapılır.
- Sayının katsayısı 10'a bölünür, yani katsayının virgülü bir basamak sola kaydırılır. Katsayıda virgül yoksa (sayı tam sayı ise) katsayının birler ve onlar basamakları arasına bir virgül konur.
- Sayının 10'un kuvveti kısmı 10'la çarpılır, yani 10'un kuvveti bir artırılır.
- Sayının bu iki kısmı sırayla 10'a bölünüp 10'la çarpıldığı için sayının değeri değişmemiş olur.
Bir sayıyı 10'un azalan kuvvetleri şeklinde yazmak için sayının katsayısında ve kuvvetinde aşağıdaki değişiklikler yapılır.
- Sayının katsayısı 10'la çarpılır, yani katsayının virgülü bir basamak sağa kaydırılır. Katsayıda virgül yoksa (sayı tam sayı ise) katsayının sonuna bir sıfır eklenir.
- Sayının 10'un kuvveti kısmı 10'a bölünür, yani 10'un kuvveti bir eksiltilir.
- Sayının bu iki kısmı sırayla 10'la çarpılıp 10'a bölündüğü için sayının değeri değişmemiş olur.
1.234 sayısının 10'un farklı kuvvetleri ile gösterimleri aşağıda verilmiştir. Bu sayıların tümü 1.234'e eşit olup sadece sayının farklı gösterimleridir.

Dikkat edilirse, tabloda yukarıya doğru çıktıkça 10'un kuvveti 1 artarken katsayıda virgül bir basamak sola kayar. Benzer şekilde, tabloda aşağıya doğru indikçe 10'un kuvveti 1 azalırken katsayıda virgül bir basamak sağa kayar. Herhangi iki satır arasında katsayı ve 10'un kuvveti kısımları 10'un aynı kuvveti ile çarpılıp bölündüğü için sayının değerinde bir değişiklik olmaz.
İkinci bir örnek olarak, \( 328,71 \times 10^6 \) sayısının 10'un farklı kuvvetleri ile gösterimleri rakamlar hizalanmış şekilde aşağıda gösterilmiştir.

10'un ortak bir kuvvetindeki sayılardan katsayısı büyük olan sayı daha büyüktür. Buna göre 10'un farklı kuvvetlerindeki sayıları karşılaştırmak için sayılar önce ortak bir kuvvete getirilmelidir.
\( a = 0,00411 \times 10^9 \)
\( b = 9,99 \times 10^5 \)
\( c = 3,25 \times 10^7 \)
sayılarını küçükten büyüğe doğru sıralayalım.
Tüm sayılarda 10'un kuvveti kısmını \( 10^5 \) yapalım.
\( a = 41,1 \times 10^5 \)
\( b = 9,99 \times 10^5 \)
\( c = 325 \times 10^5 \)
10'un ortak bir kuvvetindeki sayılardan katsayısı büyük olan sayı daha büyüktür.
\( 9,99 \times 10^5 \lt 41,1 \times 10^5 \lt 325 \times 10^5 \)
\( b \lt a \lt c \)
Farklı ülkelerde binlik ve ondalık ayracı olarak farklı semboller kullanılır. Örneğin Türkiye ve çoğu Avrupa ülkesinde binlik ayracı olarak "." ve ondalık ayracı olarak "," kullanılırken, Amerika ve İngiltere'de binlik ayracı olarak "," ve ondalık ayracı olarak "." kullanılır. Bazı ülkelerde binlik ayracı olarak boşluk da kullanılır.
Aşağıdaki eşitliklerden hangileri doğrudur?
I. \( 2345000000 = 2,345 \times 10^9 \)
II. \( 691 \times 10^{-8} = 6,91 \times 10^{-10} \)
III. \( 0,0029 \times 10^{-1} = 2,9 \times 10^{-4} \)
IV. \( 25,36 \times 10^{-10} = 2536000 \times 10^{-15} \)
Çözümü GösterI. öncül:
\( 2345000000 = 2345 \times 10^6 \)
Katsayı kısmını \( 1000 = 10^3 \) sayısına bölüp 10'un kuvveti kısmını aynı sayı ile çarpalım.
\( = 2,345 \times 10^9 \)
I. öncül doğrudur.
II. öncül:
\( 691 \times 10^{-8} \)
Katsayı kısmını \( 100 = 10^2 \) sayısına bölüp 10'un kuvveti kısmını aynı sayı ile çarpalım.
\( = 6,91 \times 10^{-6} \ne 6,91 \times 10^{-10} \)
II. öncül yanlıştır.
III. öncül:
\( 0,0029 \times 10^{-1} \)
Katsayı kısmını \( 1000 = 10^3 \) ile çarpıp 10'un kuvveti kısmını aynı sayıya bölelim.
\( = 2,9 \times 10^{-4} \)
III. öncül doğrudur.
IV. öncül:
\( 25,36 \times 10^{-10} \)
Katsayı kısmını \( 100000 = 10^5 \) ile çarpıp 10'un kuvveti kısmını aynı sayıya bölelim.
\( = 2536000 \times 10^{-15} \)
IV. öncül doğrudur.
Buna göre I., II. ve IV. öncüller doğrudur.
\( (2^{110})^5 \cdot (5^{275})^2 \) sayısı kaç basamaklıdır?
Çözümü GösterSayıyı 10'un kuvveti biçiminde yazalım.
\( (2^{110})^5 \cdot (5^{275})^2 = 2^{550} \cdot 5^{550} \)
\( = (2 \cdot 5)^{550} \)
\( = 10^{550} \)
10'un kuvveti biçiminde yazılan bir üslü sayının basamak sayısı, 10'un kuvveti kısmındaki üs değerinin bir fazlasına eşittir.
Buna göre, verilen sayı \( 550 + 1 = 551 \) basamaklıdır.
Aşağıdaki sayıları küçükten büyüğe doğru sıralayın.
\( a = 1,0047 \times 10^{10} \)
\( b = 81840 \times 10^5 \)
\( c = 0,12 \times 10^{11} \)
Çözümü GösterTüm sayılarda 10'un kuvveti kısmını \( 10^8 \) yapalım.
\( a = 1,0047 \times 10^{10} = 100,47 \times 10^8 \)
\( b = 81840 \times 10^5 = 81,84 \times 10^8 \)
\( c = 0,12 \times 10^{11} = 120 \times 10^8 \)
10'un ortak bir kuvvetindeki sayılardan katsayısı büyük olan sayı daha büyüktür.
\( b \lt a \lt c \)
Aşağıdaki ifadeleri 10'un kuvvetleri şeklinde yazınız.
(a) \( \dfrac{2^4 + 2^4 + 2^4 + 2^4 + 2^4 + 2^4}{5^{-5}} \)
(b) \( \dfrac{256 \cdot 25^3}{800} \)
(c) \( \dfrac{500 \cdot 4^{33}}{8^{21}} \)
Çözümü Göster(a) seçeneği:
\( \dfrac{2^4 + 2^4 + 2^4 + 2^4 + 2^4 + 2^4}{5^{-5}} \)
\( = \dfrac{6 \cdot 2^4}{5^{-5}} \)
\( = 2 \cdot 3 \cdot 2^4 \cdot 5^5 \)
\( = 3 \cdot 2^5 \cdot 5^5 \)
2 ve 5 tabanındaki ifadeleri 10 tabanında birleştirelim.
\( = 3 \cdot (2 \cdot 5)^5 \)
\( = 3 \times 10^5 \)
(b) seçeneği:
\( \dfrac{256 \cdot 25^3}{800} \)
Tüm sayıları asal çarpanlarına ayıralım.
\( = \dfrac{2^8 \cdot (5^2)^3}{2^5 \cdot 5^2} \)
\( = \dfrac{2^8 \cdot 5^6}{2^5 \cdot 5^2} \)
\( = 2^{8 - 5} \cdot 5^{6 - 2} \)
\( = 2^3 \cdot 5^4 \)
2 ve 5 tabanındaki ifadeleri 10 tabanında birleştirelim.
\( = 5 \cdot (2 \cdot 5)^3 \)
\( = 5 \times 10^3 \)
(c) seçeneği:
\( \dfrac{500 \cdot 4^{33}}{8^{21}} \)
Tüm sayıları asal çarpanlarına ayıralım.
\( = \dfrac{2^2 \cdot 5^3 \cdot (2^2)^{33}}{(2^3)^{21}} \)
\( = \dfrac{2^2 \cdot 5^3 \cdot 2^{66}}{2^{63}} \)
\( = 5^3 \cdot 2^{66 + 2 - 63} \)
\( = 5^3 \cdot 2^5 \)
\( = 2^2 \cdot 5^3 \cdot 2^3 \)
2 ve 5 tabanındaki ifadeleri 10 tabanında birleştirelim.
\( = 4 \cdot (5 \cdot 2)^3 \)
\( = 4 \times 10^3 \)
Ahmet \( 3,6 \times 10^3 \) saniyelik bir videonun dörtte birini izlediğine göre, videonun bitmesine kaç dakika kalmıştır?
Çözümü Göster\( 3,6 \times 10^3 \) saniyenin dörtte birini bulalım.
\( 3,6 \times 10^3 \cdot \dfrac{1}{4} = 36 \times 10^2 \cdot \dfrac{1}{4} \)
\( = 9 \times 10^2 \) saniye
Videonun tüm süresinden izlenen kısmı çıkarak kalan süreyi bulalım.
\( 3,6 \times 10^3 - 9 \times 10^2 \)
\( = 36 \times 10^2 - 9 \times 10^2 \)
\( = 27 \times 10^2 \) saniye
Videonun saniye cinsinden kalan süresini dakikaya çevirelim.
\( \dfrac{27 \times 10^2}{60} = \dfrac{27 \times 10}{6} \)
\( = 45 \) dakika bulunur.
Aşağıdaki sayılardan hangileri \( 5^{-4} \) sayısına eşittir?
I. \( 1,6 \times 10^{-3} \)
II. \( 160000 \times 10^{-9} \)
III. \( 0,0016 \)
Çözümü GösterVerilen sayıyı 10'un kuvvetleri şeklinde yazalım.
\( 5^{-4} = \dfrac{1}{5^4} \)
\( = \dfrac{10^4 \cdot 10^{-4}}{5^4} \)
\( = 2^4 \times 10^{-4} \)
\( = 16 \times 10^{-4} \)
Öncülleri \( 16 \times 10^n \) formunda yazalım.
I. öncül:
\( 1,6 \times 10^{-3} \)
Katsayı kısmını \( 10 = 10^1 \) ile çarpıp 10'un kuvveti kısmını aynı sayıya bölelim.
\( = 16 \times 10^{-4} \)
I. öncül verilen sayıya eşittir.
II. öncül:
\( 160000 \times 10^{-9} \)
Katsayı kısmını \( 10000 = 10^4 \) sayısına bölüp 10'un kuvveti kısmını aynı sayı ile çarpalım.
\( = 16 \times 10^{-5} \ne 16 \times 10^{-4} \)
II. öncül verilen sayıya eşit değildir.
III. öncül:
\( 0,0016 = 0,0016 \times 10^0 \)
Katsayı kısmını \( 10000 = 10^4 \) ile çarpıp 10'un kuvveti kısmını aynı sayıya bölelim.
\( = 16 \times 10^{-4} \)
III. öncül verilen sayıya eşittir.
Buna göre I. ve III. öncüller verilen sayıya eşittir.
\( 20^{1944} \) sayısının sağdan sıfır olmayan ilk basamağı kaçtır?
Çözümü GösterVerilen sayıyı 10'un kuvveti şeklinde yazalım.
\( 20^{1944} = (2 \cdot 10)^{1944} = 2^{1944} \cdot 10^{1944} \)
\( 10^{1944} \) sayısının ilk basamağı hariç tüm basamakları 0 olduğu için başka bir sayı ile çarpıldığında sayının sonuna üssü kadar 0 eklenir.
Bu nedenle \( 2^{1944} \) ve \( 20^{1944} \) sayıları en sondaki 0 basamakları hariç aynıdır.
2'nin tam sayı üslerinin son basamakları her 4 sayıda bir kendini tekrar eder.
\( 2^1 = 2, \quad 2^2 = 4, \quad 2^3 = 8, \quad 2^4 = 16 \)
\( 2^5 = 32, \quad 2^6 = 64, \quad 2^7 = 128, \quad 2^8 = 256 \)
1944 sayısı 4'ün tam katı olduğu için \( 2^{1944} \) sayısı 6 ile biter.
\( 2^{1944} = (\ldots 6) \)
Buna göre \( 20^{1944} \) sayısının sağdan sıfır olmayan ilk basamağı 6 olur.
\( 10^{55} - 99 \) işleminin sonucunun rakamları toplamı kaçtır?
Çözümü Göster\( 10 \)'un farklı kuvvetleri için sonucu bulalım.
\( 10^2 - 99 = 100 - 99 = 1 \)
\( 10^3 - 99 = 1000 - 99 = 901 \)
\( 10^4 - 99 = 10000 - 99 = 9901 \)
\( 10^5 - 99 = 100000 - 99 = 99901 \)
Buna göre, sonucun son iki basamağı her zaman "01" olur ve sayının başında 10'un kuvvetinin iki eksiği kadar 9 bulunur.
\( 10^{55} - 99 = \underbrace{999\ldots9}_\text{53 adet}01 \)
Sonucun rakamlarının toplamını bulalım.
\( 53 \cdot 9 + 1 = 478 \) bulunur.