İkinci Türden Stirling Sayıları
İkinci türden Stirling sayıları, \( n \) elemanlı bir kümenin elemanlarının boş olmayan \( k \) alt kümeye parçalanış sayısını hesaplar. \( n \) elemanlı bir kümenin \( k \) alt kümeye parçalanışı için Stirling sayısı \( S(n, k) \) ya da \( \genfrac\{\}{0pt}{}{n}{k} \) şeklinde gösterilir.
Örnek olarak 4 elemanlı \( A = \{ a, b, c, d \} \) kümesinin 2 alt kümeye parçalanışları aşağıdaki \( S(4, 2) = 7 \) farklı şekilde olabilir.
3 + 1 şeklindeki parçalanışlar:
\( \{ \{a, b, c\}, \{d\} \} \)
\( \{ \{a, b, d\}, \{c\} \} \)
\( \{ \{a, c, d\}, \{b\} \} \)
\( \{ \{b, c, d\}, \{a\} \} \)
2 + 2 şeklindeki parçalanışlar:
\( \{ \{a, b\}, \{c, d\} \} \)
\( \{ \{a, c\}, \{b, d\} \} \)
\( \{ \{a, d\}, \{b, c\} \} \)
Bu \( S(4, 2) = 7 \) parçalanış görsel olarak aşağıda gösterilmiştir.

Aynı kümenin 3 alt kümeye parçalanışları aşağıdaki \( S(4, 3) = 6 \) farklı şekilde olabilir.
2 + 1 + 1 şeklindeki gruplar:
\( \{ \{a, b\}, \{c\}, \{d\} \} \)
\( \{ \{a, c\}, \{b\}, \{d\} \} \)
\( \{ \{a, d\}, \{b\}, \{c\} \} \)
\( \{ \{b, c\}, \{a\}, \{d\} \} \)
\( \{ \{b, d\}, \{a\}, \{c\} \} \)
\( \{ \{c, d\}, \{a\}, \{b\} \} \)
Bu \( S(4, 3) = 6 \) parçalanış görsel olarak aşağıda gösterilmiştir.

Aynı kümenin 1 alt kümeye parçalanışları aşağıdaki \( S(4, 1) = 1 \) şekilde olabilir.
\( \{ \{a, b, c, d\} \} \)
Aynı kümenin 4 alt kümeye parçalanışları aşağıdaki \( S(4, 4) = 1 \) şekilde olabilir.
\( \{ \{a\}, \{b\}, \{c\}, \{d\} \} \)
Dikkat edilirse önceki bölümde gördüğümüz kümelerin parçalanışı bir kümenin elemanlarının \( 1 \) ve \( n \) arasında herhangi bir sayıda alt kümeye parçalanışını hesaplarken, ikinci türden Stirling sayıları sadece \( k \) sayıda alt kümeye parçalanış sayısını hesaplamaktadır. Bu açıdan baktığımızda, bir kümenin elemanlarının tüm parçalanış sayısını hesaplayan Bell sayıları (\( B_n \)) ile ikinci türden Stirling sayıları (\( S(n, k) \)) arasında aşağıdaki ilişki vardır.
\( B_n = \displaystyle\sum_{i = 1}^{n} {S(n, i)} \)
\( B_n = S(n, 1) + S(n, 2) + \ldots + S(n, n) \)
Yukarıdaki 4 elemanlı küme örneği için:
\( B_4 = S(4, 1) + S(4, 2) + S(4, 3) + S(4, 4) \)
\( B_4 = 15 \) olduğunu önceki bölümde görmüştük.
\( 15 = 1 + 7 + 6 + 1 \)
İkinci Türden Stirling Sayılarının Hesaplaması
İkinci türden Stirling sayıları aşağıdaki formülle hesaplanabilir.
\( S(n, k) = \dfrac{1}{k!}\ \displaystyle\sum_{i = 0}^{k} {(-1)^i \binom{k}{i}(k - i)^n} \)
\( n \): Kümenin eleman sayısı
\( k \): Parçalanıştaki alt küme sayısı
\( S(4, 2) = \dfrac{1}{2!}\ ((-1)^0 \binom{2}{0}(2 - 0)^4 + (-1)^1 \binom{2}{1}(2 - 1)^4 + (-1)^2 \binom{2}{2}(2 - 2)^4) \)
\( = \dfrac{1}{2}\ (16 - 2 + 0) = 7 \)
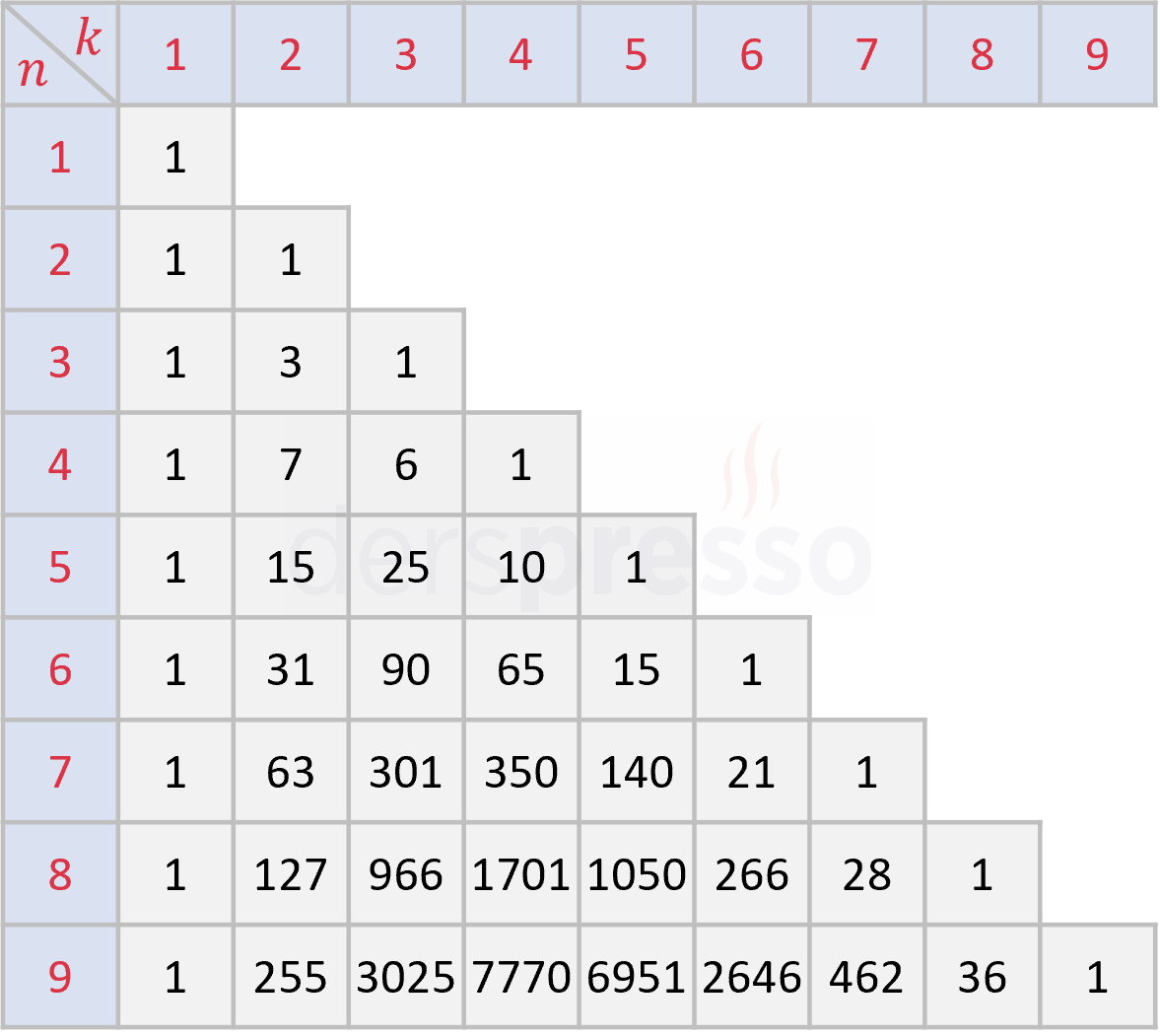
\( n \) ve \( k \)'nın 1 - 9 arası değerleri için ikinci türden Stirling sayıları aşağıdaki tabloda verilmiştir.
İkinci türden Stirling sayıları özyinelemeli bir şekilde aşağıdaki formül ile de hesaplanabilir.
\( S(n, k) = S(n - 1, k - 1) + k\ S(n - 1, k) \)
\( S(0, 0) = 1 \)
\( S(n, 0) = S(0, n) = 0 \)
\( S(5, 3) = S(4, 2) + 3\ S(4, 3) = 7 + 3 \cdot 6 = 25 \)
\( S(8, 6) = S(7, 5) + 6\ S(7, 6) = 140 + 6 \cdot 21 = 266 \)
İSPATI GÖSTER
\( n \) elemanlı \( \{ a_1, a_2, \ldots, a_n \} \) kümesinin elemanlarının \( k \) alt kümeye dağılımı iki farklı şekilde gerçekleşebilir.
1. durum: Sonuncu \( a_n \) elemanı tek başına bir alt kümede
Bu durumda diğer \( n - 1 \) eleman \( k - 1 \) alt kümeye \( S(n - 1, k - 1) \) farklı şekilde dağıtılabilir ve \( a_n \) elemanı \( k. \) alt kümeye tek eleman olarak 1 farklı şekilde konabilir. Buna göre bu durumda oluşan toplam dağıtım sayısı \( 1 \cdot S(n - 1, k - 1) = S(n - 1, k - 1) \) olur.
2. durum: Sonuncu \( a_n \) elemanı başka eleman(lar)la bir alt kümede
Bu durumda \( a_n \) elemanı dışarıda tutularak ilk \( n - 1 \) eleman \( k \) gruba \( S(n - 1, k) \) farklı şekilde dağıtılabilir. Sonrasında \( a_n \) elemanı bu \( k \) gruptan birine \( k \) farklı şekilde dağıtılabilir. Buna göre bu durumda oluşan toplam dağıtım sayısı \( k\ S(n - 1, k) \) olur.
Bu iki durum birbirinden ayrık olaylar olduğu için toplama yoluyla sayma ile dağıtım sayılarını toplayabiliriz.
\( S(n, k) = S(n - 1, k - 1) + k\ S(n - 1, k) \)
\( n \) veya \( k \)'nın sıfır olduğu durumlar için ikinci türden Stirling sayıları aşağıdaki gibidir.
\( S(0, 0) = 1 \)
\( n \ge 1 \) olmak üzere,
\( S(n, 0) = 0 \)
\( S(0, n) = 0 \)
\( n \ge 1 \) olmak üzere, \( n \) elemanlı bir kümenin 1 alt kümeye parçalanışı 1 şekilde olabilir.
\( n \ge 1 \) olmak üzere,
\( S(n, 1) = 1 \)
\( A = \{ a_1, a_2, \ldots, a_n \} \) kümesinin 1 alt kümeye parçalanışı:
\( \{ \{a_1, a_2, \ldots, a_n\} \} \)
Boş küme dahil \( n \) elemanlı bir kümenin \( n \) alt kümeye parçalanışı 1 şekilde olabilir.
\( S(n, n) = 1 \)
\( A = \{ a_1, a_2, \ldots, a_n \} \) kümesinin \( n \) alt kümeye parçalanışı:
\( \{ \{a_1\}, \{a_2\}, \ldots, \{a_n\} \} \)
\( n \) elemanlı bir kümenin 2 alt kümeye parçalanış sayısı aşağıdaki formülle hesaplanabilir.
\( S(n, 2) = 2^{n - 1} - 1 \)
\( S(7, 2) = 2^{7 - 1} - 1 = 63 \)
İSPATI GÖSTER
\( n \) elemanlı \( A = \{ a_1, a_2, \ldots, a_n \} \) kümesinin \( 2^n \) alt kümesinin herhangi birine \( A_1 \), bu kümenin tümleyenine de \( A_2 \) diyelim.
\( A = A_1 \cup A_2 \)
\( A_1 = \emptyset, A_2 = A \) olduğu ve \( A_2 = \emptyset, A_1 = A \) olduğu iki durumu hariç tutarsak, \( A_1 \) ve \( A_2 \) alt kümeleri \( A \) kümesinin 2 alt kümeli bir parçalanışı olur.
Buna göre, boş olmayan ve birleşimleri \( A \) kümesini veren \( 2^n - 2 \) farklı \( A_1 \) ve \( A_2 \) kümesi yazabiliriz.
Bu \( 2^n - 2 \) durumun her biri için \( A_1 \) ve \( A_2 \) kümesinin elemanlarının aralarında yer değiştirdiği bir durum vardır. Parçalanışlarda alt kümelerin sırası önemli olmadığı için bu durum ikilileri aynı parçalanışa karşılık gelir, dolayısıyla 2 alt kümeli parçalanış sayısı bu sayının yarısına, yani \( \dfrac{2^n - 2}{2} = 2^{n - 1} - 1 \)'e eşittir.
\( n \) elemanlı bir kümenin 3 alt kümeye parçalanış sayısı aşağıdaki formülle hesaplanabilir.
\( S(n, 3) = \frac{1}{2}(3^{n - 1} + 1) - 2^{n - 1} \)
\( S(7, 3) = \frac{1}{2}(3^{7 - 1} + 1) - 2^{7 - 1} \)
\( = 365 - 64 = 301 \)
\( n \) elemanlı bir kümenin \( n - 1 \) alt kümeye parçalanış sayısı aşağıdaki formülle hesaplanabilir.
\( S(n, n - 1) = \binom{n}{2} \)
\( S(8, 7) = \binom{8}{2} = \dfrac{8!}{2!\ 6!} = 28 \)
İSPATI GÖSTER
\( n \) elemanlı \( \{ a_1, a_2, \ldots, a_n \} \) kümesinin elemanlarının \( n - 1 \) alt kümeye parçalanışları 1 tane iki elemanlı, \( n - 2 \) tane bir elemanlı alt kümeden oluşur.
Bu şekilde örnek bir parçalanış aşağıdaki gibidir.
\( \{ \{a_1, a_2\}, \{a_3\}, \ldots, \{a_n\} \} \)
Buna göre, \( n \) elemanlı bir kümenin elemanları içinden 2 elemanın farklı seçim sayısı kadar \( n - 1 \) alt kümeye parçalanış bulunur.
\( S(n, n - 1) = \binom{n}{2} \)
\( n \) elemanlı bir kümenin \( n - 2 \) alt kümeye parçalanış sayısı aşağıdaki formülle hesaplanabilir.
\( S(n, n - 2) = \binom{n}{3} + 3\binom{n}{4}\)
\( S(8, 6) = \binom{8}{3} + 3\binom{8}{4} \)
\( = \dfrac{8!}{3!\ 5!} + 3\dfrac{8!}{4!\ 4!} = 56 + 210 = 266 \)
Örten Fonksiyon Sayısı
İkinci türden Stirling sayılarını kullanarak iki küme arasında tanımlanabilecek örten fonksiyon sayısını aşağıdaki formülle hesaplayabiliriz.
\( f: A \to B \)
\( s(A) = n, \quad s(B) = k \) olmak üzere,
Örten fonksiyon sayısı \( = k! \cdot S(n, k) \)
İSPATI GÖSTER
İkinci türden Stirling sayıları tanımı gereği, \( n \) elemanlı \( A \) kümesinin elemanları hiçbiri boş küme olmamak üzere \( k \) alt kümeye \( S(n, k) \) farklı şekilde parçalanabilir.
Bu \( k \) parça \( B \) kümesinin \( k \) elemanı ile (bu parçalar \( B \) kümesinin elemanlarını "örtecek" şekilde) \( k! \) farklı şekilde eşleştirilebilir.
Buna göre \( A \) kümesinden \( B \) kümesine bu iki sayının çarpımı kadar örten fonksiyon tanımlanabilir.
Örten fonksiyon sayısı \( = k! \cdot S(n, k) \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ a, b, c, d \} \)
olmak üzere, \( A \) kümesinden \( B \) kümesine kaç farklı örten fonksiyon tanımlanabilir?
Örten fonksiyon sayısı \( = k!\ S(n, k) \)
Yukarıdaki tabloya göre \( S(5, 4) = 10 \) olur.
Buna göre örten fonksiyon sayısı aşağıdaki gibi bulunur.
\( = 4!\ S(5, 4) = 4! \cdot 10 = 240 \)
Bu sonuç aynı örnek için dahil etme - hariç tutma prensibi ile hesapladığımız değerle aynıdır.
5 elemanlı \( A \) kümesinden 4 elemanlı \( B \) kümesine tanımlanabilecek fonksiyonlar içinde görüntü kümesi 1, 2, 3 ve 4 elemanlı olan fonksiyonların sayısı ayrı ayrı kaçtır?
Çözümü Göster4 elemanlı görüntü kümeleri:
Görüntü kümesi 4 elemanlı olan fonksiyonların sayısı bu iki küme arasında tanımlanabilecek örten fonksiyon sayısına eşittir.
Örten fonksiyon sayısı \( = k!\ S(n, k) \)
\( = 4!\ S(5, 4) = 24 \cdot 10 = 240 \)
3 elemanlı görüntü kümeleri:
Görüntü kümesi 3 elemanlı olan fonksiyonların sayısı, \( A \) kümesinden \( B \) kümesinin her bir 3 elemanlı alt kümesine tanımlanabilecek örten fonksiyon sayısına eşittir.
\( B \) kümesinin 3 elemanlı alt kümelerinin sayısı \( = C(4, 3) = 4 \)
Örten fonksiyon sayısı \( = k!\ S(n, k) \)
\( = 3!\ S(5, 3) = 6 \cdot 25 = 150 \)
Görüntü kümesi 3 elemanlı olan fonksiyonların sayısı \( = 4 \cdot 150 = 600 \)
2 elemanlı görüntü kümeleri:
Görüntü kümesi 2 elemanlı olan fonksiyonların sayısı, \( A \) kümesinden \( B \) kümesinin her bir 2 elemanlı alt kümesine tanımlanabilecek örten fonksiyon sayısına eşittir.
\( B \) kümesinin 2 elemanlı alt kümelerinin sayısı \( = C(4, 2) = 6 \)
Örten fonksiyon sayısı \( = k!\ S(n, k) \)
\( = 2!\ S(5, 2) = 2 \cdot 15 = 30 \)
Görüntü kümesi 2 elemanlı olan fonksiyonların sayısı \( = 6 \cdot 30 = 180 \)
1 elemanlı görüntü kümeleri:
Görüntü kümesi 1 elemanlı olan fonksiyonların sayısı, \( A \) kümesinden \( B \) kümesinin her bir 1 elemanlı alt kümesine tanımlanabilecek örten fonksiyon sayısına eşittir.
\( B \) kümesinin 1 elemanlı alt kümelerinin sayısı \( = C(4, 1) = 4 \)
Örten fonksiyon sayısı \( = k!\ S(n, k) \)
\( = 1!\ S(5, 1) = 1 \cdot 1 = 1 \)
Görüntü kümesi 1 elemanlı olan fonksiyonların sayısı \( = 4 \cdot 1 = 4 \)
Görüntü kümesinin farklı eleman sayıları için yukarıda hesapladığımız fonksiyon sayılarını topladığımızda, 5 elemanlı bir küme ile 4 elemanlı bir küme arasında tanımlanabilecek toplam fonksiyon sayısını elde ederiz.
\( 240 + 600 + 180 + 4 = 1024 = 4^5 \)