Düzensiz Dizilişler
Düzensiz diziliş (İngilizce: derangement) problemleri, bir kümenin belirli bir dizilişte olması beklenen elemanlarının hiçbirinin doğru pozisyonda bulunmadığı farklı diziliş sayısını hesaplar. Örnek vermek gerekirse, "54132" sayısı "12345" sayısının bir düzensiz dizilişidir, çünkü rakamların hiçbiri doğru pozisyonda değildir. "54312" sayısı ise "12345" sayısının bir düzensiz dizilişi değildir, çünkü diğer rakamlar farklı pozisyonlarda olsa da "3" rakamı doğru pozisyondadır.
\( n \) elemanlı bir küme ile oluşturulabilecek düzensiz diziliş sayısı \( D_n \) ya da \( !n \) ile gösterilir. \( !n \) ifadesine alt faktöriyel de denir.
\( n \) elemanlı bir küme ile oluşturulabilecek düzensiz diziliş sayısı aşağıdaki formülle hesaplanır.
\( n \) elemanlı bir kümenin düzensiz diziliş sayısı:
\( D_n = !n = n!\ \displaystyle\sum_{i = 0}^n \dfrac{(-1)^i}{i!} \)
\( = n!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \ldots + \dfrac{(-1)^n}{n!}) \)
\( D_3 = 3!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!}) \)
\( = 6\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6}) \)
\( = 6 \cdot \dfrac{2}{6} = 2 \)
Faktöriyel tanımı gereği boş küme için farklı diziliş sayısı \( 0! = 1 \) olur. Bu 1 diziliş "elemanın" doğru pozisyonda olduğu bir diziliş olmadığı için düzensiz bir diziliş olarak kabul edilir.
\( D_0 = 1 \)
1 elemanlı bir kümenin \( 1! = 1 \) farklı dizilişinde kümenin elemanı doğru pozisyonda olacağı için 1 elemanlı bir kümenin düzensiz dizilişi yoktur.
\( D_1 = 0 \)
Yukarıdaki formül özyinelemeli olarak aşağıdaki şekilde de yazılabilir.
\( n \ge 2 \) olmak üzere,
\( D_n = (n - 1)(D_{n - 1} + D_{n - 2}) \)
\( D_2 = (2 - 1)(D_1 + D_0) = 1 \)
\( D_3 = (3 - 1)(D_2 + D_1) = 2 \)
İSPATI GÖSTER
\( A \) ve \( B \) harflerini içeren \( n \) elemanlı bir küme için bu özyinelemeli formülü türetelim.
\( A \) elemanının düzensiz dizilişlerde orijinal pozisyonu dışında bulunabileceği \( n - 1 \) pozisyon vardır ve bu pozisyonların her biri için toplam diziliş sayısı eşit olmalıdır. \( A \) elemanının orijinal pozisyonunu 1. basamak olarak kabul ederek 2. basamakta bulunduğu düzensiz diziliş sayısını bulalım.
\( A \) elemanının 2. basamakta bulunduğu düzensiz dizilişleri iki gruba ayırabiliriz.
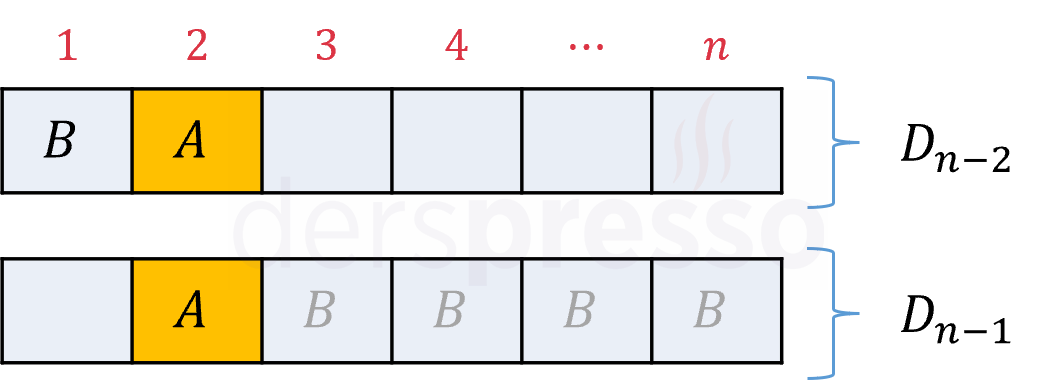
1. grupta (yukarıdaki şekildeki 1. satır) orijinal pozisyonu 2. basamak olan \( B \) elemanının \( A \) elemanının orijinal pozisyonu olan 1. basamakta bulunduğu dizilişler: Bu durumda \( A \) ve \( B \) dışındaki \( n - 2 \) elemanın \( 3. \) basamak ve sonrasındaki düzensiz diziliş sayısı \( D_{n - 2} \) olur.
2. grupta (yukarıdaki şekildeki 2. satır) \( B \) elemanının \( 3. \) basamak ve sonrasındaki pozisyonlardan birinde bulunduğu dizilişler: Bu durumda \( A \) hariç \( n - 1 \) elemanın \( 2. \) basamak dışındaki pozisyonlardaki düzensiz diziliş sayısı \( D_{n - 1} \) olur. \( B \) elemanının düzensiz dizilişleri \( 1. \) ve \( 2. \) basamaklar hariç diğer \( n - 2 \) basamak içinde, diğer \( n - 2 \) elemanın düzensiz dizilişleri de 2. basamak ve her elemanın kendi orijinal pozisyonu hariç \( n - 2 \) basamak içinde olur.
Buna göre \( A \) harfinin bir düzensiz dizilişte bulunabileceği \( n - 1 \) pozisyonun her birinde \( D_{n - 1} + D_{n - 2} \) düzensiz diziliş oluşur. Dolayısıyla toplam düzensiz diziliş sayısı aşağıdaki gibi olur.
\( D_n = (n - 1)(D_{n - 1} + D_{n - 2}) \)
2 Elemanlı Kümelerde Düzensiz Dizilişler
2 elemanlı bir kümenin tüm ve düzensiz dizilişlerini bir örnek üzerinden gösterelim.
Bir restorana gelen iki kişi girişte şemsiyelerini bırakıyorlar. Restorandan ayrılırken şemsiyeleri rastgele iade eden garson, iki kişi de yanlış şemsiyeyi alacak şekilde bu iade işlemini kaç farklı şekilde yapabilir?
2 şemsiye 2 kişiye \( 2! = 2 \) farklı şekilde iade edilebilir. Düzensiz diziliş formülünü bu 2 elemanlı duruma uyguladığımızda bu durumlardan 1'inde iki kişinin de yanlış şemsiye aldığını buluruz.
\( D_2 = 2!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!}) \)
\( = 2\ (1 - 1 + \dfrac{1}{2}) \)
\( = 2 \cdot \dfrac{1}{2} = 1 \)
2 farklı permütasyon içinden 0, 1 ve 2 şemsiyenin doğru iade edildiği durumlar aşağıda listelenmiştir. Bu gösterimde A ve B şemsiyeleri için "AB" dizilişi her iki şemsiyenin de kişilere doğru iadesine karşılık gelmektedir. Kırmızı ile işaretli harfler ilgili şemsiyenin yanlış kişiye iadesini gösterir. Düzensiz dizilişler tüm iadelerin yanlış olduğu ilk satırdaki "0 Doğru" durumuna karşılık gelmektedir.
| Doğru İade Sayısı | Permütasyon Sayısı | Permütasyonlar |
|---|---|---|
| 0 Doğru (Düzensiz dizilişler) | 1 | \( \textcolor{red}{B}\textcolor{red}{A} \) |
| 1 Doğru | 0 | \( \) |
| 2 Doğru | 1 | \( AB \) |
3 Elemanlı Kümelerde Düzensiz Dizilişler
3 elemanlı bir kümenin tüm ve düzensiz dizilişlerini bir örnek üzerinden gösterelim.
YES kelimesinin harflerinin yerleri değiştirilerek hiçbir harfin orijinal yerinde olmadığı kaç kelime yazılabilir?
\( \{ Y, E, S \} \) kümesinin elemanları ile \( 3! = 6 \) farklı kelime yazılabilir. Düzensiz diziliş formülünü bu 3 elemanlı duruma uyguladığımızda bu kelimelerden 2'sinde hiçbir harfin YES kelimesindeki yerinde olmadığını buluruz.
\( D_3 = 3!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!}) \)
\( = 6\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6}) \)
\( = 6 \cdot \dfrac{2}{6} = 2 \)
6 farklı permütasyon içinden 0, 1, 2 ve 3 harfin doğru yerinde olduğu permütasyonlar aşağıda listelenmiştir. Kırmızı ile işaretli harfler ilgili harfin yanlış pozisyonda olduğunu gösterir. Düzensiz dizilişler tüm harflerin yanlış pozisyonda olduğu ilk satırdaki "0 Doğru" durumuna karşılık gelmektedir.
| Doğru Harf Sayısı | Permütasyon Sayısı | Permütasyonlar |
|---|---|---|
| 0 Doğru (Düzensiz dizilişler) | 2 | \( \textcolor{red}{E}\textcolor{red}{S}\textcolor{red}{Y}, \textcolor{red}{S}\textcolor{red}{Y}\textcolor{red}{E} \) |
| 1 Doğru | 3 | \( Y\textcolor{red}{S}\textcolor{red}{E}, \textcolor{red}{S}E\textcolor{red}{Y}, \textcolor{red}{E}\textcolor{red}{Y}S \) |
| 2 Doğru | 0 | \( \) |
| 3 Doğru | 1 | \( YES \) |
4 Elemanlı Kümelerde Düzensiz Dizilişler
4 elemanlı bir kümenin tüm ve düzensiz dizilişlerini bir örnek üzerinden gösterelim.
Toplantı için bir şirkete gelen 4 kişi resepsiyona kimliklerini bırakıyorlar. Toplantı sonrasında kimlikleri isim ve fotoğrafları kontrol etmeden rastgele iade eden görevli, kimlikleri 4 kişi de kendisine ait olmayan bir kimlik alacak şekilde kaç farklı şekilde iade edebilir?
4 kimlik 4 kişiye \( 4! = 24 \) farklı şekilde iade edilebilir. Düzensiz diziliş formülünü bu 4 elemanlı duruma uyguladığımızda bu durumlardan 9'unda tüm kimliklerin yanlış kişilere iade edildiğini buluruz.
\( D_4 = 4!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dfrac{1}{4!}) \)
\( = 24\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6} + \dfrac{1}{24}) \)
\( = 24 \cdot \dfrac{9}{24} = 9 \)
24 farklı permütasyon içinden 0, 1, 2, 3 ve 4 kimliğin doğru iade edildiği durumlar aşağıda listelenmiştir. Bu gösterimde A, B, C, D kimlikleri için "ABCD" dizilişi tüm kimliklerin kişilere doğru iadesine karşılık gelmektedir. Kırmızı ile işaretli harfler ilgili kimliğin yanlış kişiye iadesini gösterir. Düzensiz dizilişler tüm iadelerin yanlış olduğu ilk satırdaki "0 Doğru" durumuna karşılık gelmektedir.
| Doğru İade Sayısı | Permütasyon Sayısı | Permütasyonlar |
|---|---|---|
| 0 Doğru (Düzensiz dizilişler) | 9 | \( \textcolor{red}{B}\textcolor{red}{A}\textcolor{red}{D}\textcolor{red}{C}, \textcolor{red}{B}\textcolor{red}{C}\textcolor{red}{D}\textcolor{red}{A}, \textcolor{red}{B}\textcolor{red}{D}\textcolor{red}{A}\textcolor{red}{C}, \) \( \textcolor{red}{C}\textcolor{red}{A}\textcolor{red}{D}\textcolor{red}{B}, \textcolor{red}{C}\textcolor{red}{D}\textcolor{red}{A}\textcolor{red}{B}, \textcolor{red}{C}\textcolor{red}{D}\textcolor{red}{B}\textcolor{red}{A}, \) \( \textcolor{red}{D}\textcolor{red}{A}\textcolor{red}{B}\textcolor{red}{C}, \textcolor{red}{D}\textcolor{red}{C}\textcolor{red}{A}\textcolor{red}{B}, \textcolor{red}{D}\textcolor{red}{C}\textcolor{red}{B}\textcolor{red}{A} \) |
| 1 Doğru | 8 | \( A\textcolor{red}{C}\textcolor{red}{D}\textcolor{red}{B}, A\textcolor{red}{D}\textcolor{red}{B}\textcolor{red}{C}, \textcolor{red}{C}B\textcolor{red}{D}\textcolor{red}{A}, \) \( \textcolor{red}{D}B\textcolor{red}{A}\textcolor{red}{C}, \textcolor{red}{B}\textcolor{red}{D}C\textcolor{red}{A}, \textcolor{red}{D}\textcolor{red}{A}C\textcolor{red}{B}, \) \( \textcolor{red}{B}\textcolor{red}{C}\textcolor{red}{A}D, \textcolor{red}{C}\textcolor{red}{A}\textcolor{red}{B}D \) |
| 2 Doğru | 6 | \( AB\textcolor{red}{D}\textcolor{red}{C}, A\textcolor{red}{D}C\textcolor{red}{B}, A\textcolor{red}{C}\textcolor{red}{B}D, \) \( \textcolor{red}{D}BC\textcolor{red}{A}, \textcolor{red}{C}B\textcolor{red}{A}D, \textcolor{red}{B}\textcolor{red}{A}CD \) |
| 3 Doğru | 0 | \( \) |
| 4 Doğru | 1 | \( ABCD \) |
5 Elemanlı Kümelerde Düzensiz Dizilişler
5 elemanlı bir kümenin tüm ve düzensiz dizilişlerini bir örnek üzerinden gösterelim.
Acelesi olduğu için 5 farklı daireye ait 5 elektrik faturasını posta kutularına adresleri kontrol etmeden (her posta kutusunda tek bir fatura olacak şekilde) rastgele atan bir postacı, bu işlemi hiçbir fatura doğru posta kutusuna atılmayacak şekilde kaç farklı şekilde yapabilir?
5 fatura 5 posta kutusuna \( 5! = 120 \) farklı şekilde atılabilir. Düzensiz diziliş formülünü bu 5 elemanlı duruma uyguladığımızda bu durumlardan 44'ünde hiçbir faturanın doğru posta kutusuna atılmadığını buluruz.
\( D_5 = 5!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dfrac{1}{4!} - \dfrac{1}{5!}) \)
\( = 120\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6} + \dfrac{1}{24} - \dfrac{1}{120}) \)
\( = 120 \cdot \dfrac{44}{120} = 44 \)
Daha Büyük Elemanlı Kümeler
Farklı sayıda elemandan oluşan kümeler için toplam diziliş ve düzensiz diziliş sayıları aşağıdaki tabloda verilmiştir.
| \( n \) | \( n! \) | \( D_n = !n \) | \( D_n / n! \) |
|---|---|---|---|
| 1 | \( 1! = 1 \) | \( 0 \) | \( 0,0000 \) |
| 2 | \( 2! = 2 \) | \( 1 \) | \( 0,5000 \) |
| 3 | \( 3! = 6 \) | \( 2 \) | \( 0,3333 \) |
| 4 | \( 4! = 24 \) | \( 9 \) | \( 0,3750 \) |
| 5 | \( 5! = 120 \) | \( 44 \) | \( 0,3667 \) |
| 6 | \( 6! = 720 \) | \( 265 \) | \( 0,3681 \) |
| 7 | \( 7! = 5040 \) | \( 1854 \) | \( 0,3679 \) |
| 8 | \( 8! = 40320 \) | \( 14833 \) | \( 0,3679 \) |
| 9 | \( 9! = 362880 \) | \( 133496 \) | \( 0,3679 \) |
| 10 | \( 10! = 3628800 \) | \( 1334961 \) | \( 0,3679 \) |
Bu tabloda görebileceğimiz gibi, \( n \)'nin 4 ve daha büyük değerlerinde düzensiz dizilişlerin toplam dizilişlere oranı \( 0,37 \) düzeylerinde sabitlenmektedir, dolayısıyla çok daha büyük elemanlı problemlerde de oranın bu düzeyde gerçekleşeceğini söyleyebiliriz.
\( n \) sonsuza giderken bu oranın limiti \( e \) sayısının tersine ve bulduğumuz bu orana eşittir.
\( \lim\limits_{n \to \infty} \dfrac{D_n}{n!} = \dfrac{1}{e} = 0,367879... \)
Daha büyük elemanlı bir kümenin tüm ve düzensiz dizilişlerini bir örnek üzerinden gösterelim.
Üzerlerinde 1-100 arası sayıların yazılı olduğu 100 kart karıştırıldıktan sonra birer birer açılıyor. En az bir kartın üzerindeki sayı ile aynı sırada açılma olasılığı kaçtır (örneğin 15 no'lu kartın 15. sırada açılma olasılığı)?
100 kart \( 100! \) farklı şekilde dizilebilir/farklı sırada açılabilir.
100 kartın tümünün üzerindeki sayıdan farklı bir sırada açıldığı diziliş sayısı \( n = 100 \) için düzensiz diziliş sayısına eşittir (\( D_{100} \)).
Kartların tümünün üzerindeki sayıdan farklı bir sırada açılma olasılığı \( n \)'nin büyük değerleri için yukarıda bulduğumuz sabit değere eşittir.
\( \dfrac{D_{100}}{100!} \approx 36,79\% \)
Buna göre, en az bir kartın üzerindeki sayı ile aynı sırada açılma olasılığı \( 100 - 36,79 = 63,21\% \) olarak bulunur.
6 arkadaş yılbaşında birbirlerine hediye almak istiyorlar. Kimin kime hediye alacağına karar vermek için isimlerini birer kağıda yazıyorlar ve herkes sırayla bir kağıt çekiyor.
Bu çekiliş kimse kendi ismini çekmemek koşuluyla kaç farklı şekilde sonuçlanabilir?
Çözümü GösterSoruda 6 ismin hiçbirinin olması gereken pozisyonda olmadığı farklı diziliş sayısı istenmektedir, bu da bir düzensiz diziliş problemidir.
6 kişi için bu çekiliş \( 6! = 720 \) farklı şekilde sonuçlanabilir. Düzensiz diziliş formülünü bu 6 elemanlı duruma uyguladığımızda bu durumlardan 265'inde kimsenin kendi ismini çekmediğini buluruz.
\( D_6 = 6!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dfrac{1}{4!} - \dfrac{1}{5!} + \dfrac{1}{6!}) \)
\( = 720\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6} + \dfrac{1}{24} - \dfrac{1}{120} + \dfrac{1}{720}) \)
\( = 720 \cdot \dfrac{265}{720} = 265 \) bulunur.
Bir postacı 7 dairelik bir apartmanda 7 elektrik faturasını posta kutularına üçünü doğru, dördünü hatalı olacak olacak şekilde kaç farklı şekilde atabilir?
Çözümü Göster7 posta kutusu içinden faturaların doğru atılacağı 3 posta kutusu \( C(7, 3) \) farklı şekilde seçilebilir.
Faturaların hatalı atılacağı diğer 4 posta kutusundaki düzensiz diziliş sayısı \( D_4 \) olur.
\( D_4 = 4!\ (\dfrac{1}{0!} - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dfrac{1}{4!}) \)
\( = 24\ (1 - 1 + \dfrac{1}{2} - \dfrac{1}{6} + \dfrac{1}{24}) \)
\( = 24 \cdot \dfrac{9}{24} = 9 \)
Buna göre postacı faturaların üçünü doğru, dördünü hatalı olacak şekilde posta kutularına \( C(7, 3) \cdot D_4 = 35 \cdot 9 = 315 \) farklı şekilde atabilir.