Küme Gösterim Yöntemleri
Bir kümenin elemanları üç farklı şekilde tanımlanabilir ya da gösterilebilir.
Liste Yöntemi
Bu yöntemde kümenin elemanları "\( \{ \} \)" küme parantezleri içinde ve virgülle ayrılarak listelenir.
\( A = \{ a, b, c, 1, 2 \} \)
Küme parantezlerinin içinin boş bırakılması, kümenin boş küme olduğunu gösterir.
\( A = \{ \} \)
Elemanlar arasındaki ilişki net ise listelemeyi kısa tutmak ya da elemanların sonsuza gittiğini vurgulamak için "\( \ldots \)" sembolü kullanılabilir.
\( A = \{ 0, 1, 2, 3, \ldots, 99, 100 \} \)
\( B = \{ 0, 2, 4, 6, \ldots \} \)
\( C = \{ \ldots, -2\pi, -\pi, 0, \pi, 2\pi, \ldots \} \)
Ortak Özellik Yöntemi
Kümenin elemanları arasında matematiksel ya da sözel olarak ifade edilebilen bir ilişki varsa elemanların bu ortak özellikleri belirtilerek ve elemanları tek tek listelemeye gerek kalmadan da bir küme tanımlanabilir.
Ortak özellik yönteminde önce kümenin bir elemanını temsil eden değişken ya da ifade belirtilir, "|" ya da ":" işareti konur ve bu değişkeni kullanarak kümenin elemanlarının matematiksel ya da sözel tanımlaması yapılır. Bu tanımlamada birden fazla koşul virgülle ayrılarak listelenebilir.
| Küme | Tanım |
|---|---|
| Rasyonel sayılar | \( \mathbb{Q} = \{ \frac{a}{b} \mid a, b \in \mathbb{Z}, b \ne 0 \} \) |
| İki basamaklı pozitif tam sayılar |
\( A = \{ x \mid 10 \le x \lt 100, x \in \mathbb{Z^+} \} \) \( A = \{ 10, 11, \ldots, 99 \} \) |
| Çift sayılar |
\( B = \{ 2k \mid k \in \mathbb{Z} \} \) \( B = \{ \ldots, -4, -2, 0, 2, 4, \ldots \} \) |
| Tek sayılar |
\( C = \{ 2k + 1 \mid k \in \mathbb{Z} \} \) \( C = \{ \ldots, -3, -1, 1, 3, 5, \ldots \} \) |
| Tam kare sayılar |
\( D = \{ k^2 \mid k \in \mathbb{Z^+} \} \) \( D = \{ 1, 4, 9, 16, \ldots \} \) |
| \( \pi \) radyanın tam sayı katları |
\( E = \{ k\pi \mid k \in \mathbb{Z} \} \) \( E = \{ \ldots, -2\pi, -\pi, 0, \pi, 2\pi, \ldots \} \) |
| Bir parabol fonksiyonu | \( f = \{ (x, y) \mid y = x^2 - 4, x, y \in \mathbb{R} \} \) |
Denklemler konusunda gördüğümüz reel sayı aralıkları da birer kümedir ve ortak özellik yöntemi ile de gösterilebilirler.
\( [-10, 10) = \{ x \mid -10 \le x \lt 10, x \in \mathbb{R} \} \)
\( (-\infty, 100] = \{ x \mid x \le 100, x \in \mathbb{R} \} \)
Venn Şeması
Bu yöntemde kümeye ait elemanlar kapalı bir şekil içerisinde, her elemanın başına bir nokta konularak gösterilir.

Venn şemasında kullanılan kapalı şekil; daire, elips, dikdörtgen gibi şekiller olabilir. Kullanılan şeklin büyüklüğü kümenin eleman sayısının çokluğunu göstermez.
Aşağıdaki kümeleri Venn şeması ile gösterin.
\( A_3 = \{ x \mid x \text{ 3'e tam bölünür}, x \in \mathbb{Z} \} \)
\( A_5 = \{ x \mid x \text{ 5'e tam bölünür}, x \in \mathbb{Z} \} \)
\( A_6 = \{ x \mid x \text{ 6'ya tam bölünür}, x \in \mathbb{Z} \} \)
Çözümü Göster6'ya bölünen her sayı 3'e de tam bölündüğü için \( A_6 \) kümesinin elemanları \( A_3 \) kümesinin de elemanı olur.
Bu sayılardan ikisine ya da üçüne birlikte tam bölünen sayılar bulunduğu için birden fazla kümenin elemanı olan sayılar olacaktır.
Üç kümeyi Venn şeması ile aşağıdaki şekilde gösterebiliriz.
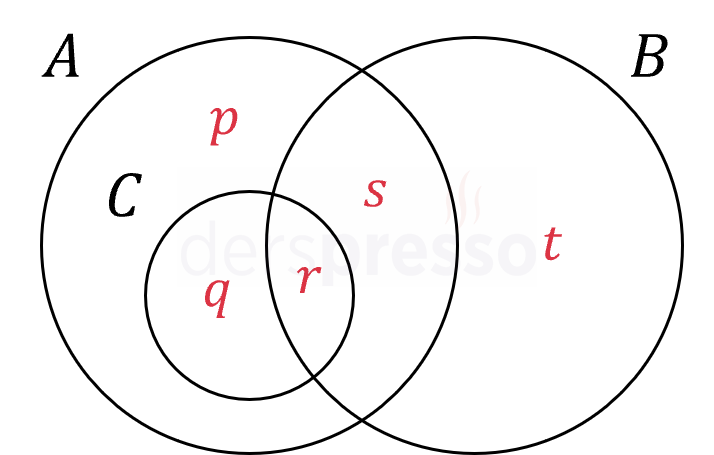
Bu şemada harflerle etiketlenmiş bölgeler aşağıdaki elemanlara karşılık gelir.
\( p \): 3 ile tam bölünen, 5 ve 6 ile tam bölünmeyen sayılar (örnek: 3)
\( q \): 3 ve 6 ile tam bölünen, 5 ile tam bölünmeyen sayılar (örnek: 6)
\( r \): 3, 5 ve 6 ile tam bölünen sayılar (örnek: 30)
\( s \): 3 ve 5 ile tam bölünen, 6 ile tam bölünmeyen sayılar (örnek: 15)
\( t \): 5 ile tam bölünen, 3 ve 6 ile tam bölünmeyen sayılar (örnek: 5)