Kümelerin Birleşimi
İki ya da daha fazla kümenin tüm elemanlarından oluşan kümeye bu kümelerin birleşim kümesi denir. Kümeler arasındaki birleşim işlemi için \( \cup \) sembolü kullanılır.
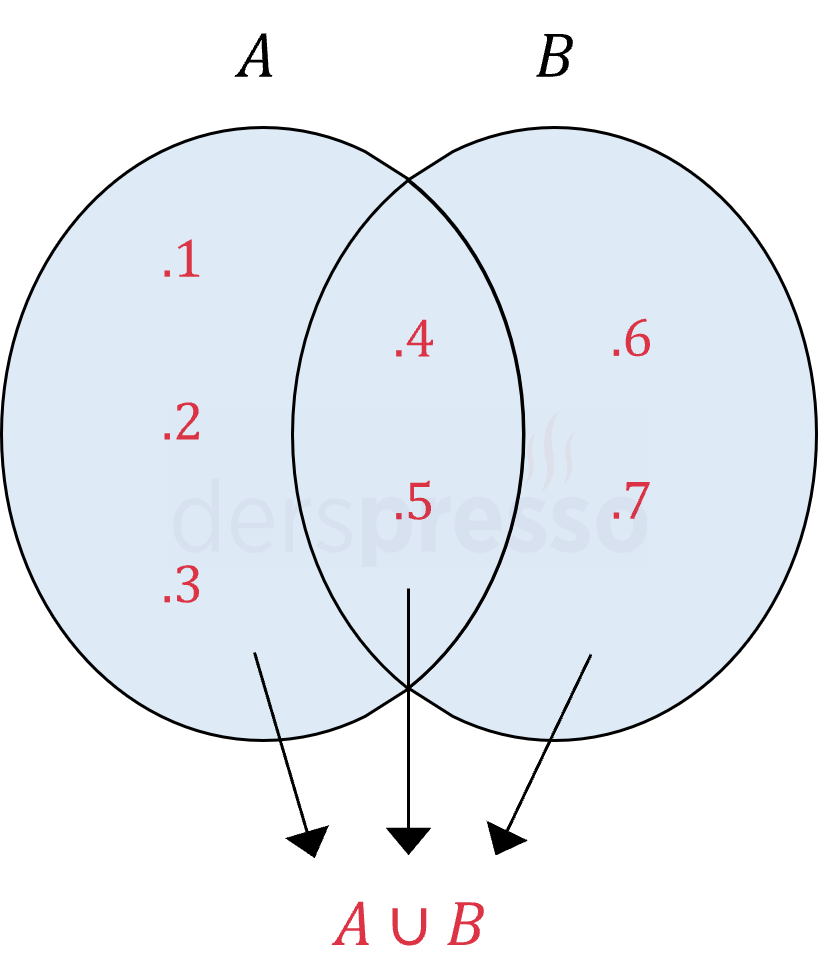
\( A \cup B = \{ x \mid x \in A \lor x \in B \} \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7 \} \)
\( A \cup B = \{ 1, 2, 3, 4, 5, 6, 7 \} \)
Bu tanıma göre, bir eleman iki (ya da daha fazla) kümeden en az birinin elemanı ise birleşim kümelerinin de elemanıdır. Benzer şekilde, bir eleman iki (ya da daha fazla) kümenin birleşim kümesinin elemanı ise bu kümelerden en az birinin elemanıdır.
İki kümenin birleşiminin eleman sayısı, kümelerin eleman sayıları toplamından kesişimlerinin eleman sayısı çıkarılarak bulunur. Bunun sebebi, iki kümenin de kesişim kümesini ayrı ayrı içermesi, dolayısıyla kümelerin eleman sayıları toplandığında kesişim kümesinin iki kez sayılmasıdır.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7 \} \)
\( A \cap B = \{ 4, 5 \} \)
\( A \cup B = \{ 1, 2, 3, 4, 5, 6, 7 \} \)
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( s(A \cup B) = 5 + 4 - 2 = 7 \)
Üç kümenin birleşim kümesinin liste ve Venn şeması gösterimleri aşağıdaki gibidir.
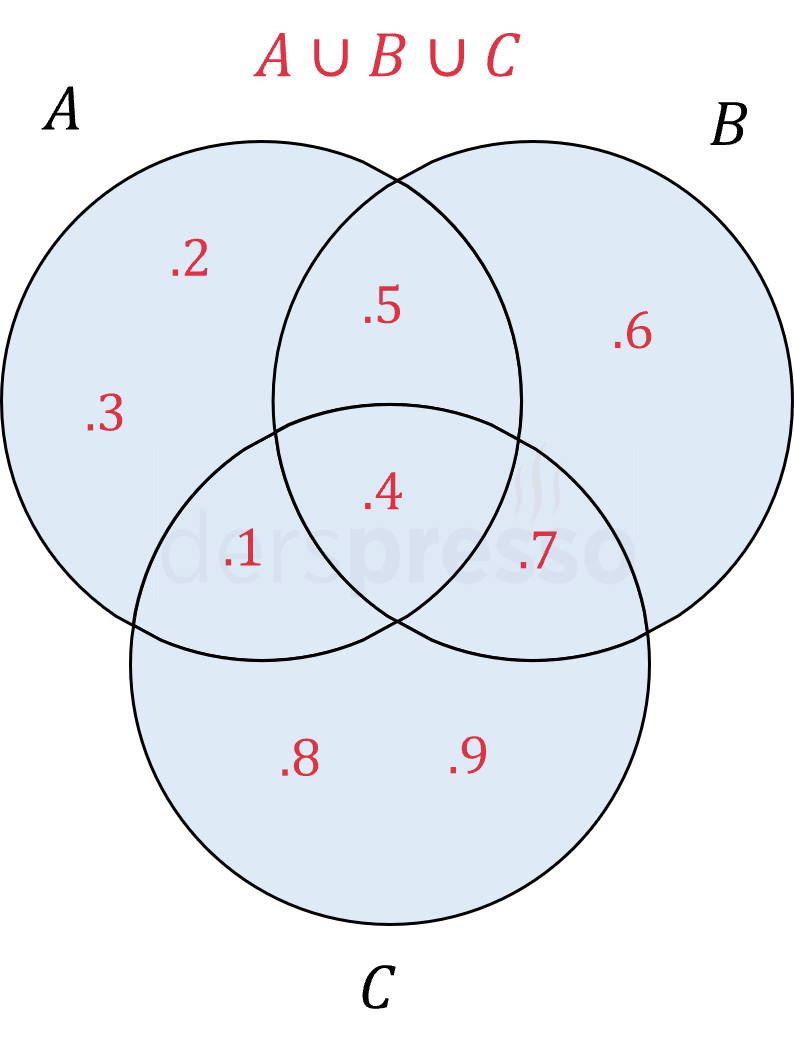
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7 \} \)
\( C = \{ 1, 4, 7, 8, 9 \} \)
\( A \cup B \cup C = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)
Bu üç kümenin ikili birleşim kümeleri aşağıdaki gibidir.
\( A \cup B = \{ 1, 2, 3, 4, 5, 6, 7 \} \)
\( A \cup C = \{ 1, 2, 3, 4, 5, 7, 8, 9 \} \)
\( B \cup C = \{ 1, 4, 5, 6, 7, 8, 9 \} \)
Üç kümenin birleşiminin eleman sayısı aşağıdaki formülle bulunur.
\( s(A \cup B \cup C) = s(A) + s(B) + S(C) \)
\( - s(A \cap B) - s(A \cap C) - s(B \cap C) \)
\( + s(A \cap B \cap C) \)
Aşağıda her bölgesi için eleman sayıları verilen üç kümenin birleşim kümesinin eleman sayısını bulalım.

\( s(A \cup B \cup C) = s(A) + s(B) + S(C) \)
\( - s(A \cap B) - s(A \cap C) - s(B \cap C) \)
\( + s(A \cap B \cap C) \)
\( = 11 + 16 + 15 - 5 - 3 - 6 + 2 = 30 \)
\( n \) tane kümenin birleşim kümesinin eleman sayısı formülü "Dahil Etme - Hariç Tutma Prensibi"ne dayanmaktadır. Bu prensibin detaylarını "Sayma" konusu altındaki "Dahil Etme - Hariç Tutma Prensibi" bölümünde inceleyeceğiz.
Birleşim İşlem Özellikleri
Birleşim işleminin değişme özelliği vardır.
\( A \cup B = B \cup A \)
İSPATI GÖSTER
\( x \) elemanı \( A \cup B \) kümesinin bir elemanı olsun.
\( x \in A \cup B \)
Birleşim kümesi tanımına göre, \( x \) \( A \) kümesinin veya \( B \) kümesinin elemanıdır.
\( x \in A \lor x \in B \)
"Veya" işleminin değişme özelliği vardır.
\( x \in B \lor x \in A \)
Birleşim kümesi tanımına göre, \( x \) \( B \) kümesinin veya \( A \) kümesinin elemanı ise birleşim kümelerinin elemanıdır.
\( x \in B \cup A \)
Birleşim işleminin birleşme özelliği vardır.
\( A \cup (B \cup C) = (A \cup B) \cup C \)
\( A = \{ 1, 2, 3, 4 \} \)
\( B = \{ 1, 2, 5, 6 \} \)
\( C = \{ 1, 3, 5, 7 \} \)
\( A \cup (B \cup C) = A \cap \{ 1, 2, 3, 5, 6, 7 \} \) \( = \{ 1, 2, 3, 4, 5, 6, 7 \} \)
\( (A \cup B) \cup C = \{ 1, 2, 3, 4, 5, 6 \} \cap C \) \( = \{ 1, 2, 3, 4, 5, 6, 7 \} \)
İSPATI GÖSTER
\( x \) elemanı \( A \cup (B \cup C) \) kümesinin bir elemanı olsun.
\( x \in A \cup (B \cup C) \)
Birleşim kümesi tanımına göre, \( x \) \( A \) kümesinin veya \( B \cup C \) kümesinin elemanıdır.
\( x \in A \lor x \in B \cup C \)
Birleşim kümesi tanımına göre, \( x \) \( B \) kümesinin veya \( C \) kümesinin elemanıdır.
\( x \in A \lor (x \in B \lor x \in C) \)
"Veya" işleminin birleşme özelliği vardır.
\( (x \in A \lor x \in B) \lor x \in C \)
Birleşim kümesi tanımına göre, \( x \) \( A \) kümesinin veya \( B \) kümesinin elemanı ise birleşim kümelerinin elemanıdır.
\( x \in A \cup B \lor x \in C \)
Birleşim kümesi tanımına göre, \( x \) \( A \cup B \) kümesinin veya \( C \) kümesinin elemanı ise birleşim kümelerinin elemanıdır.
\( x \in (A \cup B) \cup C \)
Birleşim işleminin değişme ve birleşme özellikleri olduğu için, sadece birleşim işleminden oluşan bir ifadede kümeler arasındaki parantezler kaydırılabilir ya da kaldırılabilir ve kümelerin sırası değiştirilebilir.
\( (A \cup B) \cup (C \cup D) \)
\( = A \cup (B \cup C) \cup D \)
\( = A \cup B \cup C \cup D \)
\( = D \cup B \cup A \cup C \)
Birleşim işleminin kesişim üzerinde soldan ve sağdan dağılma özelliği vardır.
\( A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
\( (A \cap B) \cup C = (A \cup C) \cap (B \cup C) \)
\( A = \{ 1, 2, 3 \} \)
\( B = \{ 2, 4, 5 \} \)
\( C = \{ 3, 4, 6 \} \)
\( A \cup (B \cap C) = A \cup \{ 4 \} \) \( = \{ 1, 2, 3, 4 \} \)
\( (A \cup B) \cap (A \cup C) \) \( = \{ 1, 2, 3, 4, 5 \} \cap \{ 1, 2, 3, 4, 6 \} \) \( = \{ 1, 2, 3, 4 \} \)
\( (A \cap B) \cup C = \{ 2 \} \cup C \) \( = \{ 2, 3, 4, 6 \} \)
\( (A \cup C) \cap (B \cup C) \) \( = \{ 1, 2, 3, 4, 6 \} \cap \{ 2, 3, 4, 5, 6 \} \) \( = \{ 2, 3, 4, 6 \} \)
İSPATI GÖSTER
\( x \) elemanı \( A \cup (B \cap C) \) kümesinin bir elemanı olsun.
\( x \in A \cup (B \cap C) \)
Birleşim kümesi tanımına göre, \( x \) \( A \) kümesinin veya \( B \cap C \) kümesinin elemanıdır.
\( x \in A \lor x \in B \cap C \)
Kesişim kümesi tanımına göre, \( x \) hem \( B \) kümesinin hem de \( C \) kümesinin elemanıdır.
\( x \in A \lor (x \in B \land x \in C) \)
"Veya" işleminin "ve" işlemi üzerinde dağılma özelliği vardır.
\( (x \in A \lor x \in B) \land (x \in A \lor x \in C) \)
Birleşim kümesi tanımına göre, \( x \) iki kümeden birincinin veya ikincinin elemanı ise birleşim kümelerinin elemanıdır.
\( (x \in A \cup B) \land (x \in A \cup C) \)
Kesişim kümesi tanımına göre, \( x \) hem \( A \cup B \) kümesinin hem de \( A \cup C \) kümesinin elemanı ise kesişim kümelerinin de elemanıdır.
\( x \in (A \cup B) \cap (A \cup C) \)
Birleşim işleminin birim (etkisiz) elemanı boş kümedir.
\( A \cup \emptyset = A \)
Birleşim İşlem Kuralları
Bir kümenin boş küme ile birleşimi kendisine eşittir.
\( A \cup \emptyset = A \)
Bir kümenin kendisiyle birleşimi kendisine eşittir.
\( A \cup A = A \)
İSPATI GÖSTER
Kümelerin eşitliği tanımına göre, \( A \cup A = A \) olduğunu göstermek için \( A \cup A \subseteq A \) ve \( A \subseteq A \cup A \) olduğunu gösterelim.
(1) \( A \cup A \subseteq A \) olduğunu gösterelim.
\( x \in A \cup A \) olsun.
Birleşim kümesi tanımına göre, \( x \) iki kümenin birleşiminin elemanı ise birinci kümenin veya ikinci kümenin elemanıdır.
\( x \in A \lor x \in A \)
\( p \lor p \equiv p \)
\( x \in A \)
\( A \cup A \subseteq A \) olduğunu göstermiş olduk.
(2) \( A \subseteq A \cup A \) olduğunu gösterelim.
\( x \in A \) olsun.
\( p \equiv p \lor p \)
\( x \in A \lor x \in A \)
\( x \in A \cup A \)
\( A \subseteq A \cup A \) olduğunu göstermiş olduk.
Kümelerin eşitliği tanımına göre, bir kümenin kendisiyle birleşimi kendisine eşittir.
\( A \cup A = A \)
Bir kümenin evrensel kümeyle birleşimi evrensel kümedir.
\( A \cup E = E \)
\( A \) kümesi \( B \) kümesinin bir alt kümesiyse birleşimleri \( B \) kümesi olur.
\( A \subset B \) ise,
\( A \cup B = B \)
İki kümenin birleşimi, her iki kümeyi de kapsar.
\( A \subseteq A \cup B \)
\( B \subseteq A \cup B \)
İSPATI GÖSTER
\( x \in A \) olsun.
Bir \( p \) önermesi doğru ise \( p \lor q \) önermesi de doğrudur.
\( x \in A \lor x \in B \)
Birleşim kümesi tanımına göre, \( x \) \( A \) kümesinin veya \( B \) kümesinin elemanı ise \( A \cup B \) kümesinin elemanıdır.
\( x \in A \cup B \)
Her \( x \in A \) için \( x \in A \cup B \) olduğuna göre, \( A \) kümesi \( A \cup B \) kümesinin bir alt kümesidir.
\( A \subseteq A \cup B \)
İki kümenin birleşiminin eleman sayısı, her iki kümenin eleman sayıları toplamından büyük olamaz.
\( s(A \cup B) \le s(A) + s(B) \)
\( s(A) = 14, s(B) = 8, s(A \cup B) = 19 \)
olduğuna göre, \( s(A \cap B) \) kaçtır?
Çözümü Gösterİki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( 19 = 14 + 8 - s(A \cap B) \)
\( s(A \cap B) = 3 \) bulunur.
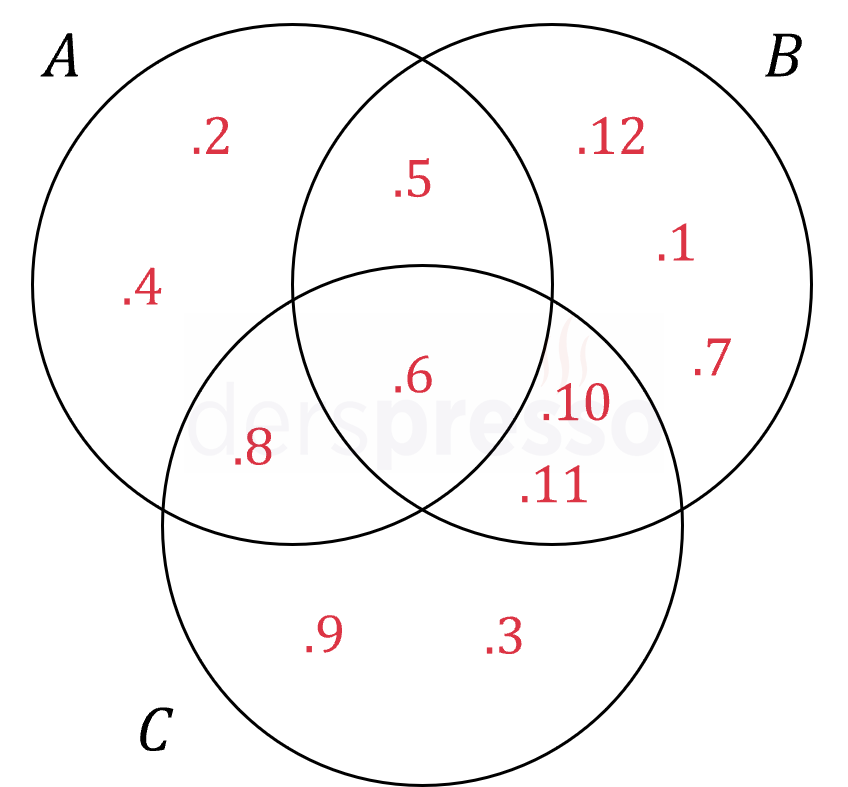
Yukarıdaki \( A, B, C \) kümeleri için aşağıdakilerden hangileri yanlıştır?
I. \( A = \{2, 4, 5, 6, 8\} \)
II. \( B \cap C = \{10, 11\} \)
III. \( (A \cap B) \cup (B \cap C) = \{5, 6, 10, 11\} \)
IV. \( s(A) + s(B) = 10 \)
V. \( s(B \cup C) = 13 \)
Çözümü GösterI. öncül doğrudur.
\( B \cap C = \{6, 10, 11\} \) olduğu için II. öncül yanlıştır.
III. öncül doğrudur.
\( s(A \cup B) = 10 \) olsa da, \( s(A) = 5 \) ve \( s(B) = 7 \) olduğu için IV. öncül yanlıştır.
\( s(B) = 7 \) ve \( s(C) = 6 \) olsa da, \( s(B \cup C) = 10 \) olduğu için V. öncül yanlıştır.
Buna göre II., IV. ve V. öncüller yanlıştır.
\( A \) kümesinin 4, \( B \) kümesinin 5 elemanı \( A \cap B \) kümesinin elemanı değildir.
\( A \cup B \) kümesinin eleman sayısı \( A \cap B \) kümesinin eleman sayısının iki katı olduğuna göre, \( A \) kümesi kaç elemanlıdır?
Çözümü GösterKesişim kümesinin eleman sayısına \( a \) diyelim.

\( s(A \cup B) = 2s(A \cap B) \)
\( 4 + a + 5 = 2a \)
\( a = 9 \)
\( s(A) = 4 + 9 = 13 \) bulunur.
\( s(A) = s(B) + 3 \), \( s(A \cup B) = 21, s(A \cap B) = 4 \)
olduğuna göre, \( s(B) \) kaçtır?
Çözümü Gösterİki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( 21 = s(B) + 3 + s(B) - 4 \)
\( 2s(B) = 22 \)
\( s(B) = 11 \) bulunur.
\( 2s(A) = 3s(B) \)
\( s(A \cap B) = 5 \)
\( s(A \cup B) = 35 \)
olduğuna göre, \( s(B) \) kaçtır?
Çözümü Göster\( 2s(A) = 3s(B) \) olduğuna göre, \( s(A) = 3k \) ve \( s(B) = 2k \) diyelim.
İki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( 35 = 3k + 2k - 5 \)
\( k = 8 \)
\( s(B) = 2k = 2 \cdot 8 = 16 \) bulunur.
\( A \cup B = \{a, b, c, d \} \)
\( A \cup C = \{b, d, e, f, k, l \} \)
\( A \cup (B \cap C) \) kümesi nedir?
Çözümü GösterBirleşim kümesinin kesişim kümesi üzerinde dağılma özelliğini kullanalım.
\( A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
\( = \{ a, b, c, d \} \cap \{ b, d, e, f, k, l \} \)
\( = \{ b, d \} \) bulunur.
\( s(A \cap B) + s(A \cup B) = s(B) \)
olduğuna göre, aşağıdakilerden hangileri kesinlikle doğrudur?
I. \( A \cup B = \emptyset \)
II. \( A = \emptyset \)
III. \( B = \emptyset \)
IV. \( A \subset B \)
V. \( A \cap B = \emptyset \)
Çözümü Göster\( s(A \cap B) + s(A \cup B) = s(B) \)
İkinci terim yerine birleşim kümesi eleman sayısı formülünün açılımını yazalım.
\( s(A \cap B) + [s(A) + s(B) - s(A \cap B)] = s(B) \)
\( s(A) + s(B) = s(B) \)
\( s(A) = 0 \)
\( A = \emptyset \)
Buna göre II. ve V. öncüller kesinlikle doğrudur.
\( B \) kümesinin boş küme olup olmamasına göre diğer öncüller doğru olabilir ya da olmayabilir.
\( s(A) = 8 \)
\( s(B) = 13 \)
\( s(A \cap B) \ne 0 \)
olduğuna göre, \( s(A \cup B) \) en fazla kaç olabilir?
Çözümü GösterBirleşim kümesi eleman sayısı formülünü kullanalım.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
Buna göre iki kümenin birleşiminin en büyük olması için kesişimleri en küçük olmalıdır.
\( s(A \cap B) = 1 \) verelim ve verilen bilgileri Venn şeması üzerinde gösterelim.

\( s(A \cup B) = 7 + 1 + 12 = 20 \) bulunur.
\( A \subset B \) olmak üzere,
\( (A \cap B) \cup (A \cap \emptyset) \) ifadesinin en sade şekli nedir?
Çözümü GösterVerilen ifadede kesişim kümesinin birleşim kümesi üzerinde dağılma özelliği uygulanmıştır.
\( (A \cap B) \cup (A \cap \emptyset) = A \cap (B \cup \emptyset) \)
\( = A \cap B \)
\( B \) kümesi \( A \) kümesini kapsadığı için kesişimleri \( A \) kümesi olur.
\( = A \) bulunur.
\( A = [-\dfrac{5}{2}, \sqrt{7}] \)
\( B = [\sqrt{2}, \dfrac{26}{3}] \)
aralıkları veriliyor. Buna göre \( (A \cup B) \cap \mathbb{Z} \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( A \cup B = [-\dfrac{5}{2}, \dfrac{26}{3}] \)
\( (A \cup B) \cap \mathbb{Z} = \{ -2, -1, 0, \ldots, 7, 8 \} \)
Kümenin eleman sayısını bulmak için ardışık sayılar terim sayısı formülünü kullanalım.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( s[(A \cup B) \cap \mathbb{Z}] = \dfrac{8 - (-2)}{1} + 1 \)
\( = 11 \) bulunur.
\( A = \{ x \mid x = 3k, k \lt 70, k \in \mathbb{Z^+} \} \)
\( B = \{ x \mid x = 5k, k \lt 48, k \in \mathbb{Z^+} \} \)
olduğuna göre, \( s(A \cup B) \) kaçtır?
Çözümü Gösterİki kümenin elemanlarını liste yöntemi ile yazalım.
\( A = \{ 3, 6, 9, \ldots, 207 \} \)
\( B = \{ 5, 10, 15, \ldots, 235 \} \)
Elemanları 3'ün katları olan bir küme ile 5'in katları olan bir kümenin kesişim kümesinin elemanları 15'in katlarından oluşur.
\( A \cap B = \{ 15, 30, 45, \ldots, 195 \} \)
Her bir kümenin eleman sayısını bulmak için ardışık sayılar terim sayısı formülünü kullanalım.
\( \text{Terim sayısı} = \dfrac{\text{Son terim} - \text{İlk terim}}{\text{Artış miktarı}} + 1 \)
\( s(A) = \dfrac{207 - 3}{3} + 1 = 69 \)
\( s(B) = \dfrac{235 - 5}{5} + 1 = 47 \)
\( s(A \cap B) = \dfrac{195 - 15}{15} + 1 = 13 \)
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( = 69 + 47 - 13 = 103 \) bulunur.
\( K \), \( L \) ve \( M \) kümeleri için aşağıdaki bilgiler veriliyor.
\( K \cap M = K \cup M \)
\( K \subseteq L \subseteq M \)
Buna göre aşağıdakilerden hangileri kesinlikle doğrudur?
I. \( K = L = M \)
II. \( s(M) \le s(K) \le s(L) \)
III. \( K \cap M = \emptyset \Rightarrow L = \emptyset \)
IV. \( s(M) \gt 0 \)
V. \( K \cap M = L \)
Çözümü Göster\( K \) ve \( M \) kümelerinin kesişim ve birleşim kümeleri eşitse bu iki küme eşit kümelerdir.
\( L \) kümesi \( K \) kümesini kapsar ve eşitse, \( M \) kümesi de \( L \) kümesini kapsar ve eşitse, \( L \) kümesi birbirine eşit olan bu iki kümeye eşit olmalıdır.
Buna göre bu üç küme eşit kümelerdir. Üç küme boş küme olabilir ya da olmayabilir.
I. öncül kesinlikle doğrudur.
Kümeler eşit olduğu için eleman sayıları da eşittir, dolayısıyla eleman sayıları arasında \( \le \) sıralaması yapılabilir. II. öncül kesinlikle doğrudur.
İki eşit kümenin kesişimi boş küme ise bu iki küme boş kümedir, dolayısıyla üç küme de boş kümedir. III. öncül kesinlikle doğrudur.
Kümeler boş küme olabilir ya da olmayabilir. Buna göre IV. öncül doğru olabilir ya da olmayabilir.
Birbirine eşit üç kümeden ikisinin kesişimi bu üç kümeye eşittir. V. öncül kesinlikle doğrudur.
Buna göre I., II., III. ve V. öncüller kesinlikle doğrudur.
\( A \) ve \( B \) ayrık olmayan iki kümedir.
\( C \cap (A \cup B) = A \cup B = \{ 1, 2, 3, 4 \} \)
\( A' = \{ 4, 5, 6, 7 \} \) olduğuna göre,
\( B - A \) kümesi nedir?
Çözümü Göster\( C \cap (A \cup B) = (A \cup B) \) eşitliği \( C \) kümesinin \( A \cup B \) kümesini kapsadığını belirtir.
Verileri Venn şeması üzerinde gösterelim.

\( B - A = \{ 4 \} \)