Silindir
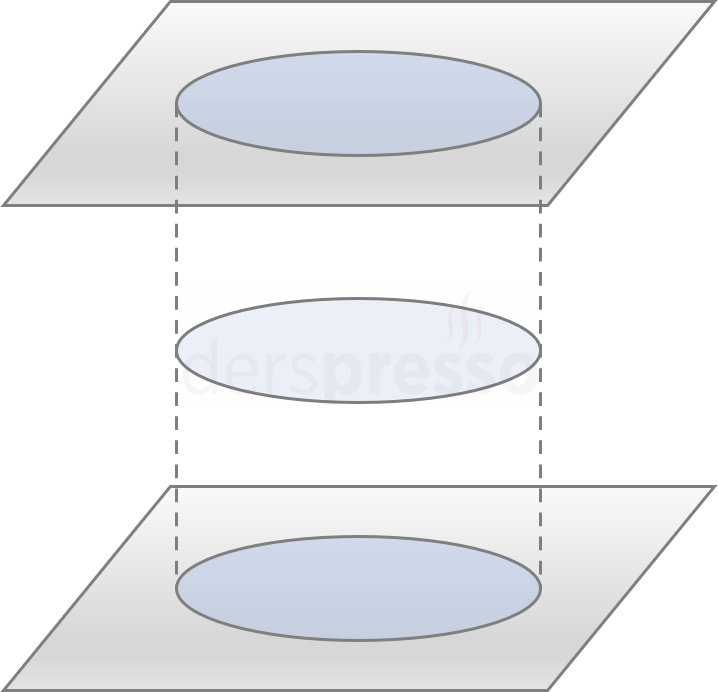
Alt ve üst tabanları özdeş birer daire olan ve birbirine paralel iki düzlem üzerinde bulunan, bu iki taban arasındaki tüm paralel kesitleri de tabanlarla özdeş olan cisme silindir denir.
Dik ve Eğik Silindir
Bir silindirin yan yüzü tabanlara dik ise bu silindire dik silindir denir. Yan yüz tabanlara dik değilse, bu silindire eğik silindir denir. Silindirlerin genel özelliği olan alt ve üst tabanların paralelliği, eğik silindirler için de geçerlidir.

Dik silindirin yan yüzü dikdörtgendir. Eğik silindirin yan yüzü paralelkenardır.
Hem dik hem de eğik silindirin yüksekliği, alt ve üst paralel tabanlar arasındaki dik ve en kısa mesafedir.
Bir silindir ve açık hali aşağıdaki gibidir.
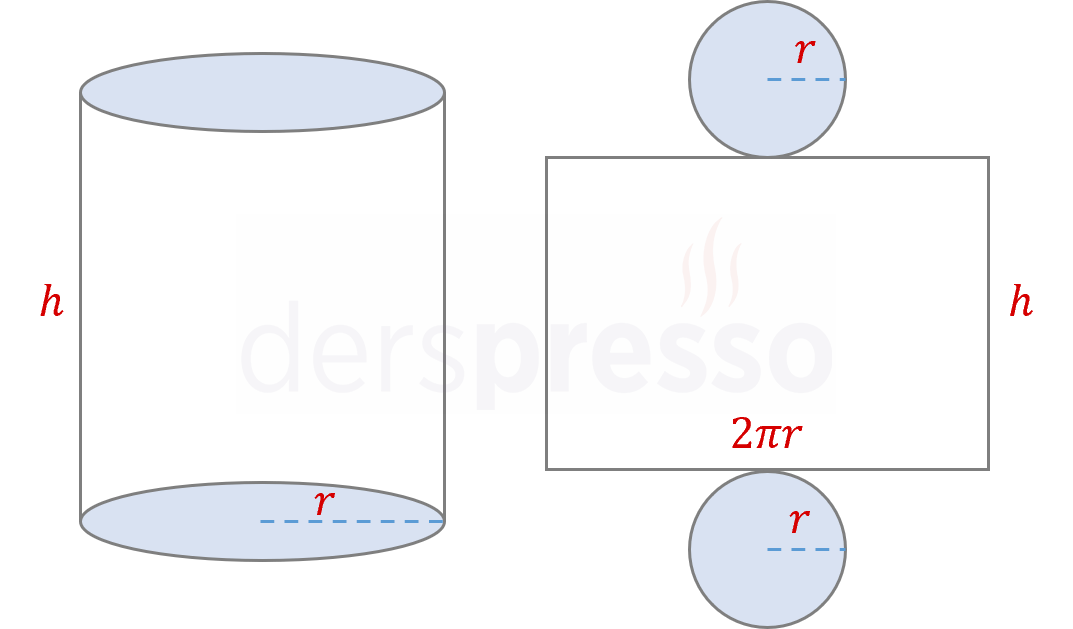
Silindirin Yüzey Alanı
Silindirin toplam yüzey alanı, taban ve yan yüz (yanal) alanlarının toplamına eşittir.
\( \text{Yüzey Alanı} = 2 \cdot \text{Taban Alanı} + \text{Yanal Alan} \)
\( \text{Yüzey Alanı} = 2 \cdot \pi r^2 + 2\pi r \cdot h \)
Silindirin Hacmi
Dik ve eğik silindirlerin hacmi, taban alanı ve yüksekliğin çarpımına eşittir. Eğik silindirde bahsettiğimiz gibi, hem dik hem de eğik silindirin yüksekliği alt ve üst tabanlar arasındaki dik ve en kısa mesafedir.
\( \text{Hacim} = \text{Taban Alanı} \cdot \text{Yükseklik} \)
\( \text{Hacim} = \pi r^2 \cdot h \)
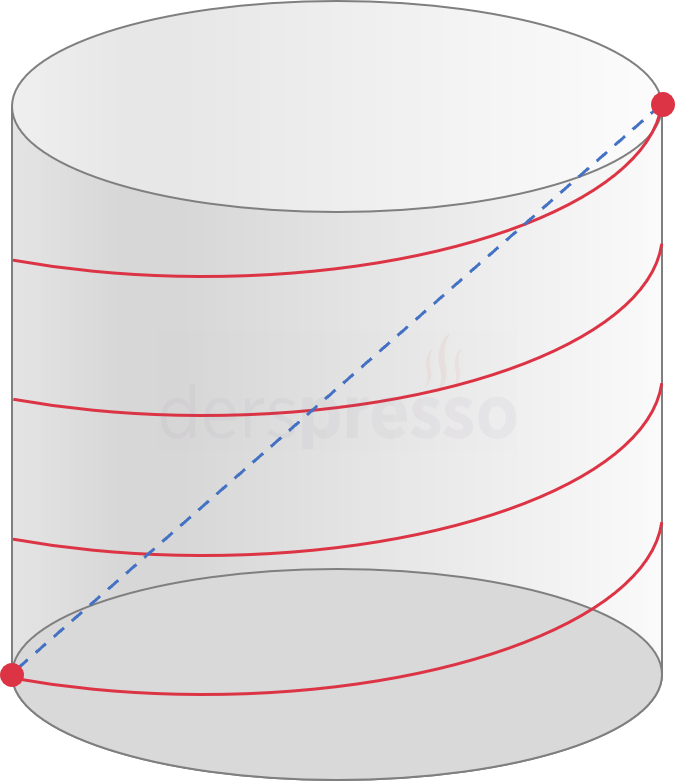
Bir ip; yüksekliği 21 cm ve taban çevre uzunluğu 8 cm olan bir silindirin etrafına, başlangıç ve bitiş noktaları silindirin köşegeninin iki uç noktası olacak şekilde şekildeki gibi sarılıyor.
İp silindirin etrafına hiç boşluk kalmayacak şekilde sarıldığına göre, ipin uzunluğu kaç cm'dir?
Çözümü Gösterİp köşegenin iki ucu arasında dikey olarak 21 cm mesafe kateder.
İp silindir etrafında 3,5 tur döndüğü için, köşegenin iki ucu arasında yatay olarak \( 8 \cdot 3,5 = 28 \) cm mesafe kateder.
İpin sardığı yan yüzeyin açılımını çizdiğimizde, ip yüksekliği 21 cm ve genişliği 28 cm olan bir dikdörtgenin köşegenine karşılık gelir.

Pisagor teoremini kullanarak köşegenin uzunluğunu bulalım.
\( d = \sqrt{21^2 + 28^2} = 35 \) cm
Buna göre ipin uzunluğu 35 cm olarak bulunur.