Piramit

Çokgen bir taban ve bu tabanı tek bir noktada birleştiren üçgen yüzlerden oluşan üç boyutlu şekle piramit denir.

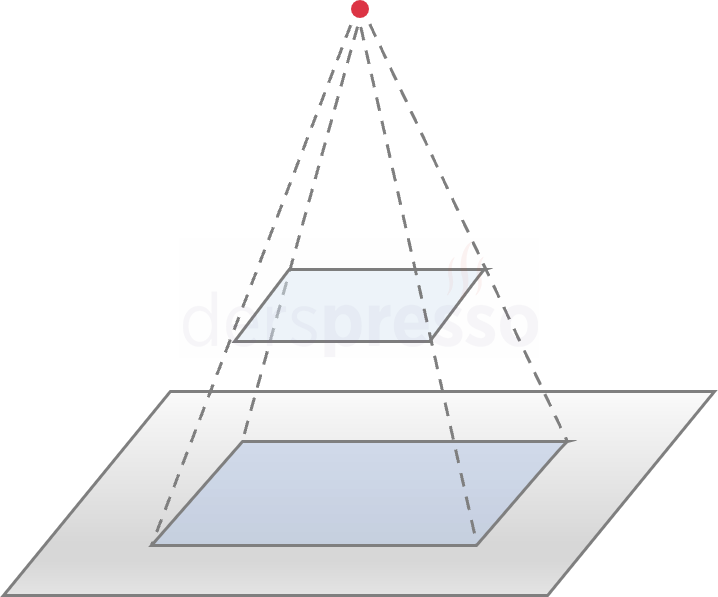
Tüm piramitlerin ortak özellikleri şunlardır:

• Tabanı bir çokgendir. Dolayısıyla, tabanı daire olan koni bir piramit değildir.
• Tabanı \( n \) kenarlı olan piramidin \( n \) tane yan yüzü vardır ve bu yan yüzler birer üçgendir.
• Piramidin tabana paralel tüm kesitleri tabanla özdeş olmasa da aynı şekle sahiptir.

Piramit Tipleri

Piramitler saydığımız ortak özellikleri dışında iki özelliğe göre farklı şekillerde ve isimlerde olabilirler.

Taban Şekline Göre Piramitler

Piramitlerin tabanı düzgün olan ya da olmayan herhangi bir çokgen şeklinde olabilir.

• Üçgen tabanlar: Normal üçgen, eşkenar üçgen, ikizkenar üçgen, dik üçgen vb.
• Dörtgen tabanlar: Dikdörtgen, kare, eşkenar dörtgen, yamuk vb.
• Çokgen tabanlar: Beşgen, düzgün altıgen, düzgün sekizgen vb.

Düzgün piramitlerde taban düzgün çokgendir.

Dik ve Eğik Piramitler

Bir piramidin tepe noktasının taban üzerindeki izdüşümü tabanın merkez noktası ise bu piramide dik piramit denir. Bu izdüşüm farklı bir noktaya karşılık geliyorsa, bu piramide eğik piramit denir.

Hem dik hem de eğik piramitlerin yüksekliği, tepe noktasından tabana indirilen dik yüksekliğin uzunluğudur.

Piramitlerin İsimlendirmesi

Piramitler tabanlarının şekillerine ve dik/eğik olma durumlarına göre isimlendirilir (dik dikdörtgen piramit, eğik kare piramit, düzgün beşgen piramit vb.). Eğer bir piramidin isminde dik ya da eğik olduğu belirtilmemişse, piramidin dik olduğu varsayılabilir (bu notlarda biz de bu varsayımla ilerleyeceğiz).

Örnek Piramitler

Piramitler çok farklı tiplerde olabilse de, en çok karşılaşacağımız piramitler aşağıdadır.

Kare Piramit

Kare piramidin tabanı bir karedir.

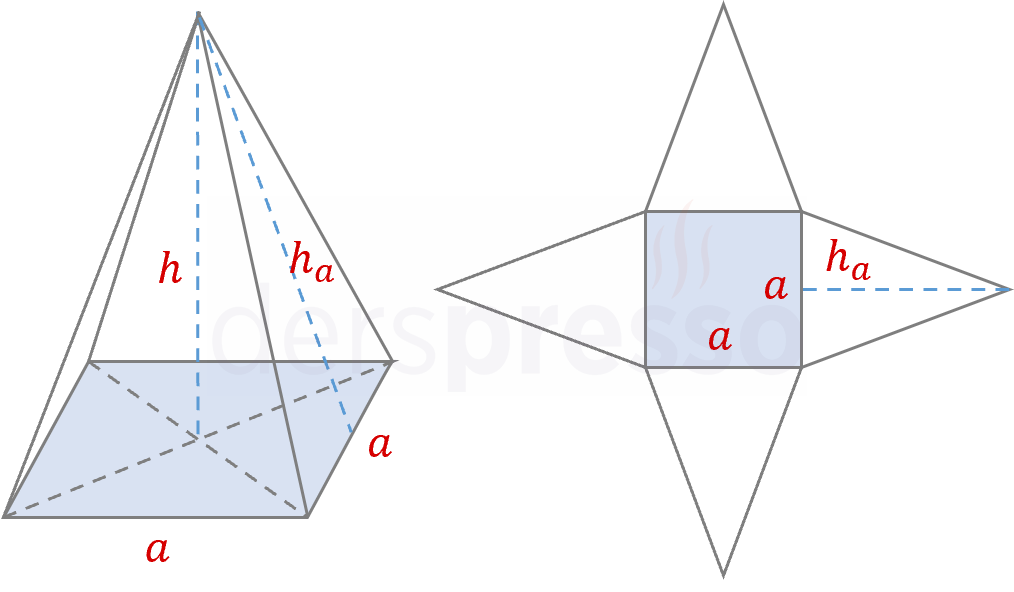
Kare piramidin dört yan yüzü vardır ve bu yan yüzler özdeş birer üçgendir.

Üçgen Piramit

Üçgen piramidin tabanı bir üçgendir.

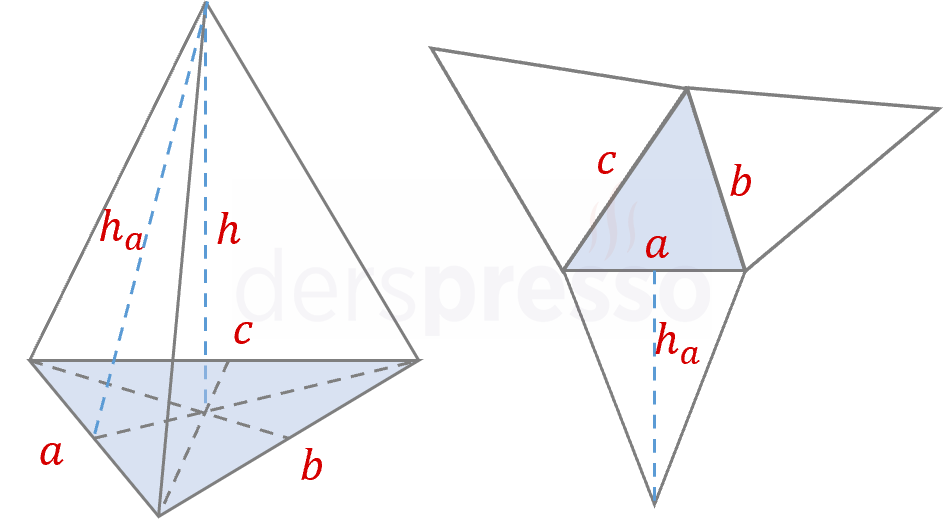
Üçgen piramidin üç yan yüzü vardır. Tabanın kenar uzunluklarına göre bu yan yüzler özdeş olabilir ya da olmayabilir.

Düzgün Dörtyüzlü

Düzgün dörtyüzlünün tabanı ve üç yan yüzü birer eşkenar üçgendir.

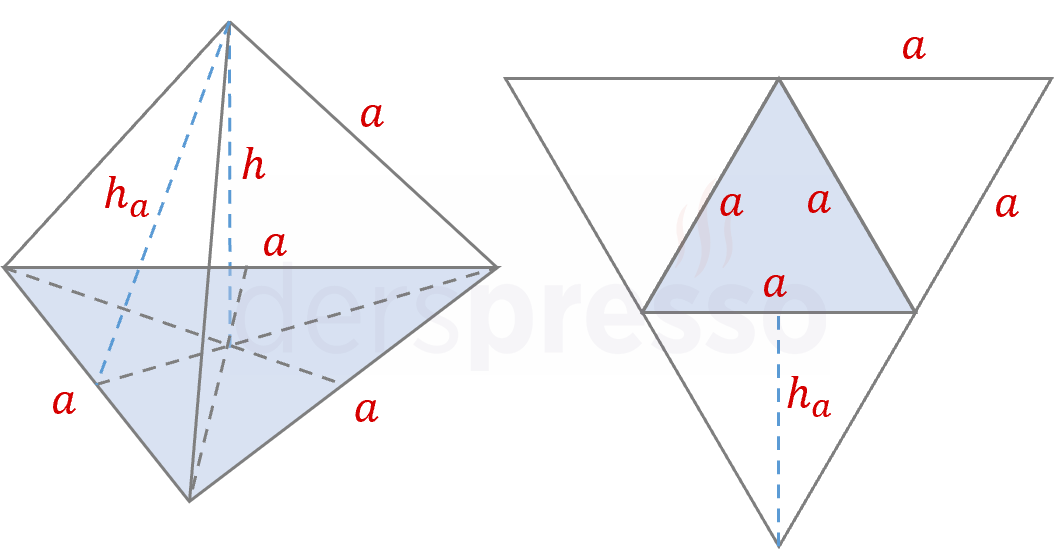
Düzgün dörtyüzlünün tüm yüzleri özdeştir.

Piramidin Yüzey Alanı

Piramidin toplam yüzey alanı, taban ve yan yüz (yanal) alanlarının toplamına eşittir. Her piramit tipi için ayrı bir alan formülü vermek yerine, aşağıdaki gibi genel bir formül vermeyi daha doğru buluyoruz.

Piramidin yüzey alan hesaplaması açısından önemli bazı noktalar şunlardır:

• Piramitlerin tüm yan yüzleri birer üçgendir.
• Dik piramitlerde uzunlukları eşit olan taban kenarlarına ait yan yüzlerin alanları birbirine eşittir.

Piramidin Hacmi

Dik ve eğik piramitlerin hacmi, taban alanı ve yüksekliğin çarpımının üçte birine eşittir. Eğik piramitlerde bahsettiğimiz gibi, hem dik hem de eğik piramitlerin yüksekliği, tepe noktasından tabana indirilen dik yüksekliğin uzunluğudur.