Prizma
Alt ve üst tabanları özdeş birer çokgen olan ve birbirine paralel iki düzlem üzerinde bulunan, bu iki taban arasındaki tüm paralel kesitleri de tabanlarla özdeş olan ve yan yüzleri düz olan cisme prizma denir.

Tüm prizmaların ortak özellikleri şunlardır:
- Alt ve üst tabanları özdeş birer çokgendir. Dolayısıyla, tabanları daire olan silindir bir prizma değildir.
- Alt ve üst tabanları birbirine paralel iki düzlem üzerinde bulunur. Buna göre, tabanları birbiriyle açı yapan cisimler prizma değildir.
- Alt ve üst tabanları arasındaki tüm paralel kesitleri de tabanlarla özdeştir.
- Yan yüzleri düzdür.
- Tabanları \( n \) kenarlı olan prizmanın \( n \) tane yan yüzü vardır ve bu yan yüzler birer paralelkenardır.
Prizma Tipleri
Prizmalar saydığımız ortak özellikleri dışında iki özelliğe göre farklı şekillerde ve isimlerde olabilirler.
Taban Şekline Göre Prizmalar
Prizmaların tabanları (ve tabanlara paralel olan kesitleri) düzgün olan ya da olmayan herhangi bir çokgen şeklinde olabilir.
- Üçgen tabanlar: Normal üçgen, eşkenar üçgen, ikizkenar üçgen, dik üçgen vb.
- Dörtgen tabanlar: Dikdörtgen, kare, eşkenar dörtgen, yamuk vb.
- Çokgen tabanlar: Beşgen, düzgün altıgen, düzgün sekizgen vb.
Dik ve Eğik Prizmalar
Bir prizmanın alt ve üst tabanlarını birleştiren yan yüzleri tabanlara dik ise bu prizmaya dik prizma denir. Yan yüzler tabanlara dik değilse, bu prizmaya eğik prizma denir. Prizmaların genel özelliği olan alt ve üst tabanların paralelliği, eğik prizmalar için de geçerlidir.

Dik prizmaların tüm yan yüzleri dikdörtgendir. Eğik prizmaların yan yüzlerinin bazıları paralelkenardır.
Hem dik hem de eğik prizmaların yüksekliği, alt ve üst paralel tabanlar arasındaki dik ve en kısa mesafedir.
Prizmaların İsimlendirmesi
Prizmalar tabanlarının şekillerine ve dik/eğik olma durumlarına göre isimlendirilir (dik dikdörtgen prizma, eğik kare prizma, dik ikizkenar üçgen prizma vb.). Eğer bir prizmanın isminde dik ya da eğik olduğu belirtilmemişse, prizmanın dik olduğu varsayılabilir (bu notlarda biz de bu varsayımla ilerleyeceğiz).
Örnek Prizmalar
Prizmalar çok farklı tiplerde olabilse de, en çok karşılaşacağımız prizmalar aşağıdadır. Taban kenarları ile yan yüzlerin ilişkisini daha net göstermek adına, prizmaların açılımları alt taban sabit kalacak şekilde verilmiştir.
Dikdörtgen Prizma
Dikdörtgen prizmanın alt ve üst tabanları özdeş birer dikdörtgendir.
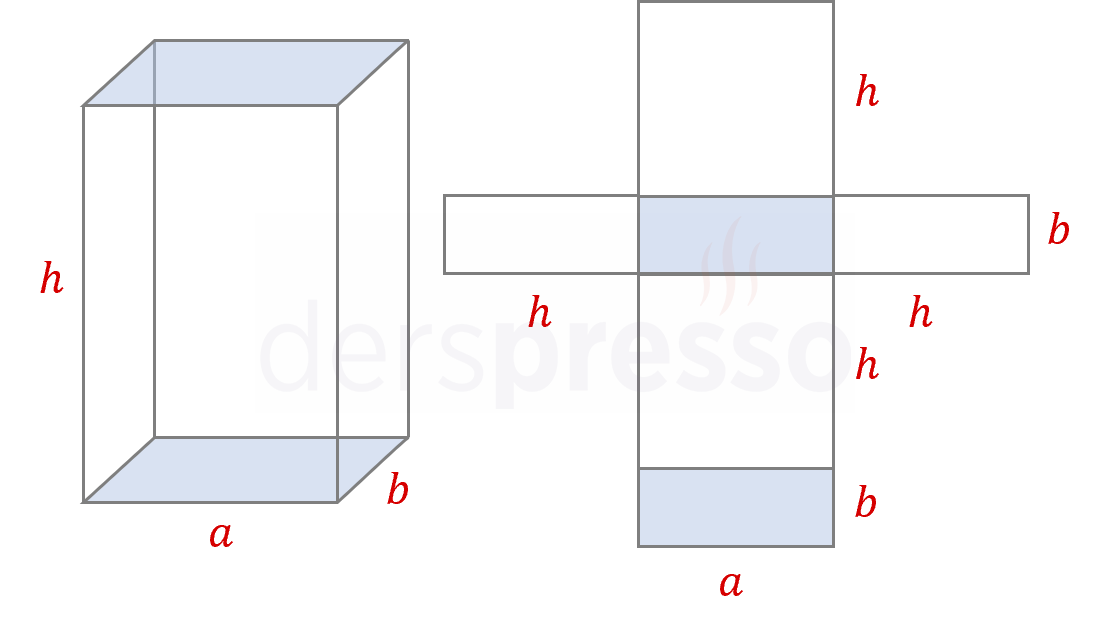
Dikdörtgen prizmanın dört yan yüzü vardır ve karşılıklı yüzler özdeştir.
Kare Prizma
Kare prizmanın alt ve üst tabanları özdeş birer karedir.

Kare prizmanın taban kenarları birbirine eşit, yüksekliği farklıdır. Kare prizmanın dört yan yüzü vardır ve tümü özdeştir.
Küp
Küpün alt ve üst tabanları özdeş birer karedir ve prizmanın yüksekliği tabanın bir kenar uzunluğuna eşittir.

Küpün tüm yüzleri özdeştir.
Üçgen Prizma
Üçgen prizmanın alt ve üst tabanları özdeş birer üçgendir.
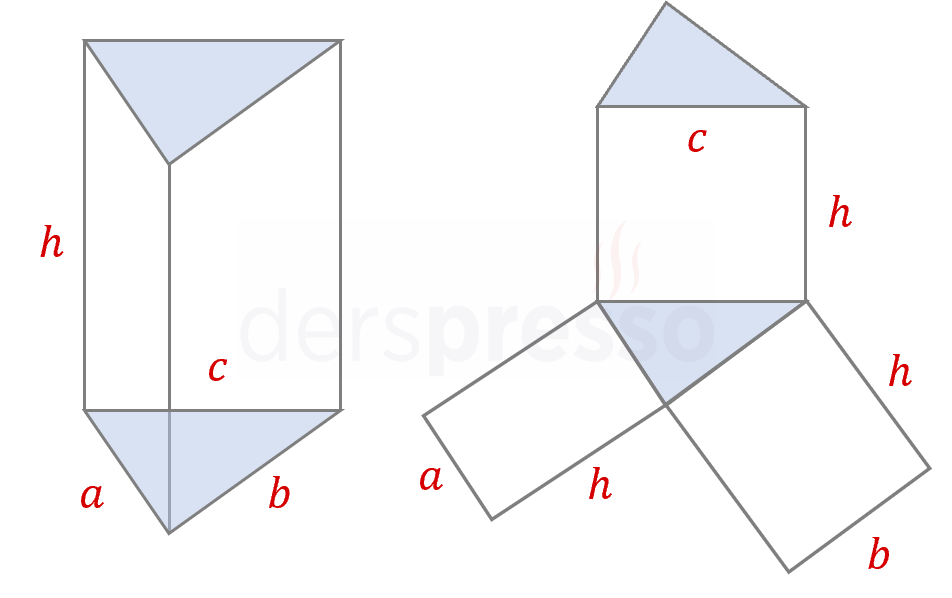
Üçgen prizmanın üç yan yüzü vardır ve bu yüzler tabanın kenar uzunluklarına göre özdeş ya da farklı olabilir.
Düzgün Beşgen Prizma
Düzgün beşgen prizmanın alt ve üst tabanları özdeş birer düzgün beşgendir.
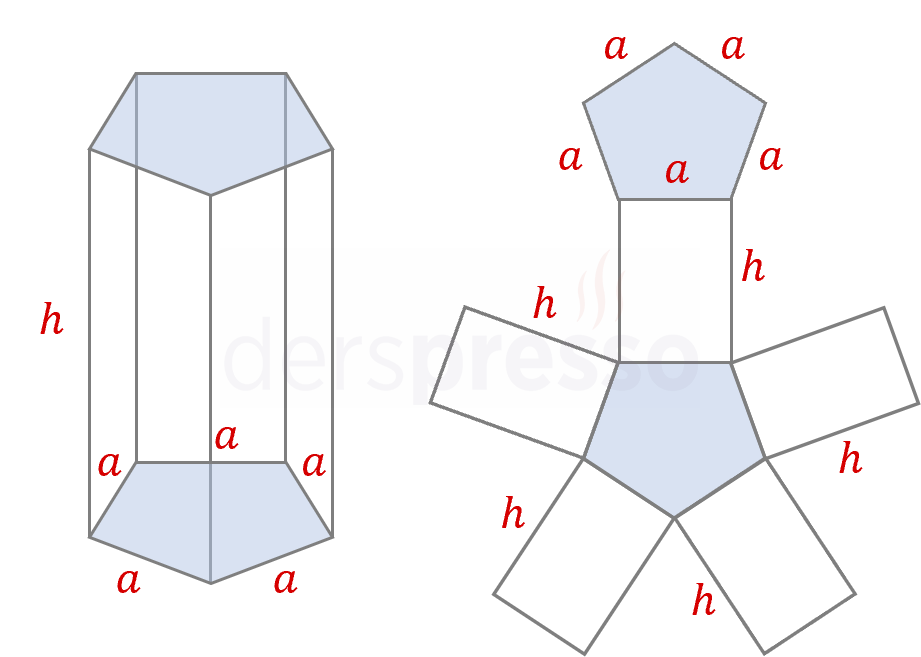
Düzgün beşgen prizmanın beş yan yüzü vardır ve kenar uzunlukları eşit olduğu için tümü özdeştir.
Prizmanın Yüzey Alanı
Prizmanın toplam yüzey alanı, taban ve yan yüz (yanal) alanlarının toplamına eşittir. Her prizma tipi için ayrı bir alan formülü vermek yerine, aşağıdaki gibi genel bir formül vermeyi daha doğru buluyoruz.
\( \text{Yüzey Alanı} = 2 \cdot \text{Taban Alanı} + \text{Yanal Alanlar} \)
Bir dik prizmanın yan yüzlerinin tümünün yüksekliği \( h \) olduğu ve yan yüzlerin genişlikler toplamı taban çevresine eşit olduğu için, yüzey alan formülünü aşağıdaki şekilde de yazabiliriz.
\( \text{Yüzey Alanı} = 2 \cdot \text{Taban Alanı} + \text{Taban Çevresi} \cdot h \)
Prizmanın yüzey alan hesaplaması açısından önemli bazı noktalar şunlardır:
- Prizmaların her iki tabanının alanları her zaman birbirine eşittir.
- Dik prizmalarda uzunlukları eşit olan taban kenarlarını birleştiren yan yüzlerin alanları birbirine eşittir.
- Buna göre, tabanları eşkenar üçgen, kare, eşkenar dörtgen ya da herhangi bir düzgün çokgen olan dik prizmaların tüm yan yüzlerinin alanları birbirine eşittir.
- Tabanları dikdörtgen ya da paralelkenar olan prizmaların karşılıklı yan yüzlerinin alanları birbirine eşittir.
- Dik prizmaların tüm yan yüzleri dikdörtgendir. Eğik prizmaların yan yüzlerinin bazıları paralelkenardır.
Prizmanın Hacmi
Dik ve eğik prizmaların hacmi, taban alanı ve yüksekliğin çarpımına eşittir. Eğik prizmalarda bahsettiğimiz gibi, hem dik hem de eğik prizmaların yüksekliği alt ve üst tabanlar arasındaki dik ve en kısa mesafedir.
\( \text{Hacim} = \text{Taban Alanı} \cdot \text{Yükseklik} \)
Prizmanın Köşegenleri
Taban Köşegeni
Dörtgenler bölümünde gördüğümüz gibi, taban köşegen uzunluğunu farklı taban tipleri için aşağıdaki formüllerle bulabiliriz.
Kare prizma ve küp:
\( \quad \text{Taban Köşegen Uzunluğu} = \sqrt{2} \cdot a \)
Dikdörtgen prizma:
\( \quad \text{Taban Köşegen Uzunluğu} = \sqrt{a^2 + b^2} \)
Cisim Köşegeni
Cisim köşegen uzunluğunu farklı prizma tipleri için aşağıdaki formüllerle bulabiliriz.
Küp:
\( \quad \text{Cisim Köşegen Uzunluğu} = \sqrt{3} \cdot a \)
Kare prizma:
\( \quad \text{Cisim Köşegen Uzunluğu} = \sqrt{2a^2 + h^2} \)
Dikdörtgen prizma:
\( \quad \text{Cisim Köşegen Uzunluğu} = \sqrt{a^2 + b^2 + h^2} \)
İki küpün hacimleri arasındaki oran \( t \) birimküp olduğuna göre, yüzey alanları arasındaki oran \( t \) cinsinden nedir?
Çözümü GösterKüplerin kenarlarına sırasıyla \( a \) ve \( b \) diyelim.
Bir kenar uzunluğu \( a \) olan küpün hacmi \( a^3 \), yüzey alanı \( 6a^2 \) olur.
İki küpün hacimleri arasındaki oran \( t \) olarak veriliyor.
\( t = (\dfrac{a}{b})^3 \)
\( \sqrt[3]{t} = \dfrac{a}{b} \)
Küplerin yüzey alanlarının birbirine oranını bulalım.
\( \dfrac{6a^2}{6b^2} = (\dfrac{a}{b})^2 \)
\( \dfrac{a}{b} \) oranı yerine bulduğumuz \( t \) değerini koyalım.
\( = (\sqrt[3]{t})^2 \)
\( = \sqrt[3]{t^2} \) bulunur.
Ayrıt uzunluğu 3 birim olan \( n \) adet özdeş küp, her birinin en az bir yüzeyi diğer bir küpün bir yüzeyiyle tam örtüşecek biçimde üst üste yapıştırılıyor.
Oluşan bu cismin cisim köşegeni \( 9\sqrt{3} \) olduğuna göre, \( n \) kaçtır?
Çözümü GösterEn alttaki küpün taban yüzeyinin köşegen uzunluğu \( \sqrt{3^2 + 3^2} = 3\sqrt{2} \) olur.
Üst üste \( n \) küpün yüksekliği ise \( 3n \) olur.
Oluşan büyük dik üçgene Pisagor teoremi uygulayalım.
\( (9\sqrt{3})^2 = (3\sqrt{2})^2 + (3n)^2 \)
\( 243 = 18 + 9n^2 \)
\( n = 5 \) bulunur.
Bir dikdörtgen prizmanın yüzey alanları sırasıyla 12, 12, 18, 18, 54, 54 birimkaredir.
Bu dikdörtgen prizmanın farklı uzunluktaki kenarlarının toplamı kaçtır?
Çözümü GösterDikdörtgen prizmanın farklı uzunluktaki kenarlarına sırasıyla \( a, b, c \) diyelim.
Yüzey alanlarını \( a, b, c \) cinsinden yazalım.
\( ab = 12, \quad bc = 18, \quad ac = 54 \)
İkinci ve üçüncü eşitlikleri taraf tarafa bölelim.
\( \dfrac{bc}{ac} = \dfrac{18}{54} \)
\( \dfrac{b}{a} = \dfrac{1}{3} \)
\( a = 3b \)
Birinci eşitlikte \( a = 3b \) koyalım.
\( ab = 12 \Longrightarrow 3b \cdot b = 12 \)
\( b^2 = 4 \)
\( b = 2 \)
Bulduğumuz \( b \) değerini kullanarak \( a \) ve \( c \) uzunluklarını bulalım.
\( ab = 12 \Longrightarrow a = 6 \)
\( bc = 18 \Longrightarrow c = 9 \)
\( a + b + c = 6 + 2 + 9 = 17 \) bulunur.
Dikdörtgenler prizması şeklindeki bir kolonun dikdörtgen yüzlerinin köşegen uzunlukları \( \sqrt{10} \), \( 3\sqrt{2} \) ve \( 4 \) cm'dir. Buna göre kolonun yüzey alanı kaçtır?
Çözümü GösterKöşegen uzunluklarını kullanarak kolonun kenar uzunluklarını bulalım.
Kolonun kenar uzunluklarına \( a \), \( b \) ve \( c \) dersek her yüze ait köşegen uzunluğunu hipotenüs teoremi kullanarak bulabiliriz.
\( a^2 + b^2 = (\sqrt{10})^2 = 10 \)
\( b^2 + c^2 = (3\sqrt{2})^2 = 18 \)
\( a^2 + c^2 = 4^2 = 16 \)
Tüm denklemleri alt alta toplayalım.
\( 2(a^2 + b^2 + c^2) = 44 \)
\( a^2 + b^2 + c^2 = 22 \)
Yukarıdaki denklemleri kullanarak kenar uzunluklarını bulalım.
\( a^2 + 18 = 22 \)
\( a = 2 \) cm
\( b^2 + 16 = 22 \)
\( b = \sqrt{6} \) cm
\( c^2 + 10 = 22 \)
\( c = \sqrt{12} = 2 \sqrt{3} \) cm
Kolonun yüzey alanını bulalım.
\( A = 2(ab + bc + ac) \)
\( = 2(2 \cdot \sqrt{6} + \sqrt{6} \cdot 2\sqrt{3} + 2 \cdot 2 \sqrt{3}) \)
\( = 4\sqrt{6} + 12\sqrt{2} + 8 \sqrt{3} \) cm bulunur.
180 \( m^3 \) su ile kısmen doldurulan dikdörtgen prizma şeklindeki bir kaptaki suyun derinliği, kabın hangi yüzeyi üzerinde durduğuna bağlı olarak 3 m, 4 m veya 6 m olmaktadır.
Buna göre, kabın hacmi \( m^3 \) cinsinden nedir?
Çözümü GösterKabın kenar uzunluklarına \( x \lt y \lt z \) olmak üzere \( x, y, z \) metre diyelim.
\( xyz \) çarpımı \( m^3 \) cinsinden kabın hacmini verir.
Soruda verilen bilgileri denklem şeklinde yazalım.
\( 6xy = 4xz = 3yz = 180 \)
\( xyz \) çarpımını elde etmek için bu eşitliğin üç tarafını birbiriyle çarpalım.
\( 6xy \cdot 4xz \cdot 3yz = 180^3 \)
\( 72(xyz)^2 = 180^3 \)
\( 72(xyz)^2 = 180 \cdot 180 \cdot 180 \)
\( (xyz)^2 = 90 \cdot 90 \cdot 10 \)
\( xyz = 90\sqrt{10} \)
Buna göre, kabın hacmi \( 90\sqrt{10} \) \( m^3 \) olarak bulunur.
Bir kenar uzunluğu 1 cm olan küçük küplerden bir kenar uzunluğu 13 cm olan büyük bir küp oluşturuluyor. Daha sonra bu küp bir boya kutusuna tamamen daldırılıp çıkarılıyor.
Büyük küpün içindeki küçük küplerden kaçının hiçbir yüzü boyanmamıştır?
Çözümü GösterBu soruyu 2 yöntemle çözebiliriz.
1. yöntem:
Büyük küp \( 13 \cdot 13 \cdot 13 = 2197 \) küçük küpten oluşur.
3 yüzü boyalı olan küçük küplerin sayısını bulalım.
3 yüzü boyalı olan küpler büyük küpün 8 köşesindeki küplerdir.
Buna göre 3 yüzü boyalı 8 küçük küp vardır.
2 yüzü boyalı olan küçük küplerin sayısını bulalım.
2 yüzü boyalı olan küpler küpün 12 ayrıtı üzerinde olup köşelerinde olmayan küplerdir.
Buna göre 2 yüzü boyalı \( 12 \cdot (13 - 2) = 132 \) küçük küp vardır.
1 yüzü boyalı olan küçük küplerin sayısını bulalım.
1 yüzü boyalı olan küpler küpün 6 yüzünün orta kısmında bulunan, ayrıtlar üzerinde bulunmayan küplerdir.
Buna göre her yüzdeki \( 13 \cdot 13 = 169 \) küpten \( 4 + 11 \cdot 4 = 48 \) küp ayrıtlar üzerindedir, dolayısıyla küpün bir yüzünde bu şekilde \( 169 - 48 = 121 \) küçük küp vardır.
Buna göre 1 yüzü boyalı \( 121 \cdot 6 = 726 \) küçük küp vardır.
Bulduğumuz adetleri toplarsak en az bir yüzü boyalı olan küplerin sayısı \( 8 + 132 + 726 = 866 \) olarak bulunur.
Hiçbir yüzü boyalı olmayan küplerin sayısı \( 2197 - 866 = 1331 \) olur.
2. yöntem:
Küpün dış yüzeyinde bulunan küçük küplerin en az bir yüzü boyalıdır. Dış yüzeydeki küçük küpleri attığımızda içteki küçük küplerin hiçbir yüzü boyalı değildir.
Dış yüzeydeki küpleri attığımızda elde edeceğimiz içteki küpün bir ayrıtında 11 küçük küp bulunur.
Bu içteki küp \( 11 \cdot 11 \cdot 11 = 1331 \) küçük küpten oluşur.