Kare
Tüm iç açıları dik açı ve kenar uzunlukları birbirine eşit olan dörtgene kare denir.

\( m(\widehat{A}) = m(\widehat{B}) = m(\widehat{C}) = m(\widehat{D}) = 90° \)
\( \abs{AB} = \abs{BC} = \abs{CD} = \abs{AD} = a \)
Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir karedir ve diğer özellikleri de taşır.
- Tüm iç açılar dik ve kenar uzunlukları eşit (kare tanımı)
- Köşegen uzunlukları eşit ve birbirine dik
Kare aynı zamanda bir paralelkenar, eşkenar dörtgen ve dikdörtgen olduğu için, dörtgenler, paralelkenar, eşkenar dörtgen, dikdörtgen bölümünde bahsettiğimiz tüm özellikler kare için de geçerlidir.
Karenin Kenar ve Köşegen Özellikleri
Karenin karşılıklı kenarları birbirine paraleldir ve tüm kenar uzunlukları birbirine eşittir.
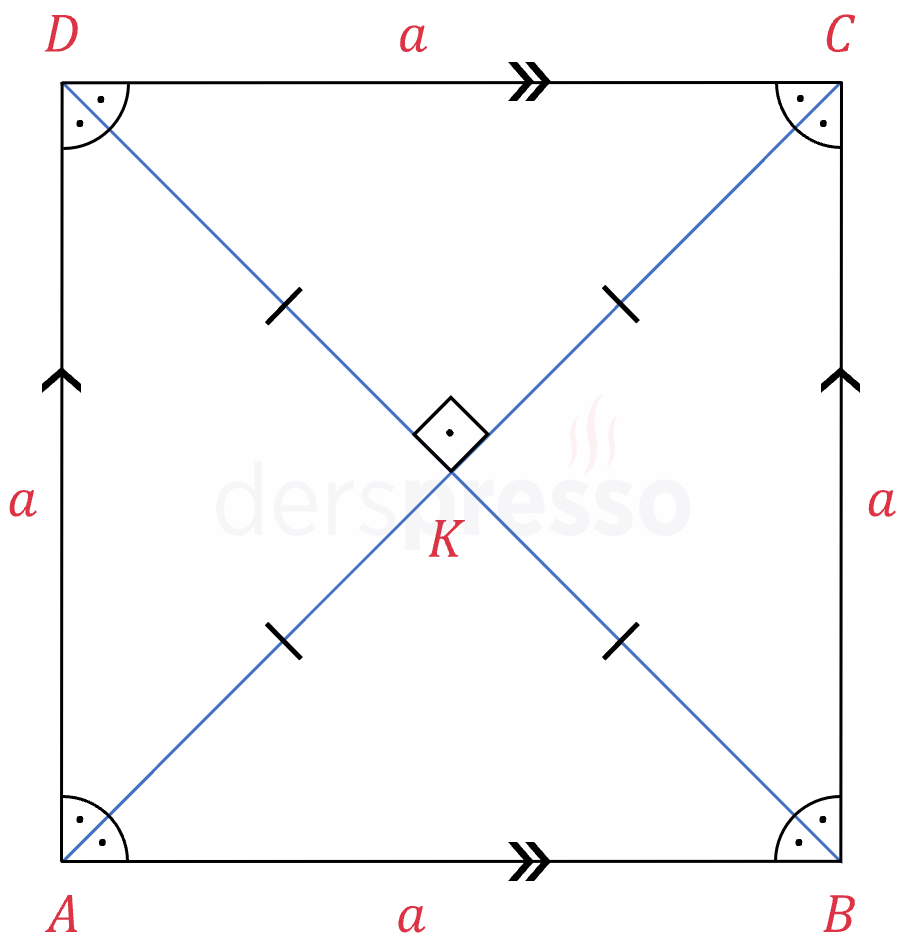
\( [AB] \parallel [DC] \) ve \( [AD] \parallel [BC] \)
\( \abs{AB} = \abs{BC} = \abs{CD} = \abs{AD} = a \)
Karenin köşegenleri birbirini ortalar, dik keser ve uzunlukları birbirine eşittir.
Karenin köşegen uzunluğu bir kenar uzunluğunun \( \sqrt{2} \) katıdır (Pisagor teoremi).
\( \abs{AC} = \abs{BD} = \sqrt{2}a \)
Karenin Açı Özellikleri
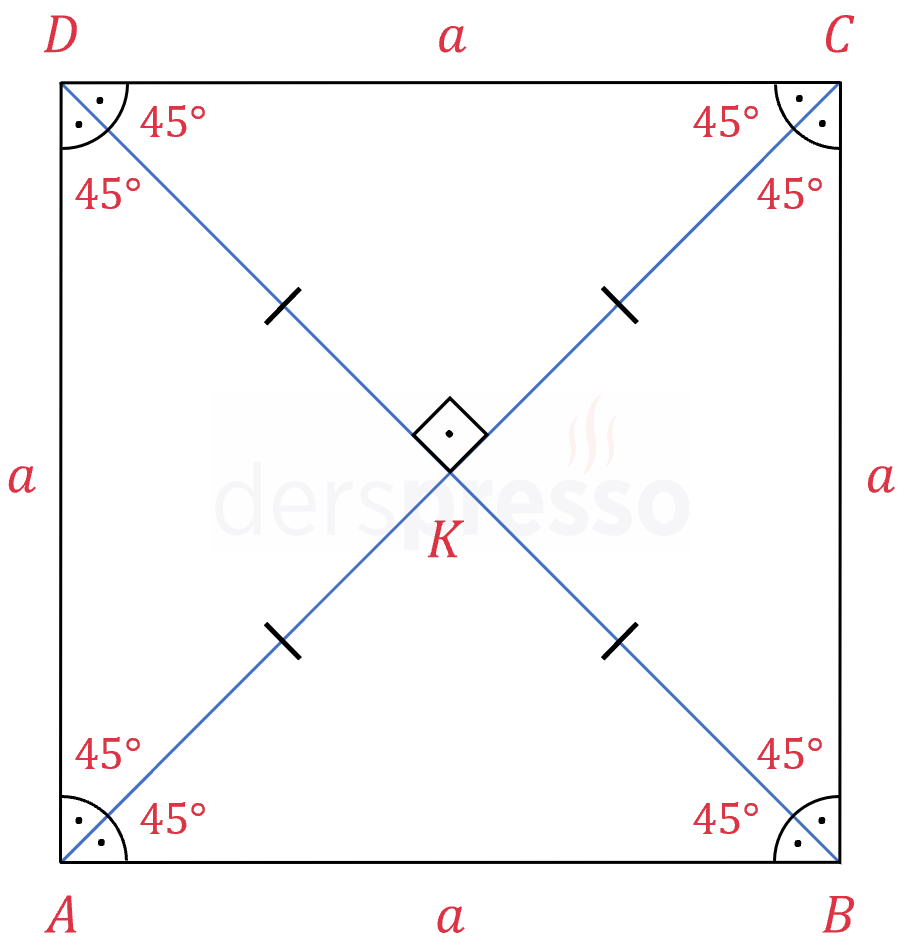
Tüm dörtgenlerde olduğu gibi, karenin hem iç açıları hem de dış açıları toplamı 360°'dir.
Karenin iç açıları eşit ve her biri 90°'dir.
\( m(\widehat{A}) = m(\widehat{B}) = m(\widehat{C}) = m(\widehat{D}) = 90° \)
Karenin köşegenleri her bir dik köşenin açıortayıdır.
Karenin Çevresi ve Alanı
Karenin çevresi, bir kenar uzunluğunun dört katına eşittir.
\( \text{Ç}(ABCD) = 4a \)
Karenin alanı, bir kenar uzunluğunun karesine eşittir.
\( A(ABCD) = a^2 \)
Karenin alanı aynı zamanda bir köşegen uzunluğunun karesinin yarısına eşittir.
Köşegenler karenin alanını dört eşit parçaya böler. Aşağıda bu kuralın tüm paralelkenarlar için geçerli olan ispatı verilmiştir.

\( A(ABK) = A(BCK) = A(CDK) = A(ADK) \)
İSPATI GÖSTER
\( ABC \) üçgeni paralelkenarla aynı tabana ve yüksekliğe sahip olduğu için, alanı paralelkenarın alanının yarısıdır.
\( A(ABC) = A(ADC) = \frac{1}{2} A(ABCD) \)
Paralelkenarda köşegenler birbirini ortaladığı için, \( ABK \) ve \( BCK \) üçgenlerinin \( [AC] \) köşegeni üzerindeki taban uzunlukları eşittir.
\( \abs{AK} = \abs{KC} \)
Bu iki üçgenin tepe noktaları aynı (\( B \) noktası) ve yükseklikleri eşit olduğu için, alanları da eşittir.
\( A(ABK) = A(BCK) = \frac{1}{2} A(ABC) \)
\( a, b \in \mathbb{Z^+} \) olmak üzere,
Bir karenin köşegeni \( a\sqrt{2} + b\sqrt{2} \) cm uzunluğundadır.
İkinci bir karenin alanı birinci karenin alanının dörtte biri olduğuna göre, ikinci karenin bir kenarı kaç cm'dir?
Çözümü GösterBir kenar uzunluğu \( x \) birim olan karenin köşegen uzunluğu \( x\sqrt{2} \) birim olur.
Buna göre birinci karenin bir kenar uzunluğu \( a + b \) cm, alanı \( (a + b)^2 \) cm\( ^2 \) olur.
İkinci karenin alanı birinci karenin alanının dörtte biri ise alanı \( \frac{(a + b)^2}{4} = (\frac{a + b}{2})^2 \) cm\( ^2 \) olur.
Buna göre, ikinci karenin bir kenarı \( \frac{(a + b)}{2} \) cm uzunluğundadır.

Yukarıdaki şekilde \( ABCD \) bir kare ve \( ALK \) bir eşkenar üçgendir.
\( ABCD \) birim kare olduğuna göre, \( ALK \) eşkenar üçgeninin bir kenarı kaç birimdir?
Çözümü Göster\( \abs{DK} = x \) birim diyelim.
Bu durumda \( \abs{KC} = 1 - x \) birim olur.
\( \abs{AD} = \abs{AB} = 1 \) ve \( \abs{AK} = \abs{AL} \) olduğu için iki dik üçgenin üçüncü kenarları da eş olur.
\( \abs{LB} = x \)
Bu durumda \( \abs{CL} = 1 - x \) birim olur.

\( ADK \) dik üçgenine Pisagor teoremini uygulayalım.
\( \abs{AK}^2 = x^2 + 1^2 \)
\( \abs{AK} = \sqrt{x^2 + 1} \)
\( KCL \) ikizkenar dik üçgeninin hipotenüs uzunluğunu bulalım.
\( \abs{KL} = (1 - x)\sqrt{2} \)
\( ALK \) eşkenar üçgen olduğu için bulduğumuz iki hipotenüs uzunluğu eşittir.
\( \abs{AK} = \abs{KL} \)
\( \sqrt{x^2 + 1} = (1 - x)\sqrt{2} \)
\( x^2 + 1 = 2x^2 - 4x + 2 \)
\( x^2 - 4x + 1 = 0 \)
İkinci dereceden denklemlerin kök bulma formülünü kullanalım.
\( x_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( = \dfrac{-(-4) \pm \sqrt{12}}{2} \)
\( = 2 \pm \sqrt{3} \)
Verilen kare birim kare olduğu için \( x \) birden küçük olmalıdır.
\( x = 2 - \sqrt{3} \)
\( ALK \) eşkenar üçgeninin bir kenar uzunluğu \( (1 - x)\sqrt{2} \) birimdir.
\( \abs{KL} = (1 - x)\sqrt{2} \)
\( = (\sqrt{3} - 1)\sqrt{2} \)
\( = \sqrt{6} - \sqrt{2} \) bulunur.

Özdeş 4 yamuk şekildeki gibi birleştirilerek bir çerçeve oluşturuluyor.
İçte ve dışta oluşan karelerin bir kenar uzunlukları oranı \( \frac{1}{3} \) olduğuna göre, içteki karenin alanının bir yamuğun alanına oranı kaçtır?
Çözümü Gösterİçteki karenin bir kenarına \( x \) dersek (yamuğun üst tabanı) dıştaki karenin bir kenarı \( 3x \) olur (yamuğun alt tabanı) .
Buna göre içteki karenin alanı \( x^2 \), dıştaki karenin alanı \( (3x)^2 = 9x^2 \) bulunur, dolayısıyla iki kare arasında kalan ve 4 eş yamuğun birleşiminden oluşan toplam alan \( 9x^2 - x^2 = 8x^2 \) olur.
4 eş yamuktan birinin alanı \( \frac{8x^2}{4} = 2x^2 \) olur.
İçteki karenin alanının bir yamuğun alanına oranı \( \frac{x^2}{2x^2} = \frac{1}{2} \) olarak bulunur.
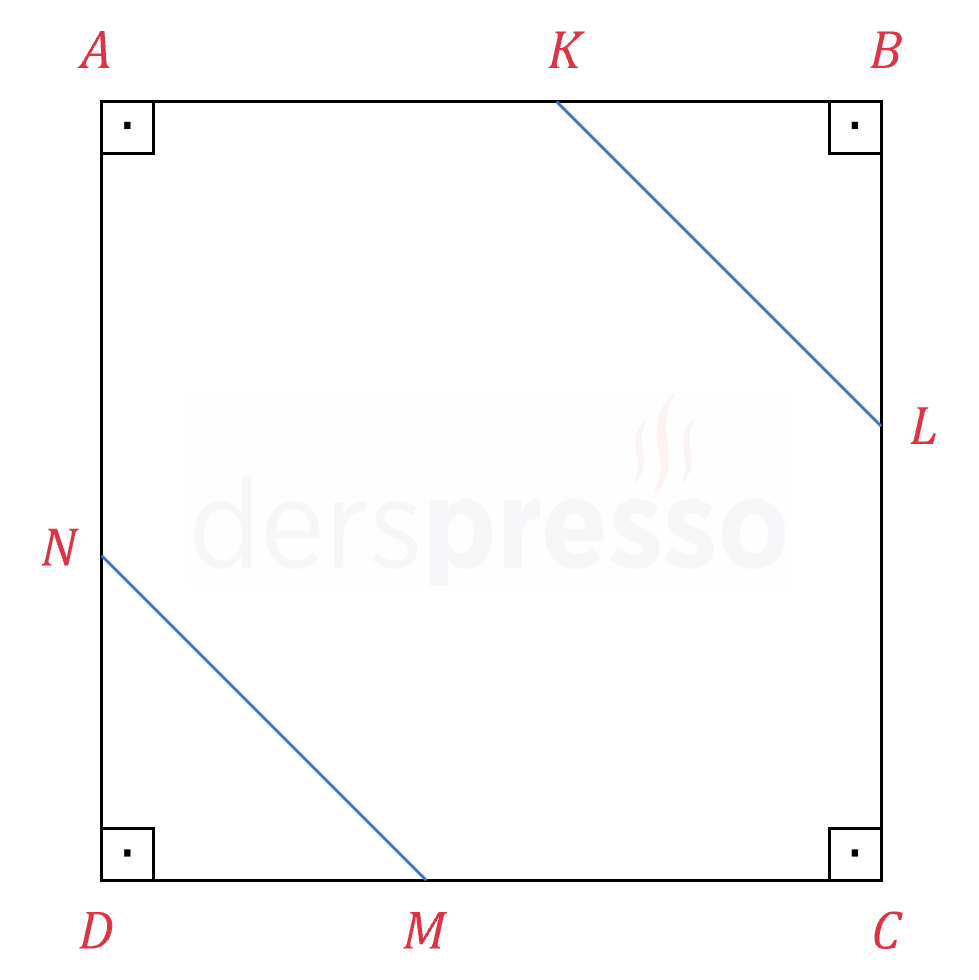
Şekildeki \( ABCD \) karesinin bir kenar uzunluğu 4 birimdir.
\( ABCD \) karesinin kenarları üzerinde bulunan \( K, L, M, N \) noktalarının oluşturduğu eşkenar \( AKLCMN \) altıgeninin bir kenar uzunluğu kaçtır?
Çözümü GösterAltıgenin bir kenar uzunluğuna \( a \) diyelim.
\( \abs{KB} = \abs{BL} = \abs{MD} = \abs{DN} = 4 - a \)
\( KBL \) ve \( MDN \) ikizkenar dik üçgenlerdir.
\( KBL \) ve \( MDN \) üçgenleri 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
Bu noktada verilen altıgenin eşkenar olduğuna, ama düzgün (eşkenar ve eş açılı) olmadığına dikkat edilmelidir.
\( \abs{KL} = \sqrt{2}\abs{KB} \)
\( a = \sqrt{2}(4 - a) \)
\( a = 4\sqrt{2} - \sqrt{2}a \)
\( a = \dfrac{4\sqrt{2}}{\sqrt{2} + 1} \)
Payı ve paydayı paydanın eşleniği olan \( \sqrt{2} - 1 \) ile çarpalım.
\( = \dfrac{4\sqrt{2}(\sqrt{2} - 1)}{(\sqrt{2} + 1)(\sqrt{2} - 1)} \)
\( = 8 - 4\sqrt{2} \) bulunur.
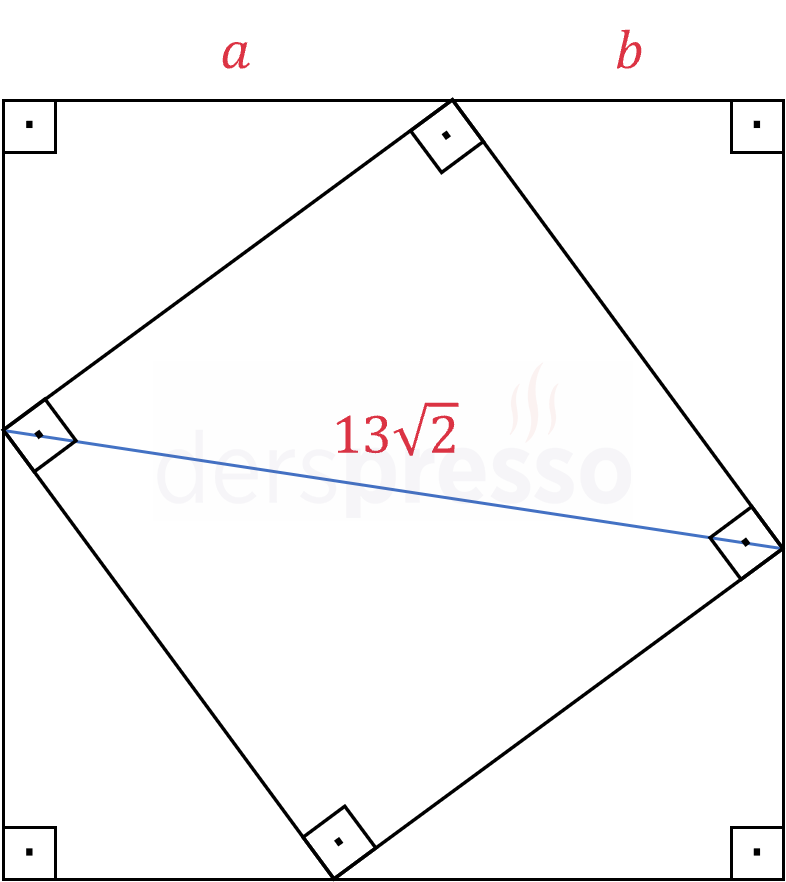
Köşegen uzunluğu \( 13\sqrt{2} \) cm olan bir kare, alanı 289 cm\( ^2 \) olan başka bir karenin içerisine şekildeki gibi yerleştiriliyor. İçteki karenin köşeleri dıştaki karenin kenarlarını uzunlukları \( a \) ve \( b \) cm olacak şekilde ikiye bölmektedir. Buna göre \( \frac{a}{b} \) oranı nedir?
Çözümü GösterKarenin kenarları eşit uzunlukta olduğu için dıştaki karenin tüm kenarları \( a + b \) cm olur.
Oluşan 4 üçgen eş üçgenler olduğu için içteki karenin tüm köşeleri dıştaki karenin kenarlarını uzunlukları \( a \) ve \( b \) cm olacak şekilde ikiye böler.
Dıştaki karenin alanı 289 cm\( ^2 \) olarak veriliyor.
\( (a + b)^2 = 289 \)
\( a + b = 17 \) cm
İçteki karenin bir kenar uzunluğuna \( c \) diyelim.

İçteki karenin köşegen uzunluğu \( 13\sqrt{2} \) cm olarak veriliyor.
Pisagor teoremini kullanarak \( c \) değerini bulalım.
\( c^2 + c^2 = (13\sqrt{2})^2 \)
\( 2c^2 = 13^2 \cdot 2 \)
\( c = 13 \) cm
Kenar uzunlukları \( a \), \( b \) ve \( c \) olan dik üçgenlerde de Pisagor teoremini kullanalım.
\( a^2 + b^2 = c^2 \)
\( a^2 + b^2 = 13^2 = 169 \)
\( a^2 + b^2 \) ifadesini aşağıdaki şekilde yazabiliriz.
\( a^2 + b^2 = (a + b)^2 - 2ab \)
Bildiğimiz değerleri bu eşitlikte yerine yazalım.
\( 169 = 17^2 - 2ab \)
\( ab = 60 \)
Soruda \( \frac{a}{b} \) oranı isteniyor.
Bu oranı bulabilmek için önce \( a - b \) ifadesinin değerini bulalım.
\( a^2 + b^2 \) ifadesini aşağıdaki şekilde de yazabiliriz.
\( a^2 + b^2 = (a - b)^2 + 2ab \)
Bildiğimiz değerleri bu eşitlikte yerine yazalım.
\( 169 = (a - b)^2 + 2 \cdot 60 \)
\( (a - b)^2 = 169 - 120 \)
\( a - b = 7 \)
\( a + b = 17 \) ve \( a - b = 7 \) denklemlerini taraf tarafa toplayarak \( a \) ve \( b \) değerlerini bulalım.
\( a = 12, \quad b = 5 \)
\( \dfrac{a}{b} = \dfrac{12}{5} \) bulunur.