Dikdörtgen
Tüm iç açıları dik açı olan dörtgene dikdörtgen denir.

\( m(\widehat{A}) = m(\widehat{B}) = m(\widehat{C}) = m(\widehat{D}) = 90° \)
Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir dikdörtgendir ve diğer özellikleri de taşır.
- Tüm iç açıları dik (dikdörtgen tanımı)
- Köşegen uzunlukları eşit ve birbirini ortalıyor.
- Karşılıklı kenarlar paralel ve köşegen uzunlukları eşit
- Karşılıklı kenarlar paralel ve iç açıların en az biri dik açı
Dikdörtgen aynı zamanda bir paralelkenar olduğu için, dörtgen ve paralelkenar bölümünde bahsettiğimiz tüm özellikler dikdörtgen için de geçerlidir.
Giriş bölümünde paylaştığımız dörtgen hiyerarşisine göre; kare dikdörtgenin ek özelliklere sahip özel birer durumu olarak düşünülebilir.
Dikdörtgenin Kenar ve Köşegen Özellikleri
Dikdörtgenin karşılıklı kenarları birbirine paraleldir ve uzunlukları eşittir.

\( [AB] \parallel [DC] \) ve \( [AD] \parallel [BC] \)
\( \abs{AB} = \abs{DC} = a \)
\( \abs{AD} = \abs{BC} = b \)
Dikdörtgenin köşegenleri birbirini ortalar ve uzunlukları birbirine eşittir.

\( \abs{AK} = \abs{KC} = \abs{DK} = \abs{KB} \)
Tüm dörtgenlerde kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır, köşegen uzunlukları eşit olan dikdörtgende bu dörtgen bir eşkenar dörtgendir. Varignon paralelkenarı adı verilen bu dörtgenle ilgili daha fazla bilgi ve dikdörtgende de geçerli olan özellikleri için dörtgenler sayfasını inceleyebilirsiniz.

Dikdörtgenin iç ve dış bölgesinden seçilen bir noktadan (\( P \) noktası) köşelere çizilen doğru parçalarının uzunlukları arasında aşağıdaki bağıntı vardır.
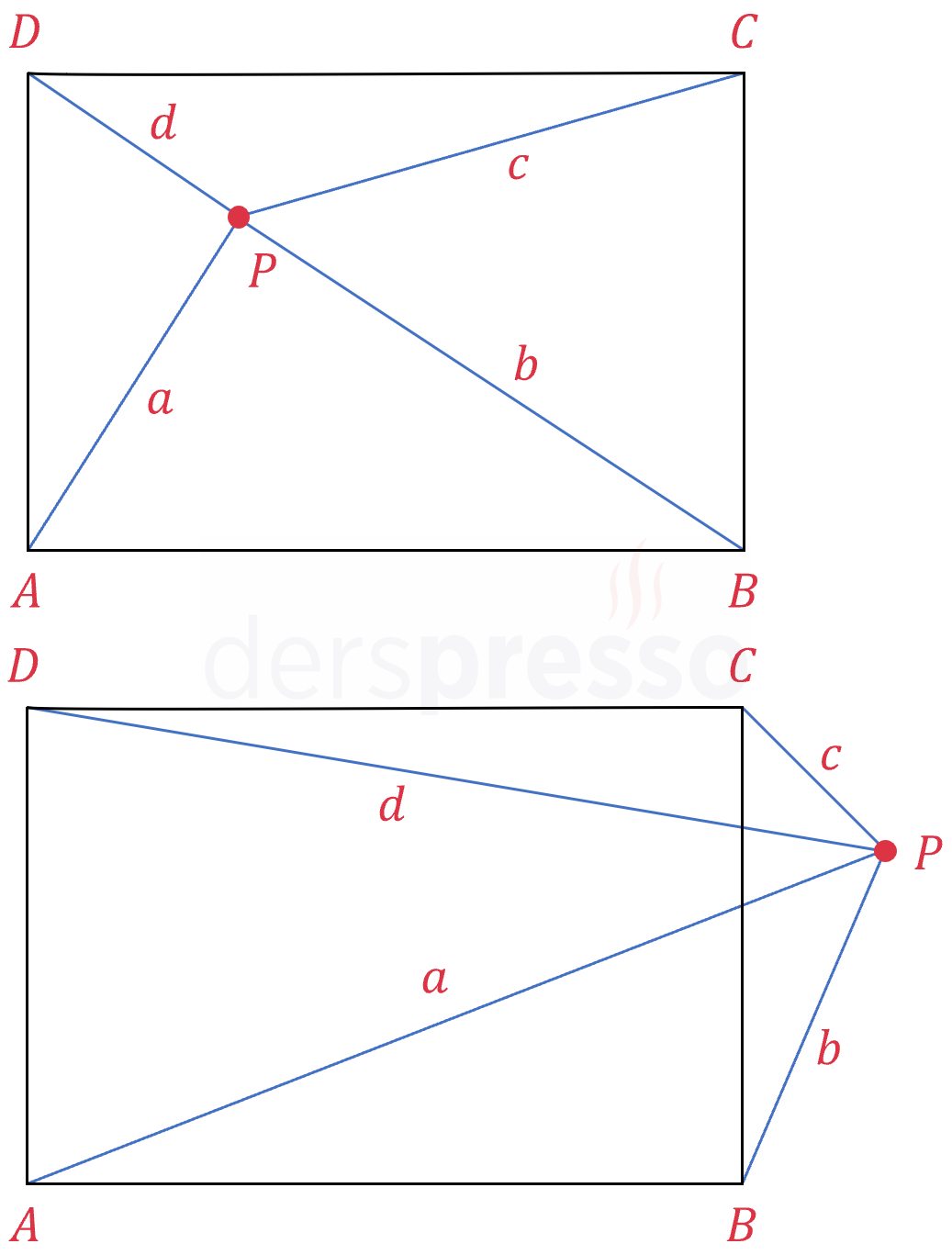
\( a^2 + c^2 = b^2 + d^2 \)
İSPATI GÖSTER
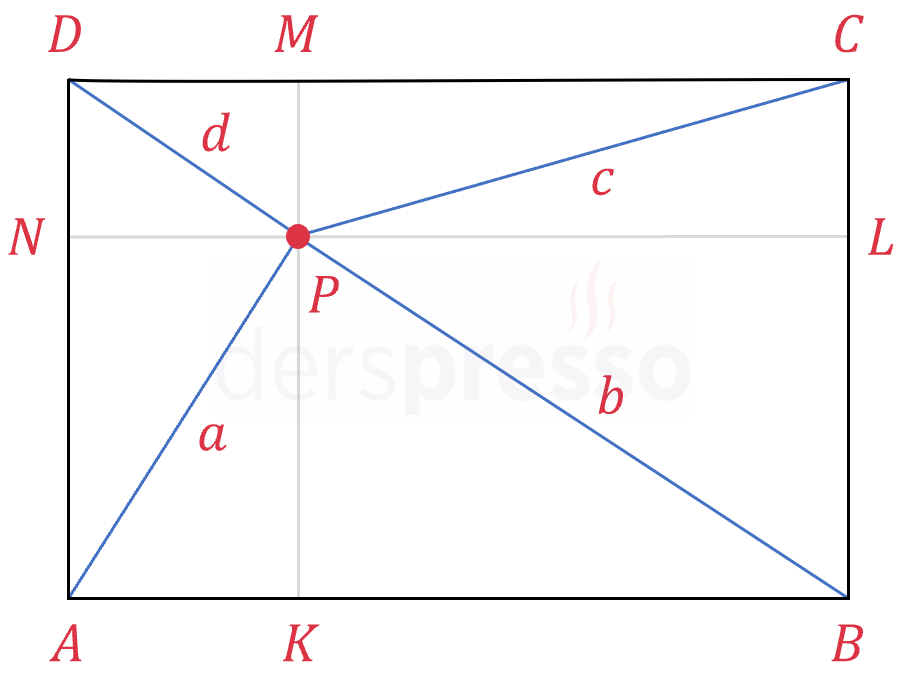
Dikdörtgenin içinde bir nokta için:
\( P \) noktasından geçen ve dikdörtgenin kenarlarına paralel \( [KM] \) ve \( [LN] \) doğrularını çizelim (kesikli gri çizgiler).
Eşitlikteki her bir kenar için Pisagor formülünü yazalım.
\( a^2 = \abs{AK}^2 + \abs{KP}^2 \)
\( b^2 = \abs{BK}^2 + \abs{KP}^2 \)
\( c^2 = \abs{CM}^2 + \abs{MP}^2 \)
\( d^2 = \abs{DM}^2 + \abs{MP}^2 \)
Aşağıdaki eşitlikleri dikkate alarak 2. ve 4. eşitlikleri tekrar yazalım.
\( \abs{BK} = \abs{CM} \)
\( \abs{DM} = \abs{AK}\)
\( b^2 = \abs{CM}^2 + \abs{KP}^2 \)
\( d^2 = \abs{AK}^2 + \abs{MP}^2 \)
\( a^2 + c^2 = b^2 + d^2 \) eşitliğindeki terimlerin karşılıklarını yazarsak her iki tarafın eşit olduğunu görürüz.
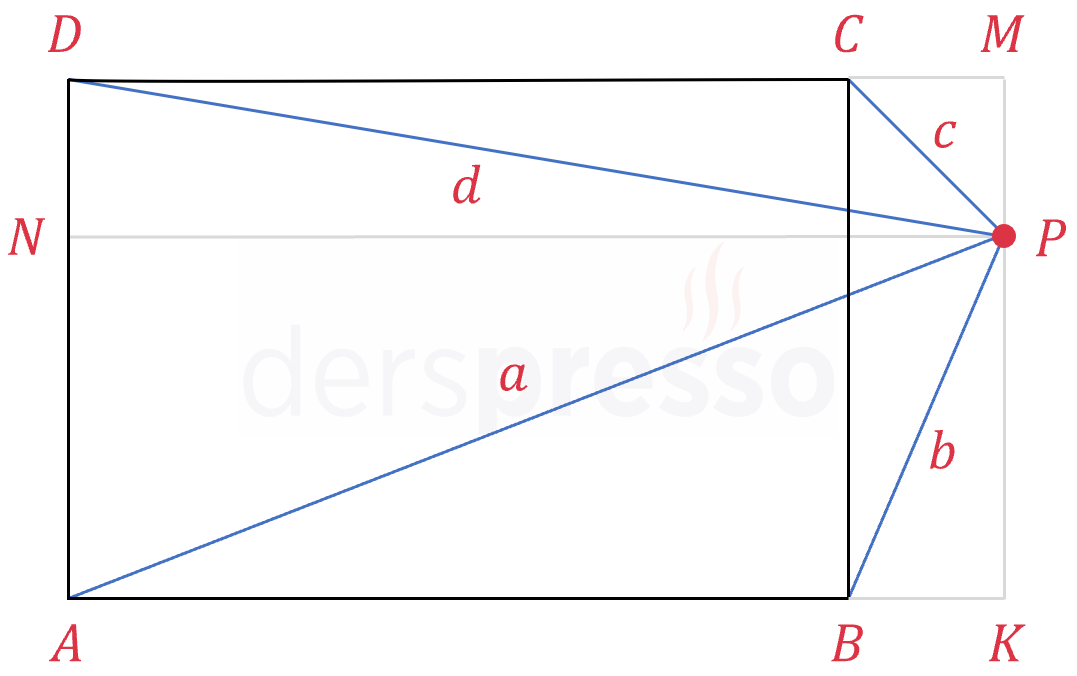
Dikdörtgenin dışında bir nokta için:
\( P \) noktasından geçen ve dikdörtgenin kenarlarına paralel \( [KM] \) ve \( [PN] \) doğrularını çizelim (kesikli gri çizgiler).
Eşitlikteki her bir kenar için Pisagor formülünü yazalım.
\( a^2 = \abs{AK}^2 + \abs{KP}^2 \)
\( b^2 = \abs{BK}^2 + \abs{KP}^2 \)
\( c^2 = \abs{CM}^2 + \abs{MP}^2 \)
\( d^2 = \abs{DM}^2 + \abs{MP}^2 \)
Aşağıdaki eşitlikleri dikkate alarak 2. ve 4. eşitlikleri tekrar yazalım.
\( \abs{BK} = \abs{CM} \)
\( \abs{DM} = \abs{AK}\)
\( b^2 = \abs{CM}^2 + \abs{KP}^2 \)
\( d^2 = \abs{AK}^2 + \abs{MP}^2 \)
\( a^2 + c^2 = b^2 + d^2 \) eşitliğindeki terimlerin karşılıklarını yazarsak her iki tarafın eşit olduğunu görürüz.
Dikdörtgenin Açı Özellikleri
Tüm dörtgenlerde olduğu gibi, dikdörtgenin hem iç açıları hem de dış açıları toplamı 360°'dir.
Dikdörtgenin tüm iç açıları eşit ve 90°'dir.
\( m(\widehat{A}) = m(\widehat{B}) = m(\widehat{C}) = m(\widehat{D}) = 90° \)
Dikdörtgenin Çevresi ve Alanı

Dikdörtgenin çevresi, kısa ve uzun kenar uzunlukları toplamının iki katına eşittir.
\( \text{Ç}(ABCD) = 2(a + b) \)
Dikdörtgenin alanı, kısa ve uzun kenar uzunluklarının çarpımına eşittir.
\( A(ABCD) = a \cdot b \)
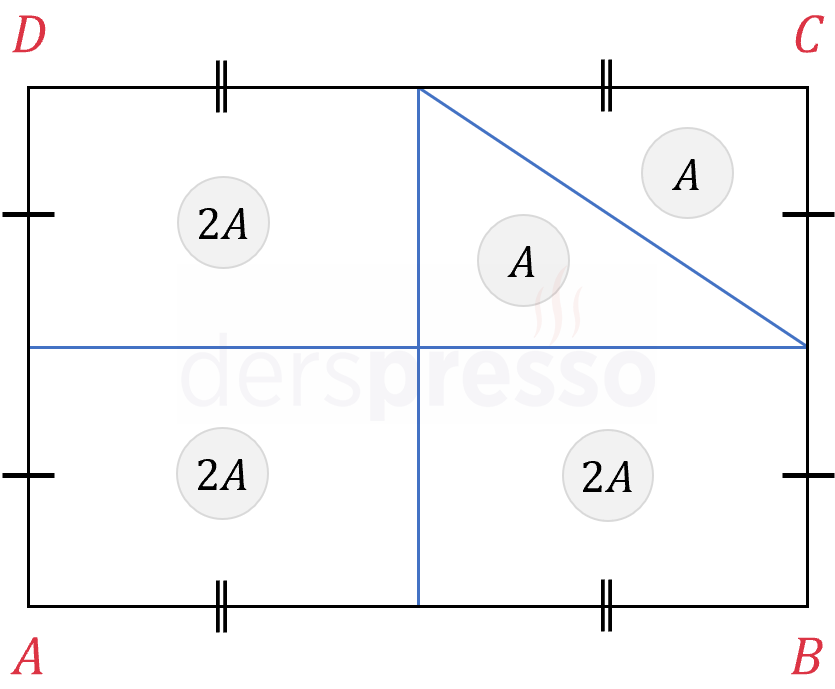
Köşegenler dikdörtgenin alanını dört eşit parçaya böler. Aşağıda bu kuralın tüm paralelkenarlar için geçerli olan ispatı verilmiştir.

\( A(ABK) = A(BCK) = A(CDK) = A(ADK) \)
İSPATI GÖSTER
\( ABC \) üçgeni paralelkenarla aynı tabana ve yüksekliğe sahip olduğu için, alanı paralelkenarın alanının yarısıdır.
\( A(ABC) = A(ADC) = \frac{1}{2} A(ABCD) \)
Paralelkenarda köşegenler birbirini ortaladığı için, \( ABK \) ve \( BCK \) üçgenlerinin \( [AC] \) köşegeni üzerindeki taban uzunlukları eşittir.
\( \abs{AK} = \abs{KC} \)
Bu iki üçgenin tepe noktaları aynı (\( B \) noktası) ve yükseklikleri eşit olduğu için, alanları da eşittir.
\( A(ABK) = A(BCK) = \frac{1}{2} A(ABC) \)
Bir dikdörtgenin farklı noktaları arasında çizilen doğru parçaları, dikdörtgenin alanını aşağıda belirtilen oranlarda böler.


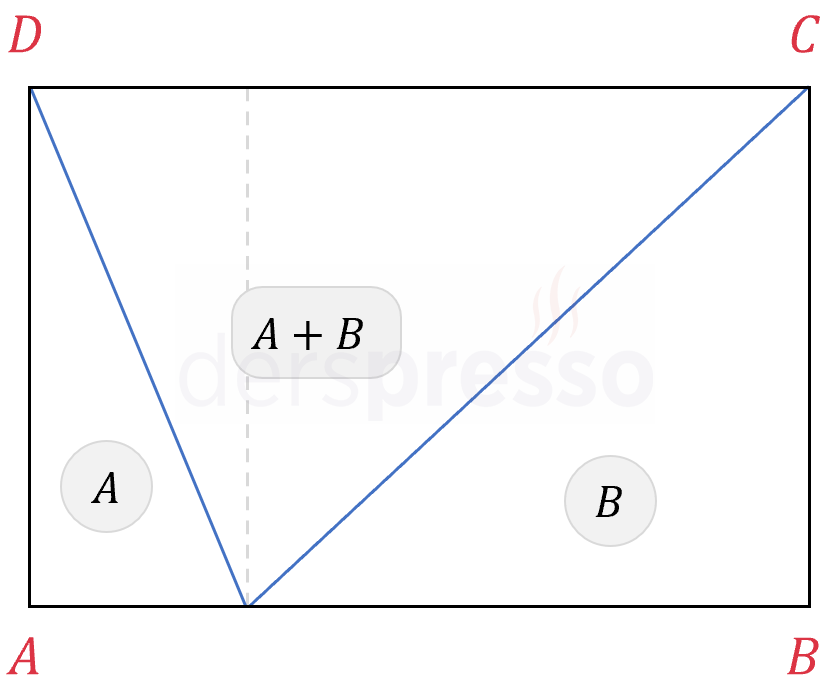

Bir dikdörtgen şekildeki gibi beş eşit dikdörtgene bölünüyor. Küçük dikdörtgenlerin her biri büyük dikdörtgen ile benzerdir.
Buna göre büyük dikdörtgenin uzun kenarının kısa kenarına oranı kaçtır?
Çözümü GösterKüçük dikdörtgenlerin kısa kenarlarına \( a \), uzun kenarlarına \( b \) diyelim.
\( a \gt b \)

Büyük dikdörtgende uzun kenar uzunluğu \( 5a \), kısa kenar uzunluğu \( b \) olur.
\( 5a \gt b \)
Küçük dikdörtgende uzun kenarın kısa kenara oranı, büyük dikdörtgende uzun kenarın kısa kenara oranına eşittir.
\( \dfrac{b}{a} = \dfrac{5a}{b} \)
\( b^2 = 5a^2 \)
\( b = \sqrt{5}a \)
Büyük dikdörtgende uzun kenarın kısa kenara oranını bulalım.
\( \dfrac{5a}{b} = \dfrac{5a}{\sqrt{5}a} = \sqrt{5} \)
Bu oranın küçük dikdörtgende de aynı olduğunu kontrol edelim.
\( \dfrac{b}{a} = \dfrac{\sqrt{5}a}{a} = \sqrt{5} \)

\( 25 \times 40 \) cm boyutlarında bir çerçevenin tüm kenarları boyunca eşit genişlikte kenar boşluğu bulunmaktadır. Kenar boşluklarının kapladığı alan çerçevenin toplam alanının %30'u olduğuna göre, kenar boşluğunun genişliği nedir?
Çözümü GösterÇerçevenin toplam alanını bulalım.
\( 25 \times 40 = 1000 \) cm\( ^2 \)
Kenar boşluklarının alanı çerçevenin alanının %30'u olduğuna göre, çerçevenin kenar boşlukları hariç alanı 700 cm\( ^2 \) olmalıdır.
Kenar boşluğunun genişliğine \( x \) diyelim.
Kenar boşluklarının içinde kalan alanı bulalım.
\( (25 - 2x)(40 - 2x) = 700 \)
\( 1000 - 50x - 80x + 4x^2 = 700 \)
\( 2x^2 - 65x + 150 = 0 \)
\( (2x - 5)(x - 30) = 0 \)
\( x = \dfrac{5}{2} \) ya da \( x = 30 \)
Çerçeve \( 25 \times 40 \) cm boyutlarında olduğu için \( x = 30 \) olamaz, dolayısıyla \( x = \frac{5}{2} \) olmalıdır.
Buna göre, kenar boşluğunun genişliği \( \frac{5}{2} = 2,50 \) cm olarak bulunur.
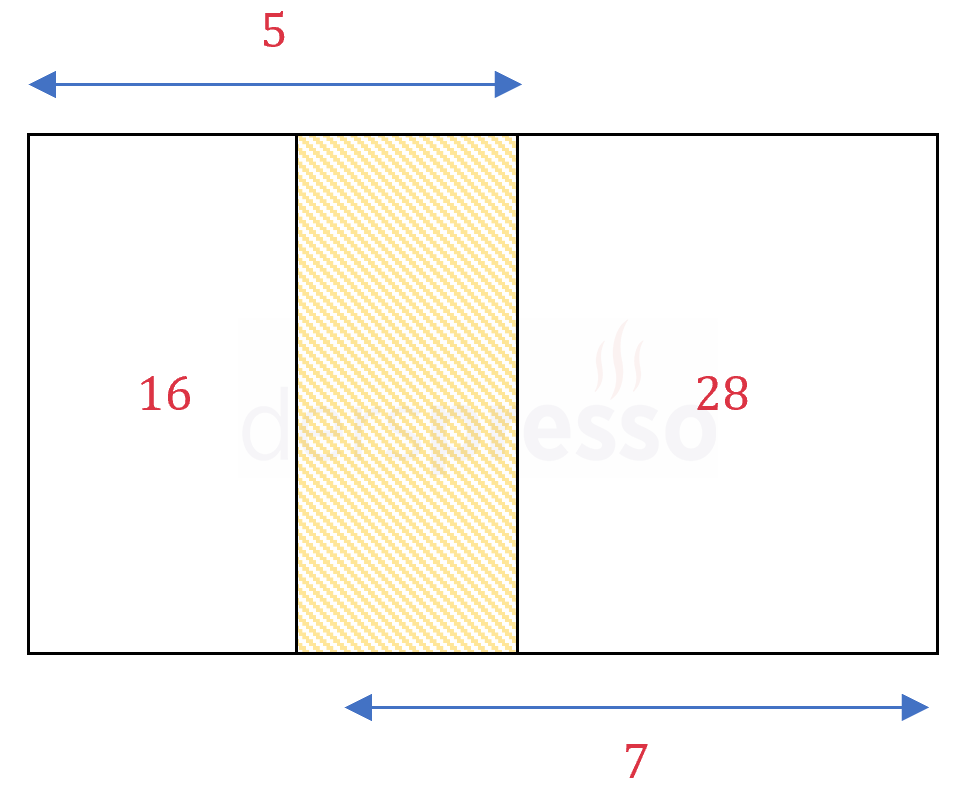
Yukarıdaki şekilde üç dikdörtgene bölünmüş bir dikdörtgen vardır.
Şekilde verilen uzunluk ve alanlara göre, ortadaki dikdörtgenin alanı kaçtır?
Çözümü GösterOrtadaki dikdörtgenin alanına \( A \), dikdörtgenlerin yüksekliklerine \( h \) diyelim.
Dikdörtgenlerin alan formüllerini yazalım.
\( 16 + A = 5h \)
\( 28 + A = 7h \)
İkinci denklemden birinci denklemi taraf tarafa çıkaralım.
\( 28 + A - (16 + A) = 7h - 5h \)
\( h = 6 \)
Bulduğumuz \( h \) değerini birinci denklemde yerine yazalım.
\( 16 + A = 5h \)
\( 16 + A = 30 \)
\( A = 14 \) bulunur.

Salih dikdörtgen şeklindeki tarlasını şekildeki gibi 9 eş dikdörtgene bölüyor.
Tarlanın çevresi 230 metre olduğuna göre, alanı nedir?
Çözümü GösterEş dikdörtgenlerin kısa kenarlarının uzunluklarına \( x \) metre, uzun kenarlarının uzunluklarına \( y \) metre diyelim.
Şekilden yararlanarak \( x \) ve \( y \) arasındaki ilişkiyi yazalım.
\( 7x = 2y \)
\( \dfrac{x}{y} = \dfrac{2}{7} \)
Eş dikdörtgenlerin kenar uzunlukları arasındaki oran \( 2 : 7 \) olduğuna göre, kısa kenarların uzunluklarına \( 2a \), uzun kenarların uzunluklarına \( 7a \) diyebiliriz.
Büyük dikdörtgenin çevresini \( a \) cinsinden hesaplayalım ve 230'a eşitleyelim.
\( 2(7a + 7a + 2a + 7a) = 230 \)
\( 46a = 230 \)
\( a = 5 \)
Büyük dikdörtgenin kenar uzunluklarını bulalım.
\( 7a + 7a = 14a \)
\( = 14 \cdot 5 = 70 \)
\( 2a + 7a = 9a \)
\( = 9 \cdot 5 = 45 \)
Büyük dikdörtgenin alanını hesaplayalım.
\( 70 \cdot 45 = 3150 \) metrekare bulunur.
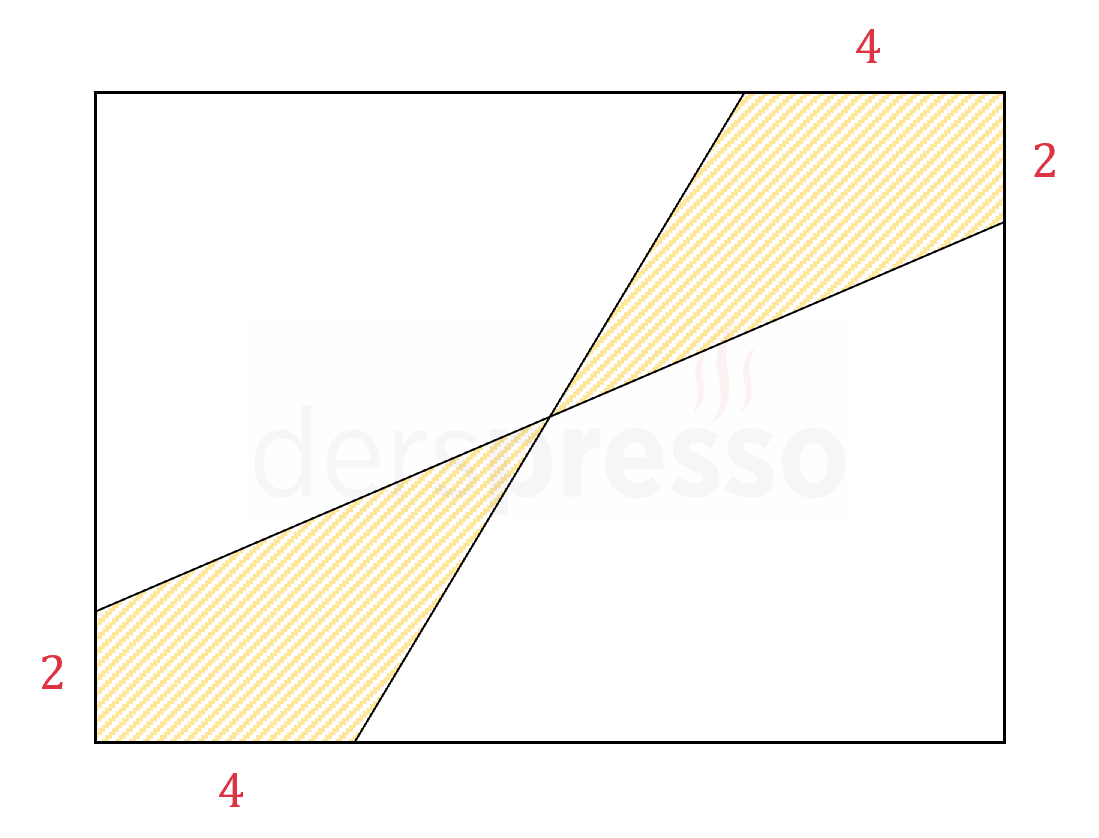
Şekildeki dikdörtgenin kenar uzunlukları 14 ve 10 birim olduğuna göre, taralı alan kaç birimkaredir?
Çözümü GösterDikdörtgenin içine çizilen doğru parçaları kenarları eşit uzunluklarda böldüğü için oluşan şekiller özdeş ve dikdörtgenin merkezine göre simetriktir.
Dikdörtgenin köşelerini ve kenar orta noktalarını şekildeki gibi birleştirelim.
Oluşan doğru parçalarının uzunluklarını yazalım.
Bir tane mavi taralı üçgenin tabanı 4 birim, yüksekliği 5 birimdir.
\( A_m = \dfrac{4 \cdot 5}{2} = 10 \) birimkare
Bir tane turuncu taralı üçgenin tabanı 2 birim, yüksekliği 7 birimdir.
\( A_t = \dfrac{2 \cdot 7}{2} = 7 \) birimkare
Tüm taralı bölgenin alanı bu iki alanın toplamının iki katına eşittir.
\( A = 2(10 + 7) = 34 \) birimkare bulunur.
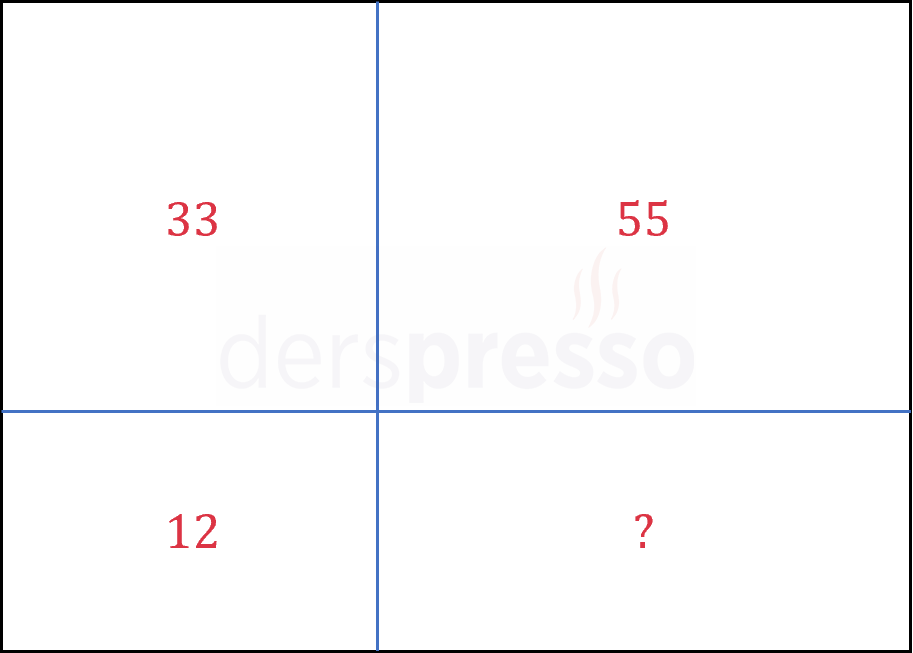
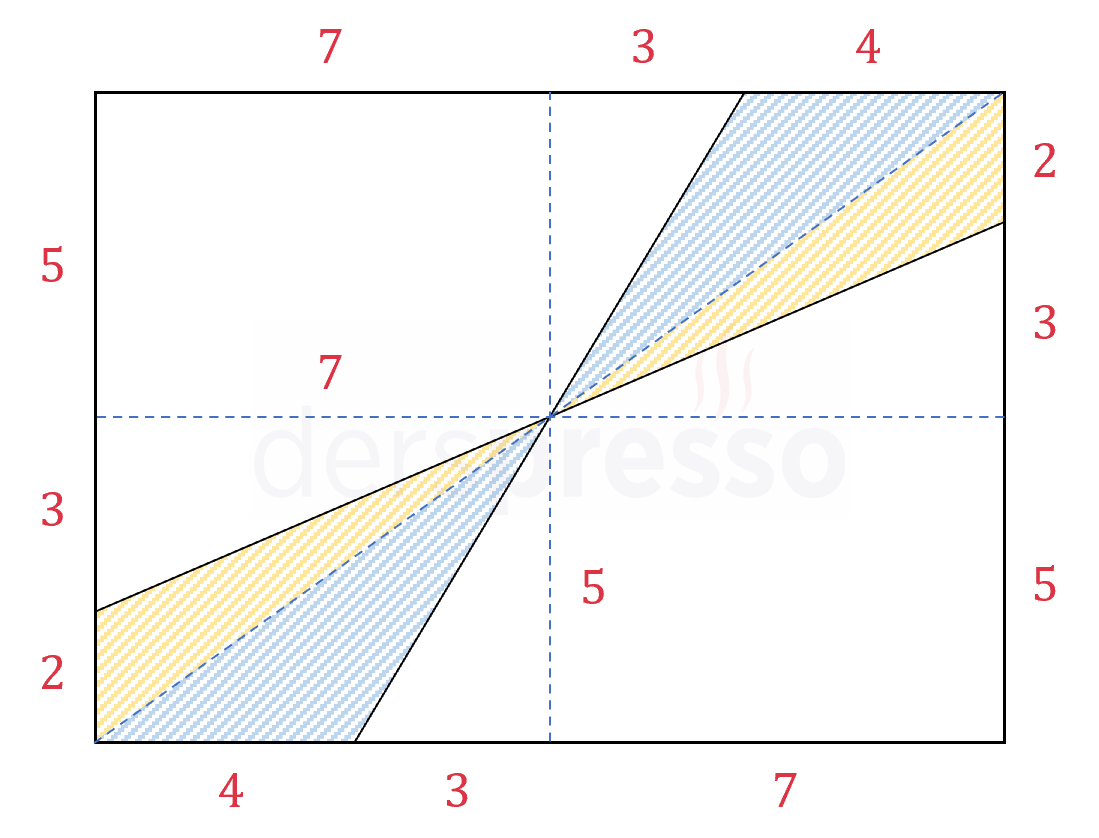
Şekildeki dikdörtgen kenarlarına paralel iki doğru parçası ile dört bölgeye ayrılmıştır. Buna göre soru işareti ile gösterilen bölgenin alanı kaç birimkaredir?
Çözümü GösterÇizilen doğru parçalarının kenarları böldüğü parçaların uzunluklarına \( a, b, c, d \) diyelim.

Soru işareti ile gösterilen alana \( x \) diyelim.
Dört bölgenin alanlarını \( a, b, c, d \) cinsinden yazalım.
\( ac = 33 \)
\( ad = 55 \)
\( bc = 12 \)
\( bd = x \)
Dört değişkeni de içeren \( ac \) ve \( bd \) ifadelerinin çarpımı yine dört değişkeni de içeren \( ad \) ve \( bc \) ifadelerinin çarpımına eşittir.
\( abcd = abcd \)
\( (ac) \cdot (bd) = (ad) \cdot (bc) \)
\( 33 \cdot x = 55 \cdot 12 \)
\( x = \dfrac{55 \cdot 12}{33} = 20 \) birimkare bulunur.

6 eş dikdörtgen şekildeki gibi yerleştiriliyor. Bu dikdörtgenlerin oluşturduğu dış dikdörtgenin alanı, iç dikdörtgenin alanının 5 katına eşittir.
Buna göre şekli oluşturan eş dikdörtgenlerin uzun kenar uzunluğunun kısa kenar uzunluğuna oranı nedir?
Çözümü GösterEş dikdörtgenlerden birinin uzun kenar uzunluğuna \( x \), kısa kenar uzunluğuna \( y \) diyelim.

Dış dikdörtgenin kısa kenarının uzunluğu \( x + y \) olur.
Dış dikdörtgenin uzun kenarının uzunluğu \( 2x + y \) olur.
İç dikdörtgenin kısa kenarının uzunluğu \( x - y \) olur.
İç dikdörtgenin uzun kenarının uzunluğu \( 2x - y \) olur.
Dış dikdörtgenin alanını bulalım.
\( (x + y)(2x + y) = 2x^2 + xy + 2xy + y^2 \)
\( = 2x^2 + 3xy + y^2 \)
İç dikdörtgenin alanını bulalım.
\( (x - y)(2x - y) = 2x^2 - xy - 2xy + y^2 \)
\( = 2x^2 - 3xy + y^2 \)
Dış dikdörtgenin alanı iç dikdörtgenin alanının 5 katına eşittir.
\( 2x^2 + 3xy + y^2 = 5(2x^2 - 3xy + y^2) \)
\( 2x^2 + 3xy + y^2 = 10x^2 - 15xy + 5y^2 \)
\( 8x^2 - 18xy + 4y^2 = 0 \)
\( 2(4x^2 - 9xy + 2y^2) = 0 \)
\( 4x^2 - 9xy + 2y^2 = 0 \)
Bulduğumuz denklemi çarpanlarına ayıralım.
\( (4x - y)(x - 2y) = 0 \)
\( 4x - y = 0 \) ya da \( x - 2y = 0 \)
\( 4x = y \) ya da \( x = 2y \)
\( x \)'i uzun kenar olarak seçtiğimiz için \( x \gt y \) olmalıdır.
Buna göre \( 4x = y \) geçerli bir çözüm değildir.
\( x = 2y \Longrightarrow \dfrac{x}{y} = 2 \)
Eş dikdörtgenlerden birinin uzun kenar uzunluğunun kısa kenar uzunluğuna oranı 2'dir.
Bir dikdörtgenin tüm köşeleri \( r \) yarıçaplı bir çemberin üzerindedir.
Dikdörtgenin çevresi 56 cm ise dikdörtgenin alanının \( r \) cinsinden eşiti nedir?
Çözümü GösterDikdörtgenin köşegenleri çember üzerinde olduğundan köşegenleri çemberin çapına eşit olur.
Bu yüzden dikdörtgenin köşegeni \( 2r \) uzunluğundadır.
Dikdörtgenin kenar uzunluklarına \( a \) ve \( b \) br diyelim.
Çember ve dikdörtgen aşağıdaki şekildeki gibidir.

\( \text{Çevre} = 2(a + b) = 56 \) cm
\( a + b = 28 \)
Dikdörtgenin alan formülünü yazalım.
\( \text{Alan} = ab \)
Dikdörtgenin kenarlarının ve köşegeninin oluşturduğu dik üçgene Pisagor teoremini uygulayalım.
\( a^2 + b^2 = (2r)^2 = 4r^2 \)
\( (a + b)^2 = a^2 + 2ab + b^2 \)
Bu eşitlikteki terimlerin yukarıda bulduğumuz değerlerini yerine koyalım.
\( 28^2 = 4r^2 + 2ab \)
Soruda istenen alan yani \( ab \) değeridir.
\( ab = \dfrac{28^2 - 4r^2}{2} \)
\( = 392 - 2r^2 \) bulunur.

\( ABCD \) bir dikdörtgendir.
\( \abs{AD} = 15, \abs{DH} = 20, \abs{HC} = 10 \)
\( [BE] \perp [AH] \) olduğuna göre, \( BEHC \) dörtgeninin alanı kaçtır?
Çözümü GösterDikdörtgenin kısa kenar uzunluğu 15, uzun kenar uzunluğu 30 birimdir.
\( ADH \) dik üçgeni 3-4-5 Pisagor üçgeninin 5 katıdır.
\( \abs{AH} = 5 \cdot 5 = 25 \)
\( m(\widehat{DAH}) = \alpha \) diyelim. Bu durumda \( m(\widehat{AHD}) = 90° - \alpha \) olur.

Z kuralını kullanarak \( AEB \) dik üçgeninin açılarını yazalım.
\( m(\widehat{BAE}) = m(\widehat{AHD}) = 90° - \alpha \)
\( m(\widehat{ABE}) = \alpha \)
\( ADH \) ve \( BEA \) dik üçgenlerinin tüm açıları eşit olduğundan bu üçgenler benzer üçgenlerdir.
\( \overset{\triangle}{ADH} \sim \overset{\triangle}{BEA} \)
Benzer üçgenlerin kenarları arasında orantı kuralım.
\( \dfrac{\abs{DH}}{\abs{EA}} = \dfrac{\abs{AH}}{\abs{BA}} \)
\( \dfrac{20}{\abs{EA}} = \dfrac{25}{30} \)
\( \abs{EA} = 24 \)
Benzerliği tekrar kullanalım.
\( \dfrac{\abs{AD}}{\abs{BE}} = \dfrac{\abs{AH}}{\abs{BA}} \)
\( \dfrac{15}{\abs{BE}} = \dfrac{25}{30} \)
\( \abs{BE} = 18 \)
\( BEHC \) dörtgeninin alanını \( ABCD \) dikdörtgeninin alanından \( ADH \) ve \( BEA \) üçgenlerinin alanlarını çıkararak bulabiliriz.
\( A(BEHC) = A(ABCD) - (A(ADH) + A(BEA)) \)
\( A(ABCD) = \abs{AB} \cdot \abs{AD} \)
\( = 30 \cdot 15 = 450 \)
\( A(ADH) = \dfrac{\abs{AD} \cdot \abs{DH}}{2} \)
\( = \dfrac{15 \cdot 20}{2} = 150 \)
\( A(BEA) = \dfrac{\abs{BE} \cdot \abs{EA}}{2} \)
\( = \dfrac{18 \cdot 24}{2} = 216 \)
Bulunan alan değerlerini denklemde yazarak istenilen alanı bulalım.
\( A(BEHC) = A(ABCD) - (A(ADH) + A(BEA)) \)
\( = 450 - (150 + 216) \)
\( = 84 \) bulunur.